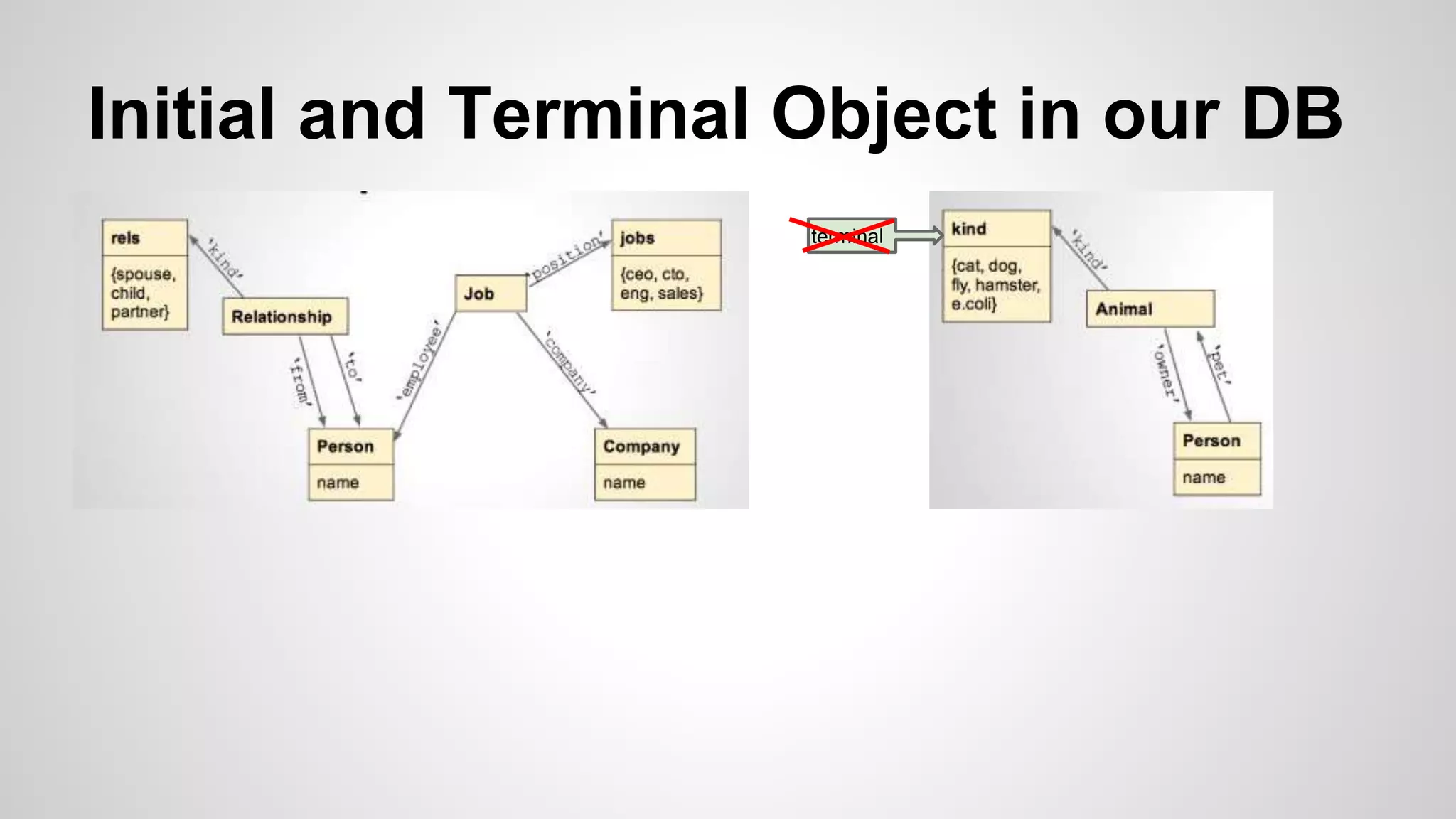
This lecture introduces several category theory concepts including initial objects, terminal objects, products, unions, equalizers, and pullbacks. Initial objects have a unique morphism from them to any other object. Terminal objects have a unique morphism to them from any other object. Products represent the "cross product" of two objects, while unions represent their disjoint combination. Equalizers capture objects where two morphisms are equal, and pullbacks capture objects where projections satisfy a relation. Examples are given for how these concepts apply to sets and databases.

1. Formal Methods in
Software
Lecture 7. Category Theory
Vlad Patryshev
SCU
2014

2. In This Lecture
• database example
• terminal object, initial object;
• products, unions
• equalizers
• pullbacks

3. Database Example
create type rels as enum (‘spouse’, ‘child’, ‘partner’);
create type jobs as enum (‘ceo’, ‘cto’, ‘eng’, ‘sales’);
create table Person (id bigint, name varchar(80), primary key (id));
create table Company (id bigint, name varchar(80), primary key (id));
create table Rel (from bigint, to bigint, kind rels,
constraint p1_fk foreign key (from references Person(id),
constraint p2_fk foreign key (yo references Person(id)
);
create table Job (company bigint, employee bigint, position jobs,
constraint c_fk foreign key (comp references Company(id),
constraint p_fk foreign key (pers references Person(id)
);

4. “Conceptual Model”
Person
id
name
Company
id
name
Job
position
company
employee
Relationship
kind
from
to
rels
{spouse,
child,
partner}
jobs
{ceo, cto,
eng, sales}

5. “More Conceptual Model”
Person
name
Company
name
Job
Relationship
rels
{spouse,
child,
partner}
jobs
{ceo, cto,
eng, sales}

6. “More Conceptual Model”
Person
name
Company
name
Job
Relationship
rels
{spouse,
child,
partner}
jobs
{ceo, cto,
eng, sales}
It’s a category!

7. Pet Database
create type kind as enum (‘cat’, ‘dog’, ‘fly’, ‘hamster’, ‘e.coli’);
create table Person (id bigint, name varchar(80), pet bigint,
primary key (id),
constraint pet_fk foreign key (pet references Animal(id));
create table Animal (id bigint, kind kind, name varchar(80), owner
bigint,
primary key (id),
constraint owner_pk foreign key owner references Person(id));

8. “More Conceptual Model”
Person
name
Animal
kind
{cat, dog,
fly, hamster,
e.coli}
Where’s composition?
kind(pet(owner(pet(“John”)))
select kind from Animal a where a.owner
in (select id from Person where pet in
(select id from Animal where owner in
(select id from person where
name=’John’)));

9. Initial Object in a Category
Definition. Given a category C, Initial Object is such an object 0 that there is
a unique function iX:0 → X for any given X. (this is its “universal property”)
Note that if we take X=0, we see that there is just one function 0 → 0. Can
you name a set (or two) with only one function S→S?
And what if there’s more than one such an object? Say 01 and 02, both have
this interesting feature. Then, for 01, we have a unique a:01 → 02; and
similarly we have a unique b:02 → 01. Composing a and b either way, we
get an identity; so they are isomorphisms.
Initial object is unique up to an isomorphism.

10. Examples of Initial Objects
• Sets: ∅, and it is unique (by sets axioms)
• Monoids: {0} - all “such monoids” are isomorphic
• Categories: empty category (whether there’s a plurality of them…)
• In this category of three objects we see no initial object:
• In this category c is initial object:
• How about more than one
initial object?
They are
isomorphic!

11. Terminal Object in a Category
Definition. Given a category C, Terminal Object is such an object 1 that
there is a unique function uX:X → 1 for any given X. (this is its “universal
property”)
Note that if we take X=1, we see that there is just one function 1 → 1, same
as with 0.
And what if there’s more than one such an object? Say 11 and 12, both have
this interesting feature. Then, for 11, we have a unique a:11 → 12; and
similarly we have a unique b:12 → 11. Composing a and b either way, we
get an identity; so they are isomorphisms.
Terminal object, like initial one, is unique up to an isomorphism.

12. Examples of Terminal Objects
• Sets: any singleton {x} is terminal. They are not equal, but are isomorphic.
• Monoids: {0} - all “such monoids” are isomorphic
• Categories: empty category (whether there’s a plurality of them…)
• In this category of three objects we see no terminal object:
• In this category c is terminal object:

13. Initial and Terminal Object in our DB
terminal

14. Cartesian Product
Definition. Given a category C, and two objects in it, X and Y, their Cartesian
Product is such an object Z=X×Y, together with two functions, pX:Z→X and
pY:Z→Y, that for any pair f:A→X and g:A→Y, f=pX∘h and g=pY∘h for some
unique h. (this is its “universal property”)
Cartesian product is unique up to an isomorphism. (proof?)

15. Examples of Cartesian Products
• Sets: AxB = {(a,b)|a∈A,b∈B}, and it is unique (by sets axioms)
• Databases: select * from A,B;
• Good programming languages, e.g. Scala: (A,B)
val intWithString: (Int, String) = (42, “Hello 42”)
• In a monoid? We have just one object!
• In a poset? It’s min(a,b)

17. Disjoint Union (dual to Product)
Definition. Given a category C, and two objects in it, X and Y, their Disjoint
Union is such an object Z=X+Y, together with two functions, iX:X→Z and
iY:Y→Z, that for any pair f:X→A and g:Y→A, f=h∘iX and g=h∘iY for some
unique h. (this is its “universal property”)
Disjoint union is unique up to an isomorphism. (proof?)

18. Examples of Disjoint Unions
• Sets: A+B = A∪B, and it is unique (by sets axioms)
• Databases: select * from A union B;
• Good programming languages, e.g. Scala: Either[A,B]
val intOrString: Either[Int, String] = Left(42)// Right(“Hello 42”)
• In a poset? It’s max(a,b)

19. Equalizers
Definition. Given a category C, two objects in it, X and Y, and two functions,
f,g:X→Y, their Equalizer is such an object E=Eq(f,g), together with a
function eq:E→X, such that that f∘eq=g∘eq for any m:O→X, m=eq∘u for
some unique u. (this is its “universal property”)
An equalizer is unique up to an isomorphism. (proof?)

20. Pullbacks
Definition. Given a category C, objects, X, Y and Z, and two functions,
f:X→Z and g:X→Z, their Pullback is such an object X×ZY, together with
functions pX:X×ZY→X and pY:X×ZY→Y, such that g∘pY = f∘pX, and for any
pair x:U→X, y:U→Y, x=pX∘h and y=pY∘h for some unique h. (this is its
“universal property”)
A pullback is unique up to an isomorphism. (proof?)

21. Examples of Pullbacks
• Sets: {(x,y)|x∈X,y∈Y,f(x)=g(y)}
• Databases: select * from A, B where A.f=B.g;
e.g. select * from Person A, Person B where A.pet=B.pet;
• In a poset? Same as min.
• Cartesian products are pullbacks.

22. References
http://www.amazon.com/Category-Computer-Scientists-Foundations-Computing/dp/0262660717
Wikipedia