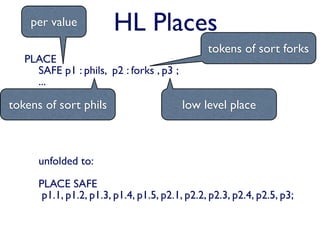
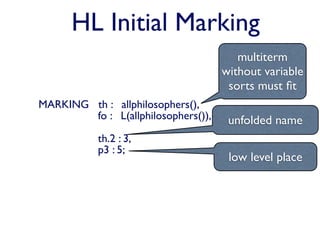
The document describes the input language for the LoLA model checker. It allows specifying Petri nets and verification tasks in a high-level algebraic style. Key elements include: 1. Defining sorts, operations, and their interpretations to specify the types and functions used. 2. Declaring high-level places and markings as terms over sorts to represent multiple low-level places and tokens. 3. Specifying high-level transitions as procedures with guards and input/output terms to represent multiple low-level transitions. 4. Providing verification tasks as logical formulas involving state predicates to check properties over the unfolded net.

1. 2. The LoLA Input Language

2. Plan
• Place/Transition nets
• Verification task
• High-Level nets
• Demo

3. Place/Transition Nets
N = [P,T,F,W,m0] treated as variables
PLACE p1, p2, p3, p4;
can be replaced as a whole
MARKING p1:2, p3:1, p1:1;
compatible with computed
markings
{ this is a comment }
TRANSITION t1
CONSUME p1:3, p2: 1;
PRODUCE p3: 2, p1 : 2;
treated as procedures
TRANSITION t2
CONSUME p3 : 1;
PRODUCE ;
only one reference per arc

4. Identifiers
Many special characters permitted, eg.
p4 23 message[x=13,from=”bla”]
Reason: easier for tools to generate such
names

5. Storage directives
If bounds for some places are known:
PLACE
default, #CAPACITY in
p0;
userconfig.H
SAFE 3: p1, p2;
SAFE 7: p3, p4;
SAFE: p5; = SAFE 1
Only for internal memory allocation, no
capacity!

6. Fairness Constraints
needed for the LTL properties only
(fair CTL is not supported so far)
TRANSITION t1 STRONG FAIR
...
TRANSITION t2 WEAK FAIR
...
TRANSITION t3
...

7. Verification Task Input
• Can be specified inline or as separate file
• For boundedness of places: ANALYSE PLACE p1
• For dead transitions: ANALYSE TRANSITION t2
• For all properties involving state predicate:
FORMULA (p1 > 3 OR p2 <= 7) AND NOT p6 = 1
• For CTL model checking:
• FORMULA EXPATH ALWAYS ALLPATH EVENTUALLY p1 > 3
• FORMULA EXPATH (p1 > 7 UNTIL p2 < 3)

8. High Level Net Input
• Main purpose: To obtain scalable sequences of models
• Deprecated for translation from other formalisms
(problem: semantic conformance)
• Will be unfolded into place/transition net anyway
• Experience: Parsing from UNIX pipe no time issue
• Style: algebraic Petri nets with explicit interpretation

9. Algebraic Petri Nets
• Signature: sorts + sorted operation symbols
• Interpretation: sets of values, n-ary functions
• Places: annotated with sort (type) symbol
• interpretation: set of values (colors)
• Transitions: annotated with set of variables, guard
expression
• interpretation: every valid assignment is firing mode
• Arcs: annotated with terms over the transition variables
• interpretation: map from firing mode of transition into color set of place
• Marking: written as multiset of terms

10. Signature: Sorts and
their interpretation
SORT
a = [ 1 , 5 ]; { 1,2,3,4,5 }
b = BOOLEAN; { TRUE, FALSE }
c = ENUMERATE red blue green END; { red, blue, green }
“successor” canonically defined on each value set
scalar arbitrary each value has
unique text
d = ARRAY [1,3] OF BOOLEAN;
representation
{ [FALSE|FALSE|FALSE], ... , [TRUE|TRUE|TRUE] }
e = RECORD
receiver : a;
sender : b;
END ; { <1|FALSE>, ...., <3|TRUE> }

11. Signature: operations
and their interpretation
SORT phils = [1 , 5 ]; forks = [1 , 5];
FUNCTION leftfork (x : phils) : forks signature
BEGIN
RETURN x
END interpretation
FUNCTION rightfork(x : phils): forks
BEGIN
RETURN x + 1
expressions evaluate
END on all integers,
FUNCTION allthinking () : phils assignments align to
VAR x : phils;
BEGIN
value set (modulo
FOR ALL x DO arithmetic)
RETURN x
END
END result is multiset

12. Statements in function body
EXIT
leave function
RETURN E
add value of E to return multiset, continue
L = E
assignment
S1 ; S2
sequential composition
WHILE E DO S END
while loop
REPEAT S UNTIL E END
until loop
FOR x := E1 TO E2 DO S END
for loop in canonical order of values
FOR ALL x DO S END
for loop through all elements of sort of x
IF E THEN s1 [ELSE S2] END
branch statement
SWITCH E
CASE E1: S1 ... CASE En: Sn
ELSE S
END
multibranch statement

13. Expressions in function body
pointwise for
X X[a + b] X.c[a + b]
arrays and
records
645 TRUE FALSE
A <-> B A -> B A AND B A OR B NOT A
A<B A <= B A>B A >= B A=B A <> B A#B
A+B A*B A-B A/B A MOD B
(E)
[ E1 | E2 | .... | En ] no modulo
bla ( E1, ...., En)
before
function must assignment
return exactly
one value

14. Example: Network
SORT dimensions = [ 1 , 3 ]; row = [ 1 , 3 ]; agent = ARRAY dimensions OF row ;
message = RECORD receiver : agent; sender : agent; END;
FUNCTION X (a:agent;b:agent):message
VAR m : message;
BEGIN
m . receiver = a; m . sender = b; RETURN m
END
FUNCTION N(z:agent):agent
VAR l : dimensions; low : row; high : row;
BEGIN
low = 1; high = low - 1; { remind canonical order }
FOR ALL l DO
IF z [ l ] > 1ow THEN z [ l ] = z [ l ] - 1; RETURN z; z[l]=z[l]+1 END;
IF z [ l ] < high THEN z [ l ] = z [ l ] + 1; RETURN z; z[l]=z[l]-1 END
END
END

15. per value HL Places
tokens of sort forks
PLACE
SAFE p1 : phils, p2 : forks , p3 ;
...
tokens of sort phils low level place
unfolded to:
PLACE SAFE
p1.1, p1.2, p1.3, p1.4, p1.5, p2.1, p2.2, p2.3, p2.4, p2.5, p3;

16. HL Initial Marking
multiterm
without variable
sorts must fit
MARKING th : allphilosophers(),
fo : L(allphilosophers()), unfolded name
th.2 : 3,
p3 : 5;
low level place

17. HL Transitions
valid for all
TRANSITION receive WEAK FAIR instances
VAR sender , receiver : agent;
GUARD is_neighbour( sender , receiver) firing mode
CONSUME channe1 : X ( sender, receiver )
PRODUCE channel : X (N(sender),sender), internal :
receiver
multiterms
unfolded to
TRANSITION receive.[sender=1,receiver=2] WEAK FAIR
CONSUME ....
Only instances with satisfied guards are generated
Isolated places are finally removed

18. HL Verification tasks
parentheses
compulsory
EXISTS x : phils : ( eating . ( x ) > 0 ) AND thinking.1 = 0
ALL y : phils : ( [y = 1] OR fo . ( L(y) ) = 0 )
any expression