The document introduces Haskell programming concepts, emphasizing that functions are first-class values focused on expression evaluation rather than execution. It discusses referential transparency, currying, and point-free programming, illustrating these ideas with code examples for calculating areas of circles and mapping functions. Additionally, it covers functors and their application in different data structures like lists and trees.

1. Introduction
to Haskell
Luca Molteni
Haskell ITA Meeting 17/10/2015

2. Topics
Basic Concepts
Currying
Functors

3. • Functions are first-class, that is, functions are
values which can be used in exactly the same
ways as any other sort of value.
• The meaning of Haskell programs is focused
around evaluating expressions rather than
executing instructions.

4. 3 * (9 + 5)
=> 3 * 14
=> 42

5. 3 * (9 + 5)
=> 3 * 9 + 3 * 5
=> 27 + 3 * 5
=> 27 + 15
=> 42

6. simple x y z = x * (y + z)

7. simple 3 9 5
=> 3 * (9 + 5)
=> 3 * 14
=> 42

8. “An expression is said to be referentially
transparent if it can be replaced with its value
without changing the behavior of a program (in
other words, yielding a program that has the
same effects and output on the same input).”
Referential transparency

9. simple a b c = simple a c b

10. simple a b c
=> { unfold }
a * (b + c)
=> { commutativity }
a * (c + b)
=> { fold }
simple a c b

11. x = x + 1

12. x = x + 1
x
=> x + 1
=> (x + 1) + 1
=> ((x + 1) + 1) +1
=> (((x + 1) +1) +1) +1
...

13. “Because a referentially transparent expression
can be evaluated at any time, it is not
necessary to define sequence points nor any
guarantee of the order of evaluation at all.
Programming done without these
considerations is called
purely functional programming.”
Referential transparency

14. totalArea r1 r2 r3
= pi * r1 ^ 2 +
pi * r2 ^ 2 +
pi * r3 ^ 2
Sum of the areas of three circles
with radii r1, r2, r3

15. circleArea r = pi * r ^ 2
totalArea r1 r2 r3
= circleArea r1 +
circleArea r2 +
circleArea r3
Sum of the areas of three circles
with radii r1, r2, r3

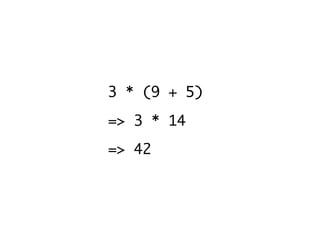
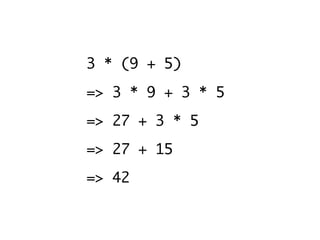
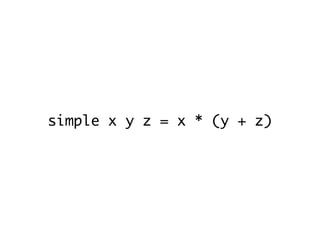
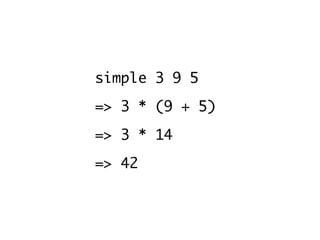
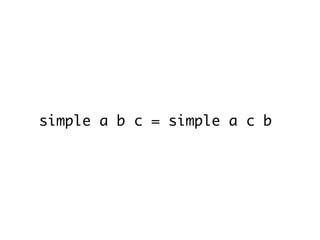
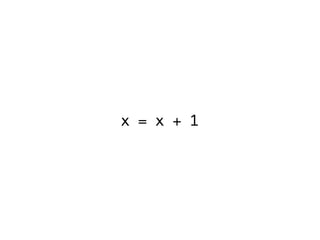
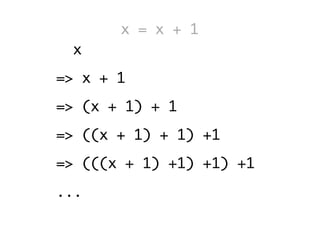
16. r1 = 3
r2 = 4
r3 = 5
radii = r1 : r2 : r3 : []
Sum of the areas of n circles?

17. radii :: [Float]
radii = r1 : r2 : r3 : []
Sum of the areas of n circles?

18. List
data List a = []
| a : List a

19. totalArea :: [Float] -> Float
totalArea [] = 0
Sum of the areas of three circles
with radii r1, r2, r3

20. totalArea :: [Float] -> Float
totalArea [] = 0
totalArea (x : xs) =
circleArea x + totalArea xs
Sum of the areas of three circles
with radii r1, r2, r3

21. square :: [Int] -> [Int]
square [] = []
square (x : xs) = (x ^ 2) : square xs
Square of list

22. Map
map :: (a -> b) -> [a] -> [b]

23. totalArea :: [Float] -> [Float]
totalArea = map circleArea
Sum of the areas of three circles
with radii r1, r2, r3

24. totalArea :: [Float] -> Float
totalArea = sum . map circleArea
Sum of the areas of three circles
with radii r1, r2, r3

25. Currying

26. simple :: (Int -> Int -> Int) -> Int
simple (x y z)
Currying

27. simple :: Int -> Int -> Int -> Int
simple x y z = x * ( y + z)
(((simple x) y) z)
Currying

28. simple 5
Partial Application

29. simple 5 :: Int -> Int -> Int
simple 5
Partial Application

30. simple :: Int -> Int -> Int -> Int
simple 5 :: Int -> Int -> Int
simple 5 2 :: Int -> Int
simple 5 2 3 :: Int
Partial Application

31. Point free programming
Tacit programming (point-free programming) is a
programming paradigm in which a function definition
does not include information regarding its arguments,
using combinators and function composition [...]
instead of variables.

32. Point free programming
map (x -> increment x) [2,3,4]
[3,4,5]
map increment [2,3,4]
[3,4,5]
map (x -> x + 1) [2,3,4]
[3,4,5]
map (+1) [2,3,4]
[3,4,5]
increment :: Int -> Int
increment x = x + 1

33. Point free programming
mf criteria operator list = filter criteria (map operator list)
mf = (. map) . (.) . filter

34. Functors

35. Functors
map :: (a -> b) -> [a] -> [b]
data List a = []
| a : List a

36. Functors
treeMap :: (a -> b) -> Tree a -> Tree b
data Tree a = Leaf a
| Branch (Tree a) (Tree a)

37. Functors
treeMap :: (a -> b) -> Tree a -> Tree b
map :: (a -> b) -> [a] -> [b]

38. Functors
thingMap :: (a -> b) -> f a -> f b

39. Functors
A typeclass is a class of types that behave
similarly.

40. Functors
class Functor f where
fmap :: (a -> b) -> f a -> f b

41. Functors
instance Functor [] where
fmap = map

42. Functors / Maybe
data Maybe a = Just a | Nothing

43. Functors
instance Functor Maybe where
fmap _ Nothing = Nothing
fmap f (Just a) = Just (f a)

44. Functors / Maybe
fmap (* 2) (Just 2)
Just 4
fmap (+ 5) (Just 2)
Just 7
fmap (+ 5) (Nothing)
Nothing

45. The End
@volothamp
It’s not about the destination.
It’s about the journey.