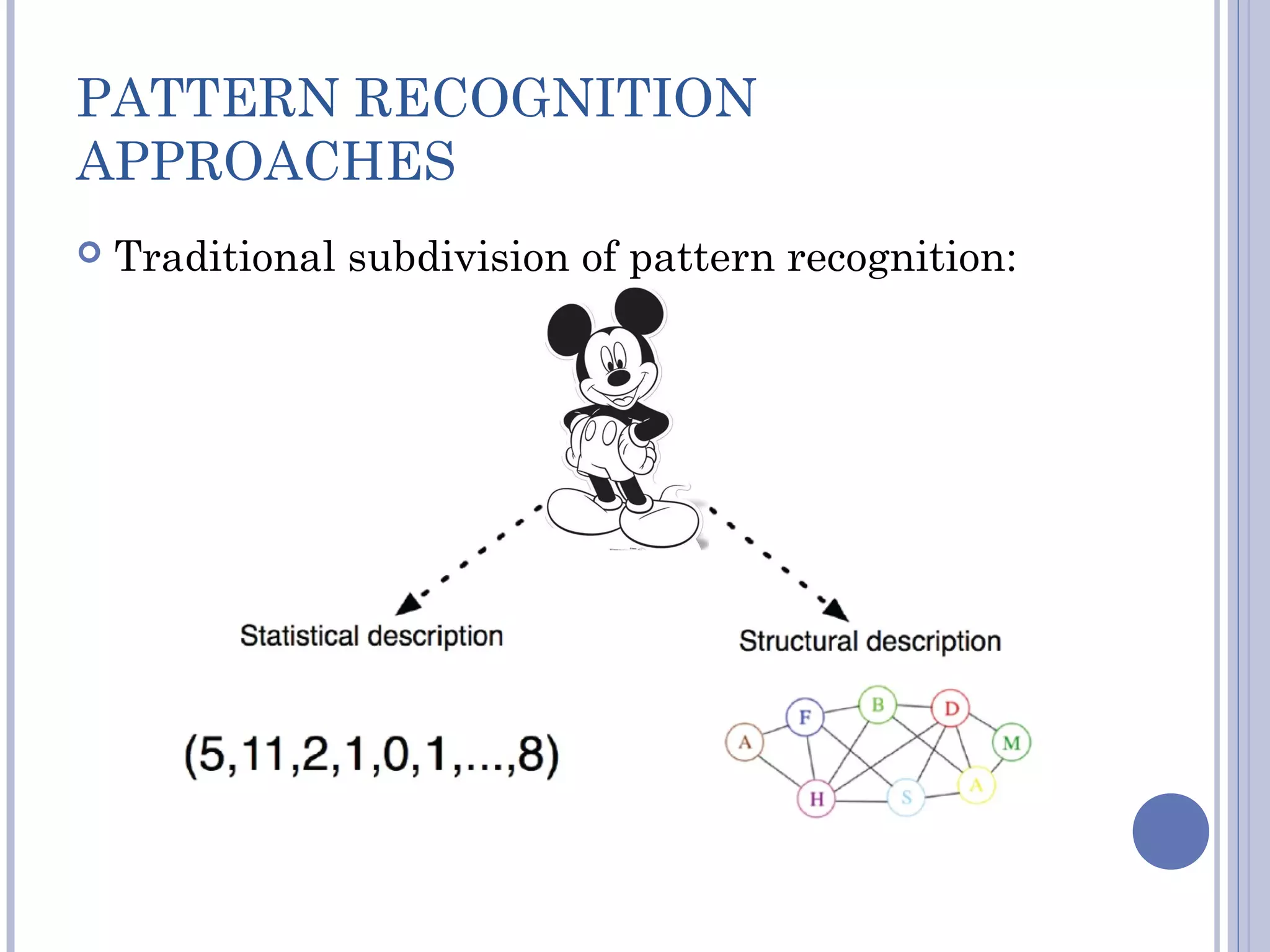
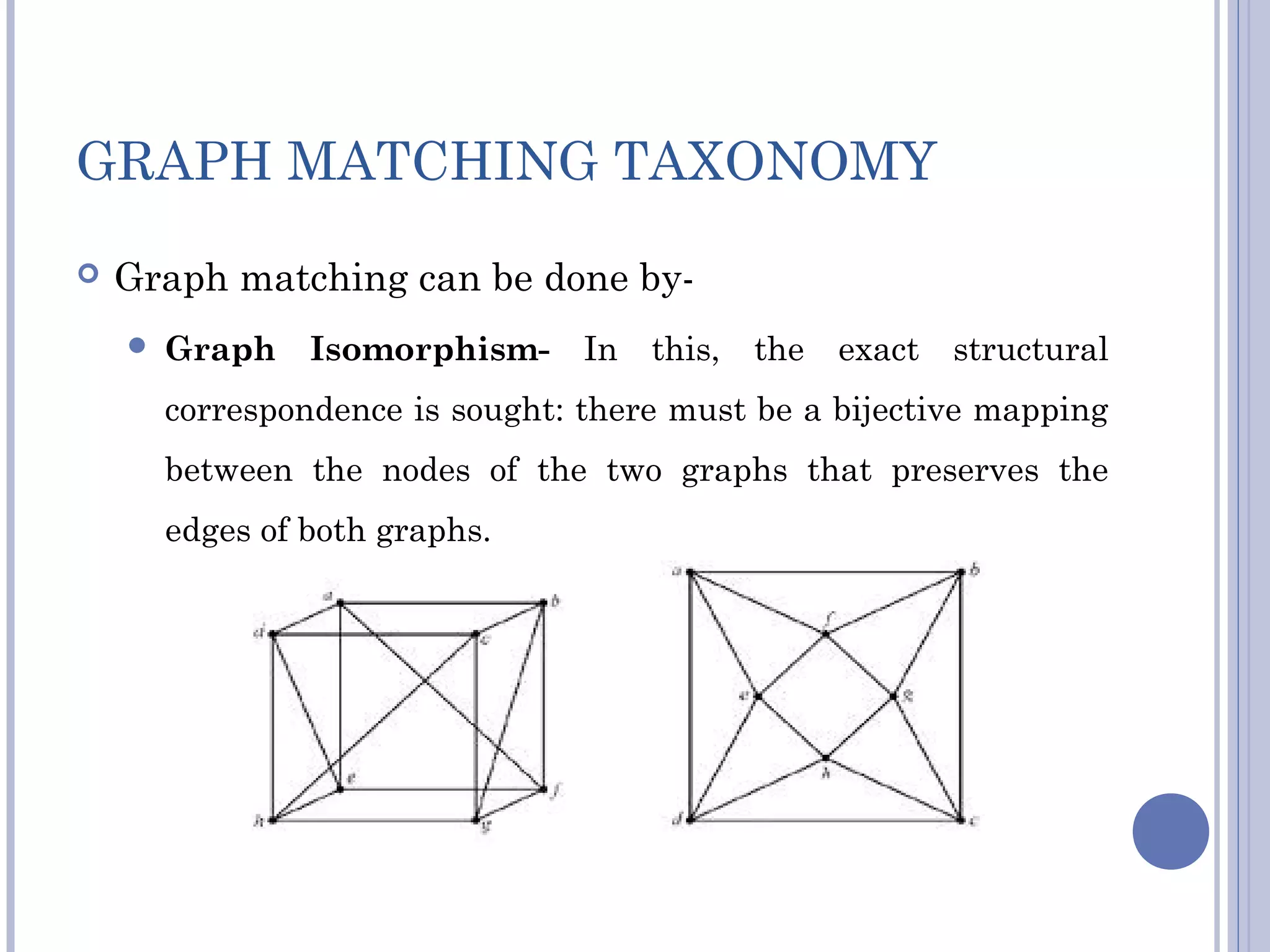
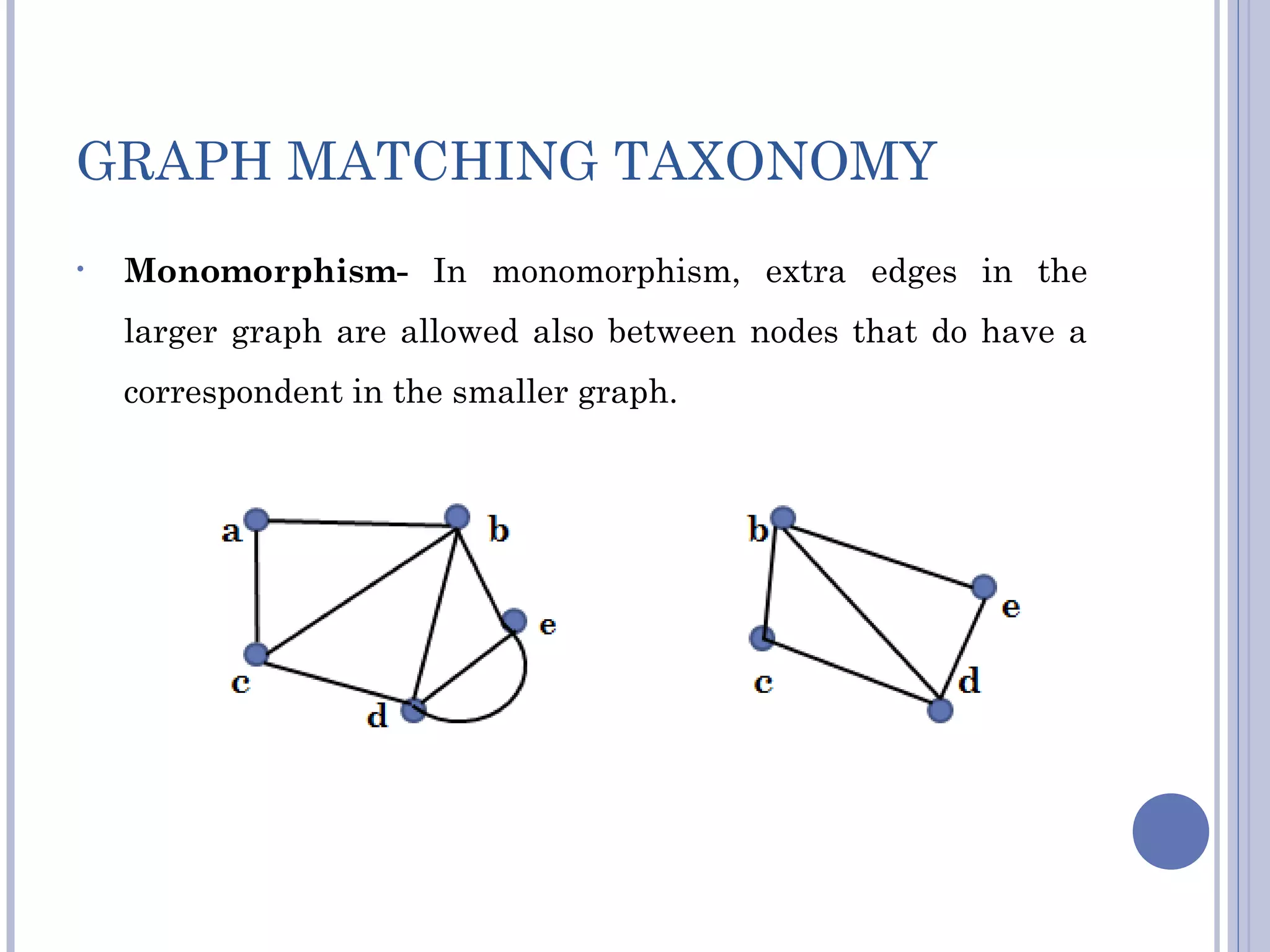
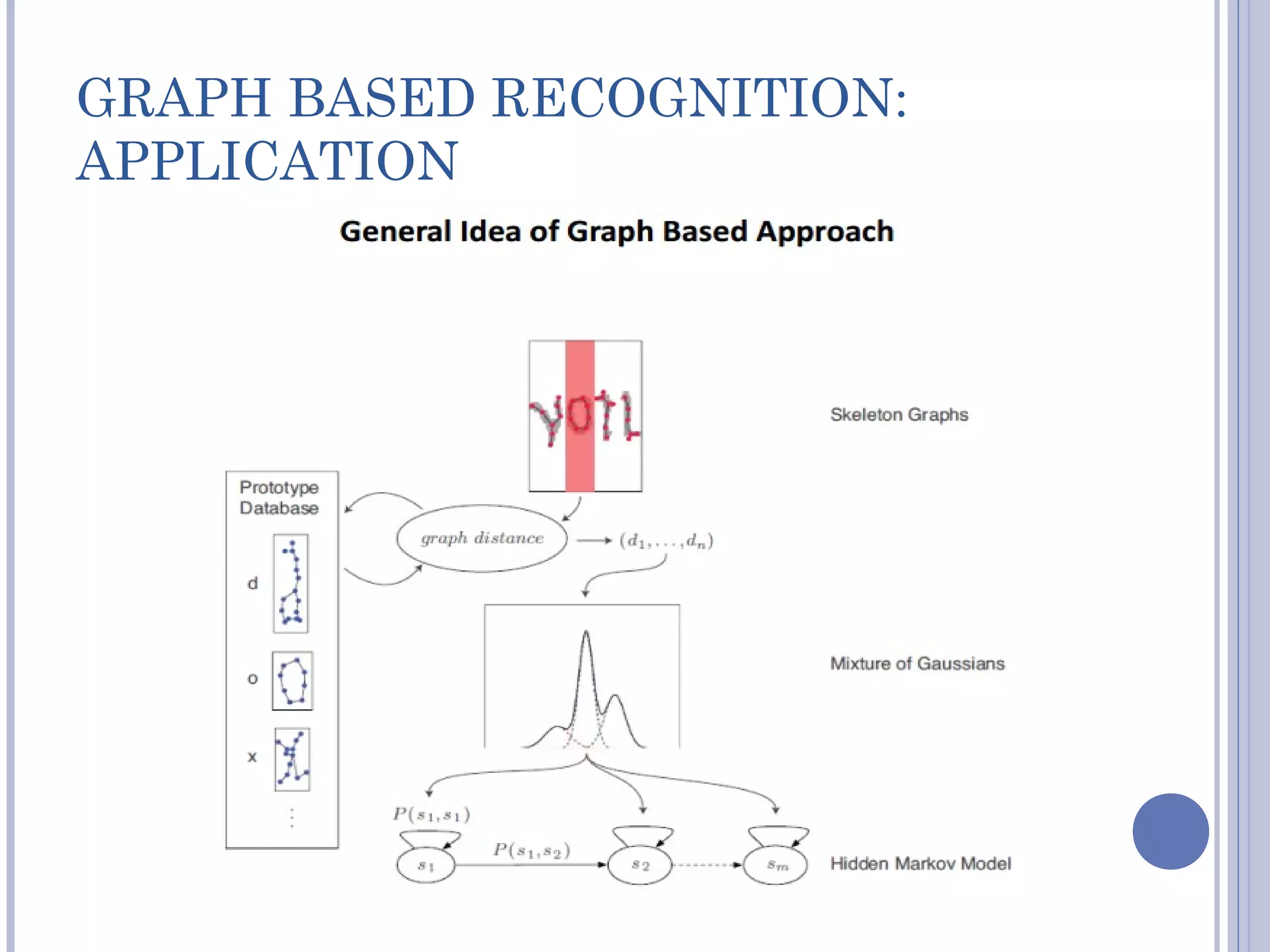
The document discusses graph matching in pattern recognition, covering various approaches, algorithms, and applications. It highlights the significance of measuring object similarity through graph representations and introduces various taxonomies such as isomorphism and graph edit distance. It concludes with future research directions and the potential efficiency of focused graph subclasses in practical applications.