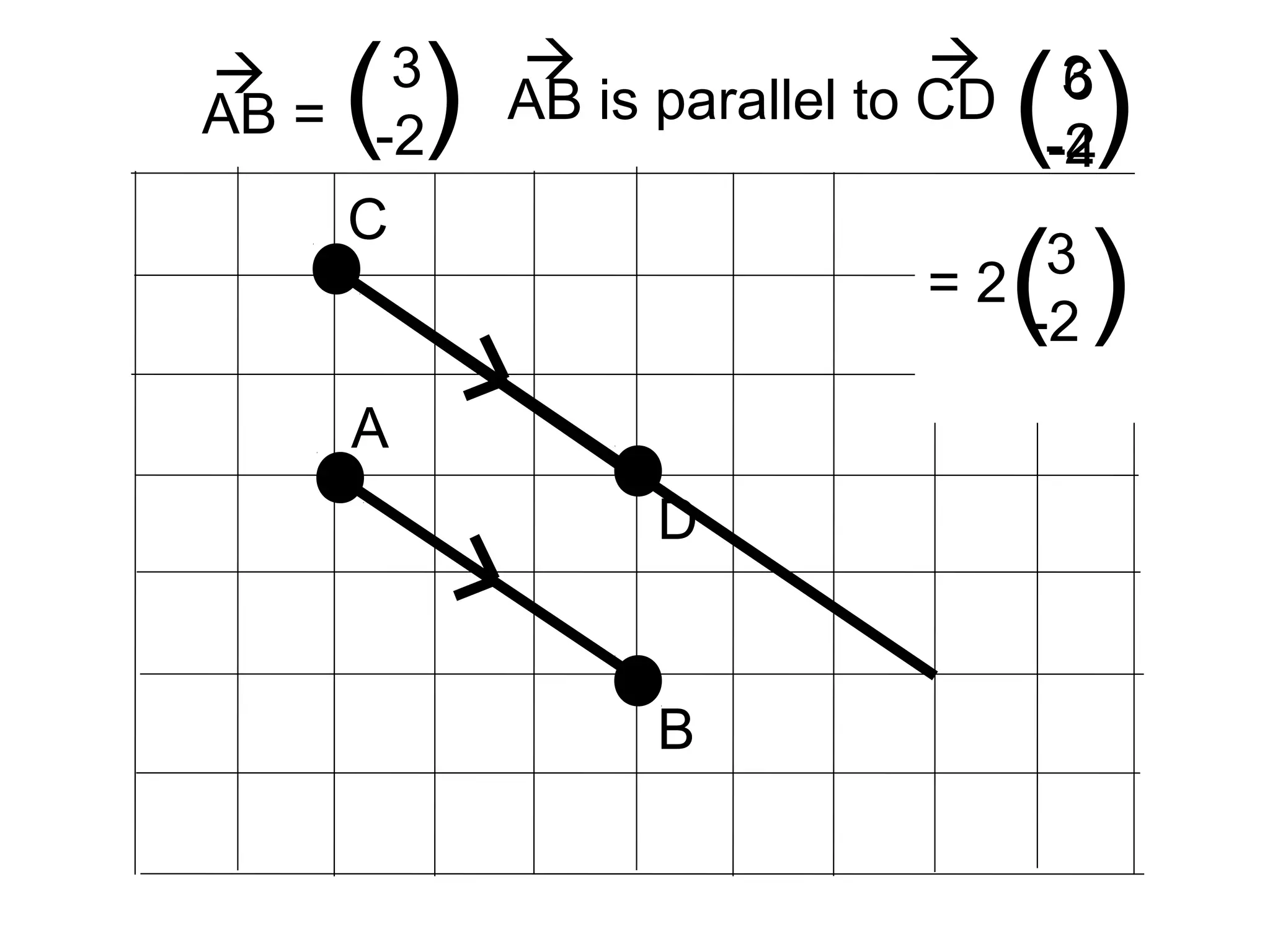
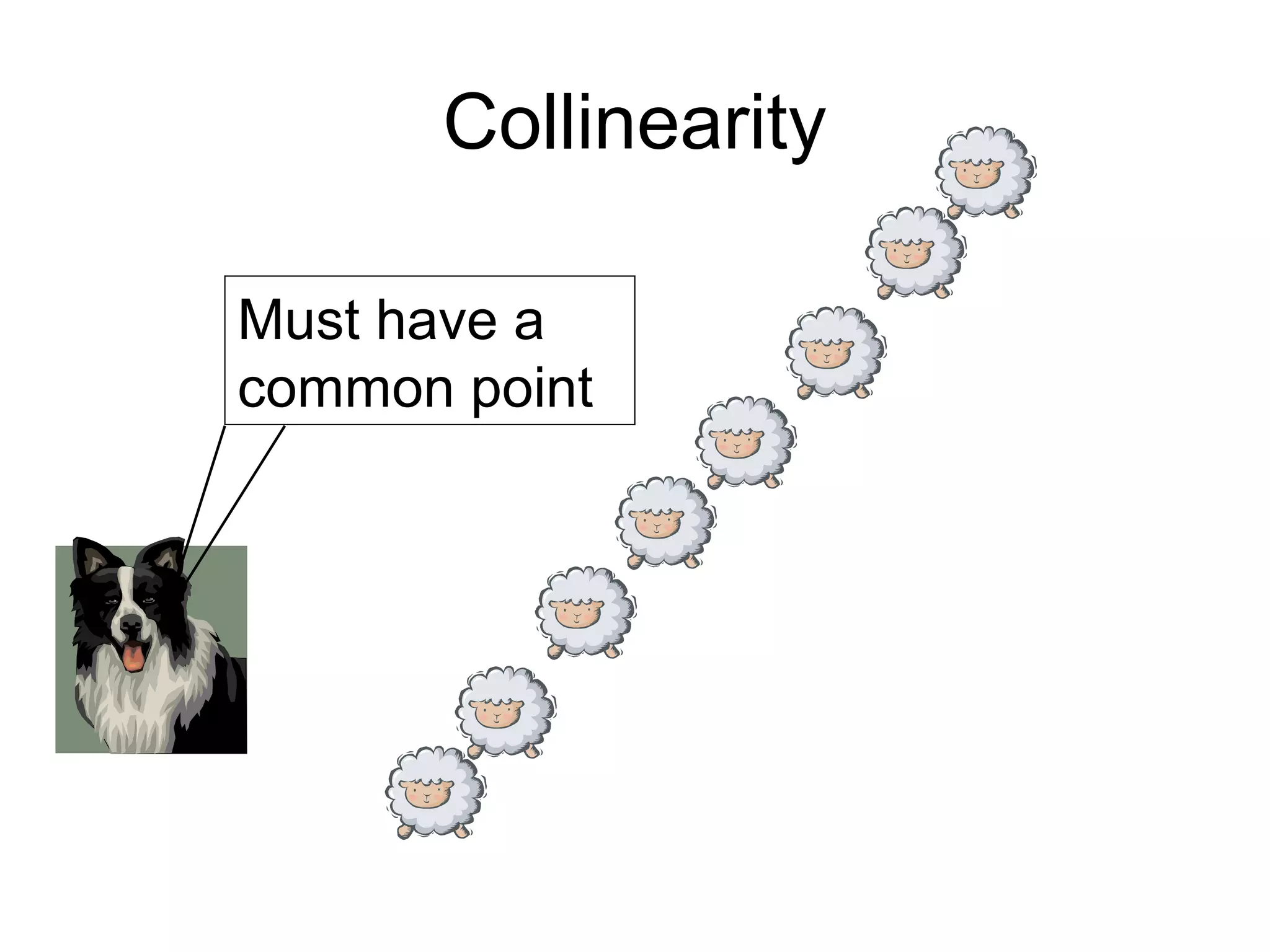
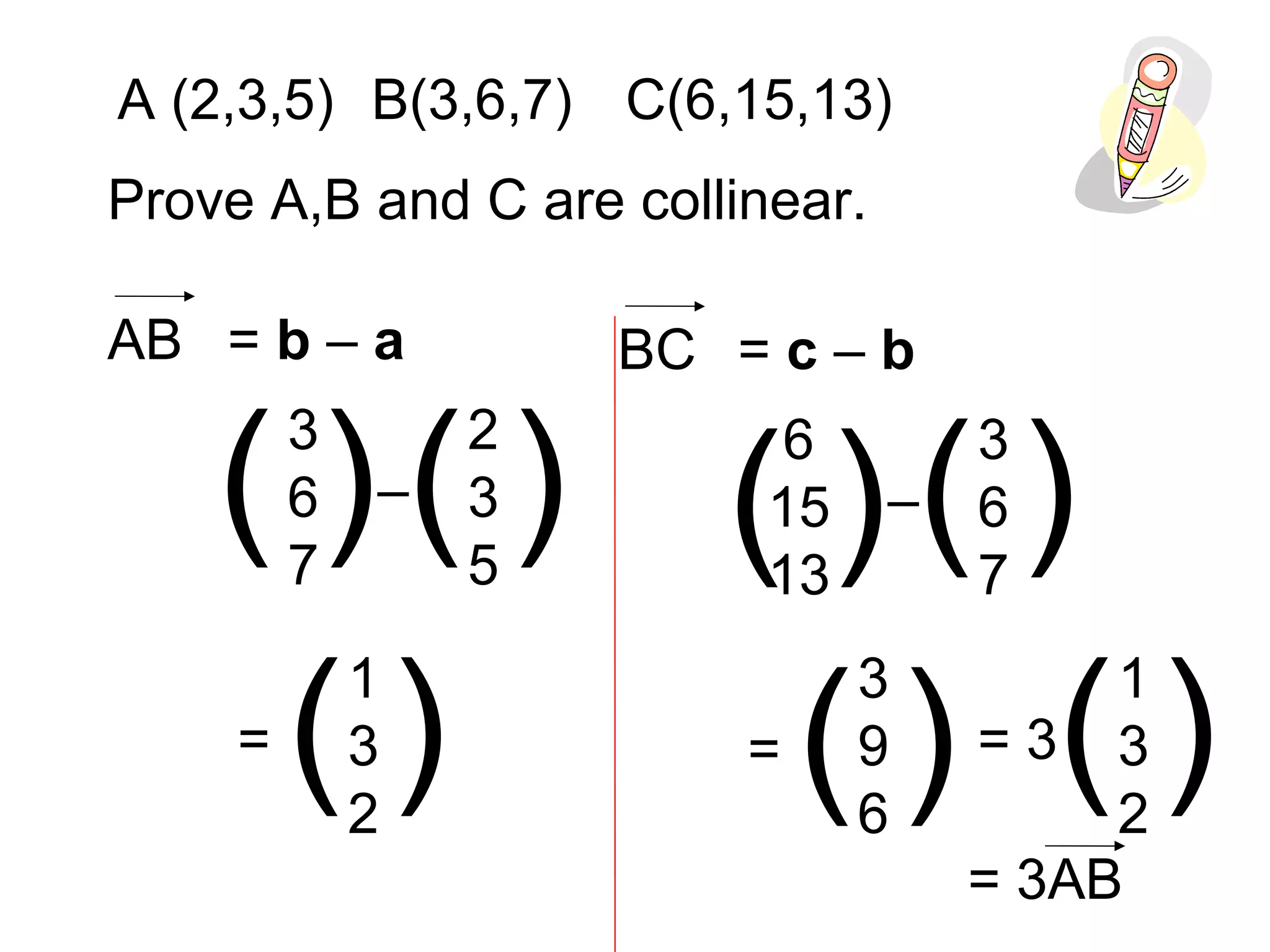
Vectors AB and CD are parallel if their direction vectors are proportional. Vectors A, B, and C are collinear if their direction vectors are proportional and they share a common point. Three examples are given to demonstrate proving vectors are parallel or collinear by showing their direction vectors are proportional.

1. Block 3
Parallel + Collinear Vectors

2. What is to be learned?
• How to identify parallel and collinear
vectors

3. = 2( )
A
B
3
-2( )AB =

C
AB is parallel to CD
 
D
3
-2( )6
-4
3
-2

4. A (1,5,7) B(3,9,8) C(0,1,5) D(4,9,7)
Prove AB and CD are parallel
AB = b – a
3
9
8
1
5
7
( ) ( )–
2
4
1
( )=
CD = d – c
4
9
7
0
1
5
( ) ( )–
( )=
4
8
2
2
4
1
( )= 2
= 2ABCD = 2AB therefore parallel

5. A (0,2,3) B(4,7,1) C(3,6,9) D(15,21,3)
Prove AB and CD are parallel
AB = b – a
4
7
1
0
2
3
( ) ( )–
4
5
-2
( )=
CD = d – c
15
21
3
3
6
9
( ) ( )–
( )=
12
15
-6
4
5
-2
( )= 3
= 3ABCD = 3AB therefore parallel

6. Collinearity
Must have a
common point

7. • If AB = kCD, then AB and CD are parallel
• If AB = kBC, then A,B and C are collinear
(common point B)
Parallel + Collinear Vectors

8. A (2,3,5) B(3,6,7) C(6,15,13)
Prove A,B and C are collinear.
AB = b – a
3
6
7
2
3
5
( ) ( )–
1
3
2
( )=
BC = c – b
6
15
13
3
6
7
( ) ( )–
( )=
3
9
6
1
3
2
( )= 3
= 3AB

9. BC = 3AB, with common point B,
therefore collinear

10. A (1,5,8) B(3,9,2) C(3,7,10) D(4,9,7)
Prove AB and CD are parallel
AB = b – a
3
9
2
1
5
8
( ) ( )–
2
4
-6
( )=
CD = d – c
4
9
7
3
7
10
( ) ( )–
( )=
1
2
-3
2
4
-6
( )= ½
= ½ ABCD = ½ AB therefore parallel
Key
Question