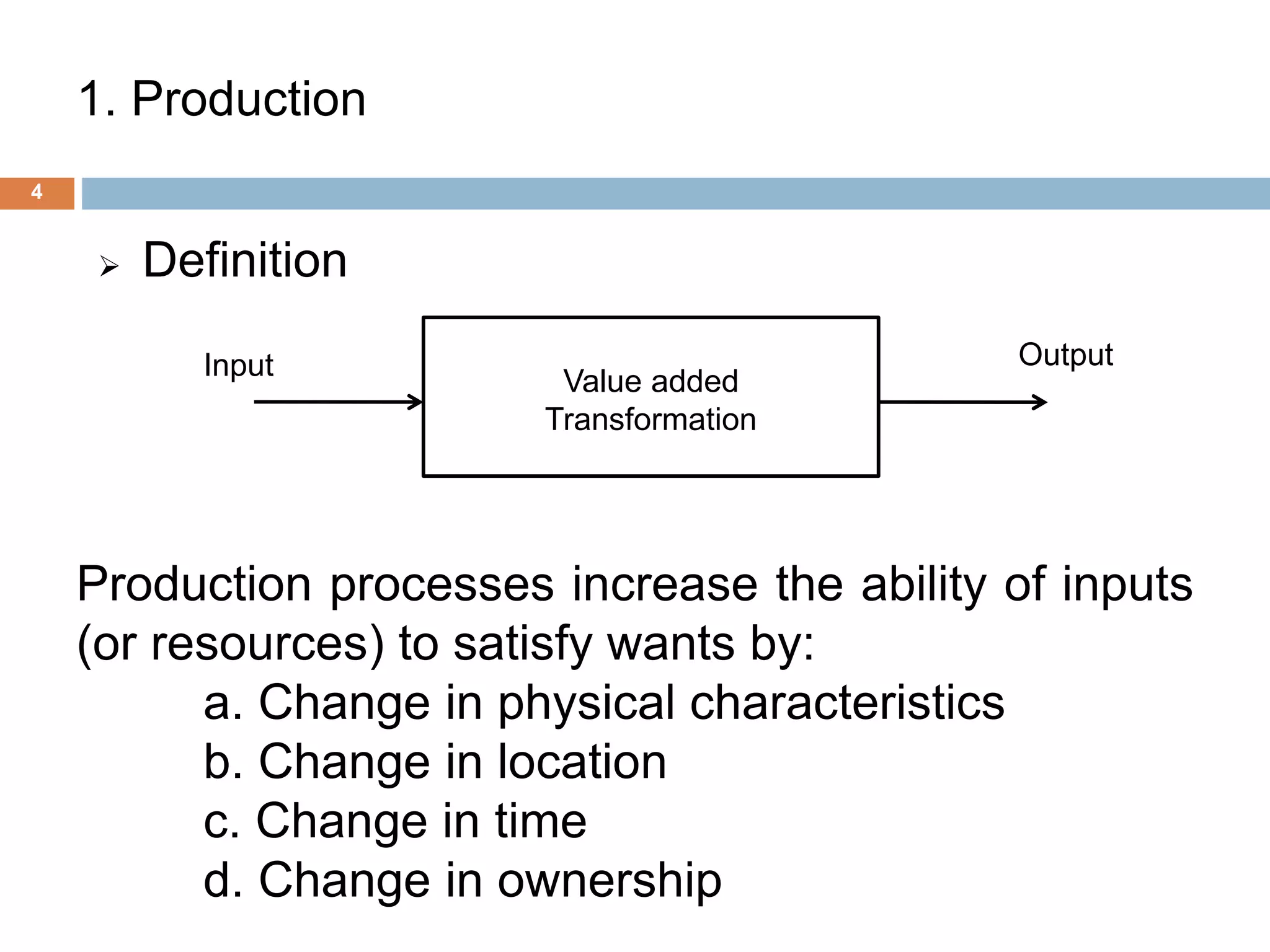
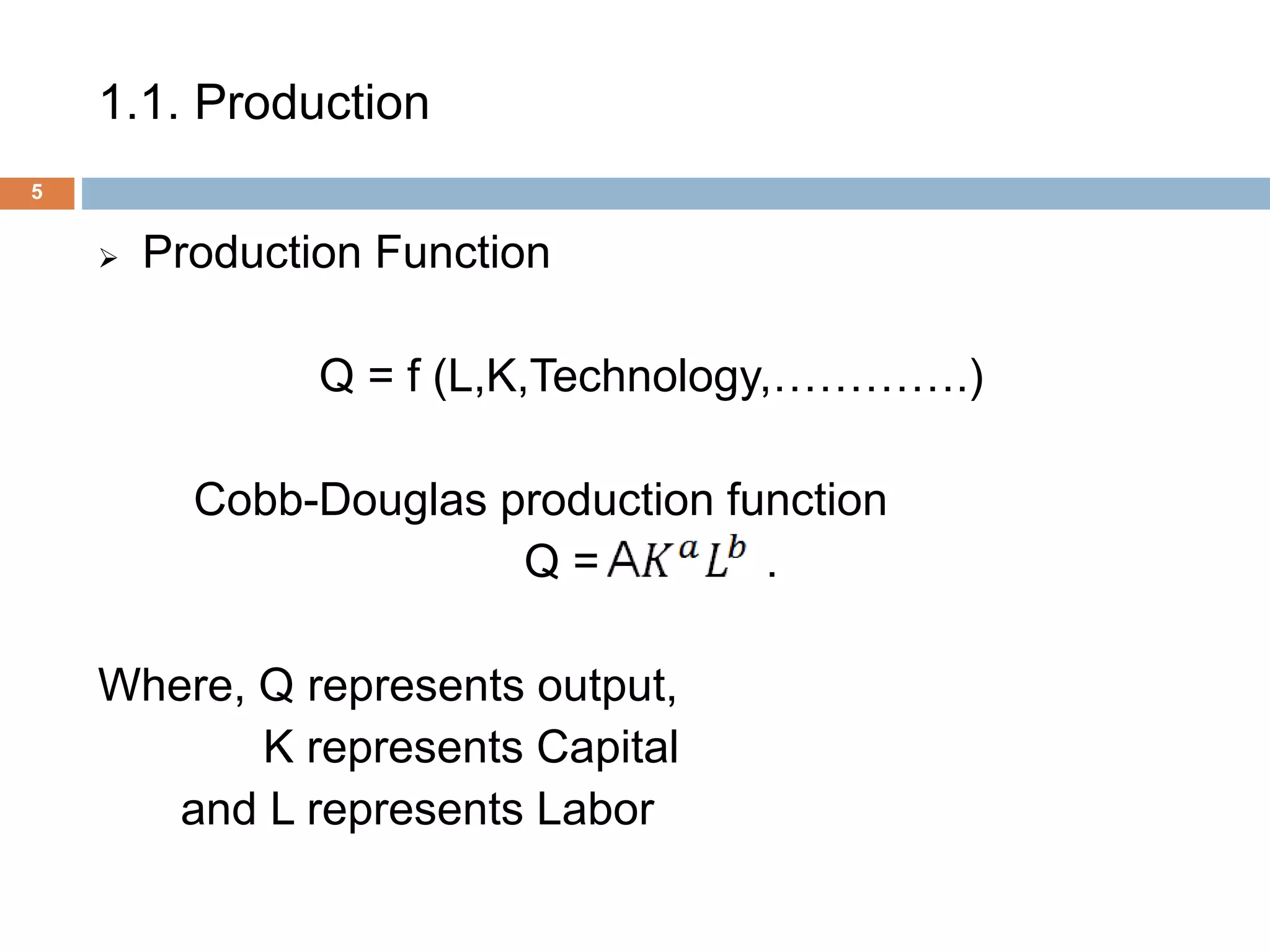
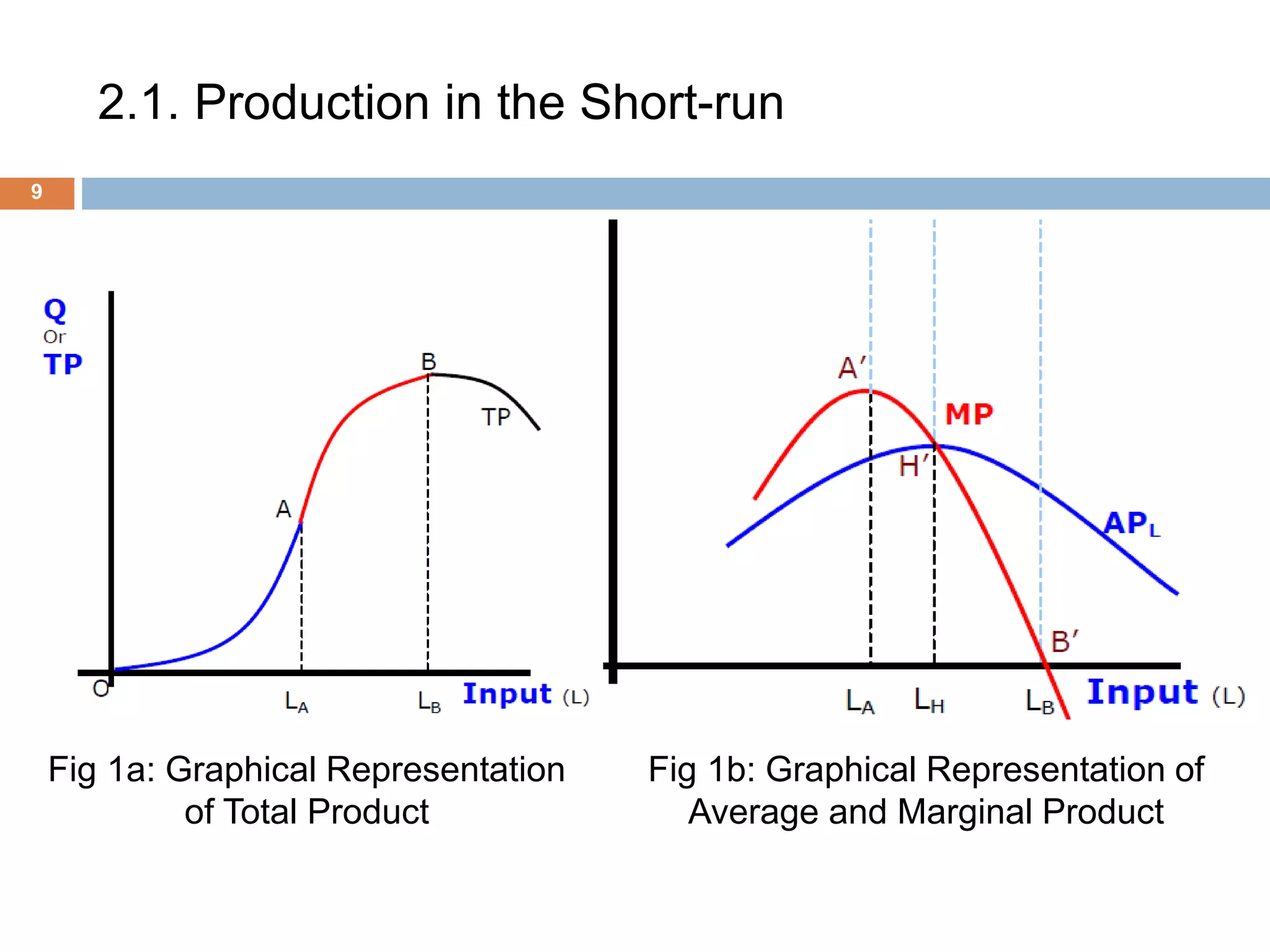
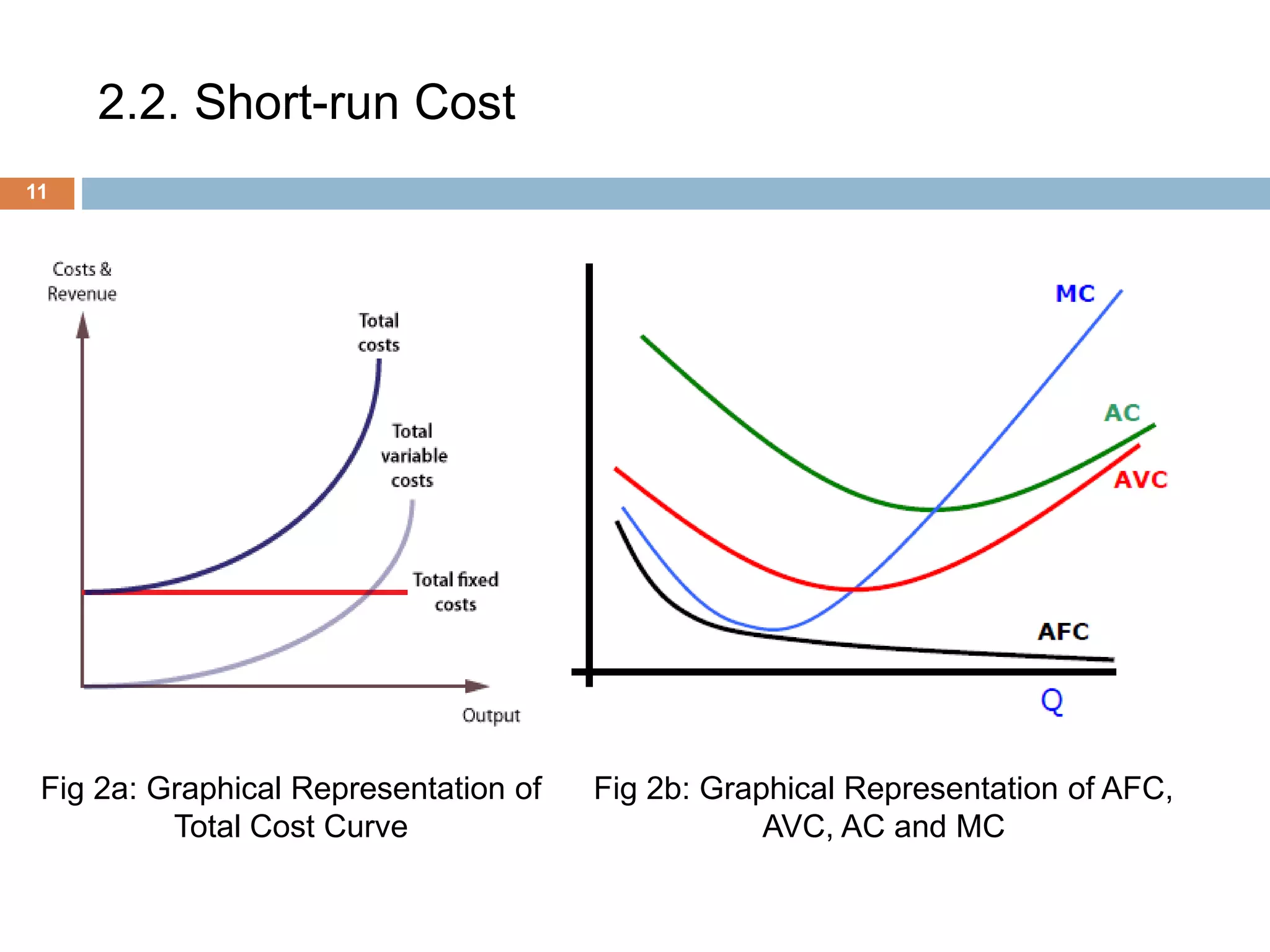
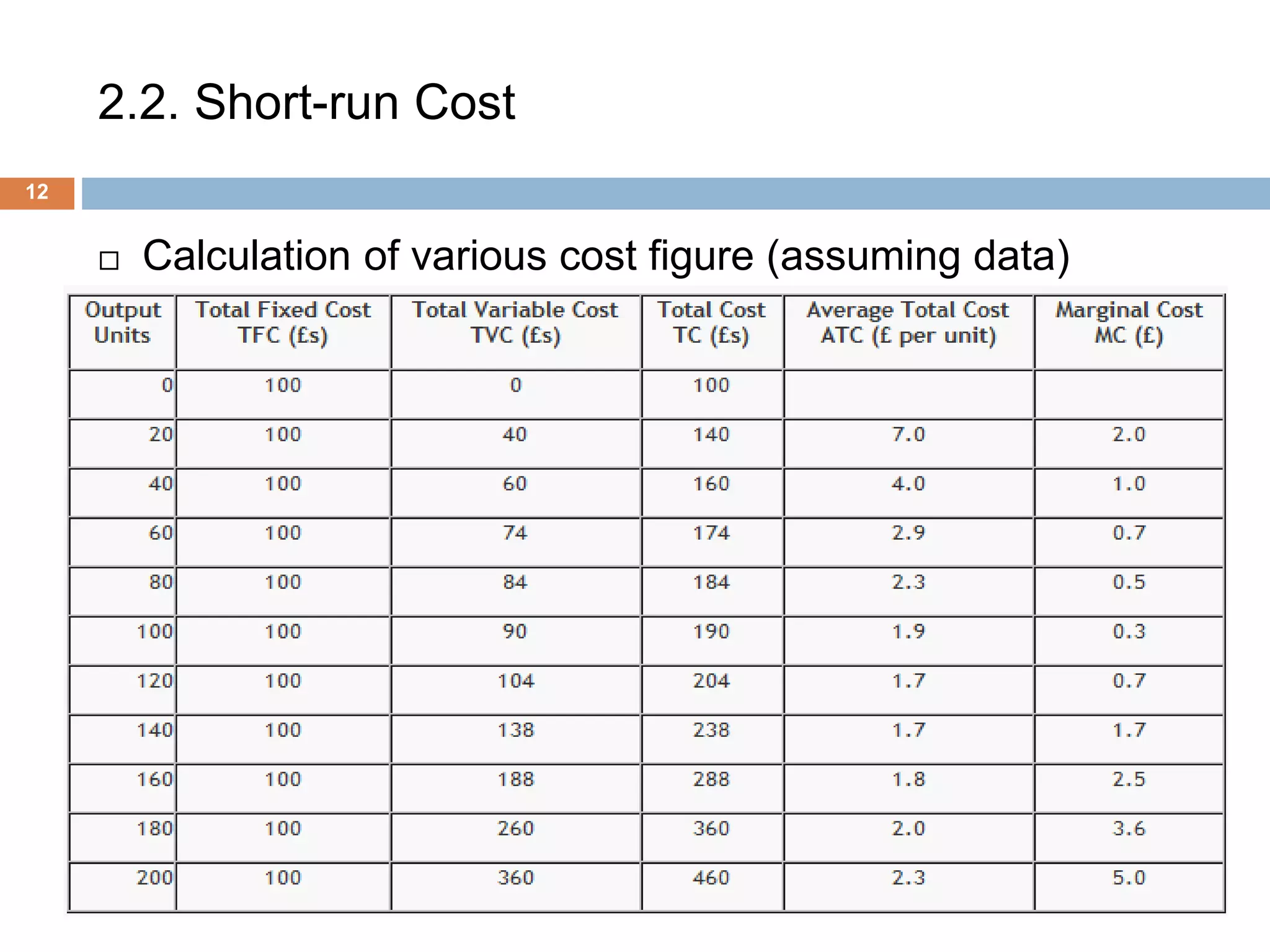
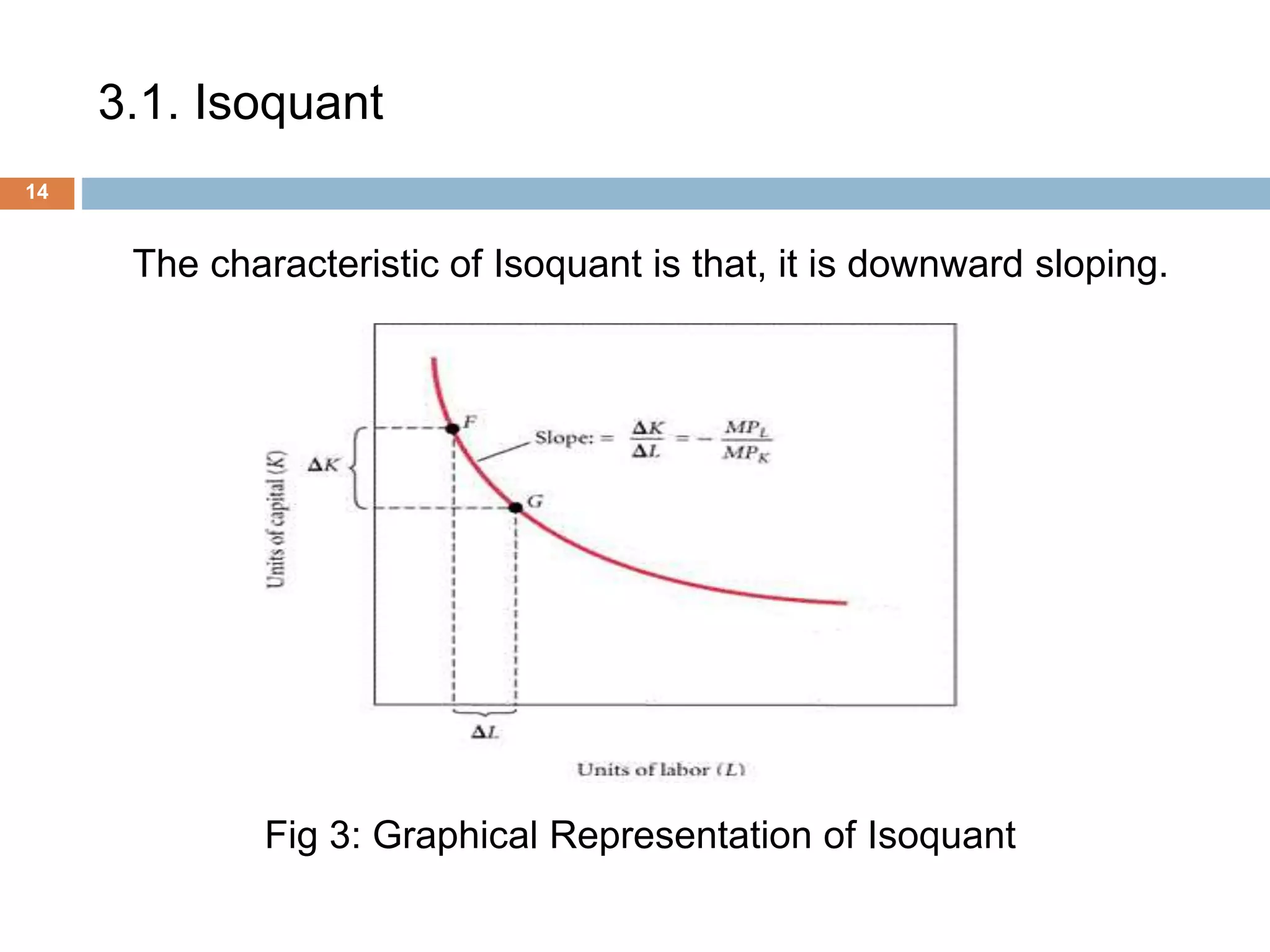
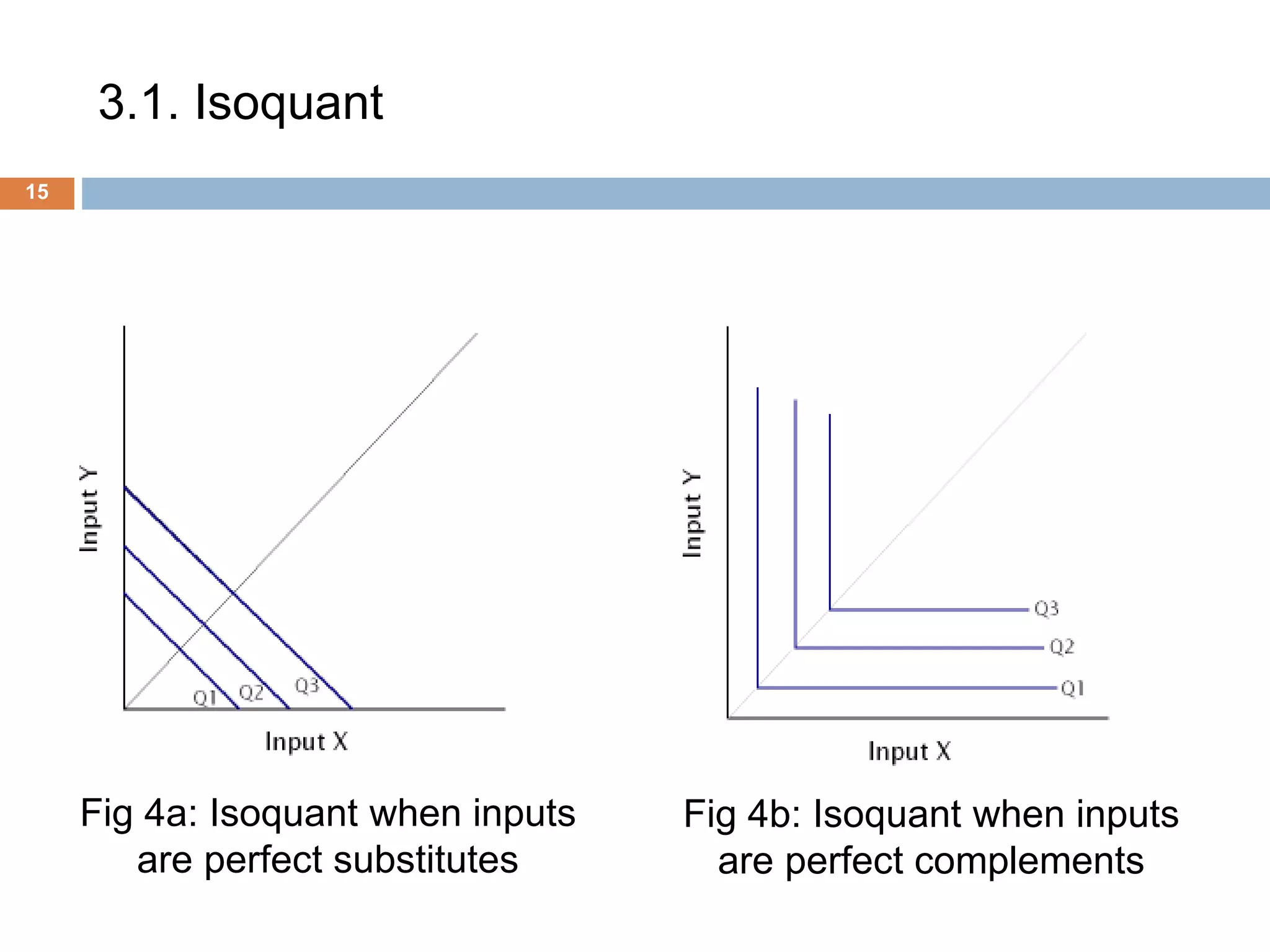
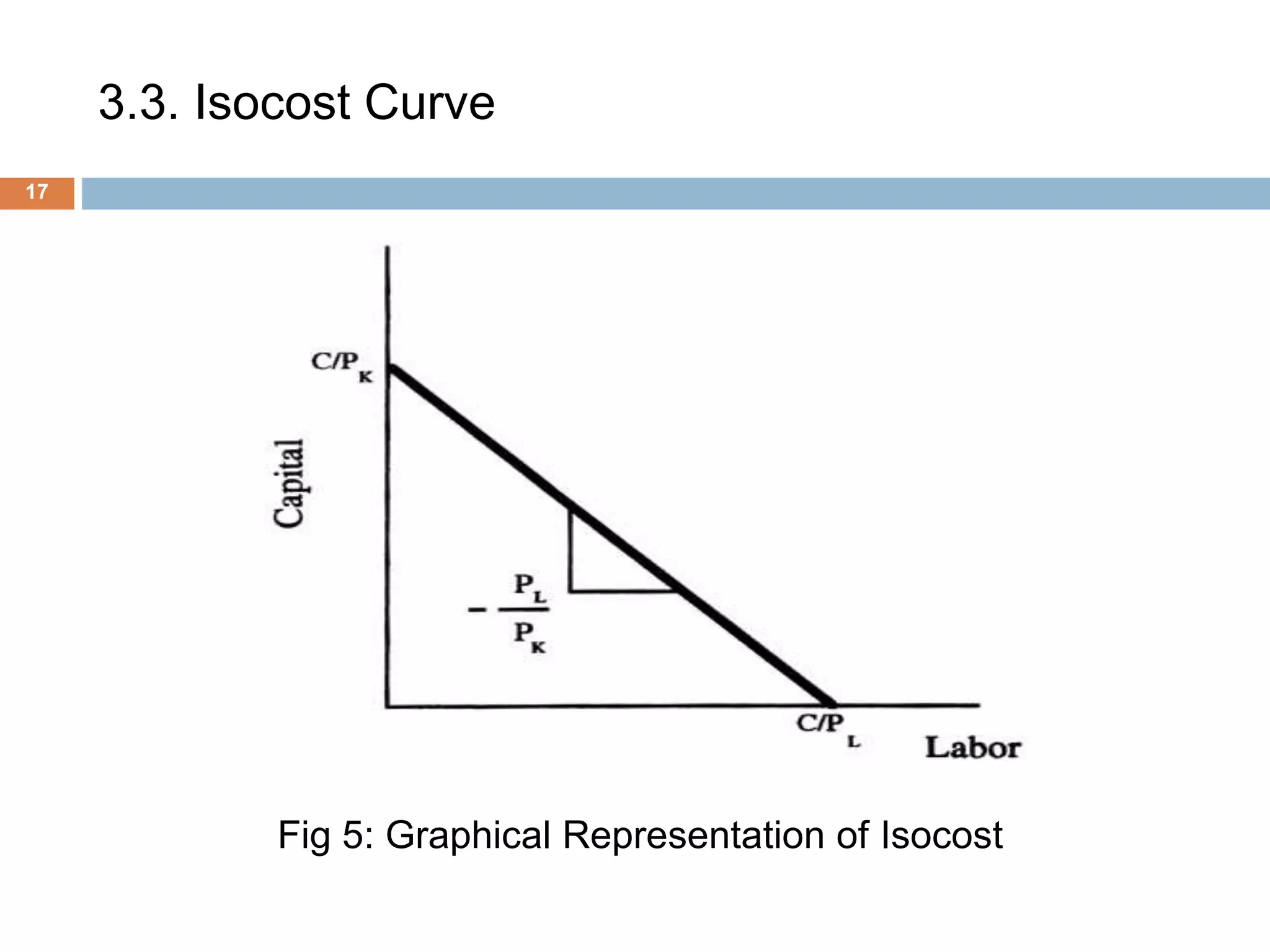
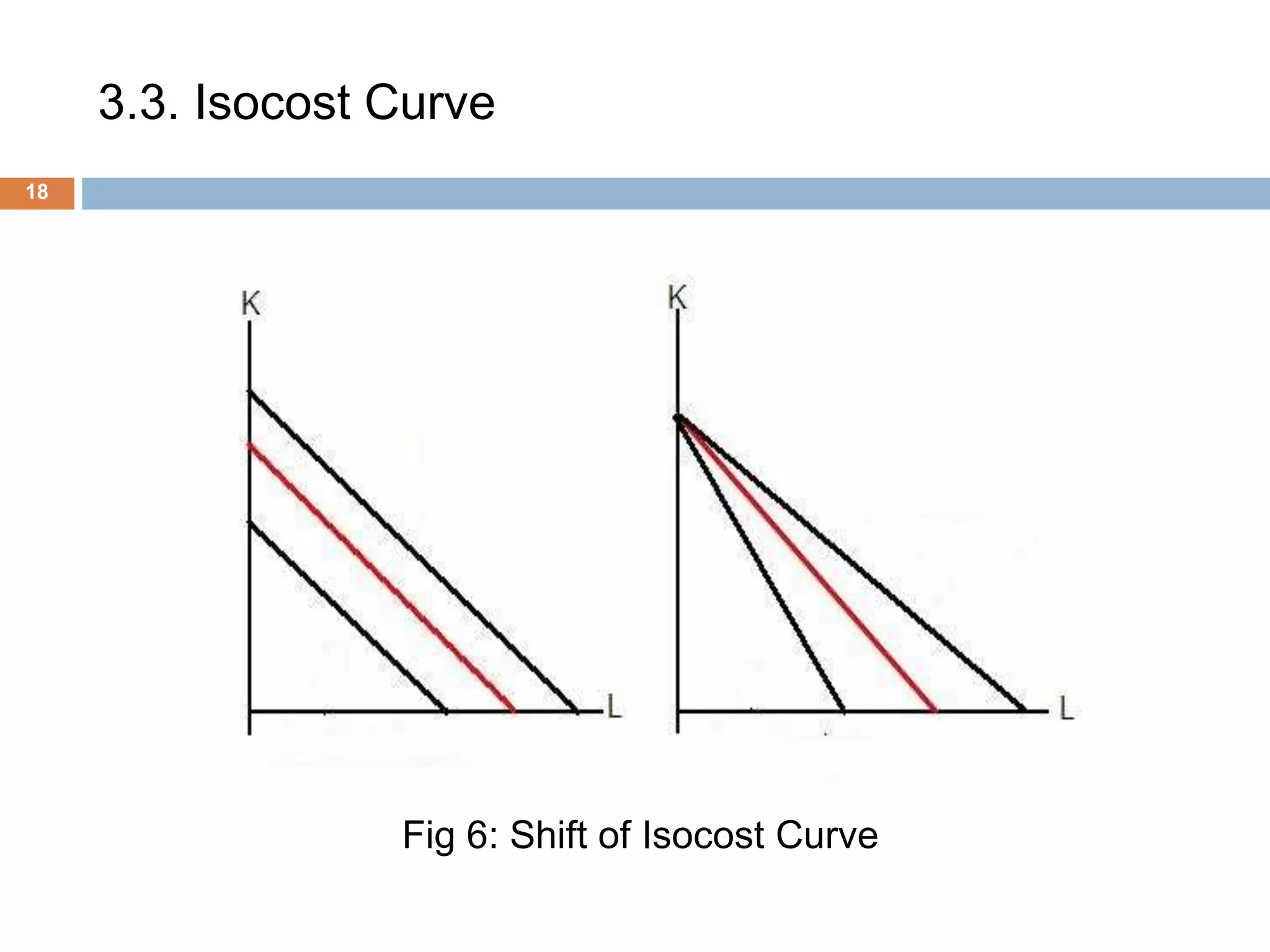
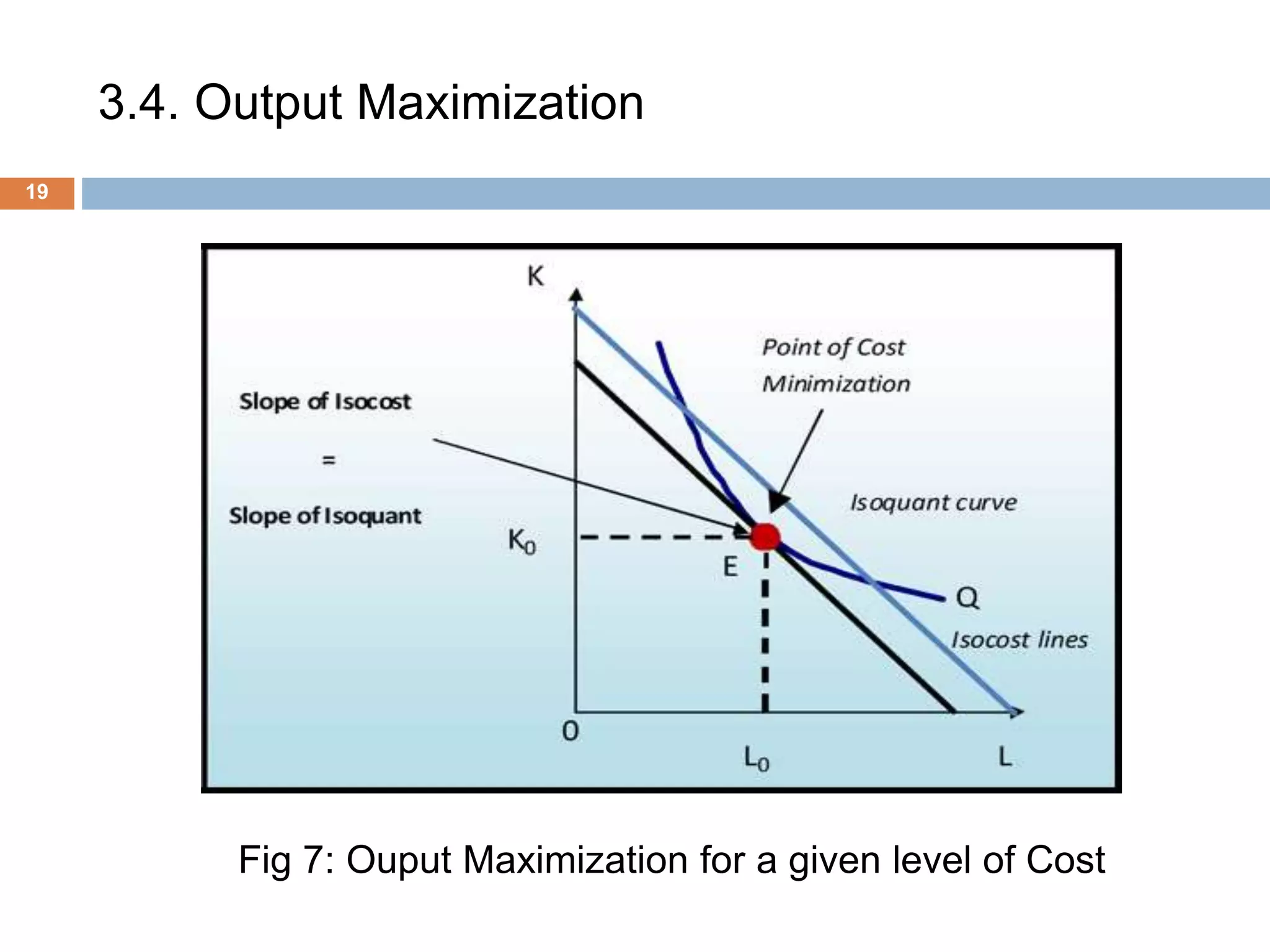
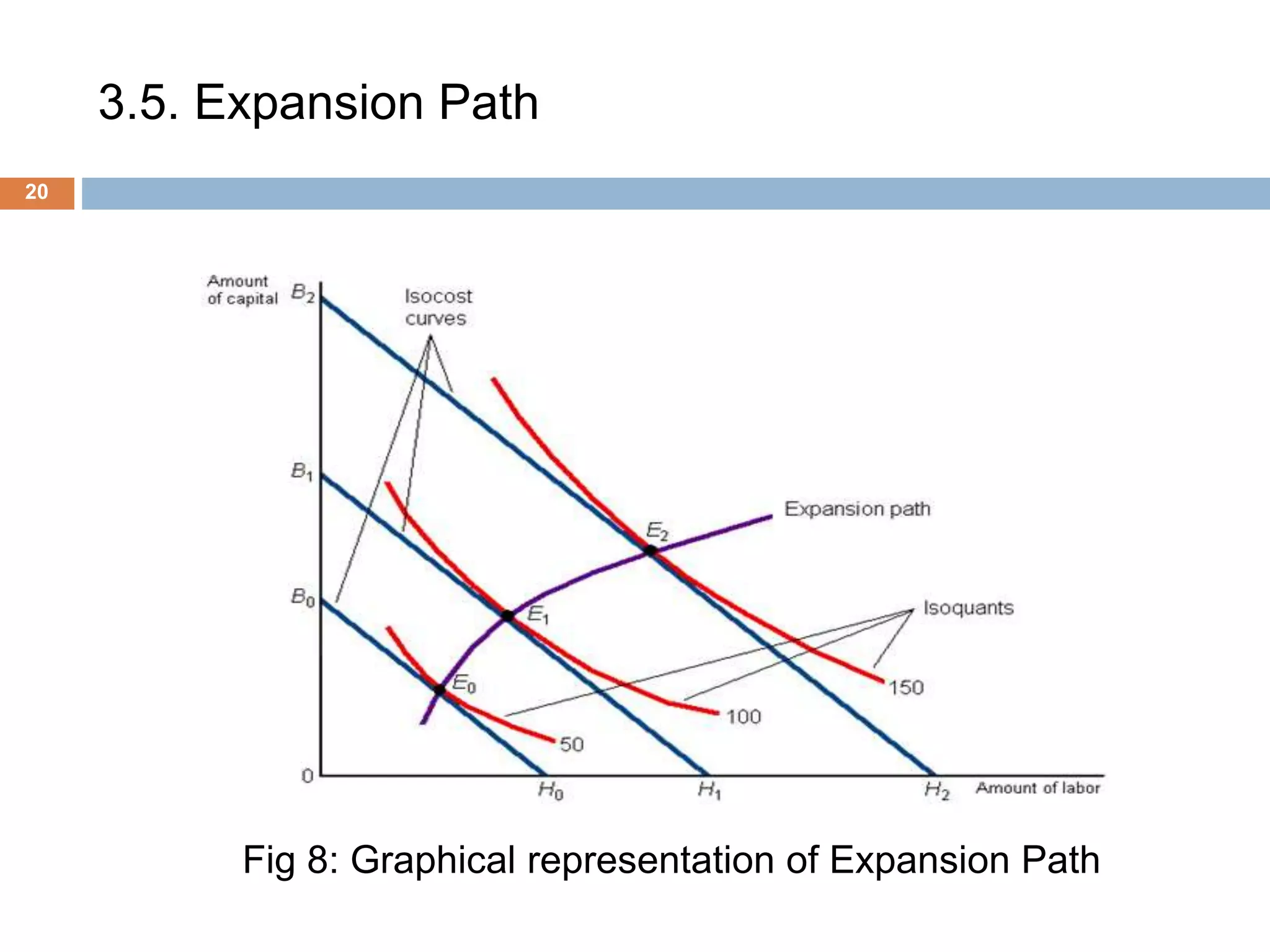
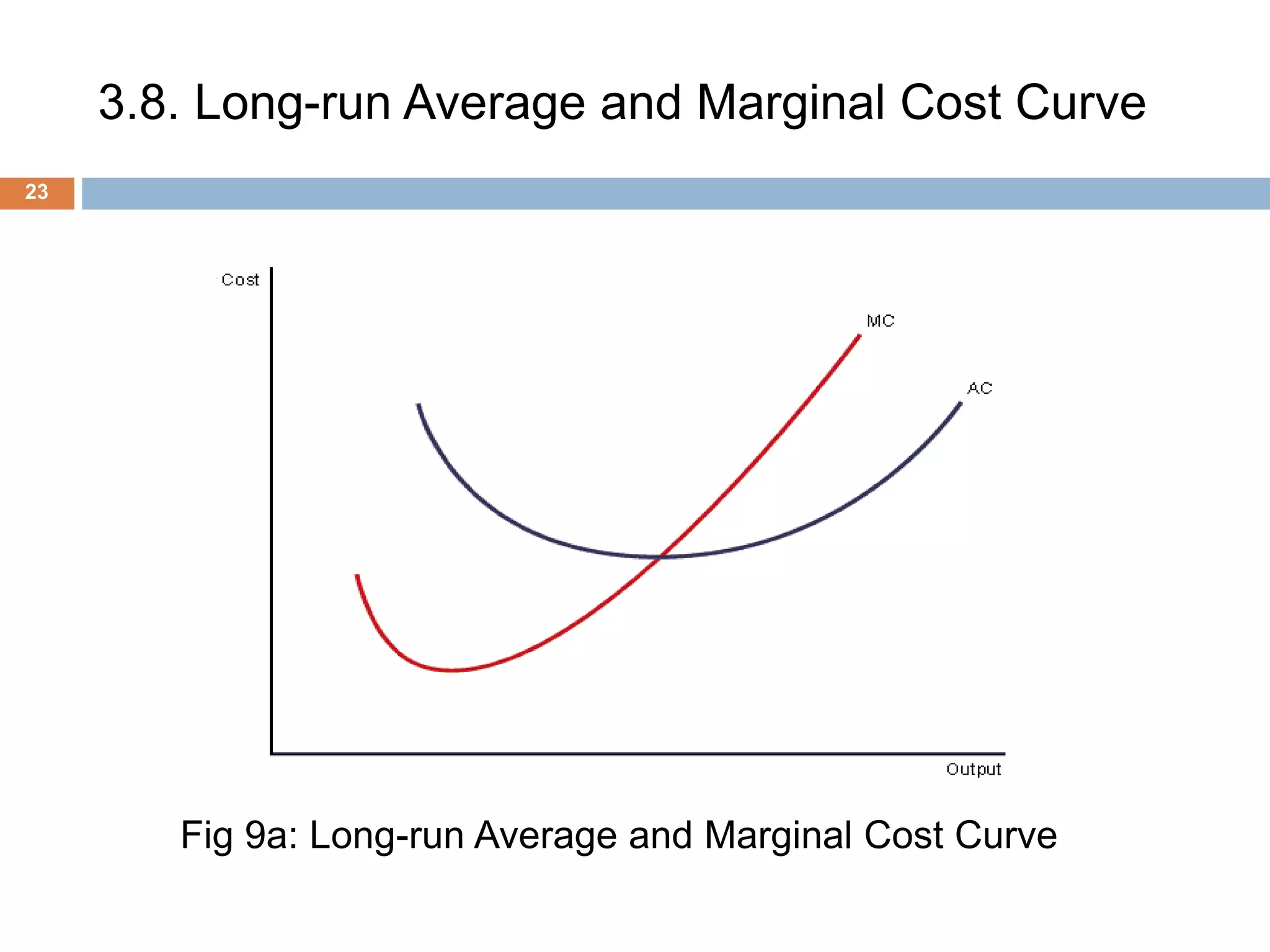
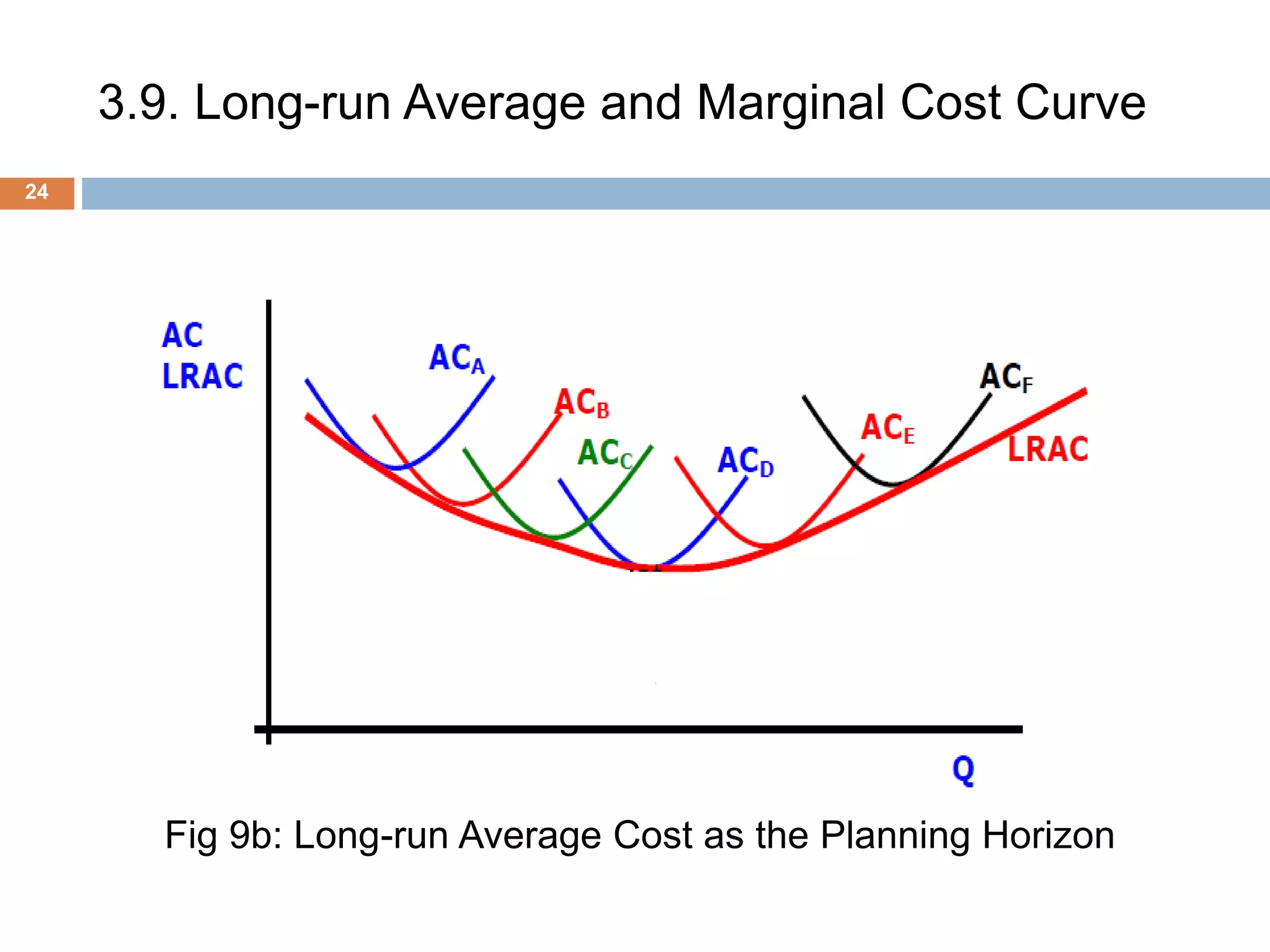
The document presents an overview of production and cost theory, outlining key concepts such as production efficiency, cost estimation, and maximizing organizational profit. It includes discussions on short-run and long-run production functions, cost components, and important economic terms like marginal cost and returns to scale. The conclusion emphasizes the significance of these theories for effective managerial decision-making and financial benefits.

1. 1
Production and Cost Theory
Prepared by
Md. Nasful Huda Prince

2. Objectives of this presentation
2
 To study about Production theory
 To study about production efficiency
 To study about Cost theory
 To relate the cost with production
 To study to achieve maximum profit for an
organization
 To study to take decision which will result
maximum financial benefit for the organization

3. Outline of Presentation
3
1. Production
2. Short-run Production and Cost
3. Long-run Production and Cost
4. Cost Estimation Technique
5. Conclusion

4. 1. Production
4
 Definition
Input Output
Value added
Transformation
Production processes increase the ability of inputs
(or resources) to satisfy wants by:
a. Change in physical characteristics
b. Change in location
c. Change in time
d. Change in ownership

5. 1.1. Production
5
 Production Function
Q = f (L,K,Technology,………….)
Cobb-Douglas production function
Q = .
Where, Q represents output,
K represents Capital
and L represents Labor

6. 1.2. Time and Production
6
Generally, four time periods are used in the
analysis of production, they are:
 Market Period
 Short-run
 Long-run
 The very Long-run
Most of the economists consider either Long-run
or short-run.

7. 2. Short-run Production and Cost
2.1. Production in the Short-run
7
Production function can be represented as
Q = f(L,K)
Here, Bar sign upon K indicates that K is fixed.
So the Production function can be represented as
Q = f(L)

8. 2.1. Production in the Short-run
8
Common Terminology:
 Total Product: Sum of total output (Q).
 Average Product: AP = =
 Marginal Product:
MP = =
 Technical Efficiency:
TE =
 Economic Efficiency:
EE=

9. 2.1. Production in the Short-run
9
Fig 1a: Graphical Representation
of Total Product
Fig 1b: Graphical Representation of
Average and Marginal Product

10. 2.2. Sort-run Cost
10
Some common Terms about cost:
 Opportunity Cost
 Implicit and Explicit Cost
 Total Cost (TC)
 Total Fixed Cost (TFC)
 Total Variable Cost (TVC)
 Average Fixed Cost (AFC)
 Average Variable Cost (AVC)
 Marginal Cost (MC)
 Average Total Cost (ATC)
 Total Revenue (TR)
 Marginal Revenue (MR)

11. 2.2. Short-run Cost
11
Fig 2a: Graphical Representation of
Total Cost Curve
Fig 2b: Graphical Representation of AFC,
AVC, AC and MC

12. 2.2. Short-run Cost
12
 Calculation of various cost figure (assuming data)

13. 3. Long-run Production and Cost
13
Long-run Production function can be represented as
Q = f(L,K)
Where, both the inputs are variable but technology is
same.
Cobb-Douglas production function can also be used
to explain this Production Function.

14. 3.1. Isoquant
14
Fig 3: Graphical Representation of Isoquant
The characteristic of Isoquant is that, it is downward sloping.

15. 3.1. Isoquant
15
Fig 4a: Isoquant when inputs
are perfect substitutes
Fig 4b: Isoquant when inputs
are perfect complements

16. 3.2. Marginal Rate of Technical Substitution
(MRTS)
16
MRTS can be defined using following equation
MRTS = - .
It is possible to relate MRTS with Marginal Product
by using following equation
MRTS = - .=

17. 3.3. Isocost Curve
17
Fig 5: Graphical Representation of Isocost

18. 3.3. Isocost Curve
18
Fig 6: Shift of Isocost Curve

19. 3.4. Output Maximization
19
Fig 7: Ouput Maximization for a given level of Cost

20. 3.5. Expansion Path
20
Fig 8: Graphical representation of Expansion Path

21. 3.6. Returns to Scale
21
Consider a production function as following form
Q = f (L,K)
Now if the input will change the variation of out can
be represented as
zQ = f (cL,cK)
Here, c & z are the proportionate change of input
and output
Now, If z>c, Increasing Returns to Scale
If z<c, Decreasing Returns to Scale
If z=c, Constant Returns to Scale

22. 3.7. Economies of Scope (SC)
22
If Joint production cost of two product is C(X,Y) and
C(X) & C(Y) are the individual production cost of
product X & Y the economies of scope will exist if
C(X,Y) < C(X) + C(Y)
The Degree to which SC exist is
SC= .
Diseconomies of scope will exist if
C(X,Y) > C(X) + C(Y)

23. 3.8. Long-run Average and Marginal Cost Curve
23
Fig 9a: Long-run Average and Marginal Cost Curve

24. 3.9. Long-run Average and Marginal Cost Curve
24
Fig 9b: Long-run Average Cost as the Planning Horizon

25. 4. Cost Estimation Technique
25
If we consider a Total Cost Function as following
TC = .
Average Total Cost can be calculated in this way
ATC = .
Marginal Cost can be calculated in this way
MC = .

26. 5. Conclusion
26
 Analysis of production and cost is very important
for an organization.
 A good manager will concentrate on technical
and economic efficiency.
 Study of production and cost will help a
manager to take decision for maximizing
organization profit.
 At last it can be concluded in this way that,
study and improvement of our knowledge about
discussed topics help us to fulfill our
presentation objectives.

27. 27
THANK YOU ALL