Pump pipeline

Water Supply and Wastewater
Removal
Pump-Pipeline
Systems
Instructor: Parjang Monajemi

Introduction
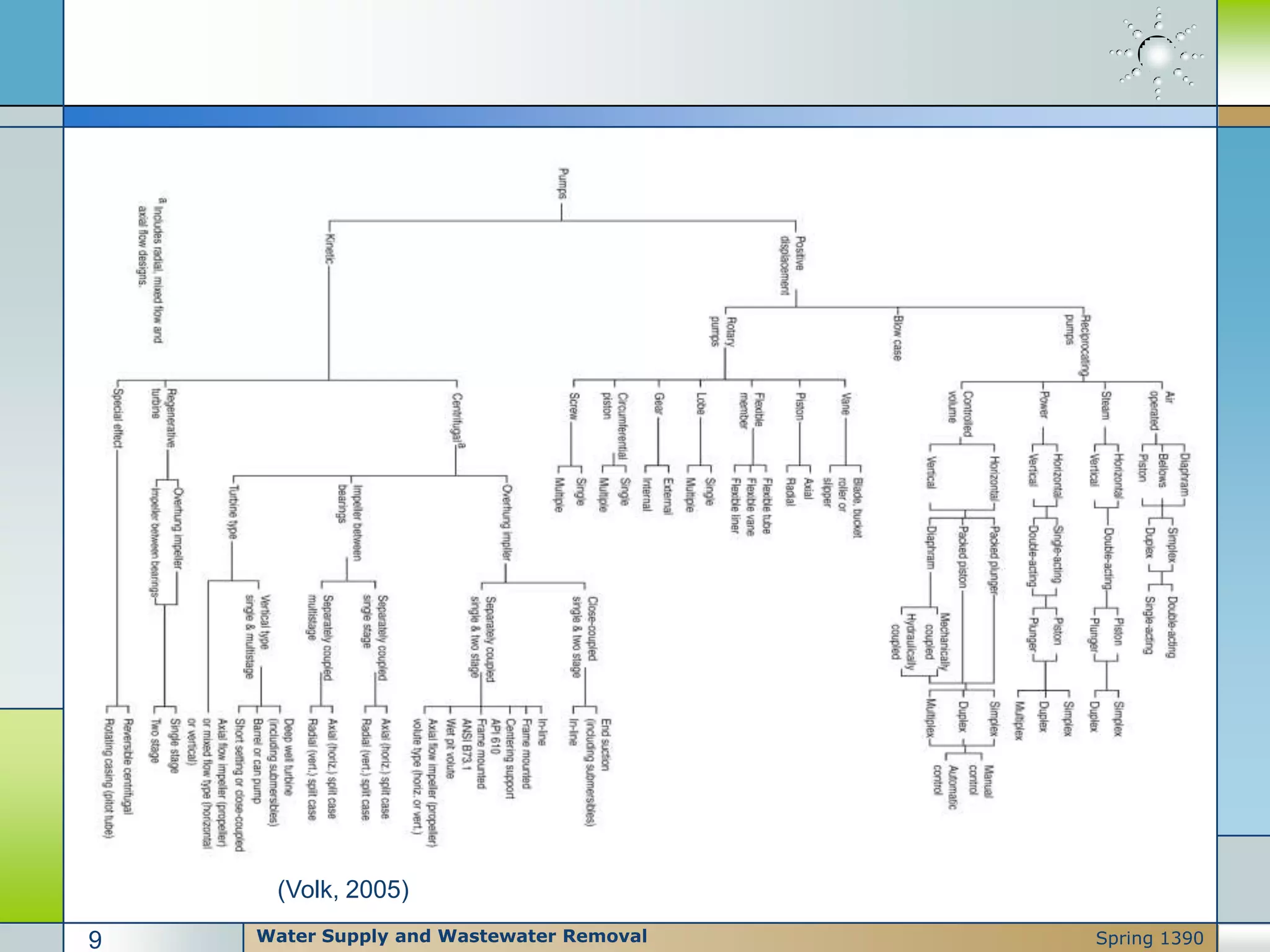
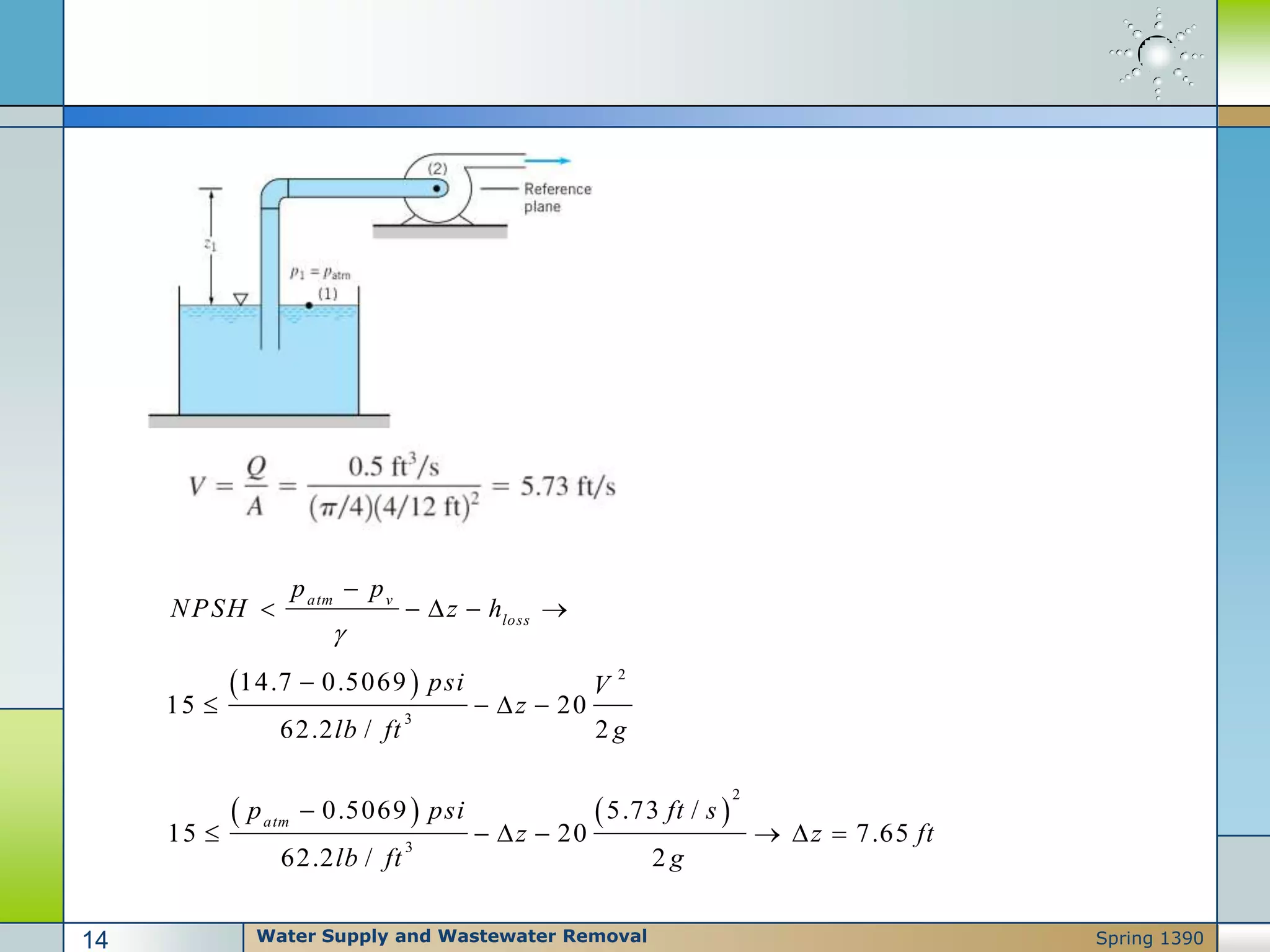
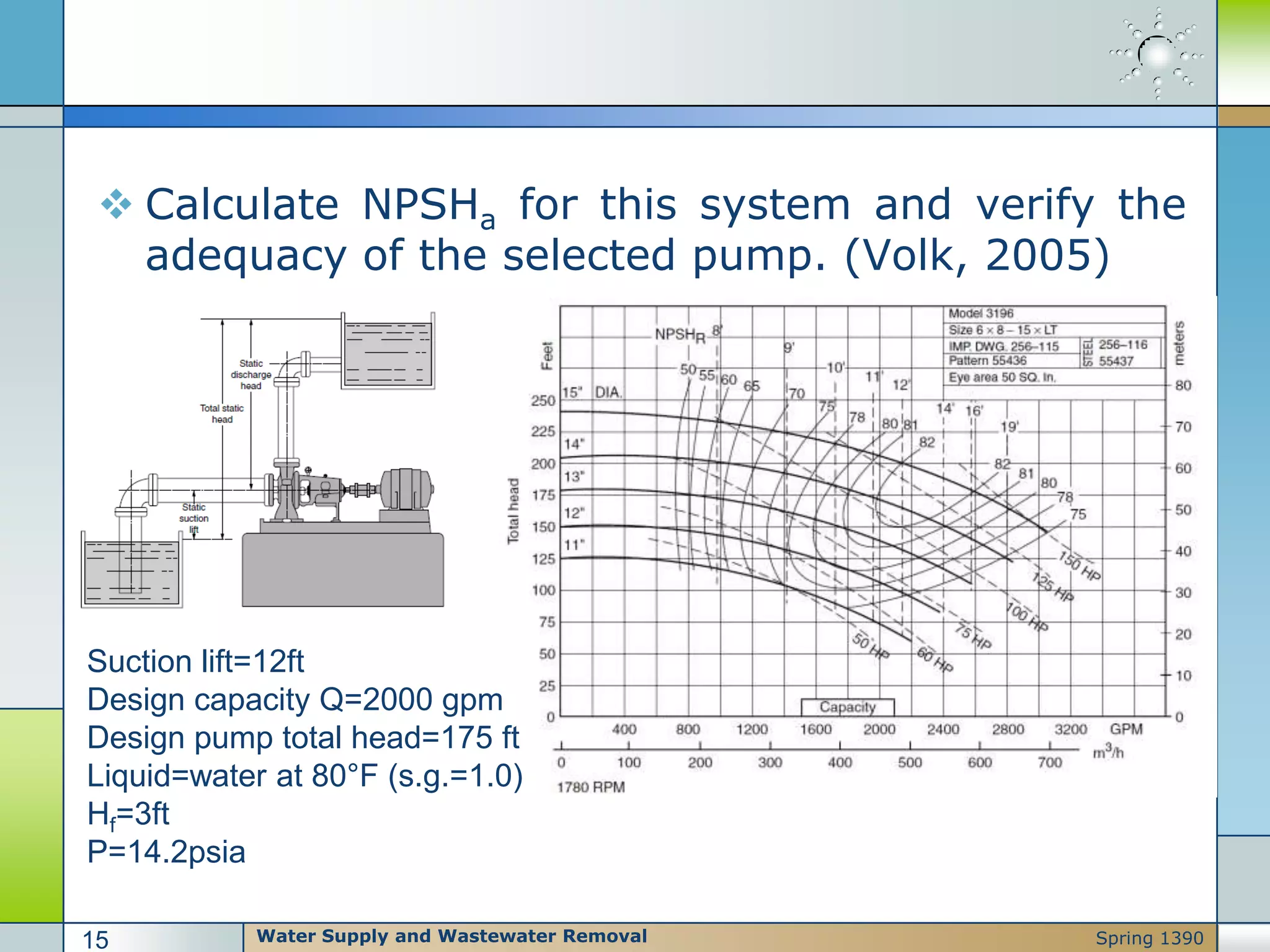
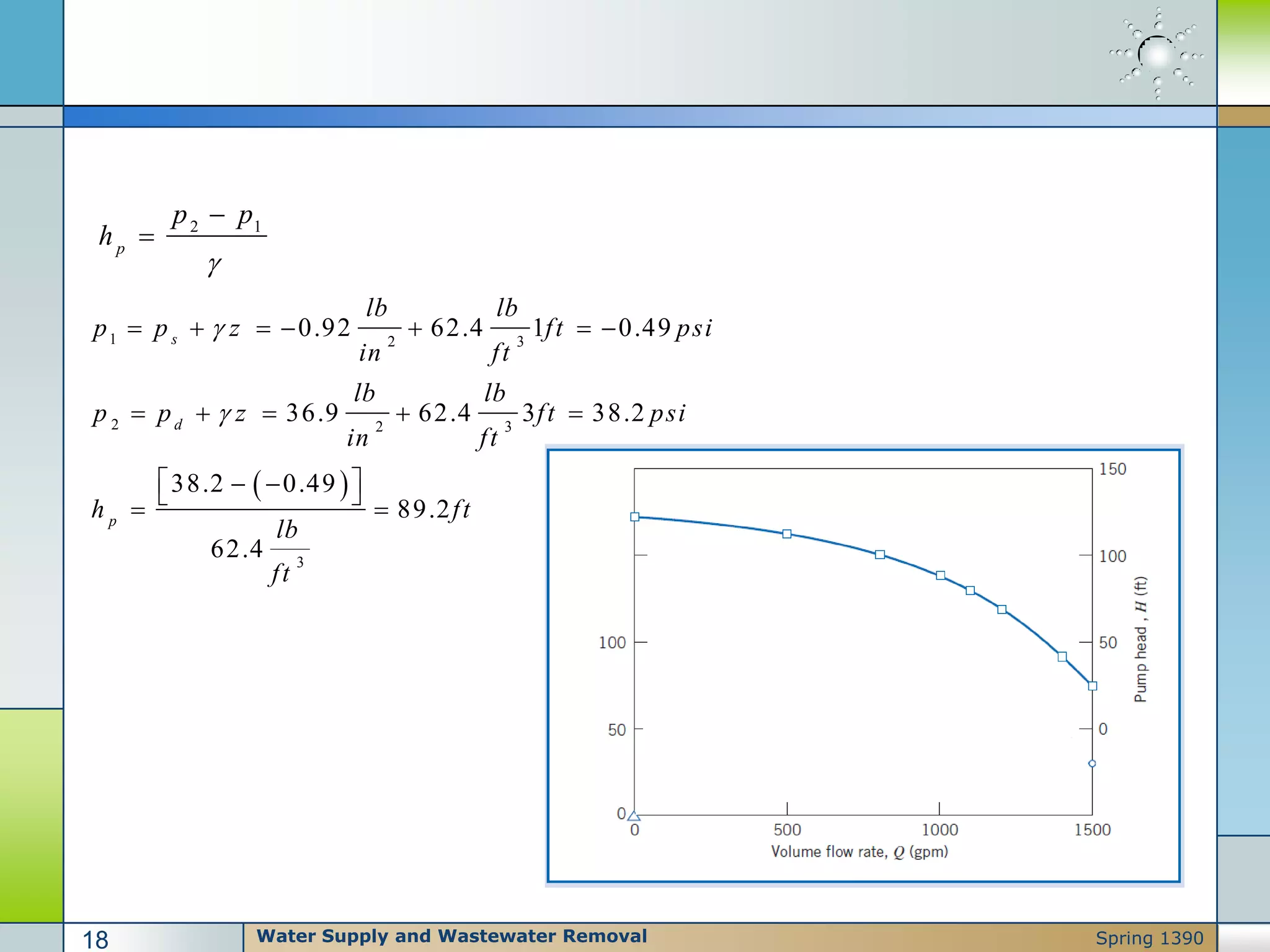
 Simply stated, a pump is a machine used to
move liquid through a piping system and to
raise the pressure of the liquid. A pump can be
further defined as a machine that uses several
energy transformations to increase the pressure
of a liquid.
 There are actually three distinct reasons for
raising the pressure of a liquid with a pump:
1. Static elevation A liquid’s pressure must be
increased to raise the liquid from one elevation
to a higher elevation. This might be necessary,
for example, to move liquid from one floor of a
building to a higher floor.
Water Supply and Wastewater Removal2 Spring 1390

2. Friction. It is necessary to increase the
pressure of a liquid to move the liquid through
a piping system and overcome frictional losses.
Liquid moving through a system of pipes,
valves, and fittings experiences frictional losses
along the way.
3. Pressure. In some systems it is necessary to
increase the pressure of the liquid for process
reasons. In addition to moving the liquid over
changes in elevation and through a piping
system, the pressure of a liquid must often be
increased to move the liquid into a pressurized
vessel, such as a boiler or fractionating tower,
or into a pressurized pipeline.

Pressure and Head
 It is important to understand the relationship
between pressure and head. Pressure is
measured in psi (pounds per square inch) or
kilopascal (kPa), bar, or kilograms per square
centimeter (kg/cm2), while the equivalent units
for head are meters (m) or feet(ft).

Classification of Pumps
 There are many ways to classify pumps:
according to their function, their conditions of
service, materials of construction, etc. The
pump industry trade association, the Hydraulic
Institute, has classified pumps as follows:
1. Kinetic: In a kinetic pump, energy is
continuously added to the liquid to increase its
velocity. When the liquid velocity is
subsequently reduced, this produces a pressure
increase. Although there are several special
types of pumps that fall into this classification,
for the most part this classification consists of
centrifugal pumps.

 Centrifugal pumps, involve a collection of
blades, buckets, flow channels, or passages
arranged around an axis of rotation to form a
rotor. Rotation of the rotor produces dynamic
effects that either add energy to the fluid or
remove energy from the fluid. centrifugal
pumps are classified as axial-flow, mixed-flow,
or radial-flow machines depending on the
predominant direction of the fluid motion
relative to the rotor’s axis as the fluid passes
the blades

 Positive Displacement In a positive
displacement pump, energy is periodically
added to the liquid by the direct application of a
force to one or more movable volumes of liquid.
This causes an increase in pressure up to the
value required to move the liquid through ports
in the discharge line. The important points here
are that the energy addition is periodic (i.e., not
continuous) and that there is a direct
application of force to the liquid. Typical
examples shown include the common tire pump
used to fill bicycle tires, the human heart, and
the gear pump.

 The following are some key application criteria
that would lead to the selection of a P.D. pump
over a centrifugal pump:
a) High viscosity
b) Self-priming
c) High pressure
d) Low flow
e) High efficiency
f) Low velocity
g) Low shear
h) Fragile solids handling capability
i) Accurate, repeatable flow measurement
j) Constant flow/variable system pressure
k) Two-phase flow

(Volk, 2005)

Cavitation in Turbomachines
 Cavitation refers to conditions at certain
locations within the turbomachine where the
local pressure drops to the vapor pressure of
the liquid, and as a result, vapor filled cavities
are formed. As the cavities are transported
through the turbomachine into regions of
greater pressure,
they will collapse
rapidly, generating
extremely high localized
pressures. Signs of
cavitation in turbopumps
include noise, vibration, and
lowering of the head-
discharge and efficiency

 On the suction side of a pump, low pressures
are commonly encountered, with the possibility
of cavitation occurring within the pump. The
requiered head at the pump inlet to keep the
liquid from cavitating or boiling is called Net
Possitive Suction Head (NPSH).
 Consider the shown operating pump. Location 1
is on the liquid surface on the suction side, and
location 2 is the point of minimum pressure
within the pump.
2
2
s s v
required
p V p
NPSH
g 
  

 The design requirement for a pump is thus
established as follows
22
1 1
1
2
1
2
2 2
2
2
s s
s loss
atm s s
s loss
atm s s
loss
atm v
loss
p Vp V
z z h
g g
p p V
z z h
g
p p V
z h
g
p p
z h NPSH
 
 
 

      
     
     

   
atm v
available loss
p p
NPSH z h


   
atm v
loss
p p
N PS H z h


   

 A centrifugal pump is to be placed above a
large, open water tank, as shown, and is to
pump water at a rate of 0.5 cfs. At this flowrate
the required net positive suction head, is 15
ft, as specified by the pump manufacturer. If
the water temperature is and atmospheric
pressure is 14.7 psi, determine the maximum
height, that the pump can be located above the
water surface without cavitation. Assume that
the major head loss between the tank and the
pump inlet is due to filter at the pipe inlet
having a minor loss coefficient k=20. Other
losses can be neglected. The pipe on the suction
side of the pump has a diameter of 4 in.
(Munson, 2009)

  2
3
14.7 0.5069
15 20
62.2 / 2
atm v
loss
p p
NPSH z h
psi V
z
lb ft g


    

   
   
2
3
0.5069 5.73 /
15 20 7.65
62.2 / 2
atm
p psi ft s
z z ft
lb ft g

      

 Calculate NPSHa for this system and verify the
adequacy of the selected pump. (Volk, 2005)
Suction lift=12ft
Design capacity Q=2000 gpm
Design pump total head=175 ft
Liquid=water at 80°F (s.g.=1.0)
Hf=3ft
P=14.2psia

 Solve the previous problem, except using water
at 160°F (Volk, 2005).
14.2 2.31
32.8
1.0
1.2
32.8 12 3 1.2 16.6
v
a
ft
H ft
NPSH ft



    
From previous figure, at 2000 gpm, NPSH = 11.2 ft,
16.6 11.2a r
NPSH ft NPSH ft  
14.2 2.31
33.5
0.98
11.2
33.5 12 3 11.2 7.3
v
a
ft
H ft
NPSH ft



     7.3 11.2a r
NPSH ft NPSH ft  

Performance Characteristics
 The flow system used to test a centrifugal pump
at a nominal speed of 1750 rpm is shown. Data
measured during the test are given in the table.
Calculate the net head delivered and the pump
efficiency at a volume flow rate of 1000 gpm.
Plot the pump head, power input, and efficiency
as functions of volume flow rate.
(Pritchard, 2011)

2 1
p
p p
h



 
1 2 3
2 2 3
3
0.92 62.4 1 0.49
36.9 62.4 3 38.2
38.2 0.49
89.2
62.4
s
d
p
lb lb
p p z ft psi
in ft
lb lb
p p z ft psi
in ft
h ft
lb
ft


      
    
   
 

Basic Output Parameters
 Usually V2 and V1 are about the same, z2 z1 is
no more than a meter or so, and the net pump
head is essentially equal to the change in
pressure head
 The power delivered to the fluid simply equals
the specific weight times the discharge times
the net head change This is traditionally
called the water horsepower. The power
required to drive the pump is the brake
horsepower where ω is the shaft
angular velocity and T the shaft torque.
2 1
p
p p
h



P Qh
bhp T

 Water at 10 °C (nu=1.3x10-6m2/s) is to flow
from reservoir A to reservoir B through a cast-
iron pipe of length 20 m at a rate of Q=0.015
m3/s as is shown. The system contains a sharp-
edged entrance and six regular threaded 90°
elbows. Determine the the required head of the
pump that must be used if the pipe diameter is
5 cm. (Munson, 2009)

 
 
3
2
0.015 /
7.65 /
0.05
4
m sQ
V m s
A 
  
7.65 0.05
Re 294231
0.0000013
VD VD
 

   
 
 
0.26
0.005
5
mm
D cm

  , Re 294000 0.03f  
       
2 2 2 2 2
2 0.5 6 1.5 1 12 0.5 9 1 65.8 63.8
2 2 2 2 2
p p
L V V V V V
h f m h m
D g g g g g
           
2 2
1 1 1 1
1 2 1 1
2 2
p p
P V P V
E h E headlosses z h z headlosses
g g 
          

 The given pump adds 25 kW to the water and
causes a flowrate of 0.04 m3/s. Determine the
flowrate expected if the pump is removed from
the system. Assume f=0.016 for either case and
neglect minor losses. (Munson, 2009)
 
2 2 2 2
1 1 2 2
1 2 1 1
31.8 30 14.2
62.5 0.16 68.7
2 2 20 0.06 20
P v P v
Z hp Z head loss Z Z m
g g 
            
 
   
 
3 3
10, 000 / 0.04 /
25000
100%
62.5
N m m s HQH
P W
H m


  
 
 
 
 
 
 
 
3 3
2 2 2 2
0.04 / 0.04 /
14.2 / 31.8 /
0.06 0.04
4 4
pipe exit
m s m s
v m s v m s
m m
 
   

222 2
1 1 2 2
1 2
22
30
68.7 0.16
2 2 20 0.06 20
30
68.7 0.16
20 0.06 20
pipeexit
pipeexit
vvP v P v
Z Z head loss
g g
vv
 
         
 
   2 2 2 2
0.06 0.04 0.44
4 4
pipe exit pipe exit
v m v m v v
 
  
 
 
     
2
2
2 2 3
0.4430
68.7 0.16 23 /
20 0.06 20
23 / 0.04 0.03 /
4
ex itex it
ex it
vv
v m s
Q m s m m s

   
 

 The efficiency is basically composed of three
parts: volumetric, hydraulic, and mechanical.
1. The volumetric efficiency is where QL
is the loss of fluid due to leakage in the
impeller-casing clearances
2. The hydraulic efficiency where hf has
three parts: (1) shock loss at the eye due to
imperfect match between inlet flow and the
blade entrances, (2) friction losses in the blade
passages, and (3) circulation loss due to
imperfect match at the exit side of the blades.
3. the mechanical efficiency is
v
L
Q
Q Q
 

1
f
h
s
h
h
  
1
f
m
p
php
  

 where Pf is the power loss due to mechanical
friction in the bearings, packing glands, and
other contact points in the machine.
 By definition, the total efficiency is simply the
product of its three parts v h m
   
Performance characteristics
for a given pump gometry
and operating speed are
usually given in the form of
plots of and bhp versus Q
commonly referred to as
capacity as is llustrated

 Water is to be pumped from one large, open
tank to a second large, open tank as shown.
The pipe diameter throughout is 6 in. and the
total length of the pipe between the pipe
entrance and exit is 200 ft. Minor loss
coefficients for the entrance, exit, and the elbow
are shown on the figure, and the friction factor
for the pipe can be assumed constant and equal
to 0.02. A certain centrifugal pump having the
given performance characteristics is suggested
as a good pump for this flow system. With this
pump, what would be the flowrate between the
tanks? Do you think this pump would be a good
choice?(Munson, 2009)

Q H η
0 89 0
400 86 30
800 81 53
1200 75 73
1600 65 86
2000 53 88
2400 28 60

As can be seen, although the
operating efficiency is not the peak
efficiency, which is about 86%, it is
close (about 84%). Thus, this pump
would be a satisfactory choice

 Solve the previous problem if two pumps were
used (a) in series, (b) in parallel
Q H η
0 89 0
400 86 30
800 81 53
1200 75 73
1600 65 86
2000 53 88
2400 28 60
Q H
0 178
400 172
800 162
1200 150
1600 130
2000 106
2400 56
Q H
0 89
800 86
1600 81
2400 75
3600 65
4000 53
4800 28
Single pump Two pumps in parallel Two pumps in series

0
20
40
60
80
100
120
0 400 800 1200 1600 2000 2400
Head,ft
Flowrate, gal/min
2 Parallel pumps
0
20
40
60
80
100
120
140
160
180
200
0 400 800 1200 1600 2000 2400
Head,ft Flowrate, gal/min
2 pumps in series
 1780 / min
88%
Q gal



 2100 / min
85%
Q gal




Dimensionless Parameters and
Similarity Laws
 As we studied earlier, we know that the
principal, dependent pump variables are the
actual head rise ha, shaft power ẃshaft, and
efficiency η. We expect that these variables will
depend on the geometrical configuration, which
can be represented by some characteristic
diameter D, other pertinent lengths L, and
surface roughness ε, In addition, the other
important variables are flowrate Q, the pump
shaft rotational speed ω, fluid viscosity μ, and
fluid density ρ.

 When the pump flow involves high Reynolds
numbers experience has shown that the effect
of the Reynolds number can be neglected. For
simplicity, the relative roughness, can also be
neglected in pumps since the highly irregular
shape of the pump chamber is usually the
dominant geometric factor rather than the
surface roughness. Thus, with these
2
Re
D 



simplification and for geometrically similar pumps
(all pertinent dimensions, scaled by a common
length scale), the dependent pi terms are
functions of only Q/ωD3 so that:
3 5
2 5
3
Power Coefficient
Head Coefficient
Flowrate Coefficient
W
H
Q
W
C
D
gH
C
D
Q
C
D









 An 8-in diameter centrifugal pump operating at
1200 rpm is geometrically similar to the 12-in
diameter pump having the shown performance
characteristics while operating at 1000 rpm. For
peak efficiency, predict the discharge, actual
head rise, and shaft horsepower for this smaller
pump. The working fluid is water at 60 °F
(Munson, 2009).

For a given efficiency the flow coefficient has the same value for a given family
of pumps.

 A centrifugal pump provides a flowrate of 500
gpm when operating at 1750 rpm against a
200-ft head. Determine the pump’s flowrate and
developed head if the pump speed is increased
to 3500 rpm. (Munson, 2009)
 
3
1 2 2
23 3 3 3
1 1 2 2 1 2
Flowrate Coefficient
500
1000
1750 3500
Q
Q
C
D
Q Q Q
Q gpm
D D D D

 

    
 
2 5
1 2 2
22 5 2 5 2 2
1 1 2 2
Head Coefficient
200
800
1750 3500
H
gH
C
D
gH gH H
H ft
D D

 

    

Specific Speed, Suction Specific
Speed
 A useful pi term named specific speed can be
obtained by eliminating diameter D between the
flow coefficient and the head rise coefficient.
 With an analysis similar to that used to obtain
the specific speed pi term, the suction specific
Speed Ss, can be expressed as

 Select a pump to deliver 500 gal/min of water
with a pressure rise of 65 psi. Assume a
rotational speed not to exceed 3600 rpm.
(Potter, 2012)
(Munson, 2009)
 
 
 3
3600 377 /
30
65 144
150
1.94 32.2
500
1.11 / sec
7.48 60
rad s
p
Hp ft
g
Q ft



  
 
  

 

   
3 / 4 3 / 4
377 1.11
0.69
32.2 150
s
p
Q
N
gH

  


 References:
1. Munson B.R., Young D. F., Okishi T. H., and Huebsch W.
W., Fundamentals of Fluid Mechanics, John Wiley and Sons
inc, Sixth Edition, 2009.
2. Potter M. C., Wiggert D. C., and Ramadan B. H., Mechanics of
Fluids, Cengage Learning, Fourth Edition, 2012.
3. Pritchard P. J., Fox and McDonald’s Introduction to Fluid
Mechanics, John Wiley and Sons inc, Eighth Edition, 2011.
4. Volk M., Pump Characteristics and Applications, Taylor &
Francis Group, Second Edition, 2005.

Pump pipeline

More Related Content

What's hot

Similar to Pump pipeline

More from Kimia Store

Recently uploaded

Pump pipeline