コンピュータビジョン最先端ガイド-2 2章3節

1. 第二章 3. ミーンシフトの理論
コンピュータ最先端ガイド勉強会
発表者 : 坪坂 正志
m.tsubosaka(at)gmail.com
2011/1/8 コンピュータ最先端ガイド勉強会 1

2. 本節の内容
• 前半(3.1-3.3)
– カーネル密度推定とミーンシフトの関係について
• 後半(3.4,3.5)
– カーネル幅の推定について(3.4)
– 理論的比較(3.5)
2011/1/8 コンピュータ最先端ガイド勉強会 2

3. 本節の内容
• 前半(3.1-3.3)
– カーネル密度推定とミーンシフトの関係について
• 後半(3.4,3.5)
– カーネル幅の推定について(3.4)
– 理論的比較(3.5)
2011/1/8 コンピュータ最先端ガイド勉強会 3

4. カーネル密度推定とは
• ノンパラメトリックな密度関数の推定法
– Parzen windowsとも呼ばれる
– ここでいうノンパラメトリックとは特定の分布関数を仮定し
ないということ
– 逆にデータが正規分布に従うなどの仮定を入れる方法の
ことをパラメトリックと呼ぶ
[Hastie+2009] The elements of
Statistical Learning : Data Mining,
Inference, and Prediction (2nd
edition)より
2011/1/8 コンピュータ最先端ガイド勉強会 4

5. カーネル密度推定の式
• データ点の集合 : = * | = 1, … , +
• カーネル関数, その幅
• カーネル密度推定による分布関数
1
= (, , )
=1
• データ点を中心とおいた幅hのカーネル関数の和と
して表される
2011/1/8 コンピュータ最先端ガイド勉強会 5

6. 本節で扱うカーネルのタイプについて
• 球対称な形のカーネルについて考える
• プロファイルと呼ばれる ≥ 0上の有界で区分的に
連続な非負値の関数()を用いて
− 2
• , , = ( )の形のカーネルを扱う
• カーネル密度推定の式
1 − 2
= ( )
=1
2011/1/8 コンピュータ最先端ガイド勉強会 6

7. カーネルの例
カーネルの名前 プロファイル関数
正規分布カーネル 1
exp(− )
2
Epanechnikovカーネル 1 − (0 ≤ ≤ 1)
0 ( > 1)
フラットカーネル 0 ≤ ≤ 1
0 ( > 1)
ここで正規化項の部分はミーンシフトの場合は比の形となる
ので簡単のため1とおく
2011/1/8 コンピュータ最先端ガイド勉強会 7

8. カーネル密度関数の勾配
• カーネル密度関数の勾配を求める
1 − 2
= +2 − ′ ( )
=1
• ここで = −′()とおくと
1 − 2
= +2 − ( )
=1
− 2
1 − 2
= × −
+2 − 2
=1
2011/1/8 コンピュータ最先端ガイド勉強会 8

9. カーネル密度関数の勾配
• カーネル密度関数の勾配を求める
1 − 2
= +2 − ′ ( )
=1
• ここで = −′()とおくと
1 − 2
= +2 − ( )
=1
− 2
1 − 2
= × −
+2 − 2
=1
ミーンシフトの更新式
2011/1/8 コンピュータ最先端ガイド勉強会 9

10. カーネル密度関数の勾配
• 整理すると
2
() = 2 () () −
• これから
2
=
2 ()
ミーンシフトのステップ 密度関数の勾配方向
• なお、このようなミーンシフトカーネルGに対応する
カーネルKをカーネルGのシャドウカーネルと呼ぶ
2011/1/8 コンピュータ最先端ガイド勉強会 10

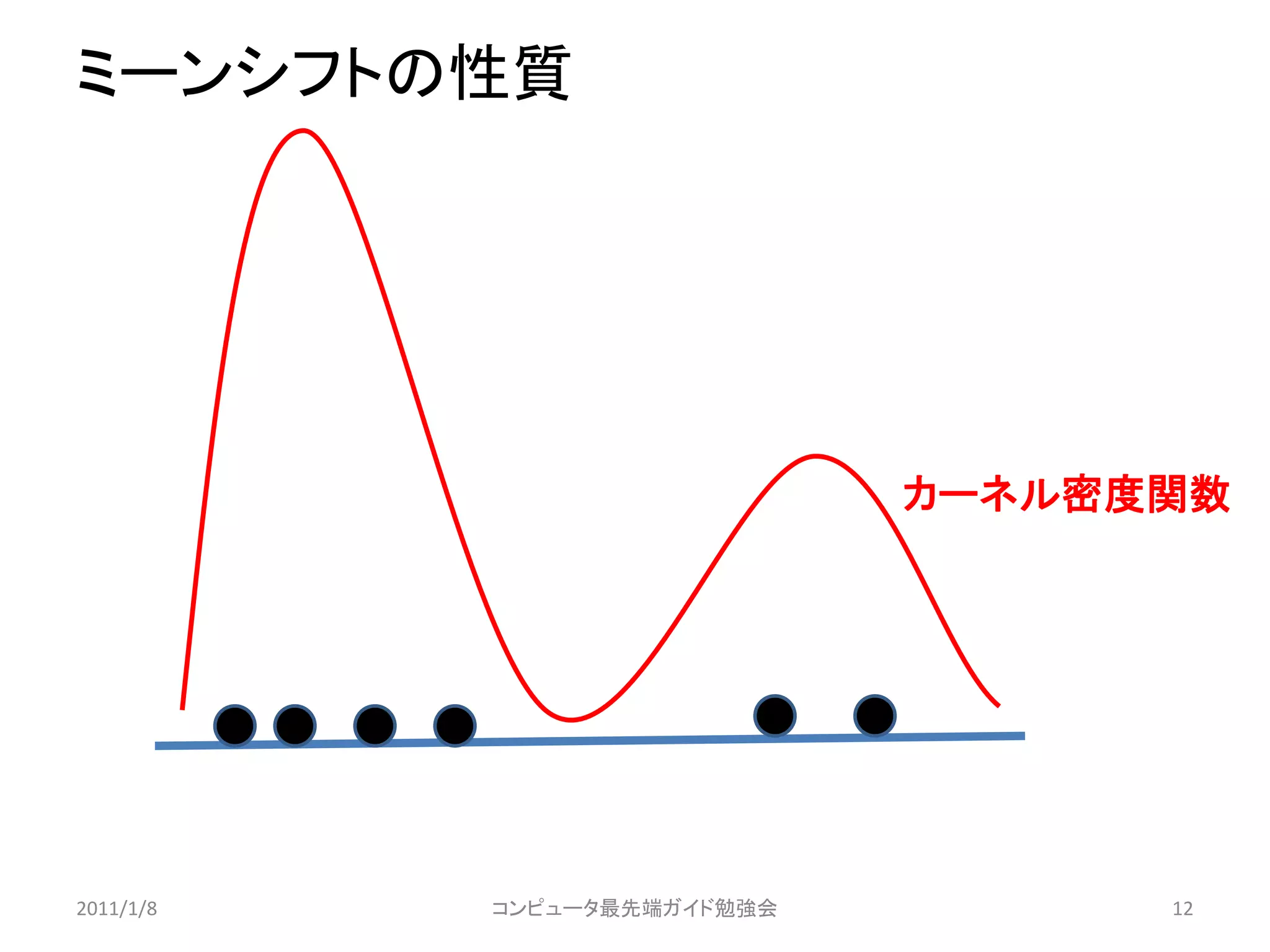
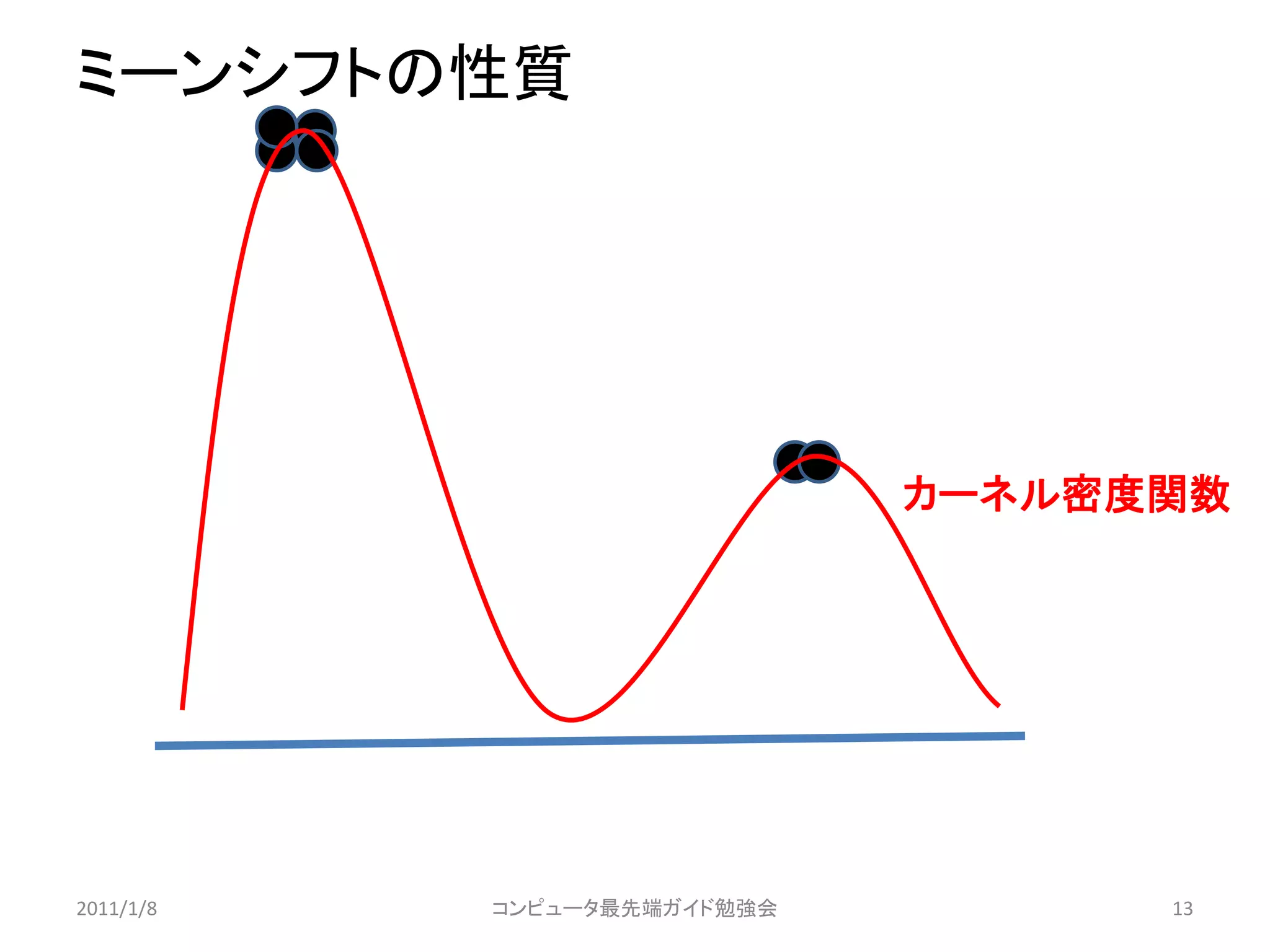
11. ミーンシフトの性質
• ミーンシフトにおける最頻値探索はカーネル密度関
数上の最頻値に収束する
– なおミーンシフトで使うカーネルと密度関数推定で使う
カーネルは一般には同じではない、ただし正規分布カー
ネルにおいては同じ。
• ステップ幅を自動設定する最急降下法とみなすこと
もできる
– 密度の小さいところではステップ幅が大きく、密度の高い
最頻値に近いところではステップ幅が小さくなる
– これにより効率的で振動のない収束が得られることが推
測できる
2011/1/8 コンピュータ最先端ガイド勉強会 11

12. ミーンシフトの性質
カーネル密度関数
2011/1/8 コンピュータ最先端ガイド勉強会 12

13. ミーンシフトの性質
カーネル密度関数
2011/1/8 コンピュータ最先端ガイド勉強会 13

14. ミーンシフトの収束定理
• ミーンシフトの収束性については以下の定理が知ら
れている[15,32]
ミーンシフトの収束定理[15 Theorem 1]
• カーネルKが凸状で単調減尐するプロファイルkを持つ
ならば, KをシャドウとするカーネルGを用いたミーンシ
フトによる最頻値探索は, Kによる密度関数上の初期
値近傍の最頻値点に必ず収束する。
2011/1/8 コンピュータ最先端ガイド勉強会 14

15. 本節の内容
• 前半(3.1-3.3)
– カーネル密度推定とミーンシフトの関係について
• 後半(3.4,3.5)
– カーネル幅の推定について(3.4)
– 理論的比較(3.5)
2011/1/8 コンピュータ最先端ガイド勉強会 15

16. 本節の内容
• 前半(3.1-3.3)
– カーネル密度推定とミーンシフトの関係について
• 後半(3.4,3.5)
– カーネル幅の推定について(3.4)
– 理論的比較 (3.5)
2011/1/8 コンピュータ最先端ガイド勉強会 16

17. カーネル幅推定の重要性
• 例えばミーンシフトを用いたクラスタリングではクラ
スタ数を与える必要はなく、データに応じてクラスタ
数が決まる
• クラスタ数はカーネルの幅に大きく作用される
But…
• 適切なカーネル幅を選ぶ必要がある
2011/1/8 コンピュータ最先端ガイド勉強会 17

18. カーネル幅による影響
• カーネル幅の値により、カーネル密度推定の結果が
大きく変わる
– 幅が小さすぎるとすべての点でピークをとるようになる
– 幅が大きすぎると単峰の分布となる
= 5
= 0.05 = 0.5
2011/1/8 コンピュータ最先端ガイド勉強会 18

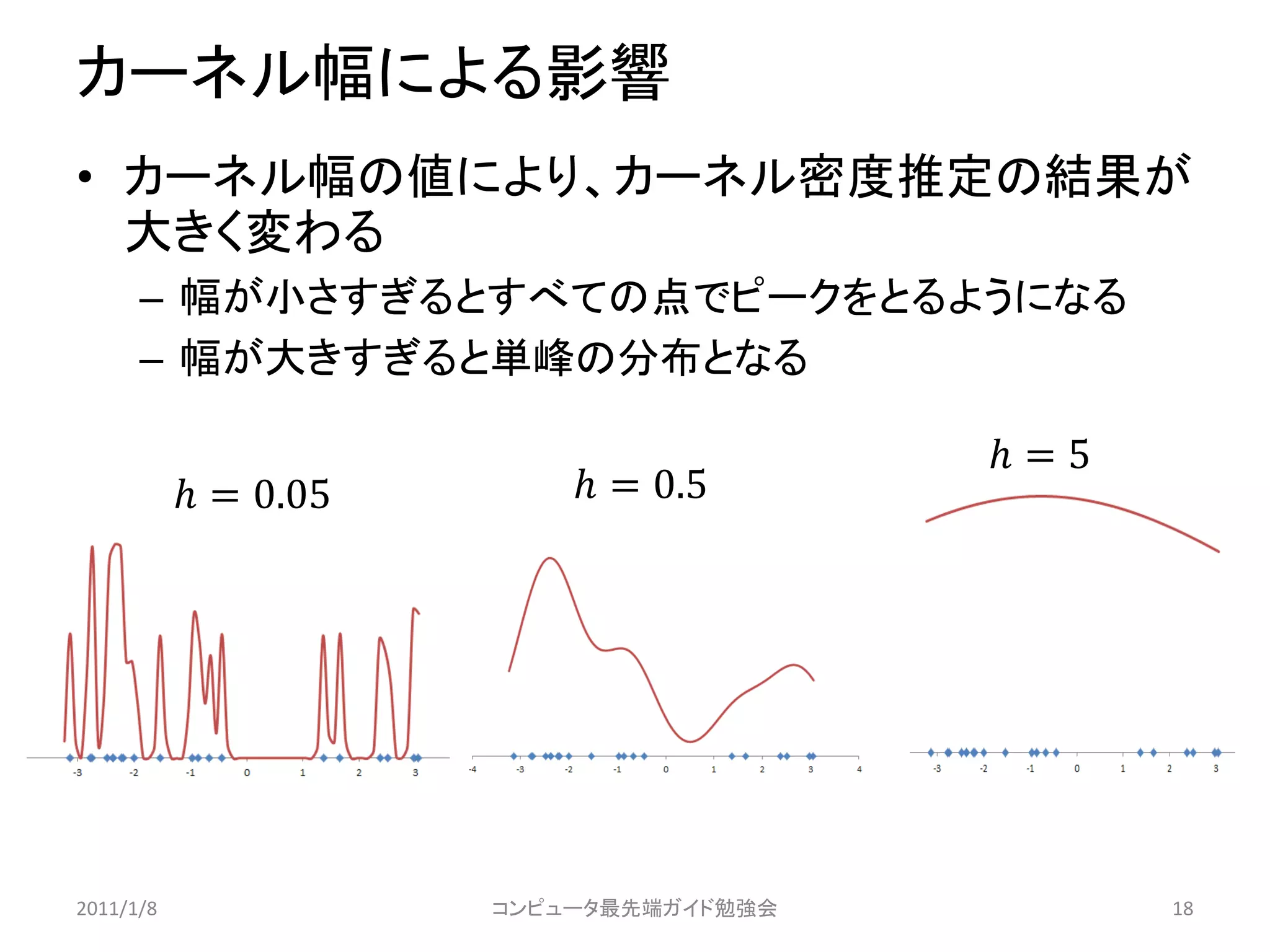
19. カーネル幅の推定手法に関する研究
• 統計的手法[46,49,58,64]
– カーネル密度推定の誤差を最小化する
– 未知の真の密度関数()とそのカーネル推定 ()の誤
差を何らかの基準 ISE(integrated squared error),
MISE(mean ISE), AMISE(asymptotic MISE)で最小化する
• ミーンシフトベクトルに基づく手法
– ミーンシフトベクトルの長さを最大化[17]
• 高次微分や非等方カーネル幅行列への拡張[37]
– SIFT法の基礎である自動スケール決定法とも関係[33]
• 安定性を指標とした手法
– クラスタ解析の安定性を最適化[23]
– ピークにガウス関数を当てはめ、結果が最も安定となる幅
を採用する手法[11,35,37,38]
2011/1/8 コンピュータ最先端ガイド勉強会 19

20. 応用利用
• 応用に関する研究
– サンプルデータから求めたカーネル幅を使って、階層的ク
ラスタリングに応用している[63]
– 安定な画像領域分割アルゴリズムへの応用[65]
• 実装に当たって
– これらの研究結果はあるが、問題の設定次第で最適化
の定義が違うため、カーネル幅の導出を行う決定的な方
法はない
– 問題によってはGUIやシステムの他部位の出力を使った
値決めも考えられる
2011/1/8 コンピュータ最先端ガイド勉強会 20

21. 本節の内容
• 前半(3.1-3.3)
– カーネル密度推定とミーンシフトの関係について
• 後半(3.4,3.5)
– カーネル幅の推定について(3.4)
– 理論的比較(3.5)
2011/1/8 コンピュータ最先端ガイド勉強会 21

22. ロバスト推定との関係
• データとして{3,4,5,8000}が与えられたとする
– 単純に平均をとると2003になる
– 8000を外れ値としてみなし、平均は4という方が妥当
– 4の近傍で注目する領域幅が十分に小さければ実際の平
均4を推定できる
– カーネル法を適応することにより外れ値(outlier)の影響を
減らせる
• また上のデータは最頻値が複数存在する分布から
データが生成されているとみなすことができる
– このような分布をマルチモーダルな分布と呼ぶ
• このようなデータからノイズに頑強に元の分布を求
める手法をロバスト推定と呼ぶ
2011/1/8 コンピュータ最先端ガイド勉強会 22

23. ロバスト推定との関係
• 最尤推定
– 元の分布のモード位置に対して尤度分布(1 , … , |)
の最尤推定はカーネル密度推定関数の最大化と理解で
きる
• M推定法
– 原点が最小値で単調増加する対象非負関数を用いて、
(| − |)を最小とするようにを最適化
– を適切に選ぶことにより、外れ値に頑強な推定ができる
– これは実はカーネル密度関数の符号を逆にしたものと一
致する
2011/1/8 コンピュータ最先端ガイド勉強会 23

24. ミーンシフト公式の理論的導出
• 前半説明したカーネル密度推定式の微分を元にし
た導出の他にも導出がある
• 界面関数最適化(variational bound optimization)の
理論に基づくもの[21,50]
– 目的関数の二次下界関数の最適化の枠組みを使い、
ミーンシフトとNewton法が同値であることが示せる[21]
– 5節で扱う最大事後確率推定への拡張へも使われている
2011/1/8 コンピュータ最先端ガイド勉強会 24

25. 高速化について
• ミーンシフトの計算においてはナイーブに行うと
(2 )かかるためコストが大きい(:データ数,
: 繰り返し数)ので高速化の手法がいくつか提案さ
れている
• 高速ガウス変換を応用したもの[68]
– カーネル和を高速に求める
• EMアルゴリズムとの同値性を利用したもの[4,6]
• Half-quadratic最適化の枠組みを使ったもの[71]
2011/1/8 コンピュータ最先端ガイド勉強会 25

26. 非線形空間への拡張
• ミーンシフトの収束先が球面状に載っているという
制約をつけたいとかを考えたとき、単純に平均をと
ると球面に載るとは限らない
– データが三次元空間にあるのではなく非線形な二次元空
間状にあると考えるとうまくいく
– Riemann多様体への拡張[51-55,59]
– 一般的な距離空間への拡張(medoidshift)[47]
– 詳しくは5節で触れる
2011/1/8 コンピュータ最先端ガイド勉強会 26