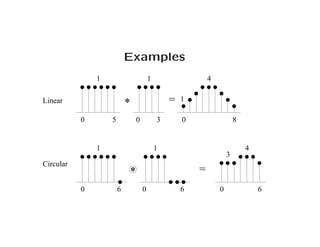
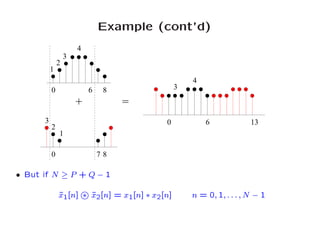
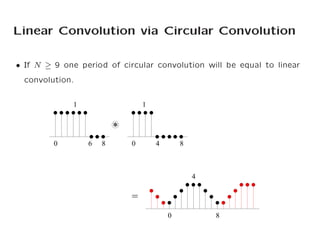
The document discusses different types of convolution operations on signals. Convolution involves taking one signal, flipping and shifting it, then multiplying it sample-by-sample with another signal and summing the results. Linear convolution produces a output signal that is the sum of the two input signal lengths minus one. Circular convolution treats the signals as if they repeat periodically, producing a periodic output signal of the same period. It can approximate linear convolution if the period is long enough. The discrete Fourier transform (DFT) and its fast version, the FFT, can also be used to efficiently compute circular convolution by multiplying the signals' Fourier transforms.

1. Convolution
The familiar one:
y[n℄ =
1
X
k= 1
x1[k℄ x2[n k℄
Leave the rst signal x1[k℄ un hanged
For x2[k℄:
{ Flip the signal: k be omes k, giving x2[ k℄
{ Shift the ipped signal to the right by n samples:
k be omes k n
x2[ k℄ ! x2[ (k n)℄ = x2[n k℄
Carry out sample-by-sample multipli ation and sum the resulting
sequen e to get the output at time index n, i.e. y[n℄

2. What happens to periodi signals?
Suppose both signals are periodi
x1[n + N℄ = x1[n℄
x2[n + N℄ = x2[n℄
Then x1[k℄ x2[n0 k℄ will also be periodi (with period N)
For ea h value of n0 we get a di erent periodi signal (periodi ity
is N in all ases)
jy[n℄j will be either 0 or 1

3. Cir ular Convolution
y[n℄ ?
=
N 1
X
k=0
~
x1[k℄ ~
x2[n k℄
y[n℄ is periodi with period N
n k an be repla ed by hn kiN (n k mod N)
Cir ular Convolution: ~
y[n℄ = ~
x1[n℄ ~
x2[n℄
~
y[n℄ def
=
N 1
X
k=0
~
x1[k℄ ~
x2[hn kiN℄ n = 0; 1; : : : ; N 1

4. Examples
0
1
0
1
=
4
0
6 6
*
0 3
0 5
4
1
0 8
=
1
1
3
6
Linear
Circular
*

5. Relationship Between Linear and Cir ular
Convolution
If x1[n℄ has length P and x2[n℄ has length Q, then x1[n℄ x2[n℄ is
P + Q 1 long (e.g., 6 + 4 1 = 9)
N max (P; Q). In general
~
x1[n℄ ~
x2[n℄ 6= x1[n℄ x2[n℄ n = 0; 1; : : : ; N 1
Cir ular onvolution an be thought of as repeating the result of
linear onvolution every N samples and adding the results (over one
period)

6. Example ( ont'd)
=
0 8
4
0 8
6
1
2
2
1
+
3
4
0
3
6
7
3
13
But if N P + Q 1
~
x1[n℄ ~
x2[n℄ = x1[n℄ x2[n℄ n = 0; 1; : : : ; N 1

7. Linear Convolution via Cir ular Convolution
If N 9 one period of ir ular onvolution will be equal to linear
onvolution.
0 8
6
1
*
=
4
0 8
0 8
4
1

8. Convolution Using the DFT
A very eÆ ient algorithm, alled the Fast Fourier Transform (FFT),
exists for omputing the DFT
Sin e x1[n℄ x2[n℄ ! X1[k℄ X2[k℄, it is more eÆ ient to ompute
ir ular onvolution using the FFT as follows:
y[n℄ = DFT 1
( X1[k℄ X2[k℄ )