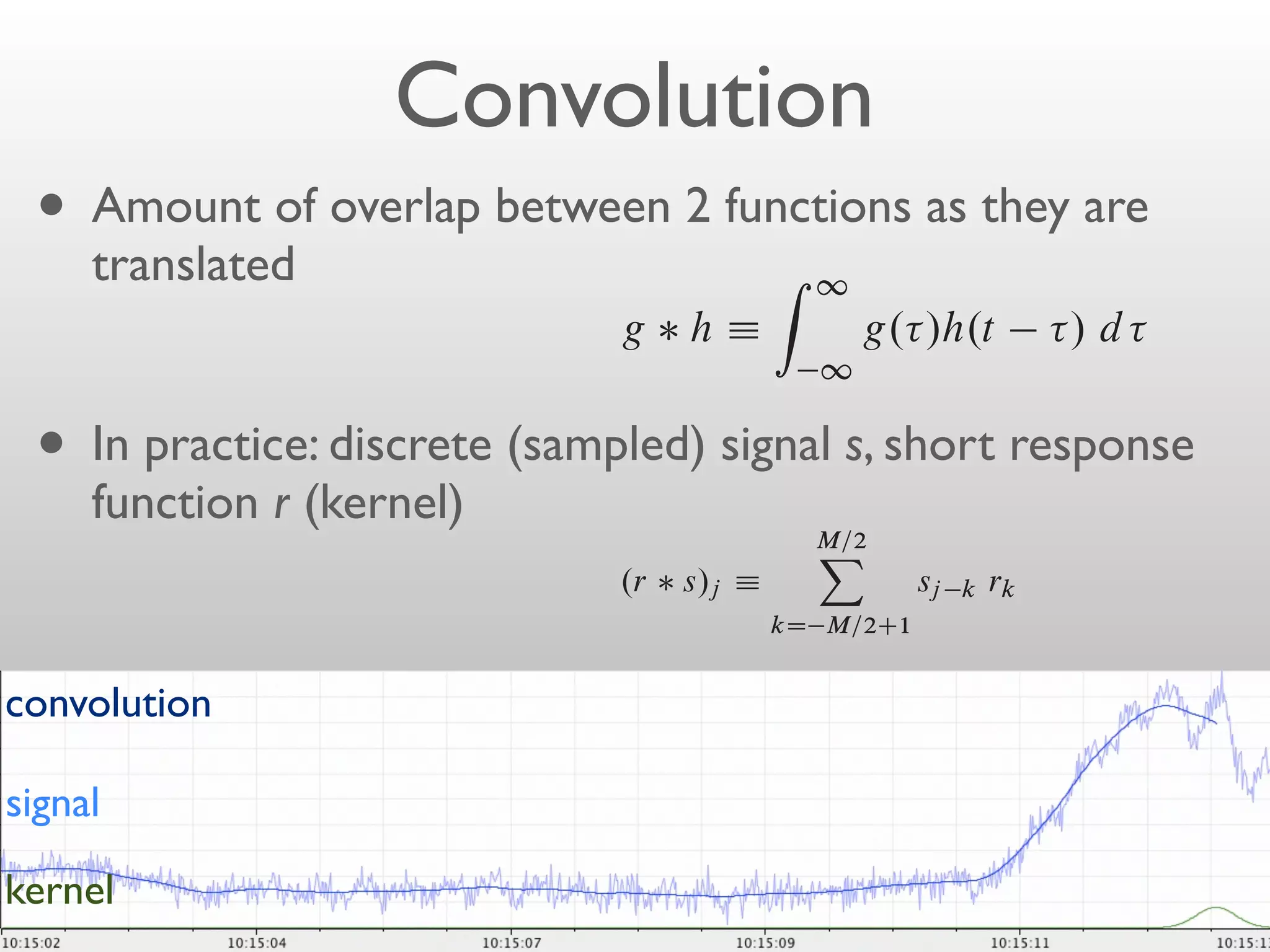
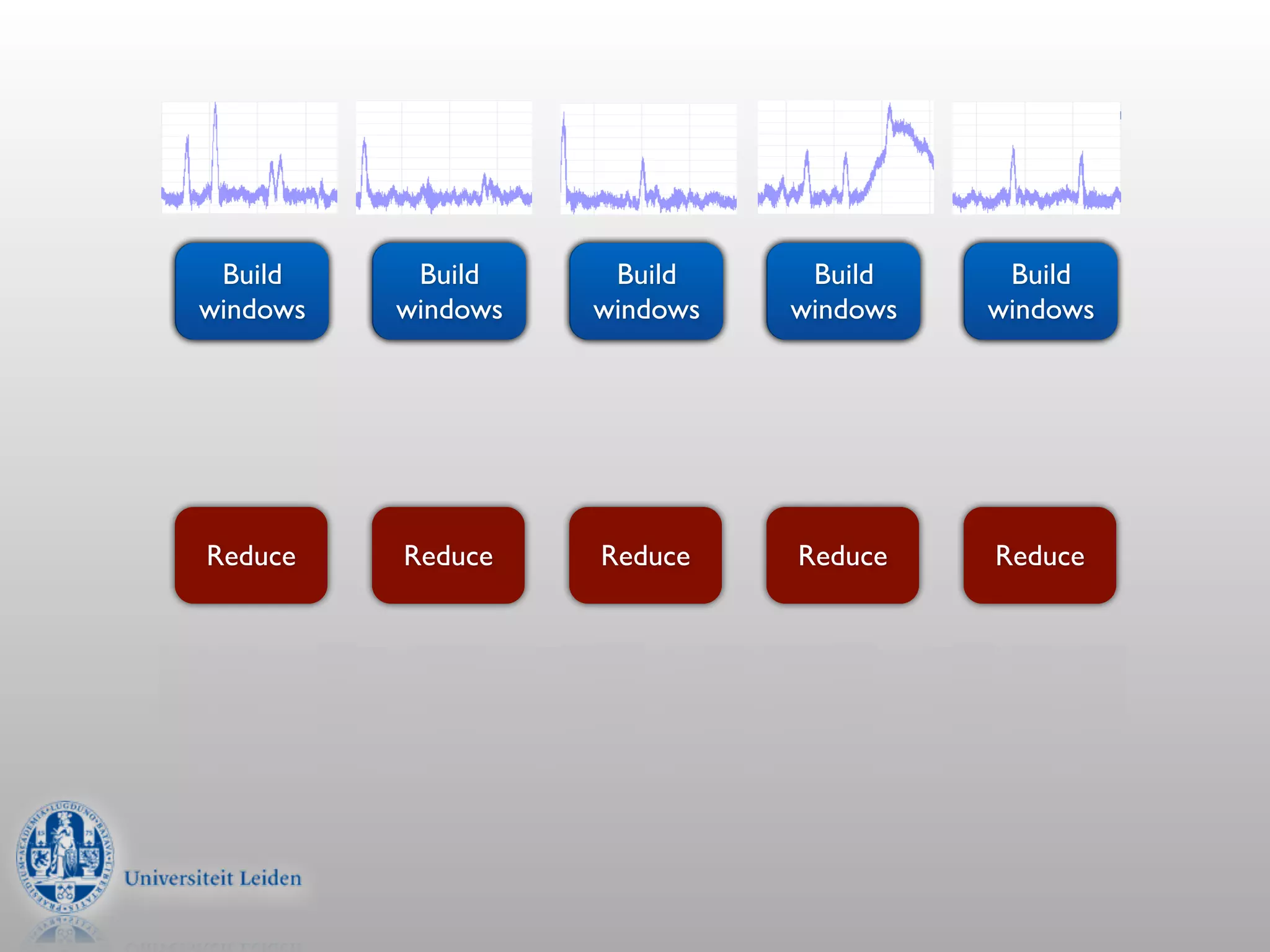
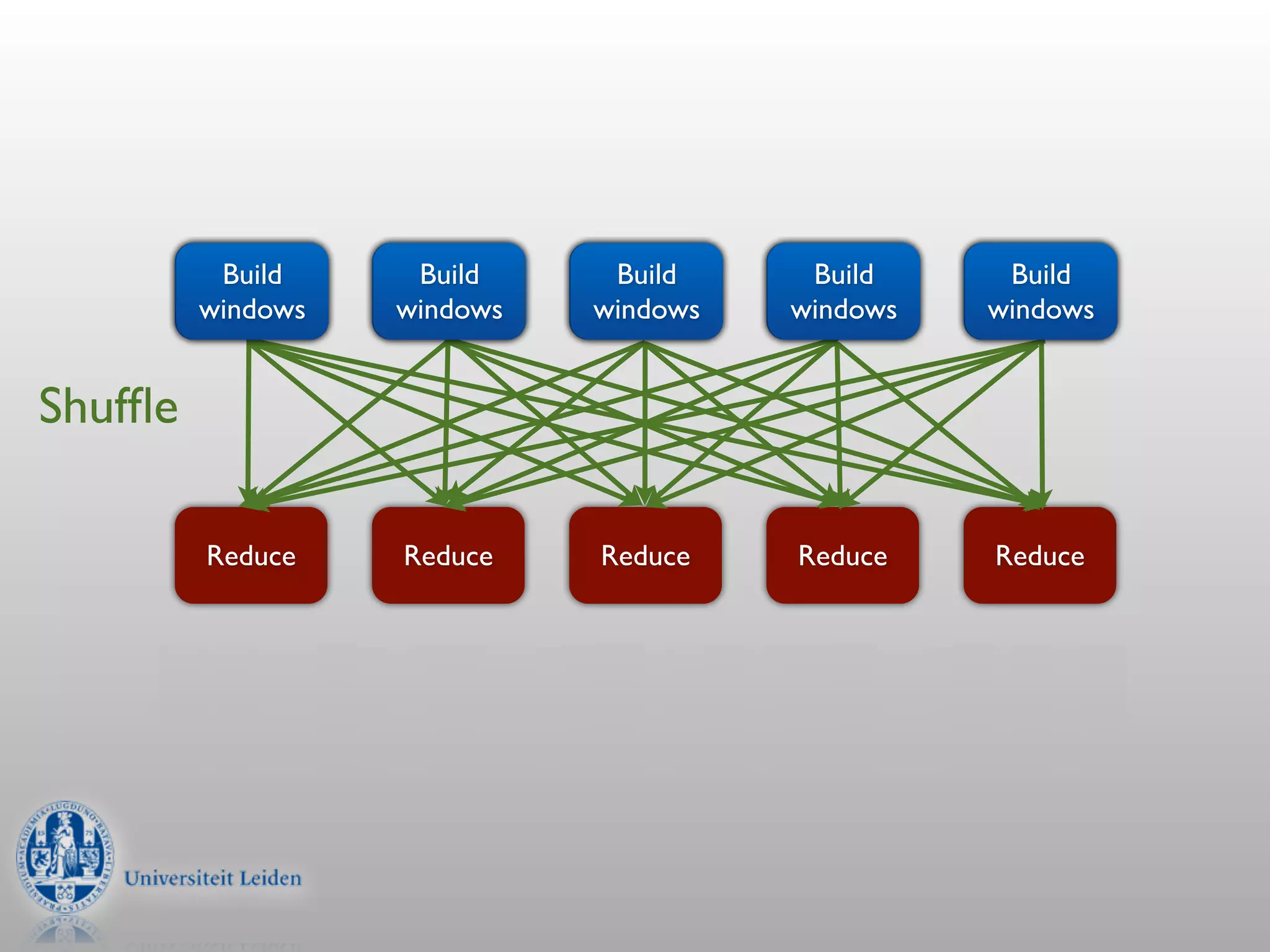
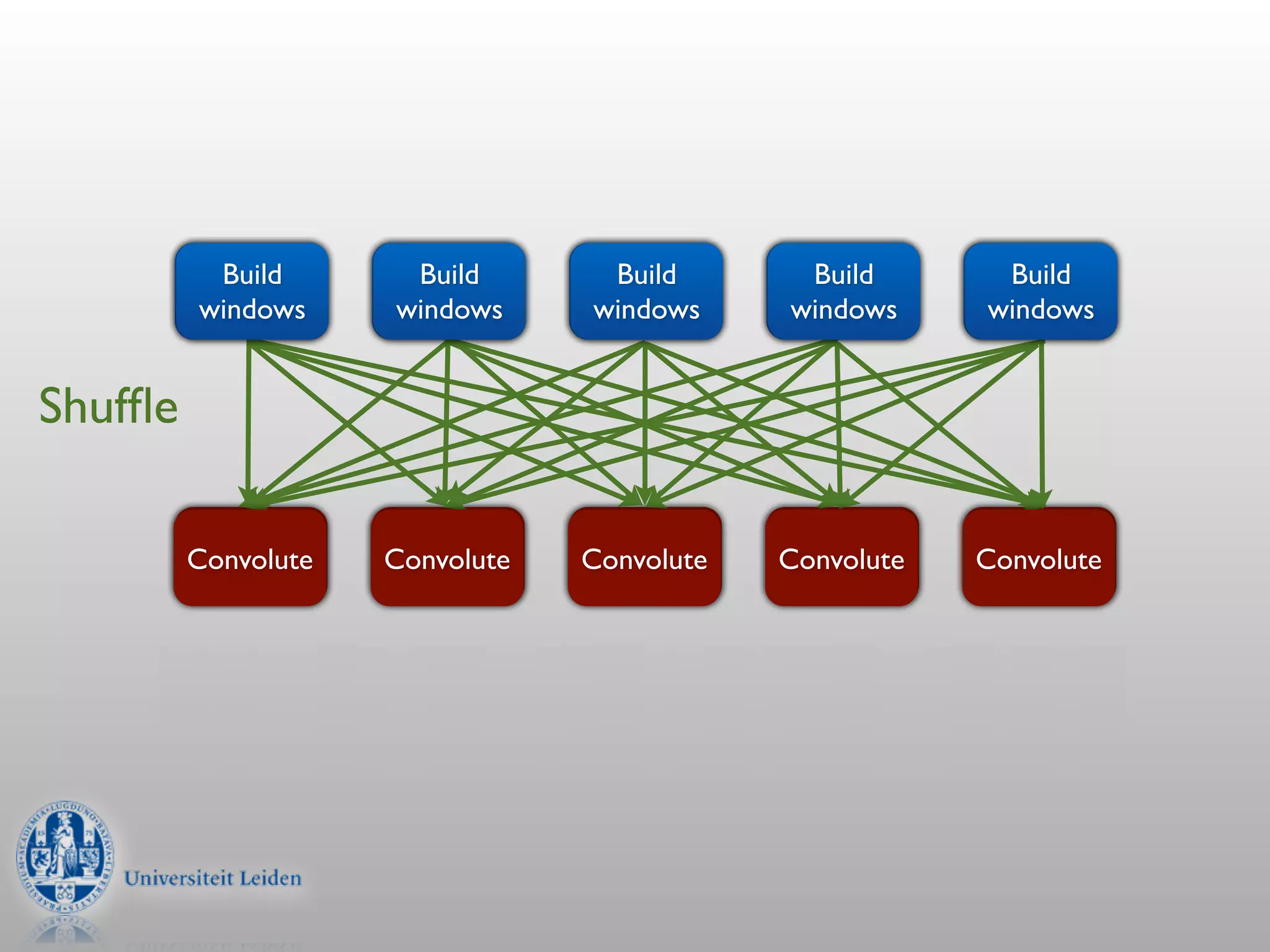
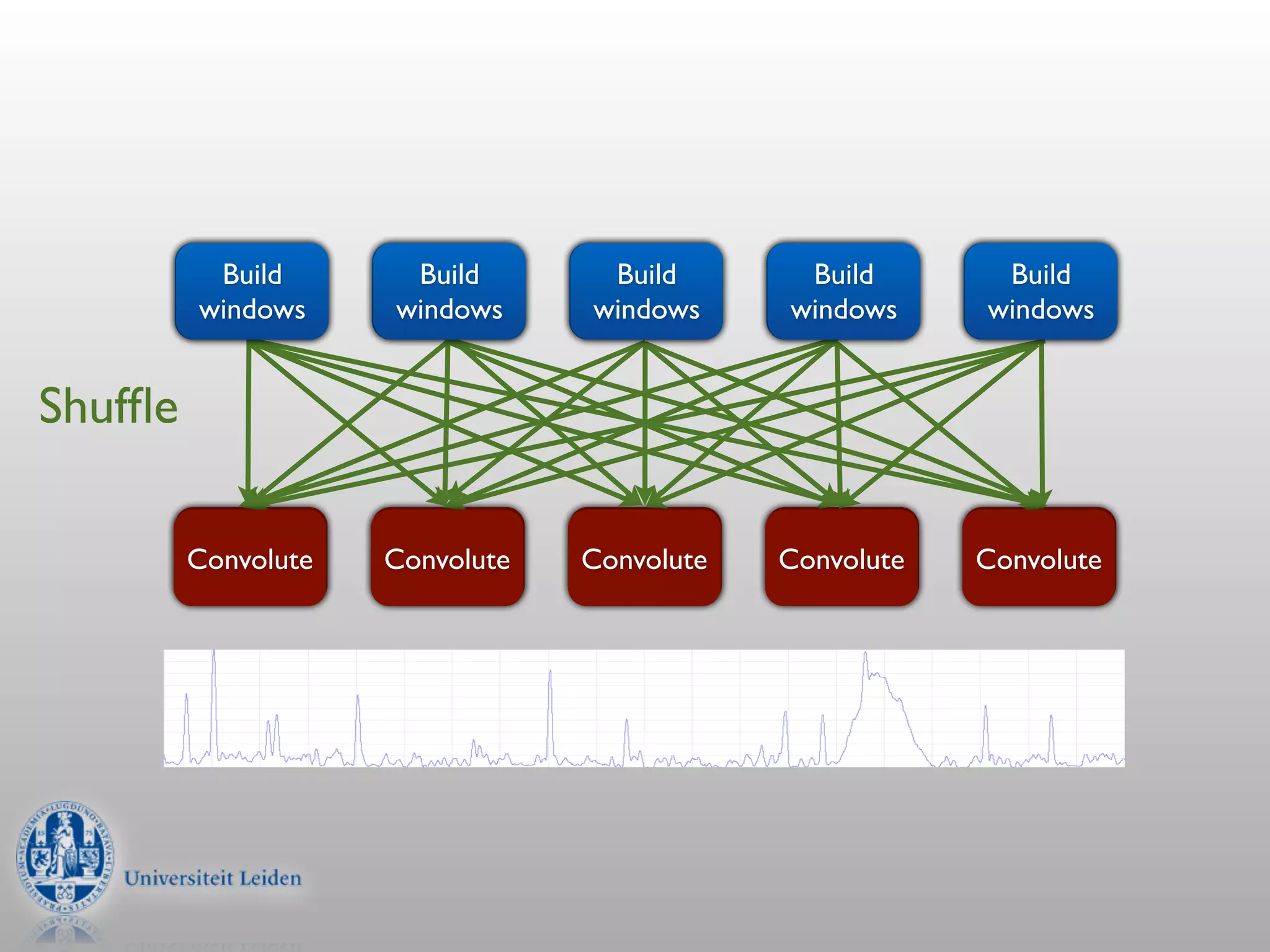
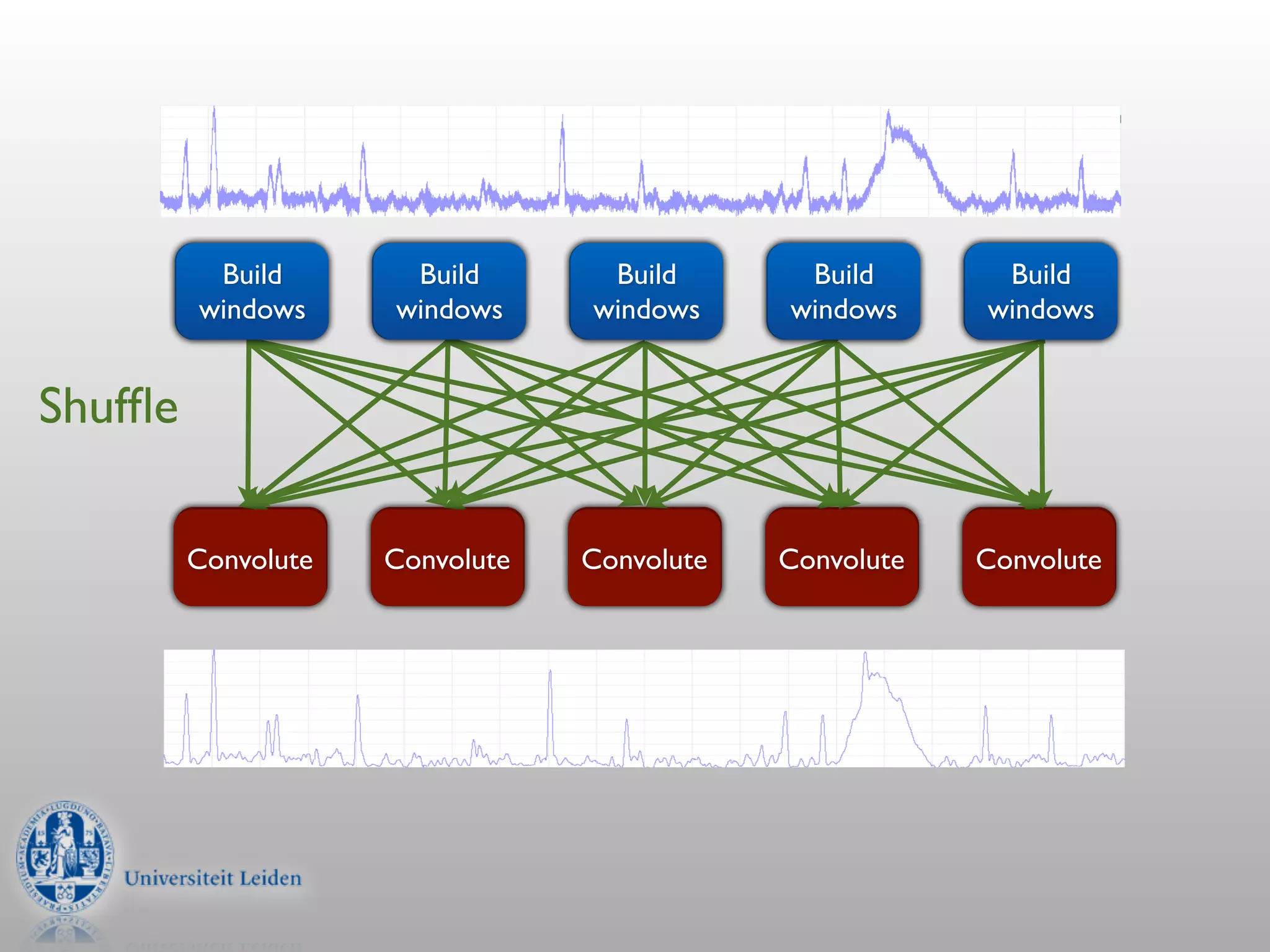
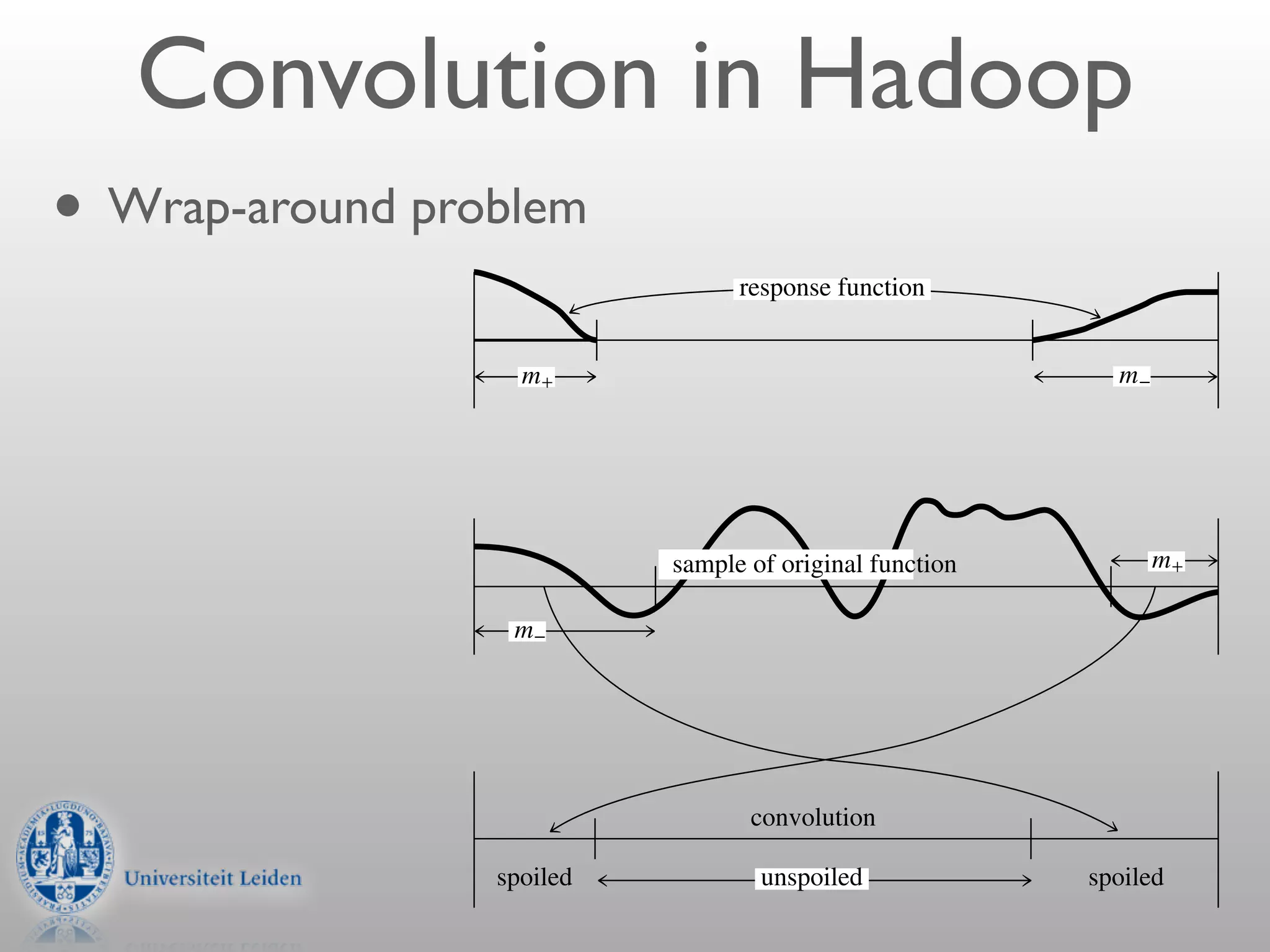
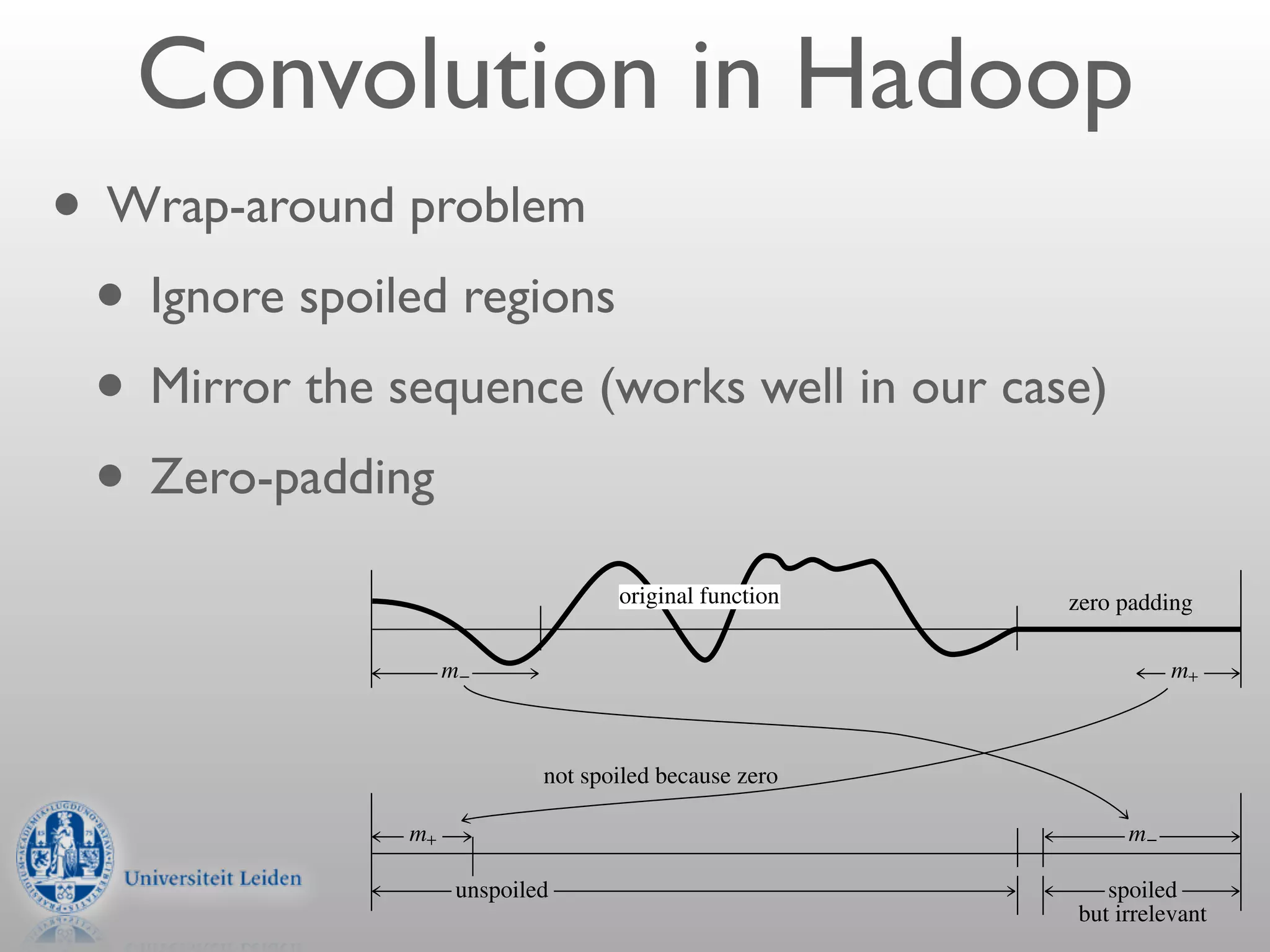
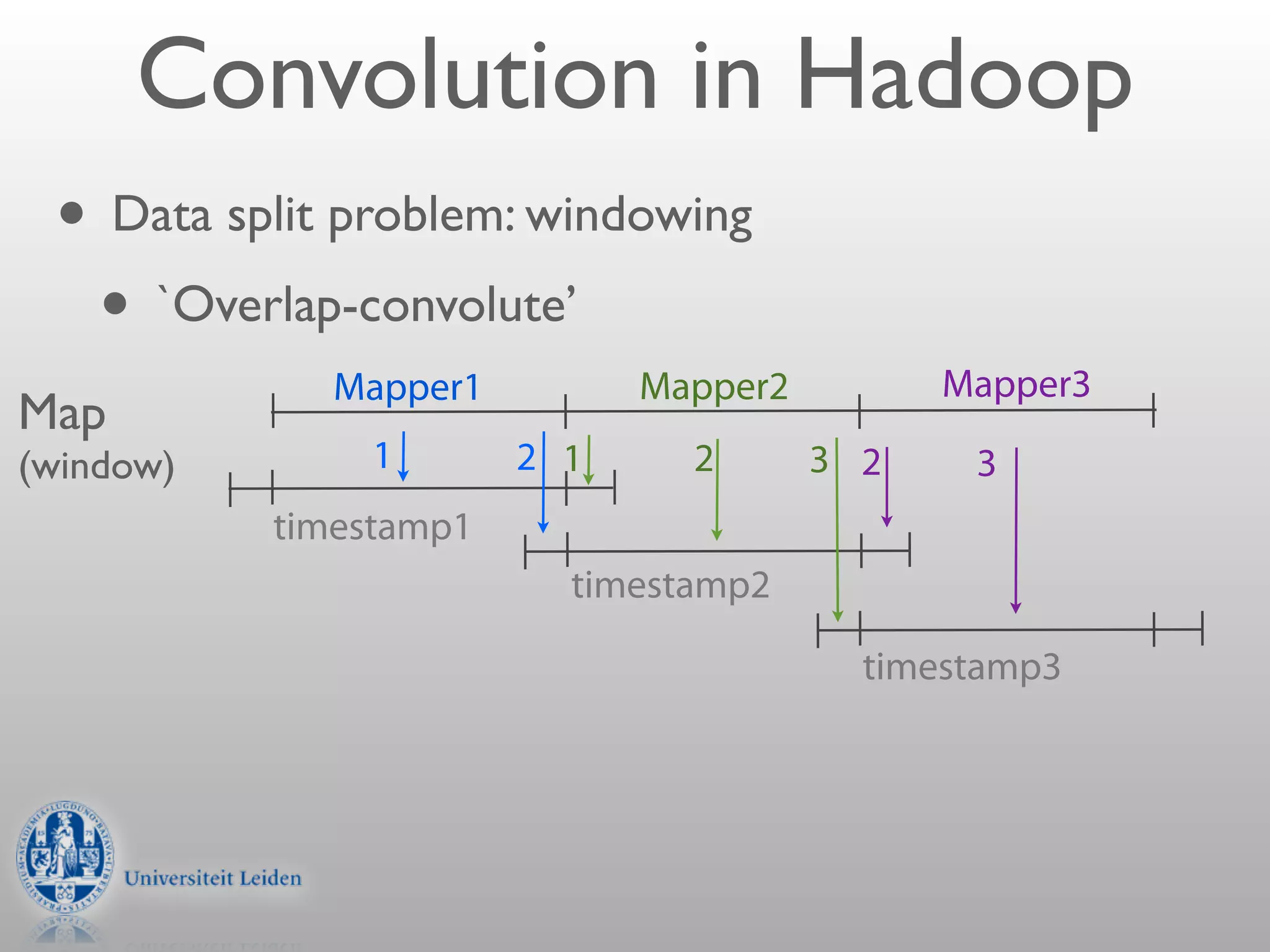
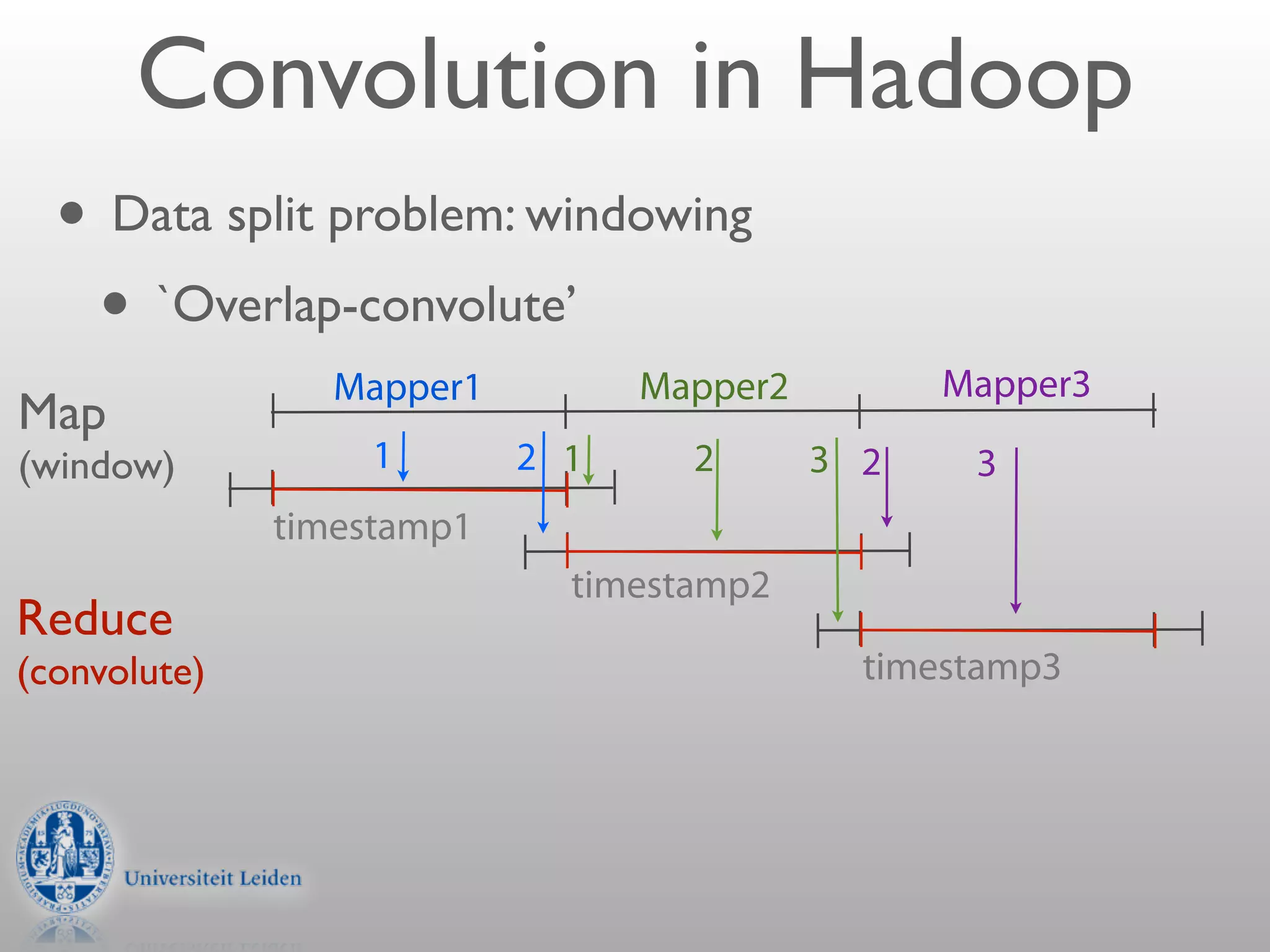
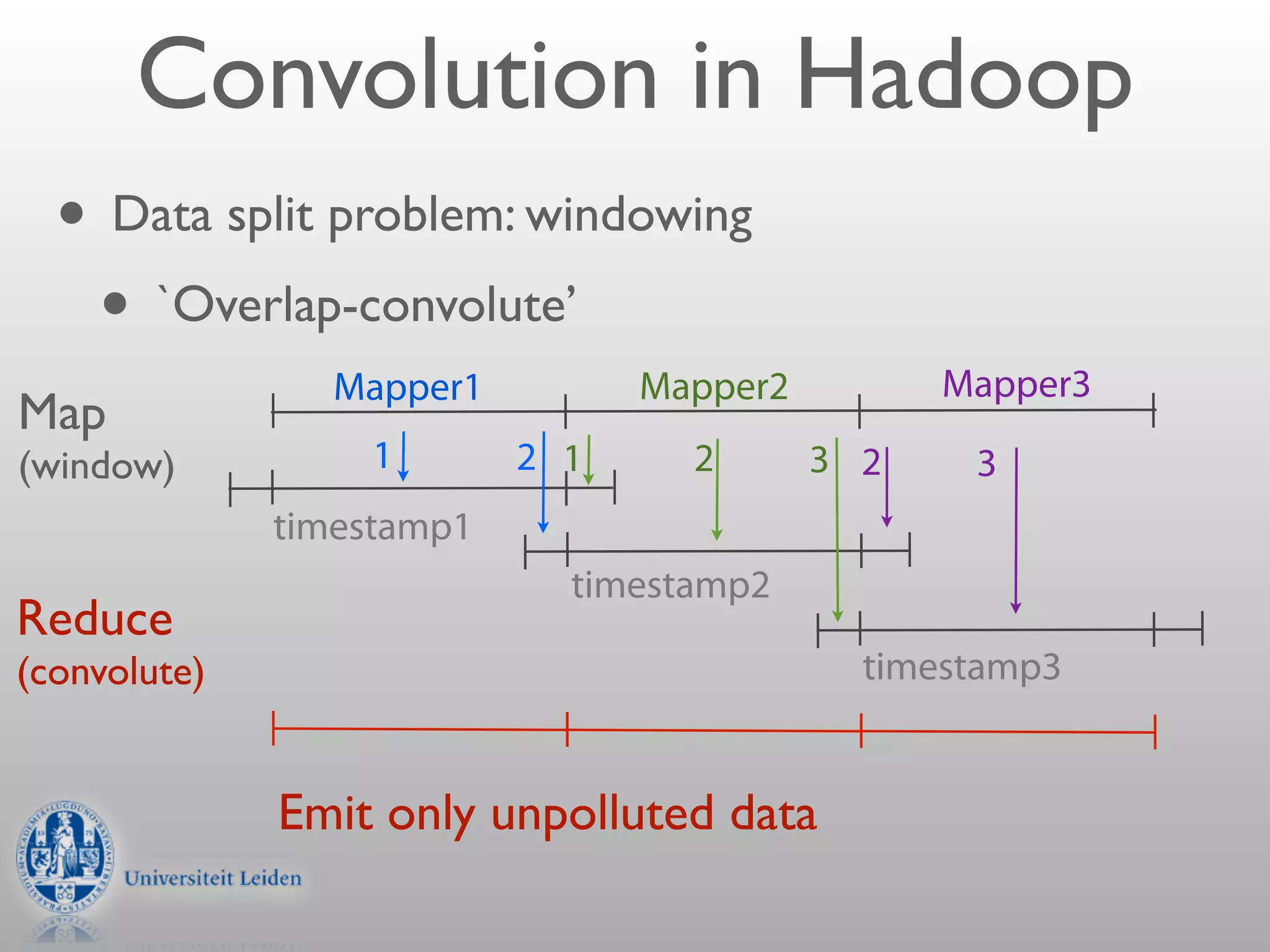
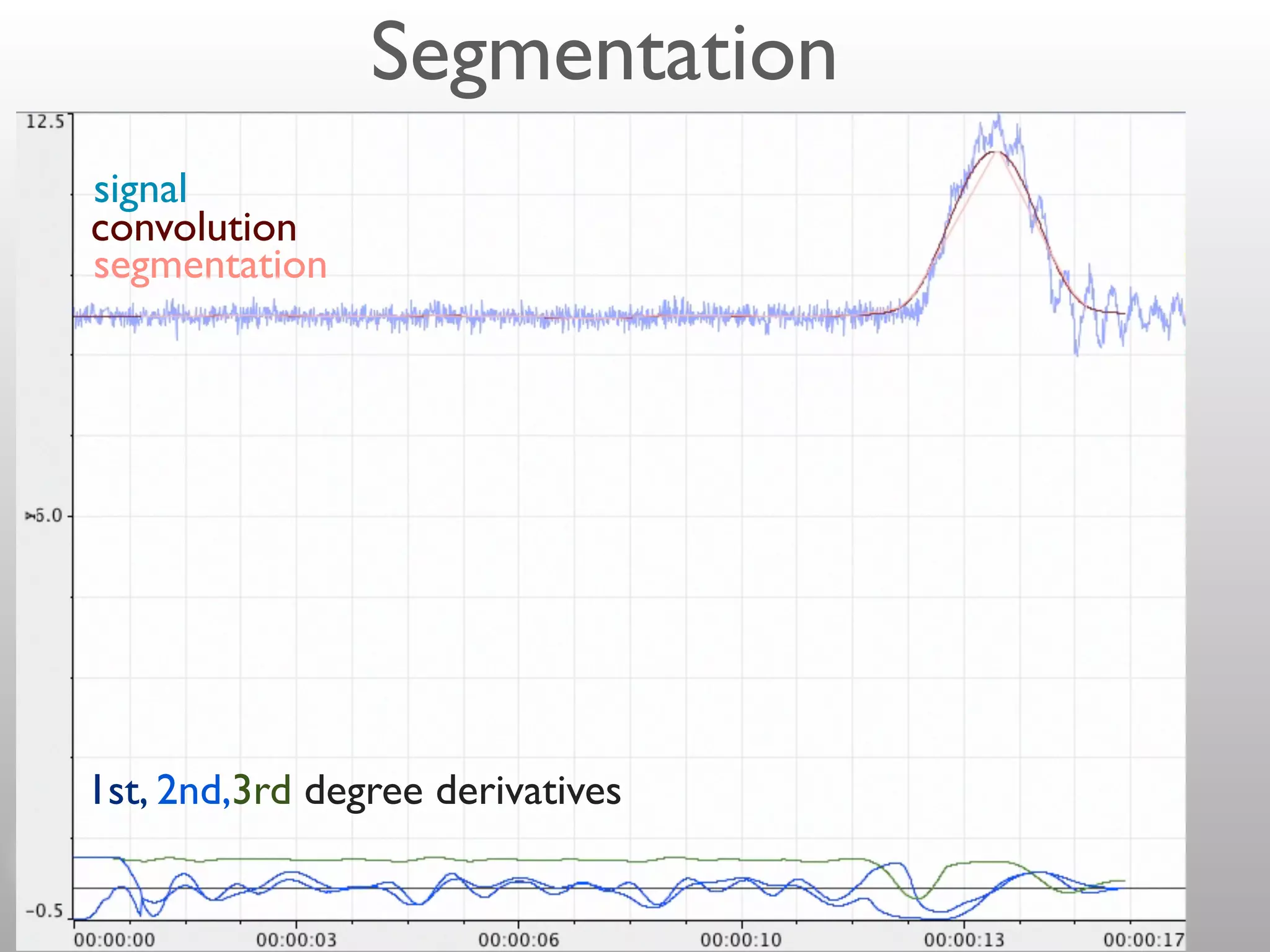
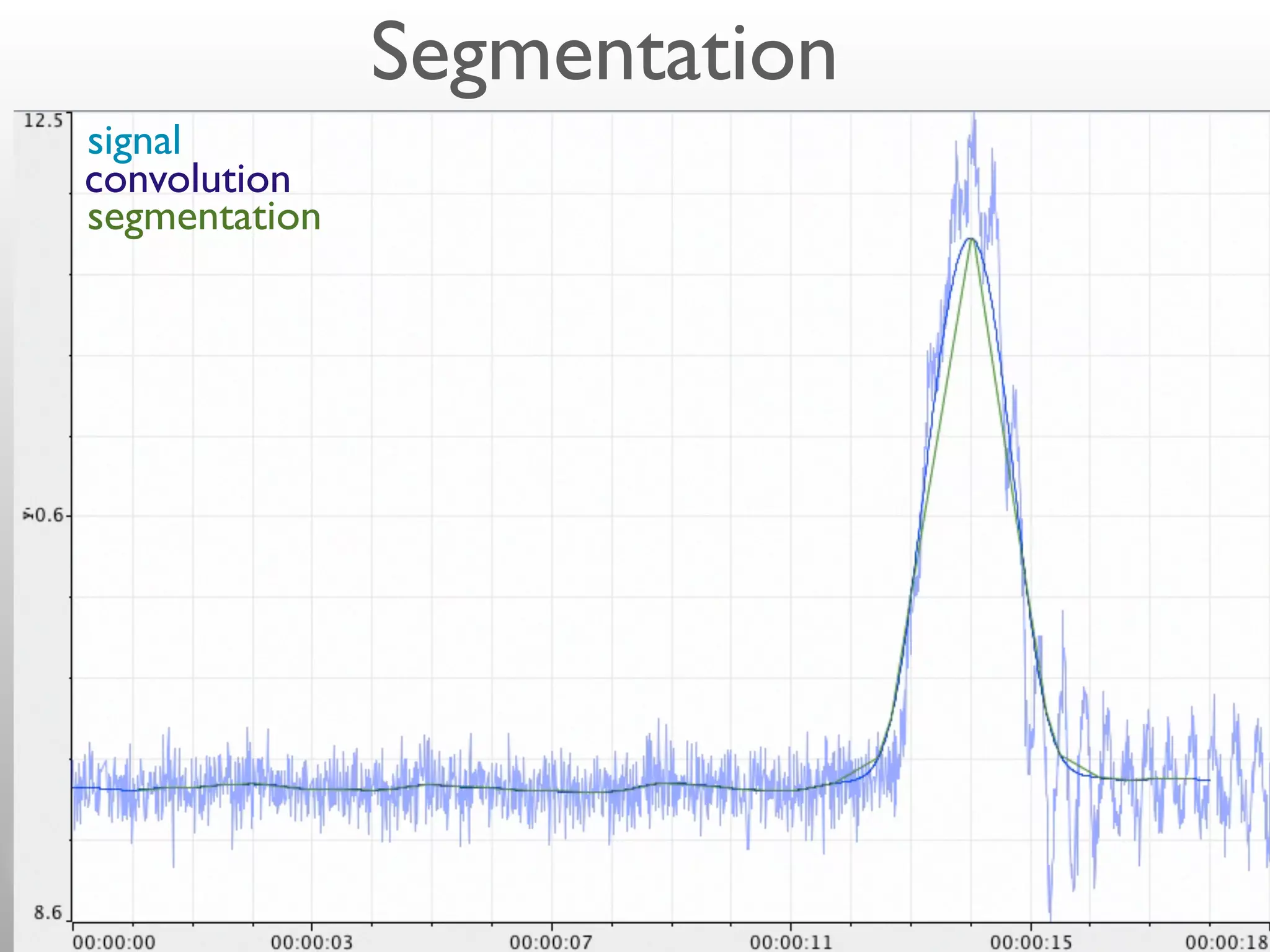
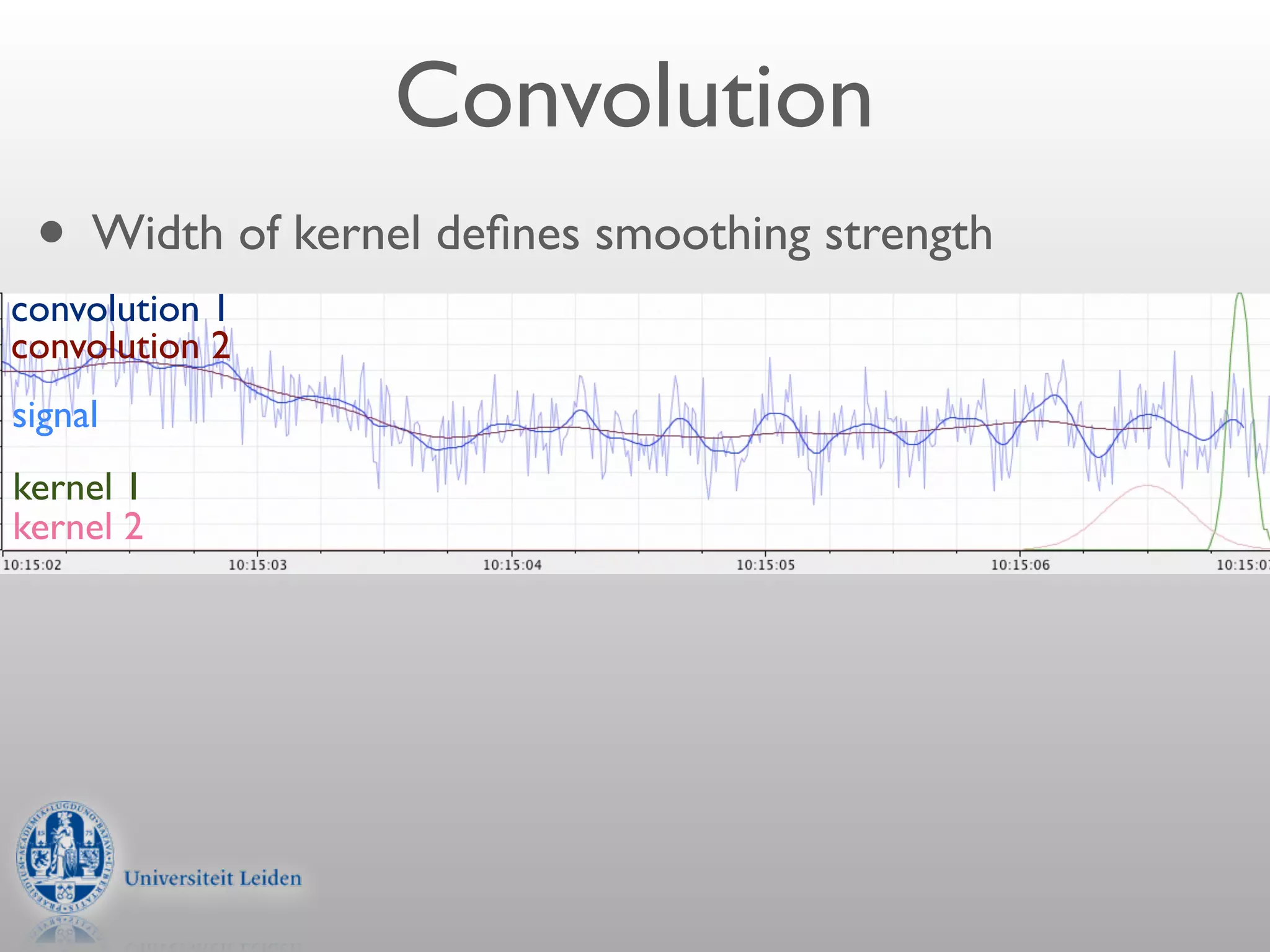
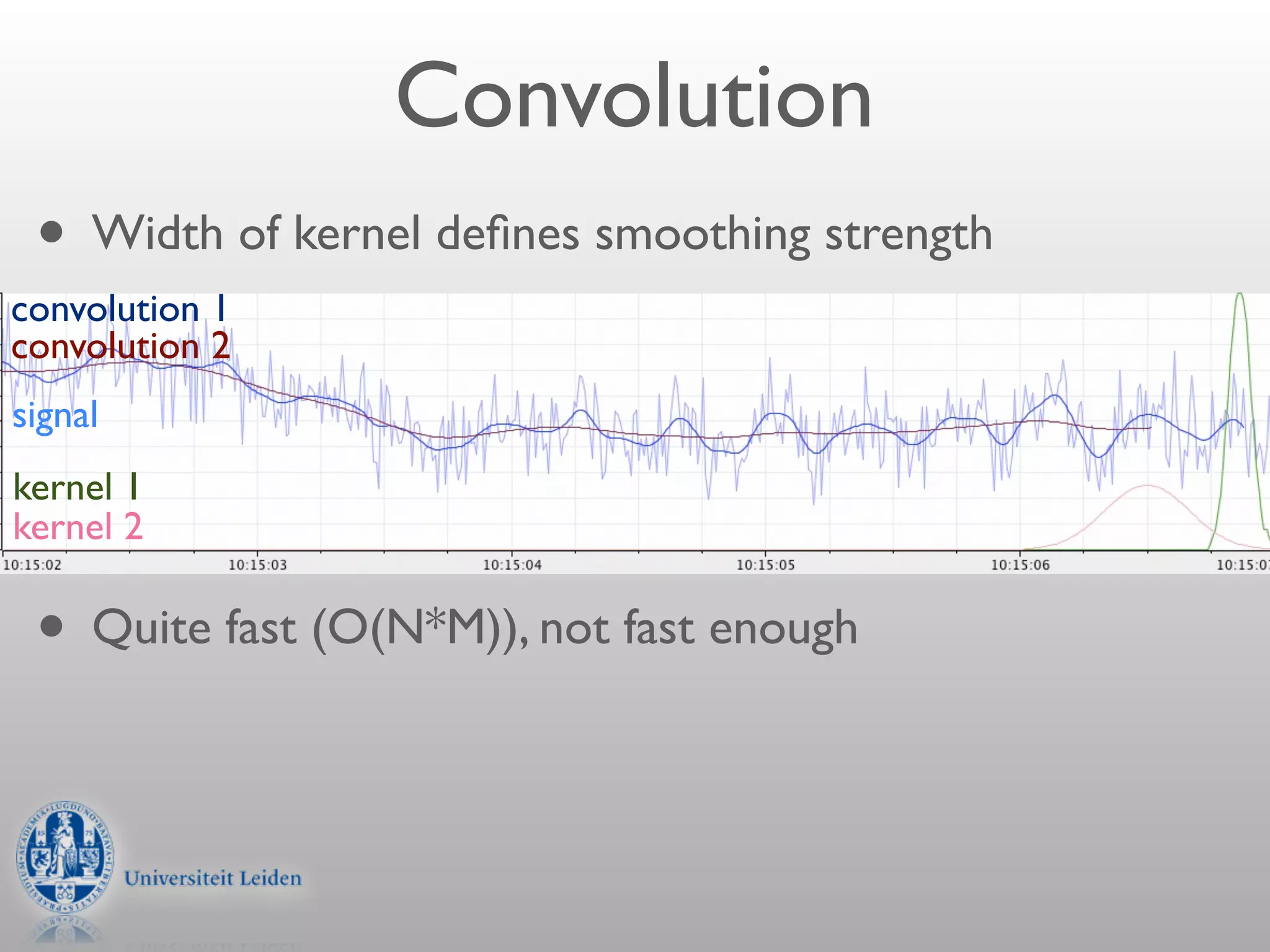
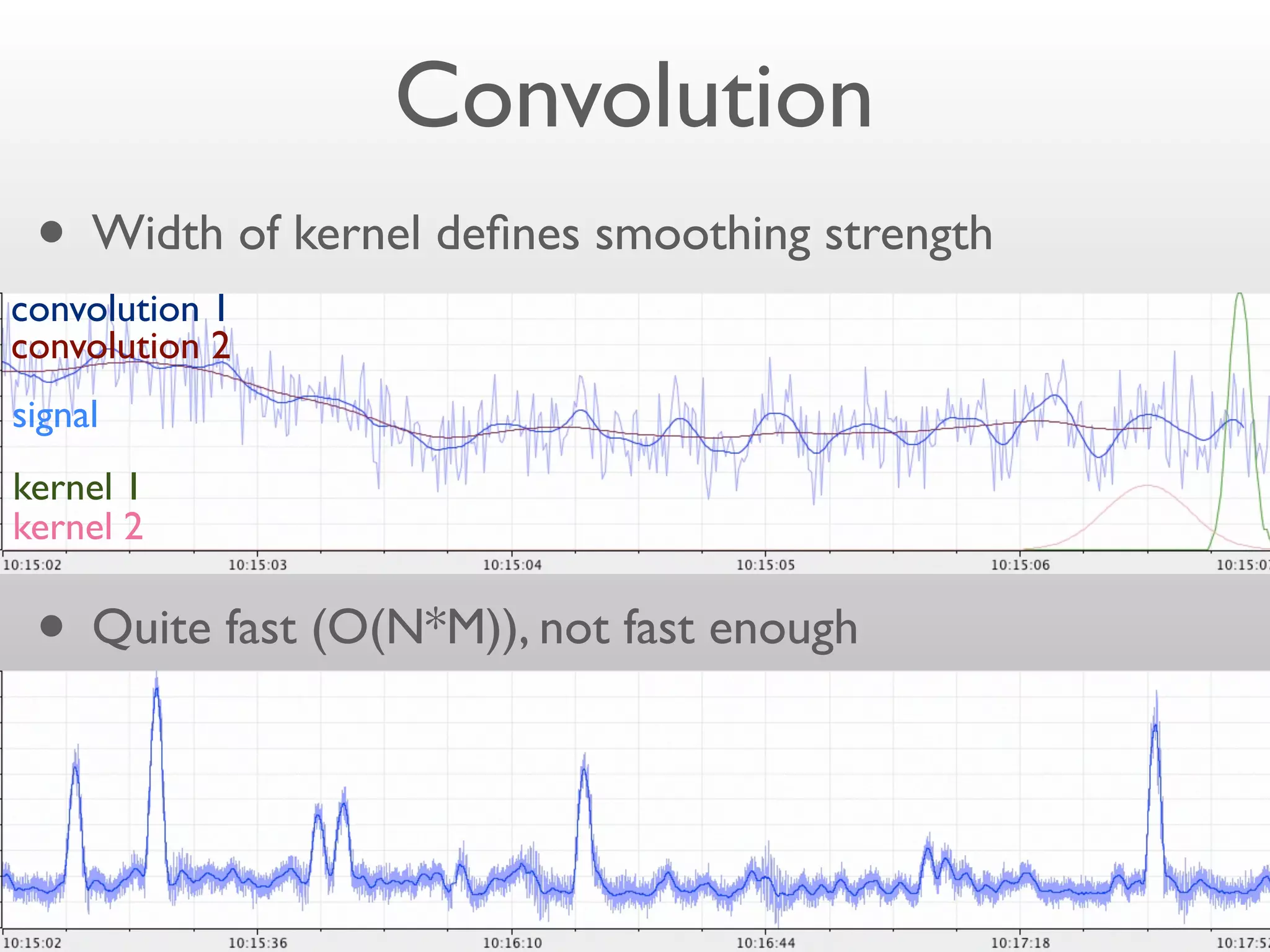
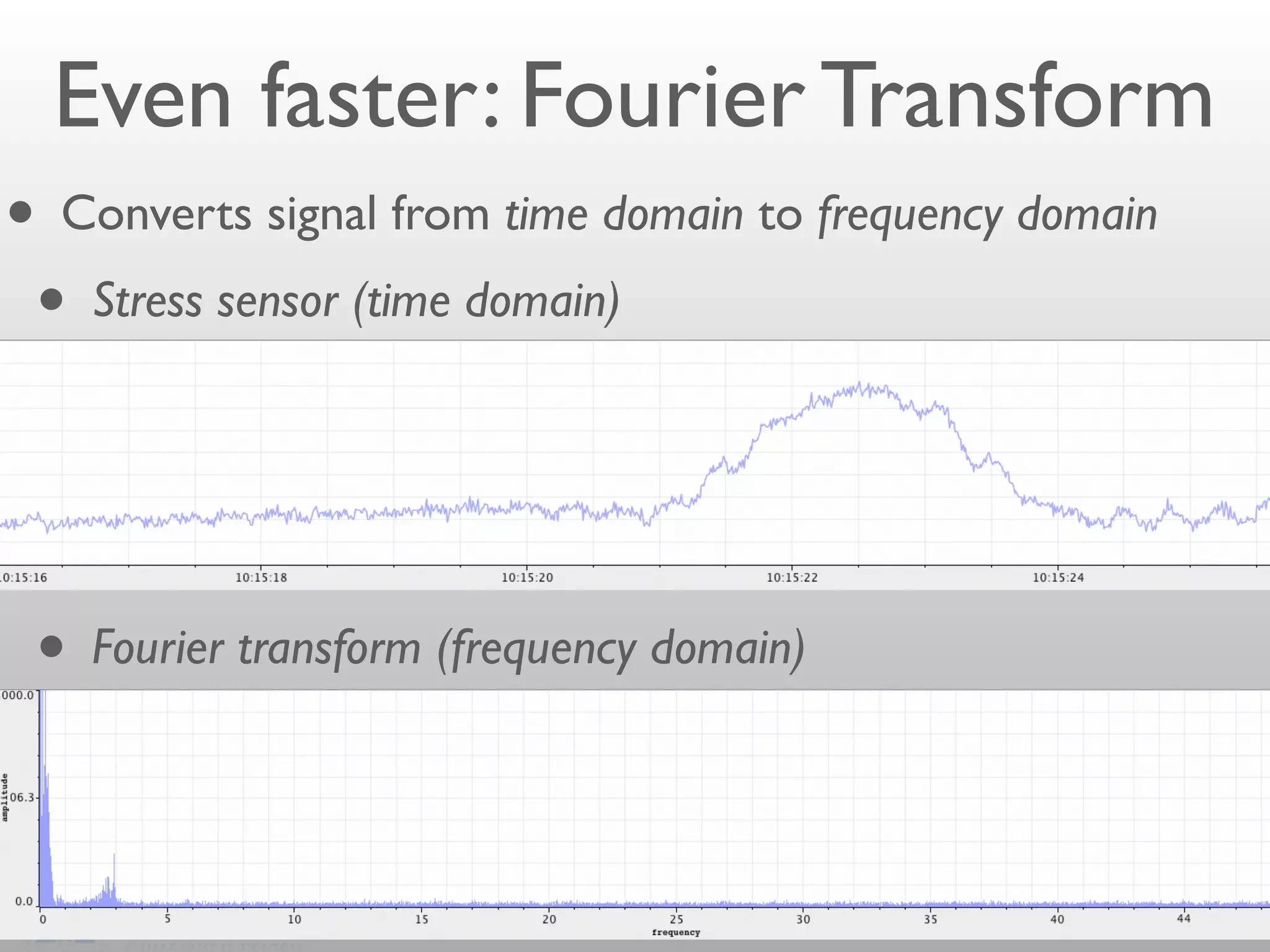
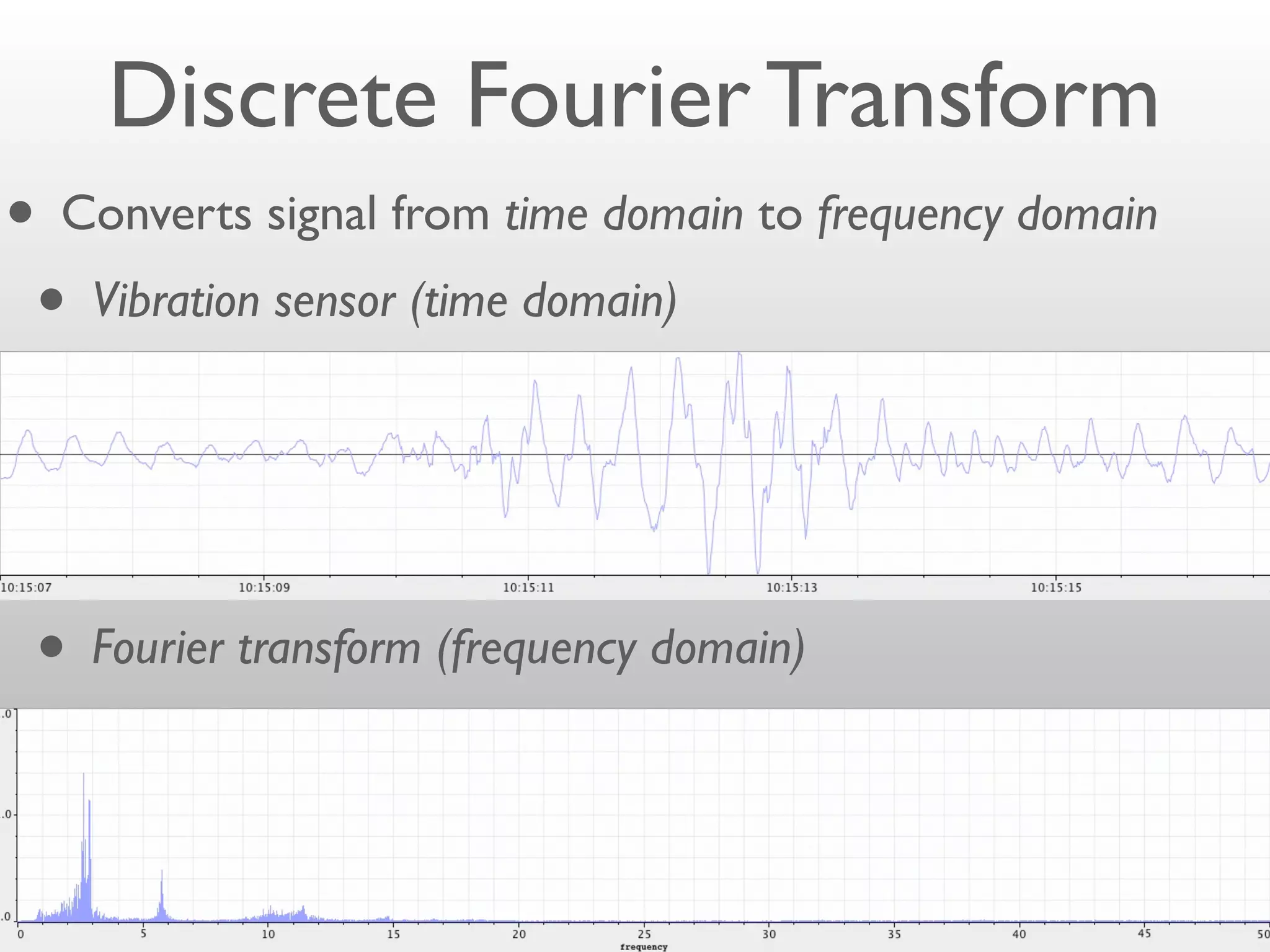
- Convolution involves multiplying two signals together to produce a smoothed output signal. - The width of the convolution kernel defines the strength of smoothing. - Convolution can be performed efficiently in Hadoop using parallel discrete Fourier transforms, which convert signals to the frequency domain where convolution becomes simple multiplication.

1. 2 if0 t
h.t / e ” H.f f / frequency shiftin
Figure 13.1.2. Convolution of discretely sampled functions. Note how the response function fo
0
Convolution
times is wrapped around and stored at the extreme right end of the array rk .
With two functions h.t / and g.t /, and their corresponding
H.f / and G.f /, we can form two combinations of special intere
• Amount of Example: Abetween g functions 1asbyall other rk ’s equal
of the two functions, denoted 2 h, is r0 D and
overlap response function with defined they are
translatedjust the identity filter. Convolution Zis1signal with this response functio
is of a
identically the signal. Another example the response function with r14 D
hÁ
all other rk ’s equal to zero.gThis produces convolved output / d is the inpu
g. /h.t that
1
multiplied by 1:5 and delayed by 14 sample intervals.
• In
Evidently, we have just described in words the following definition of
practice: discrete a(sampled) theof finitedomain M : that g h D
Note convolution witha function in signal s,duration and
that g h is response function time short response
that the function g h is one member of a simple transform pair,
function r (kernel)
M=2
X
g h ” G.f /H.f /
.r s/j Á convolution theorem
sj k rk
kD M=2C1
In other words, the Fourier transform of the convolution is just
individual Fourier transforms.is nonzero only in some range M=2 < k Ä
If a discrete response function
The correlation of two functions, denoted Corr.g; h/, is defi
where M is a sufficiently large even integer, then the response function is
finite impulse response (FIR), and its duration is M . (Notice that we are defi
Z 1
as the number of nonzero values of rk ; these values span a time interval of
Corr.g; circumstances the C t /h. / d is the
sampling times.) In most practicalh/ Á g. case of finite M
interest, either because the response really has1finite duration, or because we
a

2. 2 if0 t
h.t / e ” H.f f / frequency shiftin
Figure 13.1.2. Convolution of discretely sampled functions. Note how the response function fo
0
Convolution
times is wrapped around and stored at the extreme right end of the array rk .
With two functions h.t / and g.t /, and their corresponding
H.f / and G.f /, we can form two combinations of special intere
• Amount of Example: Abetween g functions 1asbyall other rk ’s equal
of the two functions, denoted 2 h, is r0 D and
overlap response function with defined they are
translatedjust the identity filter. Convolution Zis1signal with this response functio
is of a
identically the signal. Another example the response function with r14 D
hÁ
all other rk ’s equal to zero.gThis produces convolved output / d is the inpu
g. /h.t that
1
multiplied by 1:5 and delayed by 14 sample intervals.
• In
Evidently, we have just described in words the following definition of
practice: discrete a(sampled) theof finitedomain M : that g h D
Note convolution witha function in signal s,duration and
that g h is response function time short response
that the function g h is one member of a simple transform pair,
function r (kernel)
M=2
X
g h ” G.f /H.f /
.r s/j Á convolution theorem
sj k rk
kD M=2C1
In other words, the Fourier transform of the convolution is just
individual Fourier transforms.
convolution If a discrete response function is nonzero only in some range M=2 < k Ä
The correlation of two functions, denoted Corr.g; h/, is defi
where M is a sufficiently large even integer, then the response function is
signal finite impulse response (FIR), and its duration is M . (Notice that we are defi
Z 1
as the number of nonzero values of rk ; these values span a time interval of
Corr.g; circumstances the C t /h. / d is the
sampling times.) In most practicalh/ Á g. case of finite M
kernel interest, either because the response really has1finite duration, or because we
a

3. Convolution
• Width of kernel defines smoothing strength

4. Convolution
• Width of kernel defines smoothing strength
convolution 1
convolution 2
signal
kernel 1
kernel 2

5. Convolution
• Width of kernel defines smoothing strength
convolution 1
convolution 2
signal
kernel 1
kernel 2
• Quite fast (O(N*M)), not fast enough

6. Convolution
• Width of kernel defines smoothing strength
convolution 1
convolution 2
signal
kernel 1
kernel 2
• Quite fast (O(N*M)), not fast enough

7. Map
Reduce

8. Map
Reduce

9. Map Map Map Map Map
Reduce

10. Map Map Map Map Map
Reduce Reduce Reduce Reduce Reduce

11. Map Map Map Map Map
Reduce Reduce Reduce Reduce Reduce

12. Build Build Build Build Build
Map Map Map Map Map
windows windows windows windows windows
Reduce Reduce Reduce Reduce Reduce

13. Build Build Build Build Build
Map Map Map Map Map
windows windows windows windows windows
Reduce Reduce Reduce Reduce Reduce

14. Build Build Build Build Build
Map Map Map Map Map
windows windows windows windows windows
Shuffle
Reduce Reduce Reduce Reduce Reduce

15. Build Build Build Build Build
Map Map Map Map Map
windows windows windows windows windows
Shuffle
Reduce
Convolute Reduce
Convolute Reduce
Convolute Reduce
Convolute Reduce
Convolute

16. Build Build Build Build Build
Map Map Map Map Map
windows windows windows windows windows
Shuffle
Reduce
Convolute Reduce
Convolute Reduce
Convolute Reduce
Convolute Reduce
Convolute

17. Build Build Build Build Build
Map Map Map Map Map
windows windows windows windows windows
Shuffle
Reduce
Convolute Reduce
Convolute Reduce
Convolute Reduce
Convolute Reduce
Convolute

18. i
Convolution in Hadoop
“nr3” — 2007/5/1 — 20:53 — page 644 — #666
644
• Wrap-around problem
Chapter 13. Fourier and Spectral Applications
response function
m+ m−
sample of original function m+
m−
convolution
spoiled unspoiled spoiled

19. Convolution in Hadoop spoiled
convolution
unspoiled spoiled
• Wrap-around problem
Figure 13.1.3. The wraparound problem in convolving finite segments of a function. Not only must
the response function wrap be viewed as cyclic, but so must the sampled original function. Therefore,
a portion at each end of the original function is erroneously wrapped around by convolution with the
• Ignore spoiled regions
response function.
response function
• Mirror the sequence (works well in our case)
m+ m−
• Zero-padding
original function zero padding
m− m+
not spoiled because zero
m+ m−
unspoiled spoiled
but irrelevant

20. Convolution in Hadoop
• Data split problem: windowing
• `Overlap-convolute’

21. Convolution in Hadoop
• Data split problem: windowing
• `Overlap-convolute’
Map
(window)
timestamp1
timestamp2
timestamp3

22. Convolution in Hadoop
• Data split problem: windowing
• `Overlap-convolute’
Mapper1 Mapper2 Mapper3
Map
(window) 1 2 1 2 3 2 3
timestamp1
timestamp2
timestamp3

23. Convolution in Hadoop
• Data split problem: windowing
• `Overlap-convolute’
Mapper1 Mapper2 Mapper3
Map
(window) 1 2 1 2 3 2 3
timestamp1
timestamp2
Reduce
(convolute) timestamp3

24. Convolution in Hadoop
• Data split problem: windowing
• `Overlap-convolute’
Mapper1 Mapper2 Mapper3
Map
(window) 1 2 1 2 3 2 3
timestamp1
timestamp2
Reduce
(convolute) timestamp3
Emit only unpolluted data

25. Convolution in Hadoop
• Data split problem: windowing
• `Convolute-add’

26. Convolution in Hadoop
• Data split problem: windowing
• `Convolute-add’
Map 0 0
(convolute 0 0
with 0-padding) 0
0

27. Convolution in Hadoop
• Data split problem: windowing
• `Convolute-add’
Map
(convolute
with 0-padding)
Reduce
(add) A A+B B B+C C
Add values in overlapping regions

28. Hint: Keep mappers alive
• Mappers will be killed if you spend too much
time in a loop (e.g. during long convolutions)
• Do this in large loops:
• for(loopcount%1000==0){context.progress();}

29. Even faster: Fourier Transform
• Converts signal from time domain to frequency domain
• Stress sensor (time domain)
•f
• Fourier transform (frequency domain)

30. Discrete Fourier Transform
• Converts signal from time domain to frequency domain
• Vibration sensor (time domain)
• Fourier transform (frequency domain)

31. H.f / and G.f /, we can form two combinatio
of the two functions, denoted g h, is defined
DFT for convolution g hÁ
Z 1
g. /h
• Convolution theorem: Note that gtransform of convolution
i Fourier
h is a function in the time domai
1
is product of individualthat the 2007/5/1 — 20:53 one page 643 of a#665
Fourier transforms— member — sim
i
“nr3” — function g h is
g h ” G.f /H.f / conv
• Discrete convolution13.1 Convolution and the Fourier transform FFTthe c
theorem:
In other words, Deconvolution Using the of
individual Fourier transforms.
The correlation of two functions, denoted
N=2
X
sj k rk ” Sn Rn Z 1
• Conditions: kD N=2C1 Corr.g; h/ Á g.
1
• Signal periodic: 0-padding (see above) of t , which is call
Here Sn .n D 0; : : : ; N 1/ is the discrete Fourier transform of the valu
The correlation is a function
0; : : : ; N 1/, while Rn .n D 0; : : : ; N 1/ is the discrete Fourier t
• Signals of same length: Pad response ” G.f /H .f /0s c
domain, and it turns out to be one member of t
the values rk .k D 0; : : : ; N 1/. These values of rk are the same as f
function with
k D N=2 C 1; : : : ; N=2, but in wraparound order, exactly as was desc
end of 12.2. Corr.g; h/
13.1.1 Treatment of End Effects by Zero Paddingpai
[More generally, the second member of the

32. Discrete Fourier Transform
• DFT is O(NlogN)
• In Hadoop:
• Modification of Parallel-FFT
• Convolution:
• MR-DFT
• Take product of both FTs
• inverse MR-DFT

33. Segmentation
Windowing Windowing Windowing Windowing Windowing
Shuffle
Convolute Convolute Convolute Convolute Convolute
G’,G’’,G’’’ G’,G’’,G’’’ G’,G’’,G’’’ G’,G’’,G’’’ G’,G’’,G’’’
Emit zero-crossings

34. Segmentation
signal
convolution
segmentation
1st, 2nd,3rd degree derivatives

35. Segmentation
signal
convolution
segmentation