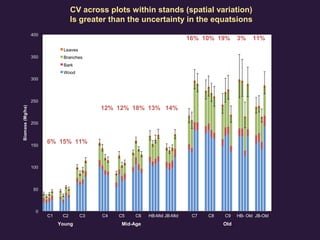
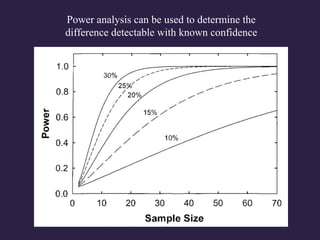
This document summarizes a workshop on tools for estimating uncertainty in ecology. It discusses various sources of uncertainty in ecosystem studies, including natural variability, measurement error, and model error. Specific examples are provided of quantifying uncertainty in nitrogen budgets, precipitation measurements, streamflow modeling, and forest biomass estimates. Monte Carlo simulation techniques are presented as a way to quantify overall uncertainty by incorporating the uncertainty in individual parameters and measurements. The importance of identifying the greatest sources of uncertainty and being able to detect meaningful differences is emphasized.