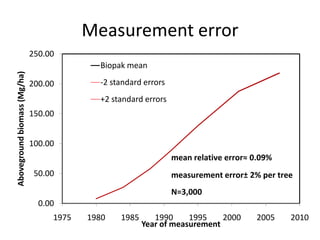
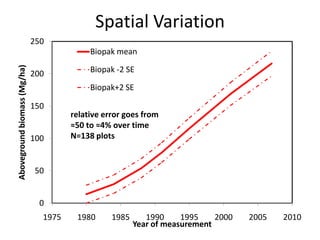
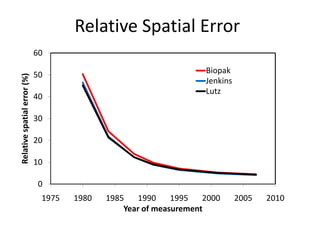
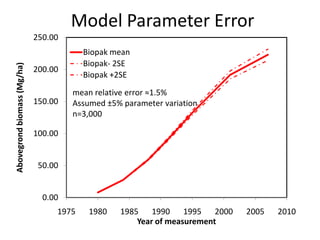
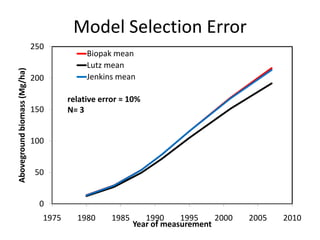
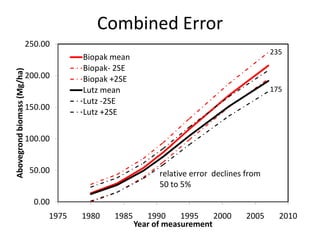
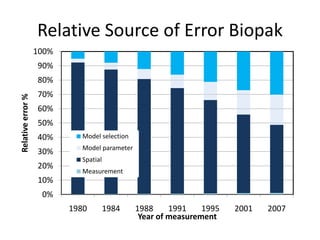
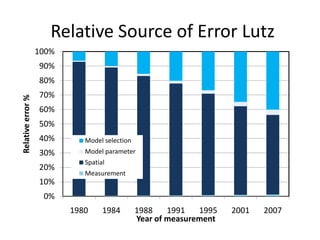
This document discusses uncertainty analysis and its importance for synthesis science. It identifies four main sources of uncertainty: measurement error, natural variation, model parameter error, and model selection error. For a case study at the H.J. Andrews Experimental Forest, it analyzes the relative contribution of each source of uncertainty over time for aboveground biomass estimates. It argues that addressing and quantifying uncertainty is essential for assessing scientific progress, improving models and knowledge, and developing standard guidelines for reporting uncertainty in synthesis science.

1. Uncertainty Analysis: An Evaluation
Metric for Synthesis Science
Mark E. Harmon
Richardson Chair and Professor
Department of Forest Ecosystems and Society
Oregon State University
ESA 2013 Organized Session

2. Two Complementary Sides to Science
• Reductionist
– Reduce down
– Simplify
– Control confounding factors
– Additive to degree possible
• Synthesis
– Build up
– Address Complexity
– Retain confounding factors
– Interactive, whole more than
sum of parts (?)
?

3. Sources of Uncertainty-1
• Measurement error (experimental error)
• Natural variation in space and time
• Model parameter error
• Model selection error

4. Sources of Uncertainty-2
• Measurement error (experimental error)
– Accuracy: how close to the truth?
– Precision: how repeatable?
– Detection limits: how small?
• Primarily considered in:
– Laboratory analyses
– Climate, hydrologic, ecophysiology
instrumentation

5. Sources of Uncertainty-3
• Natural variation in space and time
– Improve estimates of mean and variation via
sample design
– Cannot be completely eliminated
• Primarily considered in:
– Field sampling
– Field experiments
– Statistical tests

6. Sources of Uncertainty-4
• Model parameter error
– Simple to complex conversions of one variable to
another requires a model
– Uncertainty of parameter value
– Can be reduced but not eliminated completely
• Primarily considered in:
– Ecosystem estimates
– Contrast these conversions
– BA= Π*DBH2/4 vs Biomass=B1*DBHB2

7. Sources of Uncertainty-4
• Model parameter error
– Simple to complex conversions of one variable to
another requires a model
– Uncertainty of parameter value
– Can be reduced but not eliminated completely
• Primarily considered in:
– Ecosystem estimates
– Contrast these conversions
– BA= Π*DBH2/4 vs Biomass=B1*DBHB2

8. Sources of Uncertainty-5
• Model selection error
– Knowledge uncertainty of how to proceed
– Introduces a systematic, not a random error
– Can only be reduced with more knowledge
• Primarily considered in:
– Ecosystem estimates
– Simulation models
– Synthetic efforts
– Example: Are tree stems
• Cones? Neiloids? or Paraboloids?

9. Sources of Uncertainty-5
• Model selection error
– Knowledge uncertainty of how to proceed
– Introduces a systematic, not a random error
– Can only be reduced with more knowledge
• Primarily considered in:
– Ecosystem estimates
– Simulation models
– Synthetic efforts
– Example: Are tree stems
• Cones? Neiloids? or Paraboloids?

10. Watershed 1
H. J. Andrews Experimental Forest
Before
Before burning
20 yrs after burning
30 yrs after burning

11. Measurement error
0.00
50.00
100.00
150.00
200.00
250.00
1975 1980 1985 1990 1995 2000 2005 2010
Abovegroundbiomass(Mg/ha)
Year of measurement
Biopak mean
-2 standard errors
+2 standard errors
mean relative error≈ 0.09%
measurement error± 2% per tree
N=3,000

12. Spatial Variation
0
50
100
150
200
250
1975 1980 1985 1990 1995 2000 2005 2010
Abovegroundbiomass(Mg/ha)
Year of measurement
Biopak mean
Biopak -2 SE
Biopak+2 SE
relative error goes from
≈50 to ≈4% over time
N=138 plots

13. Relative Spatial Error
0
10
20
30
40
50
60
1975 1980 1985 1990 1995 2000 2005 2010
Relativespatialerror(%)
Year of measurement
Biopak
Jenkins
Lutz

14. Model Parameter Error
0.00
50.00
100.00
150.00
200.00
250.00
1975 1980 1985 1990 1995 2000 2005 2010
Abovegrondbiomass(Mg/ha)
Year of measurement
Biopak mean
Biopak- 2SE
Biopak +2SE
mean relative error ≈1.5%
Assumed ±5% parameter variation
n=3,000

15. Model Selection Error
0
50
100
150
200
250
1975 1980 1985 1990 1995 2000 2005 2010
Abovegroundbiomass(Mg/ha)
Year of measurement
Biopak mean
Lutz mean
Jenkins mean
relative error ≈ 10%
N= 3

16. Combined Error
0.00
50.00
100.00
150.00
200.00
250.00
1975 1980 1985 1990 1995 2000 2005 2010
Abovegrondbiomass(Mg/ha)
Year of measurement
Biopak mean
Biopak- 2SE
Biopak +2SE
Lutz mean
Lutz -2SE
Lutz +2SE
relative error declines from
50 to 5%
175
235

17. Relative Source of Error Biopak
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1980 1984 1988 1991 1995 2001 2007
Relativeerror%
Year of measurement
Model selection
Model parameter
Spatial
Measurement

18. Relative Source of Error Lutz
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
1980 1984 1988 1991 1995 2001 2007
Relativeerror%
Year of measurement
Model selection
Model parameter
Spatial
Measurement

19. How can we use uncertainty in
synthesis science?

20. Which set of numbers differs?
• 10 versus 10.1
• 10 versus 100

21. Which set of numbers differs?
• 10 versus 10.1
• 10 versus 100

22. Which set of numbers differs?
• 10 versus 10.1
• 10 versus 100

23. Assess scientific progress
• A goal of science is to reduce uncertainty to
the degree possible (we explain as much as
we can)
• How do we know we are making progress if
we do not honestly report uncertainty?
progress

24. Why Address Model Selection Error?
A
B
C
A
B
C
A
B B
A
B
C
A
B
C

25. Why Address Model Selection Error?
A
B
C
A
B
C
A
B B
A
B
C
A
B
C

26. Why Address Model Selection Error?
A
B
C
A
B
C
A
B B
A
B
C
A
B
C

27. Why Address Model Selection Error?
A
B
C
A
B
C
A
B B
A
B
C
A
B
C

28. Why Address Model Selection Error?
A
B
C
A
B
C
A
B B
A
B
C
A
B
C

29. Why Address Model Selection Error?
A
B
C
A
B
C
A
B B
A
B
C
A
B
C

30. Where does the uncertainty lie?
And what do we do about it?
• Measurement-improve
precision, accuracy, detection limits
• Natural variation-improve sampling design
• Model parameter-improve estimates of
parameters
• Model selection-improve knowledge or use
models that are truly general

31. Conclusions
• We need to start somewhere
– We may not know everything, but that has always
been true
– Unknown unknowns that are unknowable
– We do know uncertainty is not zero and it is not
infinite
• We need to develop:
– ways to effectively estimate uncertainty
– standard guidelines of how to report and analyze
– publication expectations

32. Thanks to:
• Becky G. Fasth
• The QUEST team
• Ruth Yanai
• Everyone that collected the WS01 data
• NSF Andrews LTER; Quest RCN; Richardson
Endowment

33. Example of Quantifying Uncertainty
• Carbon budget for WS01
• Old-growth Douglas-fir/western hemlock
forest harvested in 1964-66
• Seeded and planted numerous times
• Repeated measurement of diameter at ground
and breast height of tagged trees in 100 plus
plots
• Status of trees (live, dead, ingrowth) also
noted

34. How Can We Use Uncertainty
in a Useful Way for Synthesis Science?
• Stop hiding uncertainty
• Stop being judgmental about it
• Start reporting the building blocks
(e.g., measurement errors, model parameter
errors, etc)
• Address model selection error fully