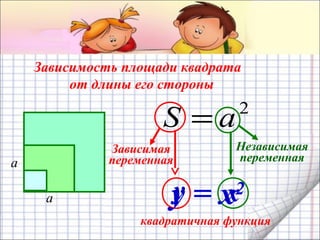
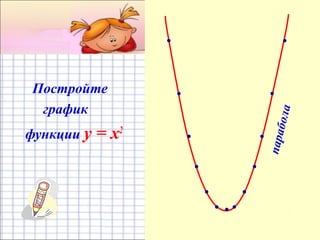
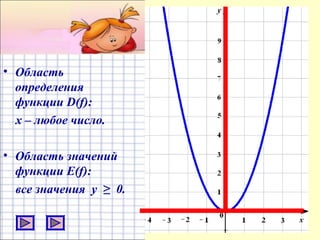
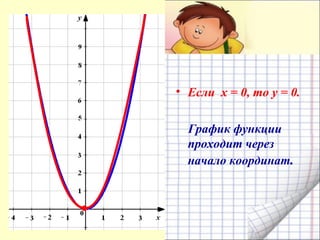
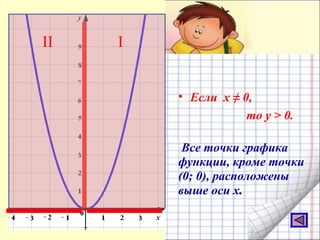
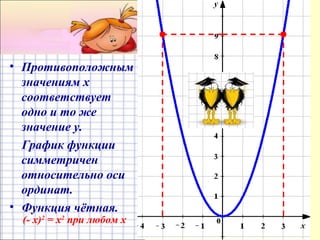
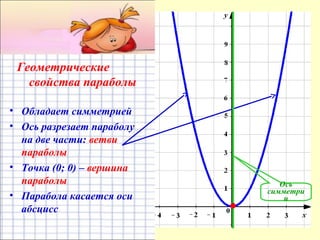
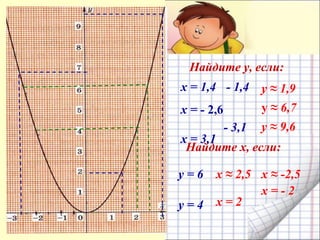
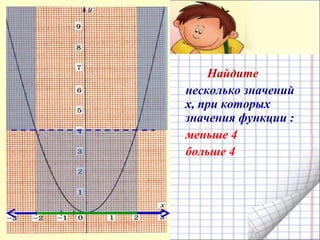
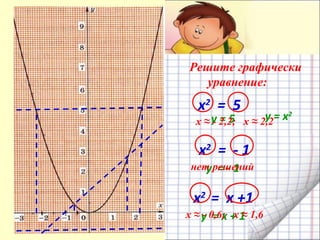
Документ представляет собой план урока для 7 класса по теме функции y = x², включая цели, понятия и практические задания. Рассматриваются свойства графика квадратичной функции, ее симметрия и область определения. Ученикам предлагается построить график функции и решить уравнения графическим способом.

1. ФункцияФункция y = xy = x22
и её графики её график
АлгебраАлгебра 7 класс7 класс
Яковлева Любовь ВикторовнаЯковлева Любовь Викторовна
МБОУ «Самосдельская СОШ им. Шитова В.А.»МБОУ «Самосдельская СОШ им. Шитова В.А.»

2. Цели урока:Цели урока:
• рассмотреть свойства и график функции
у = х2
;
• научиться строить и «читать» график
данной функции;
• научиться решать уравнения
графическим способом.

3. Назовите координаты точек,
симметричных данным точкам
относительно оси y :
(- 2; 6)
(- 1; 4)
(0; 0)
(- 3; - 5)
( 2; 6)
(1; 4)
(0; 0)
(3; - 5)
y
х

4. Найдите значение функции
y = 5x + 4, если:
х = - 1
х = - 2
х = 3
х = 5
y = - 1 y = - 19
y = - 6 y = - 29

5. Укажите
область определения функции:
y = 16 – 5x
х
y
10
−=
5
14 −
=
х
y
7
1
−
=
х
y
х ≠ 0 х ≠ 7
х – любое
число

6. Зависимость между двумя переменными, при которой
каждому значению независимой переменной
соответствует единственное значение зависимой
переменной.
Расшифруйте терминыРасшифруйте термины
Функция
Независимая переменная, значения которой
выбирают произвольно.
Аргумент
Все значения, которые принимает независимая
переменная.
Область
определения
Множество всех точек координатной плоскости,
абсциссы которых равны значениям аргумента, а
ординаты – соответствующим значениям функции.
Линейная функцияГрафик функции
Функция, заданная формулой вида y = kx + b, где
х – переменная, k и b некоторые числа, её графиком
является прямая.

7. 2
aS =
Зависимость площади квадрата
от длины его стороны
квадратичная функция
Зависимая
переменная
Независимая
переменная
а
а
y = x2y x

8. ФункцияФункция yy == xx22
МатематическоеМатематическое
исследованиеисследование

9. хх - 3- 3 -- 22,,55 - 2- 2 - 1,5- 1,5 - 1- 1 - 0,5- 0,5 00
yy
Заполните таблицу значений функции y = x2
:
х 00 0,0,55 11 1,51,5 22 2,52,5 33
y
- 9- 9 - 6,25- 6,25 - 4- 4 - 2,25- 2,25 - 1- 1 - 0,25- 0,25 00
00 2,52,5 11 2,52,5 44 6,256,25 99

10. Постройте
график
функции y = x2
парабола

11. Свойства функцииСвойства функции
y = xy = x22

12. • Область
определения
функции D(f):
х – любое число.
• Область значений
функции E(f):
все значения у ≥ 0.

13. • Если х = 0, то у = 0.
График функции
проходит через
начало координат.

14. • Если х ≠ 0,
то у > 0.
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.
III

15. • Противоположным
значениям х
соответствует
одно и то же
значение у.
График функции
симметричен
относительно оси
ординат.
• Функция чётная.
(- х)2
= х2
при любом х

16. Геометрические
свойства параболы
• Обладает симметрией
• Ось разрезает параболу
на две части: ветви
параболы
• Точка (0; 0) – вершина
параболы
• Парабола касается оси
абсцисс
Ось
симметри
и

17. «Знание – орудие,
а не цель»
Л. Н. Толстой
Найдите у, если:
х ≈ -2,5
х = - 2
у ≈ 1,9
у ≈ 6,7
у ≈ 9,6
х = 1,4
х = - 2,6
х = 3,1
у = 6
у = 4
Найдите х, если:
- 1,4
- 3,1
х ≈ 2,5
х = 2

18. Найдите
несколько значений
х, при которых
значения функции :
меньше 4
больше 4

19. • При каких значениях а точка Р(а; 64) принадлежит
графику функции у = х2
.
• Принадлежит ли графику функции у = х2
точка:
• Не выполняя вычислений, определите, какие из
точек не принадлежат графику функции у = х2
:
P(-18; 324) R(-99; -9081) S(17; 279)
(-1; 1) (0; 8)(-2; 4) (3; -9) (1,8; 3,24) (16; 0)
а = 8; а = - 8
принадлежит не принадлежит не принадлежит

20. Решите графически
уравнение:
х2
= 5
х2
= - 1
x2
= х +1
y = - 1
y = x + 1
y = х2
y = 5
нет решений
х ≈ - 2,2; х ≈ 2,2
х ≈ - 0,6; х ≈ 1,6

21. Домашнее заданиеДомашнее задание
• Изучить п. 23.
• Выполнить упр.
№ 484,
№ 486,
№ 487,
№ 494(а).

22. Удачи вам!Удачи вам!