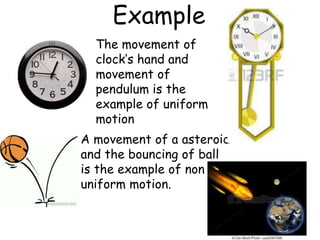
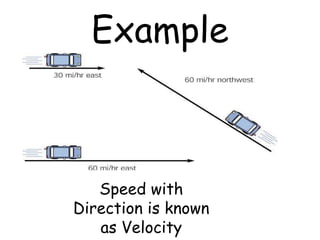
This document describes various concepts related to motion including: 1) Motion is defined as a change in position of an object over time, and can be described by distance or displacement. 2) Uniform and non-uniform motion are defined based on whether distances traveled are equal or unequal over equal time intervals. 3) Speed, velocity, average speed, average velocity, acceleration, and circular motion are defined and the relationships between related concepts like displacement, time, speed, and velocity are described. 3) Formulas for acceleration, average speed, and the three equations of motion relating displacement, time, initial velocity, final velocity, and acceleration are derived.

1. Made BY :- Sanchit
Class 9th- C

2. Describing Motion
• Motion :- Motion is the change in position
of a body with time.
• Motion can be described in terms of the (i)
distance moved or the (ii)displacement
(i)Distance moved is the actual length of the
path travelled by a body.
(ii)Displacement is the length of the shortest
path travelled by a body from initial
position to it’s final position.

3. Example of the motion
The average speed
of bullet train is
320km/hrs
A car is in
motion.
Motion of the
Ball Downward.

4. • i) Uniform motion :- If a body
travels equal distances in equal
intervals of time, it is said to be in
uniform motion.
• ii) Non uniform motion :- If a
body travels unequal distances in
equal intervals of time, it is said to
be in non uniform motion.
Uniform motion and Non
uniform motion

5. Example
A movement of a asteroid
and the bouncing of ball
is the example of non
uniform motion.
The movement of
clock’s hand and
movement of
pendulum is the
example of uniform
motion

6. • Speed :- of a body is the distance travelled
by the body in unit time.
Speed = Distance/Time
• If a body travels a distance s in time t
then its speed v is v= s/t
• The SI unit of speed is meter per second
m/s or ms -1 . Since speed has only
magnitude it is a scalar quantity.

7. Example
The red car is at the speed of
30m/s
And,
The gray car is at the speed of
40m/s

8. Average speed
Average speed :- is the
ratio of the total distance
travelled to the total time
taken.

9. Example Problems
Q. A car travels 85km from point A to B , then 45km
from point B to C . The total time took was 1.3 hrs.
What was the average speed of the Car?
Solution of the problem
Total distance=Distance covered i)A to B + ii)B to C
85km + 45km= 130km
Total Time = 1.3 hrs
Average speed = Total Distance Covered/Total time
=> 130/1.3 km/hrs
=> 100km/hrs

10. The quantity which specifies both
the direction of motion and speed
is velocity.
• Velocity of a body is the
displacement of the body per unit time.
Velocity =Displacement/time taken
•Since velocity has both magnitude and
direction, it is a vector quantity.

11. Example
Speed with
Direction is known
as Velocity

12. Average Velocity
• Average velocity :- is the ratio of the
total displacement to the total time taken.
• Average velocity =Total Displacement/Total
Time.
• Average velocity is also the mean of the
initial velocity u and final velocity v.
• Average velocity= (initial velocity + finial
velocity)/2
or
(u+v)/2
• Speed and velocity have the same units m/s
or ms -1

13. Example Problem
Q. If a car changes its speed from 10m/s to
20m/s in just 5 sec. What is the average
velocity of the car?
Sol. u = 10m/s time taken
v = 20m/s = 5sec
Average velocity = (u + v)/2
(20m/s + 10m/s)/2
30m/s/2
15m/s

14. The quantity which specifies changes
in velocity is acceleration.
• Acceleration :- is the rate of
change of velocity.
• Acceleration = (Final velocity –
initial velocity) / 2
• If the velocity of a body changes
from initial value u to final value v
in time t, then acceleration a is
a = (v-u) /2
• The SI unit of acceleration is ms - 2

15. Example
Four different ways to accelerate a
car.

16. Distance –Time Graph
• Motion can be represented on the
distance time graph.
• In the graph distance is taken on the y –
axis and time is taken on the x – axis.
• The distance time graph for uniform
speed is a straight line.
• This is because in uniform speed a body
travels equal distances in equal intervals
of time.

17. Example
Uniform Motion

18. Derivation of three formula of
motion
• Let a body is moving with initial velocity ‘u’
with uniform acceleration ‘a’ it’s velocity
become ‘v’ in time ‘t’ sec. In the meantime it
covers the distance ‘s’
• The term would be in
1. Acceleration -> m/s2
2. Initial and final velocity -> m/s
3. Time -> sec
4. Distance -> m

19. 1st Equation of motion
• Acceleration = (v – u)/t
a = (v - u)/t
 at = v – u
 u + at = v 1st
equation
of motion

20. 2nd Equation of motion
• Average velocity = (v + u)/2
• Distance Travelled = Av. Velocity + time
s = (v + u)/2 x t
Put v = u + at
 s = (u + at + u)/2 x t
 s = (2u+at)/2 x t
 s = (2ut + at2) /2
s = ut + ½ at2 2nd
Equation of
motion

21. 3rd Equation of motion
• We know that v = u + at
v – u = at
(v - u)/a = t
• Put t = (v – u)/a in eq. s = ut + ½ at2
s = u{(v – u)/a} + ½a {(v-u)/2} 2
s = (uv - u2)/a + ½a{(v2 + u2 -2uv)/a2}
 s = (uv - u2)/a + ½(v2 + u2 -2uv)/a
 s = (uv - u2)/a + (v2 + u2 -2uv)/2a
s = (2uv - 2u2 + v2 + u2 -2uv)/2a
s = (v2 - u2 )/2a
2as = v2 - u2 3rd
Equation
of motion

22. Circular motion
• The motion of a body in a circular path is called
circular motion.
• Uniform circular motion :- If a body
moves in a circular path with uniform speed, its
motion is called uniform circular motion.
• Uniform circular motion is accelerated motion
because in a circular motion a body continuously
changes its direction.
• The circumference of a circle of radius r is
given by 2лr. If a body takes time t to go once
around the circular path, then the velocity v is
given by
v = 2лr/2

23. Example