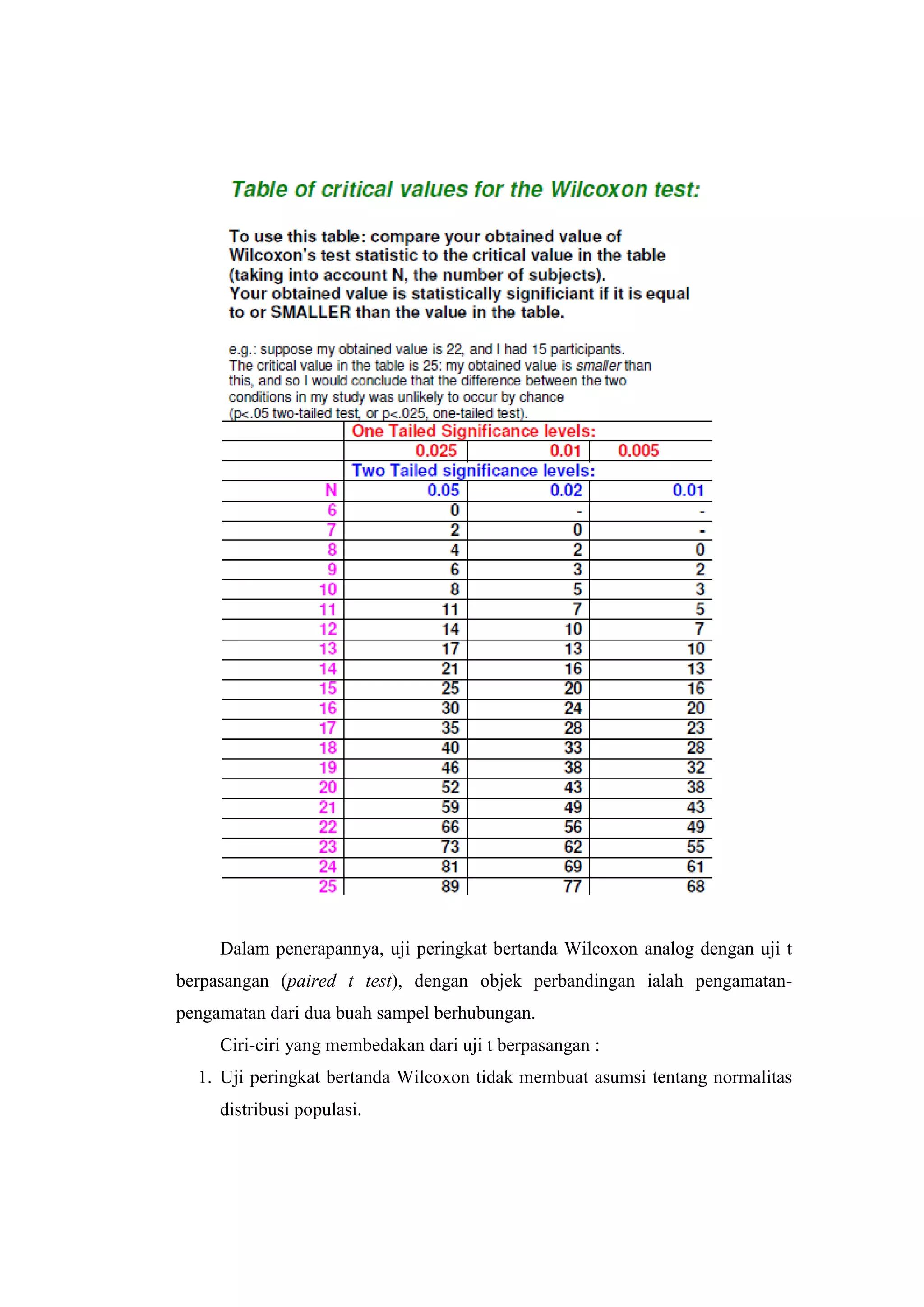
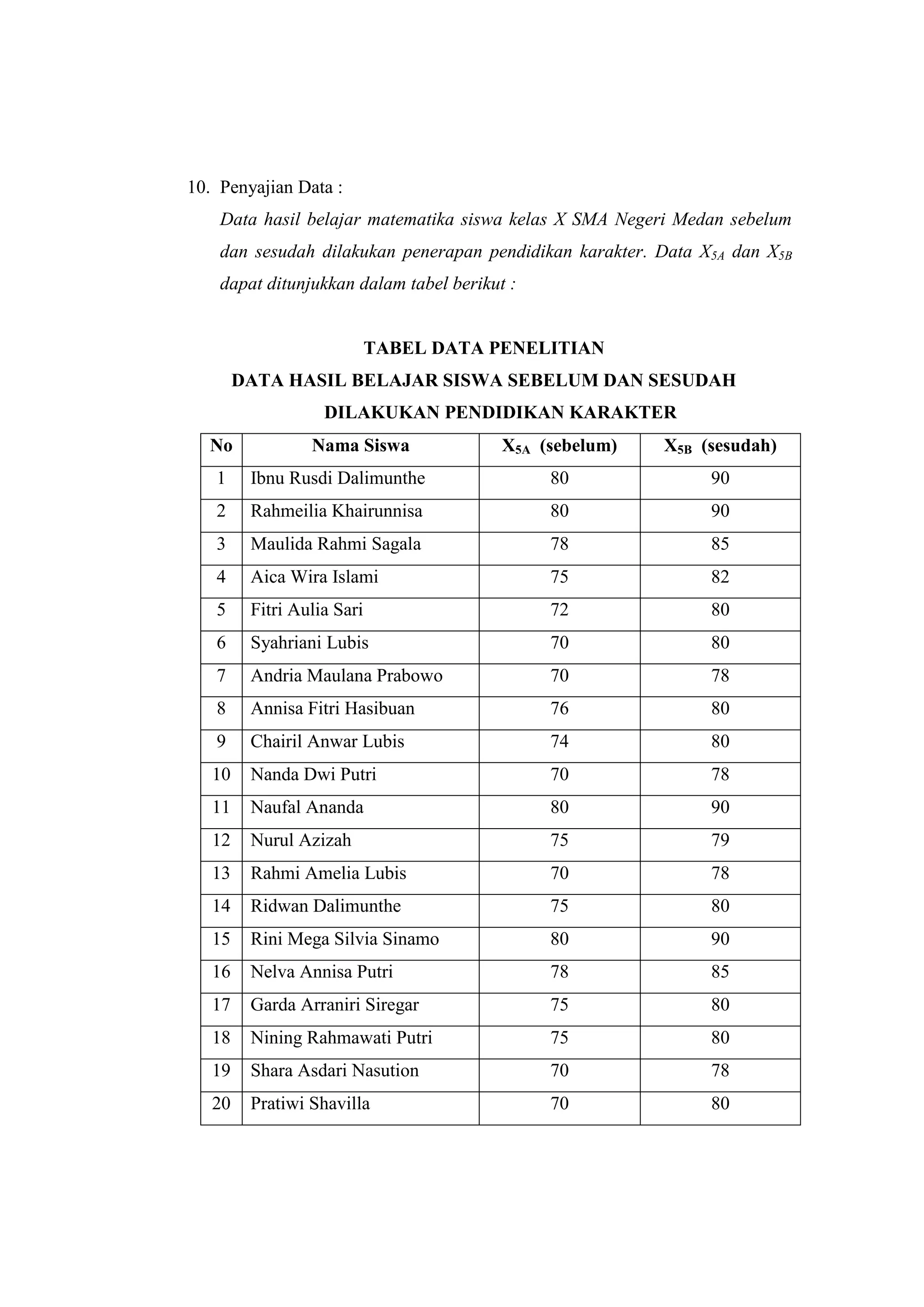
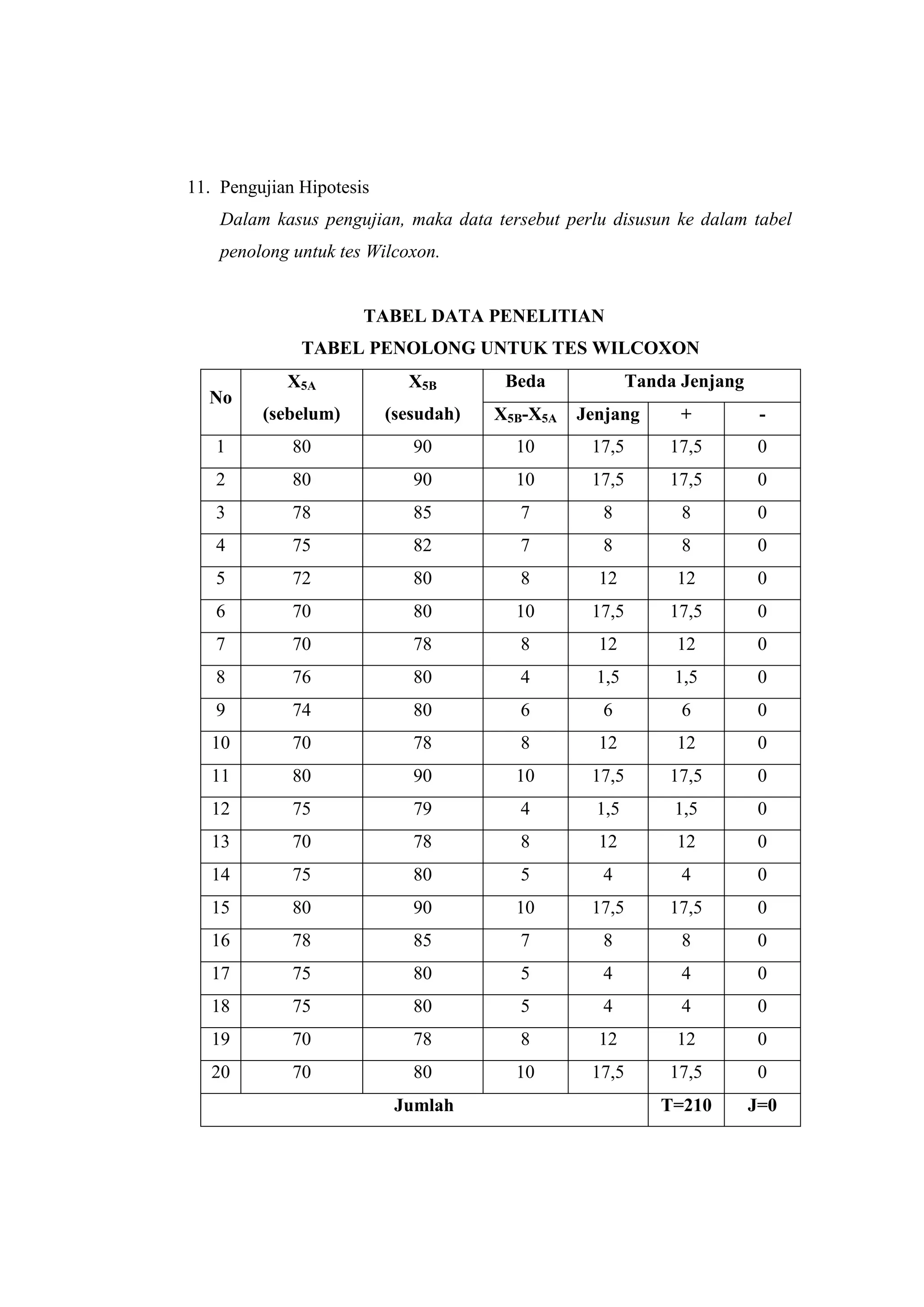
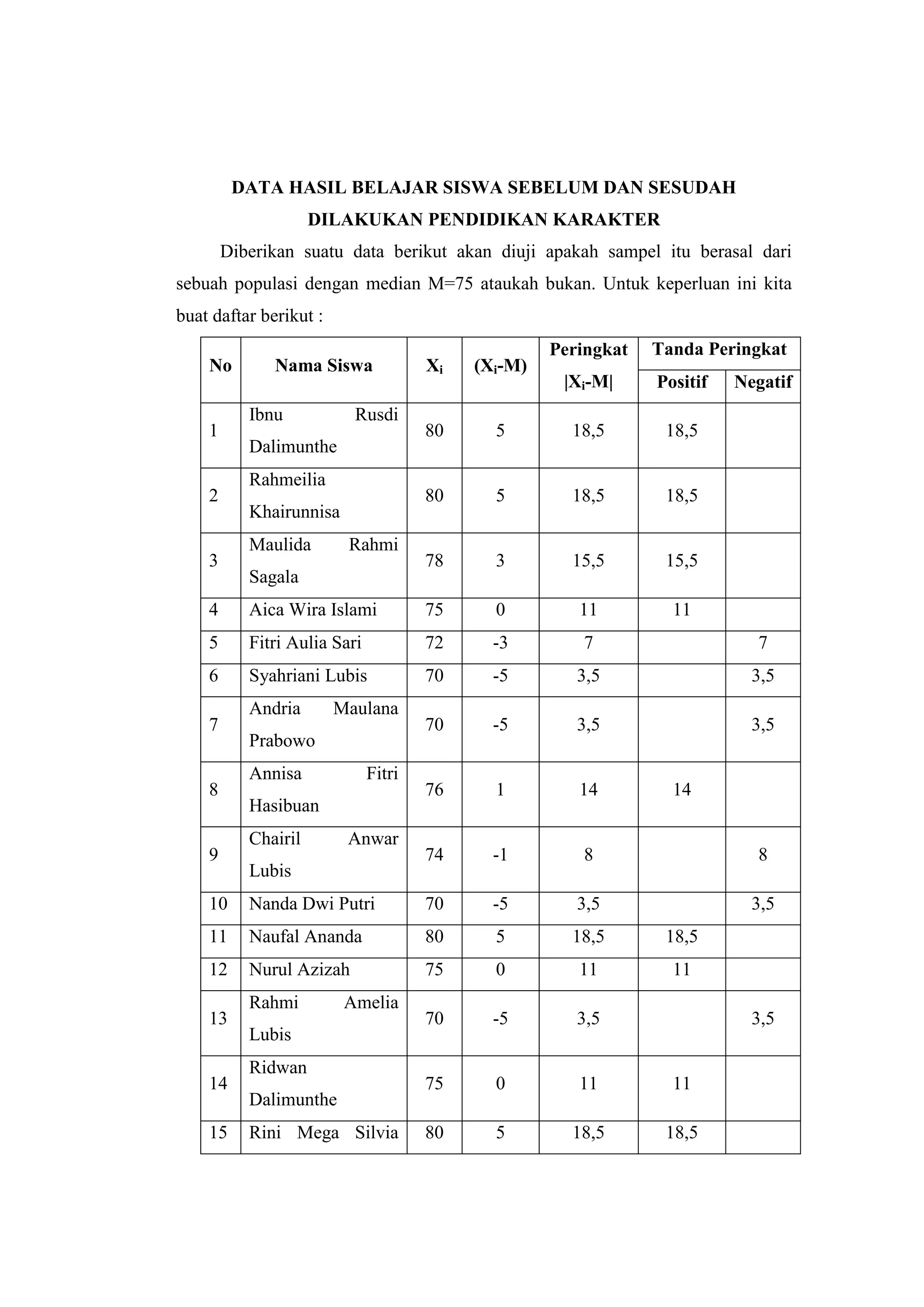
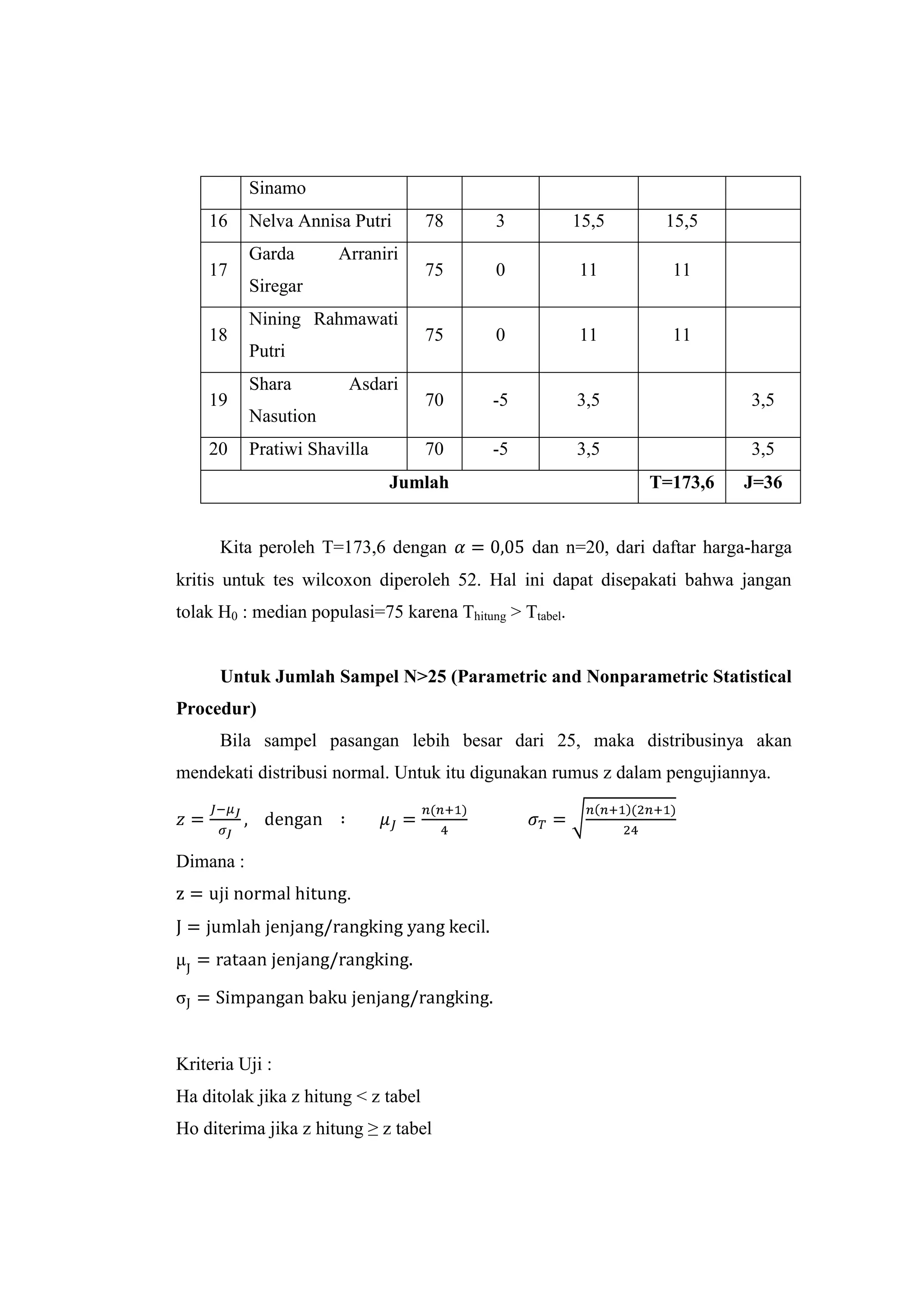
Dokumen ini membahas uji Wilcoxon untuk menghitung perbedaan antara dua sampel yang berkorelasi dengan fokus pada penerapan pendidikan karakter terhadap hasil belajar matematika siswa. Penelitian dilakukan pada 20 siswa kelas X SMA Negeri 11 Medan, yang menunjukkan bahwa penerapan pendidikan karakter memiliki pengaruh signifikan terhadap hasil belajar. Kesimpulan penelitian ini diambil berdasarkan analisis statistik dan pengujian hipotesis yang menunjukkan perbedaan yang nyata antara skor sebelum dan sesudah penerapan pendidikan karakter.

1. THE WILCOXON MATCHED-PAIRS
SIGNED-RANKS TEST
MAKALAH
Diajukan untuk Melengkapi Tugas Mata Kuliah
Statistika Non Parametrik dengan dosen pengasuh
Dr. Marwan Ramli, M.Si
Oleh
Rizki Kurniawan Rangkuti
(NPM : 7108051059)
Program Studi Pendidikan Matematika
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS ISLAM SUMATERA UTARA
MEDAN
2012

2. THE WILCOXON MATCHED-PAIRS SIGNED-RANKS TEST
Teknik ini merupakan penyempurnaan dari uji tanda (Sign Test). Kalau
dalam uji tanda besarnya selisih nilai angka antara positif dan negatif tidak
diperhitungkan sedangkan dalam uji Wilcoxon nilai selisih (X-Y) diperhitungkan,
uji ini digagas pertama kali oleh Frank Wilcoxon (1892-1965). Seperti dalam uji
tanda, teknik ini digunakan untuk menguji signifikansi hipotesis komparatif dua
sampel yang berkorelasi bila datanya berbentuk ordinal (berjenjang).
Caranya adalah sebagai berikut :
1. Beri nomor urut untuk setiap harga mutlak selisih (Xi-Yi). Harga mutlak
yang terkecil diberi nomor urut atau peringkat 1, harga mutlak selisih
berikutnya diberi nomor urut 2, dan akhirnya harga mutlak terbesar diberi
nomor urut n. Jika terdapat selisih yang harga mutlaknya sama besar, untuk
nomor urut diambil rata-ratanya.
2. Untuk tiap nomor urut berikan pula tanda yang didapat dari selisih (X-Y).
3. Hitunglah jumlah nomor urut yang bertanda positif dan juga jumlah nomor
urut yang bertanda negatif.
4. Untuk jumlah nomor urut yang didapat pada langkah 3, ambillah jumlah
yang harga mutlaknya paling kecil. Sebutlah jumlah ini sama dengan J.
Jumlah J inilah yang dipakai untuk menguji hipotesis :
H0 : tidak ada perbedaan pengaruh kedua perlakuan
Ha : terdapat perbedaan pengaruh kedua perlakuan
Untuk menguji hipotesis di atas dengan taraf nyata atau ,
kita bandingkan J di atas dengan T yang diperoleh dari harga-harga kritis untuk
tes wilcoxon. Jika J dari perhitungan lebih kecil atau sama dengan Ttabel dari daftar
berdasarkan taraf nyata yang dipilih maka terima Ha. Dalam hal lainnya H0
diterima.
Kriteria Uji :
Ha diterima jika T hitung < T tabel
H0 diterima jika T hitung ≥ T tabel

3. Dalam penerapannya, uji peringkat bertanda Wilcoxon analog dengan uji t
berpasangan (paired t test), dengan objek perbandingan ialah pengamatan-
pengamatan dari dua buah sampel berhubungan.
Ciri-ciri yang membedakan dari uji t berpasangan :
1. Uji peringkat bertanda Wilcoxon tidak membuat asumsi tentang normalitas
distribusi populasi.

4. 2. Uji peringkat bertanda Wilcoxon tidak membutuhkan informasi tentang
varians, baik varians populasi maupun populasi sampel.
3. Uji peringkat bertanda Wilcoxon bila digunakan meskipun data yang
tersedia hanya ordinal.
4. Perhatian analisis untuk membedakan satu sampel dengan sampel lainnya
pada uji peringkat bertanda Wilcoxon adalah mediannya.
Langkah – Langkah Uji Peringkat Bertanda Wilcoxon :
1. Asumsikan bahwa populasi perbedaan pasangan nilai pengamatan kedua
sampel adalah variable acak kontinu.
2. Hipotesis
Uji satu sisi :
a. Ho : W (+) = W (-) Hi : W (+) > W (-)
b. Ho : W (+) = W (-) Hi : W (+) < W (-)
Uji dua sisi :
Ho : W (+) = W (-) Hi : W (+) ≠ W (-)
W(+) : Jumlah semua peringkat selisih pasangan pengamatan (Wi , Yi)
yang bertanda positif.
W (-) : Jumlah semua peringkat selisih pasangan pengamatan (Wi , Yi)
yang bertanda negatif.
3. Untuk setiap pasangan nilai pengamatan (Xi, Yi), hitung perbedaannya (di=
Xi – Yi).
4. Berikan peringkat terhadap perbedaan nilai pasangan pengamatan, mulai
dari peringkat 1 untuk perbedaan terkecil hingga peringkat n untuk
perbedaan terbesar. Bila terdapat perbedaan nilai pasangan yang sama,
perbedaan pasangan nilai yang sama di beri peringkat rata-ratanya. Untuk
beda nol, tidak diperhatikan.
5. Bubuhkan tanda kepada peringkat yang sudah dibuat itu positif atau negatif
sesuai dengan tanda perbedaan nilai pengamatan aslinya.
6. Hitung banyaknya di yang bertanda positif (disebut W+) dan negative
(disebut W-).

5. 7. Statistik uji peringkat bertanda Wilcoxon ialah W. M yang dipakai ialah W+
atau W- yang nilainya lebih kecil :
W+= ∑ Ri (Semua peringkat positif) dan │W-│= │∑Ri│(Semua peringkat Negatif)
8. Ho ditolak bila nilai W terlalu kecil untuk dikatakan bahwa yang terlibat
hanya karena kebetulan.
Contoh :
Seorang mahasiswa pendidikan matematika Univeristas Islam Sumatera Utara
ingin mengetahui apakah penerapan pendidikan karakter berpengaruh secara
signifikan terhadap hasil belajar matematika siswa di kelas X SMA Negeri 11
Medan tahun 2012. Untuk itu dilakukan penelitian dalam hal ini di ambil satu
kelas yang sebagai sampel penelitian, katakan kelas X5 sebagai subjek penelitian
yang berjumlah 20 siswa. Data penelitian di ambil sebelum dilakukan penerapan
pendidikan karakter dan sesudah penerapan pendidikan karakter yang masing-
masing dilambangkan dengan X5A dan X5B.
Berdasarkan hal tersebut, maka :
1. Judul penelitian dapat dirumuskan sebagai berikut :
Penerapan Pendidikan Karakter Terhadap Hasil Belajar Matematika Siswa
Kelas X SMA Negeri 11 Medan Tahun Ajaran 2011-2012.
2. Variabel :
Dalam penelitian ini diketahui Pendidikan Karakter adalah variabel bebas
dan Hasil Belajar sebagai variabel terikat.
3. Rumusan Masalah Penelitian :
Apakah Penerapan Karakter pengaruh yang signifikan terhadap Hasil
Belajar siswa kelas X SMA Negeri 11 Medan.
4. Subjek Penelitian :
Subjek dalam penelitian ini adalah siswa yang akan digunakan sebagai
sampel penelitian.

6. 5. Desain Penelitian :
6. Tempat Penelitian :
SMA Negeri 11 Medan- Sumatera Utara
7. Langkah-langkah penelitian :
Menetapkan sampel penelitian yang berjumlah 20 siswa, di mana waktu
penelitiannya dilakukan selama 2 minggu. Minggu pertama dilakukan
penelitian dengan tidak menerapkan pendidikan karakter pada proses
pembelajaran matematika dan minggu kedua dilakukan penelitian dengan
menerapkan pendidikan karakter. Analisis penelitian dilakukan dengan
membandingkan data hasil belajar sebelum dan sesudah penerapan
pendidikan karakter pada proses pembelajaran.
8. Hipotesis :
H0 : Tidak terdapat pengaruh pendidikan karakter secara signifikan
terhadap hasil belajar siswa kelas X5 SMA Negeri 11 Medan Tahun Ajaran
2011-2012.
Ha : Terdapat pengaruh pendidikan karakter secara signifikan terhadap
hasil belajar siswa kelas X5 SMA Negeri 11 Medan Tahun Ajaran 2011-
2012.
9. Kriteria Penelitian :
Terima H0, bila harga jumlah jenjang yang terkecil T dari perhitungan
lebih besar dari harga T tabel (T tabel adalah harga-harga kritis untuk tes
wilcoxon).
Sebelum dilakukan
penerapan
pendidikan karakter
terhadap sampel
penelitian 20 siswa
kelas X5
Penerapan
Pendidikan
Karakter
Sesudah dilakukan
penerapan
pendidikan karakter
terhadap sampel
penelitian 20 siswa
kelas X5

7. 10. Penyajian Data :
Data hasil belajar matematika siswa kelas X SMA Negeri Medan sebelum
dan sesudah dilakukan penerapan pendidikan karakter. Data X5A dan X5B
dapat ditunjukkan dalam tabel berikut :
TABEL DATA PENELITIAN
DATA HASIL BELAJAR SISWA SEBELUM DAN SESUDAH
DILAKUKAN PENDIDIKAN KARAKTER
No Nama Siswa X5A (sebelum) X5B (sesudah)
1 Ibnu Rusdi Dalimunthe 80 90
2 Rahmeilia Khairunnisa 80 90
3 Maulida Rahmi Sagala 78 85
4 Aica Wira Islami 75 82
5 Fitri Aulia Sari 72 80
6 Syahriani Lubis 70 80
7 Andria Maulana Prabowo 70 78
8 Annisa Fitri Hasibuan 76 80
9 Chairil Anwar Lubis 74 80
10 Nanda Dwi Putri 70 78
11 Naufal Ananda 80 90
12 Nurul Azizah 75 79
13 Rahmi Amelia Lubis 70 78
14 Ridwan Dalimunthe 75 80
15 Rini Mega Silvia Sinamo 80 90
16 Nelva Annisa Putri 78 85
17 Garda Arraniri Siregar 75 80
18 Nining Rahmawati Putri 75 80
19 Shara Asdari Nasution 70 78
20 Pratiwi Shavilla 70 80

8. 11. Pengujian Hipotesis
Dalam kasus pengujian, maka data tersebut perlu disusun ke dalam tabel
penolong untuk tes Wilcoxon.
TABEL DATA PENELITIAN
TABEL PENOLONG UNTUK TES WILCOXON
No
X5A
(sebelum)
X5B
(sesudah)
Beda Tanda Jenjang
X5B-X5A Jenjang + -
1 80 90 10 17,5 17,5 0
2 80 90 10 17,5 17,5 0
3 78 85 7 8 8 0
4 75 82 7 8 8 0
5 72 80 8 12 12 0
6 70 80 10 17,5 17,5 0
7 70 78 8 12 12 0
8 76 80 4 1,5 1,5 0
9 74 80 6 6 6 0
10 70 78 8 12 12 0
11 80 90 10 17,5 17,5 0
12 75 79 4 1,5 1,5 0
13 70 78 8 12 12 0
14 75 80 5 4 4 0
15 80 90 10 17,5 17,5 0
16 78 85 7 8 8 0
17 75 80 5 4 4 0
18 75 80 5 4 4 0
19 70 78 8 12 12 0
20 70 80 10 17,5 17,5 0
Jumlah T=210 J=0

9. Berdasarkan tabel untuk harga-harga kritis dalam tes Wilcoxon untuk n=20
dengan taraf kesalahan 5% (uji pihak), diperoleh T tabel=52. Oleh karena
jumlah jenjang J yang kecil lebih kecil dari T tabel, maka jangan tolak Ha.
Dengan demikian bahwa terdapat pengaruh secara signifikan penerapan
pendidikan karakter terhadap hasil belajar siswa.
12. Kesimpulan :
Interpretasi dari penelitian ini adaalah terdapat pengaruh yang signifikan
dari penerapan pendidikan karatakter terhadap hasil belajar matematika
siswa kelas X5 SMA Negeri 11 Medan Tahun Ajaran 2011-2012.
13. Saran yang diberikan :
Perlu diterapkan pendidikan karakter di SMA guna meningkatkan hasil
belajar siswa.
Uji Median Populasi
Uji wilcoxon juga dapat digunakan untuk menguji hipotesis median
populasi, yaitu :
H0 : median populasi = M
Ha : median populasi
Berdasarkan sebuah sampel acak yang diambil dari populasi yang diduga
mempunyai M. Sudah barang tentu bahwa untuk hal ini kita hanya
memperhatikan sebuah sampel yang diambil dari sebuah populasi. Jika data
sampel berukuran n itu X1, X2, X3, . . . , Xn, maka untuk keperluan menguji
median seperti yang telah dirumuskan harus dihitung selisih (Xi-M) dan nomor
urut harga mutlak |Xi-M|. Selanjutnya ditempuh langkah 2), 3) dan 4) seperti
dijelaskan di depan. Hipotesis H0 kita tolak jika T dari perhitungan lebih kecil
atau sama dengan T dari daftar berdasarkan taraf nyata yang dipilih.

10. DATA HASIL BELAJAR SISWA SEBELUM DAN SESUDAH
DILAKUKAN PENDIDIKAN KARAKTER
Diberikan suatu data berikut akan diuji apakah sampel itu berasal dari
sebuah populasi dengan median M=75 ataukah bukan. Untuk keperluan ini kita
buat daftar berikut :
No Nama Siswa Xi (Xi-M)
Peringkat
|Xi-M|
Tanda Peringkat
Positif Negatif
1
Ibnu Rusdi
Dalimunthe
80 5 18,5 18,5
2
Rahmeilia
Khairunnisa
80 5 18,5 18,5
3
Maulida Rahmi
Sagala
78 3 15,5 15,5
4 Aica Wira Islami 75 0 11 11
5 Fitri Aulia Sari 72 -3 7 7
6 Syahriani Lubis 70 -5 3,5 3,5
7
Andria Maulana
Prabowo
70 -5 3,5 3,5
8
Annisa Fitri
Hasibuan
76 1 14 14
9
Chairil Anwar
Lubis
74 -1 8 8
10 Nanda Dwi Putri 70 -5 3,5 3,5
11 Naufal Ananda 80 5 18,5 18,5
12 Nurul Azizah 75 0 11 11
13
Rahmi Amelia
Lubis
70 -5 3,5 3,5
14
Ridwan
Dalimunthe
75 0 11 11
15 Rini Mega Silvia 80 5 18,5 18,5

11. Sinamo
16 Nelva Annisa Putri 78 3 15,5 15,5
17
Garda Arraniri
Siregar
75 0 11 11
18
Nining Rahmawati
Putri
75 0 11 11
19
Shara Asdari
Nasution
70 -5 3,5 3,5
20 Pratiwi Shavilla 70 -5 3,5 3,5
Jumlah T=173,6 J=36
Kita peroleh T=173,6 dengan dan n=20, dari daftar harga-harga
kritis untuk tes wilcoxon diperoleh 52. Hal ini dapat disepakati bahwa jangan
tolak H0 : median populasi=75 karena Thitung > Ttabel.
Untuk Jumlah Sampel N>25 (Parametric and Nonparametric Statistical
Procedur)
Bila sampel pasangan lebih besar dari 25, maka distribusinya akan
mendekati distribusi normal. Untuk itu digunakan rumus z dalam pengujiannya.
Dimana :
.
Kriteria Uji :
Ha ditolak jika z hitung < z tabel
Ho diterima jika z hitung ≥ z tabel

12. Dengan demikian :
Rumus ini dapat juga digunakan untuk membuktikan contoh diatas tentang
penerapan pendidikan karakter bagi proses pembelajaran. Harga-harga dalam
contoh disubtitusikan dalam rumus tersebut, sehingga :
Bila taraf kesalahan 0,025 (p), maka harga z tabel = 1,96 (Tabel harga-harga
kritis z dalam observasi pada distribusi normal). Harga z hitung 3,92 ternyata
lebih besar dari z tabel, dengan demikian tolak H0 dan jangan tolak Ha. Maka
penerapan pendidikan karakter berpengaruh secara signifikan terhadap hasil
belajar siswa. Kesimpulan ini sama dengan pengujian dengan sampel kecil dari uji
wilcoxon match pairs test.
Suatu data berikut dapat diuji apakah sampel itu berasal dari sebuah
populasi dengan median M. Bila sampel lebih besar dari 25, maka distribusinya
akan mendekati distribusi normal. Untuk itu digunakan rumus z dalam
pengujiannya.
Dimana :
.

13. Kriteria Uji :
Ha ditolak jika z hitung < z tabel
Ho diterima jika z hitung ≥ z tabel
Dengan demikian :
Rumus ini dapat juga digunakan untuk membuktikan contoh diatas tentang
penerapan pendidikan karakter bagi proses pembelajaran. Harga-harga dalam
contoh disubtitusikan dalam rumus tersebut, sehingga :
Bila taraf kesalahan 0,025 (p), maka harga z tabel = 1,96 (Tabel harga-harga
kritis z dalam observasi pada distribusi normal). Harga z hitung 2,56 ternyata
lebih besar dari z tabel, dengan demikian disimpulkan bahwa sampel itu berasal
dari sebuah populasi dengan median M.