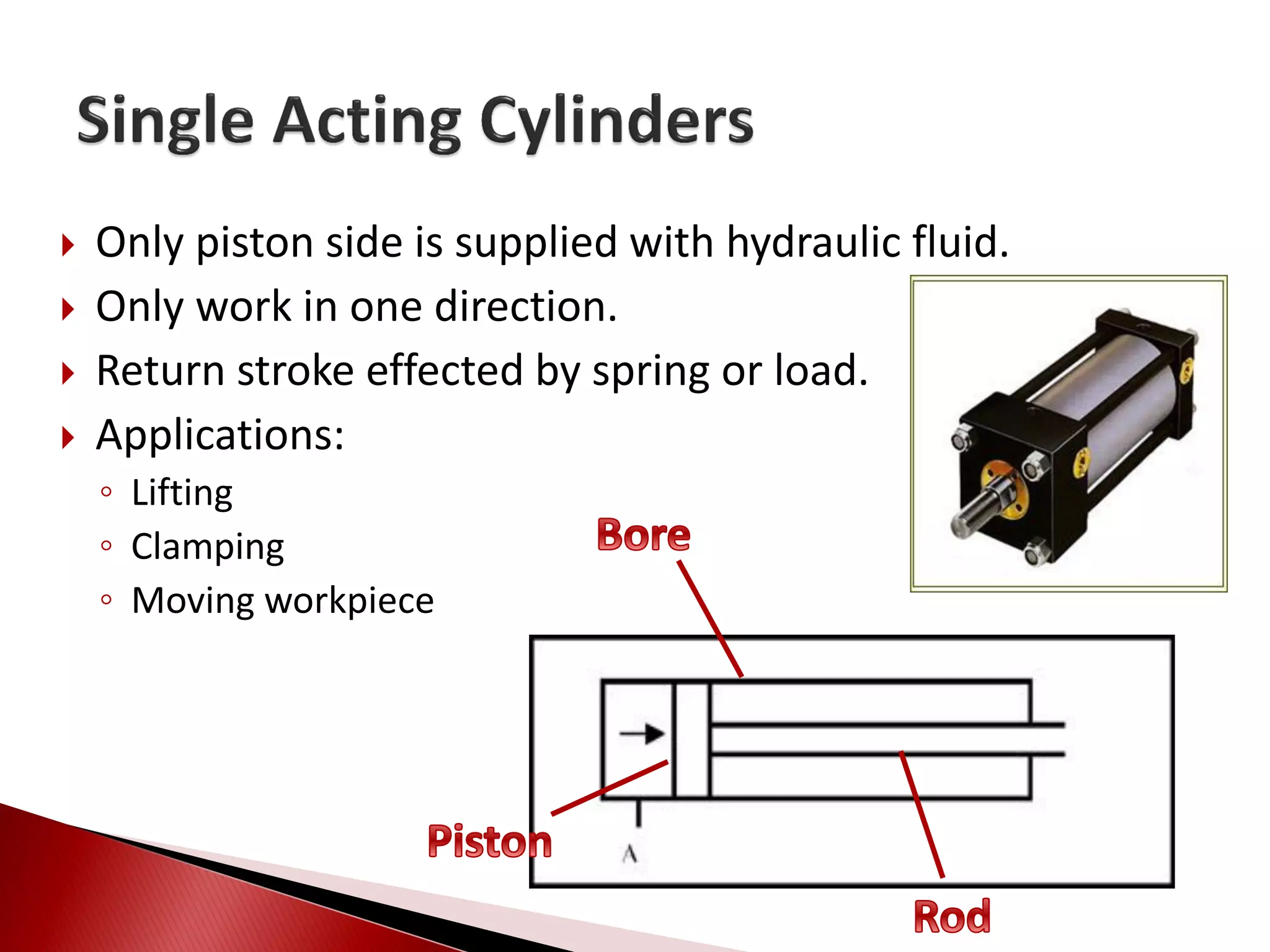
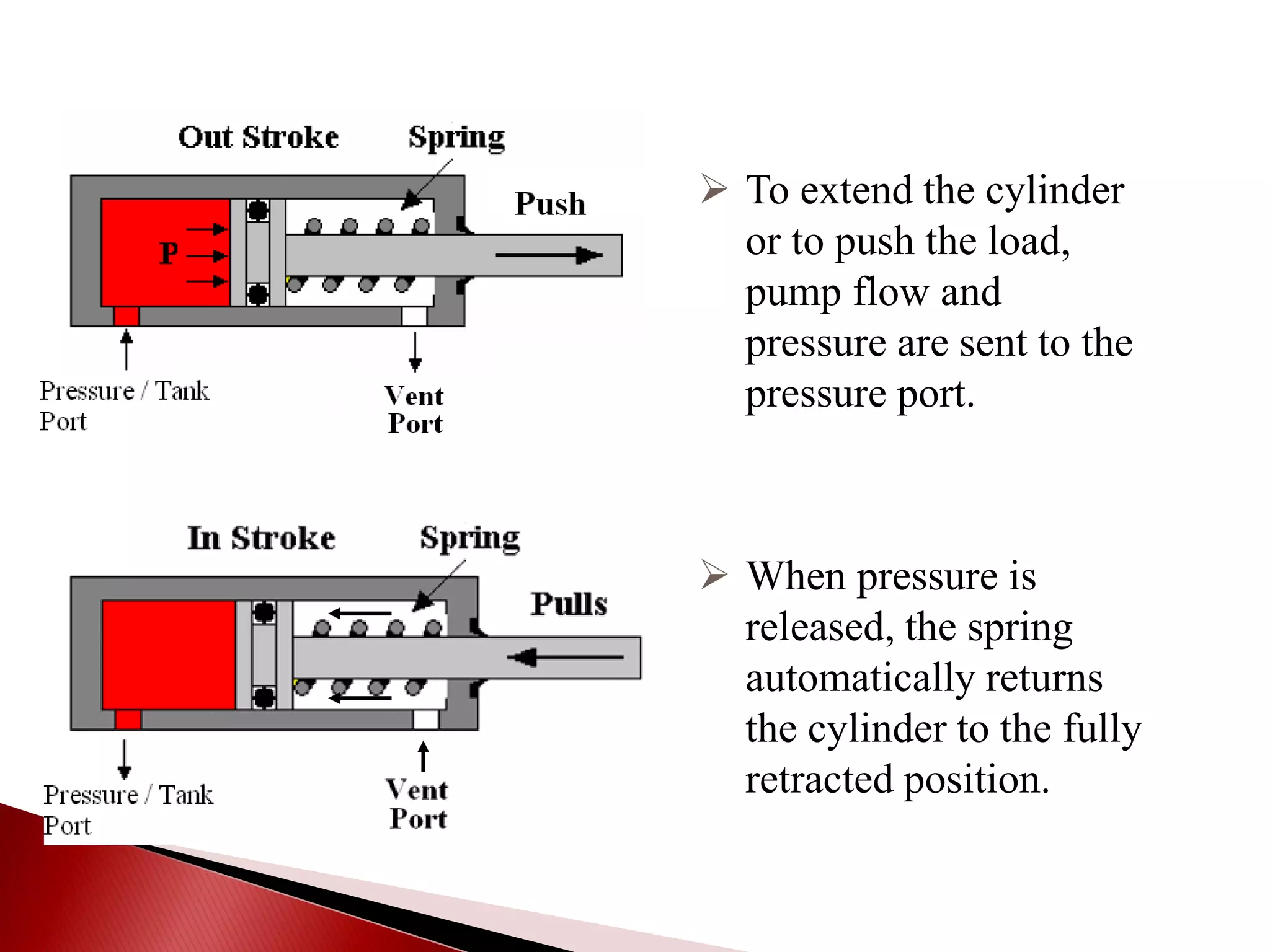
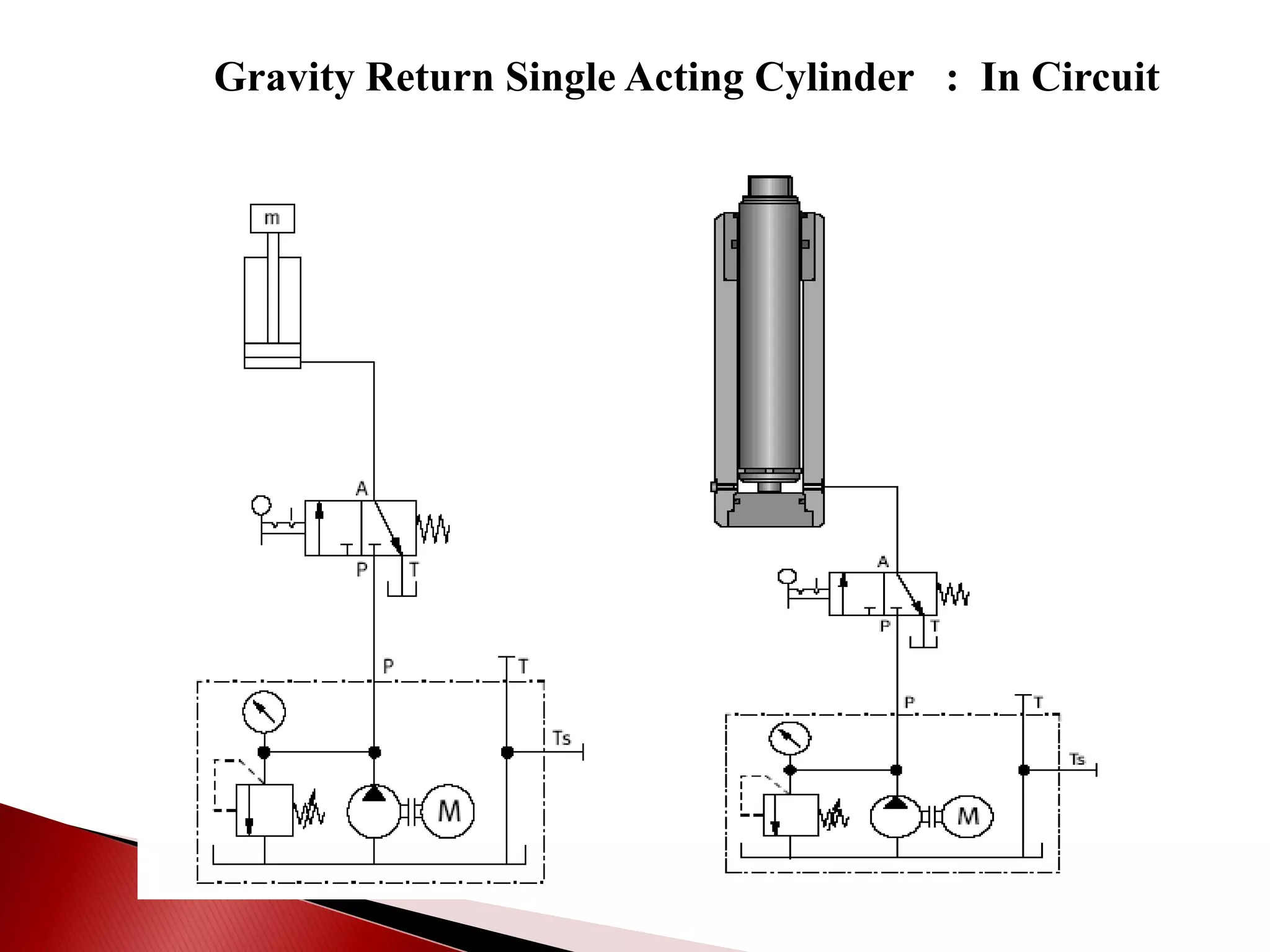
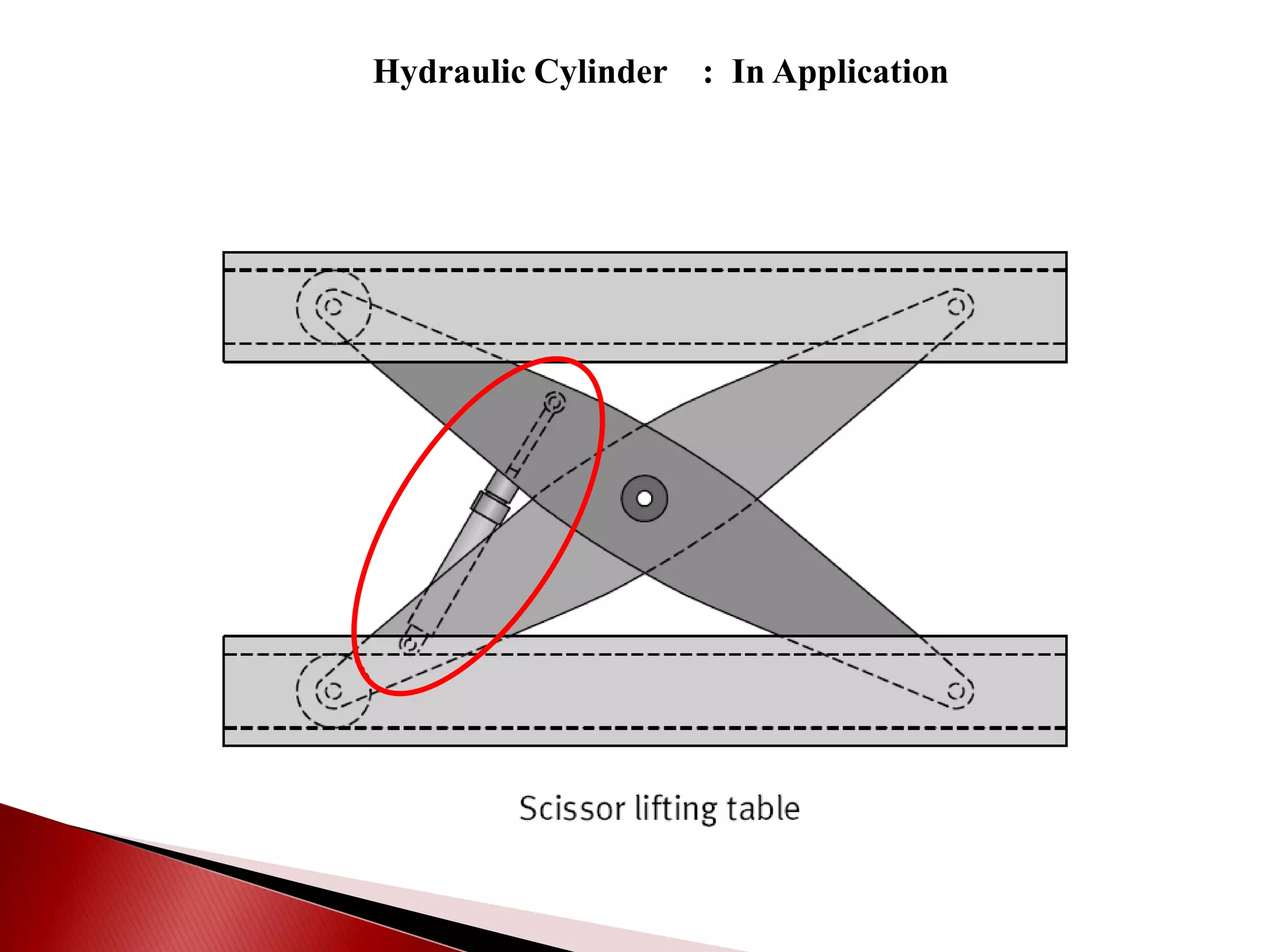
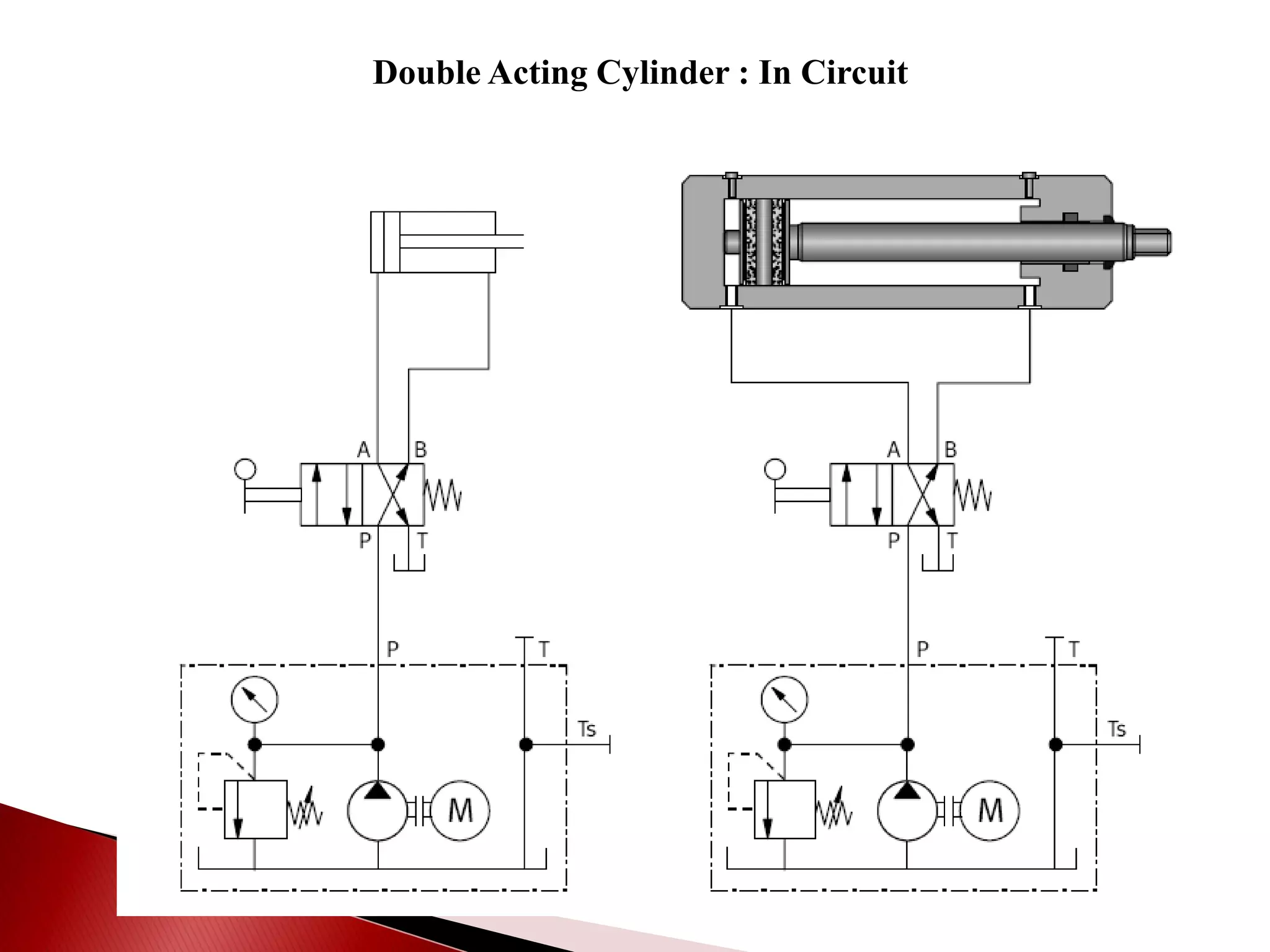
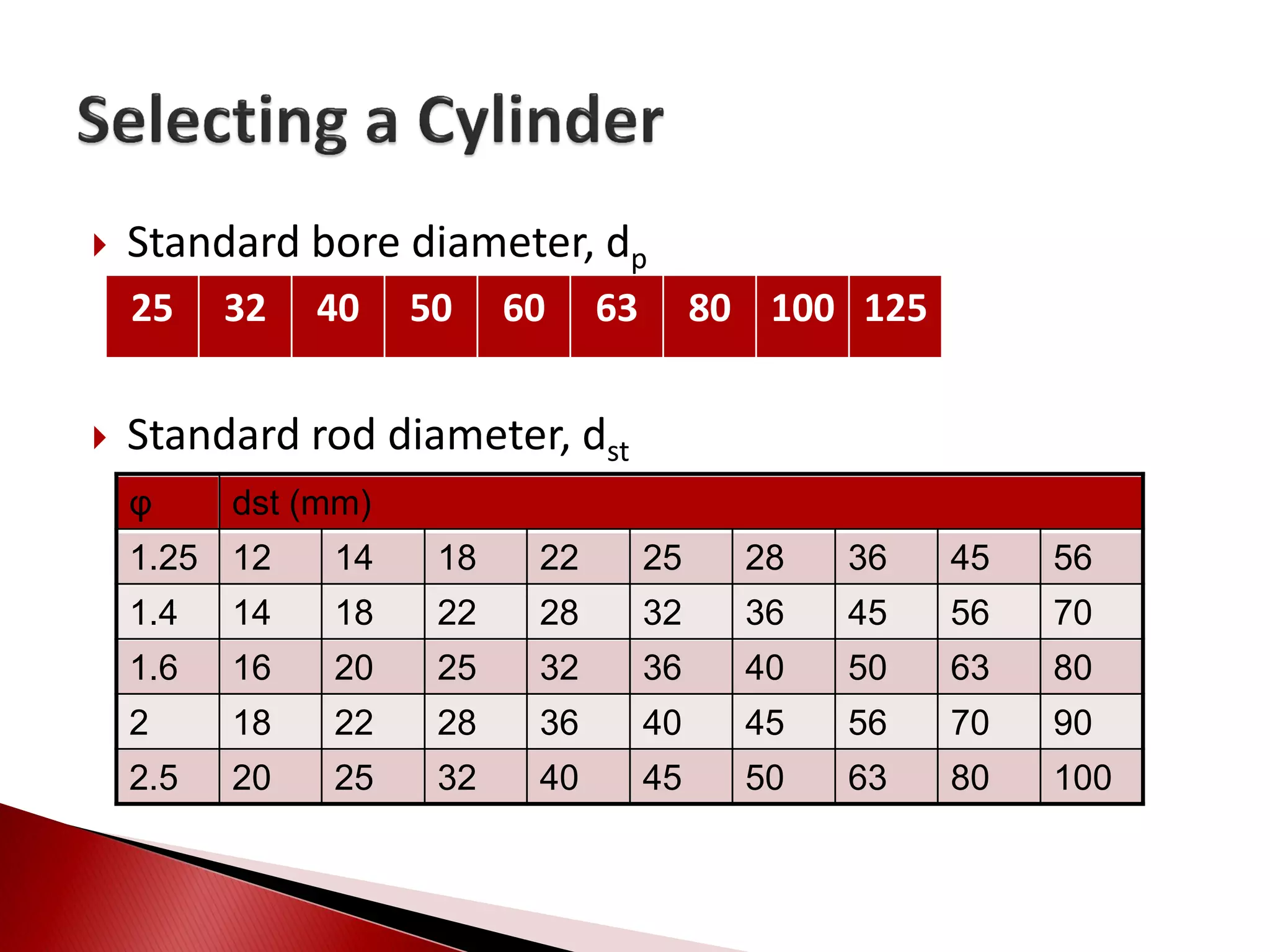
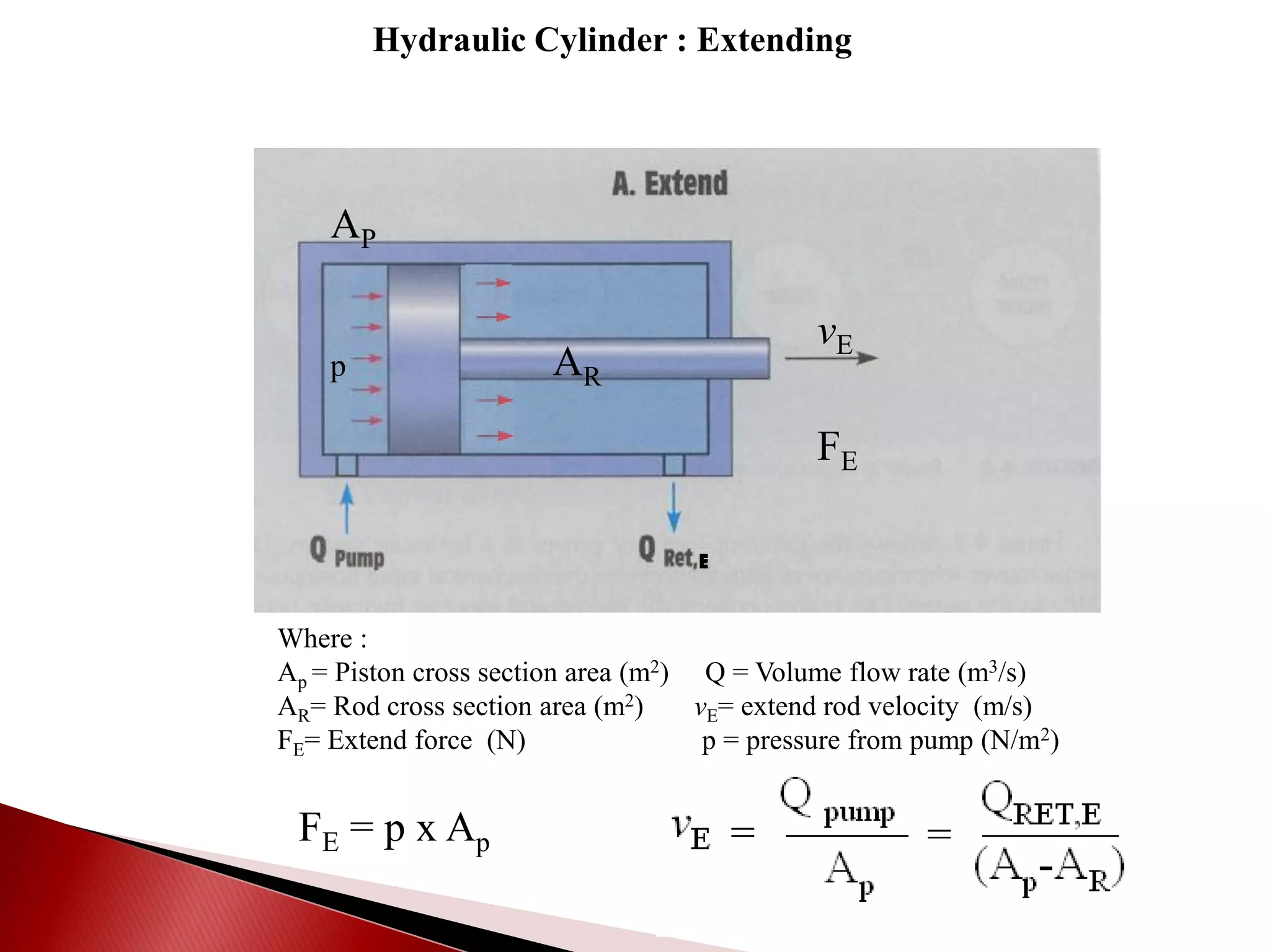
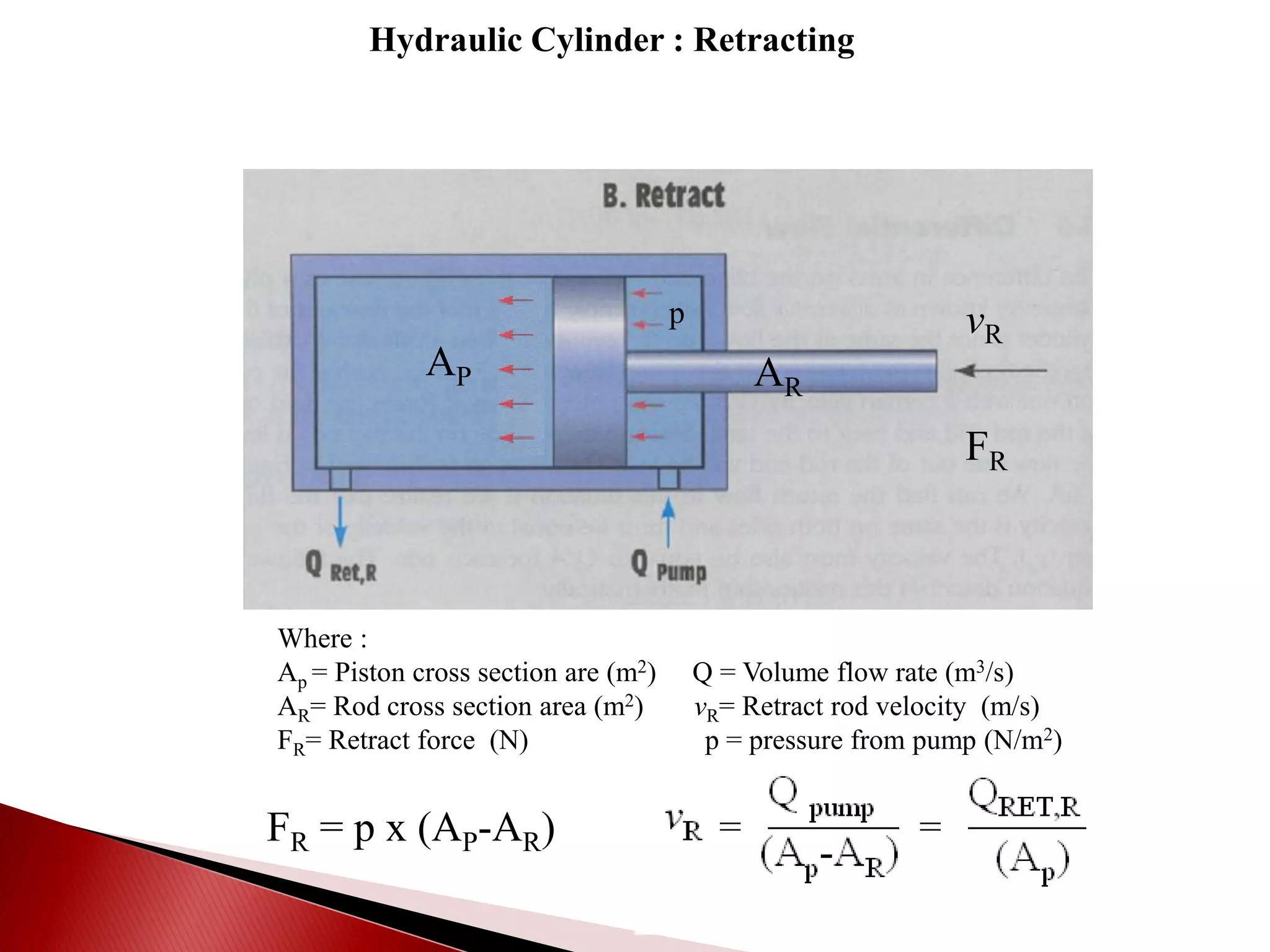
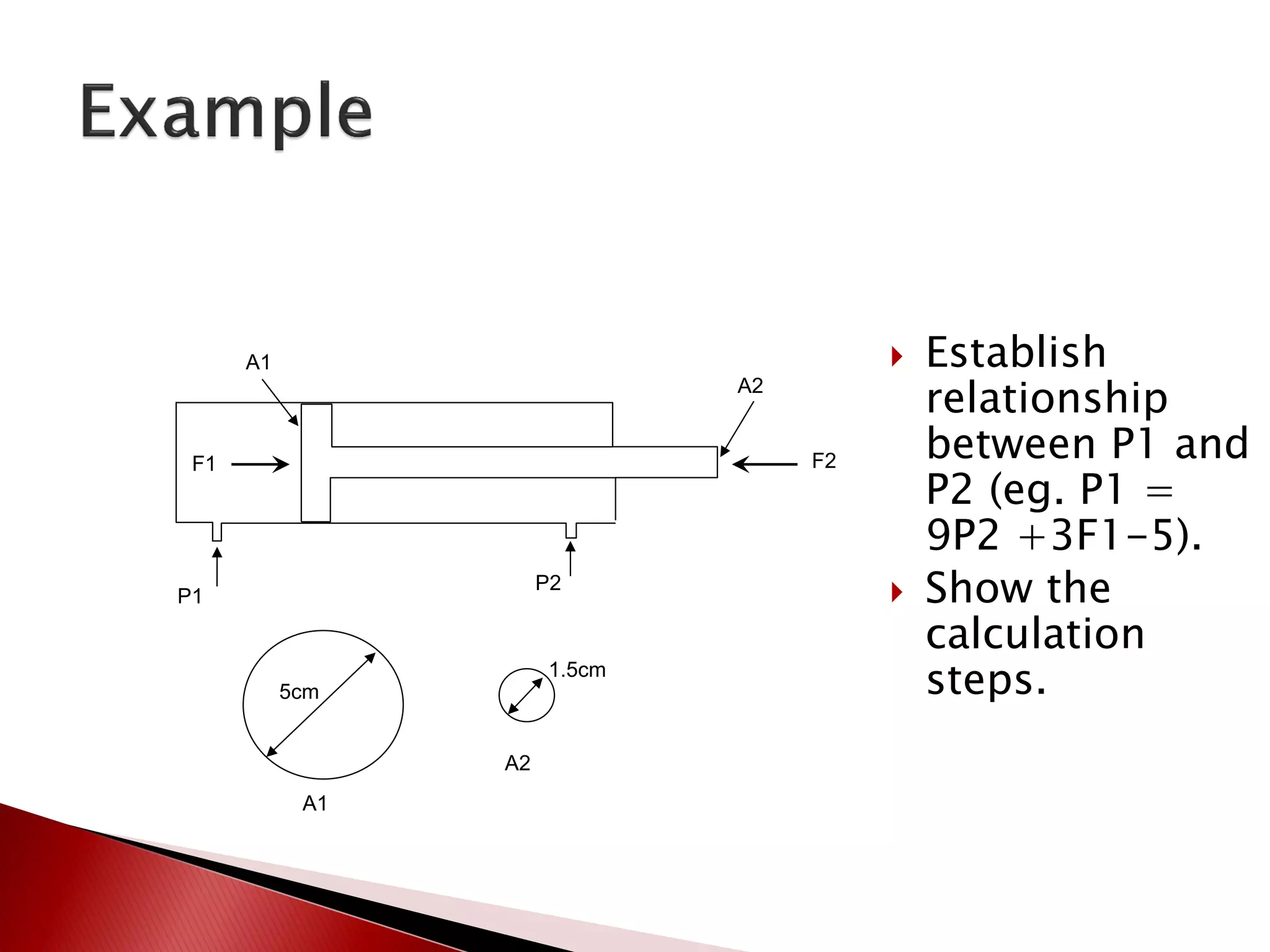
Hydraulic actuators convert hydraulic energy to mechanical motion or force. There are two main types: linear actuators like hydraulic cylinders, and rotary actuators like hydraulic motors. Hydraulic cylinders are further classified as single acting or double acting. Single acting cylinders use pressure on one side of the piston and a spring or external force for return, while double acting cylinders use pressure on both sides to push and pull the piston. Key parameters that determine cylinder selection and sizing include bore diameter, rod diameter, stroke length, working pressure, area ratio, and mechanical efficiency.

2.  Hydraulic actuators are installed to drive
loads by converting the hydraulic power into
mechanical power.
 The hydraulic actuators are classified into 2
category:
◦ Linear actuator - Hydraulic cylinders
◦ Rotary actuator - Hydraulic motors, rotary actuators

3.  Converts hydraulic energy to mechanical energy.
 Generates linear movements. Linear motors.
 Basic types:
o Single acting cylinder
o Double acting cylinder

4.  Only piston side is supplied with hydraulic fluid.
 Only work in one direction.
 Return stroke effected by spring or load.
 Applications:
◦ Lifting
◦ Clamping
◦ Moving workpiece

5. Single Acting Cylinder
 A single acting cylinder is only powered in one direction
 It needs another force to return it such as an external load
(e.g. in a car hoist or jack) or a spring.
 No hydraulic fluid is present on the low pressure side.

6.  To extend the cylinder
or to push the load,
pump flow and
pressure are sent to the
pressure port.
 When pressure is
released, the spring
automatically returns
the cylinder to the fully
retracted position.

7. Gravity Return Single Acting Cylinder : In Circuit

8. Hydraulic Cylinder : In Application

9.  Both piston surface is supplied with hydraulic fluids.
 Fluid power works in both directions (extend & retract)
 When piston extends, the fluid on rod are displaced in
reservoir.
 When piston retract, fluid in piston area are displaced
in reservoir.

10. Hydraulic Cylinder : Double Acting Cylinder
 A double acting
cylinder is powered
in both direction.
 In the case of
double-acting
cylinders, both
piston surfaces can
be pressurized.
 Pressure Port and
Vent port can be
change during
extending or
retracting.

11. Double Acting Cylinder : In Circuit

12.  Bore diameter
o Working pressure determined by bore diameter
o Larger diameter produces larger forces
 Piston rod diameter
o Normally 1/6 of bore diameter
 Stroke length
o Length by which the piston rod moves from one
extreme position to another extreme position

13.  Working pressure
o Pressure that can be handled by cylinder
o Limited by size of bore, rod and tube thickness
 Test pressure
o Pressure used during testing (by manufacturer)
o Normally 1.5~2 times of normal working pressure

14.  Area ratio
ϕ = AP/APR ; APR = AP – AST
AP : Area of Piston
AST : Area of Rod

15.  Cylinder is selected to suit application load (F = P × A).
 Can be used to calculate piston diameter. Even so,
hydraulic mechanical efficiency must be included,
2
. .
. 4
4
. .
hm
hm
hm
F p A
F d
A
p
F
d
p



 

 


16.  Standard bore diameter, dp
 Standard rod diameter, dst
25 32 40 50 60 63 80 100 125
φ dst (mm)
1.25 12 14 18 22 25 28 36 45 56
1.4 14 18 22 28 32 36 45 56 70
1.6 16 20 25 32 36 40 50 63 80
2 18 22 28 36 40 45 56 70 90
2.5 20 25 32 40 45 50 63 80 100

17.  A cylinder with area ratio 2:1 is to lift 40 kN load. The
max system pressure for pump is to be 160 bar.
Calculate the piston diameter, dp and piston rod
diameter dST for this system. The mechanical-hydraulic
efficiency of cylinder amounts is 0.95.

18.  Piston diameter, dp
24
; 40,000 ; 160 1600 /
. .
33.5
5.79
6
p
hm
F
d F N p bar N cm
p
cm
cm
 
   




19.  Piston rod diameter, dst
2
28.27
2
28.27
4
4.24
4.5
P P
PR P ST
ST
ST
A A
A A A
d
d
cm


 






20. Hydraulic Cylinder : Extending
FE = p x Ap
FE
AP
vE
AR
Where :
Ap = Piston cross section area (m2) Q = Volume flow rate (m3/s)
AR= Rod cross section area (m2) vE= extend rod velocity (m/s)
FE= Extend force (N) p = pressure from pump (N/m2)
p

21. Hydraulic Cylinder : Retracting
FR = p x (AP-AR)
AP AR
vR
FR
Where :
Ap = Piston cross section are (m2) Q = Volume flow rate (m3/s)
AR= Rod cross section area (m2) vR= Retract rod velocity (m/s)
FR= Retract force (N) p = pressure from pump (N/m2)
p

22.  Convert hydraulic energy to rotary mechanical
energy
 Motor capacity:
3
( )
( )
( )
( / min)
( )
M
p
V
Q n V
p pressure Pa
M torque Nm
V Geometricdisplacement capacity cm
Q Flowrate L
n speed rpm








23.  Example
◦ A motor with capacity of V = 10 cm3 is to operate
at a speed of 600 rpm. What flow rate is required by
the motor?

24.  Establish
relationship
between P1 and
P2 (eg. P1 =
9P2 +3F1-5).
 Show the
calculation
steps.
A1
A2
F1 F2
P1
P2
5cm
1.5cm
A1
A2

25. Cylinder Force : Examples

26. Cylinder Velocity : Examples

27. Cylinder Delivery: Examples
A
Q
v 
21 vv and