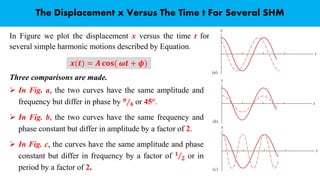
This document provides an overview of topics to be covered in Lecture 3 of the PHY-401 Waves and Oscillations course, including simple harmonic oscillation and mass attached to a spring. Simple harmonic motion occurs when the net force on an object follows Hooke's law and results in sinusoidal displacement over time. For a spring-mass system, applying Hooke's law and Newton's second law yields a differential equation relating displacement, time, spring constant, and mass. The solution to this equation gives the simple harmonic oscillation as a cosine function of angular frequency and time plus a phase constant. Comparisons are made between oscillations with different amplitudes, frequencies, and phases. Video lectures related to these topics are also provided.

1. PHY-401
Waves and Oscillations
BS Physics
4th Semester
Dr. Ejaz Ahmed
Department of Physics
Abdul Wali Khan University Mardan

2. Lecture 3: Topics to be Covered
1. Simple Harmonic Oscillation
2. Mass Attached to a Spring

3. Simple Harmonic Motion (SHM)
➢ Motion that occurs when the net force along the direction of motion obeys Hooke’s Law, or Motion
that repeats itself and the displacement is a sinusoidal function of time.
➢ Motion that occurs when the net force along the direction of motion obeys Hooke’s Law.
➢ The force is proportional to the displacement and always directed toward the equilibrium position.
➢ The motion of a spring mass system is an example of Simple Harmonic Motion (SHM).

4. Mass Attached to a Spring
By Hook’s Law 𝐹 = −𝑘𝑥
By Newton’s 2nd Law
𝐹 = 𝑚𝑎 = 𝑚
𝑑𝑣
𝑑𝑡
= 𝑚
𝑑2𝑥
𝑑𝑡2
= 𝑚 ሷ
𝑥
-----------(1)
-----(2)
From equations (1) and (2) we have;
𝐹 = 𝑚 ሷ
𝑥 = −𝑘𝑥
𝑚 ሷ
𝑥 + 𝑘𝑥 = 0
ሷ
𝑥 +
𝑘
𝑚
𝑥 = 0
ሷ
𝑥 + 𝜔2𝑥 = 0
where 𝜔2 =
𝑘
𝑚
𝜔 =
𝑘
𝑚
= 𝑎𝑛𝑔𝑢𝑙𝑎𝑟 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 = 2𝜋𝑓
x
x = 0
x = +A
x = -A
𝑇 = 2𝜋
𝑚
𝑘
= 𝑇𝑖𝑚𝑒 𝑝𝑒𝑟𝑖𝑜𝑑

5. x
x = 0
x = +A
x = -A
𝑥(𝑡) = 𝐴 cos( 𝜔𝑡 + 𝜙)
Phase
Amplitude
Phase constant
Angular frequency
Solution of the Equation
ሷ
𝑥 + 𝜔2
𝑥 = 0
𝑥(𝑡) = 𝐴 cos( 𝜔𝑡 + 𝜙)
ሷ
𝑥 = −𝜔2
𝑥
ሷ
𝒙 +
𝒌
𝒎
𝒙 = 𝟎

6. If the wave advances by a time 𝑻 = Τ
𝟐𝝅
𝝎 = 𝟐𝝅
𝒎
𝒌
the cosine function repeats
itself. This is called the time period of the oscillation i.e., the time in which the wave
repeats itself. Its unit is in sec.
𝑥(𝑡) = 𝐴 cos( 𝜔𝑡 + 𝜙)
𝝎 = 𝒂𝒏𝒈𝒖𝒍𝒂𝒓 𝒇𝒓𝒆𝒒𝒖𝒆𝒏𝒄𝒚 ൗ
𝒓𝒂𝒅𝒊𝒂𝒏𝒔
𝒔𝒆𝒄
𝑨 = 𝒂𝒎𝒑𝒍𝒊𝒕𝒖𝒅𝒆 𝒎 , for cosine function maximum displacement is ±1.
𝝓 = 𝒑𝒉𝒂𝒔𝒆 𝒂𝒏𝒈𝒍𝒆 𝒓𝒂𝒅𝒊𝒂𝒏𝒔
The frequency of the scalation is 𝒇 = Τ
𝟏
𝑻, so 𝒇 = Τ
𝝎
𝟐𝝅and it is in Hz.
𝝎𝒕 + 𝝓 = 𝒂𝒏𝒈𝒍𝒆

7. The Displacement x Versus The Time t For Several SHM
In Figure we plot the displacement x versus the time t for
several simple harmonic motions described by Equation.
➢ In Fig. a, the two curves have the same amplitude and
frequency but differ in phase by Τ
𝝅
𝟒 or 45°.
➢ In Fig. b, the two curves have the same frequency and
phase constant but differ in amplitude by a factor of 2.
➢ In Fig. c, the curves have the same amplitude and phase
constant but differ in frequency by a factor of Τ
𝟏
𝟐 or in
period by a factor of 2.
𝒙(𝒕) = 𝑨 𝐜𝐨𝐬( 𝝎𝒕 + 𝝓)
Three comparisons are made.

8. Video Lectures to Watch
1. https://www.youtube.com/watch?v=tNpuTx7UQbw (8.01x- Lect 10 - Hooke's Law, Springs,
Pendulums, Simple Harmonic Motion)
2. https://www.youtube.com/watch?v=GOdrEXTkWyI&list=PLIKpuUo6d5pIy313eSfqgHxx1P2cd5O7
n&index=181 (Energy in SHM)
3. https://www.youtube.com/watch?v=SmuCOSwuoOs&list=PLIKpuUo6d5pIy313eSfqgHxx1P2cd5O
7n&index=182 (Dynamics of SHM)