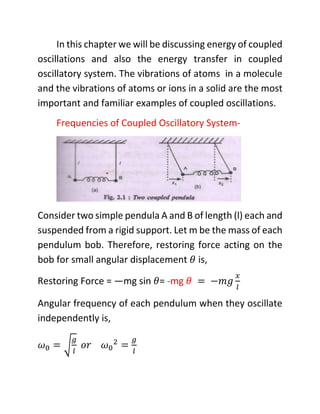
1) Coupled oscillators are oscillators connected such that energy can be transferred between them. Their motion is generally complex but can be described by normal modes. 2) Normal modes are patterns of motion where all parts of the system move sinusoidally with the same frequency and fixed phase relation. These are the natural frequencies of an oscillating system. 3) The document uses the example of two connected pendulums to illustrate normal modes. The pendulums can oscillate with two normal mode frequencies - one where they move in phase (antisymmetric mode) and one where they move out of phase (symmetric mode).

1. Coupled Oscillations
Introduction:
Coupled oscillators are oscillators connected in such
a way that energy can be transferred between them. The
general motion can be complex and may not be periodic.
However, we can find a co-ordinate frame in which each
oscillator oscillates with a well defined frequency called
normal mode. A normal mode of an oscillating system is a
pattern of motion in which all parts of the system move
sinusoidally i.e. simple harmonically with same frequency
and with a fixed phase relation. These normal modes of a
system are its natural frequencies. For any oscillating
system i.e. a physical object like a building, a bridge or a
molecule etc. has a set of normal modes whose natural
frequencies depend upon the shape, size, structure and
boundary conditions.
The most general motion of a system is a
superposition of its normal mode. In musical instruments
normal modes are called harmonics or overtones
Different modes can be excited quite independently.

2. In this chapter we will be discussing energy of coupled
oscillations and also the energy transfer in coupled
oscillatory system. The vibrations of atoms in a molecule
and the vibrations of atoms or ions in a solid are the most
important and familiar examples of coupled oscillations.
Frequencies of Coupled Oscillatory System-
Consider two simple pendula A and B of length (l) each and
suspended from a rigid support. Let m be the mass of each
pendulum bob. Therefore, restoring force acting on the
bob for small angular displacement 𝜃 is,
Restoring Force = —mg sin 𝜃= -mg 𝜃 = −𝑚𝑔
𝑥
𝑙
Angular frequency of each pendulum when they oscillate
independently is,
𝜔0 = √
𝑔
𝑙
𝑜𝑟 𝜔0
2
=
𝑔
𝑙

3. Restoring force= - m 𝜔0
2
𝑥
If pendula A and B are connected by a spring of spring
constant (k) as shown in fig. 2.1(a) and then the bobs are
slightly displaced from their equilibrium position, the two
pendula begin to oscillate.
If x1 and x2 are the displacements of the pendula at any
time (t) then depending on whether x1 > x2 or x1 < x2, the
spring is either compressed or stretched to produce a
tension k (x2 — x1) in the spring. If x2 > x1, then the
tension in the spring will assist the acceleration of A and
at the same time will oppose the acceleration of B.
Therefore, equations of motions for two pendula are,

4. Equations (2.1) and (2.2) are coupled i.e. they involve both
variables x1and x2 i.e. motion of one pendulum is affected
by the motion of other the pendula A and B are coupled.
To solve the above differential equations, we have to
decouple the equations. This can be done by adding and
subtracting eqns. (2.1) and 2.2 to get.
If we choose new co-ordinates as, q1 = x1+ x2 and q2 -= x1
– x2 , then

5. Equation &ins. (2.3) and (2.4) reduce to simple forms,
Equations (2.5) and (2.6) represent simple harmonic
motions with frequencies
𝜔1 = 𝜔0 = √
𝑔
𝑙
and 𝜔2 = √𝜔0
2 + 2𝜔2 where 𝜔2 =
𝑘
𝑚
Thus, coupled pendula oscillate simple harmonically with
two frequencies 𝜔1 and 𝜔2, which are known as normal
modes in which all the particles of the oscillating body
undergo same displacement from mean position at a
given time. Whatever may be the complicated motion of
coupled pendula, they can be described in terms of
normal Nodes. using the co-ordinates q1 and q2 which are
called normal co-ordinates.
2.3 : Normal Modes and Normal Co-ordinates

6. When a coupled system oscillates in a single mode, then
oscillating parts have same frequency and phase constant.
In a given mode the relative displacements are governed
by a characteristic constant i.e ratio of amplitudes.
The solutions for differential equations (2.5) and (2.6) can
be expressed either in the form of sine or cosine functions.
∴ 𝑞1=𝐴1 𝐶𝑜𝑠𝜔1𝑡 and
∴ 𝑞2 =𝐴2 𝐶𝑜𝑠𝜔2𝑡
Therefore, in terms of the original coordinates 𝜘1 and 𝜘2 ,
the solution become,
𝜘1 =
1
2
(𝑞1 + 𝑞2)
=
1
2
(𝐴1 𝐶𝑜𝑠𝜔1𝑡 + 𝐴2 𝐶𝑜𝑠𝜔2𝑡)
𝜘2 =
1
2
(𝑞1 − 𝑞2)
=
1
2
(𝐴1 𝐶𝑜𝑠𝜔1𝑡 − 𝐴2 𝐶𝑜𝑠𝜔2𝑡)
Case I : If 𝐴2 = 0, then equations (2.7) and (2.8) reduce to
𝜘1 =
𝐴1
2
𝐶𝑜𝑠𝜔1𝑡 and
𝜘2 =
𝐴1
2
𝐶𝑜𝑠𝜔1𝑡

7. 𝜘1 = 𝜘2
In this case both pendula oscillate with same frequency
𝜔1 = 𝜔2 = √
𝑔
𝑙
and they oscillate in-phase as shown in
fig. 2.2 (i) i.e both pendula move to the left and then to
the right simultaneously. In this case the spring is neither
stretched nor compressed i.e. both pendula
independently with same frequency 𝜔1 = 𝜔0 and this is
called a normal mode . This normal mode is also known as
antisymmetric mode.
Case II-: If 𝐴1= 0, then equations (2.7) and (2.8) reduce to

8. 𝜘1 =
𝐴2
2
𝐶𝑜𝑠𝜔2𝑡 and
𝜘2 = −
𝐴2
2
𝐶𝑜𝑠𝜔2𝑡
𝜘1 = − 𝜘2
Thus both pendula oscillate with same frequency.
𝜔2 = ( 𝜔0
2
+ 2𝜔2
)
1
2 = (
𝑔
𝑙
+ 2
𝑘
𝑚
)
1
2
In But they are out-of-phase as shown in fig. 2.2 (ii) and
(iii) i.e. both pendula move either outwards or inwards
when the spring is respectively Stretched or compressed.
It is also known as symmetric mode. It may also be noted
that 𝜔2 > 𝜔1 i.e. the frequency of symmetric is higher
than that of antisymmetric mode. Hence, antisymmetric
mode (𝜔1 )is also called slow oscillation while symmetric
mode (𝜔2 ) is known as fast mode.
Normal Co-ordinates-For any arbitory motion of coupled
system the quantity q1= x1+ x2 oscillates with frequency
𝜔1 and the quantity, q2 = x1 — x2 oscillates, with
frequency (𝜔2 ), where x1 and X2 are the displacements
of the two pendula at any time (t). These combination of
the coordinates given by q1 and q2 are known as normal

9. coordinates. These normal coordinates q1 and q2 are
associated with the normal modes 𝜔1 𝑎𝑛𝑑 𝜔2 frequencies
given by normal modes. Thus, any arbitrary motion of
coupled system may be considered as the linear
combination of normal modes.