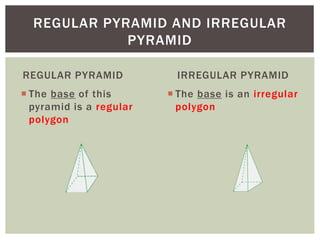
This document defines and provides details about different types of pyramids in mathematics. It begins with a brief history of pyramids and Egyptian mathematics. It then defines what a pyramid is and describes right pyramids, oblique pyramids, regular pyramids, irregular pyramids, convex pyramids, and concave pyramids. The document also covers types of pyramids based on their base, surface area, volume, frustums of pyramids, and includes examples and formulas. References for additional information on pyramids are provided at the end.

1. MEMBERS:
MEGHA,
THILINI,
MEGHASHYAM
, FARAHIYAH,
ATIQAH,
YAP YONG
XING
MATHEMATICS
PYRAMID

2. BRIEF HISTORY OF PYRAMIDS
The first precision measurements
of the pyramid were made by
Egyptologist- Sir Flinders Petrie in
1880-82 and published as The
Pyramids and Temples of Gizeh.
The great pyramids of Gizeh are the
most magnificent man made
structures in history
Egyptian mathematics was
dominated by arithmetic, with an
emphasis on measurement and
calculation in geometry. They were
only concerned with practical
application .
WHAT IS PYRAMID

3.  A pyramid is a three dimensional shape whose base is a
polygon. Each corner of a polygon is a singular apex, which
gives the pyramid its distinctive shape. each base edge and
apex form a triangle
WHAT IS PYRAMID

4. The faces of a pyramid are all triangles. If
he base is a regular polygon, the triangles
are all congruent(that is same shape and
size), and isosceles (two sides the same
length)
if the apex is directly over the centre of a
regular base as it is above, it's called a
right pyramid.
if the apex is not the centre of the base, it
is called an oblique pyramid and the faces
are not congruent.
WHAT IS PYRAMID

5. • Right Pyramid vs Oblique Pyramid
• Regular Pyramid vs Irregular Pyramid
• Convex Pyramid vs Concave Pyramid
• Types of Pyramids by their base
TYPES OF PYRAMID

6. RIGHT PYRAMID
 The apex lies directly above
the midpoint of the base
 It has isosceles triangle as
its faces
 Its base is a regular
polygon
OBLIQUE PYRAMID
 The apex is not directly
above the center of its base
 The faces are not isosceles
triangle
 It has a square base
RIGHT PYRAMID AND OBLIQUE PYRAMID

7. REGULAR PYRAMID
 The base of this
pyramid is a regular
polygon
IRREGULAR PYRAMID
 The base is an irregular
polygon
REGULAR PYRAMID AND IRREGULAR
PYRAMID

8. CONVEX PYRAMID
 It has convex polygon
as its base
- Convex means
extending outward
CONCAVE PYRAMID
 It has concave polygon
as its base
- Concave means having
an outline that goes
inward
CONVEX PYRAMID AND CONCAVE
PYRAMID

9. TRIANGULAR PYRAMID
The base is a triangle.
PENTAGONAL PYRAMID
The base is a pentagon.
SQUARE PYRAMID
The base is a pentagon.
HEXAGONAL PYRAMID
The base is a pentagon.
TYPES OF PYRAMID BY THEIR BASE

10. SURFACE AREA
The lateral surface area of a regular pyramid is the sum of the areas of its lateral
faces.
The total surface area of a regular pyramid is the sum of the areas of its lateral
faces and its base.
The general formula for the lateral surface area of a regular pyramid is
L.S.A.=1/2 pL
where p represents the perimeter of the base and l the slant height.

11. SURFACE AREA
The general formula for the total surface
area of a regular pyramid is
T.S.A.=1/2 pl + B
Where p represents the perimeter of the
base, l the slant height and B the area of
the base.

12. Find the lateral surface area of a regular
pyramid with a triangular base if each edge
of the base measures 88 inches and the slant
height is 55 inches.
The perimeter of the base is the sum of the
sides.
L.S.A = 1/2pl
p=3(8)=24inches
l= 5
L.S.A.=1/2(24)(5)=60inches^2
LATERAL SURFACE AREA

13. Find the total surface area of a regular pyramid with a square base if
each edge of the base measures 16 inches, the slant height of a side is
17 inches and the altitude is 15 inches.
T.S.A = 1/2pl + B
The perimeter of the base is 4 x s since it is a square.
p=4(16)=64inches
The area of the base is s^2
B=16^2 = 256 inches
T.S.A.=1/2(64)(17)+256
=544+256
=800inches^2
TOTAL SURFACE AREA

14.  Definition: The number of cubic units that will exactly fill a
pyramid.
VOLUME
FORMULA OF VOLUME OF
PYRAMID =
1/3 × BASE AREA ×
PERPENDICULAR HEIGHT

15.  Base as B and Height as H
 B is the area of the base of the
pyramid
H is its height. The height must
be measured as the vertical
distance from the apex down to
the base.
VOLUME
Prism can be cut into three
Different pyramid that do not Overlap . It can be shown
that these pyramid have the same volume .
Within the prism whose volume its base multiplied by its height is BH . If the
three pyramid are equal volume , then the volume of each pyramid is Bh/3

16. VOLUME
This pyramid has
base ABC and
vertex E.
This pyramid has
base ACF and
vertex E.
This pyramid
has base ACF
and vertex E.
Every pyramid, is EXACTLY one third the
volume of a triangular prism with the
same base and height . So the volume
of ANY Pyramid is (Area of its Base x
height) divided by three.

17.  It is a result of cutting a pyramid by a
plane parallel to the base and
separating the part containing the
apex.
 The lateral faces of a pyramidal
frustum are trapezoids
 The height of the pyramidal frustum is
the perpendicular distance
 The apothem is the height of any of its
sides
FRUSTUM OF PYRAMID

18. UNFOLD OF A PYRAMIDAL FRUSTUM

19. APOTHEM OF PYRAMIDAL FRUSTUM
To calculate, we have to have:
the height, the apothem of the
biggest base and the apothem of
the minor base.
Then apply the Pythagorean
theorem to determine the length of
the hypotenuse of the shaded
triangle to obtain the apothem
 Hypotenuse = square root of
(base2+ altitude2)
 So hypotenuse is equal to square
root of base square plus altitude
square

20.  Area is equal to perimeter of the large base plus perimeter of
the small base divided by two multiplied by the apothem of
the truncated pyramid
 Volume is equal to height divide by 3 multiplied by (area of
large base times small base plus square root of area of large
times small)
AREA AND VOLUME OF PYRAMIDAL
FRUSTUM

21.  http://hotmath.com/hotmath_help/topics/surface-area-of-a-
pyramid.html
 http://www.ditutor.com/solid_gometry/frustum_pyramid.html
 http://www.mathsisfun.com/geometry/pyramids.html
 http://www.ditutor.com/solid_gometry/types_pyramids.html
 http://study.com/academy/lesson/pyramid-in-math-
definition-lesson-practice-problems.html
REFERENCES