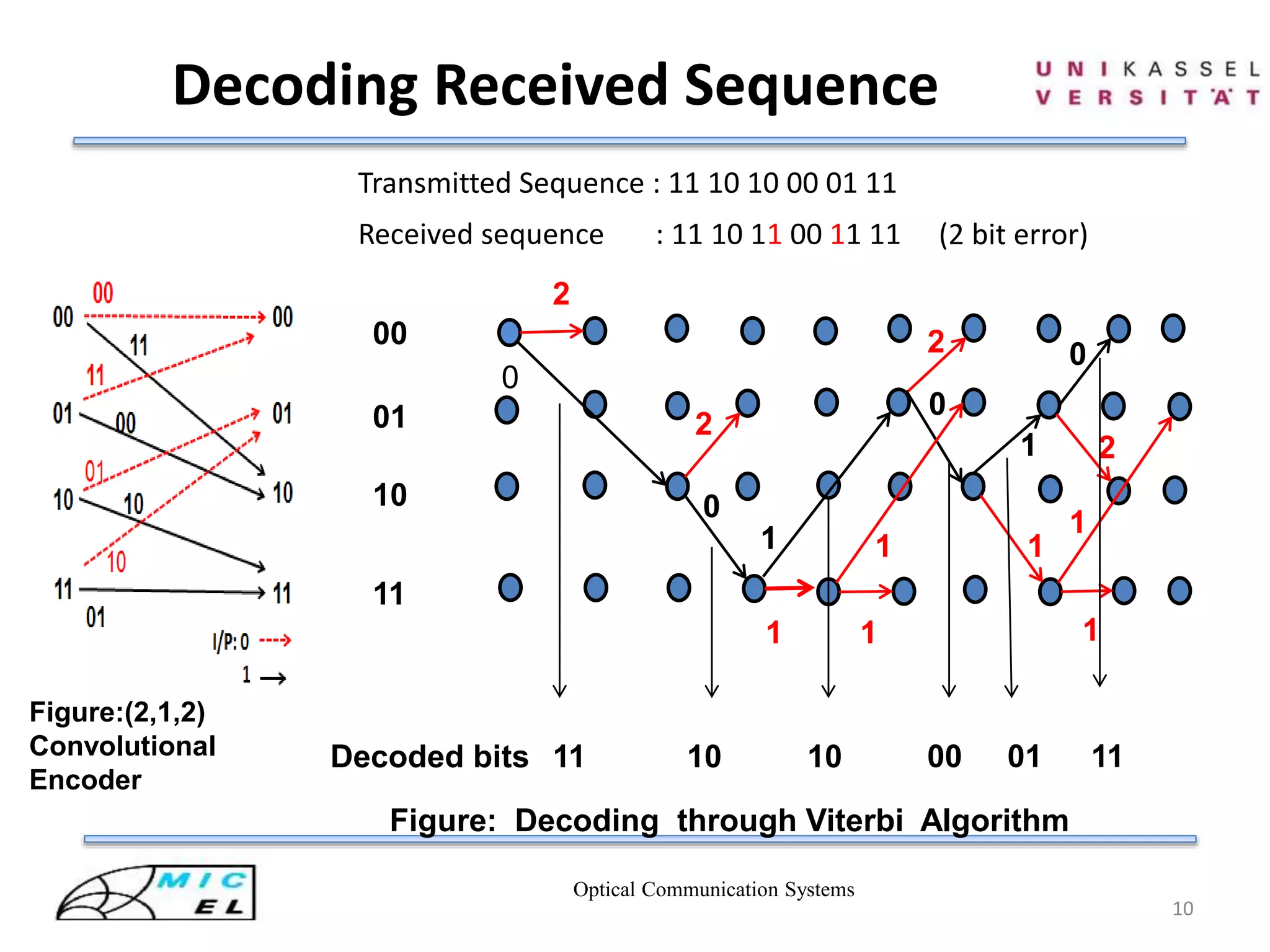
This document discusses Viterbi decoding in optical communication systems. It begins with an introduction and overview. It then covers electronic circuits for conversion, convolutional encoding including trellis diagrams, and the Viterbi algorithm for optimum decoding including computing metrics, path selection, and decoding a received sequence. It discusses the complexity of the Viterbi algorithm and recent advances like lazy Viterbi. In the end it provides a summary and references.

1. Optical Communication Systems
1
Viterbi-Decoder in Optical
Communication Systems
Prepared By : Anisuzzaman Boni
Mat No : 33109062
Date : 27th May 2014

2. Optical Communication Systems
2
Table of Contents
 Introduction
 Electronics Circuits for Conversion
 Convolutional Encoder
• Operation
• Trellis Diagram
 Optimum Decoding-Viterbi Algorithm
• Computing the Correlation Metrics
• Metrics Selection criteria
• Observation
 Decoding Received Sequence
 Complexity of Viterbi Algorithm
 Recent Advancement
 Reference
 Summary

3. Optical Communication Systems
3
Modulator
Light Source
Transmitted
Circuit
Demodulator Decoder
Fiber Optic
Cable
Encoder
Digital
Bits
01101100
00101001
Figure: Generic Model of Optical Communication System
Introduction
Electronic
Circuits
Trans. Rate In Gb/s

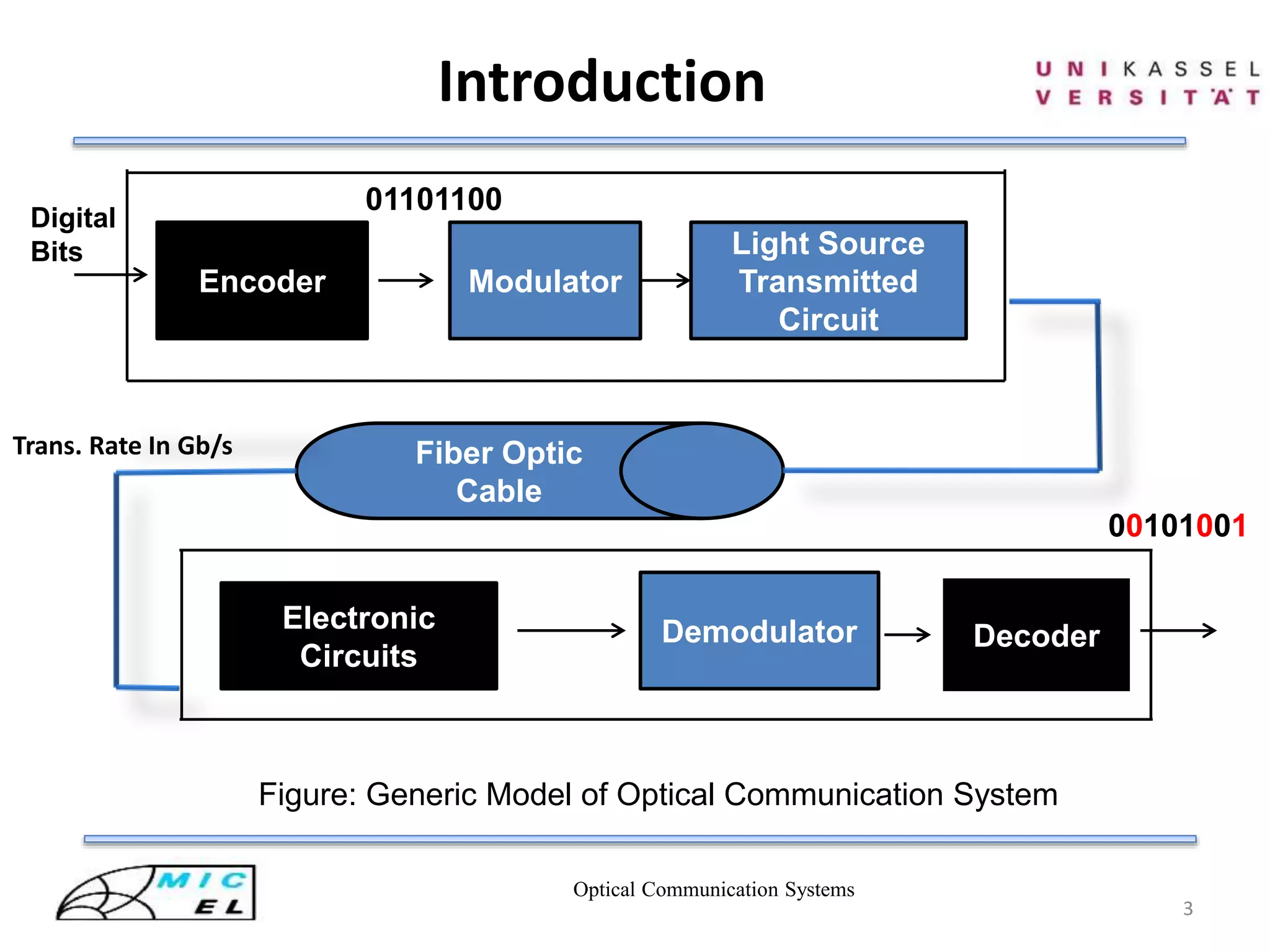
4. Optical Communication Systems
4
Figure : Block diagram of MLSE based receiver of OC-192 fiber links
Electronic Circuits for Conversion
9.9Gbps
Viterbi Decoding
Ref [3]

5. Optical Communication Systems
5
Convolutional Encoder
Features
• Code generated by passing the information into finite state shift register
• Code word-Entire data stream
• Denoted by (n,k,L) code
• Code perfectly describe by
Trellis diagram-Key concept for Viterbi algorithm
State diagram
• Better code to reach Theoretical Shannon limit

6. Optical Communication Systems
6
Convolutional Encoder
mj-2mj-1mj X1 X2
Shift Register
Encoded Bits
Figure: (2,1,2)bit Convolutional Encoder
Operation
I/P P/S N/
S
X1=mj
+mj-2
X2=mj+mj-1
+mj-2
O/P
0 0 0 00 0+0=0 0+0+0=0 00
1 0 0 10 1+0=1 1+0+0=1 11
0 0 1 00 0+1=1 0+0+1=1 11
1 0 1 10 1+1=0 1+0+1=0 00
0 1 0 01 0+0=0 0+1+0=1 01
1 1 0 11 1+0=1 1+1+0=0 10
0 1 1 01 0+1=1 0+1+1=0 10
1 1 1 11 1+1=0 1+1+1=1 01
P/S:Present State
N/S:New State
I/P:Input
O/P:Output
1 00 0 1
0 1
[2]

7. Optical Communication Systems
7
Trellis Diagram
I/P P/S N/S O/P
0 0 0 00 00
1 0 0 10 11
0 0 1 00 11
1 0 1 10 00
0 1 0 01 01
1 1 0 11 10
0 1 1 01 10
1 1 1 11 01
00
01
10
11
00
01
10
11
I/P: 0
1
00
11
11
00
01
10
10
01
Figure: Trellis diagram for (2,1,2) convolutional code
[2]

8. Optimum Decoding- Viterbi Algorithm
Optical Communication Systems
8
Computing the Correlation Metrics
• Searching through trellis for probable sequence /path
• Hamming Metrics Computation based on Hamming Distance
• Hamming Distance - the weight difference between two code words
- the no of position where two code words differ
Transmitted
Code word : 010100110
Hamming Weight
4
Received
Code word
: 100100010 3
Hamming Distance : 3

9. Optical Communication Systems
9
Metrics Selection criteria
• Select the path having higher path metrics
• Correlation path metrics CM(0),CM(1),CM(2)
Compare the metrics and if CM(0) > CM(1) >CM(2)
Select CM(0) as Survivor path and discard else path from consideration
• Same procedure repeat at each stages of trellis when new bits are
received
Observation
• Survivor paths minimize the probability of error for the received
information
Optimum Decoding-Viterbi Algorithm

10. Optical Communication Systems
10
Decoding Received Sequence
Transmitted Sequence : 11 10 10 00 01 11
Received sequence : 11 10 11 00 11 11 (2 bit error)
00
01
10
11
2
0
2
0
1
1
2
0
1
1
0
2
1
11
1
11 10 10 00 01 11Decoded bits
Figure:(2,1,2)
Convolutional
Encoder
Figure: Decoding through Viterbi Algorithm

11. Optical Communication Systems
11
Complexity of Viterbi Algorithm
Computational Complexity
• Any trellis has 2k(L-1) states
• 2k(L-1) surviving paths and 2k(L-1) metrics
• Only one path survive (most Probable path)
• Needed large memory
• Complexity increases exponentially with k and L

12. Recent Advancement
Optical Communication Systems
12
Lazy Viterbi Algorithm
• Applicable for both block and convolutional code
• Much faster compare to original one
• Running time does not depend on the constraint length
• Algorithms work by not expanding any nodes until
it really needs to
Practically found:
Code with constraint length 6,the Lazy algorithm is about 50% faster
than normal Viterbi Algorithm when SNR > 6 dB
Ref [4]

13. Optical Communication Systems
13
Summary
• Most Optimum although having some drawbacks
• Very efficient to decode a large no of data
• Algorithm very easy to understand and implementing
in software is also easy
• Algorithm universally used in CDMA,GSM technology, satellite,
Wireless LAN

14. Optical Communication Systems
14
Reference
2. Enrico Forestieri Optical Communication Theory and Techniques .3rd
edition. 2005
4. Jhon,ibrahim. A Fast Maximum-Likelihood Decoder forConvolutional Codes.
Available at:http://people.csail.mit.edu/jonfeld/pubs/lazyviterbi.pdf
3. Hyeon,jonathan,jinki.An MSLE Receiver for Electronic Dispersion Compensation of
OC-192 Fiber Links,IEEE Journal of Solid State Circuits.Vol.41,No.11,November2006
1. Arunlal,Hariprasad.An efficient viterbi decoder. International Journal
Advanced Information Technology (IJAIT) Vol. 2, No.1, February 2012