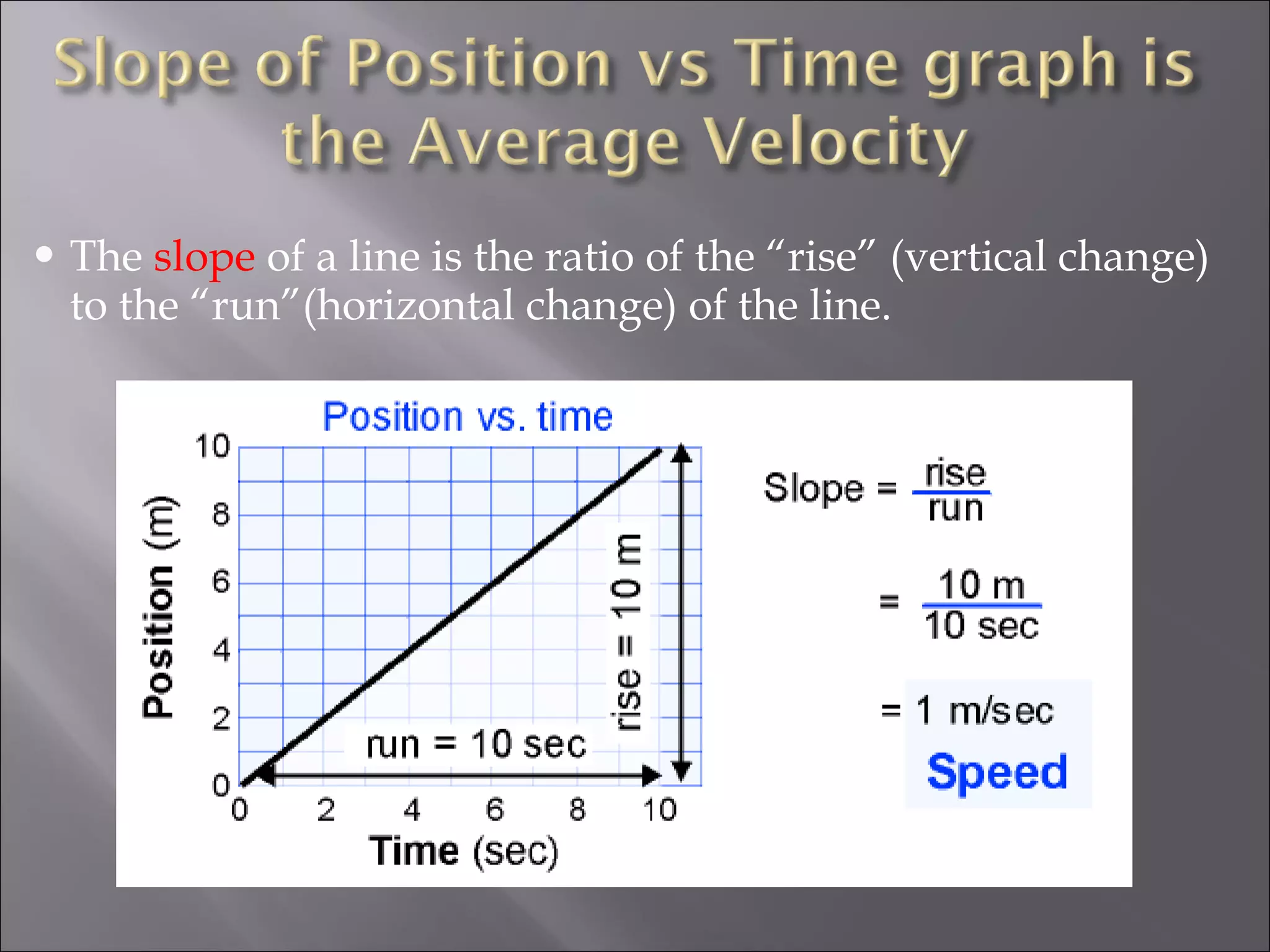
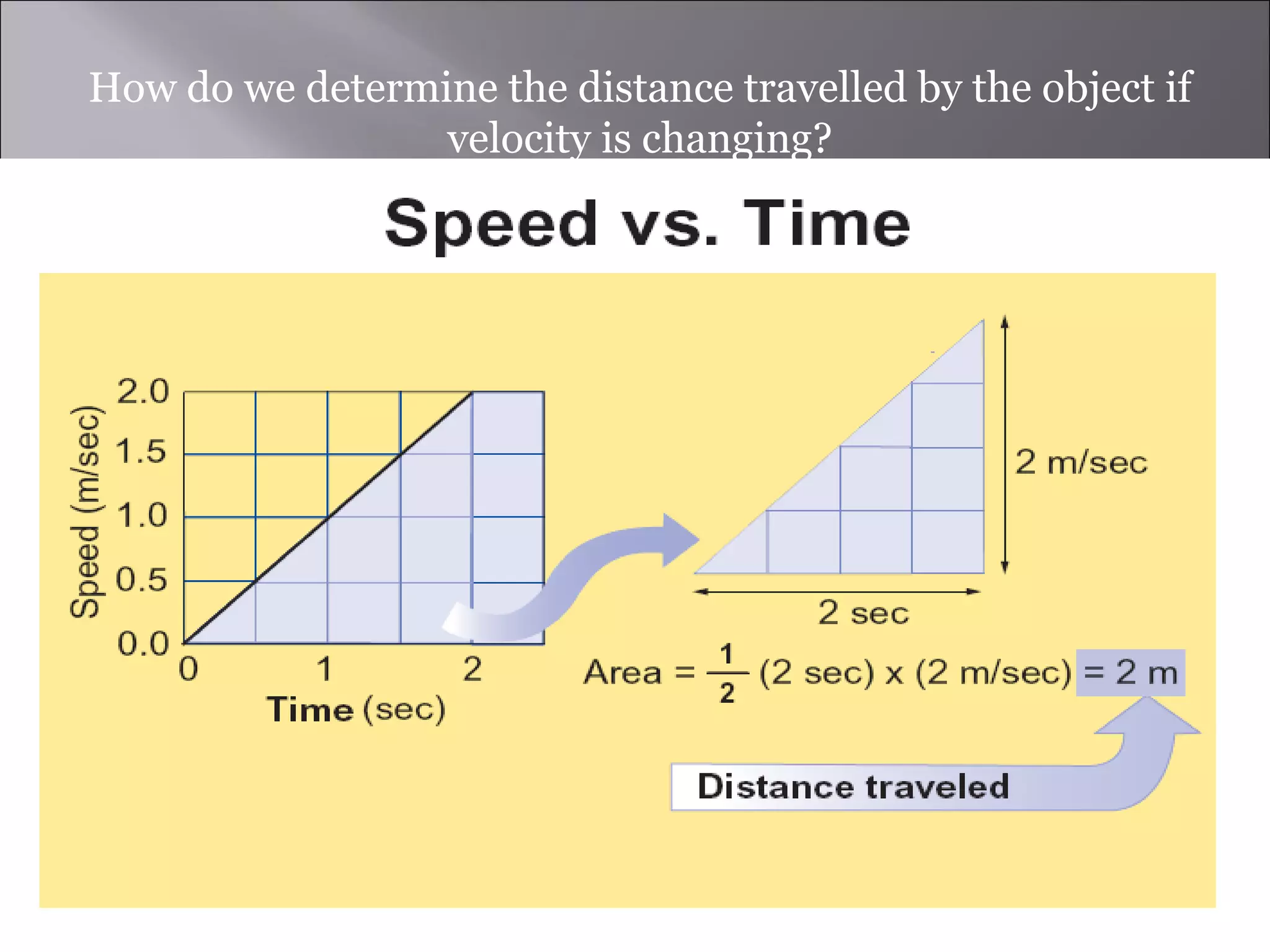
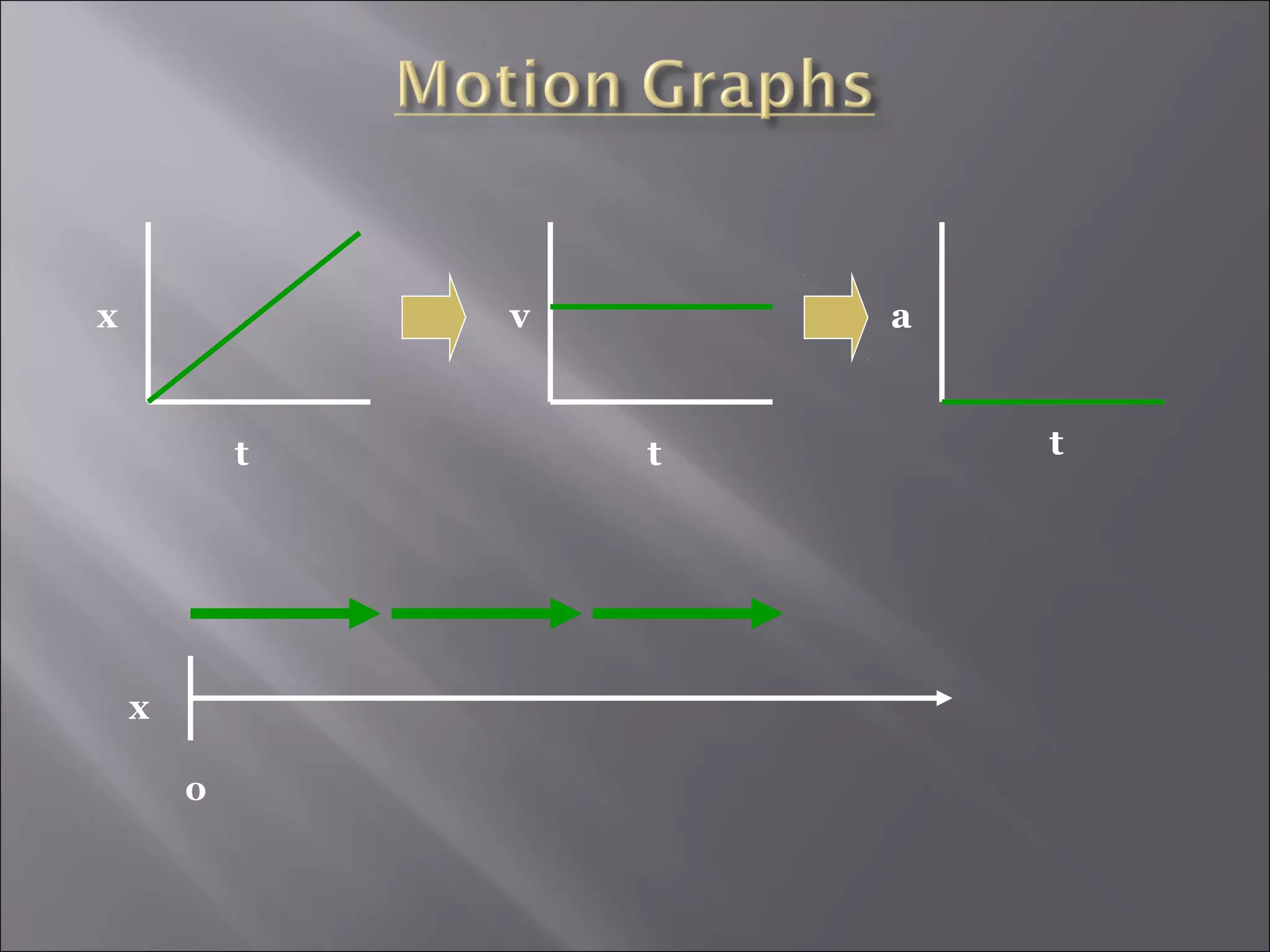
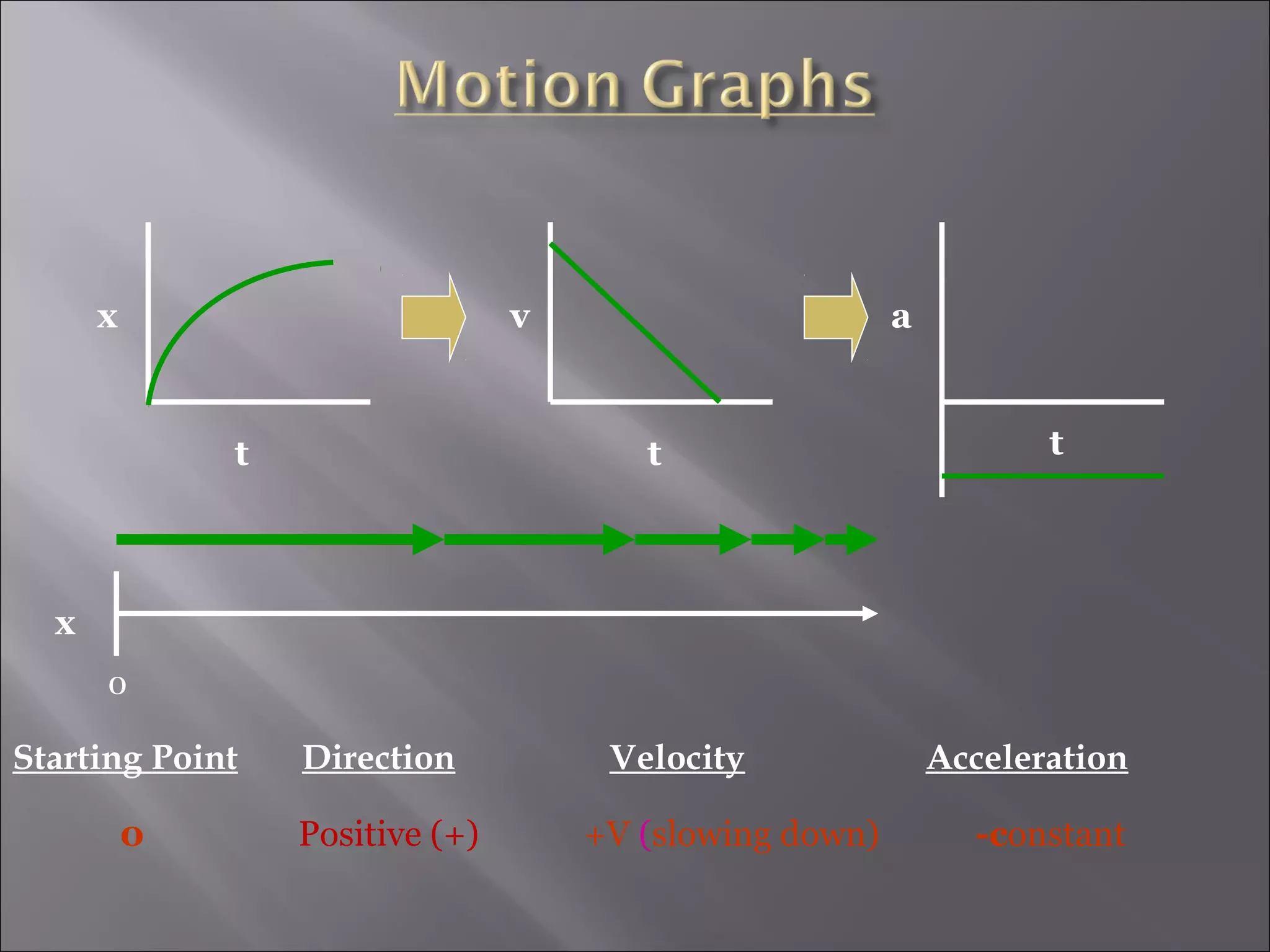
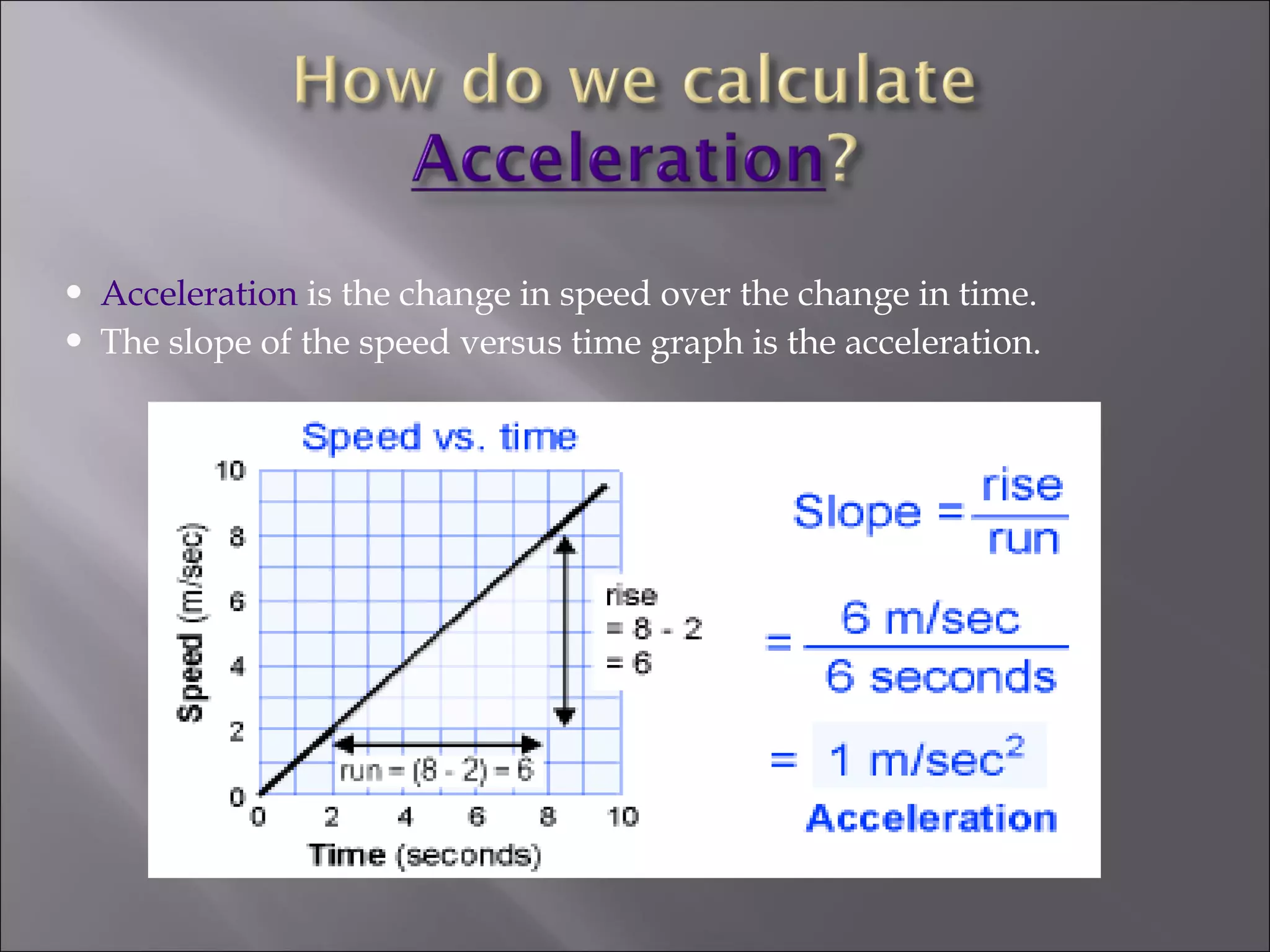
This document provides information about key concepts in kinematics including: - Velocity is defined as the rate of change of an object's position over time. Instantaneous velocity shows an object's speed at a moment in time. - Acceleration is defined as the rate of change of an object's velocity over time. It can be determined from the slope of a velocity-time graph. - The direction and sign of velocity and acceleration determine whether an object is speeding up or slowing down. Positive acceleration means speeding up while negative acceleration means slowing down.

2. v = d
t
Distance traveled (m)
Time taken (sec)
Average Velocity
(m/sec)
Instantaneous Velocity: the speed at any given
moment (like what your speedometer shows)

3.  The slope of a line is the ratio of the “rise” (vertical change)
to the “run”(horizontal change) of the line.

4.  On a Velocity vs Time graph constant velocity is a straight
line

5. Area under the velocity vs time graph is equal to the
distance travelled.

6.  Motion Diagram: Is a more sophisticated dot
diagram that conveys more information about
the situation.
•What do the arrows indicate?
•What does the length of each arrow indicate about the
motion of the object?

7.  What must you do to the first velocity arrow to get
the second velocity arrow? What direction? How
much?
•The arrow you drew to show the difference between the
velocity arrows is called a ∆v or change in velocity arrow.
•What does the ∆v arrow tell you about the motion of the
object?

10.  Using the video of the falling object we have collected the
following data:
 Draw a motion diagram.
 Plot a position time graph.
 Does this object represent an object with constant velocity?
Explain how you know.

11.  Acceleration is a vector quantity that is defined as the
rate at which an object changes its velocity
 There are 3 types of acceleration:
 If an object is increasing in speed (+ acceleration)
 If an object is decreasing in speed (- acceleration, also called
deceleration)
 Or if the object changes direction (+ or -)

12.  Acceleration is the change in speed over the change in time.
 The slope of the speed versus time graph is the acceleration.

15. How do we determine the distance travelled by the object if
velocity is changing?

18. 0
av
tt
x
t
x

19. Starting Point Direction Velocity Acceleration
0
x av
ttt
x
0 + Positive + V (speeding up) +constant

20. Δv from +5 to +10 m/s requires
a +5 m/s/s acceleration!
V (m/s) a (m/s/s)
0 +5
+ 5 + 5
+10 + 5
15 + 5

21. Starting Point Direction Velocity Acceleration
0
av
ttt
x
x
Positive (+) +V (slowing down) -constant
0

22. V (m/s) a (m/s/s)
+ 10 - 5
+ 5 - 5
0 - 5
Δv from +10 to + 5 m/s requires
a - 5 m/s/s acceleration!

23. Starting Point Direction Velocity Acceleration
0
x a
tt
v
t
x
above negative (-) -V (speeding up) -constant

24. Δv from -5 to -10 m/s requires
a -5 m/s/s acceleration!
Direction is negative (-), velocity is increasing (+)
Therefore acceleration is (-)
V (m/s) a (m/s/s)
0 -5
- 5 - 5
-10 - 5
-15 - 5

25. Starting Point Direction Velocity Acceleration
0
a
t
x
t
x
v
t
above negative (-) - V (slowing down) +constant

26. V (m/s) a (m/s/s)
- 10 + 5
- 5 + 5
0 + 5
Δv from -10 to -5 m/s requires
a +5 m/s/s acceleration!
Direction is (-), velocity is slowing down (-)
Therefore acceleration is (+)

27. V E L O C I T Y
A
C
C
E
L
E
R
A
T
I
O
N
+ -
+
Moving positive
direction; Speeding up
+ acceleration
Moving negative
direction; Slowing down
- acceleration
-
Moving positive
direction; Slowing down
- acceleration
Moving negative
direction; Speeding up
+ acceleration

28. Direction of Motion Action/Sign of
Velocity
Sign of Acceleration
Determining signs for velocity and acceleration
Increasing speed
+ direction +
Decreasing speed
+ direction
-
-
Increasing speed
- direction
Decreasing speed
- direction
+