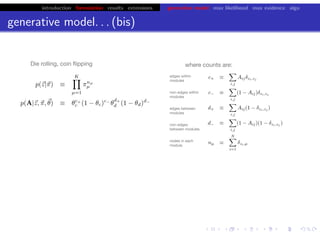
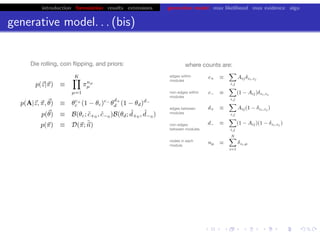
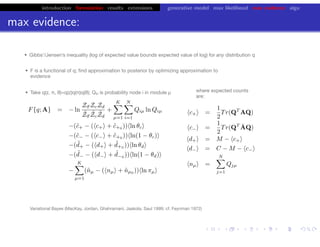
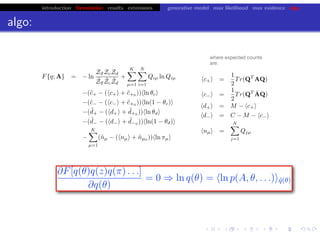
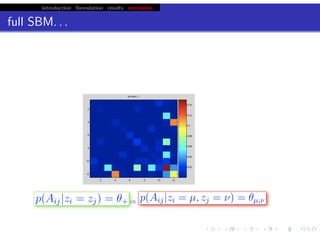
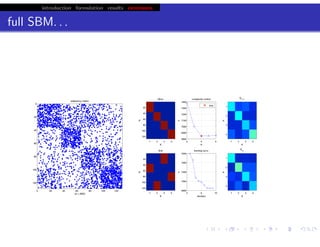
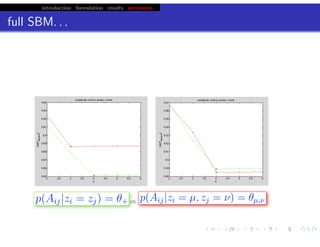
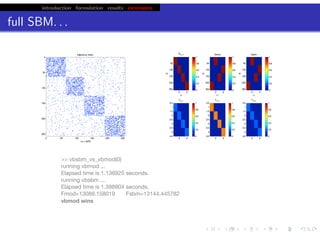
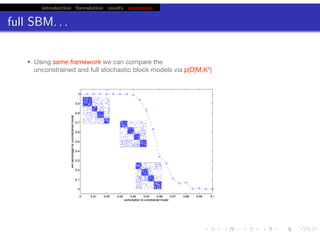
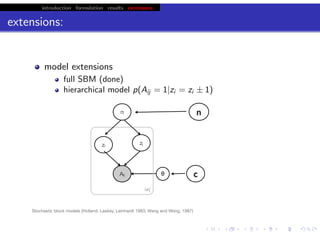
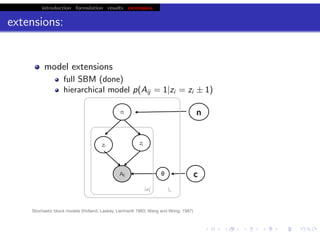
This document discusses hierarchical variational Bayesian methods and their applications in modeling biological data, particularly in network analysis. It addresses challenges such as overfitting and resolution limits in community detection within biological and social networks. The presentation is supported by algorithms and formulations for generative models, highlighting the importance of variational methods in inference and model selection.









































![bio+stats vbem/networks hierarchical biological challenges inference model selection
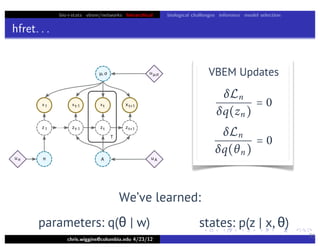
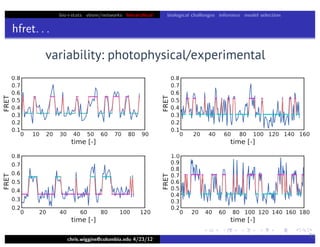
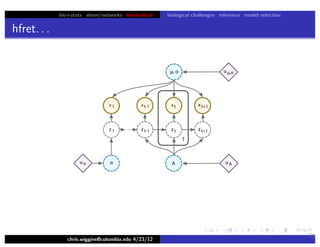
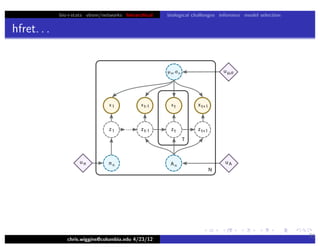
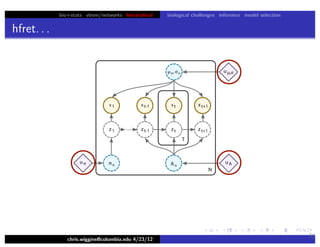
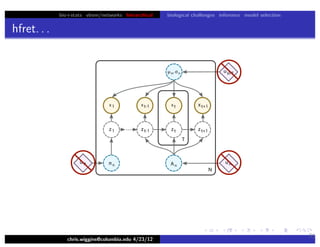
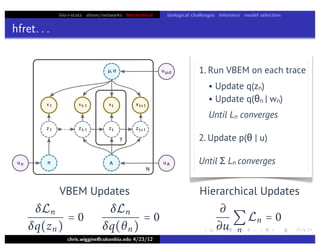
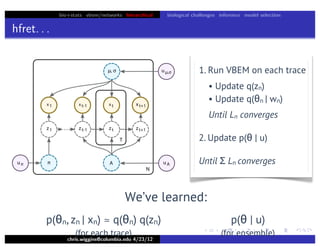
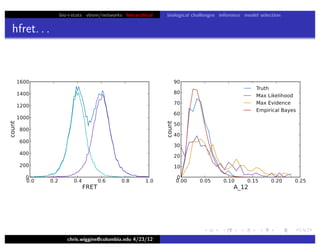
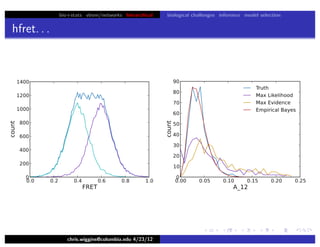
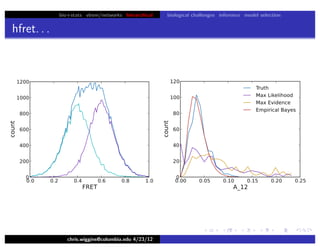
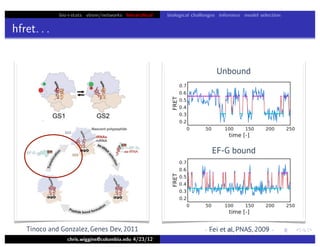
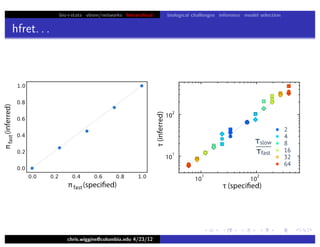
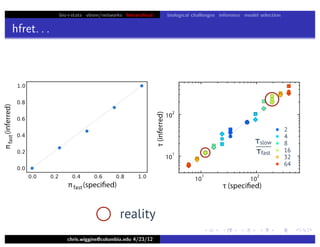
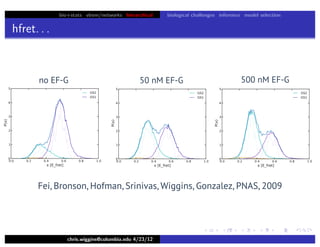
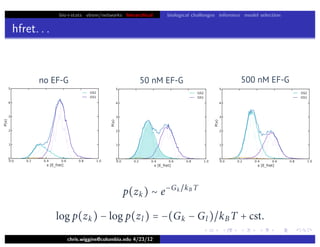
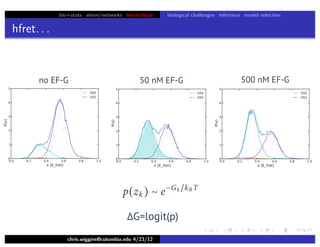
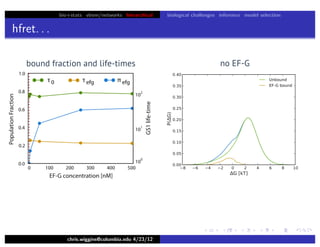
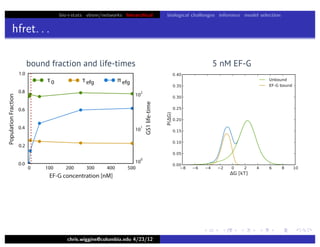
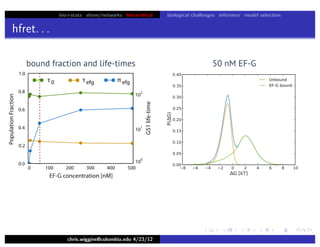
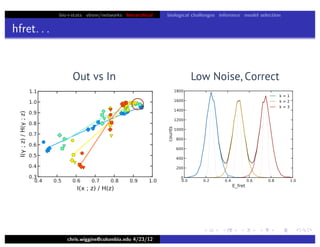
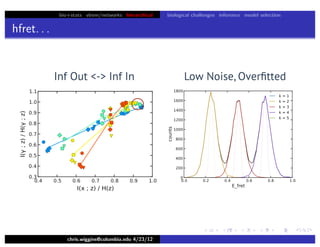
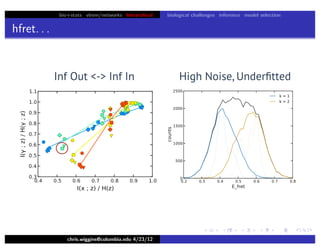
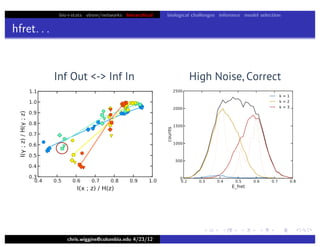
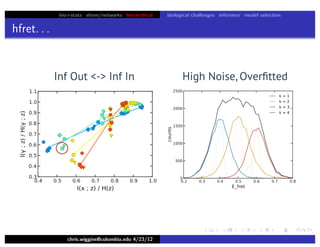
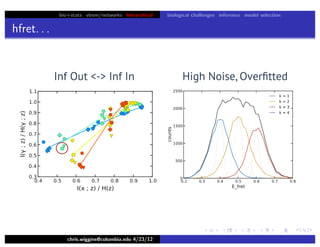
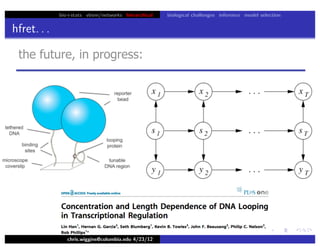
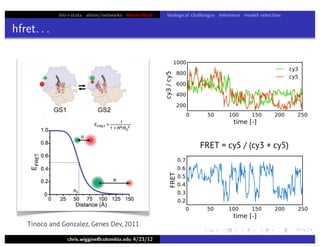
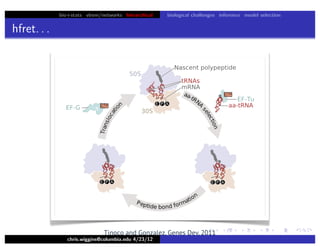
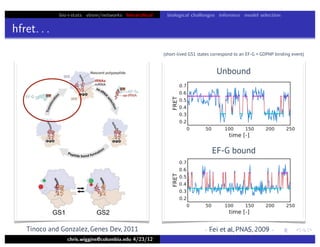
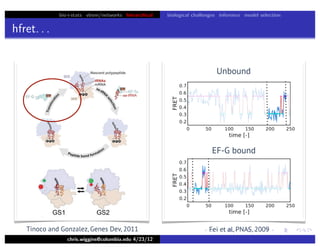
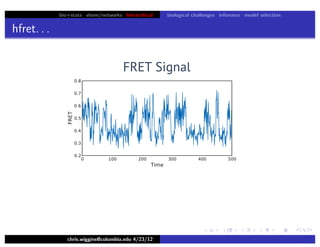
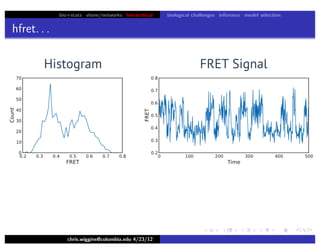
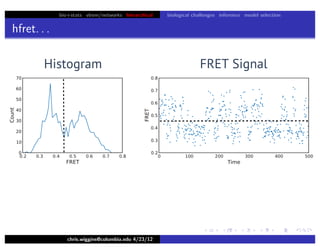
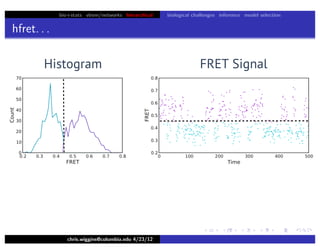
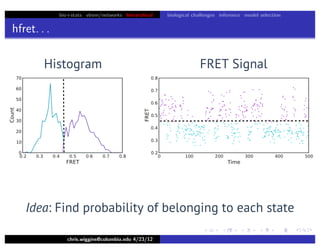
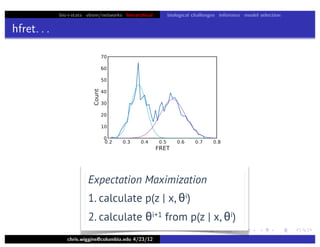
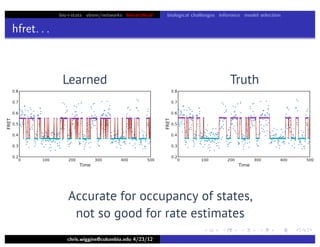
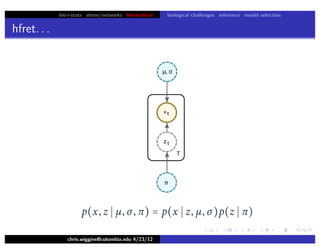
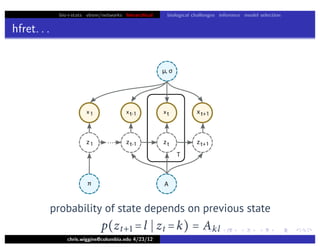
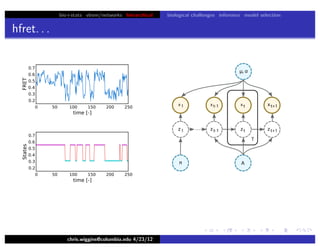
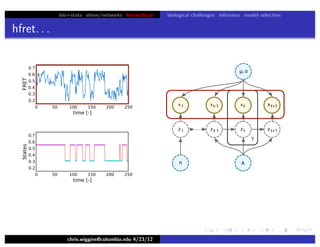
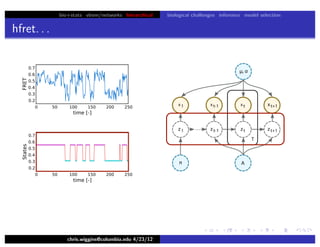
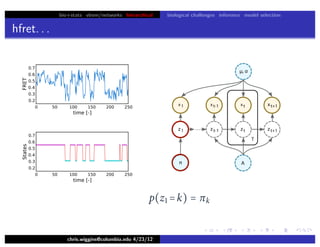
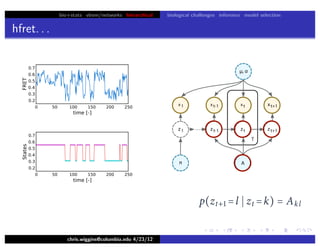
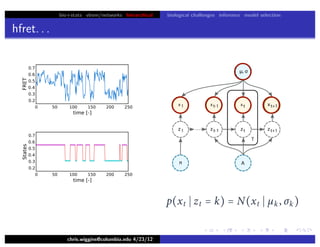
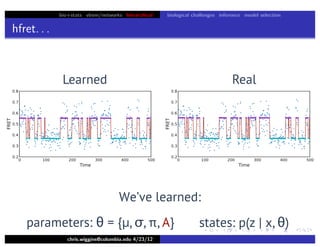
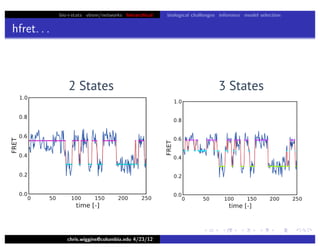
hfret. . .
chris.wiggins@columbia.edu 4/23/12
31
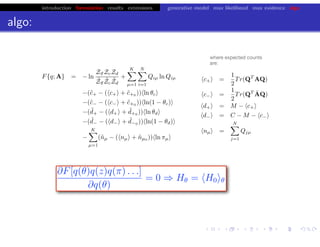
Lower bound tight for true posterior
L =
z
∫ dθ p(z, θ x)log
p(x, z, θ u)
p(z, θ x)
=
z
∫ dθ p(z, θ x)log[p(x u)]
= log p(x u)
L = log p(x u) − Dkl [q(z)q(θ w) p(z, θ x)]](https://image.slidesharecdn.com/vb-bio-130521171840-phpapp01/85/variational-bayes-in-biophysics-99-320.jpg)