Approximate Bayesian computation (ABC) is a new empirical Bayes method for performing Bayesian inference when the likelihood function is intractable or unavailable in closed form. ABC replaces the likelihood with a non-parametric approximation based on simulating data under different parameter values and comparing simulated and observed data using summary statistics. This allows Bayesian inference to be performed even when direct calculation of the likelihood is not possible. However, ABC introduces an approximation error that is unknown without extensive simulation. Some view ABC as a true Bayesian approach for an estimated or noisy likelihood, while others see it as more of a computational technique that is only approximately Bayesian.

1. (Approximate) Bayesian Computation as a new
empirical Bayes method
Christian P. Robert
Universit´e Paris-Dauphine & CREST, Paris
Joint work with K.L. Mengersen and P. Pudlo
i-like Workshop, Warwick, 15-17 May, 2013

2. of interest for i-like users
MCMSki IV to be held in Chamonix Mt Blanc, France, from
Monday, Jan. 6 to Wed., Jan. 8, 2014
All aspects of MCMC++ theory and methodology and applications
and more!
Website http://www.pages.drexel.edu/∼mwl25/mcmski/

3. Outline
Unavailable likelihoods
ABC methods
ABC as an inference machine
[A]BCel
Conclusion and perspectives

4. Intractable likelihood
Case of a well-defined statistical model where the likelihood
function
(θ|y) = f (y1, . . . , yn|θ)
is (really!) not available in closed form
cannot (easily!) be either completed or demarginalised
cannot be estimated by an unbiased estimator
c Prohibits direct implementation of a generic MCMC algorithm
like Metropolis–Hastings

5. Intractable likelihood
Case of a well-defined statistical model where the likelihood
function
(θ|y) = f (y1, . . . , yn|θ)
is (really!) not available in closed form
cannot (easily!) be either completed or demarginalised
cannot be estimated by an unbiased estimator
c Prohibits direct implementation of a generic MCMC algorithm
like Metropolis–Hastings

6. The abc alternative
Empirical approximations to the original B problem
Degrading the precision down to a tolerance ε
Replacing the likelihood with a non-parametric approximation
Summarising/replacing the data with insufficient statistics

7. The abc alternative
Empirical approximations to the original B problem
Degrading the precision down to a tolerance ε
Replacing the likelihood with a non-parametric approximation
Summarising/replacing the data with insufficient statistics

8. The abc alternative
Empirical approximations to the original B problem
Degrading the precision down to a tolerance ε
Replacing the likelihood with a non-parametric approximation
Summarising/replacing the data with insufficient statistics

9. Different worries about abc
Impact on B inference
a mere computational issue (that will eventually end up being
solved by more powerful computers, &tc, even if too costly in
the short term, as for regular Monte Carlo methods) Not!
an inferential issue (opening opportunities for new inference
machine on complex/Big Data models, with legitimity
differing from classical B approach)
a Bayesian conundrum (how closely related to the/a B
approach? more than recycling B tools? true B with raw
data? a new type of empirical Bayes inference?)

10. Different worries about abc
Impact on B inference
a mere computational issue (that will eventually end up being
solved by more powerful computers, &tc, even if too costly in
the short term, as for regular Monte Carlo methods) Not!
an inferential issue (opening opportunities for new inference
machine on complex/Big Data models, with legitimity
differing from classical B approach)
a Bayesian conundrum (how closely related to the/a B
approach? more than recycling B tools? true B with raw
data? a new type of empirical Bayes inference?)

11. Different worries about abc
Impact on B inference
a mere computational issue (that will eventually end up being
solved by more powerful computers, &tc, even if too costly in
the short term, as for regular Monte Carlo methods) Not!
an inferential issue (opening opportunities for new inference
machine on complex/Big Data models, with legitimity
differing from classical B approach)
a Bayesian conundrum (how closely related to the/a B
approach? more than recycling B tools? true B with raw
data? a new type of empirical Bayes inference?)

12. summary as an answer to Lange, Chi & Zhou [ISR, 2013]
“Surprisingly, the confident prediction of the previous generation that Bayesian methods would
ultimately supplant frequentist methods has given way to a realization that Markov chain Monte
Carlo (MCMC) may be too slow to handle modern data sets. Size matters because large data sets
stress computer storage and processing power to the breaking point. The most successful
compromises between Bayesian and frequentist methods now rely on penalization and
optimization.”
sad reality constraint that size does matter
focus on much smaller dimensions and on sparse summaries
many (fast) ways of producing those summaries
Bayesian inference can kick in almost automatically at this
stage

13. summary as an answer to Lange, Chi & Zhou [ISR, 2013]
“Surprisingly, the confident prediction of the previous generation that Bayesian methods would
ultimately supplant frequentist methods has given way to a realization that Markov chain Monte
Carlo (MCMC) may be too slow to handle modern data sets. Size matters because large data sets
stress computer storage and processing power to the breaking point. The most successful
compromises between Bayesian and frequentist methods now rely on penalization and
optimization.”
sad reality constraint that size does matter
focus on much smaller dimensions and on sparse summaries
many (fast) ways of producing those summaries
Bayesian inference can kick in almost automatically at this
stage

14. Econom’ections
Similar exploration of simulation-based and approximation
techniques in Econometrics
Simulated method of moments
Method of simulated moments
Simulated pseudo-maximum-likelihood
Indirect inference
[Gouri´eroux & Monfort, 1996]
even though motivation is partly-defined models rather than
complex likelihoods

15. Econom’ections
Similar exploration of simulation-based and approximation
techniques in Econometrics
Simulated method of moments
Method of simulated moments
Simulated pseudo-maximum-likelihood
Indirect inference
[Gouri´eroux & Monfort, 1996]
even though motivation is partly-defined models rather than
complex likelihoods

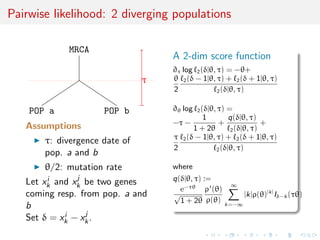
16. Indirect inference
Minimise [in θ] a distance between estimators ^β based on a
pseudo-model for genuine observations and for observations
simulated under the true model and the parameter θ.
[Gouri´eroux, Monfort, & Renault, 1993;
Smith, 1993; Gallant & Tauchen, 1996]

17. Indirect inference (PML vs. PSE)
Example of the pseudo-maximum-likelihood (PML)
^β(y) = arg max
β
t
log f (yt|β, y1:(t−1))
leading to
arg min
θ
||^β(yo
) − ^β(y1(θ), . . . , yS (θ))||2
when
ys(θ) ∼ f (y|θ) s = 1, . . . , S

18. Indirect inference (PML vs. PSE)
Example of the pseudo-score-estimator (PSE)
^β(y) = arg min
β
t
∂ log f
∂β
(yt|β, y1:(t−1))
2
leading to
arg min
θ
||^β(yo
) − ^β(y1(θ), . . . , yS (θ))||2
when
ys(θ) ∼ f (y|θ) s = 1, . . . , S

19. Consistent indirect inference
“...in order to get a unique solution the dimension of
the auxiliary parameter β must be larger than or equal to
the dimension of the initial parameter θ. If the problem is
just identified the different methods become easier...”
Consistency depending on the criterion and on the asymptotic
identifiability of θ
[Gouri´eroux & Monfort, 1996, p. 66]
Which connection [if any] with the B perspective?

20. Consistent indirect inference
“...in order to get a unique solution the dimension of
the auxiliary parameter β must be larger than or equal to
the dimension of the initial parameter θ. If the problem is
just identified the different methods become easier...”
Consistency depending on the criterion and on the asymptotic
identifiability of θ
[Gouri´eroux & Monfort, 1996, p. 66]
Which connection [if any] with the B perspective?

21. Consistent indirect inference
“...in order to get a unique solution the dimension of
the auxiliary parameter β must be larger than or equal to
the dimension of the initial parameter θ. If the problem is
just identified the different methods become easier...”
Consistency depending on the criterion and on the asymptotic
identifiability of θ
[Gouri´eroux & Monfort, 1996, p. 66]
Which connection [if any] with the B perspective?

22. Approximate Bayesian computation
Unavailable likelihoods
ABC methods
Genesis of ABC
ABC basics
Advances and interpretations
ABC as knn
ABC as an inference machine
[A]BCel
Conclusion and perspectives

23. Genetic background of ABC
skip genetics
ABC is a recent computational technique that only requires being
able to sample from the likelihood f (·|θ)
This technique stemmed from population genetics models, about
15 years ago, and population geneticists still contribute
significantly to methodological developments of ABC.
[Griffith & al., 1997; Tavar´e & al., 1999]

24. Demo-genetic inference
Each model is characterized by a set of parameters θ that cover
historical (time divergence, admixture time ...), demographics
(population sizes, admixture rates, migration rates, ...) and genetic
(mutation rate, ...) factors
The goal is to estimate these parameters from a dataset of
polymorphism (DNA sample) y observed at the present time
Problem:
most of the time, we cannot calculate the likelihood of the
polymorphism data f (y|θ)...

25. Demo-genetic inference
Each model is characterized by a set of parameters θ that cover
historical (time divergence, admixture time ...), demographics
(population sizes, admixture rates, migration rates, ...) and genetic
(mutation rate, ...) factors
The goal is to estimate these parameters from a dataset of
polymorphism (DNA sample) y observed at the present time
Problem:
most of the time, we cannot calculate the likelihood of the
polymorphism data f (y|θ)...

26. Neutral model at a given microsatellite locus, in a closed
panmictic population at equilibrium
Sample of 8 genes
Mutations according to
the Simple stepwise
Mutation Model
(SMM)
• date of the mutations ∼
Poisson process with
intensity θ/2 over the
branches
• MRCA = 100
• independent mutations:
±1 with pr. 1/2

27. Neutral model at a given microsatellite locus, in a closed
panmictic population at equilibrium
Kingman’s genealogy
When time axis is
normalized,
T(k) ∼ Exp(k(k − 1)/2)
Mutations according to
the Simple stepwise
Mutation Model
(SMM)
• date of the mutations ∼
Poisson process with
intensity θ/2 over the
branches
• MRCA = 100
• independent mutations:
±1 with pr. 1/2

28. Neutral model at a given microsatellite locus, in a closed
panmictic population at equilibrium
Kingman’s genealogy
When time axis is
normalized,
T(k) ∼ Exp(k(k − 1)/2)
Mutations according to
the Simple stepwise
Mutation Model
(SMM)
• date of the mutations ∼
Poisson process with
intensity θ/2 over the
branches
• MRCA = 100
• independent mutations:
±1 with pr. 1/2

29. Neutral model at a given microsatellite locus, in a closed
panmictic population at equilibrium
Observations: leafs of the tree
^θ = ?
Kingman’s genealogy
When time axis is
normalized,
T(k) ∼ Exp(k(k − 1)/2)
Mutations according to
the Simple stepwise
Mutation Model
(SMM)
• date of the mutations ∼
Poisson process with
intensity θ/2 over the
branches
• MRCA = 100
• independent mutations:
±1 with pr. 1/2

30. Much more interesting models. . .
several independent locus
Independent gene genealogies and mutations
different populations
linked by an evolutionary scenario made of divergences,
admixtures, migrations between populations, etc.
larger sample size
usually between 50 and 100 genes
A typical evolutionary scenario:
MRCA
POP 0 POP 1 POP 2
τ1
τ2

31. Intractable likelihood
Missing (too much missing!) data structure:
f (y|θ) =
G
f (y|G, θ)f (G|θ)dG
cannot be computed in a manageable way...
[Stephens & Donnelly, 2000]
The genealogies are considered as nuisance parameters
This modelling clearly differs from the phylogenetic perspective
where the tree is the parameter of interest.

32. Intractable likelihood
Missing (too much missing!) data structure:
f (y|θ) =
G
f (y|G, θ)f (G|θ)dG
cannot be computed in a manageable way...
[Stephens & Donnelly, 2000]
The genealogies are considered as nuisance parameters
This modelling clearly differs from the phylogenetic perspective
where the tree is the parameter of interest.

33. A?B?C?
A stands for approximate
[wrong likelihood / pic?]
B stands for Bayesian
C stands for computation
[producing a parameter
sample]

34. A?B?C?
A stands for approximate
[wrong likelihood / pic?]
B stands for Bayesian
C stands for computation
[producing a parameter
sample]

35. A?B?C?
A stands for approximate
[wrong likelihood / pic?]
B stands for Bayesian
C stands for computation
[producing a parameter
sample]
ESS=155.6
θ
Density
−0.5 0.0 0.5 1.0
0.01.0
ESS=75.93
θ
Density
−0.4 −0.2 0.0 0.2 0.4
0.01.02.0
ESS=76.87
θ
Density
−0.4 −0.2 0.0 0.2
01234
ESS=91.54
θ
Density
−0.6 −0.4 −0.2 0.0 0.2
01234
ESS=108.4
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.02.03.0
ESS=85.13
θ
Density
−0.2 0.0 0.2 0.4 0.6
0.01.02.03.0
ESS=149.1
θ
Density
−0.5 0.0 0.5 1.0
0.01.02.0
ESS=96.31
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.02.0
ESS=83.77
θ
Density
−0.6 −0.4 −0.2 0.0 0.2 0.4
01234
ESS=155.7
θ
Density
−0.5 0.0 0.5
0.01.02.0
ESS=92.42
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.02.03.0
ESS=95.01
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.53.0
ESS=139.2
Density −0.6 −0.2 0.2 0.6
0.01.02.0
ESS=99.33
Density
−0.4 −0.2 0.0 0.2 0.4
0.01.02.03.0
ESS=87.28
Density
−0.2 0.0 0.2 0.4 0.6
0123

36. How Bayesian is aBc?
Could we turn the resolution into a Bayesian answer?
ideally so (not meaningfull: requires ∞-ly powerful computer
approximation error unknown (w/o costly simulation)
true Bayes for wrong model (formal and artificial)
true Bayes for noisy model (much more convincing)
true Bayes for estimated likelihood (back to econometrics?)
illuminating the tension between information and precision

37. ABC methodology
Bayesian setting: target is π(θ)f (x|θ)
When likelihood f (x|θ) not in closed form, likelihood-free rejection
technique:
Foundation
For an observation y ∼ f (y|θ), under the prior π(θ), if one keeps
jointly simulating
θ ∼ π(θ) , z ∼ f (z|θ ) ,
until the auxiliary variable z is equal to the observed value, z = y,
then the selected
θ ∼ π(θ|y)
[Rubin, 1984; Diggle & Gratton, 1984; Tavar´e et al., 1997]

38. ABC methodology
Bayesian setting: target is π(θ)f (x|θ)
When likelihood f (x|θ) not in closed form, likelihood-free rejection
technique:
Foundation
For an observation y ∼ f (y|θ), under the prior π(θ), if one keeps
jointly simulating
θ ∼ π(θ) , z ∼ f (z|θ ) ,
until the auxiliary variable z is equal to the observed value, z = y,
then the selected
θ ∼ π(θ|y)
[Rubin, 1984; Diggle & Gratton, 1984; Tavar´e et al., 1997]

39. ABC methodology
Bayesian setting: target is π(θ)f (x|θ)
When likelihood f (x|θ) not in closed form, likelihood-free rejection
technique:
Foundation
For an observation y ∼ f (y|θ), under the prior π(θ), if one keeps
jointly simulating
θ ∼ π(θ) , z ∼ f (z|θ ) ,
until the auxiliary variable z is equal to the observed value, z = y,
then the selected
θ ∼ π(θ|y)
[Rubin, 1984; Diggle & Gratton, 1984; Tavar´e et al., 1997]

40. A as A...pproximative
When y is a continuous random variable, strict equality z = y is
replaced with a tolerance zone
ρ(y, z)
where ρ is a distance
Output distributed from
π(θ) Pθ{ρ(y, z) < }
def
∝ π(θ|ρ(y, z) < )
[Pritchard et al., 1999]

41. A as A...pproximative
When y is a continuous random variable, strict equality z = y is
replaced with a tolerance zone
ρ(y, z)
where ρ is a distance
Output distributed from
π(θ) Pθ{ρ(y, z) < }
def
∝ π(θ|ρ(y, z) < )
[Pritchard et al., 1999]

42. ABC algorithm
In most implementations, further degree of A...pproximation:
Algorithm 1 Likelihood-free rejection sampler
for i = 1 to N do
repeat
generate θ from the prior distribution π(·)
generate z from the likelihood f (·|θ )
until ρ{η(z), η(y)}
set θi = θ
end for
where η(y) defines a (not necessarily sufficient) statistic

43. Output
The likelihood-free algorithm samples from the marginal in z of:
π (θ, z|y) =
π(θ)f (z|θ)IA ,y (z)
A ,y×Θ π(θ)f (z|θ)dzdθ
,
where A ,y = {z ∈ D|ρ(η(z), η(y)) < }.
The idea behind ABC is that the summary statistics coupled with a
small tolerance should provide a good approximation of the
posterior distribution:
π (θ|y) = π (θ, z|y)dz ≈ π(θ|y) .
...does it?!

44. Output
The likelihood-free algorithm samples from the marginal in z of:
π (θ, z|y) =
π(θ)f (z|θ)IA ,y (z)
A ,y×Θ π(θ)f (z|θ)dzdθ
,
where A ,y = {z ∈ D|ρ(η(z), η(y)) < }.
The idea behind ABC is that the summary statistics coupled with a
small tolerance should provide a good approximation of the
posterior distribution:
π (θ|y) = π (θ, z|y)dz ≈ π(θ|y) .
...does it?!

45. Output
The likelihood-free algorithm samples from the marginal in z of:
π (θ, z|y) =
π(θ)f (z|θ)IA ,y (z)
A ,y×Θ π(θ)f (z|θ)dzdθ
,
where A ,y = {z ∈ D|ρ(η(z), η(y)) < }.
The idea behind ABC is that the summary statistics coupled with a
small tolerance should provide a good approximation of the
posterior distribution:
π (θ|y) = π (θ, z|y)dz ≈ π(θ|y) .
...does it?!

46. Output
The likelihood-free algorithm samples from the marginal in z of:
π (θ, z|y) =
π(θ)f (z|θ)IA ,y (z)
A ,y×Θ π(θ)f (z|θ)dzdθ
,
where A ,y = {z ∈ D|ρ(η(z), η(y)) < }.
The idea behind ABC is that the summary statistics coupled with a
small tolerance should provide a good approximation of the
restricted posterior distribution:
π (θ|y) = π (θ, z|y)dz ≈ π(θ|η(y)) .
Not so good..!
skip convergence details!

47. Convergence of ABC
What happens when → 0?
For B ⊂ Θ, we have
B
A ,y
f (z|θ)dz
A ,y×Θ π(θ)f (z|θ)dzdθ
π(θ)dθ =
A ,y
B f (z|θ)π(θ)dθ
A ,y×Θ π(θ)f (z|θ)dzdθ
dz
=
A ,y
B f (z|θ)π(θ)dθ
m(z)
m(z)
A ,y×Θ π(θ)f (z|θ)dzdθ
dz
=
A ,y
π(B|z)
m(z)
A ,y×Θ π(θ)f (z|θ)dzdθ
dz
which indicates convergence for a continuous π(B|z).

48. Convergence of ABC
What happens when → 0?
For B ⊂ Θ, we have
B
A ,y
f (z|θ)dz
A ,y×Θ π(θ)f (z|θ)dzdθ
π(θ)dθ =
A ,y
B f (z|θ)π(θ)dθ
A ,y×Θ π(θ)f (z|θ)dzdθ
dz
=
A ,y
B f (z|θ)π(θ)dθ
m(z)
m(z)
A ,y×Θ π(θ)f (z|θ)dzdθ
dz
=
A ,y
π(B|z)
m(z)
A ,y×Θ π(θ)f (z|θ)dzdθ
dz
which indicates convergence for a continuous π(B|z).

49. Convergence (do not attempt!)
...and the above does not apply to insufficient statistics:
If η(y) is not a sufficient statistics, the best one can hope for is
π(θ|η(y)) , not π(θ|y)
If η(y) is an ancillary statistic, the whole information contained in
y is lost!, the “best” one can “hope” for is
π(θ|η(y)) = π(θ)

50. Convergence (do not attempt!)
...and the above does not apply to insufficient statistics:
If η(y) is not a sufficient statistics, the best one can hope for is
π(θ|η(y)) , not π(θ|y)
If η(y) is an ancillary statistic, the whole information contained in
y is lost!, the “best” one can “hope” for is
π(θ|η(y)) = π(θ)

51. Convergence (do not attempt!)
...and the above does not apply to insufficient statistics:
If η(y) is not a sufficient statistics, the best one can hope for is
π(θ|η(y)) , not π(θ|y)
If η(y) is an ancillary statistic, the whole information contained in
y is lost!, the “best” one can “hope” for is
π(θ|η(y)) = π(θ)

52. Comments
Role of distance paramount (because = 0)
Scaling of components of η(y) is also determinant
matters little if “small enough”
representative of “curse of dimensionality”
small is beautiful!
the data as a whole may be paradoxically weakly informative
for ABC

53. ABC (simul’) advances
how approximative is ABC? ABC as knn
Simulating from the prior is often poor in efficiency
Either modify the proposal distribution on θ to increase the density
of x’s within the vicinity of y...
[Marjoram et al, 2003; Bortot et al., 2007, Sisson et al., 2007]
...or by viewing the problem as a conditional density estimation
and by developing techniques to allow for larger
[Beaumont et al., 2002]
.....or even by including in the inferential framework [ABCµ]
[Ratmann et al., 2009]

54. ABC (simul’) advances
how approximative is ABC? ABC as knn
Simulating from the prior is often poor in efficiency
Either modify the proposal distribution on θ to increase the density
of x’s within the vicinity of y...
[Marjoram et al, 2003; Bortot et al., 2007, Sisson et al., 2007]
...or by viewing the problem as a conditional density estimation
and by developing techniques to allow for larger
[Beaumont et al., 2002]
.....or even by including in the inferential framework [ABCµ]
[Ratmann et al., 2009]

55. ABC (simul’) advances
how approximative is ABC? ABC as knn
Simulating from the prior is often poor in efficiency
Either modify the proposal distribution on θ to increase the density
of x’s within the vicinity of y...
[Marjoram et al, 2003; Bortot et al., 2007, Sisson et al., 2007]
...or by viewing the problem as a conditional density estimation
and by developing techniques to allow for larger
[Beaumont et al., 2002]
.....or even by including in the inferential framework [ABCµ]
[Ratmann et al., 2009]

56. ABC (simul’) advances
how approximative is ABC? ABC as knn
Simulating from the prior is often poor in efficiency
Either modify the proposal distribution on θ to increase the density
of x’s within the vicinity of y...
[Marjoram et al, 2003; Bortot et al., 2007, Sisson et al., 2007]
...or by viewing the problem as a conditional density estimation
and by developing techniques to allow for larger
[Beaumont et al., 2002]
.....or even by including in the inferential framework [ABCµ]
[Ratmann et al., 2009]

57. ABC-NP
Better usage of [prior] simulations by
adjustement: instead of throwing away
θ such that ρ(η(z), η(y)) > , replace
θ’s with locally regressed transforms
θ∗
= θ − {η(z) − η(y)}T ^β
[Csill´ery et al., TEE, 2010]
where ^β is obtained by [NP] weighted least square regression on
(η(z) − η(y)) with weights
Kδ {ρ(η(z), η(y))}
[Beaumont et al., 2002, Genetics]

58. ABC-NP (regression)
Also found in the subsequent literature, e.g. in Fearnhead-Prangle (2012) :
weight directly simulation by
Kδ {ρ(η(z(θ)), η(y))}
or
1
S
S
s=1
Kδ {ρ(η(zs
(θ)), η(y))}
[consistent estimate of f (η|θ)]
Curse of dimensionality: poor estimate when d = dim(η) is large...

59. ABC-NP (regression)
Also found in the subsequent literature, e.g. in Fearnhead-Prangle (2012) :
weight directly simulation by
Kδ {ρ(η(z(θ)), η(y))}
or
1
S
S
s=1
Kδ {ρ(η(zs
(θ)), η(y))}
[consistent estimate of f (η|θ)]
Curse of dimensionality: poor estimate when d = dim(η) is large...

60. ABC-NP (density estimation)
Use of the kernel weights
Kδ {ρ(η(z(θ)), η(y))}
leads to the NP estimate of the posterior expectation
i θi Kδ {ρ(η(z(θi )), η(y))}
i Kδ {ρ(η(z(θi )), η(y))}
[Blum, JASA, 2010]

61. ABC-NP (density estimation)
Use of the kernel weights
Kδ {ρ(η(z(θ)), η(y))}
leads to the NP estimate of the posterior conditional density
i
˜Kb(θi − θ)Kδ {ρ(η(z(θi )), η(y))}
i Kδ {ρ(η(z(θi )), η(y))}
[Blum, JASA, 2010]

62. ABC-NP (density estimations)
Other versions incorporating regression adjustments
i
˜Kb(θ∗
i − θ)Kδ {ρ(η(z(θi )), η(y))}
i Kδ {ρ(η(z(θi )), η(y))}
In all cases, error
E[^g(θ|y)] − g(θ|y) = cb2
+ cδ2
+ OP(b2
+ δ2
) + OP(1/nδd
)
var(^g(θ|y)) =
c
nbδd
(1 + oP(1))

63. ABC-NP (density estimations)
Other versions incorporating regression adjustments
i
˜Kb(θ∗
i − θ)Kδ {ρ(η(z(θi )), η(y))}
i Kδ {ρ(η(z(θi )), η(y))}
In all cases, error
E[^g(θ|y)] − g(θ|y) = cb2
+ cδ2
+ OP(b2
+ δ2
) + OP(1/nδd
)
var(^g(θ|y)) =
c
nbδd
(1 + oP(1))
[Blum, JASA, 2010]

64. ABC-NP (density estimations)
Other versions incorporating regression adjustments
i
˜Kb(θ∗
i − θ)Kδ {ρ(η(z(θi )), η(y))}
i Kδ {ρ(η(z(θi )), η(y))}
In all cases, error
E[^g(θ|y)] − g(θ|y) = cb2
+ cδ2
+ OP(b2
+ δ2
) + OP(1/nδd
)
var(^g(θ|y)) =
c
nbδd
(1 + oP(1))
[standard NP calculations]

65. ABC as knn
[Biau et al., 2013, Annales de l’IHP]
Practice of ABC: determine tolerance as a quantile on observed
distances, say 10% or 1% quantile,
= N = qα(d1, . . . , dN)
Interpretation of ε as nonparametric bandwidth only
approximation of the actual practice
[Blum & Fran¸cois, 2010]
ABC is a k-nearest neighbour (knn) method with kN = N N
[Loftsgaarden & Quesenberry, 1965]

66. ABC as knn
[Biau et al., 2013, Annales de l’IHP]
Practice of ABC: determine tolerance as a quantile on observed
distances, say 10% or 1% quantile,
= N = qα(d1, . . . , dN)
Interpretation of ε as nonparametric bandwidth only
approximation of the actual practice
[Blum & Fran¸cois, 2010]
ABC is a k-nearest neighbour (knn) method with kN = N N
[Loftsgaarden & Quesenberry, 1965]

67. ABC as knn
[Biau et al., 2013, Annales de l’IHP]
Practice of ABC: determine tolerance as a quantile on observed
distances, say 10% or 1% quantile,
= N = qα(d1, . . . , dN)
Interpretation of ε as nonparametric bandwidth only
approximation of the actual practice
[Blum & Fran¸cois, 2010]
ABC is a k-nearest neighbour (knn) method with kN = N N
[Loftsgaarden & Quesenberry, 1965]

68. ABC consistency
Provided
kN/ log log N −→ ∞ and kN/N −→ 0
as N → ∞, for almost all s0 (with respect to the distribution of
S), with probability 1,
1
kN
kN
j=1
ϕ(θj ) −→ E[ϕ(θj )|S = s0]
[Devroye, 1982]
Biau et al. (2012) also recall pointwise and integrated mean square error
consistency results on the corresponding kernel estimate of the
conditional posterior distribution, under constraints
kN → ∞, kN /N → 0, hN → 0 and hp
N kN → ∞,

69. ABC consistency
Provided
kN/ log log N −→ ∞ and kN/N −→ 0
as N → ∞, for almost all s0 (with respect to the distribution of
S), with probability 1,
1
kN
kN
j=1
ϕ(θj ) −→ E[ϕ(θj )|S = s0]
[Devroye, 1982]
Biau et al. (2012) also recall pointwise and integrated mean square error
consistency results on the corresponding kernel estimate of the
conditional posterior distribution, under constraints
kN → ∞, kN /N → 0, hN → 0 and hp
N kN → ∞,

70. Rates of convergence
Further assumptions (on target and kernel) allow for precise
(integrated mean square) convergence rates (as a power of the
sample size N), derived from classical k-nearest neighbour
regression, like
when m = 1, 2, 3, kN ≈ N(p+4)/(p+8) and rate N− 4
p+8
when m = 4, kN ≈ N(p+4)/(p+8) and rate N− 4
p+8 log N
when m > 4, kN ≈ N(p+4)/(m+p+4) and rate N− 4
m+p+4
[Biau et al., 2012, arxiv:1207.6461]
Drag: Only applies to sufficient summary statistics

71. Rates of convergence
Further assumptions (on target and kernel) allow for precise
(integrated mean square) convergence rates (as a power of the
sample size N), derived from classical k-nearest neighbour
regression, like
when m = 1, 2, 3, kN ≈ N(p+4)/(p+8) and rate N− 4
p+8
when m = 4, kN ≈ N(p+4)/(p+8) and rate N− 4
p+8 log N
when m > 4, kN ≈ N(p+4)/(m+p+4) and rate N− 4
m+p+4
[Biau et al., 2012, arxiv:1207.6461]
Drag: Only applies to sufficient summary statistics

72. ABC inference machine
Unavailable likelihoods
ABC methods
ABC as an inference machine
Error inc.
Exact BC and approximate
targets
summary statistic
[A]BCel
Conclusion and perspectives

73. How Bayesian is aBc..?
may be a convergent method of inference (meaningful?
sufficient? foreign?)
approximation error unknown (w/o massive simulation)
pragmatic/empirical B (there is no other solution!)
many calibration issues (tolerance, distance, statistics)
the NP side should be incorporated into the whole B picture
the approximation error should also be part of the B inference
to ABCel

74. ABCµ
Idea Infer about the error as well as about the parameter:
Use of a joint density
f (θ, |y) ∝ ξ( |y, θ) × πθ(θ) × π ( )
where y is the data, and ξ( |y, θ) is the prior predictive density of
ρ(η(z), η(y)) given θ and y when z ∼ f (z|θ)
Warning! Replacement of ξ( |y, θ) with a non-parametric kernel
approximation.
[Ratmann, Andrieu, Wiuf and Richardson, 2009, PNAS]

75. ABCµ
Idea Infer about the error as well as about the parameter:
Use of a joint density
f (θ, |y) ∝ ξ( |y, θ) × πθ(θ) × π ( )
where y is the data, and ξ( |y, θ) is the prior predictive density of
ρ(η(z), η(y)) given θ and y when z ∼ f (z|θ)
Warning! Replacement of ξ( |y, θ) with a non-parametric kernel
approximation.
[Ratmann, Andrieu, Wiuf and Richardson, 2009, PNAS]

76. ABCµ
Idea Infer about the error as well as about the parameter:
Use of a joint density
f (θ, |y) ∝ ξ( |y, θ) × πθ(θ) × π ( )
where y is the data, and ξ( |y, θ) is the prior predictive density of
ρ(η(z), η(y)) given θ and y when z ∼ f (z|θ)
Warning! Replacement of ξ( |y, θ) with a non-parametric kernel
approximation.
[Ratmann, Andrieu, Wiuf and Richardson, 2009, PNAS]

77. ABCµ details
Multidimensional distances ρk (k = 1, . . . , K) and errors
k = ρk(ηk(z), ηk(y)), with
k ∼ ξk( |y, θ) ≈ ^ξk( |y, θ) =
1
Bhk
b
K[{ k−ρk(ηk(zb), ηk(y))}/hk]
then used in replacing ξ( |y, θ) with mink
^ξk( |y, θ)
ABCµ involves acceptance probability
π(θ , )
π(θ, )
q(θ , θ)q( , )
q(θ, θ )q( , )
mink
^ξk( |y, θ )
mink
^ξk( |y, θ)

78. ABCµ details
Multidimensional distances ρk (k = 1, . . . , K) and errors
k = ρk(ηk(z), ηk(y)), with
k ∼ ξk( |y, θ) ≈ ^ξk( |y, θ) =
1
Bhk
b
K[{ k−ρk(ηk(zb), ηk(y))}/hk]
then used in replacing ξ( |y, θ) with mink
^ξk( |y, θ)
ABCµ involves acceptance probability
π(θ , )
π(θ, )
q(θ , θ)q( , )
q(θ, θ )q( , )
mink
^ξk( |y, θ )
mink
^ξk( |y, θ)

79. Wilkinson’s exact BC (not exactly!)
ABC approximation error (i.e. non-zero tolerance) replaced with
exact simulation from a controlled approximation to the target,
convolution of true posterior with kernel function
π (θ, z|y) =
π(θ)f (z|θ)K (y − z)
π(θ)f (z|θ)K (y − z)dzdθ
,
with K kernel parameterised by bandwidth .
[Wilkinson, 2013]
Theorem
The ABC algorithm based on the assumption of a randomised
observation y = ˜y + ξ, ξ ∼ K , and an acceptance probability of
K (y − z)/M
gives draws from the posterior distribution π(θ|y).

80. Wilkinson’s exact BC (not exactly!)
ABC approximation error (i.e. non-zero tolerance) replaced with
exact simulation from a controlled approximation to the target,
convolution of true posterior with kernel function
π (θ, z|y) =
π(θ)f (z|θ)K (y − z)
π(θ)f (z|θ)K (y − z)dzdθ
,
with K kernel parameterised by bandwidth .
[Wilkinson, 2013]
Theorem
The ABC algorithm based on the assumption of a randomised
observation y = ˜y + ξ, ξ ∼ K , and an acceptance probability of
K (y − z)/M
gives draws from the posterior distribution π(θ|y).

81. How exact a BC?
Pros
Pseudo-data from true model and observed data from noisy
model
Interesting perspective in that outcome is completely
controlled
Link with ABCµ and assuming y is observed with a
measurement error with density K
Relates to the theory of model approximation
[Kennedy & O’Hagan, 2001]
leads to “noisy ABC”: perturbates the data down to precision
ε and proceed
[Fearnhead & Prangle, 2012]
Cons
Requires K to be bounded by M
True approximation error never assessed

82. How exact a BC?
Pros
Pseudo-data from true model and observed data from noisy
model
Interesting perspective in that outcome is completely
controlled
Link with ABCµ and assuming y is observed with a
measurement error with density K
Relates to the theory of model approximation
[Kennedy & O’Hagan, 2001]
leads to “noisy ABC”: perturbates the data down to precision
ε and proceed
[Fearnhead & Prangle, 2012]
Cons
Requires K to be bounded by M
True approximation error never assessed

83. Noisy ABC for HMMs
Specific case of a hidden Markov model summaries
Xt+1 ∼ Qθ(Xt, ·)
Yt+1 ∼ gθ(·|xt)
where only y0
1:n is observed.
[Dean, Singh, Jasra, & Peters, 2011]
Use of specific constraints, adapted to the Markov structure:
y1 ∈ B(y0
1 , ) × · · · × yn ∈ B(y0
n , )

84. Noisy ABC for HMMs
Specific case of a hidden Markov model summaries
Xt+1 ∼ Qθ(Xt, ·)
Yt+1 ∼ gθ(·|xt)
where only y0
1:n is observed.
[Dean, Singh, Jasra, & Peters, 2011]
Use of specific constraints, adapted to the Markov structure:
y1 ∈ B(y0
1 , ) × · · · × yn ∈ B(y0
n , )

85. Noisy ABC-MLE
Idea: Modify instead the data from the start
(y0
1 + ζ1, . . . , yn + ζn)
[ see Fearnhead-Prangle ]
noisy ABC-MLE estimate
arg max
θ
Pθ Y1 ∈ B(y0
1 + ζ1, ), . . . , Yn ∈ B(y0
n + ζn, )
[Dean, Singh, Jasra, & Peters, 2011]

86. Consistent noisy ABC-MLE
Degrading the data improves the estimation performances:
Noisy ABC-MLE is asymptotically (in n) consistent
under further assumptions, the noisy ABC-MLE is
asymptotically normal
increase in variance of order −2
likely degradation in precision or computing time due to the
lack of summary statistic [curse of dimensionality]

87. Which summary?
Fundamental difficulty of the choice of the summary statistic when
there is no non-trivial sufficient statistics
Loss of statistical information balanced against gain in data
roughening
Approximation error and information loss remain unknown
Choice of statistics induces choice of distance function
towards standardisation
may be imposed for external reasons
may gather several non-B point estimates
can learn about efficient combination

88. Which summary?
Fundamental difficulty of the choice of the summary statistic when
there is no non-trivial sufficient statistics
Loss of statistical information balanced against gain in data
roughening
Approximation error and information loss remain unknown
Choice of statistics induces choice of distance function
towards standardisation
may be imposed for external reasons
may gather several non-B point estimates
can learn about efficient combination

89. Which summary?
Fundamental difficulty of the choice of the summary statistic when
there is no non-trivial sufficient statistics
Loss of statistical information balanced against gain in data
roughening
Approximation error and information loss remain unknown
Choice of statistics induces choice of distance function
towards standardisation
may be imposed for external reasons
may gather several non-B point estimates
can learn about efficient combination

90. Which summary for model choice?
Depending on the choice of η(·), the Bayes factor based on this
insufficient statistic,
Bη
12(y) =
π1(θ1)f η
1 (η(y)|θ1) dθ1
π2(θ2)f η
2 (η(y)|θ2) dθ2
,
is either consistent or inconsistent
[X, Cornuet, Marin, & Pillai, 2012]
Consistency only depends on the range of Ei [η(y)] under both
models
[Marin, Pillai, X, & Rousseau, 2012]

91. Which summary for model choice?
Depending on the choice of η(·), the Bayes factor based on this
insufficient statistic,
Bη
12(y) =
π1(θ1)f η
1 (η(y)|θ1) dθ1
π2(θ2)f η
2 (η(y)|θ2) dθ2
,
is either consistent or inconsistent
[X, Cornuet, Marin, & Pillai, 2012]
Consistency only depends on the range of Ei [η(y)] under both
models
[Marin, Pillai, X, & Rousseau, 2012]

92. Semi-automatic ABC
Fearnhead and Prangle (2012) study ABC and the selection of the
summary statistic in close proximity to Wilkinson’s proposal
ABC considered as inferential method and calibrated as such
randomised (or ‘noisy’) version of the summary statistics
˜η(y) = η(y) + τ
derivation of a well-calibrated version of ABC, i.e. an
algorithm that gives proper predictions for the distribution
associated with this randomised summary statistic

93. Summary [of F&P/statistics)
optimality of the posterior expectation
E[θ|y]
of the parameter of interest as summary statistics η(y)!
[requires iterative process]
use of the standard quadratic loss function
(θ − θ0)T
A(θ − θ0)
recent extension to model choice, optimality of Bayes factor
B12(y)
[F&P, ISBA 2012, Kyoto]

94. Summary [of F&P/statistics)
optimality of the posterior expectation
E[θ|y]
of the parameter of interest as summary statistics η(y)!
[requires iterative process]
use of the standard quadratic loss function
(θ − θ0)T
A(θ − θ0)
recent extension to model choice, optimality of Bayes factor
B12(y)
[F&P, ISBA 2012, Kyoto]

95. Summary [about summaries]
Choice of summary statistics is paramount for ABC
validation/performances
At best, ABC approximates π(. | η(y)) [unavoidable]
Model selection feasible with ABC [with caution!]
For estimation, consistency if {θ; µ(θ) = µ0} = θ0 when
Eθ[η(y)] = µ(θ)
For testing consistency if
{µ1(θ1), θ1 ∈ Θ1} ∩ {µ2(θ2), θ2 ∈ Θ2} = ∅
[Marin et al., 2011]

96. Summary [about summaries]
Choice of summary statistics is paramount for ABC
validation/performances
At best, ABC approximates π(. | η(y)) [unavoidable]
Model selection feasible with ABC [with caution!]
For estimation, consistency if {θ; µ(θ) = µ0} = θ0 when
Eθ[η(y)] = µ(θ)
For testing consistency if
{µ1(θ1), θ1 ∈ Θ1} ∩ {µ2(θ2), θ2 ∈ Θ2} = ∅
[Marin et al., 2011]

97. Summary [about summaries]
Choice of summary statistics is paramount for ABC
validation/performances
At best, ABC approximates π(. | η(y)) [unavoidable]
Model selection feasible with ABC [with caution!]
For estimation, consistency if {θ; µ(θ) = µ0} = θ0 when
Eθ[η(y)] = µ(θ)
For testing consistency if
{µ1(θ1), θ1 ∈ Θ1} ∩ {µ2(θ2), θ2 ∈ Θ2} = ∅
[Marin et al., 2011]

98. Summary [about summaries]
Choice of summary statistics is paramount for ABC
validation/performances
At best, ABC approximates π(. | η(y)) [unavoidable]
Model selection feasible with ABC [with caution!]
For estimation, consistency if {θ; µ(θ) = µ0} = θ0 when
Eθ[η(y)] = µ(θ)
For testing consistency if
{µ1(θ1), θ1 ∈ Θ1} ∩ {µ2(θ2), θ2 ∈ Θ2} = ∅
[Marin et al., 2011]

99. Summary [about summaries]
Choice of summary statistics is paramount for ABC
validation/performances
At best, ABC approximates π(. | η(y)) [unavoidable]
Model selection feasible with ABC [with caution!]
For estimation, consistency if {θ; µ(θ) = µ0} = θ0 when
Eθ[η(y)] = µ(θ)
For testing consistency if
{µ1(θ1), θ1 ∈ Θ1} ∩ {µ2(θ2), θ2 ∈ Θ2} = ∅
[Marin et al., 2011]

100. Empirical likelihood (EL)
Unavailable likelihoods
ABC methods
ABC as an inference machine
[A]BCel
ABC and EL
Composite likelihood
Illustrations
Conclusion and perspectives

101. Empirical likelihood (EL)
Dataset x made of n independent replicates x = (x1, . . . , xn) of
some X ∼ F
Generalized moment condition model
EF h(X, φ) = 0,
where h is a known function, and φ an unknown parameter
Corresponding empirical likelihood
Lel(φ|x) = max
p
n
i=1
pi
for all p such that 0 pi 1, i pi = 1, i pi h(xi , φ) = 0.
[Owen, 1988, Bio’ka, & Empirical Likelihood, 2001]

102. Empirical likelihood (EL)
Dataset x made of n independent replicates x = (x1, . . . , xn) of
some X ∼ F
Generalized moment condition model
EF h(X, φ) = 0,
where h is a known function, and φ an unknown parameter
Corresponding empirical likelihood
Lel(φ|x) = max
p
n
i=1
pi
for all p such that 0 pi 1, i pi = 1, i pi h(xi , φ) = 0.
[Owen, 1988, Bio’ka, & Empirical Likelihood, 2001]

103. Convergence of EL [3.4]
Theorem 3.4 Let X, Y1, . . . , Yn be independent rv’s with common
distribution F0. For θ ∈ Θ, and the function h(X, θ) ∈ Rs, let
θ0 ∈ Θ be such that
Var(h(Yi , θ0))
is finite and has rank q > 0. If θ0 satisfies
E(h(X, θ0)) = 0,
then
−2 log
Lel(θ0|Y1, . . . , Yn)
n−n
→ χ2
(q)
in distribution when n → ∞.
[Owen, 2001]

104. Convergence of EL [3.4]
“...The interesting thing about Theorem 3.4 is what is not there. It
includes no conditions to make ^θ a good estimate of θ0, nor even
conditions to ensure a unique value for θ0, nor even that any solution θ0
exists. Theorem 3.4 applies in the just determined, over-determined, and
under-determined cases. When we can prove that our estimating
equations uniquely define θ0, and provide a consistent estimator ^θ of it,
then confidence regions and tests follow almost automatically through
Theorem 3.4.”.
[Owen, 2001]

105. Raw [A]BCelsampler
Act as if EL was an exact likelihood
[Lazar, 2003]
for i = 1 → N do
generate φi from the prior distribution π(·)
set the weight ωi = Lel(φi |xobs)
end for
return (φi , ωi ), i = 1, . . . , N
Output weighted sample of size N

106. Raw [A]BCelsampler
Act as if EL was an exact likelihood
[Lazar, 2003]
for i = 1 → N do
generate φi from the prior distribution π(·)
set the weight ωi = Lel(φi |xobs)
end for
return (φi , ωi ), i = 1, . . . , N
Performance evaluated through effective sample size
ESS = 1
N
i=1



ωi
N
j=1
ωj



2

107. Raw [A]BCelsampler
Act as if EL was an exact likelihood
[Lazar, 2003]
for i = 1 → N do
generate φi from the prior distribution π(·)
set the weight ωi = Lel(φi |xobs)
end for
return (φi , ωi ), i = 1, . . . , N
More advanced algorithms can be adapted to EL:
E.g., adaptive multiple importance sampling (AMIS) of
Cornuet et al. to speed up computations
[Cornuet et al., 2012]

108. Moment condition in population genetics?
EL does not require a fully defined and often complex (hence
debatable) parametric model
Main difficulty
Derive a constraint
EF h(X, φ) = 0,
on the parameters of interest φ when X is made of the genotypes
of the sample of individuals at a given locus
E.g., in phylogeography, φ is composed of
dates of divergence between populations,
ratio of population sizes,
mutation rates, etc.
None of them are moments of the distribution of the allelic states
of the sample

109. Moment condition in population genetics?
EL does not require a fully defined and often complex (hence
debatable) parametric model
Main difficulty
Derive a constraint
EF h(X, φ) = 0,
on the parameters of interest φ when X is made of the genotypes
of the sample of individuals at a given locus
c h made of pairwise composite scores (whose zero is the pairwise
maximum likelihood estimator)

110. Pairwise composite likelihood
The intra-locus pairwise likelihood
2(xk|φ) =
i<j
2(xi
k, xj
k|φ)
with x1
k , . . . , xn
k : allelic states of the gene sample at the k-th locus
The pairwise score function
φ log 2(xk|φ) =
i<j
φ log 2(xi
k, xj
k|φ)
Composite likelihoods are often much narrower than the
original likelihood of the model
Safe(r) with EL because we only use position of its mode

111. Pairwise likelihood: a simple case
Assumptions
sample ⊂ closed, panmictic
population at equilibrium
marker: microsatellite
mutation rate: θ/2
if xi
k et xj
k are two genes of the
sample,
2(xi
k, xj
k|θ) depends only on
δ = xi
k − xj
k
2(δ|θ) =
1
√
1 + 2θ
ρ (θ)|δ|
with
ρ(θ) =
θ
1 + θ +
√
1 + 2θ
Pairwise score function
∂θ log 2(δ|θ) =
−
1
1 + 2θ
+
|δ|
θ
√
1 + 2θ

112. Pairwise likelihood: a simple case
Assumptions
sample ⊂ closed, panmictic
population at equilibrium
marker: microsatellite
mutation rate: θ/2
if xi
k et xj
k are two genes of the
sample,
2(xi
k, xj
k|θ) depends only on
δ = xi
k − xj
k
2(δ|θ) =
1
√
1 + 2θ
ρ (θ)|δ|
with
ρ(θ) =
θ
1 + θ +
√
1 + 2θ
Pairwise score function
∂θ log 2(δ|θ) =
−
1
1 + 2θ
+
|δ|
θ
√
1 + 2θ

113. Pairwise likelihood: a simple case
Assumptions
sample ⊂ closed, panmictic
population at equilibrium
marker: microsatellite
mutation rate: θ/2
if xi
k et xj
k are two genes of the
sample,
2(xi
k, xj
k|θ) depends only on
δ = xi
k − xj
k
2(δ|θ) =
1
√
1 + 2θ
ρ (θ)|δ|
with
ρ(θ) =
θ
1 + θ +
√
1 + 2θ
Pairwise score function
∂θ log 2(δ|θ) =
−
1
1 + 2θ
+
|δ|
θ
√
1 + 2θ

114. Pairwise likelihood: 2 diverging populations
MRCA
POP a POP b
τ
Assumptions
τ: divergence date of
pop. a and b
θ/2: mutation rate
Let xi
k and xj
k be two genes
coming resp. from pop. a and
b
Set δ = xi
k − xj
k.
Then 2(δ|θ, τ) =
e−τθ
√
1 + 2θ
+∞
k=−∞
ρ(θ)|k|
Iδ−k(τθ).
where
In(z) nth-order modified
Bessel function of the first
kind

115. Pairwise likelihood: 2 diverging populations
MRCA
POP a POP b
τ
Assumptions
τ: divergence date of
pop. a and b
θ/2: mutation rate
Let xi
k and xj
k be two genes
coming resp. from pop. a and
b
Set δ = xi
k − xj
k.
A 2-dim score function
∂τ log 2(δ|θ, τ) = −θ+
θ
2
2(δ − 1|θ, τ) + 2(δ + 1|θ, τ)
2(δ|θ, τ)
∂θ log 2(δ|θ, τ) =
−τ −
1
1 + 2θ
+
q(δ|θ, τ)
2(δ|θ, τ)
+
τ
2
2(δ − 1|θ, τ) + 2(δ + 1|θ, τ)
2(δ|θ, τ)
where
q(δ|θ, τ) :=
e−τθ
√
1 + 2θ
ρ (θ)
ρ(θ)
∞
k=−∞
|k|ρ(θ)|k|
Iδ−k (τθ)

116. Example: normal posterior
[A]BCel with two constraints
ESS=155.6
θ
Density
−0.5 0.0 0.5 1.0
0.01.0
ESS=75.93
θ
Density
−0.4 −0.2 0.0 0.2 0.4
0.01.02.0
ESS=76.87
θ
Density
−0.4 −0.2 0.0 0.2
01234
ESS=91.54
θ
Density
−0.6 −0.4 −0.2 0.0 0.2
01234
ESS=108.4
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.02.03.0
ESS=85.13
θ
Density
−0.2 0.0 0.2 0.4 0.6
0.01.02.03.0
ESS=149.1
θ
Density
−0.5 0.0 0.5 1.0
0.01.02.0
ESS=96.31
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.02.0
ESS=83.77
θ
Density
−0.6 −0.4 −0.2 0.0 0.2 0.401234
ESS=155.7
θ
Density
−0.5 0.0 0.5
0.01.02.0
ESS=92.42
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.02.03.0
ESS=95.01
θ
Density
−0.4 0.0 0.2 0.4 0.6
0.01.53.0
ESS=139.2
Density
−0.6 −0.2 0.2 0.6
0.01.02.0
ESS=99.33
Density
−0.4 −0.2 0.0 0.2 0.4
0.01.02.03.0
ESS=87.28
Density
−0.2 0.0 0.2 0.4 0.6
0123
Sample sizes are of 25 (column 1), 50 (column 2) and 75 (column 3)
observations

117. Example: normal posterior
[A]BCel with three constraints
ESS=300.1
θ
Density
−0.4 0.0 0.4 0.8
0.01.0
ESS=205.5
θ
Density
−0.6 −0.2 0.0 0.2 0.4
0.01.02.0
ESS=179.4
θ
Density
−0.2 0.0 0.2 0.4
0.01.53.0
ESS=265.1
θ
Density
−0.3 −0.2 −0.1 0.0 0.1
01234
ESS=250.3
θ
Density
−0.6 −0.4 −0.2 0.0 0.2
0.01.02.0
ESS=134.8
θ
Density
−0.4 −0.2 0.0 0.1
01234
ESS=331.5
θ
Density
−0.8 −0.4 0.0 0.4
0.01.02.0
ESS=167.4
θ
Density
−0.9 −0.7 −0.5 −0.3
0123
ESS=136.5
θ
Density
−0.4 −0.2 0.0 0.201234
ESS=322.4
θ
Density
−0.2 0.0 0.2 0.4 0.6 0.8
0.01.02.0
ESS=202.7
θ
Density
−0.4 −0.2 0.0 0.2 0.4
0.01.02.03.0
ESS=166
θ
Density
−0.4 −0.2 0.0 0.2
01234
ESS=263.7
Density
−1.0 −0.6 −0.2
0.01.02.0
ESS=190.9
Density
−0.4 −0.2 0.0 0.2 0.4 0.6
0123
ESS=165.3
Density
−0.5 −0.3 −0.1 0.1
0.01.53.0
Sample sizes are of 25 (column 1), 50 (column 2) and 75 (column 3)
observations

118. Example: Superposition of gamma processes
Example of superposition of N renewal processes with waiting
times τij (i = 1, . . . , M, j = 1, . . .) ∼ G(α, β), when N is unknown.
Renewal processes
ζi1 = τi1, ζi2 = ζi1 + τi2, . . .
with observations made of first n values of the ζij ’s,
z1 = min{ζij }, z2 = min{ζij ; ζij > z1}, . . .
ending with
zn = min{ζij ; ζij > zn−1} .
[Cox & Kartsonaki, B’ka, 2012]

119. Example: Superposition of gamma processes (ABC)
Interesting testing ground for [A]BCel since data (zt) neither iid
nor Markov
Recovery of an iid structure by
1. simulating a pseudo-dataset,
(z1 , . . . , zn ), as in regular
ABC,
2. deriving sequence of
indicators (ν1, . . . , νn), as
z1 = ζν11, z2 = ζν2j2 , . . .
3. exploiting that those
indicators are distributed
from the prior distribution
on the νt’s leading to an iid
sample of G(α, β) variables
Comparison of ABC and
[A]BCel posteriors
α
Density
0 1 2 3 4
0.00.20.40.60.81.01.21.4
β
Density
0 1 2 3 4
0.00.51.01.5
N
Density
0 5 10 15 20
0.000.020.040.060.08
α
Density
0 1 2 3 4
0.00.51.01.5
β
Density
0 1 2 3 4
0.00.20.40.60.81.0
N
Density
0 5 10 15 20
0.000.010.020.030.040.050.06
Top: [A]BCel
Bottom: regular ABC

120. Example: Superposition of gamma processes (ABC)
Interesting testing ground for [A]BCel since data (zt) neither iid
nor Markov
Recovery of an iid structure by
1. simulating a pseudo-dataset,
(z1 , . . . , zn ), as in regular
ABC,
2. deriving sequence of
indicators (ν1, . . . , νn), as
z1 = ζν11, z2 = ζν2j2 , . . .
3. exploiting that those
indicators are distributed
from the prior distribution
on the νt’s leading to an iid
sample of G(α, β) variables
Comparison of ABC and
[A]BCel posteriors
α
Density
0 1 2 3 4
0.00.20.40.60.81.01.21.4
β
Density
0 1 2 3 4
0.00.51.01.5
N
Density
0 5 10 15 20
0.000.020.040.060.08
α
Density
0 1 2 3 4
0.00.51.01.5
β
Density
0 1 2 3 4
0.00.20.40.60.81.0
N
Density
0 5 10 15 20
0.000.010.020.030.040.050.06
Top: [A]BCel
Bottom: regular ABC

121. Pop’gen’: A first experiment
Evolutionary scenario:
MRCA
POP 0 POP 1
τ
Dataset:
50 genes per populations,
100 microsat. loci
Assumptions:
Ne identical over all
populations
φ = (log10 θ, log10 τ)
uniform prior over
(−1., 1.5) × (−1., 1.)
Comparison of the original
ABC with [A]BCel
ESS=7034
log(theta)
Density
0.00 0.05 0.10 0.15 0.20 0.25
051015
log(tau1)
Density
−0.3 −0.2 −0.1 0.0 0.1 0.2 0.3
01234567
histogram = [A]BCel
curve = original ABC
vertical line = “true”
parameter

122. Pop’gen’: A first experiment
Evolutionary scenario:
MRCA
POP 0 POP 1
τ
Dataset:
50 genes per populations,
100 microsat. loci
Assumptions:
Ne identical over all
populations
φ = (log10 θ, log10 τ)
uniform prior over
(−1., 1.5) × (−1., 1.)
Comparison of the original
ABC with [A]BCel
ESS=7034
log(theta)
Density
0.00 0.05 0.10 0.15 0.20 0.25
051015
log(tau1)
Density
−0.3 −0.2 −0.1 0.0 0.1 0.2 0.3
01234567
histogram = [A]BCel
curve = original ABC
vertical line = “true”
parameter

123. ABC vs. [A]BCel on 100 replicates of the 1st experiment
Accuracy:
log10 θ log10 τ
ABC [A]BCel ABC [A]BCel
(1) 0.097 0.094 0.315 0.117
(2) 0.071 0.059 0.272 0.077
(3) 0.68 0.81 1.0 0.80
(1) Root Mean Square Error of the posterior mean
(2) Median Absolute Deviation of the posterior median
(3) Coverage of the credibility interval of probability 0.8
Computation time: on a recent 6-core computer
(C++/OpenMP)
ABC ≈ 4 hours
[A]BCel≈ 2 minutes

124. Pop’gen’: Second experiment
Evolutionary scenario:
MRCA
POP 0 POP 1 POP 2
τ1
τ2
Dataset:
50 genes per populations,
100 microsat. loci
Assumptions:
Ne identical over all
populations
φ =
(log10 θ, log10 τ1, log10 τ2)
non-informative uniform
Comparison of the original ABC
with [A]BCel
histogram = [A]BCel
curve = original ABC
vertical line = “true” parameter

125. Pop’gen’: Second experiment
Evolutionary scenario:
MRCA
POP 0 POP 1 POP 2
τ1
τ2
Dataset:
50 genes per populations,
100 microsat. loci
Assumptions:
Ne identical over all
populations
φ =
(log10 θ, log10 τ1, log10 τ2)
non-informative uniform
Comparison of the original ABC
with [A]BCel
histogram = [A]BCel
curve = original ABC
vertical line = “true” parameter

126. Pop’gen’: Second experiment
Evolutionary scenario:
MRCA
POP 0 POP 1 POP 2
τ1
τ2
Dataset:
50 genes per populations,
100 microsat. loci
Assumptions:
Ne identical over all
populations
φ =
(log10 θ, log10 τ1, log10 τ2)
non-informative uniform
Comparison of the original ABC
with [A]BCel
histogram = [A]BCel
curve = original ABC
vertical line = “true” parameter

127. Pop’gen’: Second experiment
Evolutionary scenario:
MRCA
POP 0 POP 1 POP 2
τ1
τ2
Dataset:
50 genes per populations,
100 microsat. loci
Assumptions:
Ne identical over all
populations
φ =
(log10 θ, log10 τ1, log10 τ2)
non-informative uniform
Comparison of the original ABC
with [A]BCel
histogram = [A]BCel
curve = original ABC
vertical line = “true” parameter

128. ABC vs. [A]BCel on 100 replicates of the 2nd experiment
Accuracy:
log10 θ log10 τ1 log10 τ2
ABC [A]BCel ABC [A]BCel ABC [A]B
(1) .0059 .0794 .472 .483 29.3 4.7
(2) .048 .053 .32 .28 4.13 3.3
(3) .79 .76 .88 .76 .89 .79
(1) Root Mean Square Error of the posterior mean
(2) Median Absolute Deviation of the posterior median
(3) Coverage of the credibility interval of probability 0.8
Computation time: on a recent 6-core computer
(C++/OpenMP)
ABC ≈ 6 hours
[A]BCel≈ 8 minutes

129. Comparison
On large datasets, [A]BCel gives more accurate results than ABC
ABC simplifies the dataset through summary statistics
Due to the large dimension of x, the original ABC algorithm
estimates
π θ η(xobs) ,
where η(xobs) is some (non-linear) projection of the observed
dataset on a space with smaller dimension
→ Some information is lost
[A]BCel simplifies the model through a generalized moment
condition model.
→ Here, the moment condition model is based on pairwise
composition likelihood

130. Conclusion/perspectives
abc part of a wider picture
to handle complex/Big Data
models
many formats of empirical
[likelihood] Bayes methods
available
lack of comparative tools
and of an assessment for
information loss