The document provides an educational resource on complement theory, including 1's and 2's complements, along with arithmetic operations such as addition and subtraction in various number systems (binary, decimal, octal, and hexadecimal). It contains examples demonstrating the operations of 1's and 2's complement arithmetic, as well as BCD addition. Additionally, the document outlines methods for converting between different number systems and performing arithmetic calculations using these complements.

1. Lectures on Complement Theory (1’s and 2’s, 9’s
and 10’s), BCD Addition, Decimal, Octal, and
Hexadecimal Addition
for
Open Educational Resource
on
Logic Development and Programming (EC221)
by
Dr. Piyush Charan
Assistant Professor
Department of Electronics and Communication Engg.
Integral University, Lucknow

2. 2
1. Complement Theory
2. 1’s and, 2’s complement operation
Number System Continued....
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

3. 3
1.Complement Theory
Example 1 Get 1’s complement of 50
Complement Digits
50 = 110010

001101
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

4. 4
1’s Complement Arithmetic
(ADD/SUB Method)
1. Read both the operands
2. Negative operand(s) (if any) is converted into 1’s complement form
3. Add both the numbers
4. If carry is generated (i.e. =1) then the resultant number is positive.
5. Add ONE to the output of setp4, to get the final answer.
6. If carry is not generated then the answer is Negative and available in 1’s complement form.
7. Convert output of step 6 into 1’s complement to get final answer.
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

5. 5
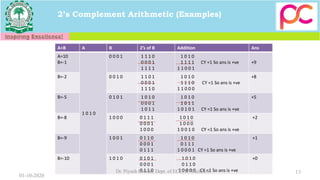
1. 1’s Complement Theory
Example 1 : Subtract 1010 from 1111 using 1’s complement theory. (15-10 Small negative)

1 0 1 0 0 1 0 1
1 1 1 1
0 1 0 1+
1] 0 1 0 0
+ 0 0 0 1
0 1 0 1 =(5)
1’s complement
Carry “1” means the answer is positive .
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

6. 6
1. 1’s Complement Theory
Example 2 : Subtract 1010 from 1000 using 1’s complement theory. (Large negative 8-10)
1 0 1 0 0 1 0 1
1 0 0 0
0 1 0 1+
0] 1 1 0 1
1’s complement
Carry “0” means the answer is negative and available in 1’s complement form.
1 1 0 1 0 0 1 0 = (2)
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

7. 7
2’s Complement Arithmetic
1. How to get 2’s complement form
2. Arithmetic operation using 2’s complement theory
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

8. 8
2’s Complement Arithmetic (How to get 2’s
complement form..?)
Example 1
Example 2
Complement Digits
Add 1
5 = 00000101
-5 = 11111011

11111010
+1
Complement Digits
Add 1
-13 = 11110011
13 = 00001101

00001100
+1
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

9. 9
2’s Complement Arithmetic
(Method)
1. Read both the operands
2. Negative operand (if any) is converted into 2’s complement form
3. Add both the numbers (2’s complement of negative operand with the other one).
4. If carry is generated (i.e. =1) then the resultant number is positive and in original form
5. If carry is not generated(when we have negative operand) then the carry is assumed =0.
6. Carry zero means the resultant number is negative and in a 2’s complement form.
7. Convert the 2’s complement form into the original form.
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

10. POS + NEG → POS Answer
10
Take the 2’s complement of the negative number and use regular binary 8-bit
addition.
000010019
+ (-5)
4
⎯→
⎯
11111011+
00000101

11111010
+1
11111011
2’s
Complement
Process
100000100
Last Bit = 1: Answer is Positive Disregard 9th
Bit
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

11. POS + NEG → NEG Answer
11
Take the 2’s complement of the negative number and use regular 8-bit
binary addition.
11110111(-9)
+ 5
-4
⎯→
⎯
00000101+
00001001

11110110
+1
11110111
2’s
Complement
Process
011111100
Last Bit = 0: Answer is Negative . Discard the last bit
11111100

00000011
+1
00000100
To Check:
Perform 2’s
Complement
On Answer
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

12. Verify the logic using following combinations:
1: (10) –(01)
2: (10) –(02)
3: (10) –(05)
4: (10) –(08)
5: (10) –(09)
6: (10) –(10)
7: (210) –(08)
8: (120) –(55)
9: (52) –(18)
01-10-2020 12Dr. Piyush Charan, Dept. of ECE, IU Lucknow

13. A+B A B 2’s of B Addition Ans
A=10
B=-1
1 0 1 0
0 0 0 1 1 1 1 0
0 0 0 1
1 1 1 1
1 0 1 0
1 1 1 1 CY =1 So ans is +ve
1 1 0 0 1
+9
B=-2 0 0 1 0 1 1 0 1
0 0 0 1
1 1 1 0
1 0 1 0
1 1 1 0 CY =1 So ans is +ve
1 1 0 0 0
+8
B=-5 0 1 0 1 1 0 1 0
0 0 0 1
1 0 1 1
1 0 1 0
1 0 1 1
1 0 1 0 1 CY =1 So ans is +ve
+5
B=-8 1 0 0 0 0 1 1 1
0 0 0 1
1 0 0 0
1 0 1 0
1 0 0 0
1 0 0 1 0 CY =1 So ans is +ve
+2
B=-9 1 0 0 1 0 1 1 0
0 0 0 1
0 1 1 1
1 0 1 0
0 1 1 1
1 0 0 0 1 CY =1 So ans is +ve
+1
B=-10 1 0 1 0 0 1 0 1
0 0 0 1
0 1 1 0
1 0 1 0
0 1 1 0
1 0 0 0 0 CY =1 So ans is +ve
+0
2’s Complement Arithmetic (Examples)
01-10-2020
13Dr. Piyush Charan, Dept. of ECE, IU Lucknow

14. Example: Perform 2’s complement subtraction on 210-08
210 = 1 1 0 1 0 0 1 0 (Subtrahend)
8= 0 0 0 0 1 0 0 0 (Minuend)
2’s complement of 8 is = 1 1 1 1 1 0 0 0
Add both the numbers:
1 1 0 1 0 0 1 0
+1 1 1 1 1 0 0 0
1 1 1 0 0 1 0 1 0
Carry = 1 means and is positive +202
01-10-2020 14Dr. Piyush Charan, Dept. of ECE, IU Lucknow

15. 15
2’s Complement Arithmetic (Examples on varying
number of bits)
Example: Perform 2’s complement arithmetic for (30)-(50) using
1: 6-bit number system
2: 8-bit number system
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow

16. Example: Perform 2’s complement arithmetic for (30)-(50) using:
(30)= 0 1 1 1 1 0
(-50)= 1 1 0 0 1 0 2’s complement 0 0 1 1 0 1
0 0 0 0 0 1
0 0 1 1 1 0
Add both the numbers
0 1 1 1 1 0
0 0 1 1 1 0
0 1 0 1 1 0 0
Carry =0 means number is negative and in 2’s compl form
(30)= 0 0 0 1 1 1 1 0
(-50)= 0 0 1 1 0 0 1 0 2’s complement 1 1 0 0 1 1 0 1
0 0 0 0 0 0 0 1
1 1 0 0 1 1 1 0
0 0 0 1 1 1 1 0
1 1 0 0 1 1 1 0
0 1 1 1 0 1 1 0 0
Carry =0 means number is negative and in 2’s compl form
0 1 0 0 1 1
0 0 0 0 0 1
0 1 0 1 0 0 = -20
0 0 0 1 0 0 1 1
0 0 0 0 0 0 0 1
0 0 0 1 0 1 0 0 = -20
Add both the numbers
1: 6-bit number system 2: 8-bit number
system
01-10-2020 16Dr. Piyush Charan, Dept. of ECE, IU Lucknow

17. BCD Numbers
01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow 17

18. 01-10-2020 Dr. Piyush Charan, Dept. of ECE, IU Lucknow 18

19. 1. Binary to decimal Conversion
2. BCD Addition
11/2/2020
Dr. Piyush Charan, Dept. of ECE, Integral University,
Lucknow
19

20. 9’s & 10’s Complement
11/2/2020 20
Dr. Piyush Charan, Dept. of ECE, Integral University,
Lucknow

21. Decimal(base 10) Addition
11/2/2020
Dr. Piyush Charan, Dept. of ECE, Integral University,
Lucknow
21

22. Octal (base 8) Addition
11/2/2020 22
Dr. Piyush Charan, Dept. of ECE, Integral University,
Lucknow

23. Hexadecimal(base 16) Addition
11/2/2020 23
Dr. Piyush Charan, Dept. of ECE, Integral University,
Lucknow