This document provides an overview of basic mathematics concepts including addition, subtraction, multiplication, and division of real numbers. It discusses key topics such as:
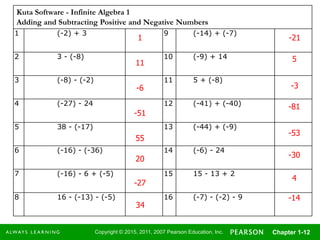
- Adding and subtracting real numbers using number lines and properties of opposites.
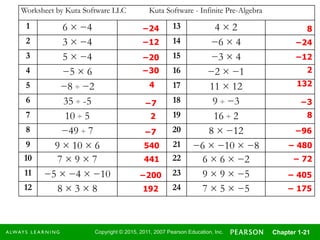
- Multiplying and dividing real numbers, including the sign of the product and quotient rules.
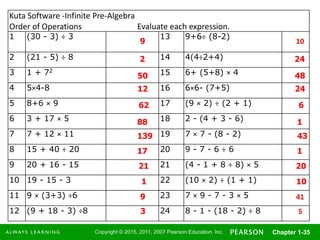
- Order of operations and evaluating expressions with exponents, parentheses, and the proper order.
- Properties of real numbers including the commutative, associative, distributive, identity, and inverse properties.

























![Copyright © 2015, 2011, 2007 Pearson Education, Inc. Chapter 1-28
Order of Operations
Evaluate:
-7 + 2 [-6 + (36 / 32 )] = Exponent
Divide
Add
-7 + 2 [-6 + (36 / 9 )] =
-7 + 2 [-6 + 4] =
-7 + 2 [-2] =
-11
Steps Taken
-7 - 4 =
Multiply](https://image.slidesharecdn.com/addition-subtraction-multi-divison6-150604022350-lva1-app6891/85/Addition-subtraction-multi-divison-6-28-320.jpg)