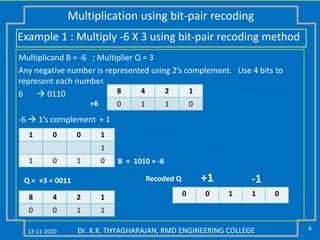
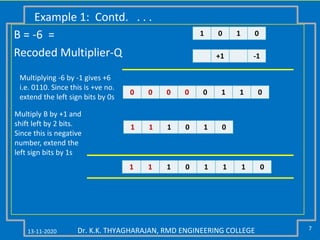
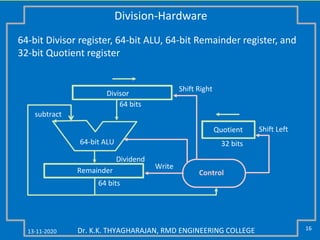
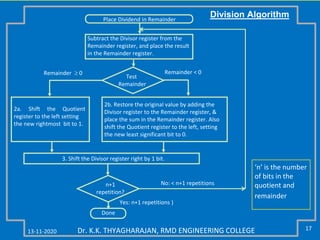
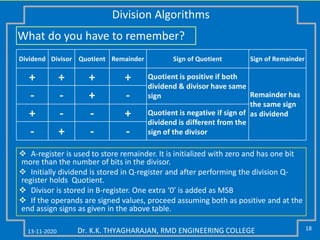
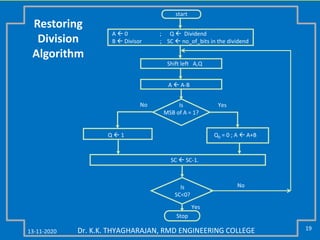
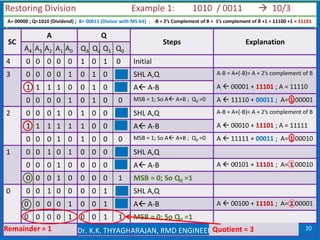
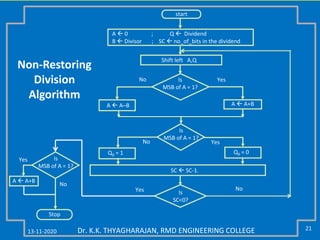
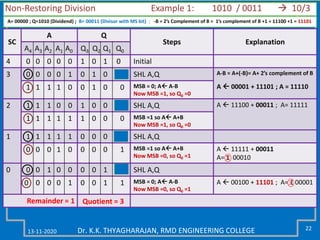
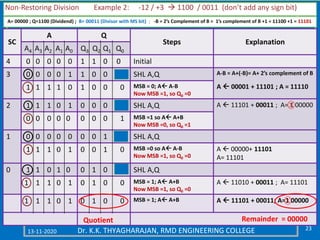
The document discusses multiplication and division algorithms in binary, specifically focusing on modified Booth's algorithm for multiplication and various division algorithms. It includes detailed examples of bit-pair recoding, handling of negative numbers using 2’s complement, and step-by-step processes for both multiplication and division within binary arithmetic. Key points include the representation of numbers, how to recode them, and the implementation of both restoring and non-restoring division methods.