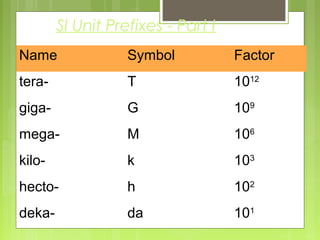
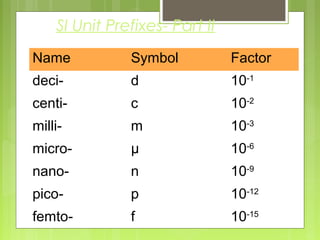
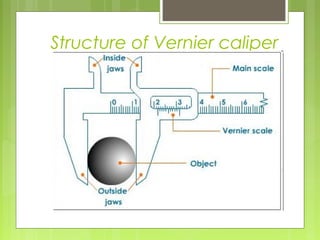
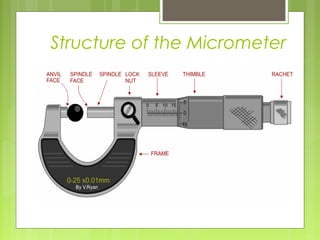
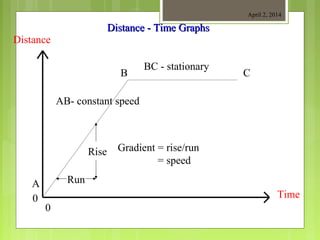
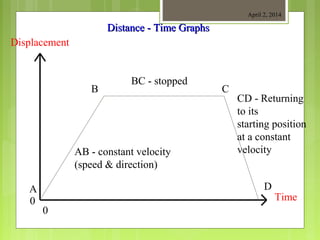
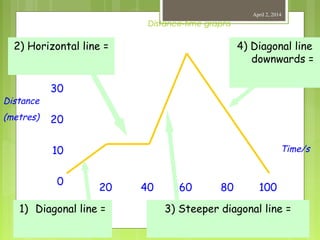
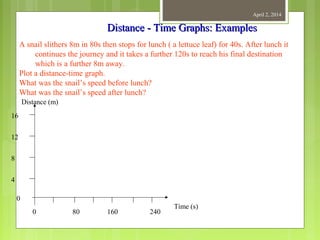
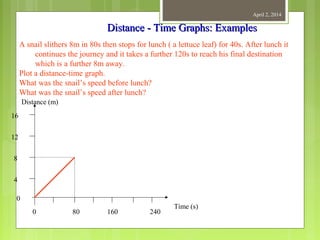
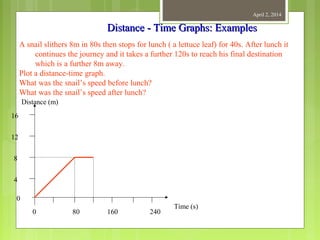
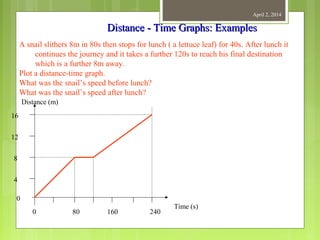
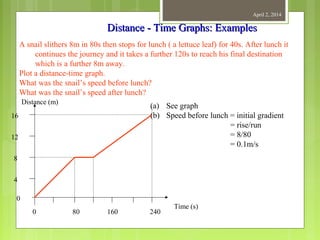
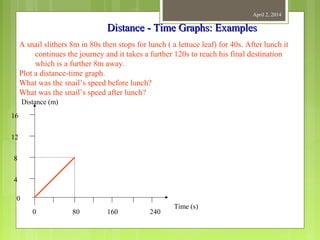
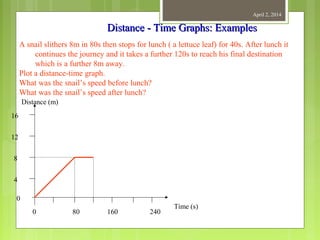
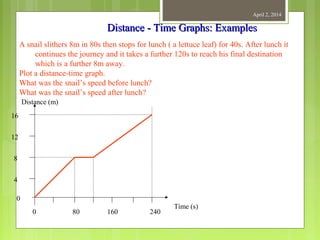
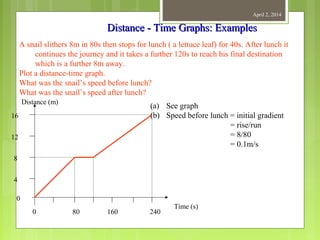
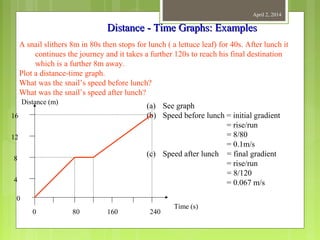
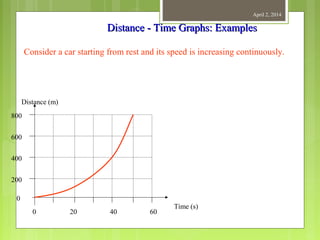
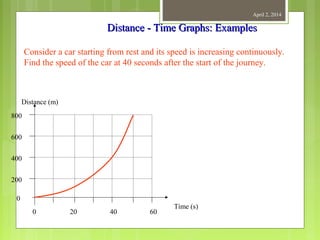
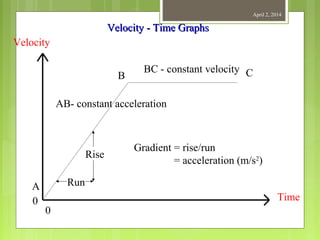
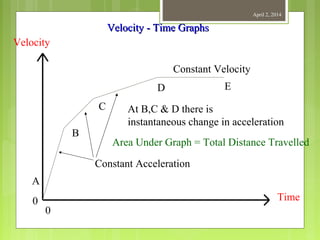
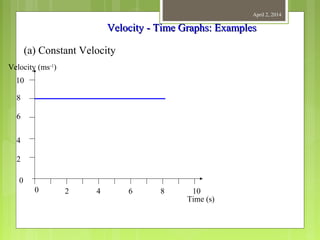
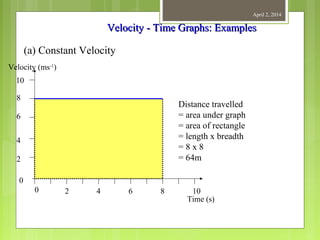
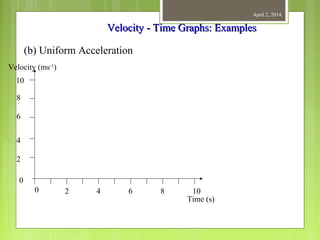
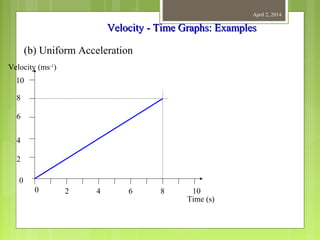
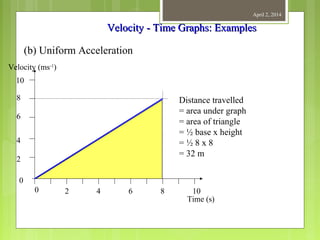
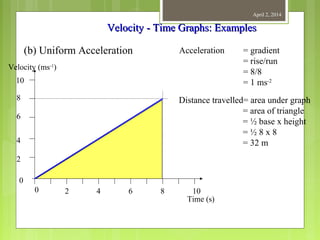
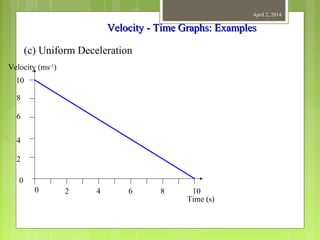
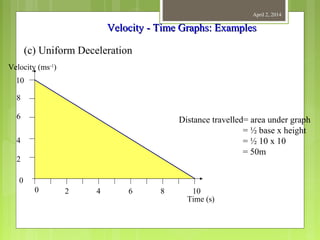
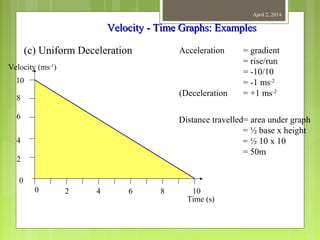
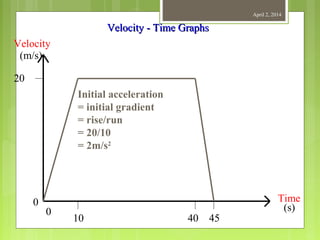
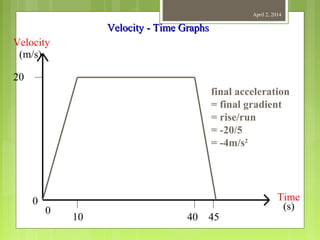
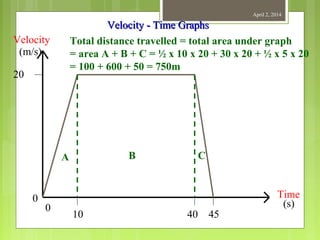
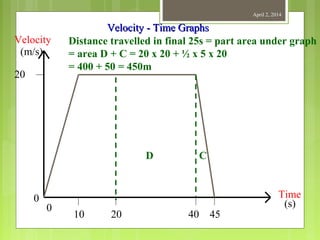
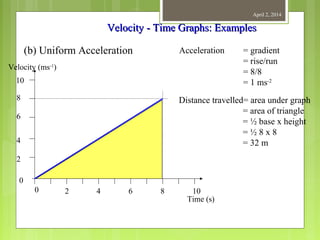
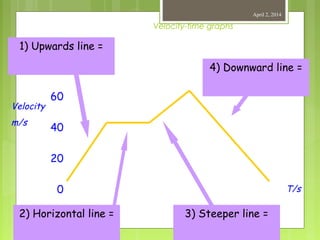
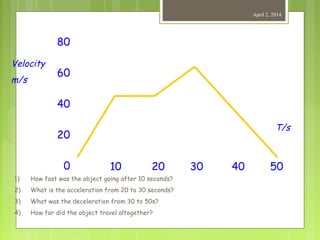
This document provides information about measurement and units of measurement. It discusses the tools used for measurement including vernier calipers and micrometers. It defines key terms like accuracy, precision, and significant figures. It also covers creating distance-time graphs and using them to determine speed and velocity. Examples are provided to demonstrate how to calculate speed from a distance-time graph and how the graph would look for an object that changes speed or stops during its motion.