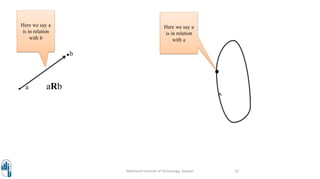
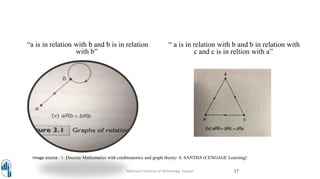
This document discusses relation matrices and graphs. It begins by defining a relation matrix as a way to represent a relation between two finite sets A and B using a matrix with 1s and 0s. An example is provided to demonstrate how to construct a relation matrix. The document then discusses how relations can be represented using graphs by connecting elements with edges. Properties of relations like reflexive, symmetric, and anti-symmetric are explained through examples using relation matrices. Finally, the conclusion restates that relation matrices and graphs can be used to represent relations between sets.

1. Relation Matrix & Graph
Ms. Rachana Pathak
(rachanarpathak@gmail.com)
Assistant Professor, Dept of Computer Science and Engineering
Walchand Institute of Technology, Solapur
(www.witsolapur.org)

2. Learning Outcome
2Walchand Institute of Technology, Solapur
At the end of this session,
Students will be able to evaluate relation matrix and graphs on it.

3. Prerequisite
• Basics of Discrete Mathematics
• Basics of Relation
Walchand Institute of Technology, Solapur 3

4. Introduction
Relation Matrix
• A relation R from a finite set A to a finite set B can be
represented by a matrix called the relation matrix of R.
• Let A ={a1,a2,a3…am} and B= {b1,b2,b3……bn} be finite set
containing m and n elements, respectively, and R be the
relation from A to B.
• Then R can be represented by an m x n matrix Mr = [rij],which
is defined as follows:
Walchand Institute of Technology, Solapur 4

5. rij = 1, if ai R bj
0, if ai R bj
Note that the matrix MR has the elements as 1’s and 0’s.
Walchand Institute of Technology, Solapur 5

6. Example
Let A = {1,2,3,4} and B ={b1,b2,b3}. Consider the relation R =
{(1,b2),(1,b3),(3,b2),(4,b1),(4,b3)}. Determine the matrix of the
relation.
Solution :
A = {1,2,3,4} B = {b1,b2,b3}.
Relation R = {(1,b2),(1,b3),(3,b2),(4,b1),(4,b3)}.
Matrix of the Relation R is written as-
Walchand Institute of Technology, Solapur 6

7. Example
b1 b2 b3
1 0 1 1
2 0 0 0
3 0 1 0
4 1 0 1
Walchand Institute of Technology, Solapur 7

8. Example
0 1 1
0 0 0
0 1 0
1 0 1
Walchand Institute of Technology, Solapur 8

9. Think & Write?
Let A = {1,2,3,4}. Find the relation R on A determined by the
matrix.
MR = 1 0 1 0
0 0 1 0
1 0 0 0
1 1 0 1
Walchand Institute of Technology, Solapur 9

10. Answer
The relation R =
{ (1,1),(1,3),(2,3),(3,1),(4,1),(4,2),(4,4) }
Walchand Institute of Technology, Solapur 10

11. Properties of a Relation in a Set
Walchand Institute of Technology, Solapur 11
• All diagonal entries must
be 1
Reflexive
• Rij = Rij for every i and jSymmetric
• Rij = 1 & Rji = 0 for i≠jAnti-symmetric

12. Reflexive
Walchand Institute of Technology, Solapur 12
MR = 1 0 1 0
0 1 1 0
1 0 1 0
1 1 0 1

13. Symmetric
MR = 1 2 3 4
1
2
3
4
Walchand Institute of Technology, Solapur 13
1 1 0 1
1 1 0 0
0 0 0 0
1 0 0 0

14. Anti-Symmetric
MR = 1 2 3 4
1
2
3
4
Walchand Institute of Technology, Solapur 14
1 0 0 0
1 1 0 0
0 0 0 0
1 0 0 0

15. Graph
Walchand Institute of Technology, Solapur 15
• A relation defined in a finite set can also be represented pictorially with
the help of a graph.
• Let R be a relation in a finite set A = {a1,a2,….an}.
• Elements of A are represented by points or circles called nodes.
• These nodes are called vertices
• Arcs are used to show the connection called as edge.
• Let us see some examples :

16. .b
. a aRb
.
Walchand Institute of Technology, Solapur 16
Here we say a
is in relation
with a
^
Here we say a
is in relation
with b

17. “a is in relation with b and b is in relation
with b”
“ a is in relation with b and b in relation with
c and c is in reltion with a”
Walchand Institute of Technology, Solapur 17
Image source : 1. Discrete Mathematics with combinatorics and graph theory- S. SANTHA (CENGAGE Learning)

18. Conclusion :
In this session, We have studied all about POSET.
Walchand Institute of Technology, Solapur 18

19. References
• 1. Discrete mathematical structures with applications to computer science -- J. P.
Tremblay & R. Manohar (MGH International)
• Reference Books:
• 1. Discrete Mathematics with combinatorics and graph theory- S. SANTHA
(CENGAGE Learning)
• 2. Discrete Mathematical Structures – Bernard Kolman, Robert C. Busby (Pearson
Education)
• 3. Discrete mathematics -- Liu (MGH)
19Walchand Institute of Technology, Solapur

20. Thank You !!!
20Walchand Institute of Technology, Solapur