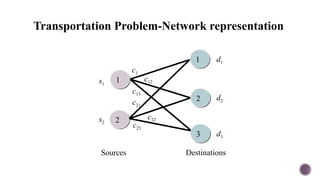
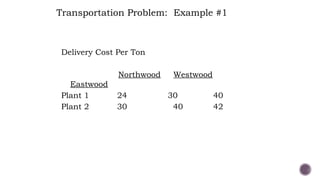
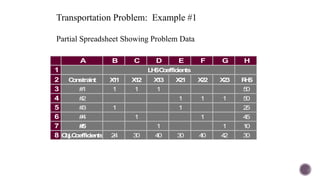
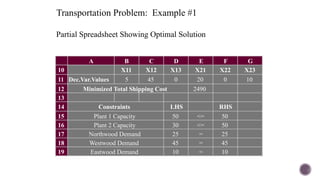
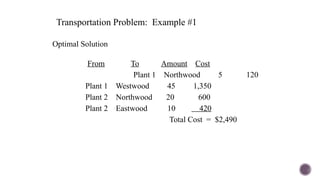
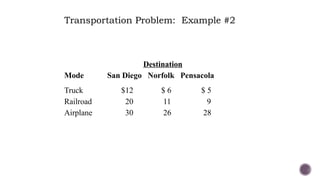
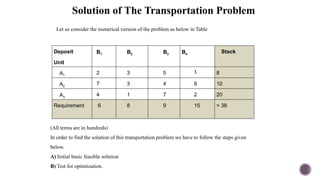
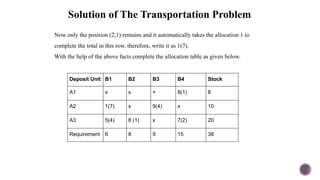
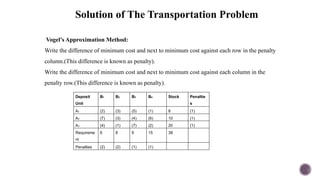
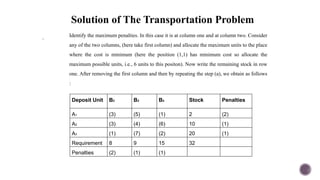
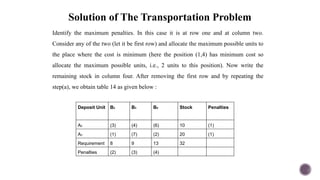
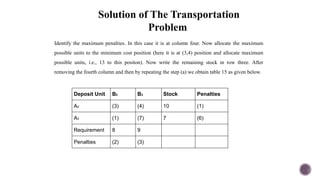
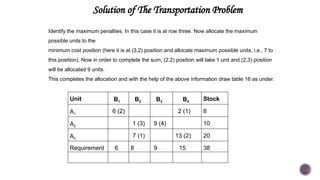
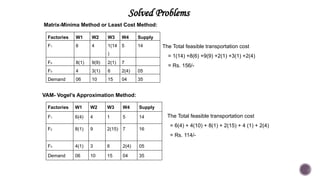
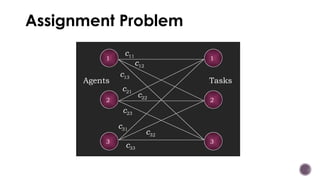
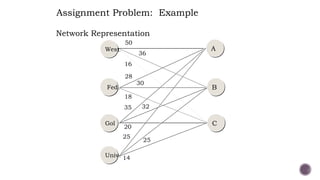
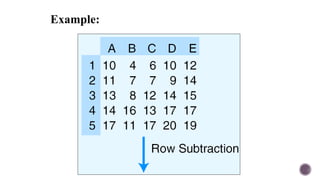
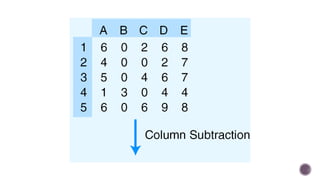
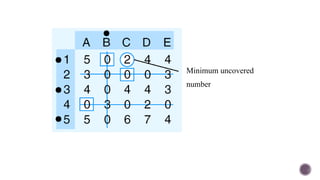
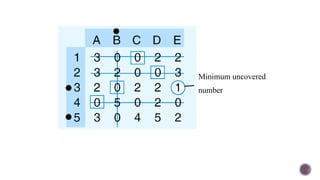
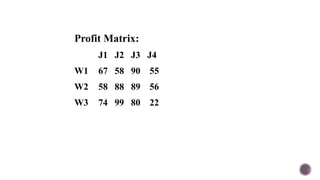
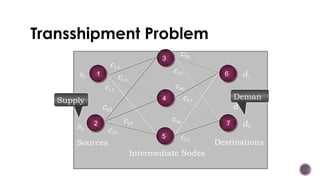
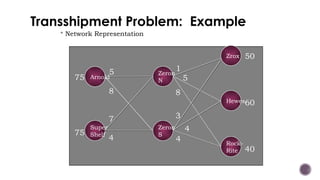
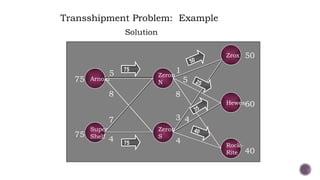
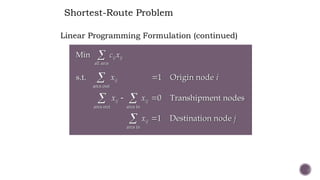
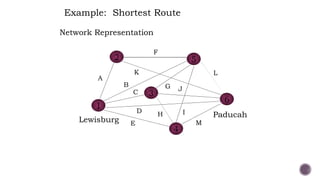
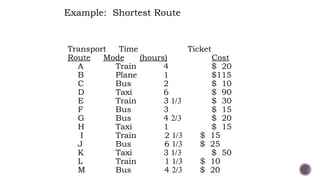
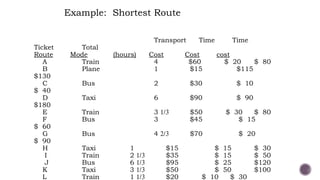
El documento presenta modelos de red en la optimización de problemas de transporte, asignación y flujo máximo, destacando su formulación y solución a través de programación lineal. Describe en detalle el problema de transporte, que busca minimizar los costos de envío al distribuir productos de varios centros de suministro a diferentes destinos. También se ofrecen ejemplos prácticos de problemas de transporte, incluyendo la formulación de funciones objetivo y restricciones necesarias para resolverlos.