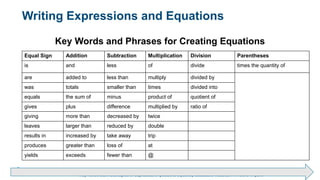
This chapter discusses using equations to solve business problems. It defines key terms related to equations such as variables, constants, expressions, and formulas. It explains how to solve basic equations by transposing terms to isolate the variable. It provides examples of solving equations with addition, subtraction, multiplication, division and multiple operations. It also discusses writing expressions and equations from word problems by identifying key words. The chapter aims to teach students how to set up and solve equations that model real-world business situations.