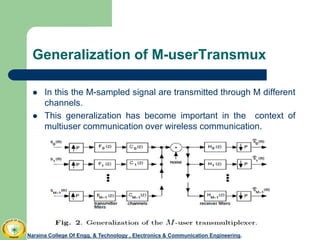
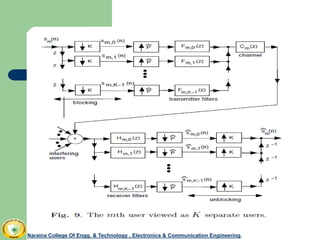
The document discusses the use of transmultiplexers as precoders in modern digital communication, focusing on their role in converting time-multiplexed signals into frequency-multiplexed signals. It covers key concepts such as bandwidth efficiency, noise optimization, and blind identification in channels. The conclusion highlights the challenges in minimizing redundancy in precoders and addressing channel nulls.