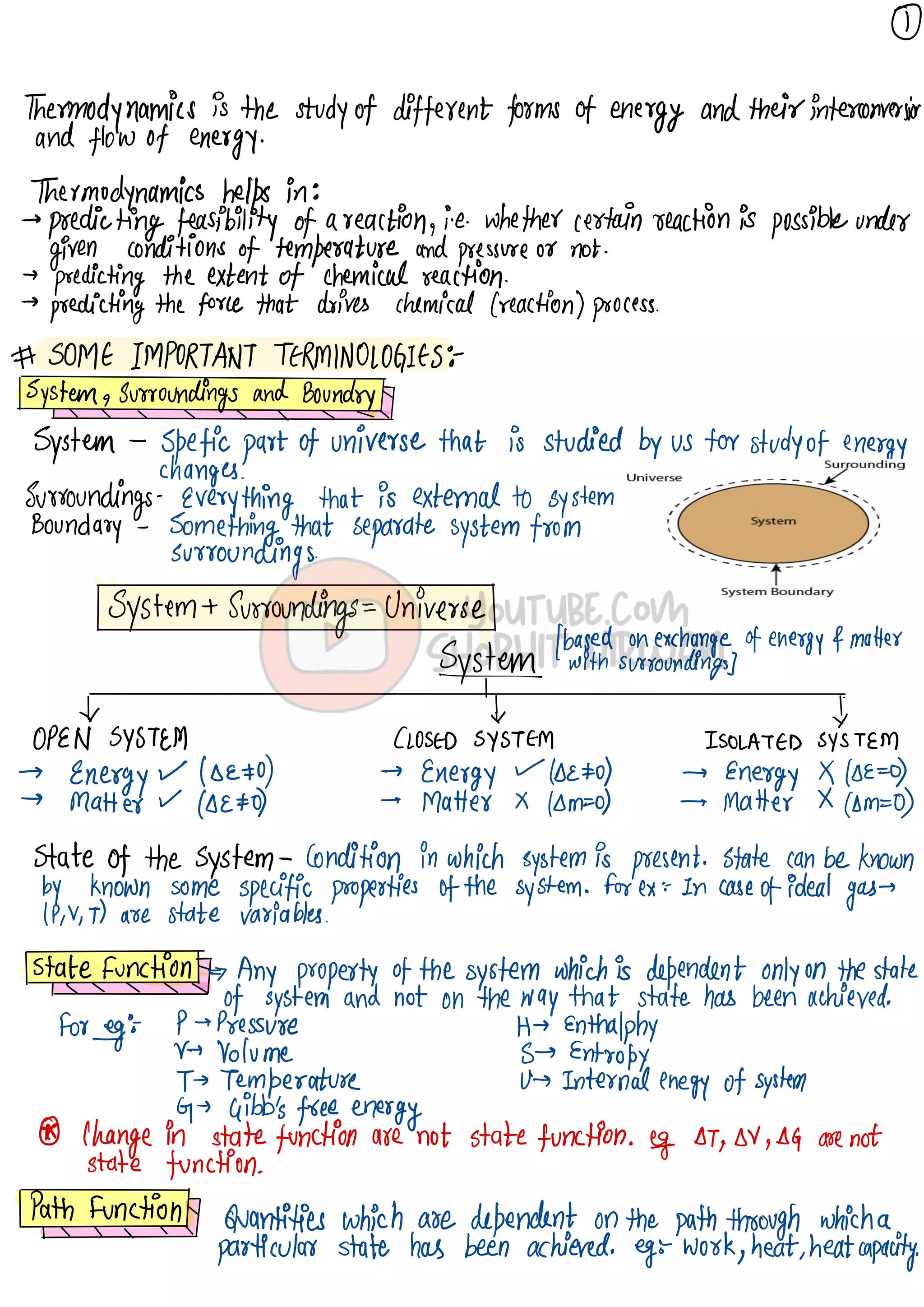
Thermodynamics is the study of energy and its transformations. It helps predict the feasibility and extent of chemical reactions based on temperature and pressure conditions. A system exchanges energy and matter with its surroundings. Thermodynamic processes include isothermal, isochoric, isobaric, and adiabatic processes. The first law of thermodynamics states that energy is conserved and the change in internal energy of a system equals heat supplied plus work done. Enthalpy is a state function that is the sum of a system's internal energy and pressure-volume work, and its change is a measure of heat absorbed or released at constant pressure.

1. THERMODYNAMICS
HANDWRITTEN NOTES
'
lPART -
H
- e
- -
✓
'
I
Designed with Emma
.
Shobhit Nierman

2. ①
Thermodynamics is the study of different forms of energy and their interconversion
and flow of energy.
Thermodynamics helps in :
→
predicting feasibility of a reaction ,
ie.
whether certain reaction is possible under
given conditions of temperature and pressure or not .
→
predicting the extent of chemical reaction.
→
predicting the force that drives chemical (reaction) process.
# SOME IMPORTANT TERMINOLOGIES :-
system , surroundings and Boundry
system -
Spetic part of universe that is studied by us for study of energy
changes.
Surroundings.
Everything that is external to system
Boundary -
something that separate system from
surroundings.
System +
Surroundings=
Universe
(based on
exchange of energy 4 matter
System with surroundings)
X N Y
OPEN SYSTEM CLOSED SYSTEM ISOLATED SYSTEM
→
Energy V (Beto) →
Energy VIDEto) →
Energy X He-0
)
→
matter V
(Beto
) -
Matter X (Dm
-
- o
) - Matter X (Dm-0
)
state of the system -
condition in which system is present. State can be known
by known some specific properties of the system. for ex :-
In case of ideal
gas
-
IPN, T) are state variables .
State function Any property of the system which is dependent only on the state
of system and not on the way that state has been achieved.
For
Igor P -
Pressure H→
Enthalpy
V→ Volume S→ Entropy
T→ Temperature vs Internal energy of system
G →
gibb's free energy
⑧ Change in state function are not state function.
of DT,
DV , DG are not
state function.
Path function Quantities which are dependent on the path through which a
particular state has been achieved.
eg:
-
work,
heat,
heat capacity.

3. ②
Extensive Property Properties which are dependent on mass or size of
system . These are additive in nature.
egfr v, men ,
total heat capacity,
total internal
energy , Hg Goss .
⑦tensive
Property which are independent of mass or size of system. These
↳Independent of properties are not additive in nature.
Forego.
-
Tg Pg motor
mass.
heat capacity , sp heat capacity ,
9 ,
concentration,
colour
,
refractive index ,
molar enthalpy g viscosity, pH ,
Eo
Trick → that term tf "
molas' '
at
"
specified elf Intensive et etat 1
Thermodynamic Process There are infinite thermodynamic process out of which
following are important or
→ Isothermal Process : T-
constant i. e.
Ti -
-
Tf
00g DT=
Old7=0
→
Isochoric Process : Volume Iv) → constant
Fe .
Vi -
-
tf
08
,
DV / dV=O
→
Isobaric Process : pressure G) →
constant
Fe.
Pi=
Pf
org DP =
OldP - O
→ Adiabatic Process :
Exchange of heat between system and surroundings
-
-
O.
i.e.
Dq=0/dq=0
→
Cyclic Process : It initial and final States after a process are same ,
then
it is known as
cyclic process.
change in stateful must be zero .
→
Reversible and Irreversible processes :-
REVERSIBLE IRREVERSIBLE
L.
It takes infinite time. I . It takes finite time.
↳
(
IIHF Process tif Reversible 4¥ ed if
321ft ET Fti step FAF tf 44T ETAT theft
TENT Reversible
process ahf ehf ett
2. The system remains in thermodynamic 2. The
system does not remains in thermodynamic
equilibrium with
surroundings throughout equilibrium with
surroundings throughout
the
process. the process .
3. Practically no
process is reversible in 3.
All process in nature are Breuersible.
nature. lie. it is ideal condition)

4. ③
#
Sign convention of Heat and work :-
← a q
-
- tore
← w ⑦re
Heat or If heat is
given to system ⑦ve system
- q-
- Ove
It heat is released Ove →
we -0ve
Werk:-
It work is done on system or compression re
It work is done by system or
expansion ve
WORK
↳ Mode of transfer of energy when system and surroundings differ in
pressure ,
till the pressures become equal.
If an object is displaced through a distance doe by a force f, the amount of
work done is
given by,
W = f x da
# Mechanical work Done by a system :-
Total volume of the
gas
-
-
V
Pressure of the
gas
=P
external Pressure =
Pex
It text > P ,
the piston moves inward till the pressure of the
gas becomes equal to external pressure lie .
p=Pext)
Now this condition F- Pert can be achieved by two ways
:(
1) It Achieve in single step lie.
Irreversible Process)
final volume =
Vt
Distance moved by piston =L
cross-sectional area of piston
-
-
A
volume change CAV) = lxA (Vt-
Vi)
Now ,
we know
Petz do f =
pxA
and we know,
W-
- f xd lie.
force x distance)
=
text xAxl
=
text t-
AV)
o :
/W=-PDT or
-
Pext ( Vf -
Vi)
-
t =
C-re) sign is used for work done by the system in case of expansion in
volume by convertors .

5. ④
NERI l 2L of an ideal gas at a
pressure of 20 atm expands isothermally
against a constant external pressure of Latin ,
until its total
volume Ps LOL . How much work is done during the expansion ?
Sofi-
W= -
Peet ( Vt -
Vi)
= -
L (Lo -
2)
= -
I 18) -
8L atm
(2) If it is Achieved in Number of steps ( ie .
Reversible Process)
It pressure is not constant at each
stage of comparison and
changes in such a manner so that it is always infinitesimally
greater than the pressure of the
gas and the volume during the
process
decreases
by an infinitesimal amount dv,
then work done is given by
the expression Vt
w = -
fpexdv
Vi
Now for compression , Pex
-
pin tdv
and for expansion , per pin-
dr
o
: In
general , Pex=
(pinIdp)
ooo Wren =
(pin Idp)dir
since, dpxdv is very small in comparison to pindv ,
so
Vt
Wren= -
I pin DV
vi
As we know
? pkn RT ( for ideal
gas)
p
-
-
mfs
Wren -
=
-
fit n RT
IF =
-
n RT
lnV¥
Wrev = -
2303 nRT
log¥
Via initial Volume
Vt =
final Volume
n =
no.
of moles
R =
gas constant
T =
absolute Temperature (in K)
⑧ Woev =
Wmax ( ie .
for getting maximum work, system should do work
in reversible process).

6. ⑤
⑧ FREEEXPANS.IO# line .
Pex - O)
↳ .
: 1×1=0 ,
whether process is reversible or
HEAT irreversible .
4 If the
energy exchange takes place because of temperature difference ,
then
it is known as heat .
Specific Heat
capacity
-
The heat required to raise the temperature of one unit
mass
by L
degree (either Celsius or Kelvin). The specific heat
capacity is
denoted by Cg formula :
q= c × m × be
q= heat required to raise temperature
by Ic
and if C is the heat capacity of n mole of the c =
specific heat
capacity
system , then its molar heat capacity cm is m
-
-
mass
given by ¥4 . at =
temperature change link)
-
Heat capacity at constant volume Kv) : The amount of heat required toraise
the temperature of one mole of a
gas by one
degree, when volume of the
gas is
kept constant.
Heat capacity at constant Pressure Kp) : The amount of heat required to
raise the temperature of one mole of a
gas by one degree ,
when pressure
of the gas is kept constant .
Now we can write equation of heat q ,
at constant volume as
q =
Cvn
at constant
pressure as
qp
=
Cp DT
k⑦ Cp and Cv are related to each other
by the expression Cp-
Cr -
n R
↳ Derivation stat shaft
•
Cpt Cv (always)
•
Cpk,
Ratio is represented by 8.
# INTERNAL ENERGY (U) :
Every system is associated with a definite
amount of energy ,
called the Internal Energy of the system.
°
It is represented by V or E.
*
° It is a state function.
Iwata
°
It is an extensive property
-
④BThe absolute value of internal Energy possessed by a substance cannot
be calculated because it is not possible to predict the exact values of
different forms of energy. Thus,
we can just calculate the change in
internal energy,
which is achieved by changing state of a system.
↳ Las

7. ⑥
First law of Thermodynamics IF LOTT
°
It is based on the law of conservation of Energy.
°
According to this total energy of the universe is always conserved and only
one form of energy changes to another energy .
£,
Consider a
system in a state initially in which internal
energy is Es . If q amount of heat is givento it and W
amount of work is done on it then its total internal
energy is Ez .
.
'
.
fz= EL +
get W
Ez-
EL =
get W
T
AV or DE -
=
ft
'
W
LIK A system does 2005 work on surroundings by absorbing 250J of heat.
Calculate the
change in internal Energy.
ans:-
=
W= -2005 fusing sign-
convention
q
= t 250J
Now, by fLOT
g
DU =
Wtq
DU =
-
200+250
DE 50 J
II:-
100J of work was done on a
spring and 155 escaped to the surroundings
as heat ,
BE or AV =
? ?.
SII.
-
DU =
qtw
= -15+100
=
857
=
E:
-
It an electric motor produced 15kt of Energy each second as mechanical
work and lost 2 KJ as heat to surroundings ,
DV =
? ? .
see:
NDE ¥4772 fas YE
-
'
Ink})
-17k¥
K3B ① If Isothermal process ( ie .
At-0
)
since DT-
- O
% DU= 0
.
'
. f- LOT
0=qtWy
1q=-W_
Pf isothermal reversible, q=
-
Wren=
2.303 nRT
dogft.to)

8. ⑦
if isothermal irreversible, f-
-
Wiser =
pex(Vt-
Vi)
② If Isochoric process ( i.e .
AV-
-
O)
since DV-
-
O
: .
into f: dW= -
Pexdv)
o
: f- LOT /DU=qT
→ this q
at constant volume fire.
qv ) .
③ If A-diabetic process lie .
Bq -0
)
-
i. f- lot
lDU=W→ work done in adiabetic process.
# limitations of floe
:O
It fails to explain the direction of process .
° It fails to explain how much heat
energy
would be transferred from one
system to another.
ENTHALPY ( H)
↳ It is defined as total heat content of the system . It is equal to the sum of
internal energy and pressure
-
volume work.
° It is a state function
° It is an extensive property.
Mathematically ,
H = Ut Pv
change in Enthalpy : It is the heat absorbed or evolved by the system at
constant pressure.
CITI UIT 34kt
)
simply g
DH=9P#-
②
also
, /DH=DUtpDV
for exothermic (system loses to
surroundings) as Gpa soDHLO
similarly , for endothermic gas q 70 :.
AH >0.
K3④ 0
In ② g if Tsochoric (i -
e.
constant volume).
DH = DU
↳ Thus
,
we can say that
"
Heat supplied at constant pressure is the
measure of enthalpy change ,
while the heat supplied at constant volume is the
measure of internal energy change
"
.
here
Dng= total moles ofgaseous
o for gaseous reactions,
DH = DU t
DngRT products minus total
moles of gaseous reactants.

9. ⑧
# Proof of Xp-
Cv-
-
R)
As we know,
BH = DU t DlpV) pv
-
- n Re
DH -
but DIRT) for A-
Lg pitRT
DH = But RD T
CpDT =
CvAT -1 RAT
Cp =
Cr t R
14-4=7
-
→
Please Read calorimetry theory from NCERT.
(DV & DH measurements)
Enthalpy change , AH of a Reaction -
Reaction Enthalpy
In a chemical reaction ,
reactants are converted into products and is
represented by '
reactants →
Products
The enthalpy change accompanying a reaction is called the reaction enthalpy.
This enthalpy change of a chemical reaction ,
is
given by the symbol Dr H.
Dr H =
(sum of enthalpies of products) -
Isum of enthalpies of reactants).
org Dr H =
⇐ Xp Hp -
Yi IHR
ni, Yi stoichiometric coefficients of products and reactants
respectively in a balanced equation.
Hp Enthalpy of formation of products.
HR Enthalpy of formation of Reactants .
forty:- C
Hylglt 2021g) -
C
02cg) t 2h20 le)
Dr H =
l H (coz ,g)
-12 HItho,
e) I -
(Hetty , g) t 2 H
Koz , g) )
k3④ On
reversing a reaction , the sign of DH is also reversed but its
magnitude remains same.
# Standard Enthalpy of Reaction : the standard enthalpy of reaction
is the enthalpy change for a reaction when all the
participating
substances are in their standard States .
The purest and most stable form of a substance at L bar and at a
specified temperature is called its standard state.

10. ⑨
# Enthalpy changes during phase transformations :
conversion of solid →
liquid is
Melting .
liquid →
gas is vaporBatton.
solid →
gas is sublimation.
These processes are
collectively known as phase transformations.
(a) Enthalpy of fusion (Itu'sHQ : The enthalpy change occurring when I
mole of solid substance in its standard state melts completely into its
liquid form is called standard or molar enthalpy of fusion .
of H2O Cs) -
H2O le)
(b) Enthalpy of Vaporisatin (ArapHo) :
The enthalpy change when one mole
of a
liquid is converted into vapours at its boiling temperature and under
standard pressure CL bar) is called enthalpy of rapon'sation or molar enthalpy
of vaporis ation .
elf: H2O le) -
H2O Cg)
(c) Enthalpy of sublimation (Dsub Ho): The enthalpy change when one mole of
a lid substance sublimes (or converted into vapours) without melting at
a temperature below its
melting point land at L bar pressure) is called the
enthalpy of sublimation or molar enthalpy of sublimation .
elf's CO2 Is) tasks coz Cv)
also, Dsub HE AfusHot trap to
- .
# Standard Enthalpy of formation :
↳ The
enthalpy change accompanying the formation of one mole of a compound
from its constituent elements, when they are in their most stable States or
reference states
,
is called standard Enthalpy of formation
of
CC
graphite,Dt 2142cg) - C Hy Cg)
2C (graphite,
s) -13
High tz 02cg) - Cz
HsOHlll.A@Hzlg1g0zlg7gCCgoaphite.s
) g Brace ) ,
S (rhombic) are the most stable States or
reference States .
The standard enthalpy of formation , Dft:
of an element in its reference
slate is taken as zero.
.
⑧ Df Ho is a special case of Dott.

11. ⑧
# Hess's law of constant Heat summation :
Heat absorbed or evolved in a
given chemical reaction is same
whether the process occurs in one step or in several steps .
A D
-7
AHH TBH,
/BH=DHiDHztDt
B →C
DHz
k3B 0
Chemical reactions can be added or subtracted to get the required
equation . (if added -
enthalpy gets added
it subtracted →
enthalpy gets subtracted ).
°
If reaction is reversed,
sign of DH also reversed .
LI.
find Bff of C0cg) it:
C (
graphite) +02cg) -
coz Cg) -
A Hex -
①
coz Cg)
-
C 0cg) +
I 02cg -
D HEY .
-
②
SEI: Haaf next of allot f tf equation that tf:
.
Target equation Ccgraphite)*
I 0dg) →
CO Cg) -
⑦
7TH A tht Hf of given equations of 3of tht use htt ett
Targeted equation at
that F1
by observation,
⑦ =
② t ②
it.
AtH =
X t
Y .
Enthalpies for different types of Reactions
# Standard Enthalpy of combustion , ACH
-0
:-
The amount of heat
ev_ed# when one mole of the substance is burnt completelyin
oxygen or air ,
and all the reactants and products are in their
standard States
,
is called the standard enthalpy of combustion.
(i.e. exothermic ,
egg
: Cy tho Cg) t
Bz 02cg) - 4 Coz Capt 5th Old
°
Simply Att FA compound TT combustion that I 3¥ Oz tf React tht
CO2 and water as a
product Hita
o Our
body also
generates energy from food by the same overall process
as combustion.

12. ④
# Enthalpy of AtomBatton , Da Ho:
The enthalpy change on
breaking one mole of bonds completely to
obtain atoms in the gas phase is called the enthalpy of atomBatton.
of City Ig) →
Ccg) t 4 H Cg)
Nats) - NaCg)
# Bond Enthalpy ,
Dbond Ho :
-
As we know that energy is required
for breaking bond and for bond making , energy is released.
simply ,
Bond list tf tht energy dat etat
Bond aid Ttt energy release etat I
⑨ fomie :.
↳ Also called Bond dissociation enthalpy →
It is the enthalpy
change accompanying the breaking of one mole of covalent
bonds of a
gaseous covalent compound to give products in the
gas phase.
←symbol.
¥
→
Bond dissociation ethalpy of dihydrogen (DH-
H Hot
Hzlg) - LH Ig)
→
Clap - 2 Cdcg) -
here Ace-
ce
Ho
(b)
forpolyatomicn-oeueo.li
Also called mean Bond enthalpy .
If we take example of CHy → here all the four C-H bonds are
identical in bond
length and energy . but
they differ in
strengths
Tre.
different amount of energy is required to break each individual
bond.
So ,
in case of polyatomic molecules ,
the mean of bond dissociation
enthalpies of all bonds present in the compounds is taken.
Thus ,
in city
f , Dc-
Htt is -
I@aHIeeanwthmdsmaf.tn
= .
of methane

13. ④
k3④ It Fs also possible to calculate enthalpy of reaction using
bond enthalpy .
Do HEEbond enthalpy
otreaastnts-Zbondenthpafopgqot.LI
:
-
calculate the enthalpy change CAH) of the following reaction .
GHzCg) t
Iz 021g) - 2 Coz Cg) t HD Cg)
Given bond enthalpies of various bonds:-
Dc-
H
HE 414 KS mot
'
Bec HE 814 KJmot
'
Do H-0=499 KT molt
A ⇐o
H-0=724 KJ mot
'
SH:-
Caegtiation tf
, elaborate af, D
Ao- HH-0=640 KImom
(H -
CE C -
H
)t
Z (0=0) → 2 (o =
⇐o
) t CH-
o-
H
)
As we know,
DrHo -
-
fsumotboenadeeannthglpiesf-
(sum of bond enthalpies
of of products ]
=
Hbc-
HH't BecHo -
IIDo H-9-
14 D⇐otto -12 Do-
H Hof
=
(2x 414 t 810T
Ex 499) -
(4×724+2×460) KT
=
(2885.5-3816) KJ
= -
930.5 KJ
←
# Enthalpy of solution , Dsoe Ho or
↳The enthalpy change when one mole of solute is dissolved completely in
specific amount of solvent or water is called enthalpy of solution.
°
It solvent Ps in excess i.e. the interactions between the ions too solute
molecules ) are
negligible then the enthalpy change is called enthalpy of solution
at infinite dilution.
°
Aoe H =
Dealtice Hot Dhyd Ho

14. ⑤
# Enthalpy of Hydration ,
Dmd Ho : when one mole of anhydrous or partially
hydrated salt combines with required number of moles of water to form a
specific hydrate .
egfr (u soy G) t 5Hall) → CUSOy .
5h20 Is)
# Enthalpy of NeutralBatton ( Dn Ho) :
-
The enthalpy change accompanying the
formation of one mole of H2O by combination of one Mol Ht ions furnished by
acid and one mole of
-
OH Tons furnished by base in dilute solutions at the
standard conditions .
• Anti offstrong acid -
strong base) -
57 .
I .
(Pattiefgaomtthnsannneo.es
will be uploaded in L-2 days on
)