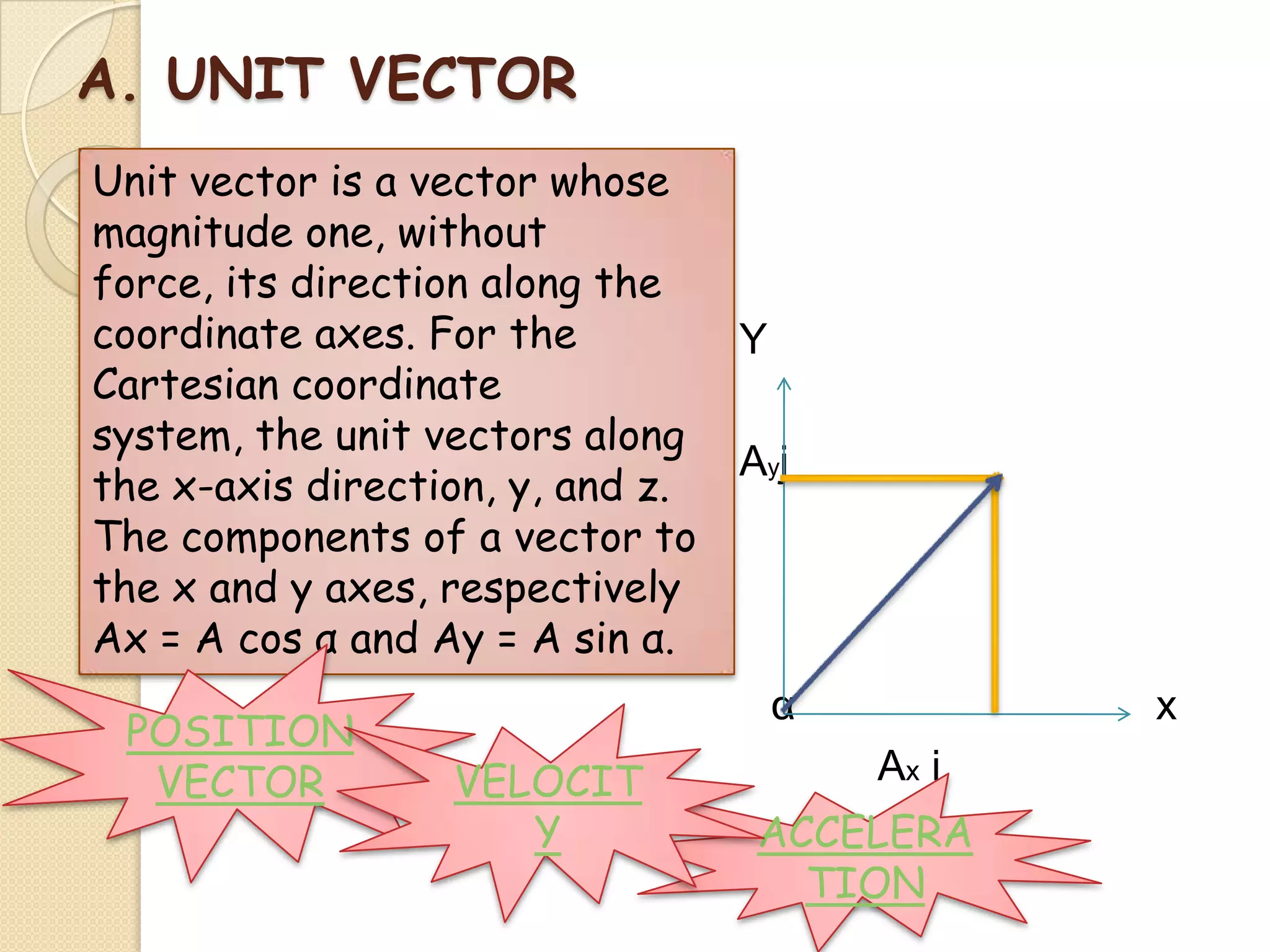
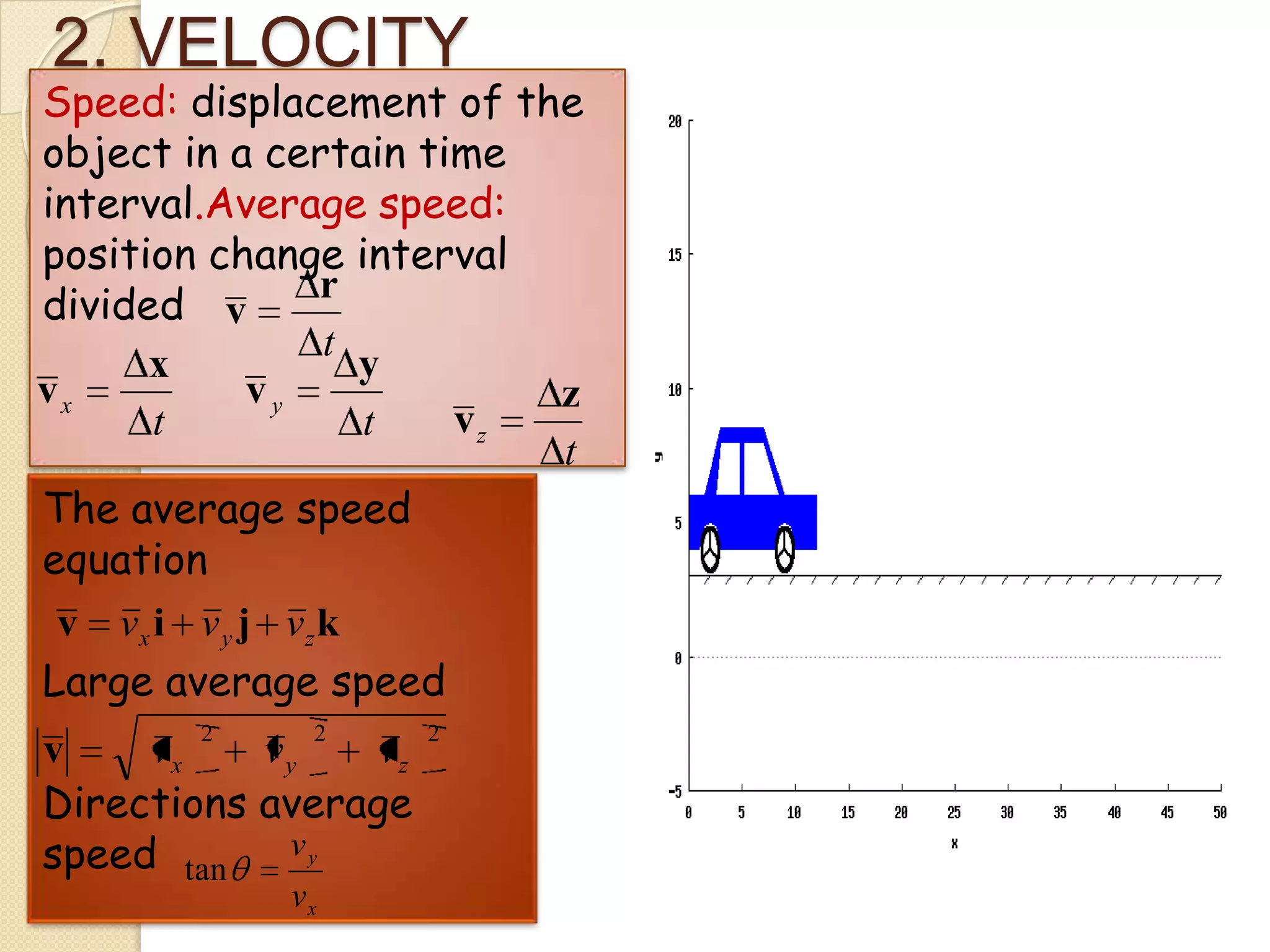
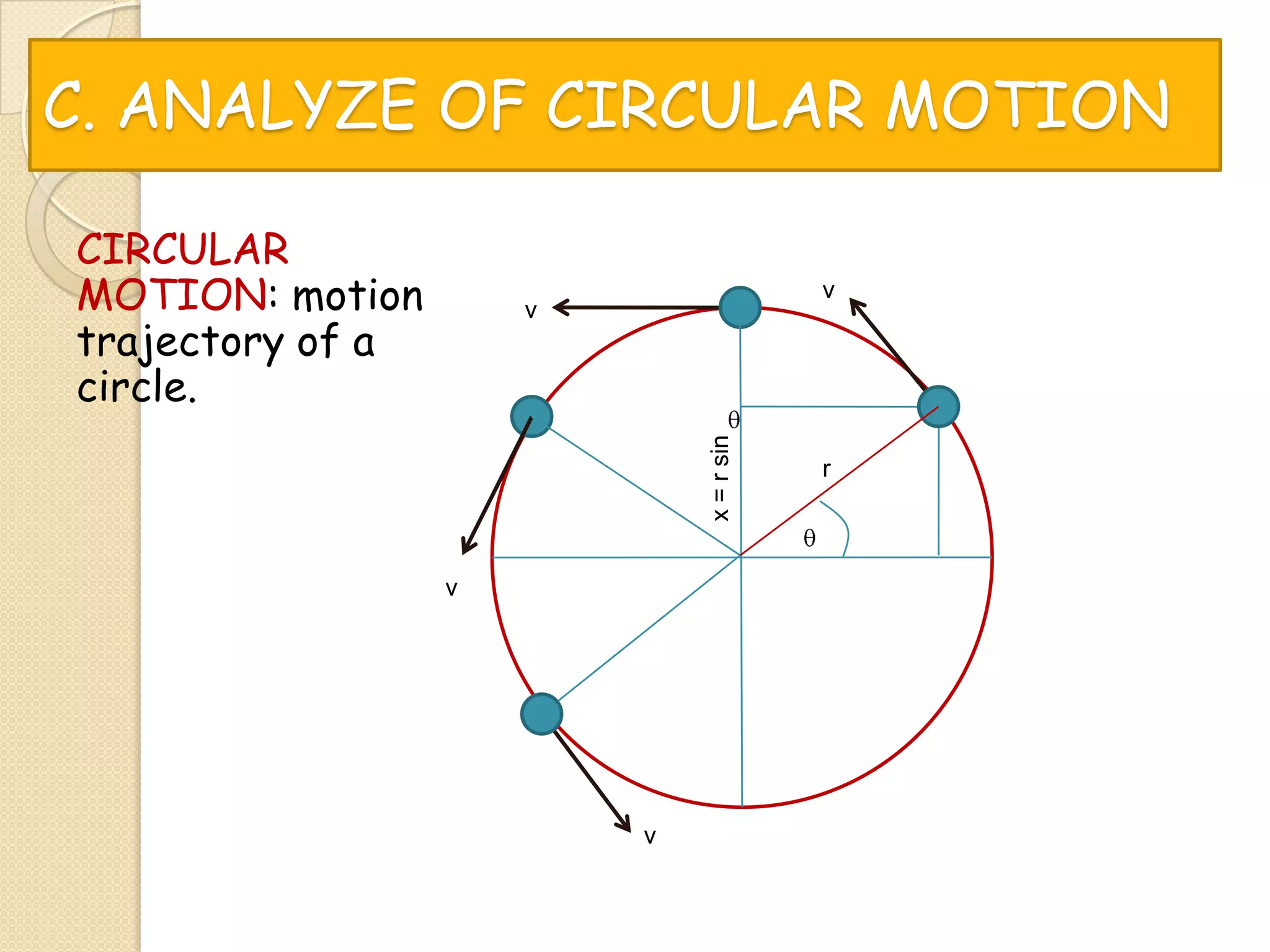
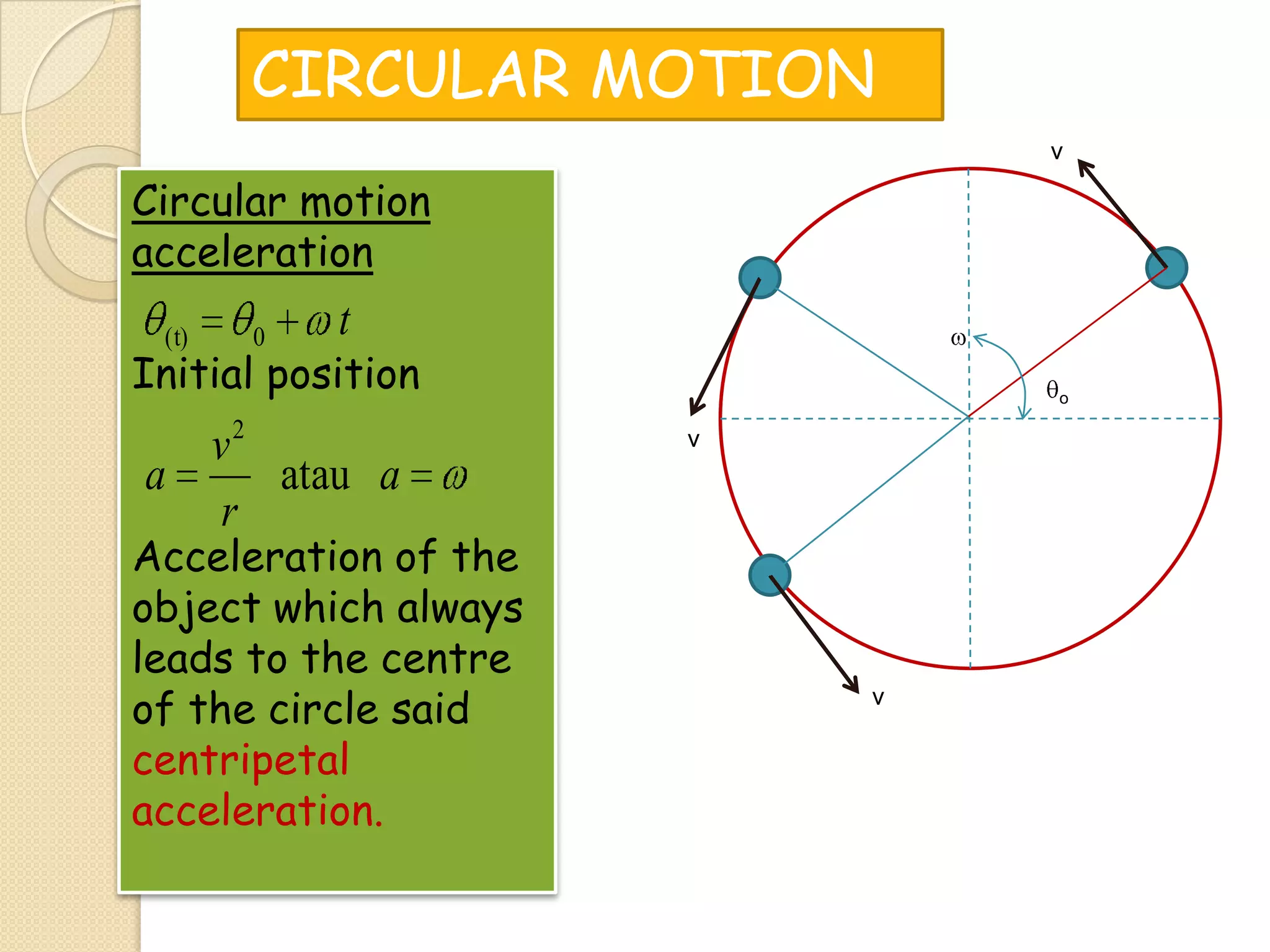
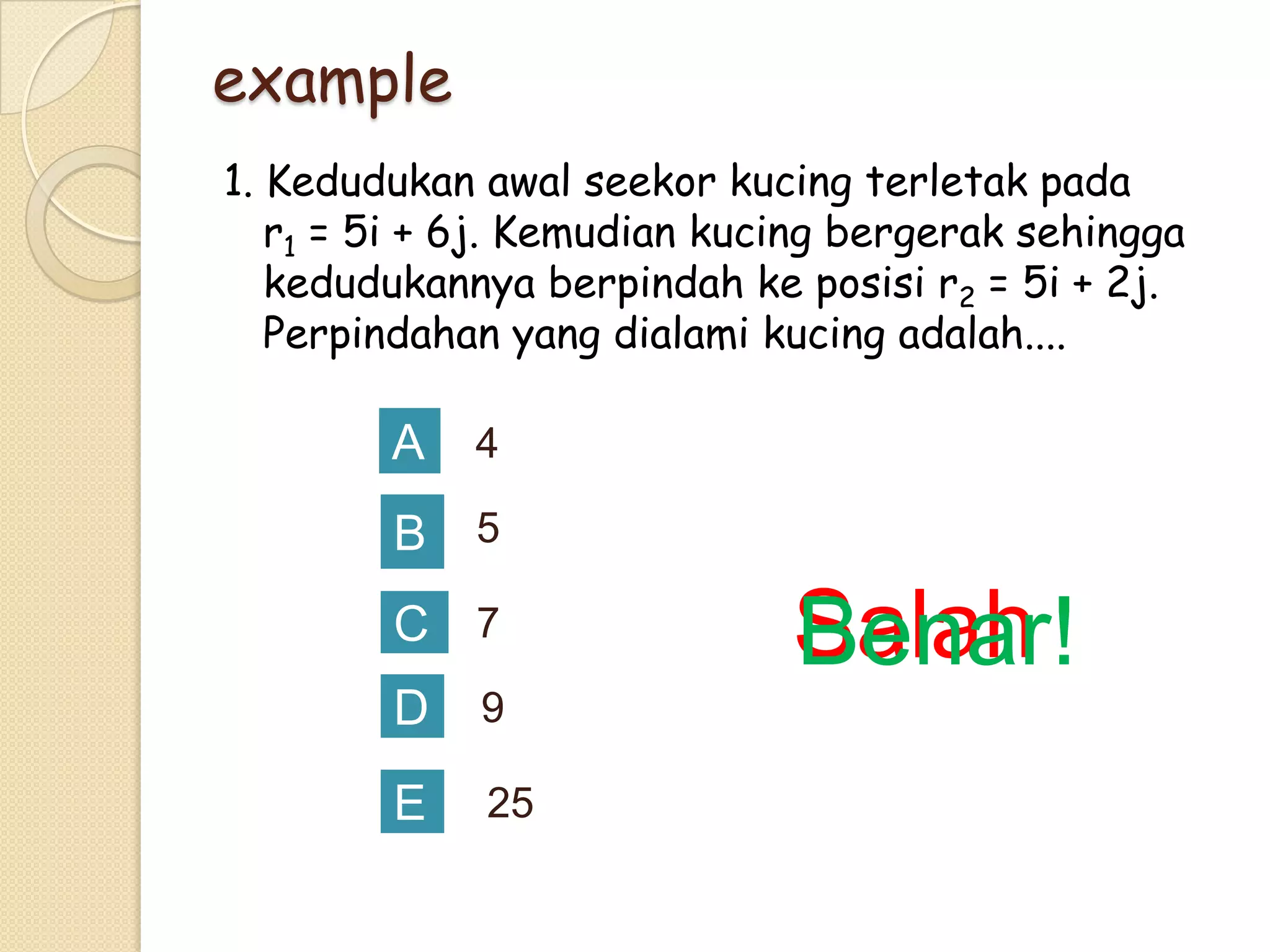
This document provides instructional materials on analyzing motion using vectors. It begins with definitions of motion and discusses rectilinear, parabolic, and circular motion. Rectilinear motion is analyzed using position, velocity, and acceleration vectors. Parabolic motion results from horizontal rectilinear motion combined with vertically accelerated motion. Circular motion is described using angular position, velocity, and acceleration. Examples are provided to demonstrate analyzing different types of motions using vectors.

1. INSTRUCTIONAL MEDIA
THE MOVEMENT WITH
VEKTOR ANALYZE
LECTURER Drs.M.HIDAYAT,M.Pd.
COMPILED BY
TUTI RESRI
YANTI
RSA1C312017

2. THE MOVEMENT WITH
VEKTOR ANALYZE
UNIT
VECTOR
THE
PARABOLIC
MOTION
CIRCULAR
MOTION

3. THE MOVEMENT WITH VEKTOR
ANALYZE
Competition standart
. Analysist of natural indication and
regularity in scope mechanics point object.
BASIC COMPETENCE
1.1 Analyze straight motion, circular
motion and using the parabolic
motion vector.

4. RECTILINEAR MOTION ANALYSIS




DEFINITIONS
MEANING OF MOTION
An object is said to move when they change the
position of other objects that serve as a reference
point.
Body is said stationary (not moving)
position when the object was not changed to other
property used as a reference point.
MOTION STRAIGHT.
object-motion trajectory straight-called rectilinear
motion. -straight motion of an object in everyday life
generally irregular.

5. A. UNIT VECTOR
Unit vector is a vector whose
magnitude one, without
force, its direction along the
coordinate axes. For the
Cartesian coordinate
system, the unit vectors along
the x-axis direction, y, and z.
The components of a vector to
the x and y axes, respectively
Ax = A cos α and Ay = A sin α.
POSITION
VECTOR
Y
Ayj
α
VELOCIT
Y
x
Ax i
ACCELERA
TION

6. 1. position vector
The position of a car (A) of
the reference point (O) can
be expressed by a position
vector (position vector), ie
OA or r.
r = x i+y j -> twodimensional
Large (long) position vector
expressed
r = x i y j z k -> three
dimensional
A
yj
r=xi+yj
O
xi

7. Displacement experienced by
the point A in the time interval
t.
r = r2 – r1
r= xi+ yj
Large displacement can be
written
r
( x) 2 ( y ) 2
Direction of movement of point
A
y
tan
x
As a function of time, the
component vector
r(t ) x(t )i y(t ) j

8. 2. VELOCITY
Speed​​: displacement of the
object in a certain time
interval.Average speed:
position change interval
r
divided v
t
y
x
vx
vy
z
vz
t
t
t
The average speed
equation
v vx i v y j vz k
Large average speed
2
2
v
vx
vy
vz
Directions average
vy
speed tan
vx
2

9. INSTANTANEOUS VELOCITY : Velocity of object
r dr
any given moment
v lim
dx
dt
vx
t
dt
dy
dt
vy
The instantaneous velocity equation
dx
dy
dz
v
i
j
k
v vx i
dt
dt
dt
The instantaneous velocity
v
vx
2
vy
2
vz
2
Instantaneous velocity direction
tan
vy
vx
vz
dz
dt
v y j vz k

10. determine position of velocity function
dx
dt
vx
x
v x dt
y
t
dx
dx
t
vx dt
x0
0
dy
v y dt
y0
0
t
x x0
t
vx dt
y
y0
v y dt
0
t
x
0
t
x0
vx dt
0
y
y0
v y dt
0
On the z axis can be obtined in the same way

11. accaleration
Acceleration: change of
velocity per unit time
a. Average acceleration: a
change of pace once in a
while
a
ax
v
t
vy
vx
ay
t
t
az
vz
t
Average acceleration
aquation :
a
ax i a y j azk
The average acceleration :
2
2
a
ax
ay
az
Average acceleration
direction
tan
ay
ax
2

12. acceleration



b. instantaneous acceleration
Instantaneous acceleration (a) is defined as
the average acceleration for the time
interval approaches zero.
Systematically, instantaneous acceleration is
formulated as follows:
However, v = dr / dt to obtain

13. acceleration
c. Determine velocity from acceleration
function
dvx
ax
a x dt dvx
dt
v
v
t
dvx
v0
t
dv y
a x dt
v0
0
a y dt
0
t
t
vx v0 x
ax dt
vy
v0 y
a y dt
0
t
vx
0
t
v0 x
ax dt
0
vy
v0 y
a y dt
0
On the z axis can be obtined in the same way

14. Parabolic motion
vy=vo sin
Blend motion trajectory uniform rectilinear
motion in the horizontal direction (x-axis)
with a uniformly accelerated motion in the
vertical direction (y-axis) is called parabolic
parabolic motion.
C
B
D
E
vx=vo cos

15. Parabolic motion
• At x axis
Velocity equation
vx
vo cos
GLB transfer equation:
x
vo cos
t
x
cos
t
At y axis
Acceleration equation

GLBB velocity equation
vy
voy
at
vy
vo sin
Transfer equation
y
y
vo sin
t
1 2
gt
2
2
ax bx
gt

16. When the bullet reaches
its highest point, bullet
velocity component in the
vertical direction is zero or
Vy = 0. thus at the highest
point applies
so the time it takes a
bullet to the highest point
substitution equation y in
the equation of uniformly
accelerated motion and
bullet time required to
produce the highest point
of maximum height
Parabolic motion
with varying elevation
angles will be obtained
by varying the maximum
height anyway. The
maximum height is
obtained if the
elevation angle α = 90 °.
Achieved the maximum
horizontal distance
defined by

17. C. ANALYZE OF CIRCULAR MOTION
CIRCULAR
MOTION: motion
trajectory of a
circle.
v
x = r sin
v
v
v
r

18. • ANGLE position
y
x r cos
r
x2
r sin
tan
y2
• angular velocity
Average angular velocity
2
t
y
x
1
t 2 t1
Instantaneous angular
velocity
lim
t
d
dt
the position of angle can
determine too : t
(t ) dt
0
0
CIRCULAR
MOTION
• Angular acceleration
2
t
1
t 2 t1
instantaneous angular
acceleration
2
d d
dt dt
d
dt 2
angular velocitu can
t
determine too :
(t ) dt
0
0

19. CIRCULAR MOTION
v
Circular motion
acceleration
(t)
0
t
Initial position
v2
a
atau a
r
Acceleration of the
object which always
leads to the centre
of the circle said
centripetal
acceleration.
o
v
v

20. CIRCULAR MOTION
In addition to centripetal acceleration, the
change uniform circular motion there is also
a tangential acceleration
v
atau aT
t
aT
r
Total acceleration possessed by objects that
undergo uniform circular motion
atotal aT as
atotal
aT
2
as
2

21. example
1. Kedudukan awal seekor kucing terletak pada
r1 = 5i + 6j. Kemudian kucing bergerak sehingga
kedudukannya berpindah ke posisi r2 = 5i + 2j.
Perpindahan yang dialami kucing adalah....
A
4
B
5
C 7
D
9
E
25
Salah
Benar!