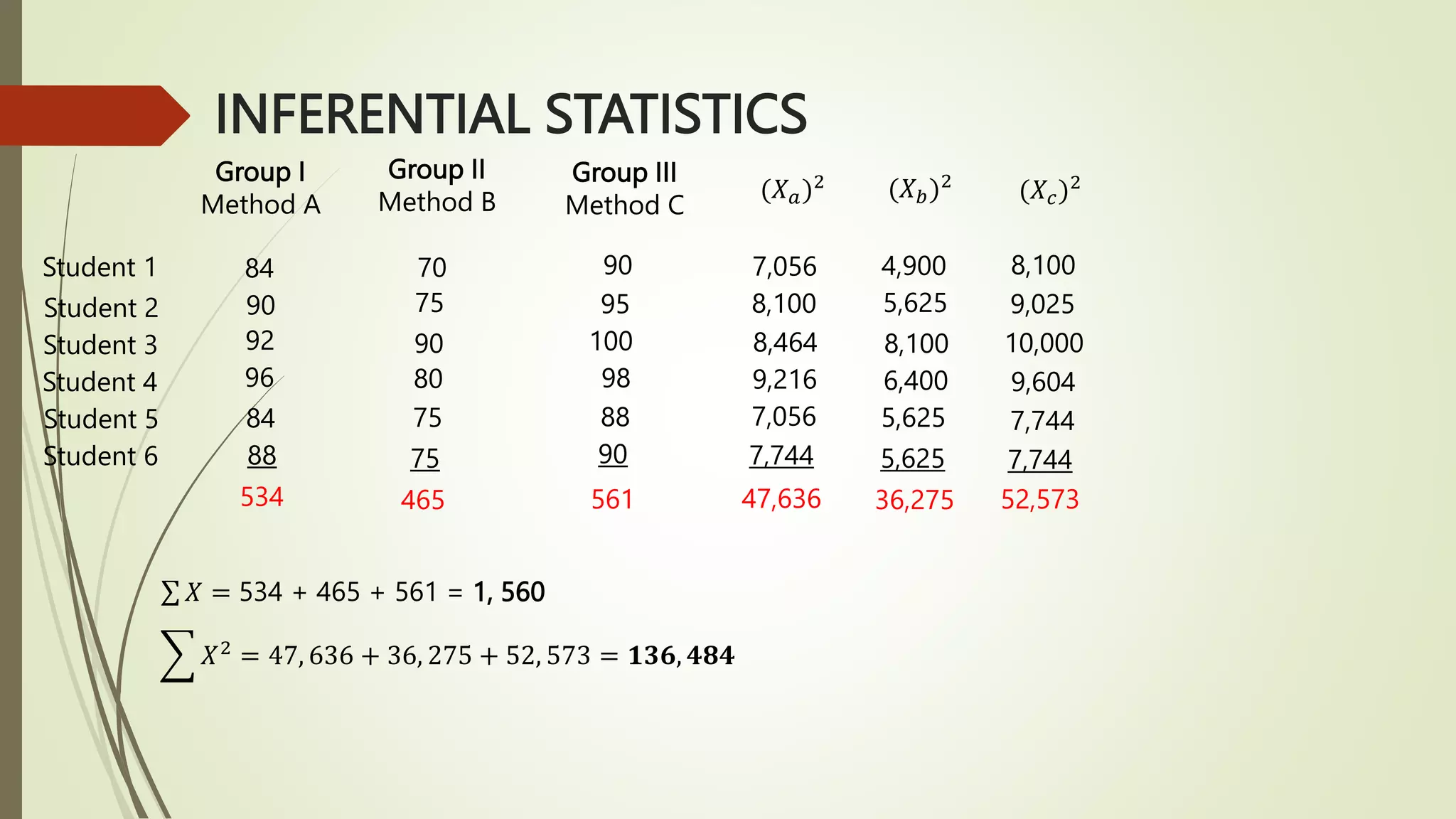
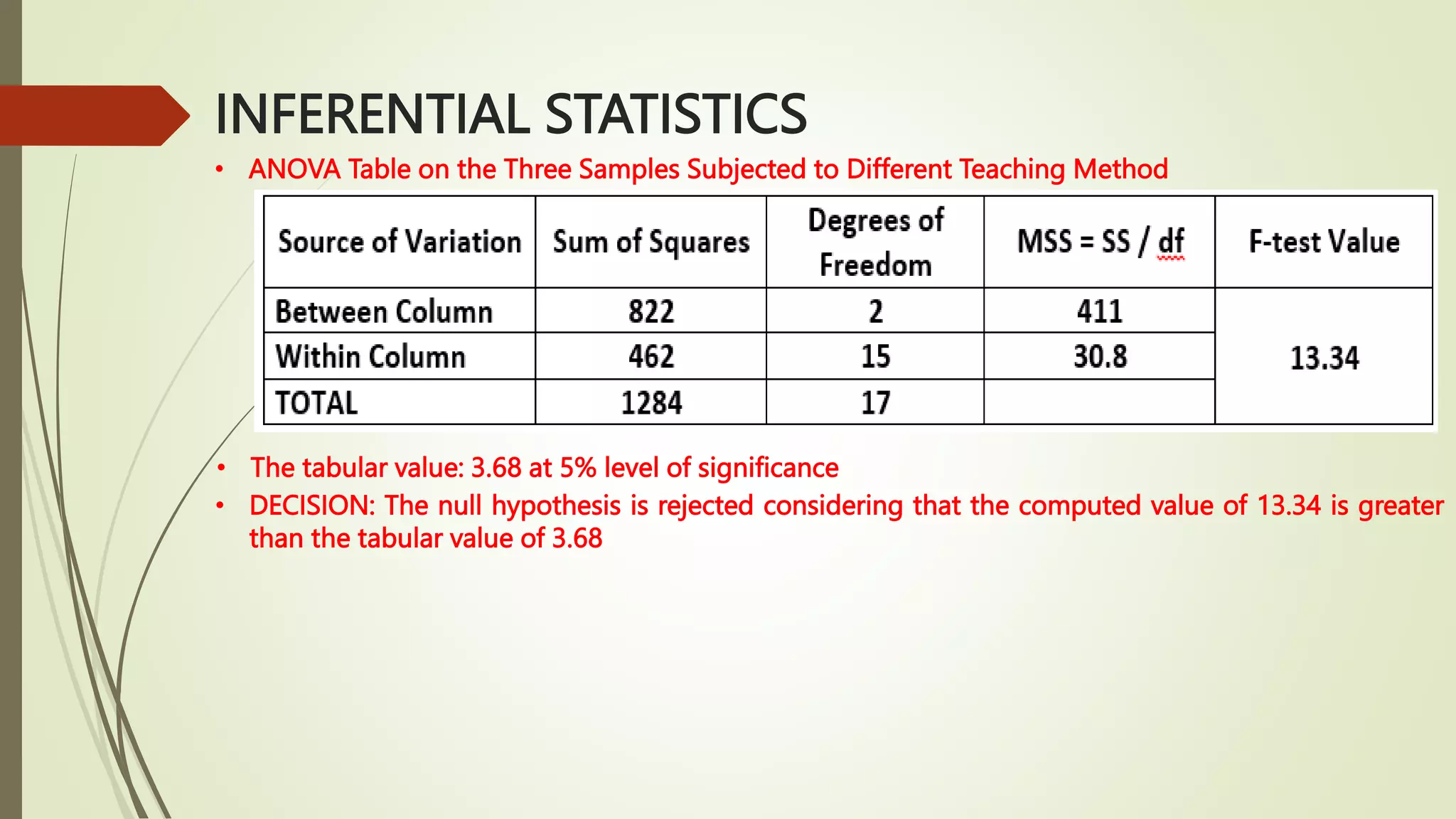
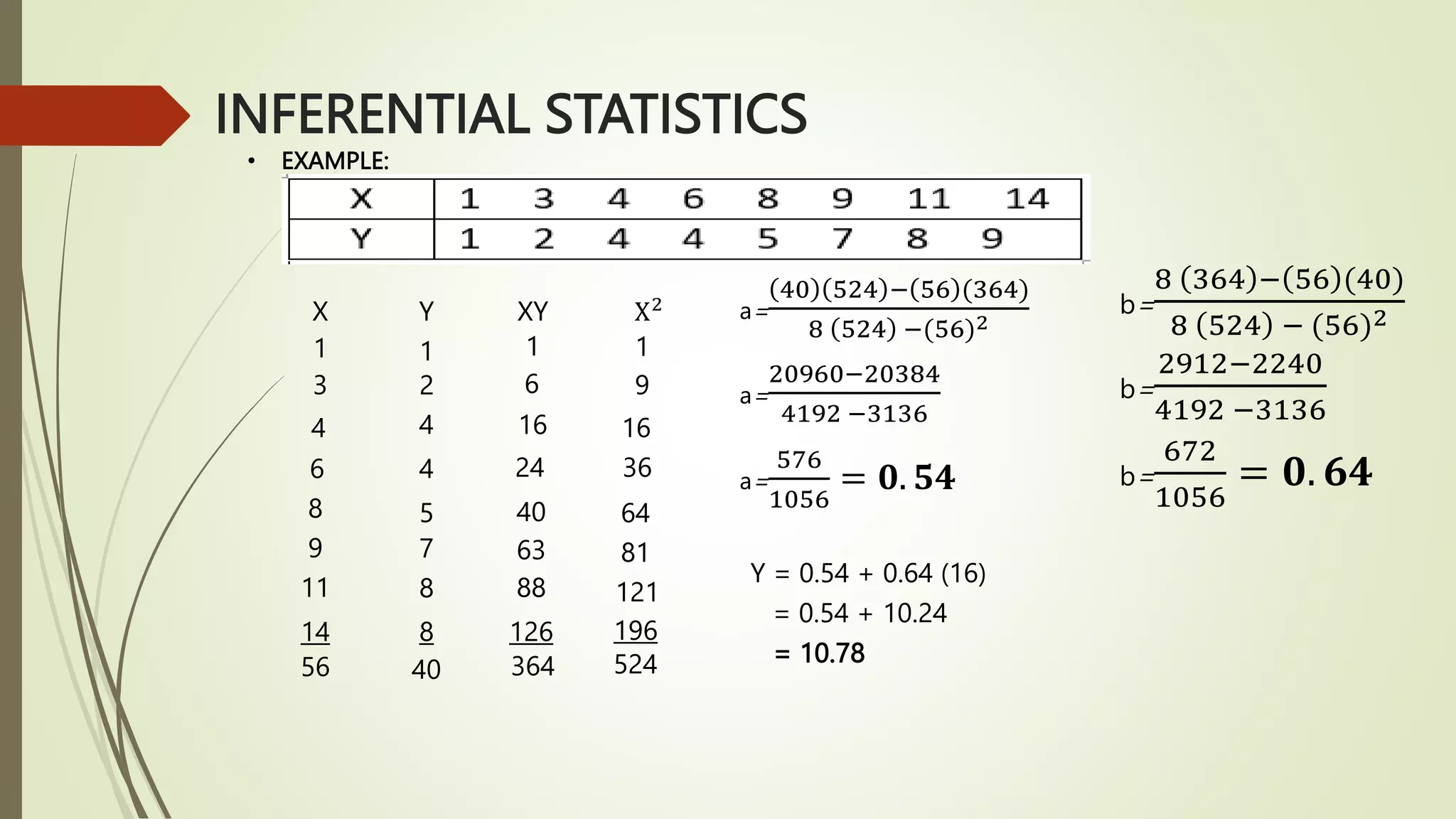
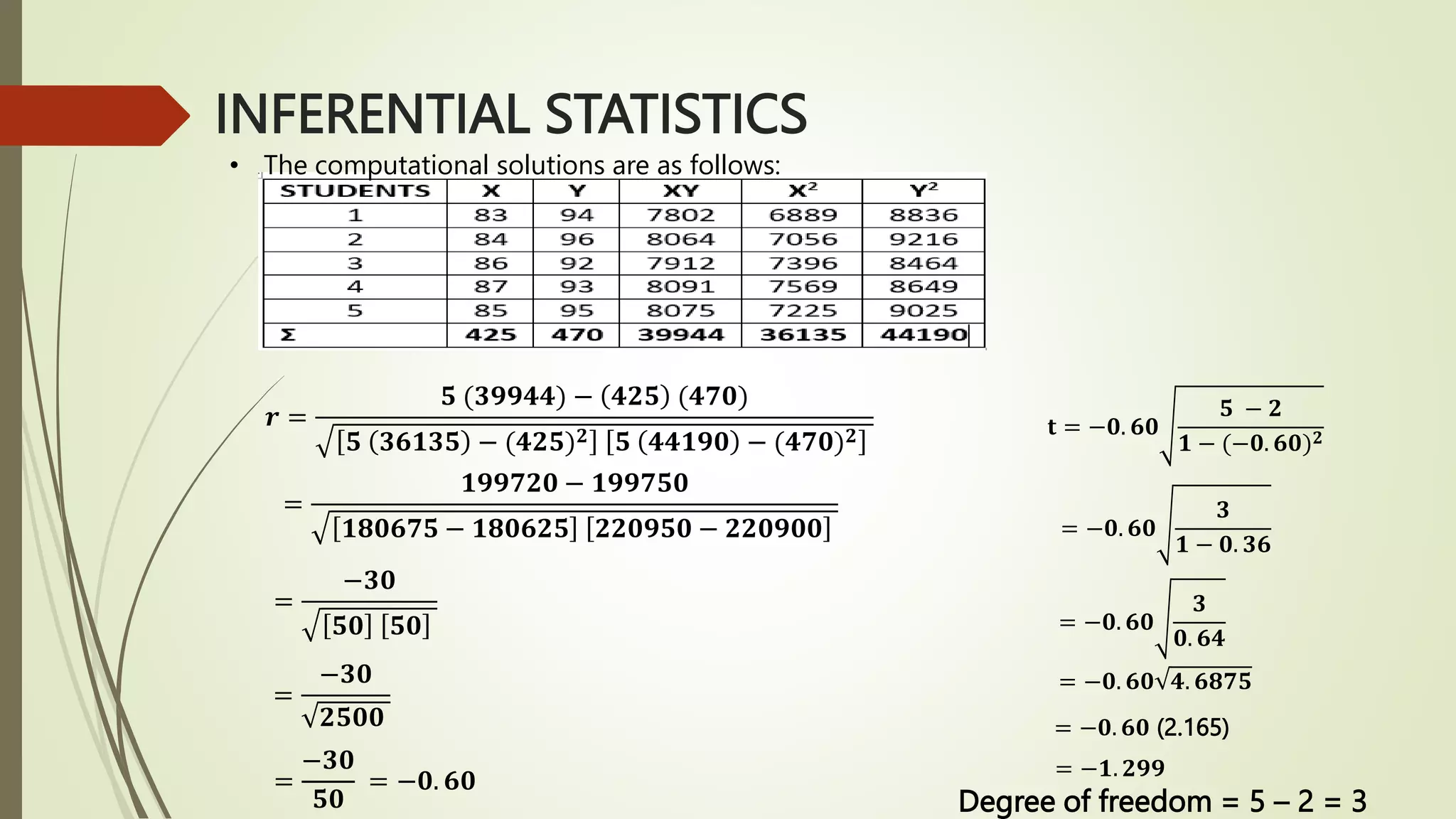
This document provides an overview of inferential statistics concepts including hypothesis testing, types of hypotheses, errors in hypothesis testing, steps in hypothesis testing, z-tests, t-tests, and analysis of variance (ANOVA). Key points covered are: hypothesis testing determines if there is a statistically significant difference between groups or a relationship between variables; the two types of hypotheses are the null and alternative; z-tests and t-tests are used to test hypotheses comparing means and proportions; and ANOVA analyzes variance between and within groups. Examples of each statistical test are provided.

1. ADVANCE STATISTICS
Jemer M. Mabazza, LLB, PhD
Graduate School
Mallig Plains Colleges

2. INFERENTIAL STATISTICS
 Inferential Statistics
• Refers to the statistical procedure used in the drawing of inferences about the
properties of population from sample data.
 Test of Hypothesis
• It is a statistical tool that determines whether there is a statistically significant
difference between two or more groups, or whether there is a statistically significant
relationship between two or more variables.
 Hypothesis
• It is a statement or tentative theory which aims to explain a facts about the real world.
• They are subjected to testing.
 If they are found to be statistically true, they are accepted
 If they are found to be statistically false, they are rejected

3. INFERENTIAL STATISTICS
 Two Kinds of Hypothesis
1. Null Hypothesis (H0). A hypothesis that may either be rejected or accepted
2. Alternative Hypothesis (Ha). It generally represents the hypothetical statement the
that the researcher wanted to prove.
• Summary:
 REJECTION of H0 implies ACCEPTANCE of Ha
 ACCEPTANCE of H0 implies REJECTION of Ha
• Possible Error when Making Decision about the Proposed Hypothesis- SUMMARY:
TYPE I and TYPE II ERRORS
DECISION H0 = TRUE Actual Condition
Ha = TRUE
Reject H0 Type I Error Correct Decision
Accept H0 Correct Decision Type II Error
• The probability of making a type 1 error or alpha error in a test is called a significance
level of a test.

4. INFERENTIAL STATISTICS
 Steps in Hypothesis Testing
1. Formulate the null hypothesis (H0) that there is no significant difference between
items being compared.
2. Set the level of significance.
3. Determine the test to be used.
4. Determine the tabular value for the test.
5. Compute for z-test or t-test as needed.
 z – test
1. Sample mean compared with Population mean
FORMULA:
z =
X − µ
σ
𝑛
where: z = z-test
X = sample mean
µ = population mean
σ = population standard deviation
n = number of items within the sample

5. INFERENTIAL STATISTICS
2. Comparing two sample mean
FORMULA: Z =
X1 − X2
σ 1
n1
+
1
n2
where: z = z-test
X1 = mean of the first sample
X2 = mean of the second sample
n1 = number of items in the second sample
σ = population standard deviation
3. Comparing two sample proportions
FORMULA:
where: P1 = proportion of the first sample
q1 = 1 - P1
P2 = proportion of second sample
q2 = 1 - P2
n1 = number of items in the first sample
n2 = number of items in the second sample
𝑧 =
P1 −
P2
P1q1
n1
+
P2q2
n2

6. INFERENTIAL STATISTICS
 EXAMPLE 1
Data from a school census show that the mean weight of college students was 45 kilos,
with a standard deviation of 3 kilos. A sample of 100 college students were found to have
a mean weight of 47 kilos. Are the 100 college students really heavier than the rest, using
.05 significance level?
Step 1: H0 : The 100 college students are not really heavier that the rest. (X = 45 kilos)
Ha : The 100 college students are really heavier that the rest. (X > 45 kilos)
Step 2: Set 0.05 level of significance
Step 3: The standard deviation given is based on the population. Therefore the z-test is to be
used
Step 4: Based on the table (critical value of z), the tabular value of z for one tailed test at 0.05
level of significance is 1.645
Step 5: The given values in the problem are:
X = 47 kilos
µ = 45 kilos
σ = 3 kilos
n = 100

7. INFERENTIAL STATISTICS
FORMULA: z =
X − µ
σ
𝑛
z =
47 −45
3
100
=
2
3
10
=
2
0.3
= 6.67
Step 6: The computed value of 6.67 is greater than the tabular value 1.645. Therefore, the null
hypothesis is rejected

8. INFERENTIAL STATISTICS
 EXAMPLE 2
A researcher wishes to find out whether or not there is significant difference between the
monthly allowance of morning and afternoon students In his school. By random
sampling, he took a sample of 239 students in the morning session. These students were
found to have a mean of monthly allowance of ₱142.00. The researcher also took a
sample of 209 students in the afternoon session. They were found to have a mean
monthly allowance of ₱148.00. The total population of students in that school has a
standard deviation of ₱40. Is there a significant difference between the two samples at
0.01 level of significance?
H0 : There is no significant difference between the samples
Ha : There is significant difference between the samples
FORMULA: Z =
X1 − X2
σ 1
n1
+
1
n2

9. INFERENTIAL STATISTICS
Z =
142 −148
40 1
239
+
1
209
=
−6
40
0.0042 +0.0048
=
−6
40
0.0090
=
−6
40 (0.095)
=
−6
3.8
= −1.579
The computed value of 1.579 is less than the tabular value of 2.58 at 0.01 level of significance.
Accept the null hypothesis

10. INFERENTIAL STATISTICS
 EXAMPLE 3
A sample survey of a television program in Metro Manila shows that 80 of 200 men
dislike the same program. We want to decide whether the difference between the two
sample proportion,
80
200
= 0.40 and
75
250
= 0.30, is significant or not at 0.05 level of
significance.
H0 : There is no significant difference between the two sample proportions
Ha : There is significant difference between the two sample proportions
The given values in the problem are:
P1 = 0.40 q1 = 1 - P1 = 1 – 0.40 = 0.60
P2 = 0.30 q2 = 1 - P2 = 1 – 0.30 = 0.70
n1 = 200 n2 = 250
𝑧 =
P1 −
P2
P1q1
n1
+
P2q2
n2
𝑧 =
0.40 − 0.30
(0.40) (0.60)
200
+
(0.30) 0.70)
250
=
0.10
0.24
200
+
0.21
250
=
0.10
0.0012 + 0.00084

11. INFERENTIAL STATISTICS
=
0.10
0.00204
=
0.10
0.045
= 2.22
The computed value of 2.22 is greater than the tabular value 1.96, the null hypothesis is
rejected

12. INFERENTIAL STATISTICS
 t – test
1. Sample mean compared with Population mean
FORMULA: t =
X − µ
𝑠
𝑛 −1
or t =
X − µ 𝑛 −1
𝑠
where: t = t-test
X = sample mean
µ = population mean
s = sample standard deviation
n = number of items in the sample
EXAMPLE: A researchers knows that the average height of Filipino women is 1.525
meters. A random sample of 26 women was taken and was found to have a mean
height of 1.56 , with standard deviation of .10 meters. Is there reason to believe that
the 26 women in the sample are significantly taller than the others .05 significance
level?
H0 : The sample is not significantly taller than the other Filipino women
Ha : The sample is significantly taller than the others

13. INFERENTIAL STATISTICS
The given values in the problem are:
X = 1.56 meters
µ = 1.525 meters
s = .10 meters
n = 26
degrees of freedom = n – 1
= 26 – 1
= 25
FORMULA: t =
X − µ
𝑠
𝑛 −1
t =
1.56 −1.525
.10
26 −1
t =
0.035
.10
25
t =
0.035
0.02
t = 1.75
The computed value of 1.75 is greater than the tabular value 1.708, the null hypothesis is
rejected

14. INFERENTIAL STATISTICS
2. Comparing two sample means
FORMULA: t =
X1 − X2
(𝑛1−1) 𝑠1
2+(𝑛2−1) 𝑠2
2
𝑛1+ 𝑛2 −2
1
𝑛1
+
1
𝑛2
where: t = t-test
X1 = mean of the first sample
X2 = mean of the second sample
𝑠1 = standard deviation of the first sample
𝑠2 = standard deviation of the second sample
𝑛1 = number of items in the first sample
𝑛2 = number of items in the second sample

15. INFERENTIAL STATISTICS
EXAMPLE: A teacher wishes to test whether or not the Case Method of teaching is more effective that
the Traditional Method. She picks two classes of approximately equal intelligence (verified trough an
administered IQ test). She gathers a sample of 18 students to whom she uses the Case Method and
another sample of 14 students to whom she uses the Traditional Method. After the experiment, an
objective tests revealed that the first sample got a mean score of 28.6 with a standard deviation of 5.9,
while the second group got a mean score of 21.7 with a standard deviation of 4.6. Based on the result
of the administered test, can we say that the Case Method is more effective that the Traditional
Method?
H0 : The Case Method is as effective as the Traditional Method
Ha : The Case Method is more effective that the Traditional Method
Given:X1 = 28.6 X2 = 21.7
𝑠1 = 5.9 𝑠2 = 4.6
𝑛1 = 18 𝑛2 = 14
degrees of freedom = 𝑛1 + 𝑛2 - 2
= 18 + 14 – 2
= 30

16. INFERENTIAL STATISTICS
FORMULA: t =
X1 − X2
(𝑛1−1) 𝑠1
2+(𝑛2−1) 𝑠2
2
𝑛1+ 𝑛2 −2
1
𝑛1
+
1
𝑛2
t =
28.6 −21.7
18−1 5.9 2+(14−1) 4.6 2
18 +14 −2
1
18
+
1
14
t =
6.9
17 (34.81)+(13) (21.16)
32 −2
0.06+0.07
t =
6.9
591.77+275.08
30
0.13
t =
6.9
28.895 0.13
t =
6.9
3.756
t =
6.9
1.94
t =3.56
The computed t-value of 3.56 is greater than the tabular value 1.697, therefore the null
hypothesis is rejected

17. INFERENTIAL STATISTICS
 Analysis of Variance (ANOVA)
FORMULA:
F =
MSS𝑏
MSS𝑤
• ANOVA is based upon two sources of variation – (1) the between – column variance;
(2) the within – column variance
• The two variance was sometimes called as between – column sum of squares (𝐒𝐒𝒃)
and the within – column sum of squares (𝑺𝑺𝑤). The sum of the two variances make up
the total sum of squares (TSS).
FORMULA: TSS = 𝑥2 −
( 𝑥)2
𝑁
where: x = refers to the value of each entry
N = refers to the total number of items
EXAMPLE: Let us take three groups of 6 students each, where each group is subjected to
one of three types of teaching method. The grades of the students are taken at the end
of the semester and enumerated according to grouping. The one way classification
model will look like this:

18. INFERENTIAL STATISTICS
Group I
Method A
Group II
Method B
Group III
Method C
Student 1
Student 2
Student 3
Student 4
Student 5
Student 6
84
90
92
96
84
88
70
75
90
80
75
75
90
95
100
98
88
90
(𝑋𝑎)2 (𝑋𝑏)2
(𝑋𝑐)2
7,056
8,100
8,464
9,216
7,056
7,744
4,900
5,625
8,100
6,400
5,625
5,625
8,100
9,025
10,000
9,604
7,744
7,744
534 465 561 47,636 36,275 52,573
𝑋 = 534 + 465 + 561 = 1, 560
𝑋2 = 47, 636 + 36, 275 + 52, 573 = 𝟏𝟑𝟔, 𝟒𝟖𝟒

19. INFERENTIAL STATISTICS
• The total sum of squares is computed as follows:
TSS = 136, 484 -
(1,560)2
18
= 136, 484 -
2,433,600
18
= 136, 484 - 135, 200
= 1, 284
• The between-column variance or between-column sum of squares is of the sum of the squares
of the column sum, minus the correction term, where r refers to the number of rows.
1
𝑟
𝑆𝑆𝑏 =
1
𝑁𝑜. 𝑜𝑓 𝑅𝑜𝑤𝑠
(𝑠𝑢𝑚 𝑜𝑓 𝑒𝑎𝑐ℎ 𝑐𝑜𝑙𝑢𝑚𝑛)2
−
( 𝑥)
2
𝑁
𝑆𝑆𝑏 =
1
6
(5342
+ 4652
+ 5612
) −
(1, 560)2
18
𝑆𝑆𝑏 =
1
6
(285, 156 + 216, 255 + 314, 721) −
(2, 433, 600)
18
𝑆𝑆𝑏 =
816, 132
6
−
(2, 433, 600)
18
𝑆𝑆𝑏 = 136, 022 − 135, 200
𝑆𝑆𝑏 = 822
TSS = 𝑥2
−
( 𝑥)2
𝑁

20. INFERENTIAL STATISTICS
• The within-column variance or within-column sum of squares is the difference between the total
sum of squares and the between-column sum of squares.
𝑆𝑆𝑤 = TSS − SS𝑏
= 1, 284 − 822
= 462
• We can make use any of the following in getting the “degrees of freedom”:
Total degress of freedom (df) = N − 1
= 18 − 1
= 𝟏𝟕
Total degress of freedom (df) = rk − 1
= (3 x 6) − 1
= 18 − 1
= 𝟏𝟕
Between-column df = Number of Columns – 1
= 3 − 1
= 𝟐
Within-column df = total df – between column df
= 17 − 2
= 𝟏𝟓

21. INFERENTIAL STATISTICS
• To compute for the Mean Sum of Squares
𝑀𝑆𝑆𝑏 =
SS𝑏
df𝑏
=
822
2
= 411
𝑀𝑆𝑆𝑤 =
SS𝑤
df𝑤
=
462
15
= 30.8
• To compute for the F-test
F =
MSS𝑏
MSS𝑤
F =
411
30.8
= 13.34

22. INFERENTIAL STATISTICS
• ANOVA Table on the Three Samples Subjected to Different Teaching Method
• The tabular value: 3.68 at 5% level of significance
• DECISION: The null hypothesis is rejected considering that the computed value of 13.34 is greater
than the tabular value of 3.68

23. INFERENTIAL STATISTICS
 Chi-square Test (𝑿𝟐
)
• Use of Chi-square Test
1. For estimating how closely an observed distribution matches an expected
distribution, also known as good-of-fit test.
2. For estimating whether two random variables are independent, also called as test
of independence.
FORMULA: For Good-of-Fit Test
𝑋2
=
(OF − EF)2
EF
FORMULA: For Test of Independence
𝑋2
=
(OF − EF)2
EF
EF =
Row Total x Column Total
n

24. INFERENTIAL STATISTICS
 EXAMPLE
• Chi-square for a Good-of-Fit Test
 A two dice (dice A and B) with six sides was rolled out 10 times with a chance of any
particular number coming out was the same: 1 in 6. If the dice is loaded, there are certain
numbers which will have a greater chance of appearing, while others will have a lower
chance. The researcher observed the following in one dice (A).
𝑥2
=
(18−10)2
10
+
(5−10)2
10
+
(9−10)2
10
+
(7−10)2
10
+
(5−10)2
10
+
(16−10)2
10
𝑥2 = 6.4 + 2.5 + 0.1 + 0.9 + 2.5 + 3.6
𝑥2 = 16 CONCLUSION: There is very low chance that these rolls came from a fair dice considering that the calculated
value of 16 is greater that the tabular value of 11.07. This means that there is statistically significant difference
between the two dices.

25. INFERENTIAL STATISTICS
• Chi-square Test for Independence
• Test the hypothesis that academic performance does not depend on IQ at 1% significance level.
• Degrees of Freedom (df) = (r – 1) (k – 1)
= (2 – 1) (3 – 1)
= 2
• COMPUTATION: Getting the 𝐅𝒆
 Where 𝑓𝑜 = 31, 𝑓𝑒 =
32 x 80
100
= 25.6
 Where 𝑓𝑜 = 1, 𝑓𝑒 =
32 x 20
100
= 6.4
 Where 𝑓𝑜 = 45, 𝑓𝑒 =
49 x 80
100
= 39.20
 Where 𝑓𝑜 = 4, 𝑓𝑒 =
49 x 20
100
= 9.80
 Where 𝑓𝑜 = 4, 𝑓𝑒 =
19 x 80
100
= 15.2
 Where 𝑓𝑜 = 15, 𝑓𝑒 =
19 x 20
100
= 3.80

26. INFERENTIAL STATISTICS
• Replacing the above values into the chi-square formula, we shall have:
𝑋2 =
(OF − EF)2
EF
𝑋2
=
(31 −25.6)2
25.6
+
(1 −6.4)2
6.4
+
(45 −39.2)2
39.2
+
(4 −9.80)2
9.80
+
(4 −15.2)2
15.2
+
(15 −3.80)2
3.80
𝑋2 =
29.16
25.6
+
29.16
6.4
+
33.64
39.2
+
33.64
9.80
+
125.44
15.2
+
125.44
3.80
𝑋2 = 1.139 + 4.556 + 0.858 + 3.433 + 8.253 + 33.011
𝑋2 = 51.25
• Since the computed Chi-square value of 51.25 is greater than the tabular value of 9.21, the null
hypothesis is rejected. For the 100 students, academic performance depends on IQ

27. INFERENTIAL STATISTICS
 Simple Regression Analysis
• Regression analysis is concerned with the problem of estimation and forecasting.
 TYPES OF RELATIONSHIP
1. Direct Relationship. The slope of the line is positive because Y increases as X also
increases
2. Inverse Relationship. The slope of the line is negative because Y decreases as X also
increases
• Least Square Regression Line or LSRL is a statistical technique that analyses the
relationship between the independent and dependent variables.
 EQUATION:
Y = a + bX
 NORMAL EQUATIONS:
1. ΣY = aN + bΣX
2. ΣXY = aΣX + bΣ𝑿𝟐

28. INFERENTIAL STATISTICS
WHERE: ΣY = sum of the values of Y, the dependent variable
N = the number of pairs of X and Y
ΣX = sum of the values of X, the independent variable
ΣXY = the sum of the column XY, which is derived by multiplying the paired values of X and Y
Σ𝐗𝟐
= the sum of the column 𝐗𝟐
is derived by squaring the values of X
• Based on the given data of X and Y, we can determine all of the above which means
that the two normal equations now consist of a system of two linear equations with
two unknowns – a and b
• FORMULAS:
a=
𝚺𝐘 𝚺𝐗𝟐 − 𝚺𝐗 (𝜮𝑿𝒀)
𝐍 𝜮𝐗𝟐 −(𝜮𝐗)𝟐
b=
𝐍 𝜮𝐗𝐘 − 𝜮𝐗 (𝜮𝐘)
𝐍 𝜮𝐗𝟐 − (𝜮𝐗)𝟐

29. INFERENTIAL STATISTICS
• EXAMPLE:
X Y XY X2
1
3
4
6
8
9
11
14
56
1
2
4
4
5
7
8
8
40
1
6
16
24
40
63
88
126
1
9
16
36
64
81
121
196
364 524
a=
40 524 − 56 (364)
8 524 −(56)2
a=
20960−20384
4192 −3136
a=
576
1056
= 𝟎. 𝟓𝟒
b=
8 364 − 56 (40)
8 524 − (56)2
b=
2912−2240
4192 −3136
b=
672
1056
= 𝟎. 𝟔𝟒
Y = 0.54 + 0.64 (16)
= 0.54 + 10.24
= 10.78

30. INFERENTIAL STATISTICS
 Simple Correlation Analysis
• Correlation analysis concerned with the relationship in the changes of such variables.
• Degrees of correlation or relationship between two variables
1. Perfect correlation (negative and positive)
2. Some degrees of correlation (negative and positive)
3. No correlation
• The concept of correlation in terms of computed value is called correlation coefficient.
The value of the correlation coefficient ranges from -1 to +1.
• Pearson r test. The Pearson Product-Moment Coefficient of Correlation, otherwise
known as Pearson r is the most commonly used correlation coefficient.
• Pearson r, as the most widely used measure of correlation has two basic assumptions,
to wit:
1. The existence of linear relationship; and
2. The level of measurement of the data for the two variables are either in interval or
ratio scale.

31. INFERENTIAL STATISTICS
• The value of r (degree of linear relationship) can be interpreted according to the use of
range of values for the Pearson Product Moment of Correlation Coefficient, as follows:
• Notably, Pearson r is not a measure of causality. The significant of the obtained
correlation coefficient can be determined through the use of t-test for testing the
significance of r.
𝐭 = 𝐫
𝐧 − 𝟐
𝟏 − 𝐫𝟐
WHERE: t = t-test
r = obtained Pearson r value
n = paired sample size
FORMULA:
Degree of freedom = n – 2

32. INFERENTIAL STATISTICS
FORMULA for Pearson r:
𝒓 =
𝐍 𝚺𝐗𝐘 − 𝚺𝐗 (𝚺𝐘)
𝐍 𝜮𝐗𝟐 − (𝜮𝐗)𝟐 𝐍 𝜮𝐘𝟐 − (𝜮𝐘)𝟐
Where: r = correlation coefficient
N = total number of pair variables
X = the first variable under study
Y = the second variable under study
EXAMPLE:
A researcher wants to find out about the relationship between the performance of a sample
of five Peace and Security students in Political Science and Peace Security subjects:

33. INFERENTIAL STATISTICS
• The computational solutions are as follows:
𝒓 =
𝟓 (𝟑𝟗𝟗𝟒𝟒) − 𝟒𝟐𝟓 (𝟒𝟕𝟎)
𝟓 𝟑𝟔𝟏𝟑𝟓 − (𝟒𝟐𝟓)𝟐 𝟓 𝟒𝟒𝟏𝟗𝟎 − (𝟒𝟕𝟎)𝟐
=
𝟏𝟗𝟗𝟕𝟐𝟎 − 𝟏𝟗𝟗𝟕𝟓𝟎
𝟏𝟖𝟎𝟔𝟕𝟓 − 𝟏𝟖𝟎𝟔𝟐𝟓 𝟐𝟐𝟎𝟗𝟓𝟎 − 𝟐𝟐𝟎𝟗𝟎𝟎
=
−𝟑𝟎
𝟓𝟎 𝟓𝟎
=
−𝟑𝟎
𝟐𝟓𝟎𝟎
=
−𝟑𝟎
𝟓𝟎
= −𝟎. 𝟔𝟎
𝐭 = −𝟎. 𝟔𝟎
𝟓 − 𝟐
𝟏 − (−𝟎. 𝟔𝟎)𝟐
= −𝟎. 𝟔𝟎
𝟑
𝟏 − 𝟎. 𝟑𝟔
= −𝟎. 𝟔𝟎
𝟑
𝟎. 𝟔𝟒
= −𝟎. 𝟔𝟎 𝟒. 𝟔𝟖𝟕𝟓
= −𝟎. 𝟔𝟎 (2.165)
= −𝟏. 𝟐𝟗𝟗
Degree of freedom = 5 – 2 = 3

34. INFERENTIAL STATISTICS
• Thus, there is moderate negative relationship between the performance of a sample of five Peace
and Security students in Political Science and Peace Security subjects
• The significance of t-value to determine whether to reject 𝐇𝐎 and accept 𝐇𝐚 or otherwise, thus the
researcher can generalize whether there is direct, indirect or no correlation between variables.
 Computed t value = -1.30
 Critical value of t at 0.05 level of significance = 2.353
 If computed t-value > critical value of t = REJECT 𝐇𝐎
If the computed t-value < critical value of t = ACCEPT 𝐇𝐎
 CONCLUSION: Since the computed t-value is lesser than the critical value of t, the null
hypothesis, is ACCEPTED
• Hence, we can say that the performance of the five students of Peace and Security in Political
Science and Peace Security subjects had a moderate negative correlation with no significant
relationship exist between the said variables.