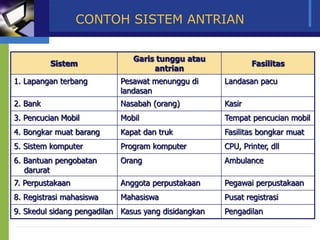
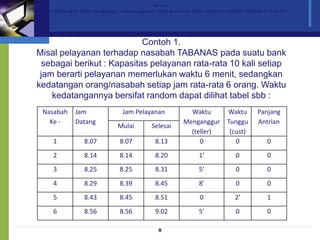
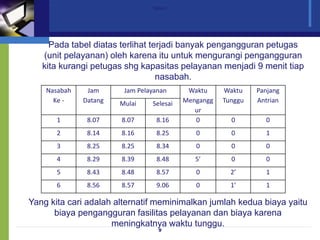
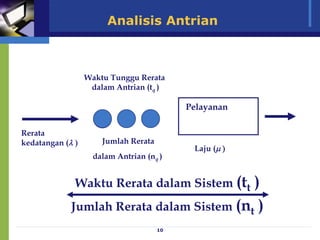
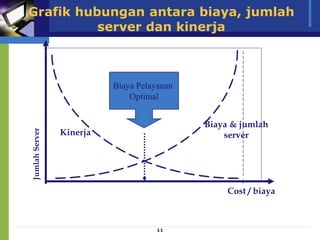
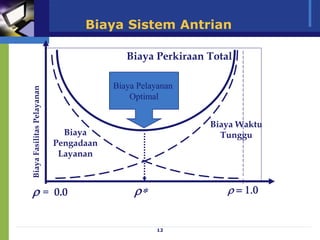
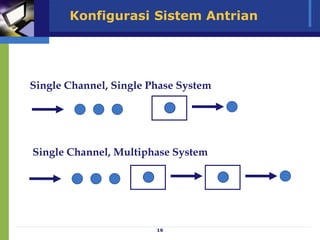
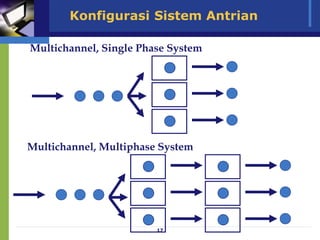
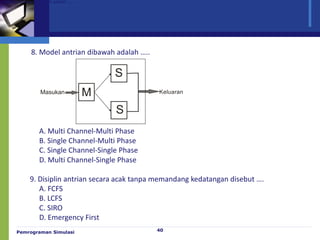
Dokumen ini membahas model antrian dan penerapan teori antrian dalam meningkatkan efisiensi pelayanan di berbagai fasilitas, seperti bank dan toko. Analisis mengenai waktu tunggu, biaya pelayanan, serta strategi untuk meminimalkan waktu antrian dan biaya terkait juga diuraikan. Beragam konfigurasi sistem antrian dan praktik terbaik dalam pengelolaan antrian serta pemodelan matematis juga disajikan.

1. LOGO
Model Antrian
Ir Tito Adi Dewanto

2. Menunggu dalam suatu antrian
adalah hal yang paling sering terjadi
dalam kehidupan sehari-hari
Intro

3. Theatre 1
Siapapun yang pergi berbelanja atau ke bioskop
telah mengalami ketidaknyamanan
dalam mengantri untuk membeli atau membayar tiket
Skip
Intro

4. Dengan memperhatikan hal ini, banyak
perusahaan mengusahakan untuk mengurangi
waktu menunggu sebagai komponen utama
dari perbaikan kualitas.
Skip
Intro

5. Umumnya, perusahaan dapat mengurangi waktu
menunggu dan memberikan pelayanan yang lebih
cepat dengan menambah jumlah pelayanan, seperti
jumlah teller pada bank atau jumlah kasir pada
supermarket.
Skip
Intro

6. Namun, menambah kapasitas pelayanan memerlukan
biaya dan dasar analisi waktu menunggu adalah
adanya trade-off antara biaya perbaikan pelayanan dan
biaya yang berasal dari waktu menunggu pelanggan.
Next
Intro
Teori Antrian :
 Menunggu giliran untuk
mendapatkan pelayanan dari
suatu fasilitas
 Antrian terjadi karena
kemampuan pelayanan tidak
bisa mengimbangi kebutuhan
pelayanan

7. CONTOH SISTEM ANTRIAN
Sistem
Garis tunggu atau
antrian
Fasilitas
1. Lapangan terbang Pesawat menunggu di
landasan
Landasan pacu
2. Bank Nasabah (orang) Kasir
3. Pencucian Mobil Mobil Tempat pencucian mobil
4. Bongkar muat barang Kapat dan truk Fasilitas bongkar muat
5. Sistem komputer Program komputer CPU, Printer, dll
6. Bantuan pengobatan
darurat
Orang Ambulance
7. Perpustakaan Anggota perpustakaan Pegawai perpustakaan
8. Registrasi mahasiswa Mahasiswa Pusat registrasi
9. Skedul sidang pengadilan Kasus yang disidangkan Pengadilan

8. Nasabah
Ke -
Jam
Datang
Jam Pelayanan Waktu
Menganggur
(teller)
Waktu
Tunggu
(cust)
Panjang
Antrian
Mulai Selesai
1 8.07 8.07 8.13 0 0 0
2 8.14 8.14 8.20 1’ 0 0
3 8.25 8.25 8.31 5’ 0 0
4 8.29 8.39 8.45 8’ 0 0
5 8.43 8.45 8.51 0 2’ 1
6 8.56 8.56 9.02 5’ 0 0
8
Tabel 1
Hubungan kedatangan, waktu menganggur, waktu tunggu dan panjang anterian dalam pelayanan nasabah TABANAS di Bank XYZ
Contoh 1.
Misal pelayanan terhadap nasabah TABANAS pada suatu bank
sebagai berikut : Kapasitas pelayanan rata-rata 10 kali setiap
jam berarti pelayanan memerlukan waktu 6 menit, sedangkan
kedatangan orang/nasabah setiap jam rata-rata 6 orang. Waktu
kedatangannya bersifat random dapat dilihat tabel sbb :

9. Nasabah
Ke -
Jam
Datang
Jam Pelayanan Waktu
Mengangg
ur
Waktu
Tunggu
Panjang
Antrian
Mulai Selesai
1 8.07 8.07 8.16 0 0 0
2 8.14 8.16 8.25 0 0 1
3 8.25 8.25 8.34 0 0 0
4 8.29 8.39 8.48 5’ 0 0
5 8.43 8.48 8.57 0 2’ 1
6 8.56 8.57 9.06 0 1’ 1
9
Tabel 2
Pada tabel diatas terlihat terjadi banyak pengangguran petugas
(unit pelayanan) oleh karena itu untuk mengurangi pengangguran
kita kurangi petugas shg kapasitas pelayanan menjadi 9 menit tiap
nasabah.
Yang kita cari adalah alternatif meminimalkan jumlah kedua biaya yaitu
biaya pengangguran fasilitas pelayanan dan biaya karena
meningkatnya waktu tunggu.

10. 10
Pelayanan
Analisis Antrian
Rerata
kedatangan ( Jumlah Rerata
dalam Antrian (nq )
Waktu Rerata dalam Sistem (tt )
Jumlah Rerata dalam Sistem (nt )
Waktu Tunggu Rerata
dalam Antrian (tq )
Laju (

11. 11
Grafik hubungan antara biaya, jumlah
server dan kinerja
Jumlah
Server
Biaya & jumlah
server
Kinerja
Biaya Pelayanan
Optimal
Cost / biaya

12. 12
Biaya Sistem Antrian
 = 1.0
= 0.0
Biaya
Fasilitas
Pelayanan
Biaya Perkiraan Total
Biaya Waktu
Tunggu
Biaya
Pengadaan
Layanan
Biaya Pelayanan
Optimal
*

13. 13
Karakteristik Kedatangan
Ukuran Populasi Kedatangan
 Tak terbatas (essentially infinite)
 Terbatas (finite)
Pola kedatangan pada sistem
 Terjadwal
 Secara acak  distribusi Poisson
 
!
x
e
x
P x




=
 
!
x
e
x
P x




=

14. Komponen sistem antrian
1. Populasi masukan
Berapa banyak pelanggan potensial yang masuk sistem antrian
2. Distribusi kedatangan
Menggambarkan jumlah kedatangan per unit waktu dan dalam
periode waktu tertentu berturut-turut dalam waktu yang berbeda
3. Disiplin pelayanan
Pelanggan yang mana yang akan dilayani lebih dulu : a. FCFS (first
come, first served) b. LCFS (last come, first served) c. Acak (SIRO)
d. Prioritas (UGD)
4. Fasilitas Pelayanan
mengelompokkan fasilitas pelayanan menurut jumlah yang tersedia
: a. Single-channel b. multiple-channel
5. Distribusi Pelayanan
a. Berapa banyak pelanggan yang dapat dilayani per satuan waktu
b. Berapa lama setiap pelanggan dapat dilayani
6. Kapasitas sistem pelayanan
memaksimumkan jumlah pelanggan yang diperkenankan masuk
dalam sistem
6. Karakteristik sistem lainnya
pelanggan akan meninggalkan sistem jika antrian penuh, dsb

15. Notasi dalam sistem antrian
 nt = jumlah pelanggan dalam sistem
 Pn = probabilitas kepastian n pelanggan dalam sistem
 λ = jumlah rata-rata pelanggan yang datang persatuan waktu
 µ = jumlah rata-rata pelanggan yang dilayani per satuan waktu
 Po = probabilitas tidak ada pelanggan dalam sistem
 p = tingkat intensitas fasilitas pelayanan
 nt = jumlah rata-rata pelanggan yang diharapkan dlm sistem
 nq = jumlah pelanggan yang diharapkan menunggu dalam antrian
 tt = waktu yang diharapkan oleh pelanggan selama dalam sistem
 tq = waktu yang diharapkan oleh pelanggan selama menunggu
dalam antrian
 1/µ = waktu rata-rata pelayanan
 1/λ = waktu rata-rata antar kedatangan
 S = jumlah fasilitas pelayanan
 Ct = Biaya Total = S.Cs + nt.Cw

16. 16
Konfigurasi Sistem Antrian
Single Channel, Single Phase System
Single Channel, Multiphase System

17. 17
Konfigurasi Sistem Antrian
Multichannel, Single Phase System
Multichannel, Multiphase System

18. 18
Disiplin Antrian
 Bagaimana pelanggan diseleksi dari antrian untuk
dilayani?
 First Come First Served (FCFS)
 Last Come First Served (LCFS)
 Served in Random Order (SIRO)
 Priority (jobs are in different priority classes)/UGD
 Untuk kebanyakan model diasumsikan FCFS
Pemrograman Simulasi

19. 19
Penamaan Antrian
X / Y / k (notasi Kendall)
X = distribusi kedatangan (iid)
Y = distribusi waktu pelayanan (iid)
 M = distribusi eksponensial untuk waktu
layanan dan kedatangan
 Ek = distribusi Erlang k
 G = general (antrian secara umum)
 D = deterministic (layanan dan kedatangan
konstan)
k = jumlah server
Pemrograman Simulasi

20. 20
Model Antrian
1. M/M/1 atau M/M/I/I/I
2. M/M/s atau M/M/S/I/I
3. Model Waktu Pelayanan Konstan
4. G/G/k
5. Model Populasi Terbatas

21. 21
Antrian M/M/1

22. 22
Asumsi M/M/1
Laju kedatangan  (distribusi Poisson)
Laju pelayanan  (distribusi exponential)
Server tunggal (satu fasilitas pelayanan)
First-come-first-served (FCFS)
Panjang antrian tak terbatas
Jumlah pelanggan tak terbatas

23. SINGLE CHANNEL MODEL
Model yang paling sederhana yaitu model saluran
tunggal atau sistem M/M/1
1. Populasi input tak terbatas
2. Distribusi kedatangan pelanggan potensial
mengikuti distribusi poisson
3. Disipliln pelayanan mengikuti FCFS
4. Fasilitas pelayanan terdiri dari saluran tunggal
5. Distribusi pelayanan mengikuti distribusi
poisson
6. Kapasitas sistem diasumsikan tak terbatas
7. Tidak ada penolakan maupun pengingkaran

24. 24
Karakteristik Operasi M/M/1
Faktor Utilitas
Rerata Waktu Tunggu
Rerata Jumlah Pelanggan


 =




=
L


 =


 =


 =




=
t
n
)
(
2





=
q
n
)
( 




=
q
t


 =
= s
n

 
=
1
t
t

25. 25
Karakteristik Operasi M/M/1
Persentasi Waktu Luang
Prob ada n Pelanggan dalam Sistem
Biaya Pengeluaran Total



=1
0
P
1

 







=
k
k
n
P


Total Cost = Waiting Cost + Service Cost



=1
0
P
n
n
P 
















=




1
Total Cost = Waiting Cost + Service Cost



=1
0
P
Pemrograman Simulasi
Ct = Biaya Total = nt.Cw + S.Cs

26. 26
Contoh 1
Sebuah bank memiliki 1 mesin ATM.
Kenyataanya :
 Waktu rata-rata untuk melayani customer 50 detik
 Rata-rata customer yang akan memakai atm 60 org/jam
 Dirancang pembuatan mesin ATM yang baru.
 Pihak bank ingin mengetahui probabilitas seorang customer pasti harus
mengantri untuk memakai ATM
Penyelesaian :
  =Tingkat kedatangan = 60 org/jam
  = tingkat layanan = 1 org/50 detik x 3600 detik /1 jam= 72 org/jam
Sehingga tingkat kesibukan = 60/72 = 0,833
 Rata waktu tunggu dalam antrian = 0,0694 jam = 4,167menit
 Artinya P(seorang customer harus mengantri) = 0,833
 Lama menunggu rata-rata = 4,167 menit
 Rata jumlah customer dalam antrian = 4,2 = 4 org


 =
)
( 




=
q
t
)
(
2





=
q
n
Pemrograman Simulasi

27. 27
Contoh 2
Suatu toko variasi mobil memiliki data sbb: Selama 1 jam rata-rata ada 3
pembeli yang datang. Kapasitas pelayanan yang ada rata-rata setiap jam
mampu melayani 8 langganan/pembeli.
Hitunglah :
 A. Rata-rata jumlah langganan yang antri sebelum dilayani
 B. Rata-rata jumlah langganan dalam sistem
 C. Rata-rata lama langganan sebelum dilayani
 D. Rata-rata lama langganan dalam sistem
 E. Prob ada n langganan dalam sistem
 F. Rata-rata banyak langganan yang sedang dilayani
 G. Kalau biaya pelayanan setiap jam Rp 500 dan biaya karena langganan
menunggu setiap jam Rp 100, maka hitunglah jumlah seluruhnya setiap
jam.
Pemrograman Simulasi

28. Pemrograman Simulasi 28
 =Tingkat kedatangan = 3 org/jam
 = tingkat layanan = 8 org/jam
225
,
0
)
(
2
=

=





q
n
A
6
,
0
3
8
3
=

=

=




t
n
B
075
,
0
)
3
8
(
8
3
)
(
=

=

=





q
t
C
2
,
0
3
8
1
1
=

=

=



t
t
D
8
3
=
=




F
G> E(Ct) = S.Cs + nt.Cw = 1.500 + 0,6.100=560
n
n
P
E 
















=





1
n 0 1 2 3 4 5 6 7 >8
P 0,625 0,324 0,088 0,012 0,005 0,002 0,001 0

29. Contoh 3
PT CIARD mengoperasikan satu buah pompa bensin dengan satu
operator. Rata-rata tingkat kedatangan kendaraan mengikuti
distribusi poisson yaitu 20 kendaraan per jam. Operator dapat
melayani rata-rata 25 mobil per jam, dengan waktu pelayanan
setiap mobil mengikuti distribusi probabilitas eksponensial. Jika
diasumsikan model sistem antrian yang digunakan operator
tersebut (M/M/1), hitunglah :
1. Tingkat intensitas (kegunaan) pelayanan (p)
2. Jumlah rata-rata kendaraan yang diharapkan dalam sistem
3. Jumlah kendaraan yang diharapkan menunggu dalam antrian
4. Waktu yang diharapkan oleh setiap kendaraan selama dalam sistem
(menunggu pelayanan)
5. Waktu yang diharapkan oleh setiap kendaraan untuk menunggu dalam
antrian
Mobil antri menunggu
pelayanan
s
1 pompa bensin
melayani 20 mobil per
jam
Kedatangan
mobil, 15 per
jam
Mobil Keluar
SPBU CIARD
Fasilitas
Pelayanan

30. Penyelesaian
λ = 20 dan µ = 25
1. Tingkat intenstas (kegunaan) pelayanan atau 80
,
0
25
20
μ
λ
p =
=
=
Angka tersebut menunjukkan bahwa operator akan
sibuk melayani kendaraan selama 80% dari waktunya.
Sedangkan 20% dari waktunya
(1 – p) yang sering disebut idle time akan digunakan
operator untuk istirahat, dll
2 atau
,
4
20
25
20
λ
-
μ
λ
nt =

=
=
4
80
,
0
1
80
,
0
p
-
1
p
nt =

=
=
Angka tersebut menunjukkan bahwa operator dapat
mengharapkan 4 mobil yang berada dalam sistem

31. 3 20
,
3
125
400
)
20
25
(
25
)
20
(
λ)
-
μ(μ
λ
nq
2
2
=
=

=
=
Angka tersebut menunjukkan bahwa mobil yang
menunggu untuk dilayani dalam antrian sebanyak 3,20
kendaraan
4 menit
12
atau
jam
20
,
0
25
1
20
25
1
λ
-
μ
1
tt =
=

=
=
Angka tersebut menunjukkan bahwa waktu rata-rata
kendaraan menunggu dalam sistem selama 12 menit
5 menit
9,6
atau
jam
16
,
0
125
20
)
20
25
(
25
20
λ)
-
μ(μ
λ
tq =
=

=
=
Angka tersebut menunjukkan bahwa waktu rata-rata
kendaraan menunggu dalam antrian selama 9,6 menit

32. 32
Antrian M/M/s
Pemrograman Simulasi

33. 33
Asumsi M/M/s
Laju kedatangan of  (distribusi Poisson)
Service rate of  (distribusi exponential)
Dua/lebih server
First-come-first-served (FCFS)
Panjang antrian tak terbatas
Jumlah pelanggan tak terbatas
Laju pelayanan sama pada semua server
Pemrograman Simulasi

34. 34
Karakteristik Operasi M/M/s
Faktor Utilitas/rata-rata banyaknya objek dalam
fasilitas pelayanan
Rerata Waktu Tunggu
Rerata Jumlah Pelanggan



.
M
=



= L
Lq



.
M
=



.
M
=

1

= q
t t
t
S
q
S
S
S
Po
t )
.(
)
/
(
1
)(
!
( 2




 
=



.
S
=



= q
t n
n
0
2
.
)
(
)!
1
(
)
/
(
P
S
S
n
S
q







=
Pemrograman Simulasi

35. 35
Karakteristik Operasi M/M/s
Persentasi Waktu Luang

































=


= S
S
S
n
P S
S
n
n
!
1
!
1
1
1
0
0
Pemrograman Simulasi

36. 36
Contoh 4
Sebuah supermaket memiliki 4 jalur keluar/pembayaran.
Kedatangan customer dengan tingkatan 100 org/jam. Rata-
rata 1 customer dilayani 2 menit.
Ingin diketahui :
 Berapa jumlah customer berada dalam antrian !
 Probabilitas customer tidak harus antri !
Penyelesaian :
M = 4
 = 100 org/jam
 = 30 org/jam  1 jam = ?? Org
1 org = 2 menit
1 jam = 60/2 = 30 org
Sehingga = 0,8331
Dari dan diperoleh nq = 3,29 org



.
M
=










= 0
2
.
)
(
)!
1
(
)
/
(
P
S
S
n
S
t



= t
q n
n

37. Pemrograman Simulasi 37
SOAL UJIAN OPERATION RESEARCH
TEORIANTRIAN
1. Pengertian Sistem Antrian adalah …….
A. Pelayanan kepada pelanggan
B. Pelayanan setiap pelanggan dating
C. Keseluruhaan dari layanan yang diberikan kepada pelanggan sejak ia
datang sampai selesai dilayani.
D. Keseluruhan dari layanan sejak pelanggan datang.
2. Penyebab timbulnya antrian adalah ……
A. Orang yang perlu dilayani terlalu banyak
B. Fasilitas layanan sedikit
C. Antri yang lama mendatangkan kepuasan
D. Kedatangan orang yang ingin dilayani persatuan waktu lebih tinggi dari
lama pelayanan persatuan waktu.

38. Pemrograman Simulasi 38
3. ‘Traffic Intencity’ merupakan perbandingan rata-rata kedatangan dengan
rata-rata kemampuan pelayanan. Formulanya adalah ….
A. 
B. 
C. /
D. /
4. Suatu toko variasi mobil memiliki data sebagai berikut : Selama 1 jam rata-
rata ada 3 pembeli yang datang. Kapasitas pelayanan yang ada rata-rata
setiap jam mampu melayani 8 langganan. Traffic Intencity adalah …..
A. 3/8
B. 8/3
C. 24
D. 2 2/3

39. 39
MASUKAN M S M S KELUARAN
•Lihat diagram berikut :
PHASE 1 PHASE 2
5. Model antrian diatas adalah …..
A. Multi Channel-Single Phase
B. Multi Channel-Multi Phase
C. Single Channel-Multi Phase
D. Single Channel-Single Phase
6. Tingkat pelayanan dalam suatu periode tertentu dalam antrian ……
A. 
B. /
C. /
D. 
7. Model distribusi kedatangan memiliki ketentuan jumlah …
A. Macam fasilitas pelayanan banyak
B. System lebih dari 1
C. Kapasitas antrian terbatas
D. Masukan tidak terhingga

40. Pemrograman Simulasi 40
•Model antrian dibawah adalah …..
M
S
S
Masukan Keluaran
A. Multi Channel-Multi Phase
B. Single Channel-Multi Phase
C. Single Channel-Single Phase
D. Multi Channel-Single Phase
9. Disiplin antrian secara acak tanpa memandang kedatangan disebut ….
A. FCFS
B. LCFS
C. SIRO
D. Emergency First
8. Model antrian dibawah adalah …..

41. Pemrograman Simulasi 41
10. Toko jujur setiap jam dikunjungi 4 pembeli. Kapasitas pelayanan setiap jam di toko
jujur adalah 6 orang. Hitung rata-rata waktu antrian sebelum dilayani….
A. 0,30
B. 0,31
C. 0,32
D. 0,33
11. Objek yang datang atau masuk ke dalam system yang memerlukan pelayanan
disebut dengan ….
A. Antri
B. Antrian
C. Input
D. Output
12. Struktur yang dipakai di Rumah Sakit adalah …..
A. Multi Channel-Single Phase
B. Multi Channel-Multi Phase
C. Single Channel-Multi Phase
D. Single Channel-Single Phase