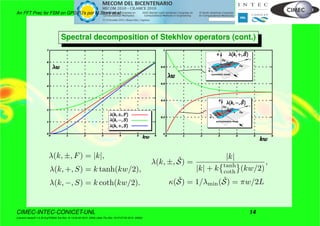
The document discusses an FFT preconditioning technique for solving incompressible Navier-Stokes flows using fractional step methods on GPU hardware. It highlights the inefficiencies of global memory access on GPUs, the advantages of structured meshes, and presents the accelerated global preconditioning (AGP) algorithm, which provides better convergence than the iterated orthogonal projection (IOP) method. The implementation details, performance metrics, and comparisons of both methods are also covered, indicating that AGP is more efficient for stable and quick simulations in engineering applications.












![An FFT Prec for FSM on GPGPU’s por M.Storti et.al.
Implementation details on the GPU
• We use the CUFFT library.
• Per iteration: 2 FFT’s and
Poisson residual
evaluation. The FFT on the
GPU Tesla C1060 performs
at 27 Gflops, where the
operations are counted as
5N log2(N). The new
Tesla C2050 (Fermi) GPU
has a performance of
80 Gflops for the FFT.
• For a grid of 128x128x64
8ms/iter (2x4ms, for each
FFT), so the cost per time
step (Poisson only,
assuming 3 iterations) is of
24ms.
0
5
10
15
20
25
30
10^{3} 10^{4} 10^{5} 10^{6} 10^{7} 10^{8}
FFTcomputingrate[Gflops]
Number of cells
CIMEC-INTEC-CONICET-UNL 15
((version texstuff-1.0.35-8-g7f2f93d Tue Nov 16 13:02:45 2010 -0300) (date Thu Nov 18 07:27:53 2010 -0300))](https://image.slidesharecdn.com/gpuslides-101118150243-phpapp01/85/Gpuslides-15-320.jpg)