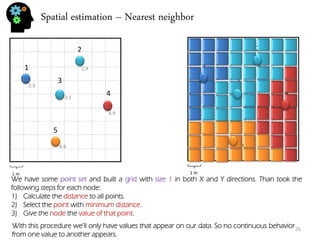
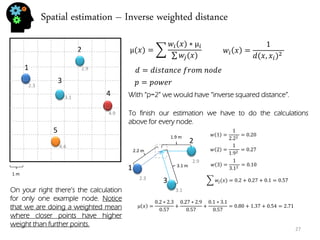
The document provides an index and overview of topics related to geostatistics including: - Types of data (point data and grid data), file formats, and viewing data - Statistical parameters like mean, variance, and percentiles - Univariate analysis methods like histograms and boxplots - Bivariate analysis like scatterplots and correlation - Spatial estimation techniques including kriging and sequential simulation - Variography and building variograms - Stochastic modeling procedures like sequential Gaussian simulation

1. Student Garden
Geostatistics course
1

2. INDEX
•Types and purpose of data
•Point data (s.3)
•Point data file format (s.4)
•Viewing point data (s.5-7)
•Grid data (s.8)
•Grid data file format and viewing (s.9-10)
•Grid spatial parameters (s.11-12)
•Statistical parameters
•Basic parameters (s.13)
•Mean (s.14)
•Variance (s.15)
•Percentile (s.16)
•Univariate analysis
•Histogram (s.17)
•Boxplot (s.18)
•Lineplot (s.19)
•Bivariate analysis
•Scatterplot (s.20)
•Correlation and regression (s.21)
•Stereonet (s.22)
•Special scatterplots (s.23)
•Spatial estimation
•Purpose (s.24)
•Nearest neighbor (s.25)
•Inverse weighted distance (s.26)
•Variography
•Anisotropy (s.27)
•Building a variogram (s.28-31)
•Kriging
•Simple kriging (s.32-35)
•Ordinary kriging (s.36)
•Sequential simulation
•Uncertainty (s.37-38)
•Random walk (s.39)
•Node value as hard value (s.40)
•Probability function generation (s.41-42)
•Procedures (s.43)
•Sequential Gaussian Simulation (s.44)
•Direct Sequential Simulation (s.45)
2

3. INDEX
•Simulation post-processing
•Getting mean and variance of simulations (s.47)
•Co-located co-simulation
•When to use… (s.48)
•How to do… (s.49-51)
•Sequential indicator simulation
•Categorical data (s.52)
•Indicator function (s.53)
•Indicator variogram (s.54)
•How to do… (s.55)
•Indicator simulation post-processing
•Getting most-likely value and entropy of simulations (s.56)
•Stochastic Genetic procedures
•Genetic algorithms (s.57)
•Global stochastic inversion (s.58)
•Convolution (s.59-61)
•Objective function (s.62-65)
3

4. Types and purpose of data – point data
Place where a sample was gathered
Objective
•Study the dispersion of a contaminant in the flooding areas of a river.
We’ve gathered samples in the areas where flooding occurred and retrieved the following variables:
•X coordinate
•Y coordinate
•Z coordinate
•Iron content
•Organic content
We call this point-data (and hard- data because it was retrieved with direct methods resulting in a physical sample).
4

5. Types and purpose of data – point data file format
Flooding_contents_project 5 X Y Z Iron_content Organic_content 4.1 4 0.9 0.11 0.09 3.8 6.6 1.1 0.10 0.09 3.2 7.2 1.3 0.12 0.11 4.4 7.9 1.2 0.09 0.09 2.6 8.2 1.3 0.08 0.10 3.5 8.6 1.1 0.07 0.09 2.9 8.8 0.9 0.07 0.11 2.4 9.6 0.7 0.06 0.07 3.9 9.8 1.4 0.03 0.04 3.3 10.3 1.5 0.01 0.03
x
y
z
5
6
7
8
9
10
3
4
5
This is an example of an ASCII (text) point- data file (GEOEAS format because it has an header). On the right you can see the plot of the data in the file. One of the points is even indicated ( ) both in the file and plot.
5

6. Types and purpose of data – viewing point data
We usually view variables as colors. Each color indicates a specific range of values for that variable. For this example we’ll use the “Jet” color mapping (sometimes called colorbar). Let’s view the iron content:
Flooding_contents_project 5 X Y Z Iron_content Organic_content 4.1 4 0.9 0.11 0.09 3.8 6.6 1.1 0.10 0.09 3.2 7.2 1.3 0.12 0.11 4.4 7.9 1.2 0.09 0.09 2.6 8.2 1.3 0.08 0.10 3.5 8.6 1.1 0.07 0.09 2.9 8.8 0.9 0.07 0.11 2.4 9.6 0.7 0.06 0.07 3.9 9.8 1.4 0.03 0.04 3.3 10.3 1.5 0.01 0.03
0.01 , 0.021, 0.032, 0.043, 0.054, 0.065, 0.076, 0.087, 0.098, 0.109, 0.12
x
y
z
5
6
7
8
9
10
3
4
5
6

7. Types and purpose of data – viewing point data
We’ve used the colorbar but how do we build one? I want to make a colorbar with 10 colors which means having 10 value ranges.
0.01 , 0.021, 0.032, 0.043, 0.054, 0.065, 0.076, 0.087, 0.098, 0.109, 0.12
a)I retrieve the minimum from the variable to be color mapped: 0.01
b)I retrieve the maximum from the same variable: 0.12
c)I calculate the range between them: 0.12 – 0.01 = 0.11
d)I divide that range by 10 (because I want 10 colors): 0.11/10 = 0.011
e)Than i calculate the interval in each bin by summing the superior limit from last bin to the calculated bin range.
f)0.01 + 0.011 = 0.021 so first bin is [0.01, 0.021[
g)0.021 + 0.011 = 0.032, second bin is [0.021,0.032[
h)0.032 + 0.011 = 0.043, third bin is [0.032,0.011[
i)And so on…, until the last bin
Each color is given by a RGB triplet (it may be RGB-A but the last value is transparency).
•R for red
•G for green
•B for blue
•(optional) A for alpha
It is quite common that every software that gives the user opportunity to choose color to have a color dialog where you insert the exact RGA triplet you want..
•Red is: 255;0;0 (255 is the max).
•Green is: 0;255;0
•Blue is: 0;0;255
•Purple is: 128;0;128
To build purple we need 128 parts in 255 of red, 0 of green, and 128 parts in 255 of blue.
7

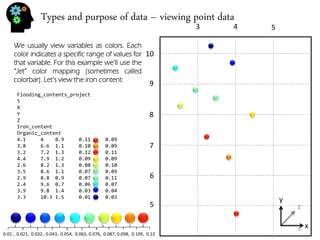
8. Types and purpose of data – viewing point data
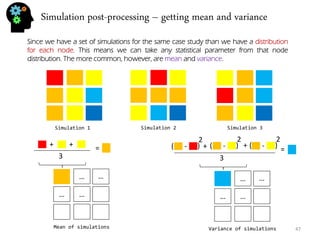
There are many kinds of colorbar. Many have been developed to achieve some specific purpose like display a colored image in black and white or getting the best contrast between positive values, negative values and zero values in a seismic cube. Like this:
min.
max.
This color map is usually called “Seismic” colormap or “RdBu” (for red to blue or blue to red). Notice that in the seismic cube this colormap will show negatives in blue colors, positives in red colors and near zero values in whites. It gets very simple to retrieve the strength of the seismic signal.
min.
max.
The “Jet’ color map (sometimes called “rainbow”) on the other hand was made to show easily a wider range of values although there is still the felling of continuity.
RGB triplets from blue to red “Jet” [ 0 0 143] [ 0 0 239] [ 0 79 255] [ 0 175 255] [ 15 255 255] [111 255 159] [207 255 63] [255 223 0] [255 127 0] [255 31 0] [191 0 0]
8

9. Types and purpose of data – grid data
On the left you have a grid. In this case we are viewing that grid as a surface but it is still a grid. Let’s make a definition. - A grid is a mesh of cells, each with its own position, and its own value (or values if multiple variables).
x=1
x=2
x=3
x=4
y=1
y=2
y=3
y=4
y=5
y=6
This is a regular rectangular mesh (geostatistics grid with constant cell size for each axis) but there are other kinds of meshes.
9

10. Types and purpose of data – grid data
Let’s see some other examples of grids.
Regular grid (geostatistics)
Irregular grid (size may change)
Structured grid (the shape of cell changes as well as size)
Structured grid (the shape of cell changes as well as size)
In geostatistics we usually use the regular grid with rectangular cells. However it would be possible to do in other formats.
10

11. Types and purpose of data – grid data file format and viewing
Flooding_contents_project 1 Iron_content 0.09 0.10 0.09 0.08 0.07 0.05 0.05 0.03 0.01
x=1
x=2
x=3
y=1
y=2
y=3
0.09
0.12
0.09
0.08
0.07
0.05
0.05
0.03
0.01
This is an example of an ASCII (text) grid- data file (GEOEAS format because it has an header). On the right you can see the disposition of the variables values in the column in-file.
0.01 , 0.021, 0.032, 0.043, 0.054, 0.065, 0.076, 0.087, 0.098, 0.109, 0.12
min.
max.
x=1
x=2
x=3
y=1
y=2
y=3
0.09
0.12
0.09
0.08
0.07
0.05
0.05
0.03
0.01
11

12. Types and purpose of data – grid spatial parameters
size y = 2
size x = 1
First Y coordinate = 1
First X coordinate = 2.2
The parameters that define this regular grid are:
a)Number of cells in X: 3
b)Number of cells in Y: 3
c)Number of cells in Z: 1
d)Size of cell in X: 1
e)Size of cell in Y: 2
f)Size of cell in Z: 1
g)First coordinate in X: 2.2
h)First coordinate in Y: 1
i)First coordinate in Z: 0
We use these parameters to put the grid with correct disposition, dimensions, and location. Without them we only have a column of values.
12

13. Types and purpose of data – grid spatial parameters
Typical problem of misplacing the grid with the hard-data due to wrong size and first coordinate. Ensure both point-data and grid- data are in the same spatial units and correctly positioned.
13

14. Statistical parameters – basic parameters
30, 5, 32, 26, 18, 9, 11, 11, 13, 7, 24, 25, 28, 8, 9, 9, 7,24, 32, 27, 26, 18, 12
Let’s use a few sample values:
Some basic parameters important to understand you r data are:
•Minimum: 5
•Maximum: 32
•Arithmetic mean: 17.86
•Standard deviation: 9.03
•Variance: 81.67
•Percentile 25: 9
•Percentile 50 (median): 18
•Percentile 75: 26
Let’s think about each one of them. There are many types of mean:
•Arithmetic mean
•Geometric mean
•Harmonic mean
•Etc…
Each has it’s own advantages but throughout this course you’ll consider mainly two: the arithmetic mean and the weighted mean.
14

15. Statistical parameters – mean
The arithmetic mean is given by:
μ= 푥푖 푛푖 =1 푛
μ= 푤푖푥푖 푛푖 =1 푛
The weighted mean is given by:
, where “W” is the weight for each sample value.
, where “X” is the sample “i" value.
We’ll talk later about weighted mean but we use it every time we want to calculate a mean from some samples but some samples are more important than others. Examples are kriging and inverse weighted distance. The samples are worth more depending on their distance and/or direction (also depends on other stuff but for now let’s take it easy).
The arithmetic mean is used to achieve a representative value (a central tendency meaning your distribution is clustered around this value) for a distribution that could have many samples therefore difficult to study as an entity. But using only the mean has a problem:
30, 5, 32, 26, 18, 9, 11, 11, 13, 7, 24, 25, 28, 8, 9, 9, 7,24, 32, 27, 26, 18, 12
17.86, 17.86, 17.86, 17.86,17.86, 17.86, 17.86, 17.86,17.86, 17.86, 17.86, 17.86,17.86, 17.86, 17.86, 17.86,17.86, 17.86, 17.86, 17.86,17.86, 17.86, 17.86
Set 1:
Set 2:
Both sets have the same mean. However one varies a lot, the other doesn’t vary at all. We need something to tell us the level of variation.
15

16. Statistical parameters – variance
One possible way of measuring the variability of a distribution is by calculating the distance of each value to the mean (the most arithmetically representative value of a distribution). We call this the absolute deviation:
푑=μ−푥푖
Of course we still need to get a representative value for the variability so we do the mean of absolute deviations:
푑μ= μ−푥푖 푛푖 =1 푛
Unfortunately the modulus is not a straightforward function (it’s actually the result a square root of a squared number, or a composed function). So someone replaced the modulus by an exponential of 2, therefore making the mean of squared deviations, also called the variance:
σ2= (μ−푥푖)2푛푖 =1 푛
The problem with variance is that you change the order of magnitude so it’s pretty common to put a square root in variance, calling this the standard deviation:
σ= (μ−푥푖)2푛푖 =1 푛
16

17. Statistical parameters – percentile
The percentile is a ways of calculating a number that limits a given quantity in a distribution. For example if I have the samples (notice they are sorted): 2,2,3,4,5,8,13,20,21
3 is the number that divides the first 25% of values with the other 75%, thus 3 is the percentile 25. There are two numbers to the left of 3 and 6 numbers to the right of 3.
I also know that 5 is the number that divides the first 50 % of my data with the last 50 %. Thus 5 is the percentile 50 (median) with 4 numbers on the left, and four numbers on the right.
So percentile is about quantity, about local quantity in a distribution. Imagine that you want to compare two distributions of samples. They have the same mean and same variance, as well same maximum and minimum value. Are the two distributions equal? You can’t really state that. In fact the percentiles may be different meaning that the data is clustered in a different manner throughout the distribution.
Before we finish this section let’s just see exactly what the mode is. The mode is the value that appears most often in a set of data. In the case of continuous variables the mode is the value at which its probability density function has its maximum value, so, informally speaking, the mode is at the peak. This is the reason some distributions are called bi-modal, because they have two peaks (also multi-modal, meaning multiple peaks).
17

18. Univariate analysis - histogram
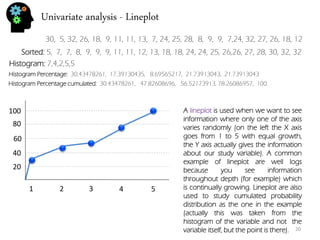
30, 5, 32, 26, 18, 9, 11, 11, 13, 7, 24, 25, 28, 8, 9, 9, 7,24, 32, 27, 26, 18, 12
Let’s use the sample values from the previous section:
Univariate analysis means that you’re studying the variable by itself. In fact the previous section (about mean, variance and so on) was already univariate analysis. Now we’re going to plot our data. The most typical univariate plot is the histogram. To do an histogram I must:
•Calculate the maximum (32) and minimum (5) and calculate the difference (32-5=27).
•Now we calculate the bin (for 7 bins) size which is 27/5=5.4.
•Now we build de limits of our bins: 1º:[5,10.4[, 2º:[10.4,15.8[, 3º:[15.8,21.2[, 4º:[21.2,26.6[, 5º:[26.6,32]
•And see how many values are inside each bin: 1º:7 , 2º:4, 3º:2, 4º:5, 5º:5
•Finally we plot the intervals on the X-axis, and the frequency (number of values per bin) in the Y- axis.
Sorted: 5, 7, 7, 8, 9, 9, 9, 11, 11, 12, 13, 18, 18, 24, 24, 25, 26,26, 27, 28, 30, 32, 32
5
10.4
15.8
21.2
26.6
32
2
4
6
8
18

19. Univariate analysis - boxplot
5
10.4
15.8
21.2
26.6
32
2
4
6
8
With an histogram you can see how probable a given bin is. The mean from this data-set is 17.86 which actually stands on the bin less probable. You can actually see some resemblance to two peaks or two populations. This could mean that more than one phenomena is involved with this variable.
This is a boxplot. It shows minimum (5), maximum (32), percentile 25 (9), percentile 50 (18), percentile 75 (26), and mean (17.86). The boxplot is very useful when studying data by it’s quantities. The bigger the blue box the wider the interval between percentile 25 and percentile 75. In this distribution you’ll notice a tendency towards the left side of the variable range. The first 25 % of data have the least variability.
5
9
18
26
17.86
32
variable
19

20. Univariate analysis - Lineplot
Sorted: 5, 7, 7, 8, 9, 9, 9, 11, 11, 12, 13, 18, 18, 24, 24, 25, 26,26, 27, 28, 30, 32, 32
30, 5, 32, 26, 18, 9, 11, 11, 13, 7, 24, 25, 28, 8, 9, 9, 7,24, 32, 27, 26, 18, 12
Histogram: 7,4,2,5,5
Histogram Percentage: 30.43478261, 17.39130435, 8.69565217, 21.73913043, 21.73913043
Histogram Percentage cumulated: 30.43478261, 47.82608696, 56.52173913, 78.26086957, 100.
1
20
40
60
80
100
2
3
4
5
A lineplot is used when we want to see information where only one of the axis varies randomly (on the left the X axis goes from 1 to 5 with equal growth, the Y axis actually gives the information about our study variable). A common example of lineplot are well logs because you see information throughout depth (for example) which is continually growing. Lineplot are also used to study cumulated probability distribution as the one in the example (actually this was taken from the histogram of the variable and not the variable itself, but the point is there).
20

21. Bivariate analysis - scatterplot
21
Flooding_contents_project 5 X Y Z Iron_content Organic_content 4.1 4 0.9 0.11 0.09 3.8 6.6 1.1 0.10 0.09 3.2 7.2 1.3 0.12 0.11 4.4 7.9 1.2 0.09 0.09 2.6 8.2 1.3 0.08 0.10 3.5 8.6 1.1 0.07 0.09 2.9 8.8 0.9 0.07 0.11 2.4 9.6 0.7 0.06 0.07 3.9 9.8 1.4 0.03 0.04 3.3 10.3 1.5 0.01 0.03
Remember the point data from slide 2? We have two variables. Let’s see how they relate.
This is a scatterplot. From a scatterplot you can see the relation between two variables. In this case you’ll notice that there seems to be something similar to a linear positive (when one grows the other also grows) relation between iron content and organic content. Numerically we could retrieve the correlation coefficient and the linear regression line (plotted as dashed red).
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
Iron_content
Organic_content

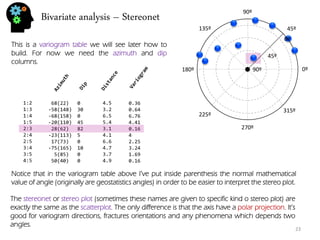
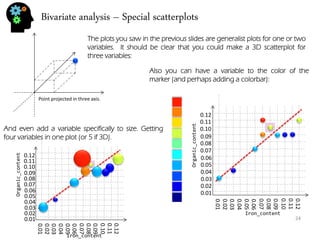
22. Bivariate analysis – correlation and regression
22
There are many methods to measure relation and dependence between two or more variables. In fact there are quite a few correlation coefficient. The most usual is the Pearson correlation coefficient.
ρ= 퐸[푋−μ푥푌−μ푦] σ푋σ푌
The Pearson coefficient is between -1 and 1. Numbers closer to 1 (or -1) indicate stronger correlation being positive if close to 1, and negative (one variable increases, the other decreases) if closer to -1. Numbers around 0 mean no Pearson correlation exists (normally they appear as clouds with little to no shape).
To do linear regression means to find a line that represents the general relation of your data (if it is at all linear or similar). That means discovering this:
푌=푚∗푋+푏
“Y” and “X” are know to us. They’re the variable data that stands on the Y-axis and X-axis. The only problem is how to discover both “m” and “b”. The formulas are:
푏= 푌−푚∗ 푋 푛
푋= 푥푖 ,푌=푌푖
푚= 푛∗ 푋푌− 푋 푌 푛∗ 푋2−( 푋)2

23. Bivariate analysis – Stereonet
23
1:2 1:3 1:4 1:5 2:3 2:4 2:5 3:4 3:5 4:5
68(22) -58(148) -68(158) -20(110) 28(62) -23(113) 17(73) -75(165) 5(85) 50(40)
0 30 0 45 82 5 0 10 0 0
4.5 3.2 6.5 5.4 3.1 4.1 6.6 4.7 3.7 4.9
0.36 0.64 6.76 4.41 0.16 4 2.25 3.24 1.69 0.16
This is a variogram table we will see later how to build. For now we need the azimuth and dip columns.
0º
45º
90º
135º
180º
225º
270º
315º
90º
45º
0º
Notice that in the variogram table above I’ve put inside parenthesis the normal mathematical value of angle (originally are geostatistics angles) in order to be easier to interpret the stereo plot.
The stereonet or stereo plot (sometimes these names are given to specific kind o stereo plot) are exactly the same as the scatterplot. The only difference is that the axis have a polar projection. It’s good for variogram directions, fractures orientations and any phenomena which depends two angles.

24. Bivariate analysis – Special scatterplots
24
The plots you saw in the previous slides are generalist plots for one or two variables. It should be clear that you could make a 3D scatterplot for three variables:
Point projected in three axis.
Also you can have a variable to the color of the marker (and perhaps adding a colorbar):
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
Iron_content
Organic_content
And even add a variable specifically to size. Getting four variables in one plot (or 5 if 3D).
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
Iron_content
Organic_content

25. Spatial estimation - Purpose
25
1
2
3
4
5
1 m
2.3
2.9
3.1
4.4
4.9
Look at the data on your left. We only know what is going on where point data exists and we need a map in order to have a real notion of how a phenomena or variable behaves in space.
There are 2 terms that specifically manage this kind of problem: interpolation and estimation. The difference will depend on the author but for the purpose of this course when referring by those terms I mean to do an exercise that demands calculating a value in a place where it does not exist.
There are many methods for spatial estimation (interpolation). Most are transversal to any number of dimensions (from 1 dimension to “n” dimensions). Specifically we’ll train how to do this in spatial dimensions (2D or 3D, for “x ;y ;z”). Notice however that nothing stops us from using time or any other variable as a dimension.

26. Spatial estimation – Nearest neighbor
26
1
2
3
4
5
1 m
2.3
2.9
3.1
4.4
4.9
We have some point set and built a grid with size 1 in both X and Y directions. Than took the following steps for each node:
1)Calculate the distance to all points.
2)Select the point with minimum distance.
3)Give the node the value of that point.
With this procedure we’ll only have values that appear on our data. So no continuous behavior from one value to another appears.

27. Spatial estimation – Inverse weighted distance
27
1
2
3
4
5
1 m
2.3
2.9
3.1
4.4
4.9
μ(푥)= 푤푖(푥)∗μ푖 푤푗(푥)
푤1= 12.22 =0.20
푑=푑푖푠푡푎푛푐푒 푓푟표푚 푛표푑푒
푝=푝표푤푒푟
With “p=2” we would have “inverse squared distance”.
To finish our estimation we have to do the calculations above for every node.
2.3
2.9
3.1
1
2
3
2.2 m
1.9 m
3.1 m
푤2= 11.92 =0.27
푤3= 13.12 =0.10
푤푗(푥)=0.2+0.27+0.1=0.57
μ푥= 0.2∗2.30.57+ 0.27∗2.90.57+ 0.1∗3.10.57=0.80+1.37+0.54=2.71
On your right there’s the calculation for only one example node. Notice that we are doing a weighted mean where closer points have higher weight than further points.
푤푖푥= 1 푑(푥,푥푖)2

28. Variography - anisotropy
28
We’ll be calling anisotropy a measure of how one direction has more continuity than the other. Let’s see an example:
Can you guess which direction as a greater sense of continuity? In the horizontal direction you’ll be following more or less the same geological layer so probably you’ll find things that are more similar to your starting point. The more the similarity the greater the range of continuity. On the other hand the vertical direction is transversal to the three example layers, thus less likely to find anything similar to your starting point.
We can say that we have anisotropy where the horizontal is more continuous than the vertical but we need some way to study this numerically. And we do know how to study variability. We use a formula similar to variance to calculate a variogram. The tool that can give us a numeric account of anisotropy.

29. Variography – building a variogram
These are 5 point-data each with a value, location, and a number ID (1 to 5). Let’s make the variogram table:
0º
90º
68º
122º
-58º
112º
-68º
160º
-20º
28º
208º
-23º
17º
-75º
5º
50º
1
2
3
4
5
1 m
2.3
2.9
3.1
4.4
4.9
1:2 1:3 1:4 1:5 2:3 2:4 2:5 3:4 3:5 4:5
68 -58 -68 -20 28 -23 17 -75 5 50
0 0 0 0 0 0 0 0 0 0
4.5 3.2 6.5 5.4 3.1 4.1 6.6 4.7 3.7 4.9
0.36 0.64 6.76 4.41 0.16 4 2.25 3.24 1.69 0.16
Mean: 3.52 , Variance: 0.94
0.36/2 0.64/2 6.76/2 4.41/2 0.16/2 4/2 2.25/2 3.24/2 1.69/2 0.16/2
29
2γ푥,푦=퐸(푍푥−푍(푦)2)

30. Variography – building a variogram Exercise 1
1:2 1:3 1:4 1:5 2:3 2:4 2:5 3:4 3:5 4:5
68 -58 -68 -20 28 -23 17 -75 5 50
0 0 0 0 0 0 0 0 0 0
4.5 3.2 6.5 5.4 3.1 4.1 6.6 4.7 3.7 4.9
0.36 0.64 6.76 4.41 0.16 4 2.25 3.24 1.69 0.16
0º
90º
68º
122º
-58º
112º
-68º
160º
-20º
28º
208º
-23º
17º
-75º
5º
50º
I want to make a variogram in azimuth = 20º with tolerance 10º and 3 bins.
a) Let’s get all angles from [20-tol,20+tol[ = [10,30[
b) Maximum distance is 6.6 so our lag distance for 3 bins is 6.6/3 = 2.2.
Sill = 0.94
2.2
4.4
6.6
0.5
1.0
1.5
2.0
2.5
NOTE: I’m plotting semi-variogram values which are half the normal variogram values.
30

31. Variography – building a variogram Exercise 2
1:2 1:3 1:4 1:5 2:3 2:4 2:5 3:4 3:5 4:5
68 -58 -68 -20 28 -23 17 -75 5 50
0 0 0 0 0 0 0 0 0 0
4.5 3.2 6.5 5.4 3.1 4.1 6.6 4.7 3.7 4.9
0.36 0.64 6.76 4.41 0.16 4 2.25 3.24 1.69 0.16
I want to make a variogram in azimuth = -70º with tolerance 15º and 3 bins.
a) Let’s get all angles from [-70-tol,-70+tol[ = [-85,-55[
b) Maximum distance is 6.5 so our lag distance for 3 bins is 6.5/3 = 2.16.
0º
90º
68º
122º
-58º
112º
-68º
160º
-20º
28º
208º
-23º
17º
-75º
5º
50º
Sill = 0.94
2.16
4.32
6.5
0.5
1.0
1.5
3.0
4.0
NOTE: for the third bin ( ) I’ve calculated the mean ( ) of values ( ) inside that bin.
31

32. Variography – building a variogram
0º
90º
68º
122º
-58º
112º
-68º
160º
-20º
28º
208º
-23º
17º
-75º
5º
50º
If my main direction is azimuth = -70º than the minor 1 will be the orthogonal (-70+90) 20º.
To do this for a 3D case in which we may manipulate the azimuth, dip and rake of the main direction we must do a series of rotations (using linear algebra) to find which directions are the orthogonal.
0º
90º
68º
122º
-58º
112º
-68º
160º
-20º
28º
208º
-23º
17º
-75º
5º
50º
Let’s take an example of direction azimuth 90º with tolerance of 10º. The considered interval should be [90- 10,90+10[ = [80,100[. Usually in geostatistics only ranges between -90 and 90 are used so the actual considered interval is a composition of [80,90[ U [-90,-80[.
32

33. Kriging – simple kriging
33
“0;0” – North (Y)
1.5
“90;0” – East (X)
3.2
3.2
1.5
γℎ= 퐶0+퐶1∗(1−푒 −3ℎ 푎 )
We’ve studied a set of point data and got the following variograms that were adjusted with an exponential model. The ellipsoid is on your right. The exponential model formula is above. Notice that the main direction (with highest range) is the “90;0”, and minor 1 “0;0”. There’s no minor 2 since this is a 2D study case.
γℎ=0+1∗(1−푒 −3ℎ 푎(θ) )

34. Kriging – simple kriging
34
1
2
3
4
5
1 m
2.3
2.9
3.1
4.4
4.9
We intend to estimate the value of this node using 3 point data and simple kriging method. Let’s start by studying point 1:
2.3
2.9
3.1
1
2
3
2.2 m
1.9 m
3.1 m
( 푥 푎 )2+( 푦 푏 )2=1
푥=푎∗cos (θ)
푦=푏∗sin (θ)
푟θ= 푥2+푦2
푥1푝=3.2∗cos (45) = 2.26
푦1푝=1.5∗sin (45) = 1.06
푟1푝θ= 푥2+푦2=2.49
푥12=3.2∗cos (28) = 2.82
푦12=1.5∗sin (28) = 0.70
푟12θ= 푥2+푦2=2.91
1
3.2
1.5
45º
28º
-32º = 32
3
2
p
2.2 m
4.1 m
2.8 m
푥13=3.2∗cos (32) = 2.71
푦13=1.5∗sin (32) = 0.79
푟13θ= 푥2+푦2=2.82
γ4.1=0+1∗1−푒 −3∗4.12.91 =0.98
γ2.8=0+1∗1−푒 −3∗2.82.82 =0.94
γ2.2=0+1∗1−푒 −3∗2.22.49 =0.92

35. Kriging – simple kriging
35
1
2
3
3.4 m
1.9 m
3.2 m
3.2
1.5
225º = 45º
180º = 0º
250º = 70º
푥23=3.2∗cos (70) = 1.09
푦23=1.5∗sin (70) = 1.40
푟23θ= 푥2+푦2=1.78
γ3.2=0+1∗1−푒 −3∗3.21.78 =1
p
푟21θ= 푟12θ = 2.91
γ4.1=0.98
푟2푝θ= 푥2+푦2=1.78
γ1.9=0+1∗1−푒 −3∗1.93.2 =0.83
1
2
3
3.1 m
3.2
1.5
2.8 m
3.2 m
푟31θ= 푟13θ = 2.82
γ2.8=0.94
푟32θ= 푟23θ = 1.78
γ2.8=1
푥3푝=3.2∗cos (70) = 0.55
푦3푝=1.5∗sin (70) = 1.47
푟3푝θ= 푥2+푦2=1.57
γ3.1=0+1∗1−푒 −3∗3.11.57 =1
70º
100º=80º
148º=32º

36. Kriging – simple kriging
36
1
2
3
1
2
3
p
0
0
0
0.98
0.94
0.98
1
0.94
1
w3
w1
w2
1
0.92
0.83
We need to find w1, w2 and w3. So we must solve the system.
I’ve solved it:
•w1 = 0.45
•W2 = 0.57
•W3 = 0.38
So to get the kriged value I must do:
2.3
2.9
3.1
1
2
3
2.2 m
1.9 m
3.1 m
푣푝=2.3−μ푝∗0.45+2.9−μ푝∗0.57+3.1−μ푝∗0.38+μ푝 = 2.75
μ푝= (2.3+2.9+3.1) 3 =2.76
2.75
To achieve simple kriging we would have to do this procedure for all cells in our grid. But this is pretty much it.
, this mean can be user input.

37. Kriging – ordinary kriging
37
The difference between simple and ordinary kriging is that in ordinary we must ensure that the sum of weights is equal to 1. Therefore the following system modification is required:
1
2
3
1
2
3
p
0
0
0
0.98
0.94
0.98
1
0.94
1
w3
w1
w2
1
0.92
0.83
1
0
0
0
1
1
1
0
!
I’ve solved it:
•w1 = 0.32 (aprox)
•W2 = 0.42 (aprox)
•W3 = 0.24 (aprox)
There is another value but it’s not used to calculate the kriged value.
So to get the kriged value I must do:
푣푝=2.3∗0.32+2.9∗0.42+3.1∗0.24 = 2.68
To achieve ordinary kriging we would have to do this procedure for all cells in our grid.

38. Sequential simulation - uncertainty
38
The first thing you need to know before studying sequential simulation methods is why do we use simulation (stochastic) methods in the first place. Let’s start by an easy example:
Time (x)
Distance (y)
1
2
3
4
1
2
3
4
5
We have a relation between time and distance that is:
푦=푚∗푥 ,푚 푖푠 푐표푛푠푡푎푛푡
The problem is we don’t know with certainty the value of “m”. However we estimate that it is somewhere between 0.7 and 1.3. Which mean that in any given time we have several possibilities of distance. This can be seen on the plot to your left.
This is uncertainty. Mathematical uncertainty since even the retrieving of the model with value “m” is an estimation. This problem is easily solved since the “m” has a constant value throughout time. But what if it doesn’t? What if even doesn’t follow any recognizable function? Perhaps we should try stochastic methods.

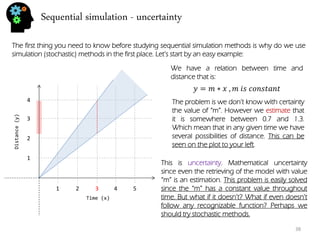
39. Sequential simulation - uncertainty
39
Time (x)
Distance (y)
1
2
3
4
1
2
3
4
5
I’ve done 3 simulations, each with it’s own color. To do this simulation I’ve randomly generated a distance(y) for time=1 that followed the given formula (m = [0.7,1.3]).
푦=푚∗푥 ,푚 푖푠 푛표푡 푐표푛푠푡푎푛푡
Than for time =2 I’ve randomly generated a distance that depends on time=1 (otherwise we could have points outside of “m” value).
I’ve followed this procedure for all time steps and done 3 stochastic simulations.
With three simulations we got a much better sense of uncertainty range for time step 3. In fact if we would want to decrease all this uncertainty we could introduce new data like with time = 3, distance = 2.9. This way the distances that preceded and the ones that followed are going to be conditioned to the distance value of time=3. In fact we could call it hard-data.
Stochastic simulation follows the same concept. Let’s see what parameters are randomized for these procedures.

40. Sequential simulation – random walk
40
1
2
3
4
5
1 m
2.3
2.9
3.1
4.4
4.9
1
2
3
4
5
…
When we do kriging, or any other conventional estimation method, only the hard-data is used to estimate any point on the grid.
For this reason we could estimate the cells from first to last, or from last to first that it wouldn’t make a difference.
In simulation, however, when you estimate (simulate actually) a cell, that cell can be used to simulate the following values. Which means the simulating from the first cell to the last, or from the last to the first does have differences (and probably a lot, depending on the case).
To avoid tendencies in the simulation the cells are simulated considering a random walk which says that the first cell to be simulated is in x,y = 3,9, the second x,y=5,2, and so on… (this is an example). So we actually randomly generated the time when a node is simulated.
1
5
9
6
7
3
8
4
2
3
9
5
8
6
2
4
7
1
5
8
3
4
9
6
1
7
2
Examples of 3 random walks in a 3x3 grid.

41. Sequential simulation – node value as hard value
41
1
2
3
4
5
1 m
2.3
2.9
3.1
4.4
4.9
2.3
2.9
3.1
1
2
3
2.2 m
1.9 m
3.1 m
2.3
2.9
3.1
1
2
3
First value being simulated…
1
2
3
4
5
6
7
8
9
10
11
…
Second value being simulated…
As said before the simulated nodes can be used as hard-data to simulate new ones. The procedure above show the two first nodes simulated with a given random walk (only a few numbers appear).

42. Sequential simulation – probability function generation
42
The random walk is one of two stochastic steps when doing a simulation. When we krige a node, the kriged value won’t be (or probably wont be…) the simulated value. There is something that happens in between. When you do kriging you can retrieve two things. The kriging mean (which we already saw how to calculate) and kriging variance.
So to get the kriging mean on the slide 25 example we would do:
푣푝=2.3−μ푝∗0.45+2.9−μ푝∗0.57+3.1−μ푝∗0.38+μ푝 = 2.75
μ푝= (2.3+2.9+3.1) 3 =2.76
푘푣푝=0.45∗0.92+0.57∗0.83+0.38∗1
1
2
3
1
2
3
p
0
0
0
0.98
0.94
0.98
1
0.94
1
w3
w1
w2
1
0.92
0.83
1
0
0
0
1
1
1
0
!
And the kriging variance would be:
NOTE: this is just for illustration purposes in fact we usually solve the kriging matrix with correlogram and not variogram values.

43. Sequential simulation – probability function generation
43
So if we have a mean and a variance we can build a Gaussian distribution. And inside that distribution randomly generate a value which is more probable around the mean (closer to the mean).
Value range
Probability
Value range
Probability
So I generate a probability from 0 to 1.
An retrieve the respective simulated value.
This is a probability function of Gaussian distribution with given mean and variance.
This is the cumulated probability function of Gaussian distribution with given mean and variance.

44. Sequential simulation - procedures
44
So sequential simulation has two fundamental stochastic steps:
a)The random walk.
b)The random value retrieved from probability distributions.
To do a sequential simulation we would do for all nodes:
1)See which node is to be simulated in the random walk.
2)Search for the neighboring nodes and hard-data.
3)Get the kriged value and kriging variance with those nodes and points.
4)Build a probability function based on the kriged value and kriging variance.
5)Generate a probability and retrieve the value that corresponds with that probability.
Point 4 is an important point because the main differences between procedures of sequential simulation are here. We will see two types of procedures: Sequential Gaussian Simulation and Direct Sequential Simulation. They’re almost identical except in the way they build the probability distribution function.

45. Sequential simulation – Sequential Gaussian Simulation
45
To do sequential gaussian simulation we must do a transformation to our variable distribution, a gaussian transformation, which means transforming the real values into gaussian values. From this point on we would proceed with the normal sequential simulation procedure:
1)See which node is to be simulated in the random walk.
2)Search for the neighboring nodes and hard-data.
3)Get the kriged value and kriging variance with those nodes and points.
Here in point 4) we would use the mean and variance kriging to build a local gaussian distribution. And from that distribution we would retrieve our simulated value.
Since all values simulated are from a gaussian transformation in the end we would have to transform all simulated gaussian values into normal values. Meaning we would do the exact opposite of the first step.
Sequential Gaussian Simulation assumes a Gaussian behavior for variables and may have problems when this is far from truth. It is still widely used although another algorithm was developed to avoid doing the gaussian transformation and instead doing a procedure which, while still using Gaussian distributions, is much closer to the real data. We call it Direct Sequential Simulation.

46. Sequential simulation – Direct Sequential Simulation
46
Equivalent Gaussian interval
Sampled interval in real data
In Direct Sequential Simulation we would do the common procedure for sequential simulation and than when getting a kriging mean and variance we would convert that interval (in real distribution) into a Gaussian distribution. From the Gaussian interval we would build a local Gaussian function and randomly generate a probability there. That probability has an equivalent in the global Gaussian distribution. And the global as an equivalent in the real distribution. This would be our final simulated value.
It is important to use Gaussian distributions to ensure that the values closer to the mean are more probable, and values further less probable. If we didn’t do this we would not have any guarantee that the variogram would be replicated in the simulation (the input variogram ellipsoid).
Sequential simulations usually reproduce both the distribution of the real data (can be seen on a histogram for example) and the input variogram (can be seen on a mesh variogram). Also usually (depending on the procedure), the limits of the data (minimum and maximum) remain the same.

47. Simulation post-processing – getting mean and variance
47
Simulation 1
Simulation 2
Simulation 3
Mean of simulations
+
+
=
3
…
…
…
…
Variance of simulations
…
…
…
…
=
3
-
(
)
2
(
-
)
2
-
)
2
+
+
(
Since we have a set of simulations for the same case study than we have a distribution for each node. This means we can take any statistical parameter from that node distribution. The more common, however, are mean and variance.

48. Co-located co-simulation – When to use…
48
Sometimes we have to variables that are correlated to each other:
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
Iron_content (we use this…)
Organic_content (to estimate this…)
If so we can measure that correlation and retrieve a number. If we have an image we know has little or less uncertainty than the correlated variable we intend to estimate than we could use that image as a secondary variable and estimate the primary variable with co-located co-kriging methods.
That said let’s see how to perform this in a stochastic sequential simulation (doing, therefore, co-located co-simulation).
(using this linear correlation)

49. Co-located co-simulation – How to do…
49
2γℎ=퐸푍푥−푍푥+ℎ2
γℎ=퐶0−퐶(ℎ)
,푏푒푖푛푔 푓푢푛푐푡푖표푛 퐸 푡ℎ푒 푒푥푝푒푐푡푒푑 푣푎푙푢푒 (푚푒푎푛)
,푏푒푖푛푔 퐶0 푡ℎ푒 푠푖푙푙 푎푛푑 퐶ℎ 푡ℎ푒 푐표−푣푎푟푖푎푛푐푒
ρℎ= 퐶(ℎ) 퐶(0)
,푏푒푖푛푔 ρℎ 푡ℎ푒 푐표푟푟푒푙표푔푟푎푚
So far we’ve been dealing directly with the variogram value in the kriging matrix but actually normally we use correlogram value (or co-variance with sill =1). Let’s see how to calculate the correlogram from the variogram.
Subtracting the variogram value to the sill will give use the co-variance value. The co- variance divided by the sill will give us the correlogram. Since the sill is 1 for out study case the correlogram equals the co-variance. The difference in a plot would be:
Variogram
Co-variance or correlogram
Correlation = 1
Correlation = 0

50. Co-located co-simulation – How to do…
50
So if we would assume the study case from slide 25 (actually the kriging matrix from slide 42 in simulation) and we would want to do co-simulation, than we should have a secondary image and correlation for that node.
2.3
2.9
3.1
1
2
3
2.2 m
1.9 m
3.1 m
푐푐=0.7 푎푛푑 푉푠 푓표푟 푠푒푐표푛푑푎푟푦 푣푎푙푢푒
So our kriging matrix should be this one (notice the variogram values were transformed into correlogram and the changes that appear in purple). The correlation value is cc=0.7.
1
2
3
1
2
3
p
1
1
1
0.02
0.06
0.02
0
0.06
0
w3
w1
w2
0
0.08
0.17
cc
cc*0.08
cc*0.17
cc*0
1
1
1
1
ws
1
1
1
1
!
1
0.08
0.17
0
1
1
s
s

51. Co-located co-simulation – How to do…
51
푣푝=2.3−μ푝∗0.10+2.9−μ푝∗0.15+3.1−μ푝∗0.07+푉푠−μ푝∗0.74+μ푝
W = 0.10812852, 0.15659974, 0.07054397, 0.74175945, (!)-0.07703169
μ푝= (2.3+2.9+3.1) 3 =2.76
We know the weights and the value Vs = 2.7. So the kriged value is:
푣푝=2.3−μ푝∗0.10+2.9−μ푝∗0.15+3.1−μ푝∗0.07+2.7−μ푝∗0.74+μ푝=2.71
Notice we use the secondary image value as a sample which has a weight. There is another important point thought. We must ensure the secondary variable has the same range as the primary variable. For this reason we must, before anything else, do a linear transformation for the secondary variable to have the same minimum and maximum as the primary. You can do it using this formula:
푉푠= 푉푠−min푉푠∗(max푉푝−m푖푛푉푝) (max푉푠−m푖푛푉푠) +m푖푛푉푝
Vs is the secondary variable. Vp is the primary.

52. Sequential indicator simulation – categorical data
52
Until now we’ve used only continuous variables but sometimes it’s useful to estimate and/or simulate discrete variables which we commonly call categorical because they’re largely based on categories. One possible example would be the estimation of the area covered by a specific kind of vegetation. In this case you would have two categories: covered, and uncovered. You can also have the same example but with more than one type of cover (different types of vegetation). The first case would be binary (or indicator, I’ll explain latter why), the second multiphasic (multiple phases or categories).
The example on your left shows a map which has two colors, meaning two different categories. It is likely a simulation of dissemination of some kind of phenomena (either exists or not) because the blue color (or whatever that may be) seems to fill the entire study area as opposition of the orange which is quite more scattered.

53. Sequential indicator simulation – indicator function
53
The first thing you need to understand when developing with indicator algorithms is that each class or category is a variable. A variable whose nature is the probability of the category itself. This means that for every sample that exists we have two possible outcomes: either probability 1( category exists in that position) or 0 (category does not exist on that position).
1
2
3
4
Categorical_project 5 X Y Z Category_1 Category_2 Category_3 Category_4 1 2 0 1 0 0 0 2.8 1.6 0 0 0 1 0 2 2 0 0 1 0 0 2.4 0 0 0 0 0 1
This example of file (whose format will depend on the software) show the real nature of the information in that data. In each of the samples one category has probability 1, all the others 0.
퐼퐶푥≔ 1,푥∈퐶 0,푥∉퐶
So each category has the following function. We call this function indicator function because it either gives us 1 in “x” belong to the category “C” or 0 if it does not.

54. Sequential indicator simulation – indicator variogram
54
We usually do variograms for continuous variables but a set of “n” categories are “n” different variables. So we need to do a variogram for each of those variables.
2γ퐼푧푥,푥+ℎ=퐸(퐼푧푥−퐼푧(푥+ℎ)2)
For the case study in the previous slide we would have four different indicator variograms because of the four different categories. The correct procedure to simulate or krige indicator variables is using all of the variogram ellipsoids (for the several categories) and use them to build the kriging matrix. However sometimes a multiphasic variogram is used which is built by the sum of the variograms of all variables. Other times a mean approximate is used. Depends largely on the intended result.
If the variables only have between 1 and 0 values you can probably guess the variogram model will be something like a probability model for that specific category.
Think about this. Imagine that we have four categories, therefore 4 variogram models and we intend to use a multiphasic to do simulation. The problem is that one of categories is so rare that using it’s variogram for the multiphasic could endanger the correct simulation of other categories. I could consider building a multiphasic with all categories except that one…

55. Sequential indicator simulation – how to do…
55
Assuming you have the all the variogram ellipsoids or simply the multiphasic we pretty much build the kriging matrix as in the normal continuous sequential simulation as show in slide 42.
Once you have the weights you need to multiply them by each of the samples values meaning for sample 1 in slide 53: 1;0;0;0
This means you’ll have a kriged mean for each of the samples (ex: 0->0.3 , 1->0.2, 2-> 0.4, 3-> 0.1) meaning a probability for each category. So know we can build the our distribution (we actually normalize these values first by dividing them by their total sum):
0.1
0.3
0.6
0.9
1
0
1
2
3
So I generate a probability from 0 to 1.
An retrieve the respective simulated category.
Notice that some categories, because they have a bigger probability are more likely to be generated.

56. Indicator simulation post-processing – most likely and entropy
56
Simulation 1
Simulation 2
Simulation 3
We’ve seen this before for continuous variables. Right now however we have 3 simulations. And for teach of the nodes we may have 3 different categories. The most likely value is the category, for each node, that appears more often (it’s actually the mode). Entropy gives us a level of uncertainty based on an entropy.
Most likely value
…
…
…
…
Entropy
…
…
…
…
푒=− 푝푘∗log푝푘
Pk is actually the probability of category k.

57. Stochastic genetic procedures – genetic algorithms
57
Using stochastic simulation for basic parameters uncertainty studies is only one of the possible uses. In fact since stochastic sequential simulations explore multiple solutions to a single parameterization we can use it in optimization algorithms by genetic approach.
Genetic algorithms is the name given to a procedure which relies on different generations, each created using the previous, and evaluated through an objective function (quantifying fitness, if using the original expression). Let’s see a general illustration for a genetic procedure.
Generation 0
Fitness evaluation
Best fit individuals for Generation 0
Generation 1 (created from best individuals in generations 0)
Fitness evaluation
Best fit individuals for Generation 1
Generation 2 (created from best individuals in generations 1)
So we decide many parameters like the number of individuals for generations, the objective function that evaluates fitness, the number of generations, etc.

58. Stochastic genetic procedures – global stochastic inversion
58
Global stochastic inversion (GSI) is a type of genetic approach to build a model of acoustic impedance by evaluating the fitness of each generation using an objective function which compares the real seismic data to the synthetics seismic data from each generation. The best locations (more similar to the real data) are used to create the individuals for the next generation.
Simulation “n”
Simulation 2
Simulation 1
Simulation 0
Generation 0 uses hard-data to do simulation
Fitness evaluation (comparing simulated data with real data)
Best image from generation 0
Simulation “n”
Simulation 2
Simulation 1
Simulation 0
Generation 1 uses hard-data and best image to do co- simulation
So how does the evaluation actually occurs? And what is a best image?

59. Stochastic genetic procedures – convolution
59
On the left you have the real seismic (profile). On the right you have a simulation of acoustic impedance (the same profile).
So how do we compare the real seismic data with the simulation of acoustic impedance? Well, we actually build a synthetic seismic from the simulation using a procedure called convolution.
To do a convolution we need a wavelet which is usually built using the real well log data (acoustic impedance) and the seismic data in the same location. Let’s see how a wavelet looks like.

60. Stochastic genetic procedures – convolution
60
-4.000 588.006 -3.000 -567.287 -2.000 -2130.426 -1.000 -3632.075 0.000 -4242.837 1.000 -3562.341 2.000 -1889.319 3.000 -104.545 4.000 1097.485
0
1
2
3
4
-1
-2
-3
-4
To the left you have a plot of a wavelet. To the right you have an example of a wavelet file (not the same example as on the left).
The X-axis gives us the depth step, the Y-axis the wavelet magnitude.
Wavelets can transform reflection data into seismic data. But from this point we still need to calculate the reflections from the acoustic impedance simulation. We do this for each vertical trace in simulation.
푅푖= (퐴퐼푖+1−퐴퐼푖) (퐴퐼푖+퐴퐼푖+1)
So for every trace in every depth position “i” we calculate a reflectivity using the following formula (and from this point on we have a reflectivity image for our simulation):
i
i+1

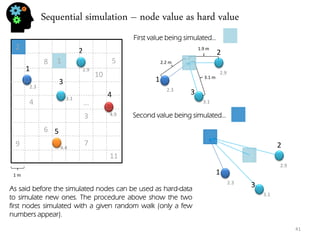
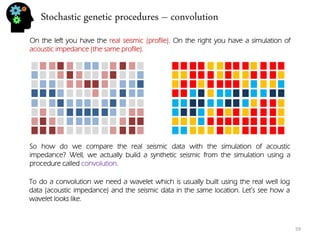
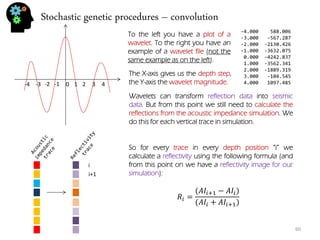
61. Stochastic genetic procedures – convolution
61
0
1
2
3
4
-1
-2
-3
-4
=
+
.
wavelet
Using the reflectivity image, for every trace, in every depth position “i“, we calculate a value which is the result of convolution. Notice however that if I start in position i=0 (first value in trace) the calculation will be done not only in position “i“ but also in the interval [i-wavelet up size, i+wavelet down size]. So the same point is going to get involved in multiple operations. For instance if the wavelet up size =3 than i=0 will be transformed when calculating on position i=0, i=1,i=2,i=3 because the interval for that trace is [i-3,i+3] = [0,6] if i=3. If i=4 the interval is [1,7] and i=0 is no longer considered. So we can say that the calculation of each position happens following this procedure:
푆푖= 푅푖+푅푖∗푊푖
Notice however that, although I’m saying Si is a seismic value, that can only be true when the trace is fully convolved. Ri would be reflectivity, Wi is wavelet value for position i.

62. Stochastic genetic procedures – Objective function
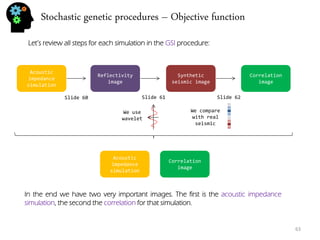
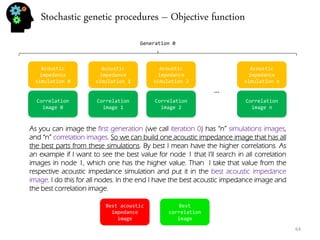
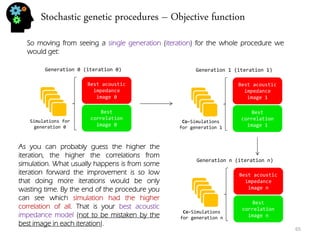
62
So now that we have a synthetic seismic and the real seismic we can compare both by doing the correlation between them (the following is Pearson correlation, others can be used).
ρ= 퐸[푋−μ푥푌−μ푦] σ푋σ푌
푋= 푥푖 ,푌=푌푖
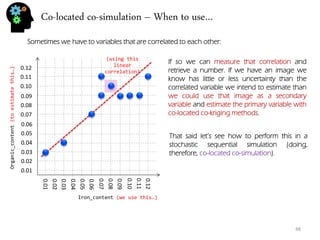
The correlation is done using something we call layer map. The layer map is a instruction (stochastically generated for each generation) for the series used in the correlation so for instance:
=
Layer 1 with a series of 3 values
Correlation trace
Layer 2 with a series of 5 values
The correlation is done for each trace using the series defined in the layer map. In the end we have a correlation image for the acoustic impedance simulation.

63. Stochastic genetic procedures – Objective function
63
Let’s review all steps for each simulation in the GSI procedure:
Acoustic impedance simulation
Reflectivity image
Synthetic seismic image
Correlation image
Slide 60
Slide 61
Slide 62
We use wavelet
We compare with real seismic
Acoustic impedance simulation
Correlation image
In the end we have two very important images. The first is the acoustic impedance simulation, the second the correlation for that simulation.

64. Stochastic genetic procedures – Objective function
64
Acoustic impedance simulation 0
Correlation image 0
Acoustic impedance simulation 1
Correlation image 1
Acoustic impedance simulation 2
Correlation image 2
Acoustic impedance simulation n
Correlation image n
…
Generation 0
As you can image the first generation (we call iteration 0) has “n” simulations images, and “n” correlation images. So we can build one acoustic impedance image that has all the best parts from these simulations. By best I mean have the higher correlations. As an example if I want to see the best value for node 1 that I’ll search in all correlation images in node 1, which one has the higher value. Than I take that value from the respective acoustic impedance simulation and put it in the best acoustic impedance image. I do this for all nodes. In the end I have the best acoustic impedance image and the best correlation image.
Best acoustic impedance image
Best correlation image

65. Stochastic genetic procedures – Objective function
65
So moving from seeing a single generation (iteration) for the whole procedure we would get:
Generation 0 (iteration 0)
Best acoustic impedance image 0
Best correlation image 0
Simulations for generation 0
Generation 1 (iteration 1)
Best acoustic impedance image 1
Best correlation image 1
Co-Simulations for generation 1
Generation n (iteration n)
Best acoustic impedance image n
Best correlation image n
Co-Simulations for generation n
As you can probably guess the higher the iteration, the higher the correlations from simulation. What usually happens is from some iteration forward the improvement is so low that doing more iterations would be only wasting time. By the end of the procedure you can see which simulation had the higher correlation of all. That is your best acoustic impedance model (not to be mistaken by the best image in each iteration).

66. Template
66

67. Template
67

68. Template
68