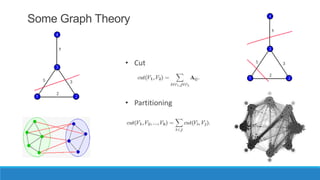
This document discusses using graph-based approaches for gene expression clustering. It describes representing gene expression data as graphs, with genes as vertices and edge weights representing similarity. It covers partitioning graphs into clusters using simple graph partitioning that finds minimum cuts, and spectral graph partitioning that uses the eigenvectors of the graph Laplacian matrix. Spectral partitioning is shown to provide better, more qualitative clusters than simple partitioning. The document provides an overview of key graph theory concepts used in these clustering methods like cuts, partitioning, degrees, and Laplacian matrices.

1. GENE EXPRESSION
CLUSTERING
GRAPH BASED APPROACHES
A P R E S E N T A T I O N B Y GOVIND M (M120432CS)
MTECH COMPUTER SCIENCE AND ENGINEERING
N AT I O N A L I N S T I T U T E O F T E C H N O L O G Y C A L I C U T
govindmaheswaran@gmail.com

2. Clustering and Graph Theory
Using Graphs in
Clustering
Simple Graph Partitioning Outline
Spectral Graph Partitioning
Conclusion

3. Clustering
• Process of Grouping a set of data objects, in terms of similarity
• Same Cluster => Similar Objects and vice versa.
• Widely used in data mining, market analysis etc.
• Used to make sense of Bioinformatics data.
• Two major purposes, in Bioinformatics
• Find properties of genes ( Relationship among genes, deduce the functions of genes etc)
• Predict more relevant factors (eg. Clustering cancerous and non cancerous
genes, finding the effect of a medication)

4. Graphs
• Data Structure
• Used in multiple domains
• Key Terms
• Edge
• Vertex
• Weighted Graph

5. Some Graph Theory
• Cut
• Partitioning

6. Clustering using Graphs
Involves 3 steps
1. Preprocessing
◦ Convert data set into a graph
◦ Using Adjacency matrix and Degree Matrix representation
◦ Similarity between nodes can be taken as the weight of an edge.
2. Partitioning
◦ Partition the graph
3. Clustering
◦ Repeat until required number of clusters are obtained
◦ Alternatively, extra iterations followed by joinings may also be implemented.

7. Simple Graph Partitioning
• Weight of an edge = Similarity between the nodes
• Find Minimum Cut
• Edge Value decreases, cluster differs

8. Simple Graph Partitioning : The
Algorithm
Input : Graph G<V,E>, Number of Clusters k
Output: Cluster of Graphs
Repeat k-1 times
Low_val = infinity
For each edge e of the graph
Calculate Cut_Cost, cost of a CUT at that edge
if Cut_Cost < Low_val
Low_Val = cut_cost
Cut_Edge = e
Cut at edge e

9. Simple Graph Partitioning (cont..)
• Advantage
• Simple to implement
• Uses the concept of Min Cut.
• Disadvantage
• What about intra-cluster similarity..?

10. Spectral Graph Partitioning
• Is widely used
• Uses Eigen Vectors of Laplacian Matrix
• Recursive algorithm
• Qualitatively Good
• Computationally Better than SGP.

11. Some graph theory…
d1 = 7
• Degree : d2 = 3
d3 = 1
d4 = 0
0 2 5 0
• Affinity Matrix : 0 0 3 0
0 0 0 1
0 0 0 0
7 0 0 0
0 3 0 0
• Degree Matrix 0 0 1 0
0 0 0 0
-7 2 5 0
0 -3 3 0
• Laplacian Matrix : 0 0 -1 1
0 0 0 0

12. Some more Graph Theory…
• Spectrum : Eigen vectors, arranged in the order of magnitude of eigen values.
• Eigen Values of Graphs
• Calculated as Eigen values of Laplacian matrix of the graph
• Corresponidngly Eigen Vectors too
• Fiedler Theorm
• Correlation b/w eigen vectors and graph properties
• Principal Eigen Vectors. Kth Principal Eigen Vector.
• Principal Eigen Vector : Centrality of Vertices
• 2nd Principal Eigen Vector : algebraic connectivity
• Called Fiedler Vector
• Matrix of positive and negative values
• Partition is decided by the Sign of the value.

13. Spectral Graph Partitioning
Input : Graph G<V,E>
Output: Graphs G1< V1,E1>, G2< V2,E2>
Create the Laplacian Vector L, of the Graph G.
Calculate the Fiedler Vector F
for each vertex vi in G
if F[i]>0
V1.append(v)
else
V2.append(v)

14. SPG : Example
2nd Principal Vector = <0.415, 0.309, 0.069, −0.221, 0.221, −0.794>
2nd Principal Vector = <0.415, 0.309, -0.190, 0.169, >
(of 1235)

15. SGP : Bipartitioning Method
(contd.)
• Recursive Algorithm
• Although better than Simple Graph Partitioning, not optimum
• Multiple times bipartitioning.
• Can be improved by Multipartitioning
• Use more eigen vectors.

16. Conclusion
• Clustering is Based on simple concepts of graph theory
• Optimal results (Spectral methods)
• Can give better performance than traditional clustering.
• Preprocessing overhead.

17. References
1. Yanhua Chen; Ming Dong; Rege, M., "Gene Expression Clustering: a Novel Graph Partitioning
Approach," Neural Networks, 2007. IJCNN 2007. International Joint Conference on
, vol., no., pp.1542,1547, 12-17 Aug. 2007, doi: 10.1109/IJCNN.2007.4371187
URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4371187&isnumber=4370
891
2. Hagen, L.; Kahng, A.B., "New spectral methods for ratio cut partitioning and clustering,"
Computer-Aided Design of Integrated Circuits and Systems, IEEE Transactions on
, vol.11, no.9, pp.1074,1085, Sep 1992, doi: 10.1109/43.159993
URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=159993&isnumber=4190
3. Donath, W.E.; Hoffman, A.J., "Lower Bounds for the Partitioning of Graphs," IBM Journal of
Research and Development, vol. 17, pp. 420-425, 1973.
4. Pavla Kabel´ıková , “Graph Partitioning Using Spectral Methods”, Thesis, VˇSB - Technical
University of Ostrava, 2006.
5. Chung, F.R.K., "Spectral Graph Theory," American Mathematical Society, 1997.