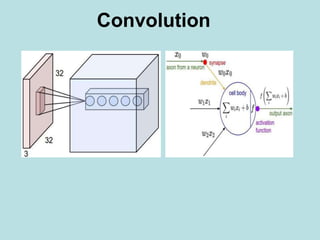
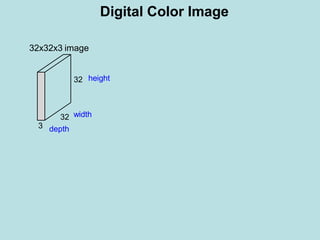
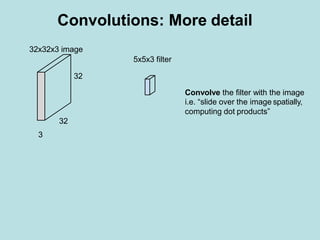
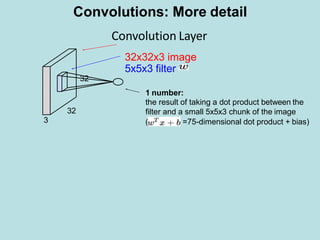
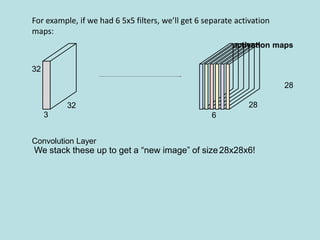
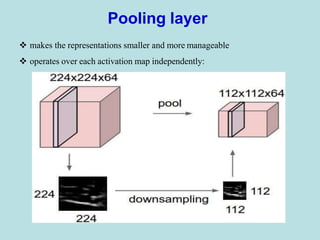
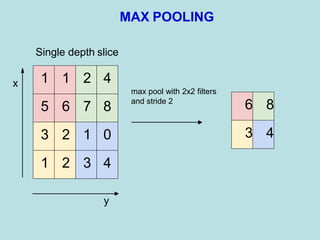
The document discusses deep learning and convolutional neural networks. It provides details on concepts like convolution, activation maps, pooling, and the general architecture of CNNs. CNNs are made up of repeating sequences of convolutional layers and pooling layers, followed by fully connected layers at the end. Convolutional layers apply filters to input images or feature maps from previous layers to extract features. Pooling layers reduce the spatial size to make representations more manageable.

1. Deep Learning
Dr. Baljit Singh Khehra
Professor
CSE Department
Baba Banda Singh Bahadur Engineering College
Fatehgarh Sahib-140407, Punjab, India

2. Convolution


 

M1 N1
N1
f * g (x, y)
f * g (x) 
 
0

   f (,)g(x , y  )
 0 0
 f (,)g(x , y  )dd
f ()g(x )
 f ()g(x )d
2D(continuous, discrete) :
1D(continuous, discrete) : Input
Kernel
Output is
sometimes called
Feature map

3. Convolution

4. 32
3
32x32x3 image
width
height
32
depth
Digital Color Image

5. 32x32x3 image
5x5x3 filter
32
Convolve the filter with the image
i.e. “slide over the image spatially,
computing dot products”
32
3
Convolutions: More detail

6. 32
3
Convolution Layer
32x32x3 image
5x5x3 filter
32
1 number:
the result of taking a dot product between the
filter and a small 5x5x3 chunk of the image
(i.e. 5*5*3 =75-dimensional dot product + bias)
Convolutions: More detail

7. 32
3
activation mapConvolution Layer
32x32x3 image
5x5x3 filter
32
1
28
28
convolve (slide) over all
spatial locations
Convolutions: More detail

8. 32
3 6
28
For example, if we had 6 5x5 filters, we’ll get 6 separate activation
maps:
activation maps
32
28
Convolution Layer
We stack these up to get a “new image” of size28x28x6!

9. Size of Image after Convolution
 Input Image of Size M×N denoted as
 If Number of Filter: NF applied on input image, then Activation Maps will be NF
 Size of each filter is m×n
 Filters are denoted as
 Let stride be s and padding be p
 Then, size of each activation map
),(),(),(
:),(
yxByxGyxR
yxf
fff
),(,..........),,(),,( 21 yxgyxgyxg NF
),(),(),(
.....................................
),(),(),(
),(),(),(
222
111
kjhkjhkjh
kjhkjhkjh
kjhkjhkjh
b
NF
g
NF
r
NF
bgr
bgr
















1
2
1
2
s
npN
s
mpM

10. Example
 Input Image of Size M×N=32×32 denoted as
 If Number of Filter: NF=6 applied on input image, then Activation Maps will be
NF=6
 Size of each filter is m×n=5×5
 Filters are denoted as
 Let stride be s=1 and padding be p=0
 Then, size of each activation map will be 28×28
),(),(),(
:),(
yxByxGyxR
yxf
fff
),(,..........),,(),,( 621 yxgyxgyxg
),(),(),(
.....................................
),(),(),(
),(),(),(
666
222
111
kjhkjhkjh
kjhkjhkjh
kjhkjhkjh
bgr
bgr
bgr












1
1
50*232
1
1
50*232

11. Input Image: 32x32x3
10 5x5 filters with stride (s)= 1,
pad (p)=2
Output volume size: ?
Another Example

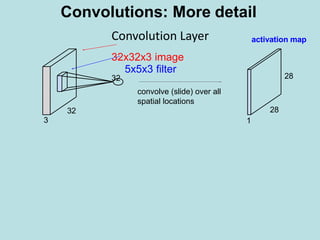
12. Input volume: 32x32x3
10 5x5 filters with stride 1, pad 2
Output volume size:
[(32+2*2-5)/1+1]×[(32+2*2-5)/1+1] = 32×32
spatially, so
32x32x10
Output

13. • 7
• 7x7 input (spatially)
assume 3x3 filter
• 7
A closer look at spatial dimensions:
Convolutions: More detail

14. • 7
• 7x7 input
(spatially)
assume 3x3
filter
• 7
A closer look at spatial dimensions:
Convolutions: More detail

15. • 7
• 7x7 input (spatially)
assume 3x3 filter
• 7
A closer look at spatial dimensions:
Convolutions: More detail

16. • 7
• 7x7 input
(spatially)
assume 3x3
filter
• 7
A closer look at spatial dimensions:
Convolutions: More detail

17. 7
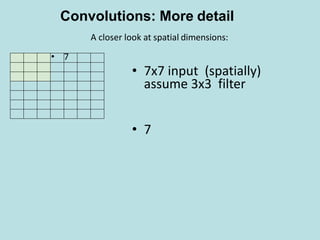
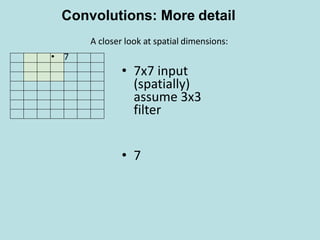
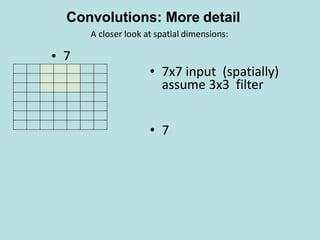
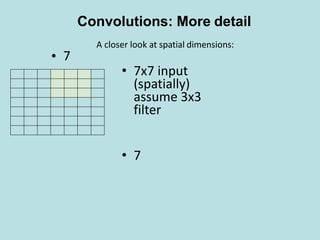
• • 7x7 input (spatially)
assume 3x3 filter
7
A closer look at spatial dimensions:
Convolutions: More detail
[(7+2*0-3)/1+1]×[(7+2*0-3)/1+1] = 5×5 Output

18. 7x7 input (spatially)
assume 3x3 filter
applied with stride
2
7
7
A closer look at spatial dimensions:
Convolutions: More detail

19. 7x7 input (spatially)
assume 3x3 filter
applied with stride
2
7
7
A closer look at spatial dimensions:
Convolutions: More detail

20. 7x7 input (spatially)
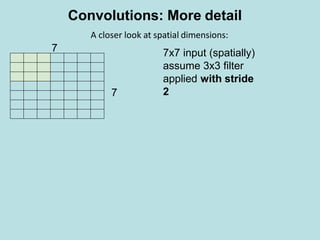
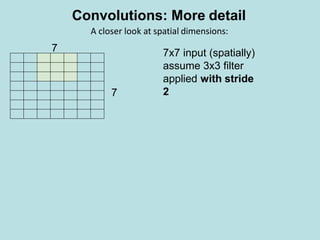
assume 3x3 filter
applied with stride
2
=> 3x3 output!
7
7
A closer look at spatial dimensions:
Convolutions: More detail
[(7+2*0-3)/2+1]×[(7+2*0-3)/2+1] = 3×3 Output

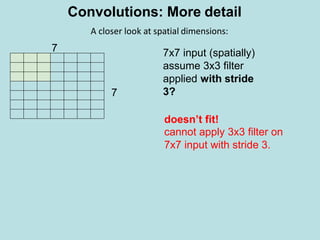
21. 7x7 input (spatially)
assume 3x3 filter
applied with stride
3?
7
7
A closer look at spatial dimensions:
Convolutions: More detail
[(7+2*0-3)/3+1]×[(7+2*0-3)/3+1] = [4/3+1]×[4/3+1] =2.33×2.33

22. 7x7 input (spatially)
assume 3x3 filter
applied with stride
3?
7
7
A closer look at spatial dimensions:
doesn’t fit!
cannot apply 3x3 filter on
7x7 input with stride 3.
Convolutions: More detail

23. In practice: Common to zero pad the border
0 0 0 0 0 0
0
0
0
0
e.g. input 7x7
3x3 filter, applied with stride 1
pad with 1 pixel border => what is theoutput?
Convolutions: More detail
[(7+2*1-3)/1+1]×[(7+2*1-3)/1+1] = 7×7 Output

24. In practice: Common to zero pad the border
e.g. input 7x7
3x3 filter, applied with stride 2
pad with 1 pixel border => what is theoutput?
0 0 0 0 0 0
0
0
0
0
Convolutions: More detail
[(7+2*1-3)/2+1]×[(7+2*1-3)/2+1] = 4×4 Output

25. In practice: Common to zero pad the border
0 0 0 0 0 0
0
0
0
0
Convolutions: More detail
e.g. input 7x7
3x3 filter, applied with stride 3
pad with 1 pixel border => what is theoutput?
[(7+2*1-3)/3+1]×[(7+2*1-3)/3+1] = 3×3 Output

26. Preview: ConvNet is a sequence of Convolution Layers, interspersedwith
activation functions
32
32
3
28
28
6
CONV,
ReLU
e.g. 6
5x5x3
filters
Convolutions: More detail

27. RELU Activation Function






0
00
)(
zifz
zif
zR

28. Preview: ConvNet is a sequence of Convolutional Layers, interspersed with activation
functions
32
32
3
CONV,
ReLU
e.g. 6
5x5x3
filters
28
28
6
CONV,
ReLU
e.g. 10
5x5x6
filters
POOL
Andrej Karpathy
….
10
24
24
Convolutions: More detail

29. Pooling layer
 makes the representations smaller and more manageable
 operates over each activation map independently:

30. 1 1 2 4
5 6 7 8
3 2 1 0
1 2 3 4
Single depth slice
x
y
max pool with 2x2 filters
and stride 2
6 8
3 4
MAX POOLING

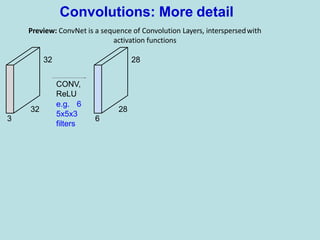
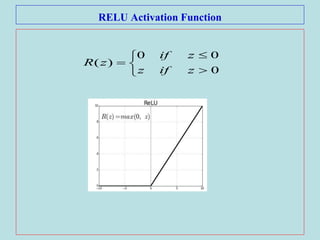
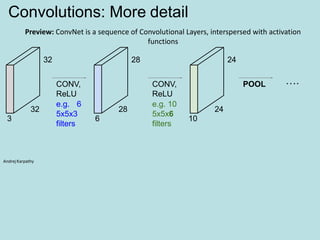
31. [(CONVRELU)*NPOOL]*MFC
N: up to 5
M is Large
FC: Contains neurons that connect to the
entire input volume, as in ordinary Neural
Networks
General Architecture of CNNs

32. Example to recognize Car from Car, truck,
airplane, ship and horse