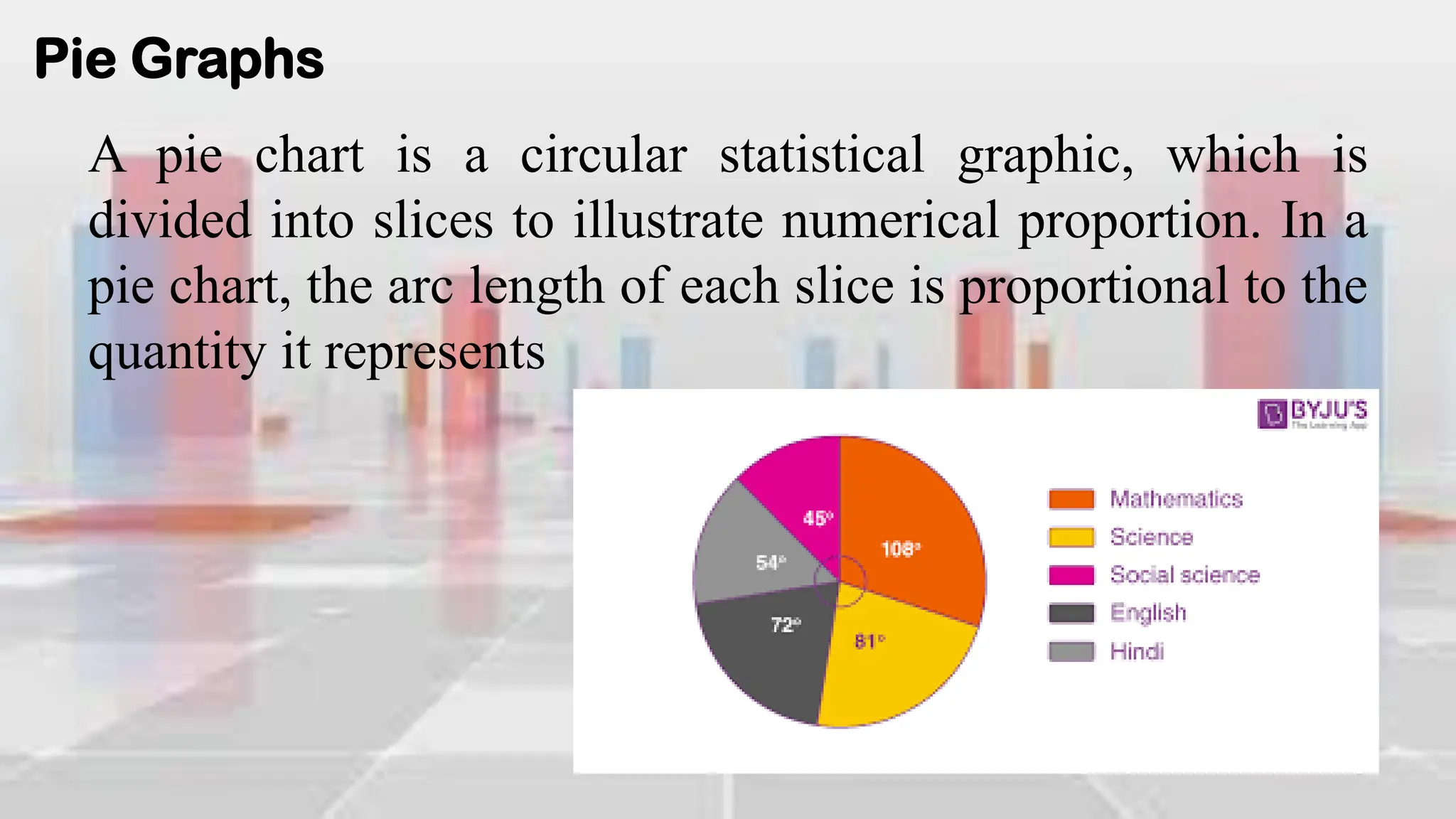
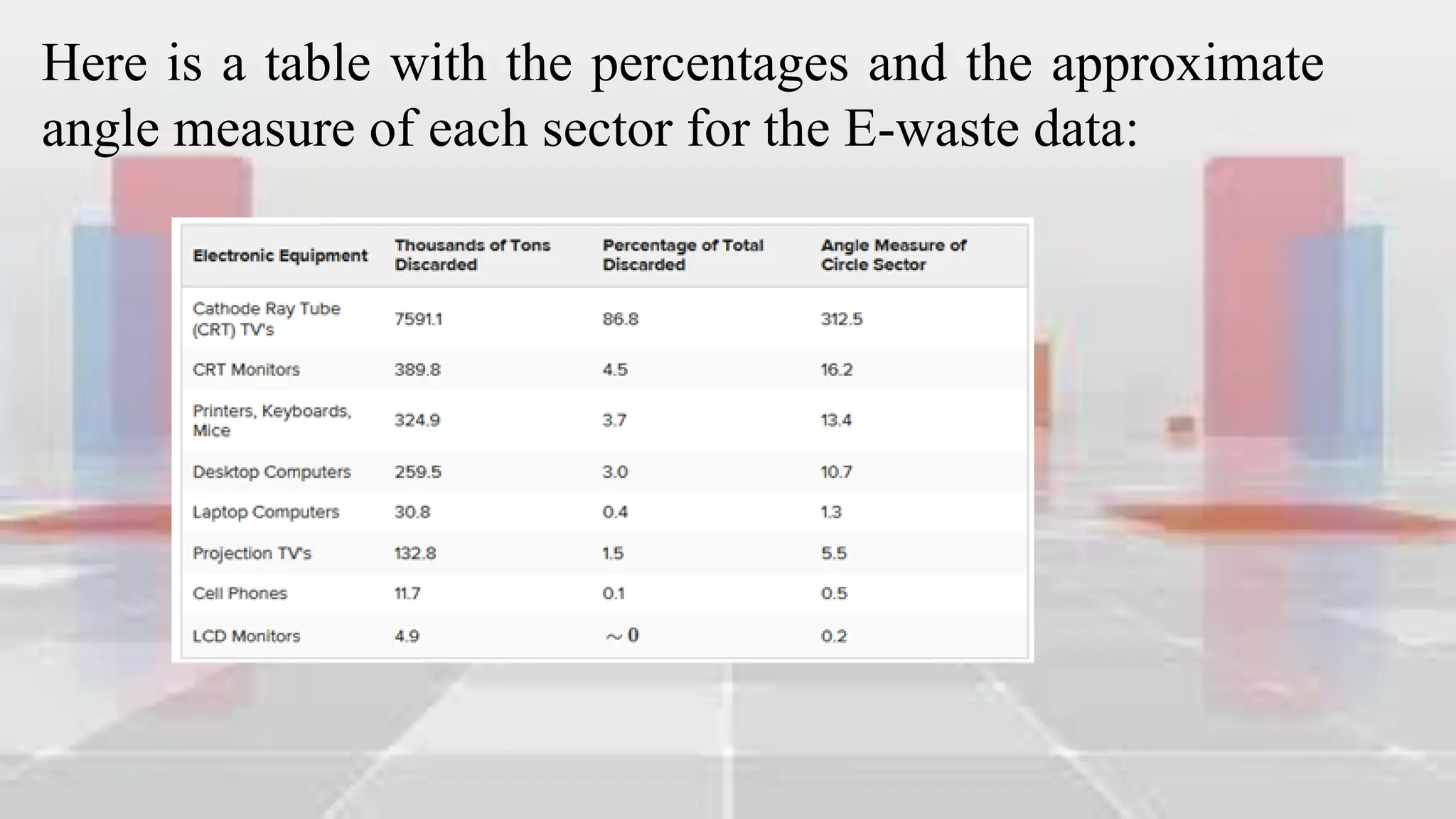
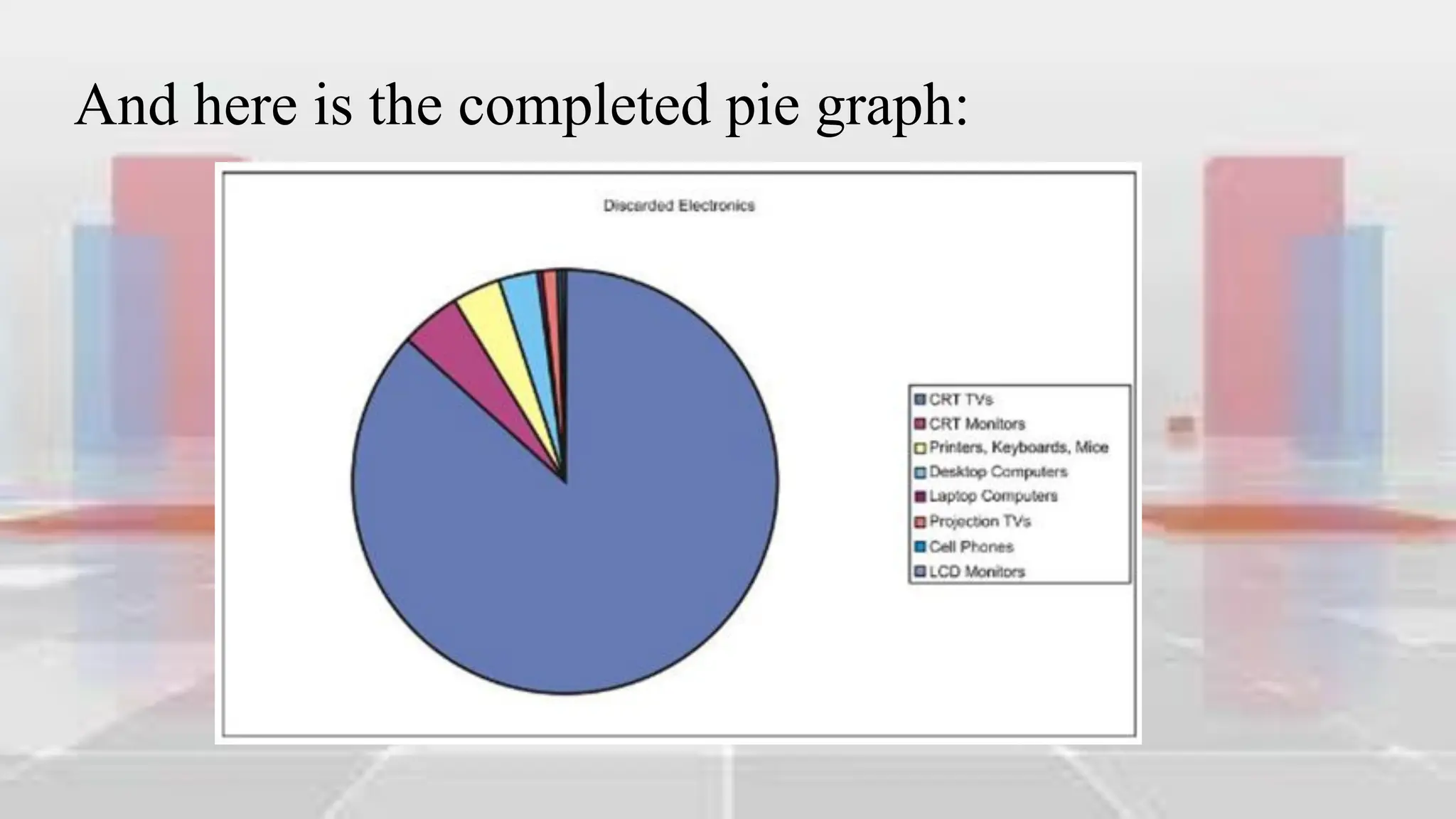
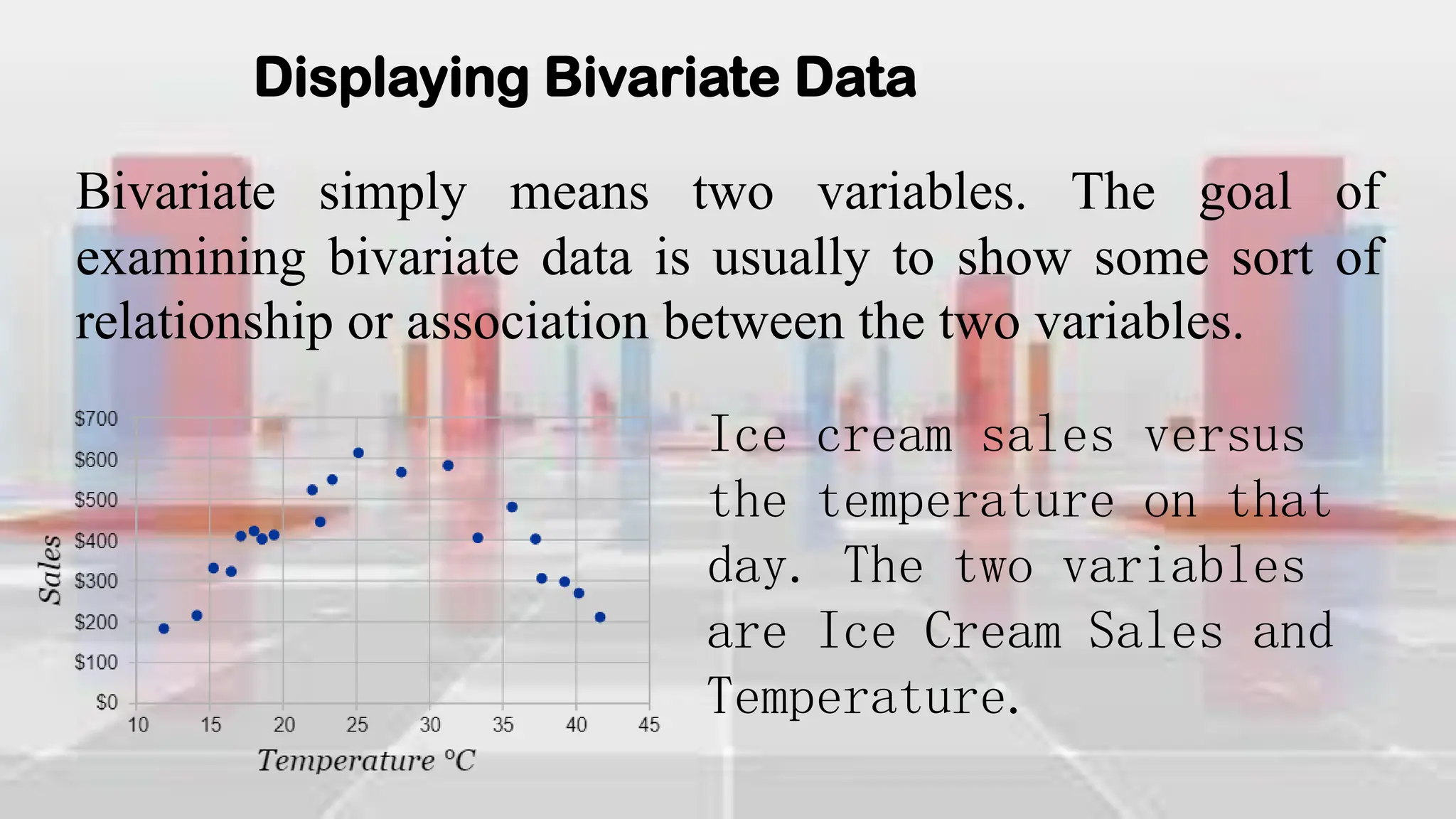
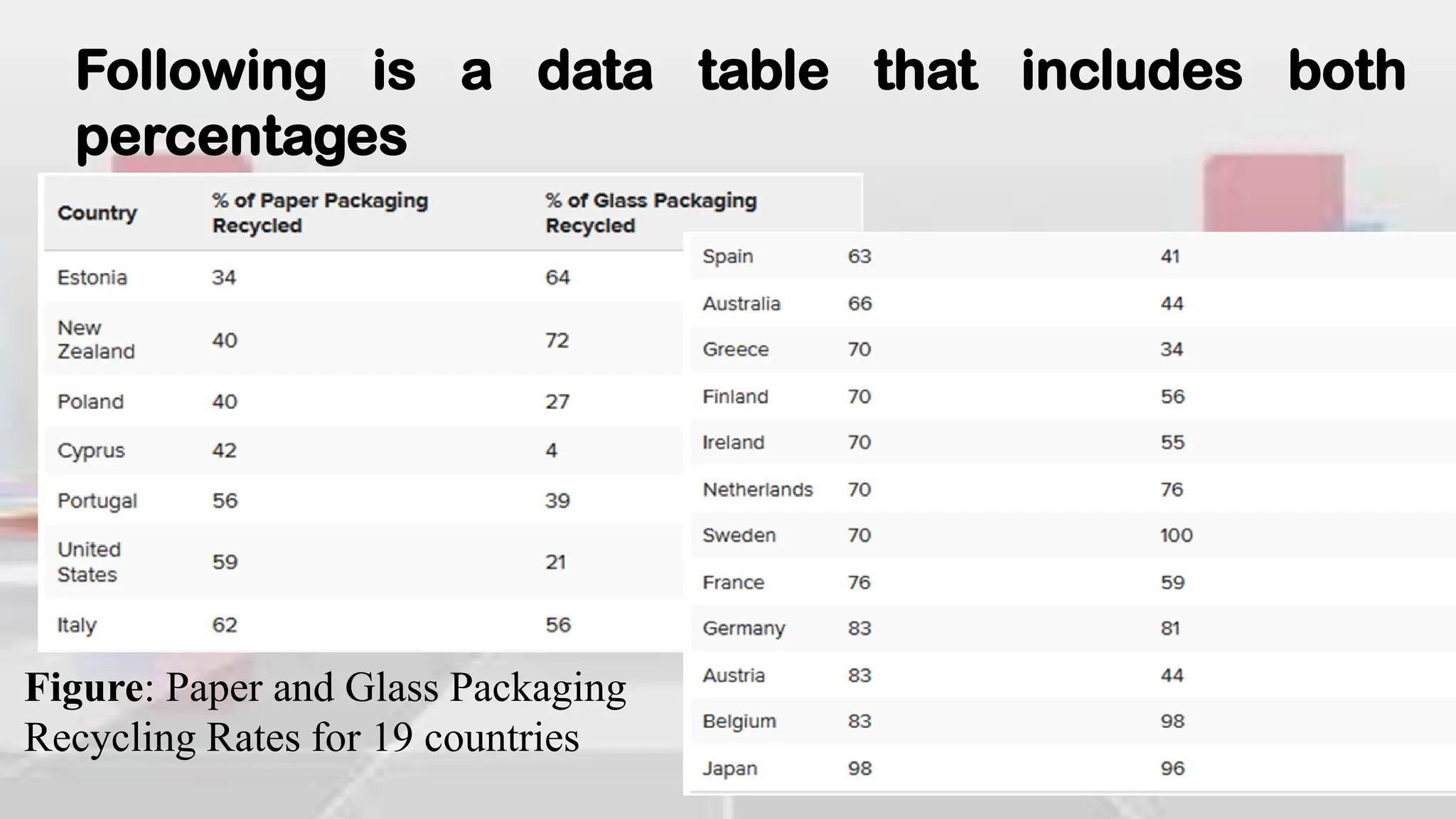
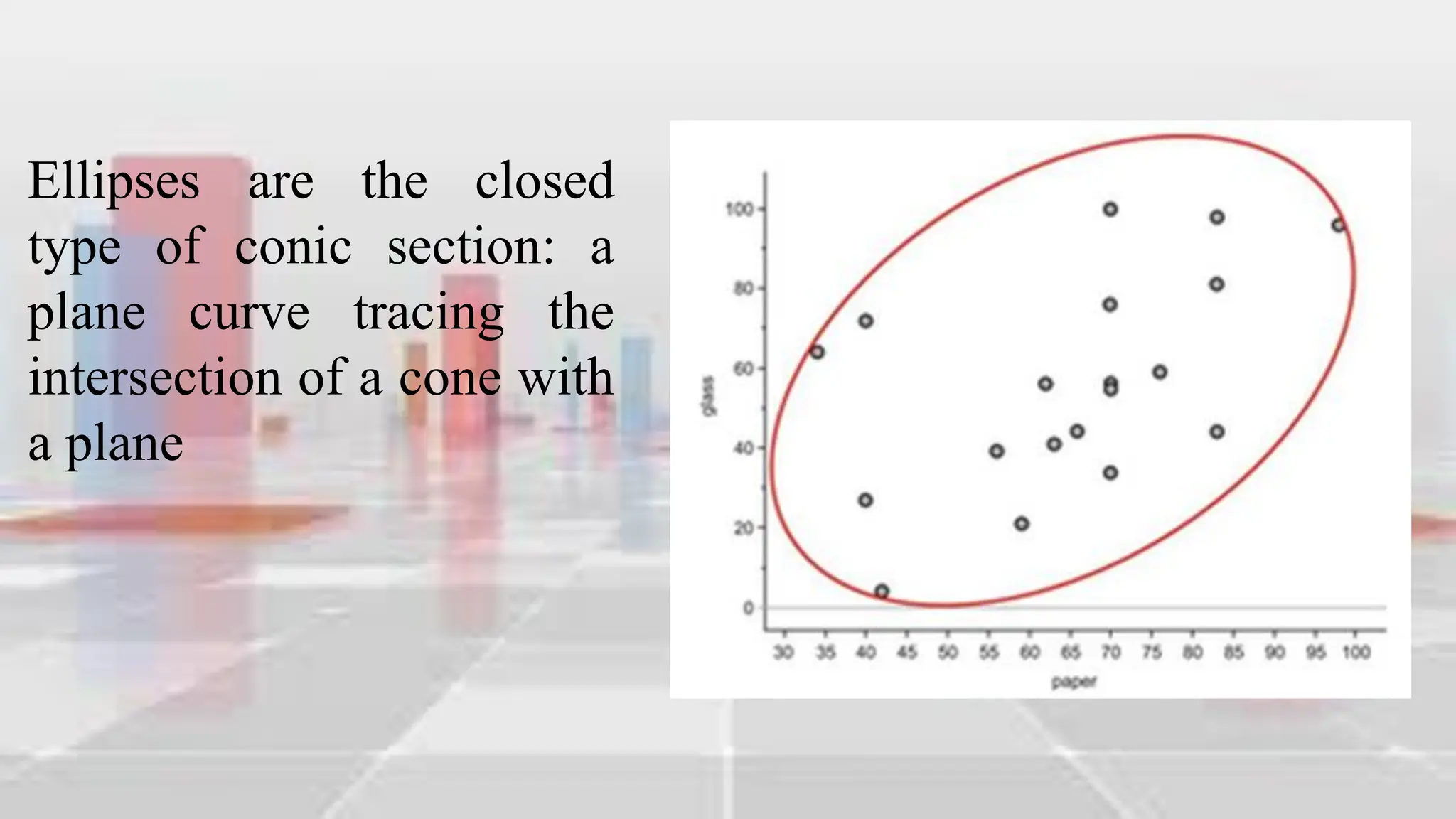
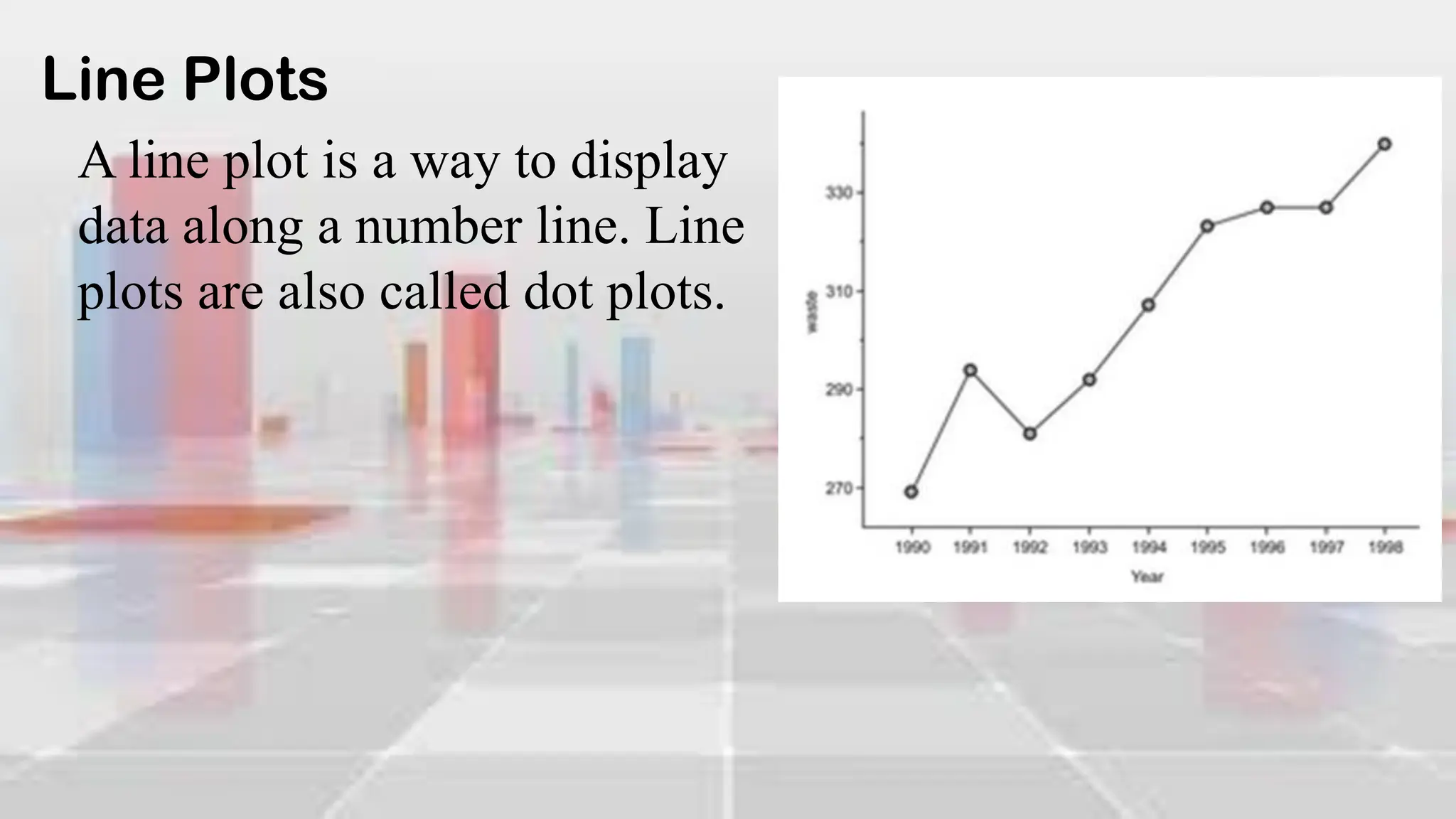
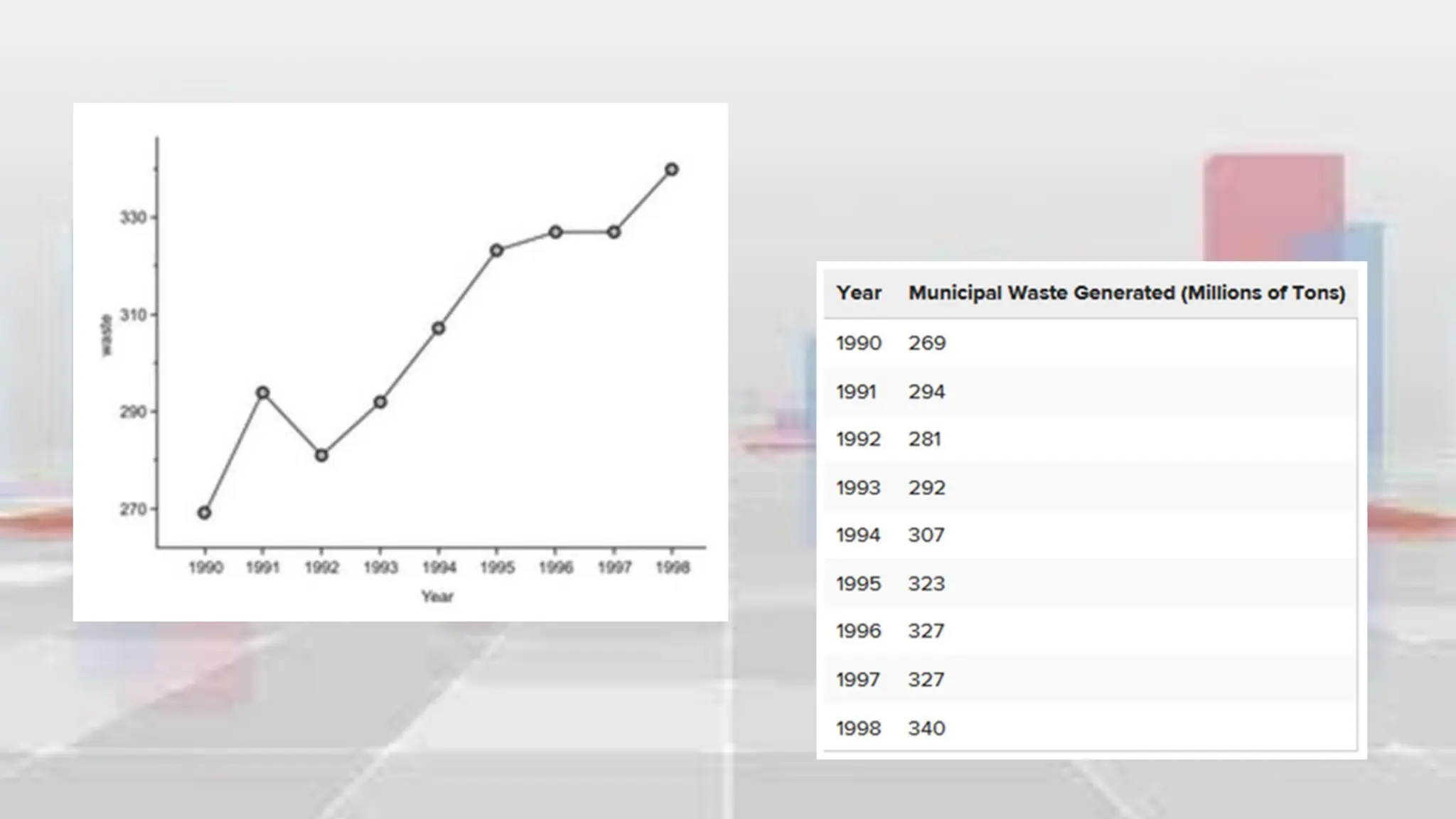
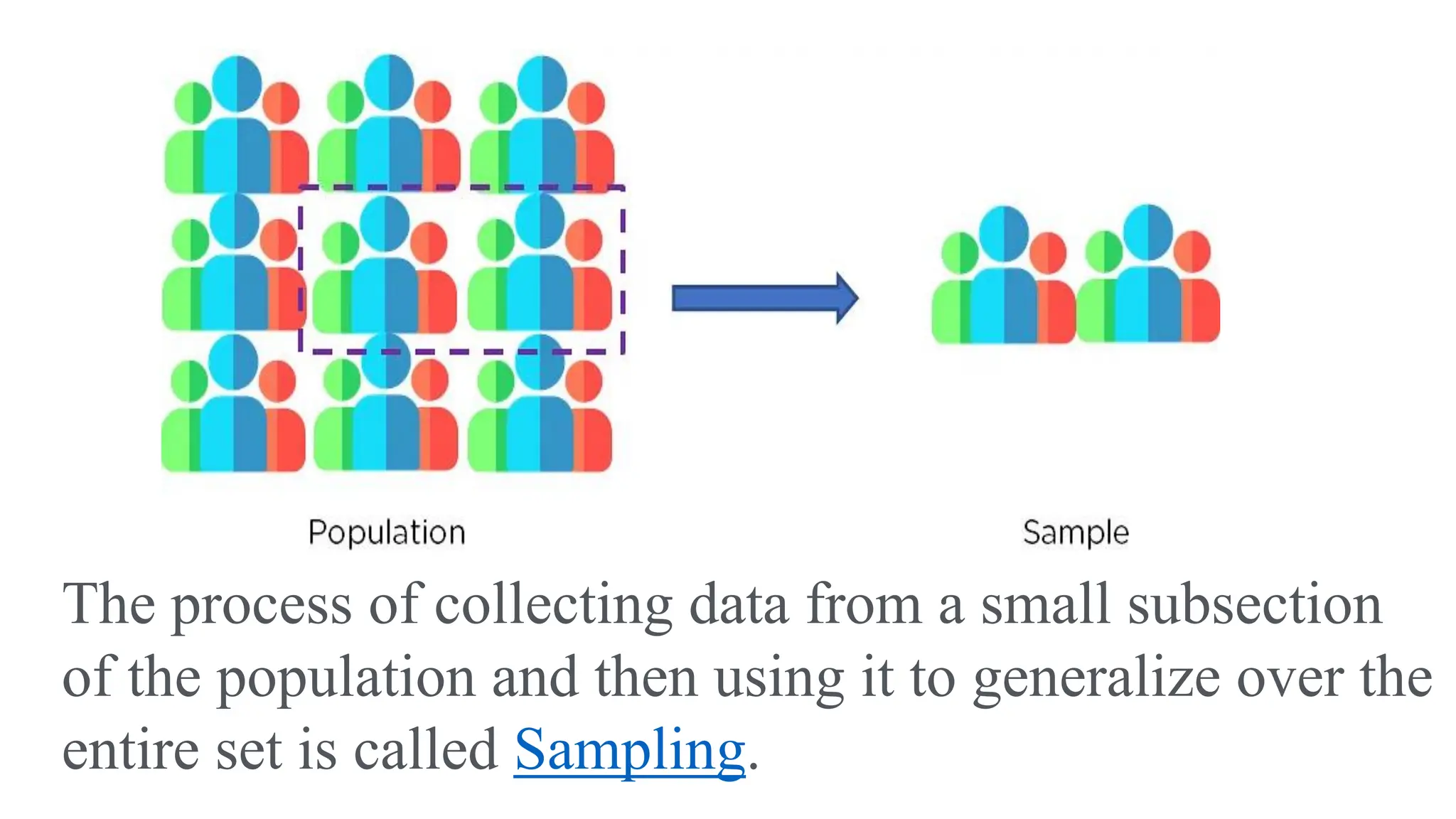
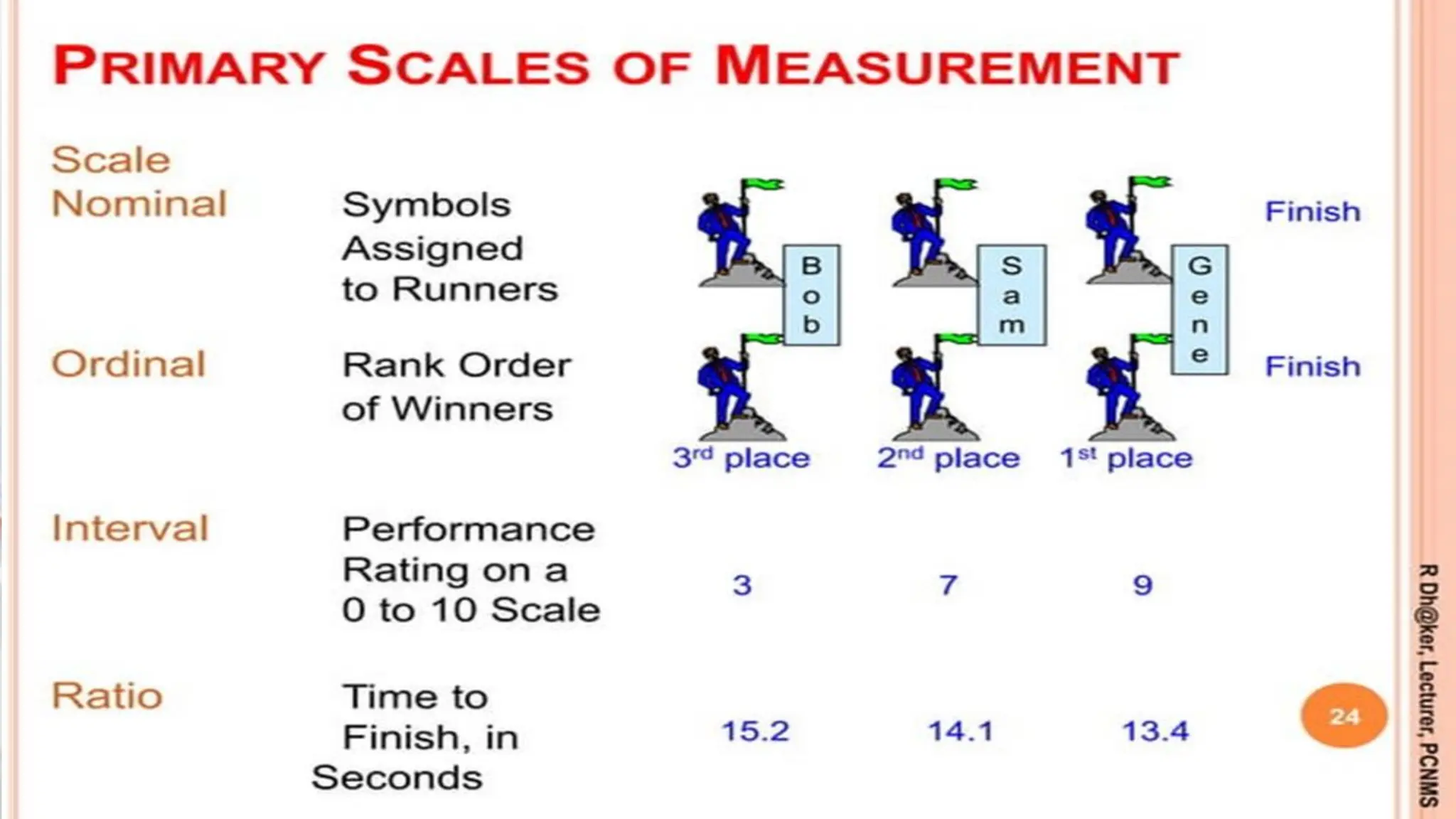
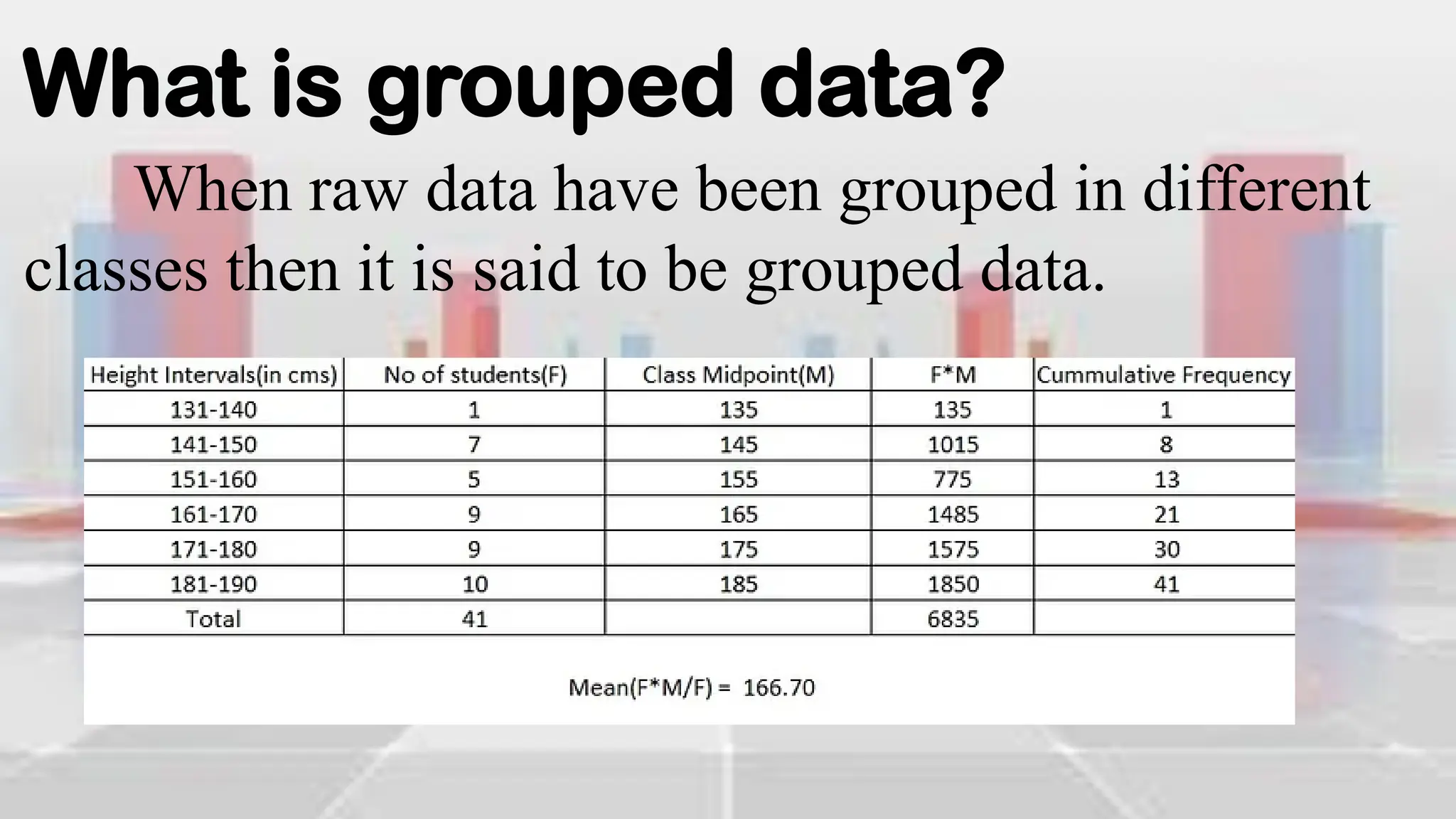
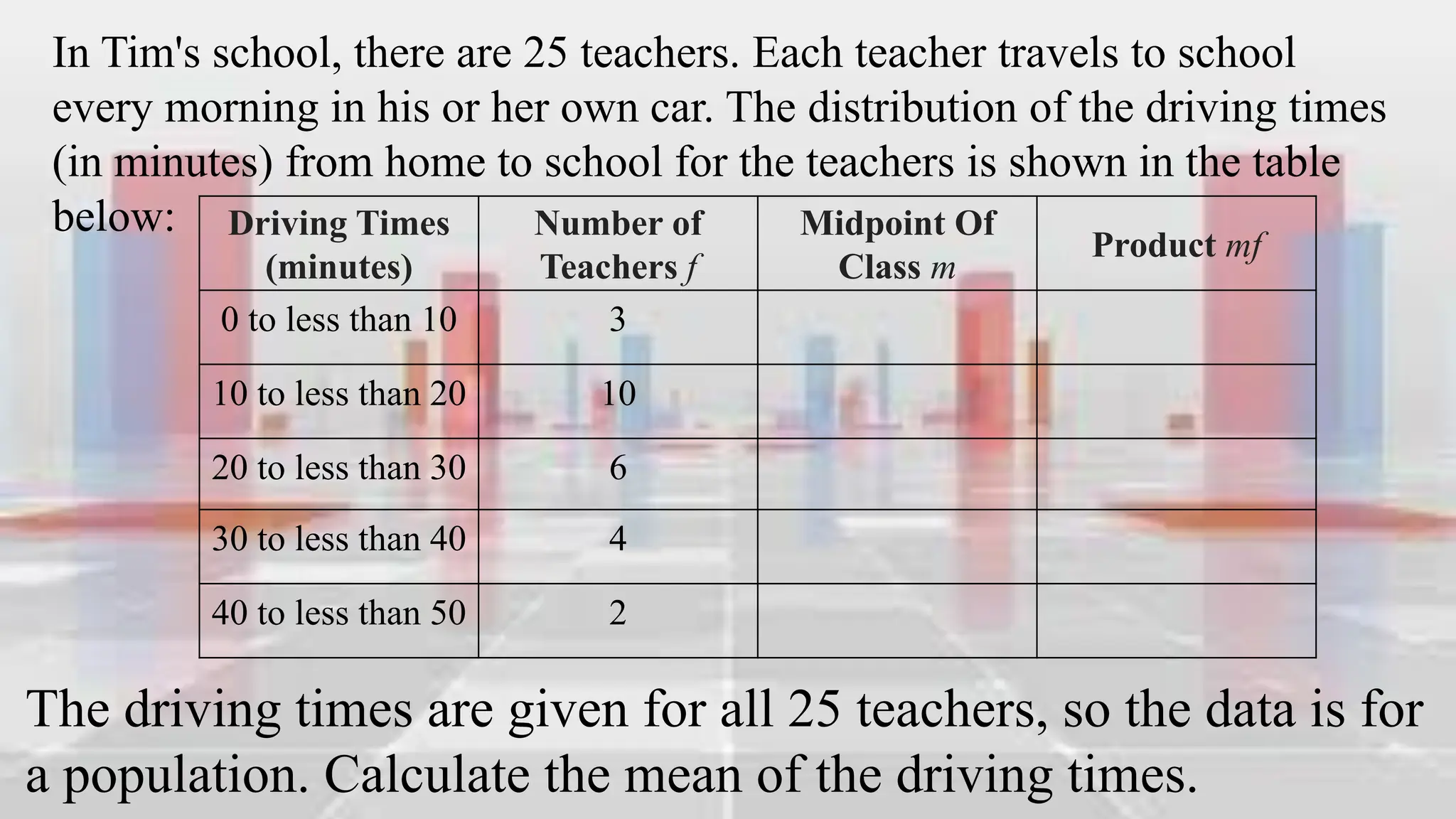
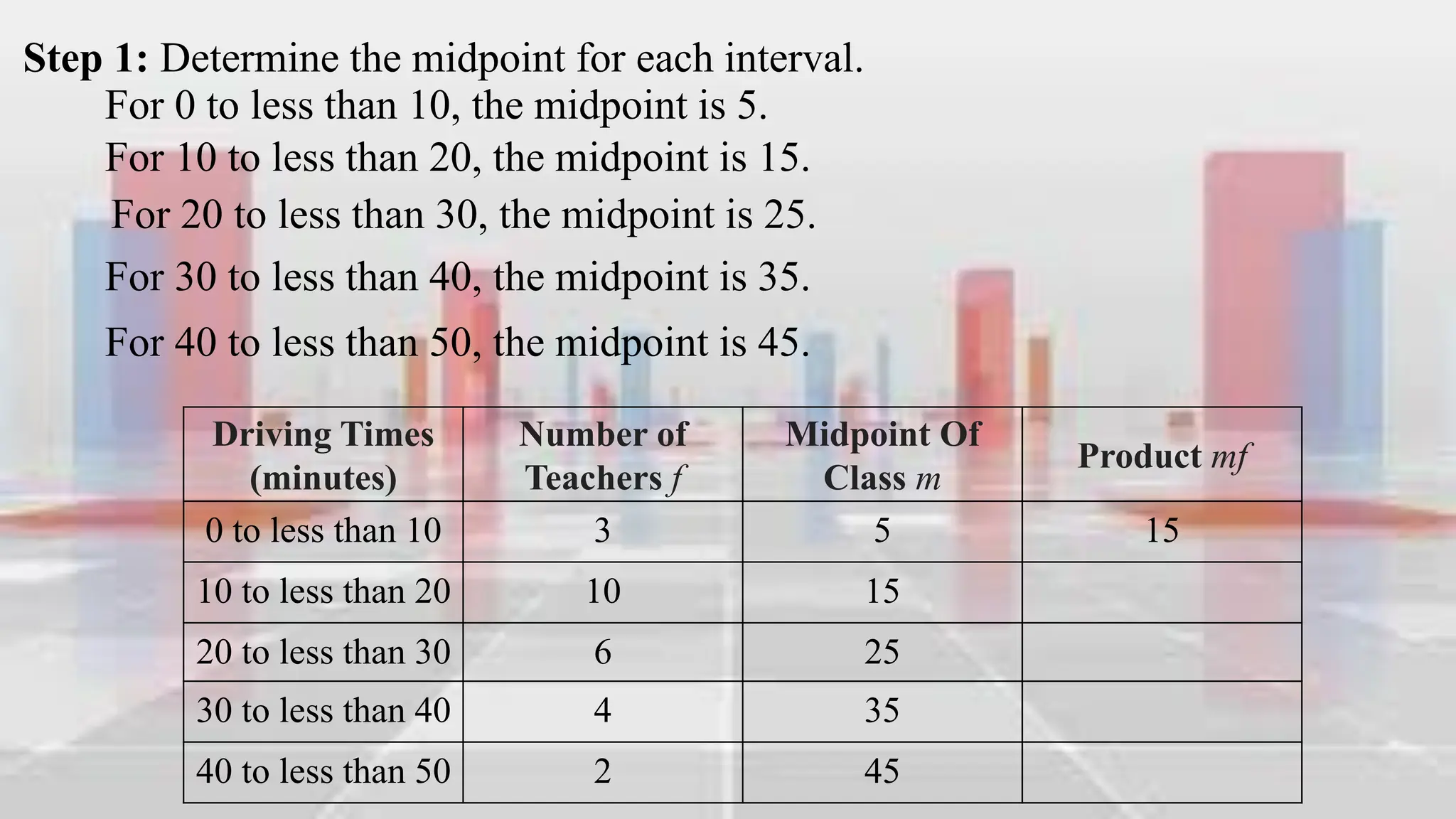
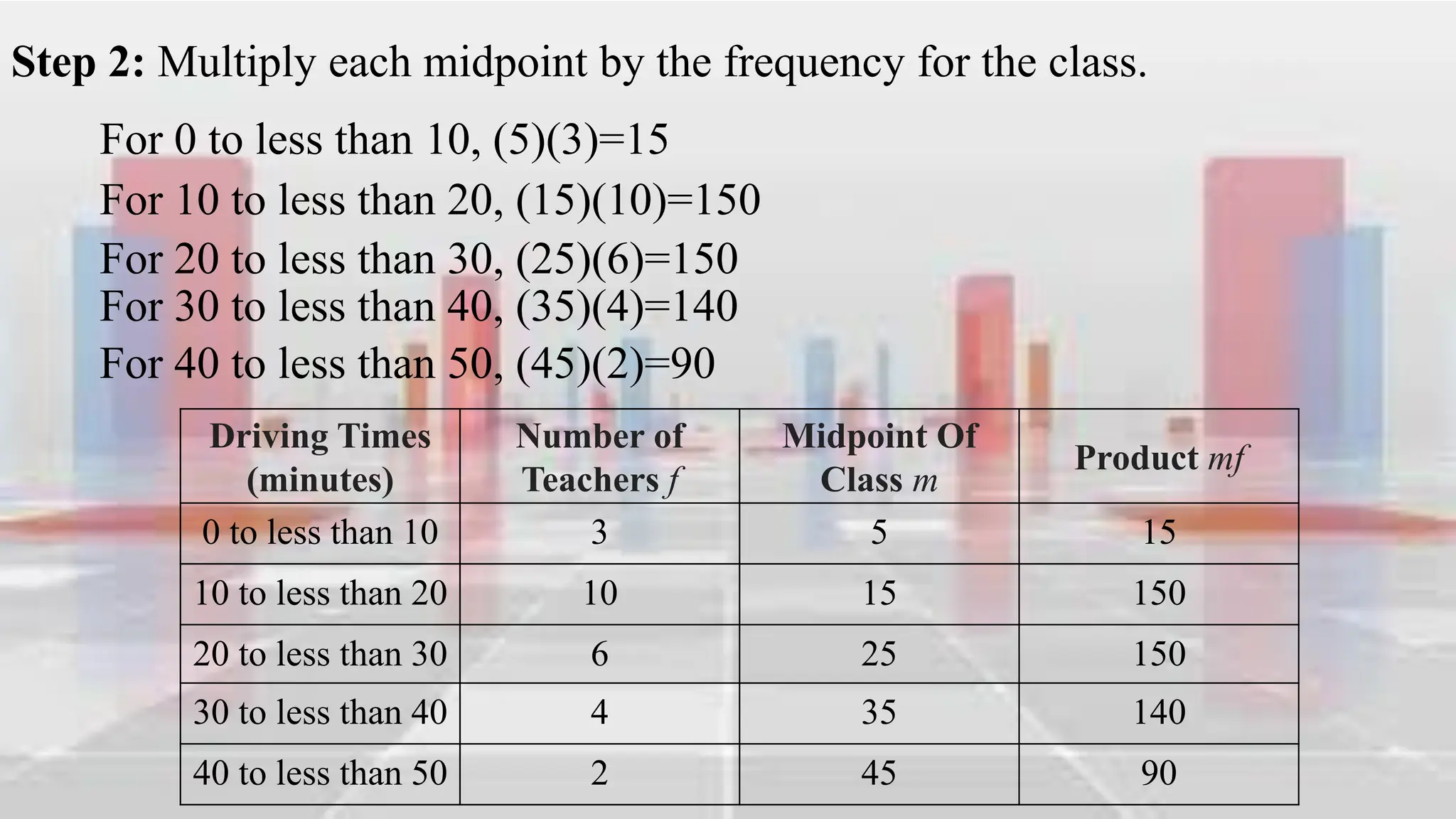
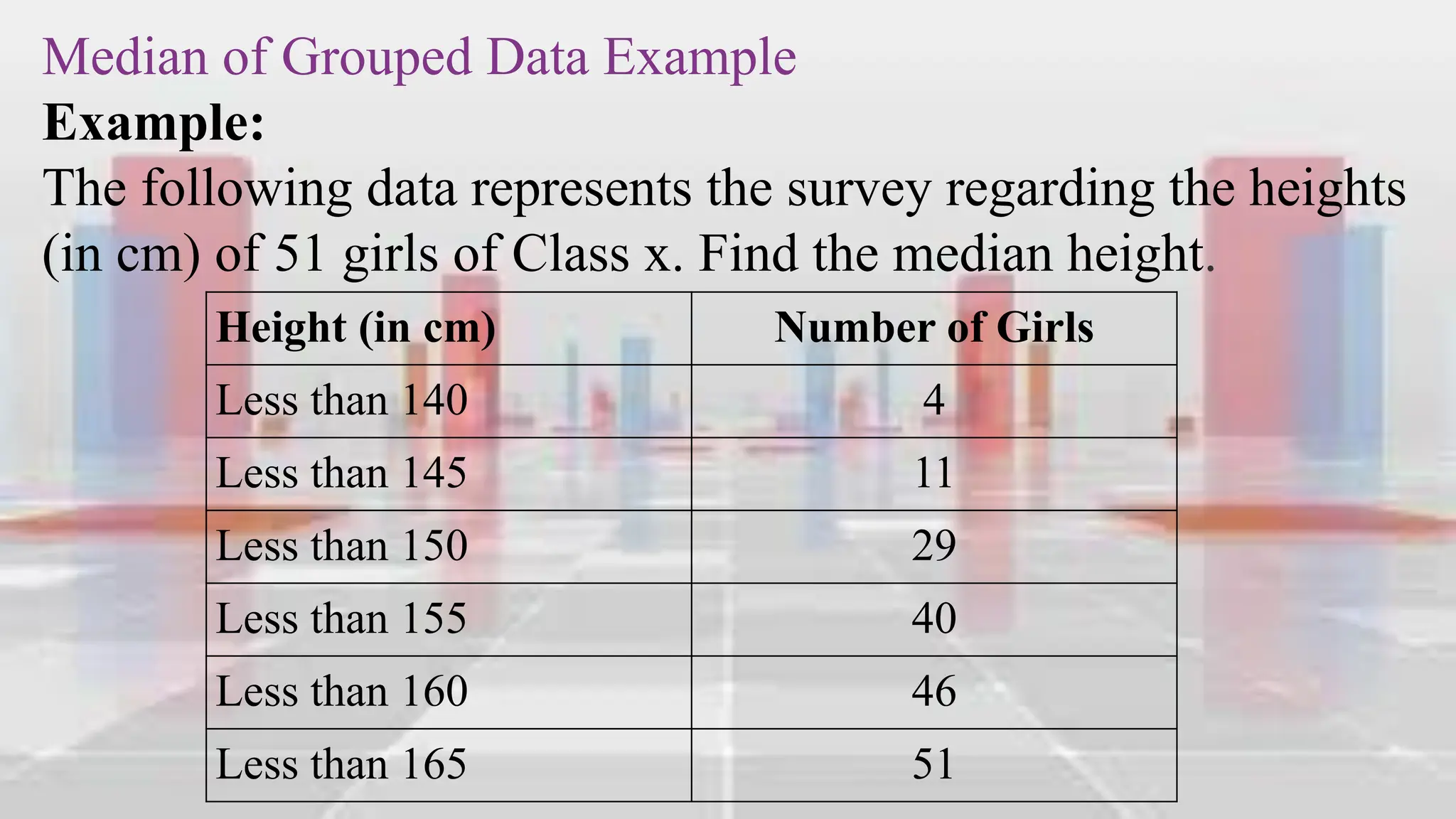
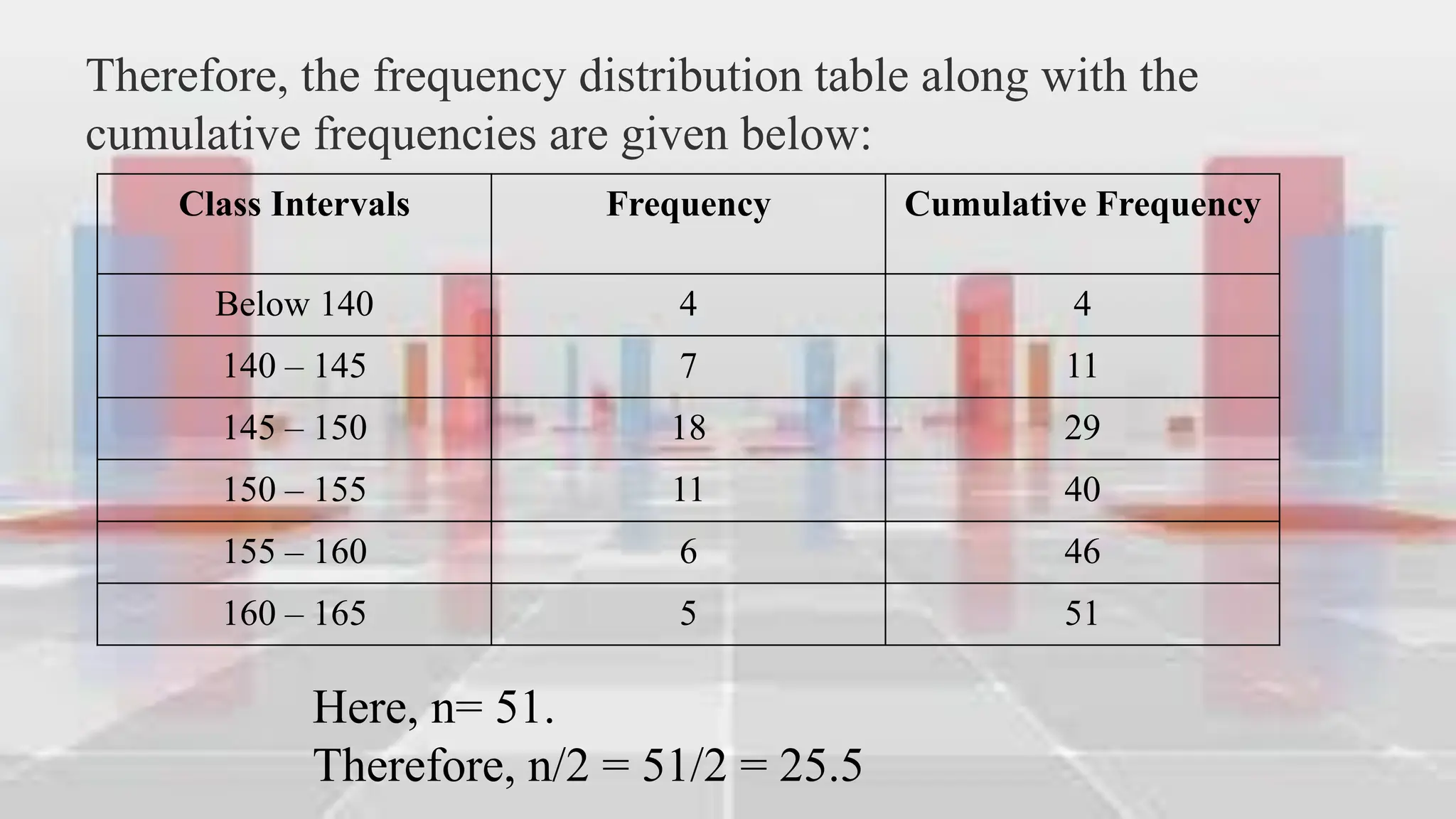
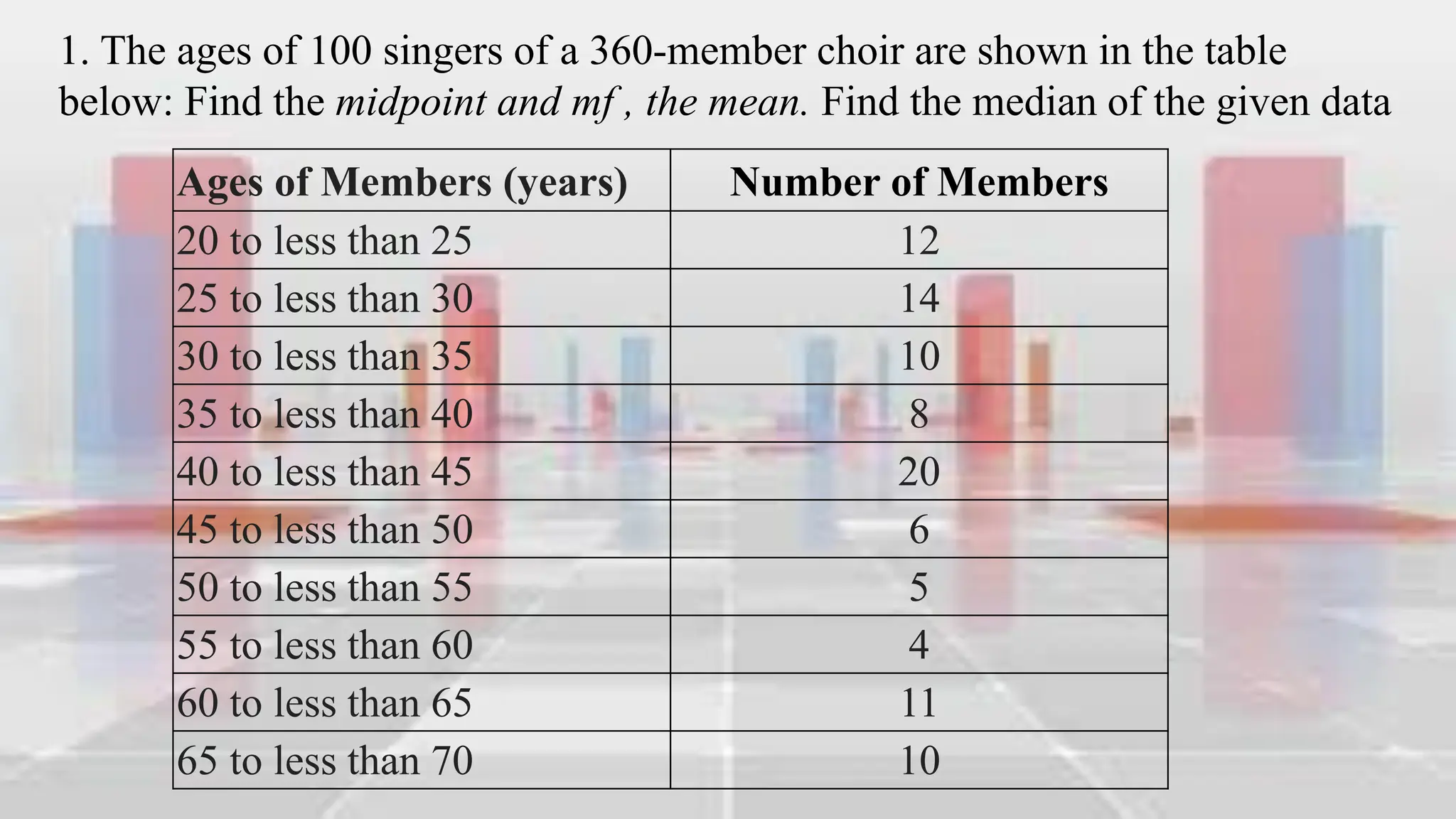
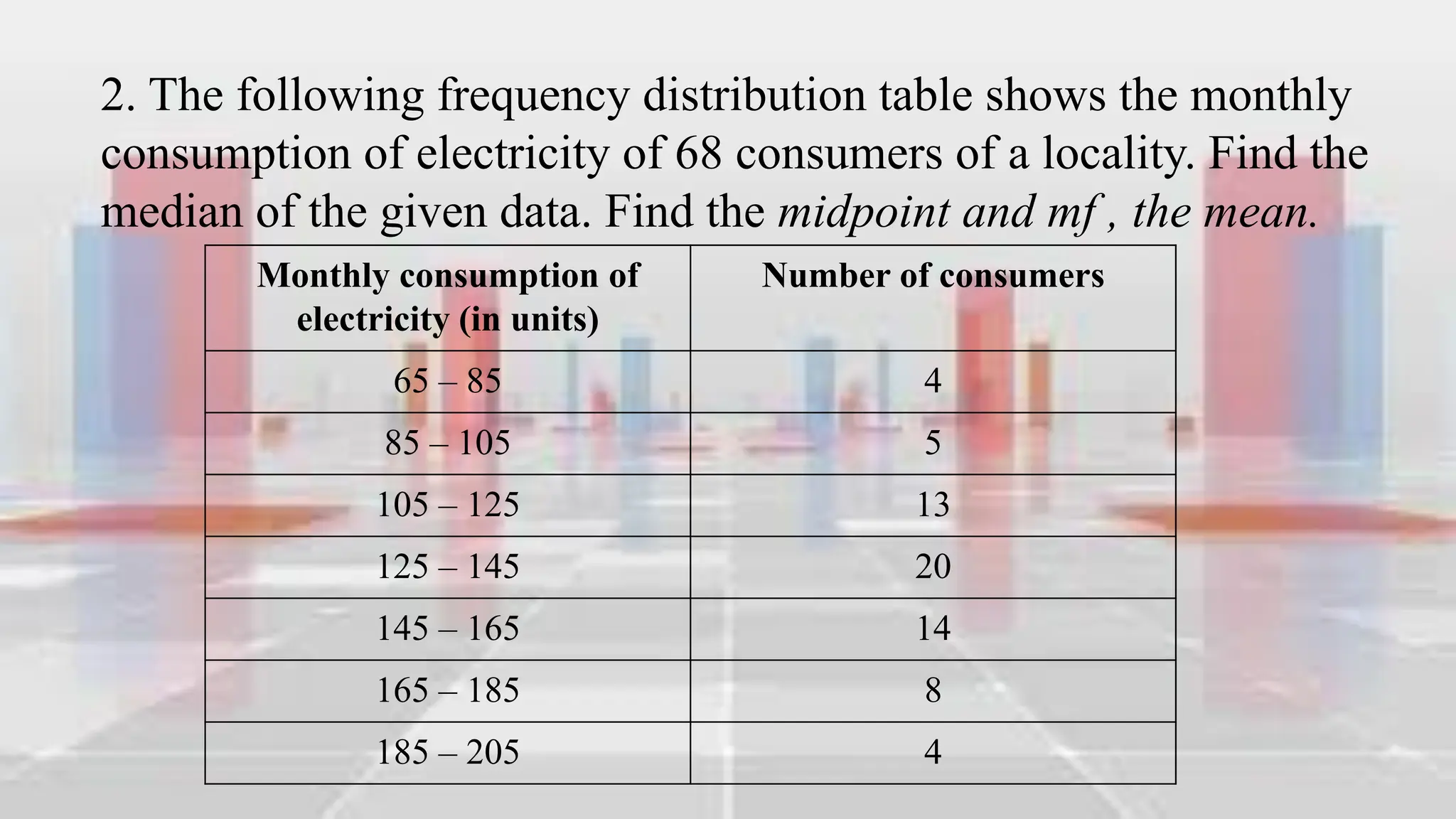
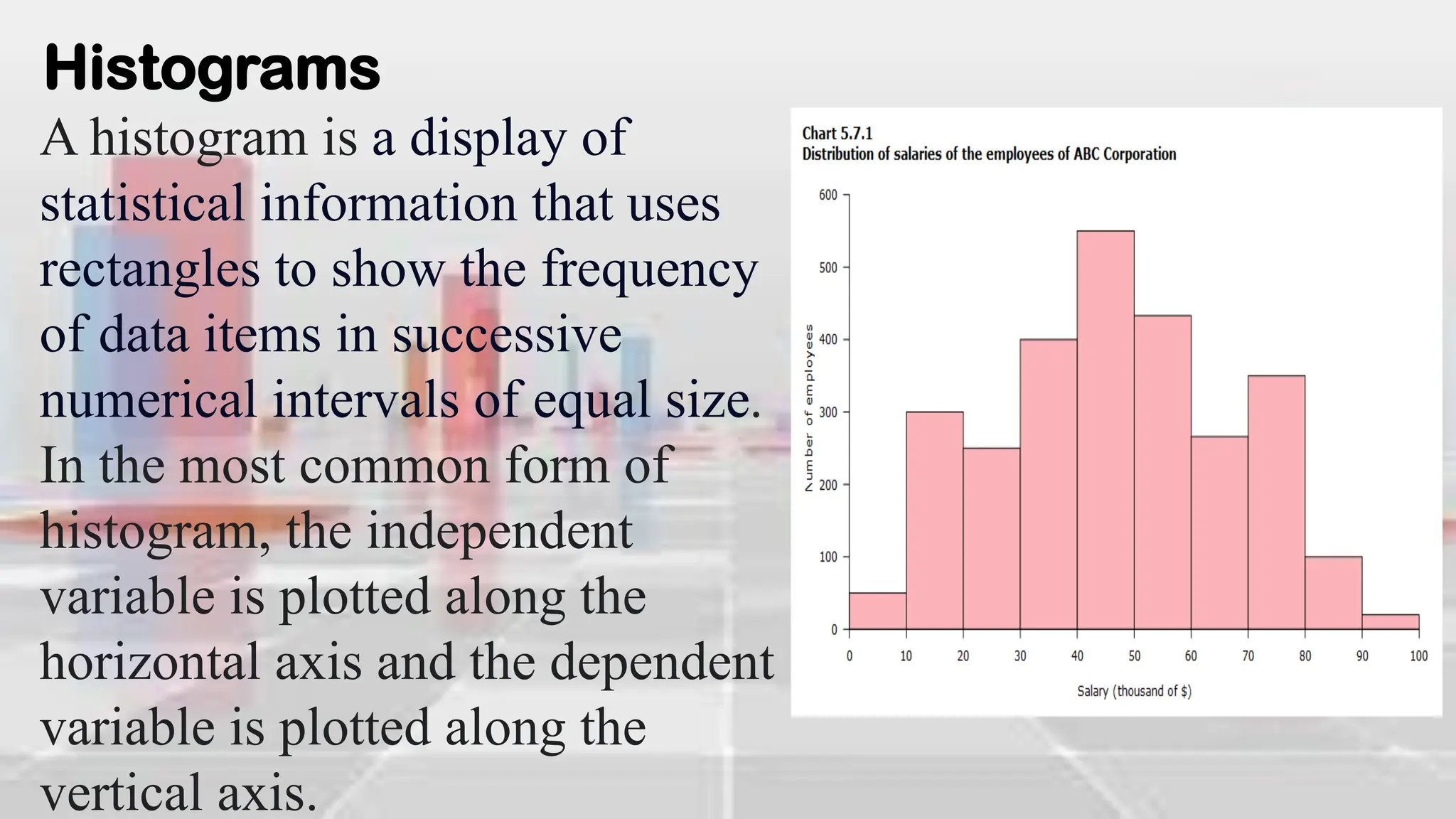
This document provides an introduction to statistical analysis and key concepts such as populations, samples, measures of central tendency (mean, median, mode), and grouped vs. ungrouped data. It explains that a population is the entire set being studied, while a sample is a subset used to make inferences about the population. It also defines nominal, ordinal, interval, and ratio levels of measurement for variables. The document demonstrates how to calculate the mean, median, and mode for both ungrouped and grouped data sets. It provides examples of finding the mean, median, and midpoint of intervals for grouped driving time and height data.

1. Introduction to
Analyzing Statistical
Data

2. Statistics
---is a branch of applied mathematics that involves the
collection, description, analysis, and inference of
conclusions from quantitative data.

3. Introduction to Data and
Measurement Issues

4. Classifying Variables
Statisticians refer to an entire group that is being
studied as a population. Each member of the population is
called a unit.

5. Population
vs.
Sample

6. Population is the entire set
of items from which you
draw data for a statistical
study. It can be a group of
individuals, a set of items,
etc. It makes up the data
pool for a study.

7. An example of a population would be the entire
student body at a school. It would contain all the
students who study in that school at the time of data
collection. Depending on the problem statement, data
from each of these students is collected. An example is
the students who speak Hindi among the students of a
school.

8. A sample is defined as a smaller and more
manageable representation of a larger group. A
subset of a larger population that contains
characteristics of that population. A sample is used
in statistical testing when the population size is too
large for all members or observations to be
included in the test

9. The process of collecting data from a small subsection
of the population and then using it to generalize over the
entire set is called Sampling.

10. Samples are used when :
1. The population is too large to collect data.
2. The data collected is not reliable.
3. The population is hypothetical and is unlimited in
size. Take the example of a study that documents
the results of a new medical procedure. It is
unknown how the procedure will affect people
across the globe, so a test group is used to find out
how people react to it.

11. Errors in Sampling
The researcher has to accept that there could be variations
in the sample due to chance that lead to changes in the
population estimate. A statistician would report the estimate
of the parameter in two ways: as a point estimate (e.g., 915)
and also as an interval estimate. The difference between the
true parameter and the statistic obtained by sampling is called
sampling error. It is also possible that the researcher made
mistakes in her sampling methods in a way that led to a
sample that does not accurately represent the true population.

12. This type of systematic error in sampling is called
bias. Statisticians go to great lengths to avoid the
many potential sources of bias. We will
investigate this in more detail in a later chapter.

13. Levels of
Measurement

14. Nominal measurement
A nominal measurement is one in which the values of the
variable are names.
Examples of nominal scales:
You can categorize your data by labelling them in mutually exclusive
groups, but there is no order between the categories.
• City of birth
• Gender
• Ethnicity
• Car brands
• Marital status

15. Ordinal measurement
An ordinal measurement involves collecting information of
which the order is somehow significant. The name of this
level is derived from the use of ordinal numbers for ranking
(1st, 2nd, 3rd, etc.).
Ex. High school men soccer players classified by their athletic
ability: Superior, Average, Above Average
Likert-type questions (e.g., very dissatisfied to very satisfied)

16. Interval measurement
With interval measurement, there is significance to the
distance between any two values
Example:
• Test scores (e.g., IQ or exams)
• Personality inventories
• Temperature in Fahrenheit or Celsius

17. Ratio measurement
A ratio measurement is the estimation of the ratio between a
magnitude of a continuous quantity and a unit magnitude of
the same kind. A variable measured at this level not only
includes the concepts of order and interval, but also adds the
idea of 'nothingness', or absolute zero.
Example:
• Height
• Age
• Weight
• Temperature in Kelvin

19. What is ungrouped data?
When the data has not been placed in any categories
and no aggregation/summarization has taken placed on the
data then it is known as ungrouped data. Ungrouped data is
also known as raw data
Height of students:
(171,161,155,155,183,191,185,170,172,177,183,190,139,149,
150,150,152,158,159,174,178,179,190,170,143,165,167,187,
169,182,163,149,174,174,177,181,170,182,170,145,143):

20. What is grouped data?
When raw data have been grouped in different
classes then it is said to be grouped data.

21. Measures of Central
Tendency and Dispersion

22. Central Tendencies
Central tendency is the central location in a
probability distribution. There are many measures
for central tendencies like mean, mode, median,
interquartile range, percentiles, geometric mean,
harmonic mean.

23. Measurements of Center
The students in a statistics class were asked to report the number of
children that live in their house (including brothers and sisters
temporarily away at college). The data are recorded below:
1, 3, 4, 3, 1, 2, 2, 2, 1, 2, 2, 3, 4, 5, 1, 2, 3, 2, 1, 2, 3, 6
Once data are collected, it is useful to summarize the data set by
identifying a value around which the data are centered. Three
commonly used measures of center are the mode, the median, and the
mean.

24. Mode
The mode is defined as the most frequently occurring number in a
data set. The mode is most useful in situations that involve categorical
(qualitative) data that are measured at the nominal level.
When a data set is described as being bimodal, it is clustered about
two different modes. Technically, if there were more than two, they
would all be the mode.
If there is an equal number of each data value, the mode is not
useful in helping us understand the data, and thus, we say the data set
has no mode.
eg 7,11,14.25,15,15,15,15,15,19,19,29,81. Mode is 15

25. Mean
Another measure of central tendency is the arithmetic
average, or mean. This value is calculated by adding all the
data values and dividing the sum by the total number of data
points. The mean is the numerical balancing point of the data
set.
eg, The mean of “15,11,14,3,21,17,22,16,19,16,5,7,9,20,4”
is 13.26667.

26. Median
The median is simply the middle number in an
ordered set of data.
Suppose a student took five statistics quizzes and
received the following grades:
80, 94, 75, 96, 90
When there is an even number of numbers, no one of the
data points will be in the middle. In this case, we take the
average (mean) of the two middle numbers.

27. Driving Times
(minutes)
Number of
Teachers f
Midpoint Of
Class m
Product mf
0 to less than 10 3
10 to less than 20 10
20 to less than 30 6
30 to less than 40 4
40 to less than 50 2
In Tim's school, there are 25 teachers. Each teacher travels to school
every morning in his or her own car. The distribution of the driving times
(in minutes) from home to school for the teachers is shown in the table
below:
The driving times are given for all 25 teachers, so the data is for
a population. Calculate the mean of the driving times.

28. Step 1: Determine the midpoint for each interval.
For 0 to less than 10, the midpoint is 5.
For 10 to less than 20, the midpoint is 15.
For 20 to less than 30, the midpoint is 25.
For 30 to less than 40, the midpoint is 35.
For 40 to less than 50, the midpoint is 45.
Driving Times
(minutes)
Number of
Teachers f
Midpoint Of
Class m
Product mf
0 to less than 10 3 5 15
10 to less than 20 10 15
20 to less than 30 6 25
30 to less than 40 4 35
40 to less than 50 2 45

29. Step 2: Multiply each midpoint by the frequency for the class.
For 0 to less than 10, (5)(3)=15
Driving Times
(minutes)
Number of
Teachers f
Midpoint Of
Class m
Product mf
0 to less than 10 3 5 15
10 to less than 20 10 15 150
20 to less than 30 6 25 150
30 to less than 40 4 35 140
40 to less than 50 2 45 90
For 10 to less than 20, (15)(10)=150
For 20 to less than 30, (25)(6)=150
For 30 to less than 40, (35)(4)=140
For 40 to less than 50, (45)(2)=90

30. Step 3: Add the results from Step 2 and divide the sum by 25.
For the population, N=25 and ∑ mf =545, so using the
formula µ=
∑ 𝑚𝑓
𝑁
, the mean would be
µ=
545
25
=21.8.

31. Median of Grouped Data Example
Example:
The following data represents the survey regarding the heights
(in cm) of 51 girls of Class x. Find the median height.
Height (in cm) Number of Girls
Less than 140 4
Less than 145 11
Less than 150 29
Less than 155 40
Less than 160 46
Less than 165 51

32. Solution:
To find the median height, first, we need to find the class
intervals and their corresponding frequencies.
The given distribution is in the form of being less than
type,145, 150 …and 165 gives the upper limit. Thus, the class
should be below 140, 140-145, 145-150, 150-155, 155-160
and 160-165.

33. From the given distribution, it is observed that,
4 girls are below 140. Therefore, the frequency of class intervals
below 140 is 4.
11 girls are there with heights less than 145, and 4 girls with
height less than 140
Hence, the frequency distribution for the class interval 140-145 =
11-4 = 7
Likewise, the frequency of 145 -150= 29 – 11 = 18
Frequency of 150-155 = 40-29 = 11
Frequency of 155 – 160 = 46-40 = 6
Frequency of 160-165 = 51-46 = 5

34. Therefore, the frequency distribution table along with the
cumulative frequencies are given below:
Class Intervals Frequency Cumulative Frequency
Below 140 4 4
140 – 145 7 11
145 – 150 18 29
150 – 155 11 40
155 – 160 6 46
160 – 165 5 51
Here, n= 51.
Therefore, n/2 = 51/2 = 25.5

35. Thus, the observations lie between the class interval 145-150, which
is called the median class.
Therefore,
Lower class limit = 145
Class size, h = 5
Frequency of the median class, f = 18
Cumulative frequency of the class preceding the median class, cf =
11.

36. Median = 149.03.
M = l + (
n/2 − 𝑐𝑓
𝑓
) * h
Median = 145+ (25.5.11) x 5
Median = 145 + (72.5/18)
Median = 145 +4.03

37. 1. The ages of 100 singers of a 360-member choir are shown in the table
below: Find the midpoint and mf , the mean. Find the median of the given data
Ages of Members (years) Number of Members
20 to less than 25 12
25 to less than 30 14
30 to less than 35 10
35 to less than 40 8
40 to less than 45 20
45 to less than 50 6
50 to less than 55 5
55 to less than 60 4
60 to less than 65 11
65 to less than 70 10

38. 2. The following frequency distribution table shows the monthly
consumption of electricity of 68 consumers of a locality. Find the
median of the given data. Find the midpoint and mf , the mean.
Monthly consumption of
electricity (in units)
Number of consumers
65 – 85 4
85 – 105 5
105 – 125 13
125 – 145 20
145 – 165 14
165 – 185 8
185 – 205 4

39. Midrange
The midrange (sometimes called the midextreme) is
found by taking the mean of the maximum and
minimum values of the data set.
Consider the following quiz grades: 75, 80, 90, 94,
and 96. The midrange would be:
Since it is based on only the two most extreme values, the midrange
is not commonly used as a measure of central tendency.

40. Trimmed Mean
To calculate a trimmed mean you remove the maximum
and minimum values and divide by the number of values that
remain.
Consider the following quiz grades: 75, 80, 90, 94, 96.
A trimmed mean would remove the largest and smallest values, 75
and 96, and divide by 3.

41. Visualizations of Data
Data visualization is the representation of data through
use of common graphics, such as charts, plots, infographics,
and even animations. These visual displays of information
communicate complex data relationships and data-driven
insights in a way that is easy to understand

42. Histograms
A histogram is a display of
statistical information that uses
rectangles to show the frequency
of data items in successive
numerical intervals of equal size.
In the most common form of
histogram, the independent
variable is plotted along the
horizontal axis and the dependent
variable is plotted along the
vertical axis.

43. Creating Frequency Tables
Frequency tables simply display each value of the
variable, and the number of occurrences (the frequency) of
each of those values.
In this example, the variable is the number of plastic
beverage bottles of water consumed each week.
Consider the following raw data:
6, 4, 7, 7, 8, 5, 3, 6, 8, 6, 5, 7, 7, 5, 2, 6, 1, 3, 5, 4, 7, 4, 6, 7,
6, 6, 7, 5, 4, 6, 5, 3

44. Figure: Imaginary Class Data on Water Bottle Usage

45. The following data set shows the countries in the world
that consume the most bottled water per person per year.

46. A bracket, '[' or ']', indicates that the
endpoint of the interval is included in the
class. A parenthesis, '(' or ')', indicates that
the endpoint is not included. It is common
practice in statistics to include a number
that borders two classes as the larger of the
two numbers in an interval. For example,
[80−90) means this classification includes
everything from 80 and gets infinitely close
to, but not equal to, 90. 90 is included in
the next class, [90−100).
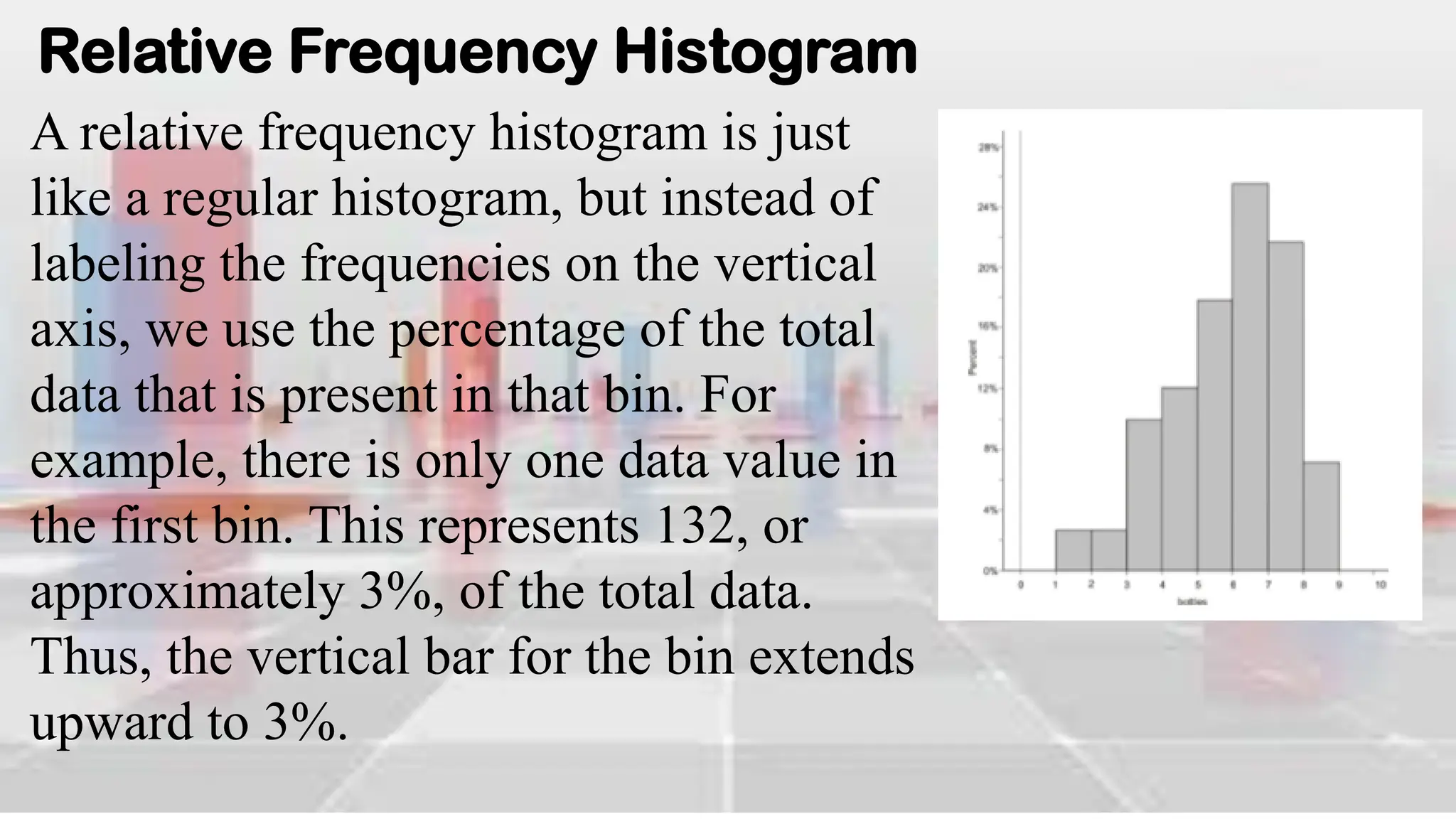
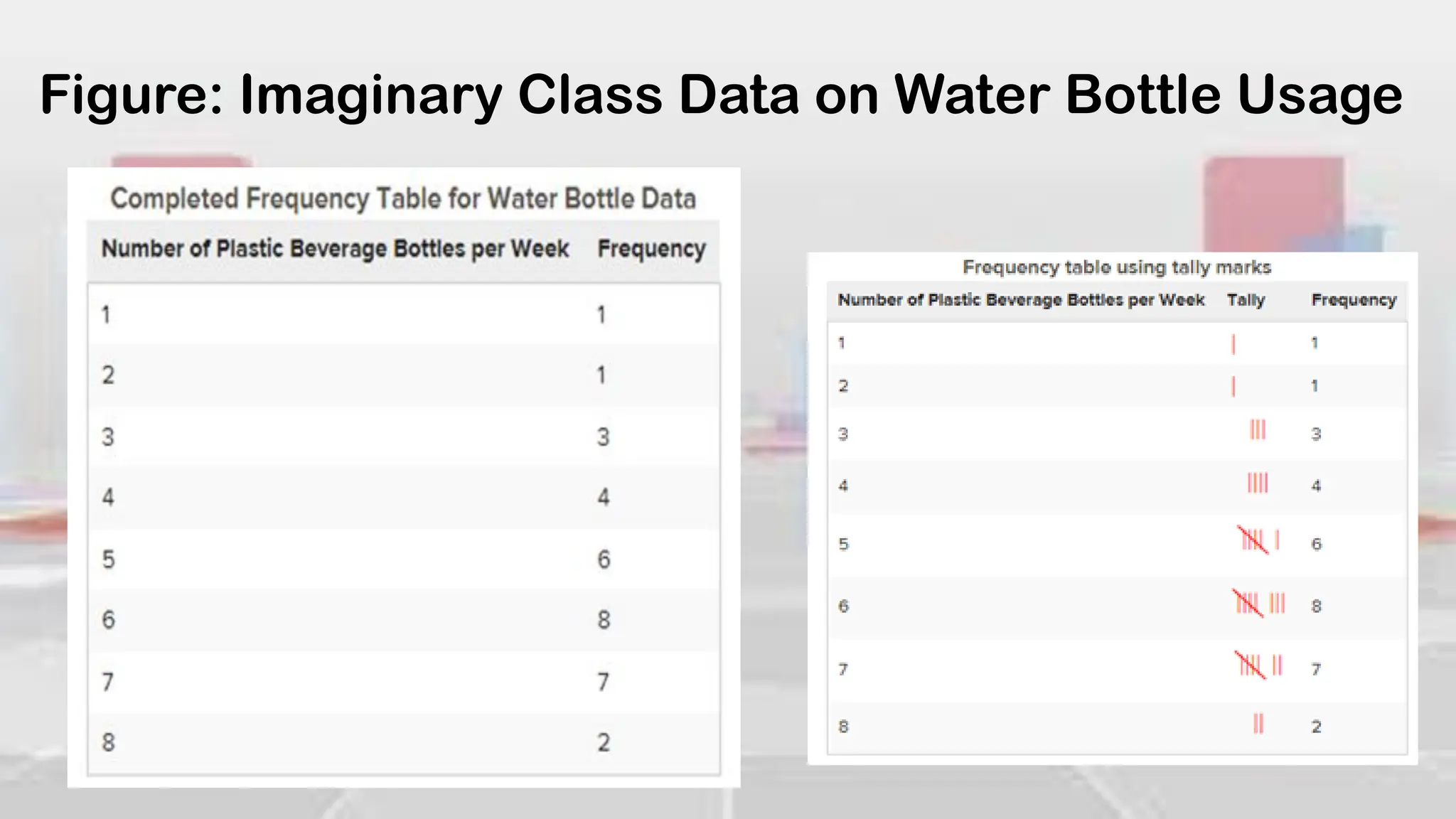
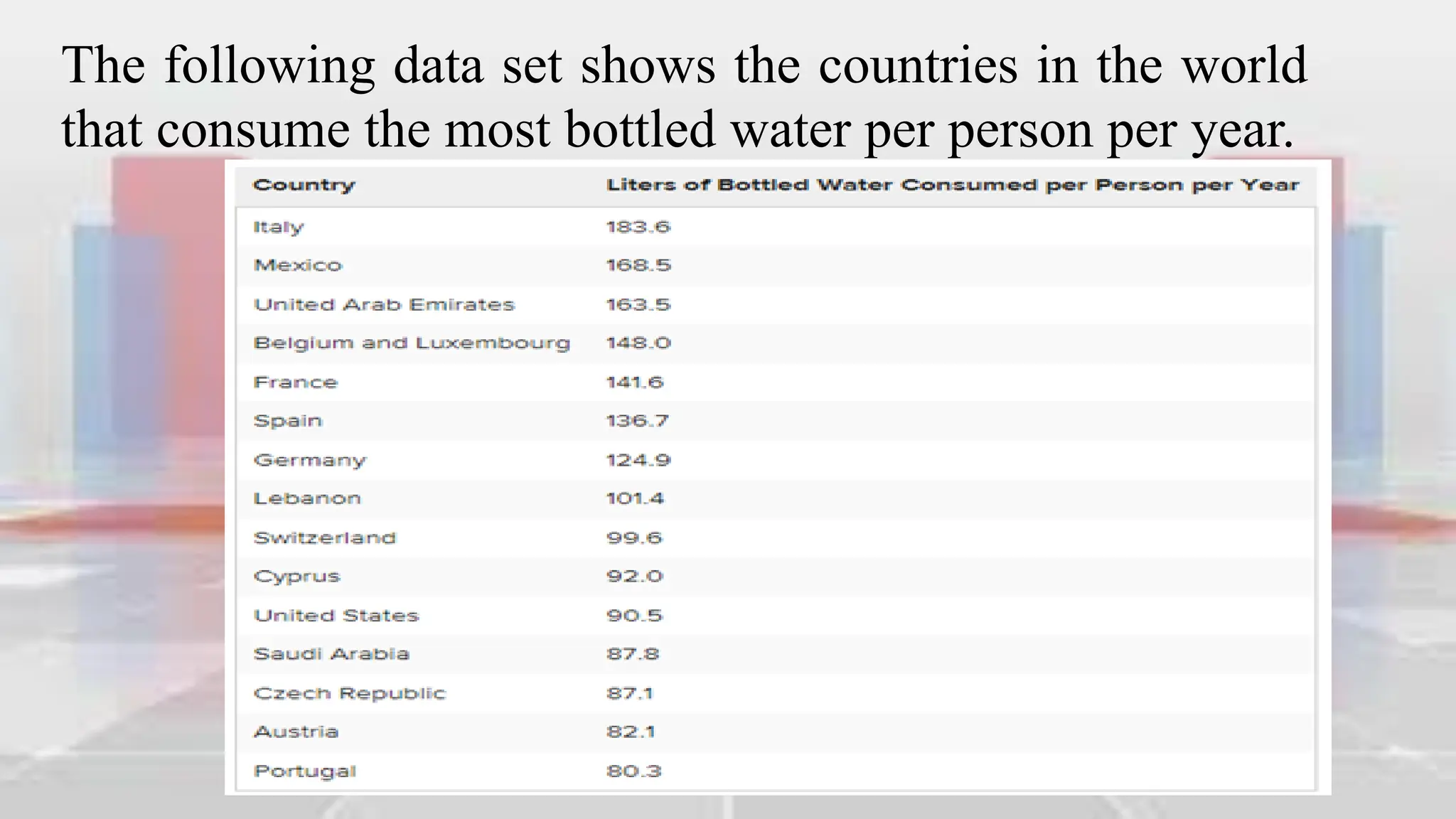
Figure: Completed Frequency Table for World Bottled Water
Consumption Data (2004)

47. Relative Frequency Histogram
A relative frequency histogram is just
like a regular histogram, but instead of
labeling the frequencies on the vertical
axis, we use the percentage of the total
data that is present in that bin. For
example, there is only one data value in
the first bin. This represents 132, or
approximately 3%, of the total data.
Thus, the vertical bar for the bin extends
upward to 3%.

48. Frequency Polygons
A frequency polygon is similar to
a histogram, but instead of using
bins, a polygon is created by
plotting the frequencies and
connecting those points with a
series of line segments.

49. Graphs for Categorical Data
We live in an age of unprecedented access to increasingly sophisticated and
affordable personal technology. Cell phones, computers, and televisions
now improve so rapidly that, while they may still be in working condition,
the drive to make use of the latest technological breakthroughs leads many
to discard usable electronic equipment. Much of that ends up in a landfill,
where the chemicals from batteries and other electronics add toxins to the
environment. Approximately 80% of the electronics discarded in the
United States is also exported to third world countries, where it is disposed
of under generally hazardous conditions by unprotected workers. The
following table shows the amount of tonnage of the most common types of
electronic equipment discarded in the United States in 2005.
E-Waste and Bar Graphs

50. Figure: Electronics Discarded in the US (2005). Source: National Geographic, January
2008.
The type of electronic equipment is a categorical variable,
and therefore, this data can easily be represented using a bar
graph.

51. Creating a Bar Graph
While this looks very similar to a histogram, the
bars in a bar graph usually are separated
slightly. The graph is just a series of disjoint
categories

52. Pie Graphs
A pie chart is a circular statistical graphic, which is
divided into slices to illustrate numerical proportion. In a
pie chart, the arc length of each slice is proportional to the
quantity it represents

53. Here is a table with the percentages and the approximate
angle measure of each sector for the E-waste data:

54. And here is the completed pie graph:

55. Complete the chart below to show the approximate
percentage of the total number of grades, and Create a pie
graph for this data.

56. Stem-and-Leaf Plots
A stem-and-leaf plot is a similar plot in which it is much
easier to read the actual data values. In a stem-and-leaf plot,
each data value is represented by two digits: the stem and
the leaf.

58. Displaying Bivariate Data
Bivariate simply means two variables. The goal of
examining bivariate data is usually to show some sort of
relationship or association between the two variables.
Ice cream sales versus
the temperature on that
day. The two variables
are Ice Cream Sales and
Temperature.

59. Following is a data table that includes both
percentages
Figure: Paper and Glass Packaging
Recycling Rates for 19 countries

60. Scatterplots
A scatter plot is a type of data visualization that shows the
relationship between different variables. This data is shown
by placing various data points between an x- and y-axis.
Essentially, each of these data points looks “scattered” around
the graph, giving this type of data visualization its name.

61. Ellipses are the closed
type of conic section: a
plane curve tracing the
intersection of a cone with
a plane

62. Line Plots
A line plot is a way to display
data along a number line. Line
plots are also called dot plots.

63. Figure: Total Municipal Waste
Generated in the US by Year in
Millions of Tons
In this example, the time in years is considered the explanatory
variable, or independent variable, and the amount of municipal
waste is the response variable, or dependent variable. It is not
only the passage of time that causes our waste to increase.
Other factors, such as population growth, economic
conditions, and societal habits and attitudes also contribute as
causes. However, it would not make sense to view the
relationship between time and municipal waste in the opposite
direction.
When one of the variables is time, it will almost always be the
explanatory variable. Because time is a continuous variable,
and we are very often interested in the change a variable
exhibits over a period of time, there is some meaning to the
connection between the points in a plot involving time as an
explanatory variable. In this case, we use a line plot. A line
plot is simply a scatterplot in which we connect successive
chronological observations with a line segment to give more
information about how the data values are changing over a
period of time. Here is the line plot for the US Municipal
Waste data:

65. Box-and-Whisker Plots
A boxplot, also called a box and whisker plot, is a way
to show the spread and centers of a data set. Measures of
spread include the interquartile range and the mean of the
data set. Measures of center include the mean or average
and median (the middle of a data set).