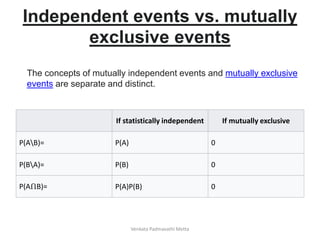
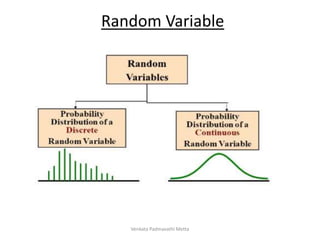
The document covers fundamental concepts of probability theory including sample spaces, events, and conditional probability, along with the axioms of probability. It provides examples to illustrate key concepts such as random variables, binomial-theorem, and the use of Bayes' theorem for calculating conditional probabilities. Additionally, it addresses counting principles and the inclusion-exclusion principle in probability calculations.