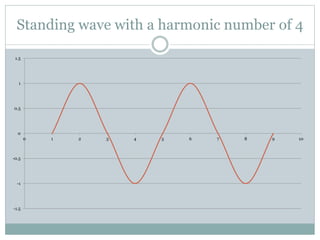
1) A standing wave is formed by the interference of two waves traveling in opposite directions with the same amplitude, frequency, and wavelength. 2) Nodes are points of zero amplitude, while antinodes are points of maximum amplitude. 3) Harmonics refer to allowed frequencies that are integer multiples of the fundamental frequency. The harmonic number is the integer multiplier. 4) For a string fixed at both ends, allowed wavelengths are λm = 2L/m, where m is the harmonic number. The number of antinodes equals the harmonic number.

1. STANDING WAVES ON STRINGS
PHYSICS 101
SECTION 226
MARCH.8/2015
Learning Object 6

2. What is a Standing Wave?
 A standing wave is when you combine two harmonic waves that have the same
amplitude, frequency, and wavelength as each other but they need to be
traveling in opposite directions than each other.
 The two waves have the wave function:
D(x,t) = A sin(kx±ωt)
 + ωt is when the wave is moving in the negative x direction
 - ωt is when the wave is moving in the positive x direction
The resulting wave function of the 2 waves moving in opposite directions is:
D(x,t) = D1 (x,t) + = D2 (x,t)
= A sin [sin(kx-ωt)+sin(kx+ωt)]
Using trigonometry, the wave function becomes:
D(x,t) = 2A sin(kx) cos (ωt)
Note: This wave function equation describes a standing wave.

3. What is a Node and Antinode?
 A node is a point on a standing wave on a string that
has an amplitude of zero and is therefore at rest.
Nodes have these characteristics at all times.
 An antinode is a point on a standing wave on a
string that has the maximum amplitude that it can.
The maximum amplitude is ±2A (as shown in the
wave function on the previous slide).

4. What is a Harmonic and Harmonic Number of a
Standing Wave on a String?
 A harmonic refers to the allowed frequency of a
wave that is a whole number multiple of the
fundamental (reference) frequency of a wave.
 The fundamental frequency is the frequency that
gives the longest wavelength of 2L. It is also called
the first harmonic.
 A harmonic is also called a resonant frequency.

5. Continued………
 A harmonic number is the integer that is
multiplied to the fundamental frequency to get a
particular resonant frequency.
For example:
fm = mf1 where m = 1,2,3,4,……
f4 = 4f1
To get f4, you need to multiply f1 by, so f4 is the fourth
harmonic meaning its harmonic number is 4.

6. Wavelengths of a Standing Wave on a String
With Both Ends Fixed
 The allowed wavelengths that a standing wave on a
string can oscillate with, if it has both of its ends
fixed, is given by:
λm = 2L where m = 1,2,3,4,……
m
• This equation gives the longest wavelength of 2L, so
λ1 = 2L. λ1 corresponds to the fundamental frequency
f1.

7. How is the number of antinodes in a standing wave on a string
with fixed ends equal to the harmonic number of that standing
wave?
Note: To explain this, I am going to use an example.
 Let’s consider the fourth harmonic meaning that it
has a harmonic number of 4. Using the equation fm =
mf1 where m = 1,2,3,4,……, we get f4 = 4f1.
 Using the same value of m and plugging it into the
equation λm = 2L/m where m = 1,2,3,4,……, we get:
λ4 = 2L/4 = L/2

8. Continued……
 λ = v/f rearranging this to get f = v/ λ
 The fundamental frequency f1 = v/ λ1 = 1/(2L )
 Because the fundamental frequency has no nodes,
the sine wave corresponding to it has the phase (π/2)
at length L. The fourth harmonic has the phase (π/2)
at L/4.
 This means that while the fundamental frequency
has one arch at length L, the fourth harmonic has 4
times the number of arches as the fundamental
frequency.

9. Continued……
 The fourth harmonic has 4 arches that are
alternating with consecutive arches being reflections
of each other in the x-axis moved to the right(looks
like shape of 2 sine waves).
 This also makes sense because the wavelength of the
sine wave for the fourth harmonic wave is L/2,
meaning that 2 sine waves of this wavelength fit in a
total length of L.

10. Continued……
 Since each sine wave has an amplitude at (π/2), each sine
wave reaches its amplitude at 2 points (π/2) and (3π/2).
Therefore, 2 sine waves reach the amplitude at 4 points.
 These four points are written in terms of the length L and
in radians:
1) L/8 = (π/2)
2) 3L/8 = (3π/2)
3) 5L/8 = (5π/2)
4) 7L/8 = (7π/2)

11. Continued……
 4 arches = 4 antinodes because the antinodes are
located at the point of greatest displacement of each
arch so there are 4 such points for 4 arches.
 Because an antinode is a point on a standing wave on
a string that has the maximum
amplitude(greatest displacement on an arch),
there are 4 antinodes.

12. Standing wave with a harmonic number of 4
-1.5
-1
-0.5
0
0.5
1
1.5
0 1 2 3 4 5 6 7 8 9 10

13. Description of Graph
• The points at 2, 4, 6, and 8 on the x-axis correspond
to the amplitudes at L/8 = (π/2), 3L/8 = (3π/2),
5L/8 = (5π/2), and 7L/8 = (7π/2) respectively. This
is where the antinodes are located.