Документ содержит основные методы решения линейных уравнений с одной переменной, описывая процесс упрощения уравнений, включая избавление от знаменателей и раскрытие скобок. Приведены примеры решения уравнений с различными сложностями, а также проверка корректности решений. Кроме того, обсуждаются свойства корней уравнений и приводятся дополнительные примеры для закрепления материала.

1. Раздел I. ЛИНЕЙНЫЕ УРАВНЕНИЯ
С ОДНОЙ ПЕРЕМЕННОЙ
§ 1. Общие сведения об уравнениях
При решении уравнения надо его упростить и свести к линейному урав­
нению вида ах = Ъ. Для этого необходимо:
• избавиться от знаменателей, если они есть;
• разделить уравнение на линейные, если оно предоставлено в виде
равного нулю произведения сумм;
• раскрыть скобки, если они есть;
• перенести члены с переменными в левую часть, а без переменных —
в правую;
• привести подобные члены.
Кроме того, если после раскрытия скобок сложного уравнения получи­
ли много членов в любой его части, то целесообразно сначала привести
подобные члены, а потом делать переносы. После этого найти корни.
Иногда данное уравнение целесообразно привести к виду, когда в пра­
вой части находится произведение выражений, а в левой нуль. При этом
следует помнить: произведение равняется нулю, если хотя бы один из
множителем равняется нулю.
8.Решим уравнения:
а) 25 + х = 37; х = 37 - 25; х = 12.
б) х - 12 = 23; х = 23 + 12; х = 35.
в) 24 - х —18; —х = 18 —24; - х = - 6; х - 6.
г) 3,7 - х = 1,9; ~х - 1,9 - 3,7; -х = -1 ,8 ; х = 1,8.
2 2 1
д) 1= —+ г, х = 1 — ; х - —.
3 3 3
е) 13 = 74 - х; х = 74 - 13; х = 61.
9. Решим уравнения:
а) 6х = 30; х = 30 : 6; х = 5. б) Ьу - 0; у = 0 : 5; у = 0.
в) Аг - - 8; г = -8 : 4; г - -2 . г) 2х + 3 = 19; 2х = 19 - 3; х = 16 : 2; х = 8.
д) Зу - 4 = 1; Зу = 1 + 4; Зу = 5;у = 5 : 3; у - 1~.
«ж
е) 1 - Зх = 25; -З х = 2 5 - 1 ; -З х = 24; х = 24 : (-3); х = - 8.
10. Решим уравнения:
2 2 3 15 „1
а ) —х ~ 5 ; х ~ 5 : х = 5 •—; х = — ; х = 1 —ш
3 3 2 2 2
* 5б>-?*'=!; *=1:(-? ) ®=1{ - | ) *=~1;
ч ^ 3 5 3 5 3 3 3 4 1
в) 1— х - — х = ----- 1; — х —— ; х - ; х ——.
4 8 4 8 4 8 8 3 2
11. а) Члены уравнения Зх - 5= 12: Зх; —5; 12.
б) Члены уравнения 18 - Ьх - 4 4- 2x1 18; -5 х ; 4; 2х.
в) Члены уравнения 0,8л: + 3 = 4,6: 0,8*; 3; 4,6.
12. а) В уравнении 2х + 35 = 24 выражение 2х + 35 — левая часть, число
24 — правая часть.
б) В уравнении 47# - 15 = 83 выражение 47у - 15 — левая часть, число
83 — правая часть.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

2. в) В уравнении342 - 15- 282+ 3 выражение342 -1 5 — леваячасть, выражение
282+ 3 — правая часть.
13. Чтобы определить, какое число надо вписать в квадратики, чтобы по­
лучилось правильное равенство, обозначим это число через х и решим
полученное уравнение:
а) Зх + 11 = 32; Зх = 32 - 11; Зх = 21; х = 21 : 3; х = 7.
Ответ: в квадратик надо вписать число 7.
б) 2х - 9 = 15 - х; 2х + х = 15 + 9; Зле = 24; х = 24 : 3; х = 8.
Ответ: в квадратик надо вписать число 8.
14. Покажем, что уравнение:
а) х - 2 = Зх имеет решение х —- 1.
Ответ: дс= —1 является решением, потому что при подстановке в уравнение
-1 вместо х9 получим правильное равенство: - 1-2 = 3* ( - 1); —3 = —3.
б) 82 - 5 = 5г имеет решение 2=
Ответ: г —— является решением, потому что при подстановке в урав-
3
нение ~ вместо 2, получим правильное равенство: 8-
- - 5 = — ; 13—~ 5 —8-і; 8- = 8- .
3 3 3 3 3 3
(О
15. Покажем, что уравнение:
а) х(х - 3) = 0имеет решения х - 0, х = 3.
Произведение х(х —3) при данных значениях х всегда будет равняться О,
так как хотя бы один из множителей будет равняться О: или х = О, или
х - 3 = Опри х = 3. Ответ: уравнение имеет решения х = О, х = 3.
б) 2(2- 2)(2+ 3) = Оимеет решения 2= О, 2= 2, 2= “3.
Произведение 2(2- 2)(2+ 3) при данных значениях г всегда будет рав­
няться О, так как хотя бы один из множителей всегда будет равняться О:
ИЛИ2= 0, ИЛИ2 - 2 = 0 при 2= 2, ИЛИ 2 + 3 = 0 при 2= -3 .
Ответ: уравнение имеет решения г = 0, 2= 2, г = -3 .
17. Смотри объяснение к упражнениям 8-10.
а) х - (3 - 2х) = 9; х - 3 + 2х = 9; Зх = 9 + 3; Зх = 12; х = 12 : 3; х - 4.
Проверка: найдем значение левой части уравнения при * = 4:
4 - ( 3 - 2 -4 ) = 4 - ( 3 - 8 ) = 4 + 5 = 9.
Значения левой и правой частей уравнения равны: 9 = 9.
Ответ: х = 4.
б) 8 - (3* - 2) = 13; 8 - Зх + 2 = 13; -З х = 13 - 8- 2; -3 * = 3;
х = 3 : (—3); л; = - 1.
П роверка: найдем значение левой части уравнения При дс = -1 :
8- (3 •(-1) -2 ) = 8- (-3 - 2) = 8 + 5 = 13.
Значения левой и правой частей уравнения равны: 13 = 13.
Ответ: д: = —1.
в) 3(х - 2 ) = 27; * - 2 = 27 :3 ; * - 2 = 9; * = 9 + 2 ; * = 11.
П роверка: найдем значение левой части уравнения при х = 11:
3(11 - 2) = 3 * 9 = 27.
Значение левой и правой частей уравнения равны: 27 = 27.
Ответ: х = 11.
Решим уравнения 18—23. Смотри объяснение к упражнениям 8—10.
18. й) 2(х - 3) = 36; х - 3 = 18; х = 18 + 3; х = 21.
б) 4(5 - х) = 12; 5 - * = 3; -х = 3 - 5; - х = -2 ; х = 2.
в) 0,1(дс + 1) = 1;дс + 1 = 1 : 0,1; х + 1 = 10; х = 10 - 1; х = 9.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

3. 19. а) 3(x + 5) = 27; * + 5 = 2 7 :3 ;л : + 5 = 9;л: = 9 - 5 ;д : = 4.
б) 5(jc - 3) = 15; x -3 = 15 : 5; x -3 = 3; x = 3 + 3; x = 6.
в) 8(3 - x) = 40; 3 - x = 40 : 8; 3 - x = 5; -x *- 5 - 3; —x = 2; x = -2 .
20. a) 4(* + 1) + 11 = 31; 4(* + 1)= 31 - 11; 4(x + 1) = 20; x + 1 = 20 ; 4;
x + 1 = 5; x = 5 - 1; x = 4.
б) 10 + 3(z - 2) = 1; 3(z - 2) = 1 - 16; 3(z- 2) = -1 5 ; z - 2 = -1 5 : 3;
z - 2 = -5 ; z = -5 + 2; z = -3 .
в) ö(y ~ 3) - 12 = 73; 5(1/ - 3) = 73 + 12;5(у - 3)= 85; (у- 3)* 85:5;
у - 3 = 17; у - 17 + 3; у = 20.
г) 47 + 2{х + 4) = 7; 2(х -i- 4) = 7 - 47; 2(х + 4)= -4 0 ; х +4 =-4 0 :2;
л: + 4 = -2 0 ; jc = -2 0 - 4; х = -2 4 .
21- а) 5(2* - 3) = 50; 2х - 3 = 50 : 5; 2х - 3- 10; 2х = 10+ 3; 2* =13;
х = 13 : 2; х = 6,5.
б) 37(8* - 23) = 37; 8л: - 23 = 37 : 37; 8л: - 23 = 1; 8* = 1 + 23; 8х = 24;
х = 24 : 8; х = 3.
в) 52(17 - 8л:) = 52; 17 - 8х = 52 : 52; 17 - 8х = 1; - 8л: = 1 - 17;
- 8л: = -1 6 ; л: = -1 6 : ( - 8); х = 2.
г) 84(37 - 17z) = 168; 37 - 17 z = 168 : 84; 37 - 17z = 2; -17z = 2 - 37;
OK 1
-17z = -3 5 ; z = -3 5 : (-17); z = — ; z = 2 — .
17 17
22. a) 3x + (7 - je) = 10; 3x + 7 —x = 10; 2x = 10 - 7; 2л: = 3; ж= 3 : 2; л: = 1,5.
б) 2л: - (3 —x) = 18; 2x - 3 + x = 18; 3# = 18 + 3; 3x = 21; x = 21 : 3; x = 7.
в) 8z - (5 - 3z) = 17; 8z - 5 + 3z = 17; 11z = 17 4- 5; 11z = 22; z * 2.
г) 12y + (5 - 2y) = -1 5 ; 12y + 5 - 2y = -1 5 ; lOy = -1 5 - 5; lOy = -2 0 ;
у = —20 : 10; у - - 2.
23. а) 2л: - (х - 3) = 20; 2л: - х + 3 = 20; х = 20 - 3; х = 17.
б) 5 - (4i/ -i/) = 10; 5 - Зу = 10; -Зу = 1 0 - 5 ; -Зу = 5; у = - l | .
в) 4z - (7 + 3z) = 2; 4z - 7 - 3z = 2; z = 2 + 7; z = 9.
r) 17y + (8- 15y) = 4; 17y + 8- 15y = 4; 2y = -4 ; у = -4 ; 2; у = -2 .
24. За три тетради и толковый словарь заплатили 16,2 грн. Известно, что
толковый словарь стоит вдвое больше, чем три тетради. Найдите стоимость
толкового словаря и трех тетрадей.
Решение. Пусть стоимость трех тетрадей х грн., тогда стоимость словаря
будет 2х грн. Их общая стоимость — (л: + 2л:) грн., которая по условию
задачи равняется 16,2 грн. Составим уравнение:
х + 2х = 16,2; Зле = 16,2; х = 16,2 : 3; х = 5,4.
2х = 5,4 *2; 2х = 10,8.
Стоимость 3-х тетрадей — 5,4 грн. Стоимость толкового словаря — 10,8 грн.
П роверка: 1) стоимость толкового, словаря вдвое больше стоимости трех
тетрадей: 10,8 : 5,4 = 2;
2) за толковый словарь и три тетради заплатили 16,2 грн.:
10,8 + 5,4 = 16,2.
Ответ: стоимость трех тетрадей — 5,4 грн.; стоимость толкового слова­
ря — 10,8грн.
25« Решение. Чтобы найти задуманное число, нужно составить уравнение.
Для этого обозначим это число буквой х . Умножив его на 3, получим Зл:.
Если к произведению прибавим 18, получится (Зл: + 18).
Составим уравнение:
Зх + 18 = 63; Зл: = 63 - 18; Зл: = 45; л: = 45 : 3; л: = 15.
Ответ: 15 — задуманное число.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

4. 26- Решение. Обозначим задуманное число буквой х . Если его умножить
на 7, получим 7х, после вычитания от произведения числа 16 получим
(7л: —16). Так как по условию задачи это число равняется 33, составим
уравнение: 7л: - 16 = 33.
7х - 16 * 33; 7л: = 33 + 16; 7л: = 49; х = 49 : 7; х = 7.
Ответ: 7 — задуманное число.
Решим уравнения 27—29. Смотри объяснение к упражнениям 8—10.
27. а) —(б-9ж ) = 15; - в - - - 9 х = 15; 4 - 6 * = 15; - 6* = 11; х = - 1 - .
З у ' 3 3 6
б) - - ( 12- * ) = ? ; 12- * = ® : - ; 12- * = 2; - х = 2- 12; * = 10.
. С м Д . . . . ц . - . . м ,
5 5 5 5
28. а) (3* - 2) : 2 = 18; 3* - 2 = 18 * 2; 3* - 2 = 36; 3* = 36 + 2;
2
Зл: = 38; х = 38 : 3; х —12—.
3
б) (5* - 3) : 3 = 9; 5л: ~ 3 = 9 •3; 5* - 3 = 27; 5л: = 27 + 3; 5* - 30;
х = 30 : 5; х = 6.
в) (41 - х) : 9 = 4;41 - х = 4 * 9; 41 - х = 36;- х =36 - 41; - х = -5 ;.
х = - 5 : (-1); х = 5.
29. а) 2(3* - 2) + 4 = 30; 2(3л: - 2) = 30 - 4; 2(3л: - 2) = 26; Зл: - 2 = 26 : 2;
Зх - 2 = 13; 3* = 13 + 2; 3* = 15; х = 15 : 3; х = 5.
б) 3(2 - л:) + 25 = 28; 3(2 - х) = 28 - 25; 3(2 - л:) = 3; 2 - х = 3 : 3;
2- х = 1; - х = 1- 2; - * = —1; л: = 1.
2 / ч 1 2 / ч 1 2 а 2 2 2
в) - - {л :- 4 ) + ~ = 5; - ( л : - 4 ) = 5 - - ; -* (д :-4 ) = 4 - ; л :-4 = 4 ~ : - ;
3 1 ' 3 3 1 } 3 3 1 ’ 3 3 3
14 3 ^ гг гг ^ 4х~ 4 - ------- ; * - 4 = 7; * = 7 + 4; х = 11.
3 2
г ) | (1- 2*) + | = - 2; | .(1- 2х) = - 2- 1; | -(1- 2х) = - 2 ± ;
1 - 2 * = - 2 —: —; 1 - 2 * = - — *—; 1 - 2 * = -5 ; ~2х = - 5 - 1 ; - 2дс= - 6;
7 7 7 3
л: = - 6: ( - 2); * = 3.
Решим уравнения 30—32. Смотри также объяснение к упражнениям 8—10.
Чтобы решить уравнения, записанные в виде пропорции (равенства отно­
шений чисел), необходимо преобразовать уравнение, пользуясь основным
свойством пропорции: если пропорция правильная, то произведение ее
крайних членов равняется произведению средних членов.
30- а) 6* : 8= 3 : 2; 6* •2 = 8 •3; 12л: = 24; х = 24 : 12; х = 2.
б) 5 : (2*) = 3 : 18; 2х •3 = 5 18; 6* = 90; * = 90 : 6; * = 15.
в) 1 : (Зл:) = 4 : 12; Зх * 4 = 1 ■12; 12* = 12; х = 12 : 12; х = 1.
31. а) (л: - 5) : 2 = 3 : 4; 4(* - 5) = 2 * 3; 4(х - 5) = 6; х - 5 = 6 : 4;
х - 5 = 1,5; х = 1,5 + 5; х = 6,5.
б) 5 : (с - 3) = 2 : 3; 2(с - 3) = 5 - 3;2(с - 3)= 15; с - 3 = 15 : 2;
с - 3 = 7,5; с = 7,5 + 3; с = 10,5.
в) 7 : 4 = 5* : 3; 4 •5* = 7 •3; 20* = 21; * =21 :20; * = 1,05.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

5. 3 2 . а) 2 : т = т : 8; т •т = 2 - 8; т2 = 16; т —-4 ; т = 4 ( т = ±4).
б) х : 10 = ОД : х; х *х = 10 •ОД; х2= 1; зс = —1; л; = 1 (х = ±1).
в) 2п : 9 = 2 : п; 2п •п = 9 *2; 2л2= 18; п2= 9; п = —3; п = 3 (п = ±3).
Решите уравнения 33—35, проверку сделайте самостоятельно.
Чтобы решить уравнения, в которых неизвестное находится под знаком
модуля, надо сделать перенос членов уравнения из одной части урав­
нения в другую так, чтобы выражение, которое находится под знаком
модуля, было в левой части уравнения, а другие члены уравнения —
в правой. Таким образом получим уравнение, которое можно решить,
пользуясь примером 3) раздела «Хочешь знать еще больше?», с. 8—9
учебника.
33. а) |х|+ 5 = 12; х~ 12 - 5; |х|= 7; х = —7 или х = 7. Ответ: -7 ; 7.
б) |х|- 8= —3; |х|= —3 + 8; х= 5; х = -5 или х = 5. Ответ: —5; 5.
в) 2|х|+ 3 = 25; 2|лс|= 2 5 - 3 ; 2|х|= 22; [х|= 22 : 2; |х|= 11; х = -11 или * = 11.
Ответ: —11; 11.
34. а) х + 4|= О; х + 4 = 0; х = -4 . Ответ: -4 .
б) |* - 2| = 12; * - 2 = -1 2 ; х = -1 2 + 2; х = -1 0 ;
или х - 2 = 12; х = 12 + 2; х = 14. Ответ: -10; 14.
в) |х - 1| + 7 = 3; |х - 1|= 3 - 7; |х —1| = - 4 . Ответ: уравнение решений
не имеет, так как равенство |х —1|= -4 неверное, потому что модуль любого
выражения является числом неотрицательным.
35. а) |2х - 3|= 5; 2х - 3 = -5 ; 2х = - 5 + 3; 2х = -2 ; х - -2 : 2; х = -1 ;
или 2х —3 = 5; 2х = 5 + 3; 2х = 8; х = 8 : 2; х = 4. Ответ: —1; 4.
б) |2х| - 3 = 5; |2х|= 5 + 3; |2х|= 8; 2х = - 8; х = -8 : 2; х = -4 ;
или 2х = 8; х = 8 : 2; х = 4. Ответ: -4 ; 4.
в) 2|х - 3|= 5; х- 3|= 5 : 2; |х -3( = 2,5; х - 3 = -2 ,5 ; х = -2,5 + 3; х = 0,5;
или х - 3 = 2,5; х = 2,5 + 3; х = 5,5. Ответ: 0,5; 5,5.
36*. Чтобы определить, при каком значении а уравнение будет иметь задан­
ный корень, подставим значение переменной х в это уравнение, тогда по
определению корня уравнения получим правильное равенство, которое
содержит неизвестное а. Решим полученное уравнение относительно а .
а) Зах + 96 = 0 имеет корень х = —8.
Тогда: За *(—8) + 96 = 0; -24а = —96; а = —96 : (-24); а = 4.
Ответ: при а = 4 — х = -8 является корнем данного уравнения.
^ а 1 ЛГ¥, а п 1 ^ а 1
б) 1 х = — имеет корень х = 2. Тогда: 1 ------ 2= — ; 1----- = — ;
4 2 4 2 2 2
1 ! 1 ^1 Л1 ( ^ 3 ( 01; а = - 1—; а = -1- : — ; а = ------(-2);
2 2 2 2 2 ) 2 у }
а
а
~ 2
Ответ: при а = 3 корнем данного уравнения является — х = 2.
в) 4(а - 3)х = 72 имеет корень х = 6. Тогда:
4(а - 3) - 6= 72; 24(а - 3) = 72; а - 3 = 72 : 24; а - 3 = 3 ;а = 3 -*-3 ;а = 6.
Ответ: при а = 6корнем данного уравнения является — х = 6.
37*. Чтобы определить, при каком значении т заданные уравнения будут
иметь общий корень, надо решить уравнение, которое не имеет парамет­
ра т 9 найденное значение х подставить в другое уравнение, полученное
уравнение решить относительно переменной т.
а) 2(х + 3) = 36; х + 3 = 3 6 : 2 ; х + 3 = 18; х = 18 —3; х = 15.
х = 15 является корнем уравнения х : 3 + 2т = 19, поэтому 15 : 3 + 2т = 19 —
верное равенство. Найдем т:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

6. 15 : 3 + 2т = 19; 5 + 2т = 19; 2т = 1 9 - 5 ; 2т = 14; т - 14 : 2; т = 7.
Ответ: при т - 7 уравнения имеют общий корень.
б) (8- х) 7 = 28; (8-х ) = 28 : 7; 8- х = 4; - х = 4 - 8; - х = -4 ; х = 4.
х = 4 является корнем уравнения 5(2х —3т) = 0, поэтому 5(2 *4 —Зт) = 0 —
верное равенство. Найдем т: 5(2 *4 - З т) = 0; 5(8 - З т) = 0;
2
8- З т = 0 : 5; 8 - З т = 0; -З т = —8; т = -8 : (-3); т - 2 —.
3
2
Ответ: при т - 2 — уравнения имеют общий корень.
3
в) (Зх - 2) : 2= 17; Зх - 2 = 17 - 2; Зх - 2 = 34; Зх = 34 + 2; Зх = 36;
х = 36 : 3; х = 12. х = 12 является корнем уравнения (х : 3 + 8 )2т = 48,
поэтому (12 : 3 + 8)2т = 48 — верное равенство.
(4 + 8 )2 т = 48; 12 - 2 т = 48; 2 4 т = 48; т = 48 : 24; т = 2.
Ответ: при т - 2 уравнения имеют общий корень.
38*. Определим, при каком значении к уравнение не будет иметь корней:
а) Уравнение х2= Ъ. не будет иметь корней при отрицательных значени­
ях ку так как квадрат любого числа принимает только неотрицательные
значения. Ответ: при отрицательных значениях И уравнение не будет
иметь корней.
б) Выполним преобразование уравнения |х|+ к - 0; |х|= -к . Модуль лю­
бого числа является числом неотрицательным, поэтому уравнение не
будет иметь корней, если —к будет принимать отрицательные значения,
то есть, если к будет принимать положительные значения. Ответ: при
положительных значениях к уравнение не будет иметь корней.
в) Выполним преобразование уравнения к + 2х = 2(х —3); к + 2х = 2х —6;
&+ 2х - 2х = - 6; к = - 6. Так как получили равенство, которое не зависит
от х, то заданное уравнение не будет иметь корней, если равенство к = —6
будет неверным. Равенство &= -6будет неверным, если к будет принимать
любое значение, кроме - 6.
Ответ: при любом значении к * - 6уравнение не будет иметь корней.
39. Обозначим ширину прямоугольника как х см, тогда длина прямоуголь­
ника будет Зх см, так как по условию задачи она втрое больше, чем ши­
рина. Периметр прямоугольника считается по формуле Р = 2(а + Ь), где
а и Ъ — ширина и длина прямоугольника. Периметр данного прямоуголь­
ника 2(х + Зх) см, что по условию задачи составляет 60 см.
Составим уравнение: 2(х + Зх) = 60; 2- 4х = 60; 8х = 60; х = 60 : 8; х = 7,5.
Ответ: ширина прямоугольника 7,5 см.
40. Обозначим ширину прямоугольника как х см, тогда его длина 2х см. Пе­
риметр прямоугольника составляет 2(х + 2х) см, что по условию равняется
50 см. Составим уравнение: 2(х + 2х) = 50; 2 •Зх = 50; 6х = 50;
1 1 2
х = 50 : 6; х = 8—. Длина прямоугольника: 2х = 2 •8—; 2х = 16 —.
3 3 3
2
Ответ: длина прямоугольника: 1 6 - см.
3
41. Обозначим длину стороны меньшего квадрата как х см, тогда длина
стороны большего квадрата будет 2х см, так как по условию задачи она
вдвое больше. Периметр большего квадрата (4 - 2х) см, а меньшего 4х см.
Учитывая, что разность периметров большего и меньшего квадратов рав­
няется 50 см, составим уравнение:
4 * 2х - 4х = 50; 8х - 4х = 50; 4х = 50; х = 50 : 4; х = 12,5.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

7. Длина стороны большего квадрата: 2х - 2 * 12,5; 2х = 25.
Ответ: 25 см.
42. Обозначим половицу возраста дедушки как х лет, тогда возраст де­
душки будет составлять 2х лет. Если дедушка проживет еще столько же
и еще половину, это будет составлять 2х + 2х + х, что по условию задачи
составляет 200 лет. Составим уравнение: 2х + 2х + х = 200; Ъх - 200;
х = 200 : 5; х = 40. Возраст дедушки 2х = 2 *40; 2х - 80.
. Ответ: возраст дедушки 80 лет.
43. Обозначим через х количество лет, через которое дочь будет вдвое младше,
чем отец. Через х лет отцу будет (34 + х) лет, дочери — (12 + х) лет. Учи­
тывая, что дочь будет в это время вдвое младше отца, составим уравнение:
34 + х - 2(12 + х); 34 + х = 24 + 2х х —2х - 24 - 34; - х = -1 0 ; х - 10.
Ответ: через 10 лет дочь будет вдвое младше отца.
44. Решение.
I способ. Обозначим количество быков в череде как х. Треть череды состав­
ляет быков, а две трети от —составляют —-—, или 70 быков. Получаем
3 3 3 3
0 V о.у
уравнение: —*—= 70; — = 70; 2х = 9 •70; 2х = 630; х ?=630 : 2; х - 315.
3 3 9
I I способ. Обозначим треть от трети всей череды как х быков, тогда треть
всей череды составляет Зх быков, а вся череда 3 •Зх быков, то есть 9х
быков. Так как пастух вел две трети от трети череды, то он вел 2х быков,
что составило 70 быков. Составим уравнение: 2х = 70; х = 70 : 2; х = 35.
Количество быков в череде 9х быков. 9х = 9 *35; 9х = 315.
Ответ: в череде 315 быков.
45. а) 3,7 - 1,2 : 0,4 * 3,7 - 12 : 4 = 3,7 - 3 = 0,7;
б) 2,8 + 8,1 : 2,7 = 2,8 + 81 : 27 = 2,8 + 3 = 5,8;
в) (7 - 8,5) : 0,5 = -1 ,5 : 0,5 = -1 5 : 5 = -3 ;
г) —4,9 : (2,3 - 1,6) = -4 ,9 : 0,7 = -4 9 : 7 = -7 ;
д) 3 : 0,2 + 8 •2,5 * 30 : 2 + 20 = 15 + 20 = 35;
е) 12,1 : 0,11 + 1 : (-0,2) = 1210 : 11 - 10 : 2 = 110 - 5 = 105;
е) 0,2® + 0,32= 0,008 + 0,09 = 0,098;
з) (-0 ,4 )2- 1,22= 0,16 - 1,44 = -1 ,2 8 ;
ж) (3 - 1,4) : 0,22= 1,6 : 0,04 = 160 : 4 =*40.
46. а) Если а = 2, то 2 а + 5 = 2 * 2 + 5 = 4 4 -5 = 9;
б) если т = 8, то 2,3 - 3т - 2,3 - 3 * 8 = 2,3 - 24 = - 21,7;
1в) если а = — и с = 0,5, то
3 2 3
о О 2 3 4 + 9 13 0 1
2а + Зс - 2 - + 3 0,5 = - + 1,5 = - + - = --------= — = 2 - ;
3 3 3 2 6 6 6
г) если а = — и с ~ 0,5, то
3
2 (а + 3с) = 2 Г| + 3 0,б) =
( 2 3
( Ь 1-5) -
Г2 3>
1 3
—+ —
3 2
= о 2 + 9 _ _ 11 1 1 ^ 11 э 2
6 6 0 Я 3 ~ 3
47, Обозначим коэффициент пропорциональности как х %тогда первое число
составляет 2х, второе — Зх, третье — 5х. Сумма этих чисел 2х + Зх + Ьх,
что по условию задачи равняется 300. Составим уравнение:
2х + Зя + Ъх - 300; 10х = 300; х = 30.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

8. Тогда первое число 2х = 2 *30, 2х = 60; второе число Зх = 3 * 30, Зх = 90;
третье число 5* = 5 * 30, 5х - 150.
Отпветг число 300 является суммой чисел 60, 90, 150.
§ 2. Равносильные уравнения
Чтобы доказать равносильность уравнений, надо доказать, что они име­
ют одни и те же корни или совсем не имеют,корней. Можно также путем
выполнения преобразований из одного уравнения получить другое, ему
равносильное. Для этого можно в любой части уравнения раскрыть скоб­
ки, свести подобные члены; перенести любой член из одной части урав­
нения в другую, заменив его знак на противоположный; обе части урав­
нения умножить или разделить на одно и то же число, отличающееся от
нуля. В результате указанных действий всегда, кроме исключительных
случаев, получим уравнение, равносильное данному. Исключительными
являются случаи, когда в результате преобразований хотя бы в одной
из частей уравнения исчезает деление на выражение с переменной или
сокращается квадратный корень из выражения с переменной. В таком
случае следует указывать значения переменной, при которых возникает
деление на нуль или извлечение квадратного корня из отрицательного
числа, и исключить эти значения из решения уравнения, об этом вы
узнаете в следующем классе.
ш
I
ш
X
о
к
гО-I
о
53. Подберем к каждому из уравнений равносильное, используя основные
свойства уравнений.
а) Если в уравнении 7х + 8 = 10 перенести слагаемое 8 в правую часть,
получим равносильное уравнение 7х = 10 - 8.
б) Если в уравнении 12 - Зх = 0 перенести уменьшаемое 12 в правую часть,
получим равносильное уравнение -З х = - 12.
в) Если в уравнении 5х - 2 = 2х —5 члены уравнения, которые содержат
х, перенести в левую часть, а те, которые не содержат х, в правую, полу­
чим равносильное уравнение 5х - 2х = —5 + 2.
ос^ 3
г) Если обе части уравнения -------= 3 —х умножить на 5, получим рав-
5
носильное уравнение х + 3 = 15 - 5х.
1 3
д) Если обе части уравнения —•(3 - 6х) = —умножить на 4, получим рав-
2 4
носильное уравнение 2(3 - 6х) = 3.
е) Если обе части уравнения —+ Зх = х умножить на 3, получим равно-
3
сильное уравнение 1 + 9х = Зх.
54. Перенесем члены с переменными из правой части в левую, а без пере­
менных — в правую:
а) 12х - 3 = х + 2; б) 152 + 8 = 2г; в) - т - —- 3 - —пг;
12* - * = 2 + 3. 15г - 2г = - 8. 2 3 2
1 1 о 2—т + —т = 3 + —.
2 2 3
55. Перенесем члены с переменными из левой части в правую, а без пере­
менных — в левую:
а) 7х + 4 = 9х; б) 3 8 - 2 п - 2п; в) 1 - 0,5г = 1,5з;
4 = 9х - 7х. 38 = 2п + 2л. 1 = 1,5г -I- 0,5г.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

9. Решим уравнения 56—59. Смотри объяснение к упражнениям 8—10.
56. Решим уравнения: ^
а) 12у + 3 = 1/ - 7;. 12у - у = -7 - 3; Н у = -1 0 ; у = -1 0 : 11; у = - — .
2
б) 5х + 2х + 5 = 4л:; 5л: - 4л: + 2х = -5 ; Зх = -5 ; * - - 5 : 3 ; х = - 1 —.
О
в) 0,7 - 2с = Зс + 1,7; -2 с - Зс = 1,7 - 0,7; -5 с = 1; с = 1 : (-5); с = -0 ,2 .
57. а) 2л: - 1 = Зх; 2л: - Зх = 1; - х = 1; х = -1 .
б) 5у + 6= 2у; 5у - 2у = - 6; 3у = - 6; у = -6 : 3; у = -2 .
в) 0,82- 1 = 0,32; 0,8г - 0,32 = 1; 0,52 = 1; г = 1 : 0,5; 2= 2.
2
г) 2 + 37* = 40*; 37* - 40* = -2 ; -3* = -2 ; * = -2 : (-3); * = - .
О
д) 1 - 0,5с = 0,5с; -0,5с - 0,5с = -1 ; -1 *с = -1 ; с = 1.
е) 3 + 4,7л: = 4,7л:; 4,7* - 4,7х = -3 ; 0 = -3 , что является неверным ра­
венством. Решений нет.
5 8 . а) 3(х - 5) = 2х - 7; Зх - 15 = 2л: - 7; Зх - 2х = -7 + 15; зс = 8.
б) 4(£ - 0,9) = 1,2 + 21; 41 - 3,6 = 1,2 + 21; 4 1 -2 1 = 1,2 + 3,6;
21 = 4,8; I = 4,8 : 2; I = 2,4.
в) 7л: - 4(х - 3) = 12; 7х ~ 4л: + 12 = 12; Зл: = 12 - 12; Зх = 0; х = 0.
г) 16 - (2 - 5лг) = 29; 16 - 2 + 5х = 29; 5* = 29 - 16 + 2; 5х = 15; х = 3.
59. а) —ас = 1 2 - * ; - * + * = 12; * + — = 12; - * = 12; * = 1 2 - - ; * = 9.
3 3 3 3 4
2 2 „ 2у + 3у „ 5 „ 3 27 .2
б) -г / = 9~у; дУ+г/ = 9; — = *» д» = 9; !/ = 9' 5; у = ~5“: у 5-
, 1 1 1 1 2- 6г 1 5
в)—2= —+ 2; - 2-2 = —; ---------= —; — 2= —; 2
6 3 6 3 6 3 6 3
1 6 2
2= ; 2= .
3 5 5
5 5 . 5 5 . 5
г )5 у = — + у; 5у - у = - - ; у = ; У = ~32*
2 2 2д) —л: + 8= 8; - х = 8 - 8 ; —х = 0; х = 0.
3 3 3
ч . 1 1 . 1 1 -28с + с 1 1е) -4с = с; -4с + —с = —; ------------= —; -27с = 1; с = ------- .
7 7 7 7 7 7 27
60. а) Так как 2х - 3 равняется х + 17, то 2х - 3 = х + 17.
2х —3 = х + 17; 2х - х = 17 + 3; х = 20.
Ответ: х = 20.
б) Так как х + 37 вдвое больше, чем х —15, то х + 37 = 2(х —15).'
х + 37 = 2х - 30; х - 2х = -3 0 - 37; - х = -6 7 ; х = 67.
Ответ: 67.
Решим уравнения 61—68. Смотри объяснение к упражнениям 8—10.
6 1 .а) —( 2 * -3 ) = 1; —-5 (2 * -3 ) = 1-5; 2 * - 3 = 5; 2* = 8; * = 8 :2 ; * = 4.
5 5
б) ~ ( 4 + 3*) = | ; | -9 (4 + 3*) = | 9; 4 + 3* = 3; 3* = —1; * = ~ £-
в ) | ( 2 - 3 * ) = ф ^ -7 (2 -3 * ) = ~ 7 ; 3 (2 -3 * ) = 1; 6 - 9 * = 1;
5
-9 х = 1 - 6 ; -9 х - -5; х = —.
9
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

10. 9у 7 2х. 7 1
62. а) — + —= 1 ; ----- 9 + —-9 = 1-9; 2ж-3 + 7 = 9; 6х = 9 - 7 ; 6х = 2; х = —.
3 9 3 9 3
б) — - — = 7; — 1 0 - — 10 = 7-10; З с 2 - с = 70; 6с - с = 70;
5 10 5 10
5с = 70; с = 70 : 5; с = 14.
В) ^ _ ^ = _2; —-8- — •8= -2•8; л 2г-3л = -16; -л = -16; л = 16.
4 8 . 4 8
63. а) —+ ———= —; —•9 + ——- -9 = —-9; 2 + 3(х - 2) = 5; 2 + Зх - 6= 5;
9 3 9 9 3 9
Зх - 4 = 5; Зх = 5 + 4; Зх = 9; х = 9 : 3; х = 3.
б) 1 _ 1'± Ё = _2^ ; —•8- 1 ^ 5 .8= - 2—■8; 3 - 4 (1/ + б) = -18;
8 2 4 8 2 4 ' ’ ,
3 - 4# - 20 = —18; -4у = - 1 8 - 3 + 20; -4у = -1; {/ = - 1 :( - 4 ) ; у = - .
4
х —3 2х х —3 2х
в) —— - — —= 2; — -9 - — -9 = 2-9; (х - 3) * 3 - 2х =18;
3 9 3 9
Зх - 2х - 9 = 18; х = 18 + 9; х = 27.
64. а) 5(0,6/71 - 2) = 2{т - 3,6); 3т —10 = 2т - 7,2; 3т - 2т = —7,2 + 10;
тп= 2,8.
б) 3(1,2л + 8) = 4(5 —0,1л); 3,6л + 24 = 20 - 0,4л; 3,6л + 0,4л = 20 - 24;
4л = -4 ; л = - 4 : 4; л = -1 .
в) 2(11 - 6х) - 3(7 - 4х) = 1; 22 —12х - 21 + 12х = 1; 1 = 1.
Так как равенство верно, х — любое число.
г) 7(у + 6) = 4(3*/ - 5) - 3; Чу + 42 = 12у - 20 -3 ; 7у - 12у =-2 3 - 42;
-5у = -6 5 ; у = -6 5 : (-5); у = 13.
д) --(б + *) = —(2*-15); — 3(б + *) = - ( 2 * -1 5 )-3 ; 6+ * = 2 (2 * -1 5 );
3 3 3 3
6+ х = 4х - 30; х - 4х = -3 0 - 6; -Зх = -36; х = -36 : (-3 ); х = 12.
*> ^(7 " 2*) = | (8* + 4 ! ) | -4 (7 -2 * ) = | ( 8* + 4 | }-4 ;
2(7- 2*) = з|в;с + у 1 ; 14 - 4* = 24* +14; -2 8 * = 0; * = 0 :(-2 8 ); * = 0..
6 5 .а) - ( * - 2 ) = - ( 5 * - 2 4 ) ; - ( * - 2 ) - 5 = - ( 5 * - 2 4 ) - 5 ; 3(х - 2) = 2(5* - 24);
5 5 5 5
Зх - 6 = 10х - 48; Зх - 10х = -4 8 + 6; —7х = -42; х = -4 2 : (-7); х = 6.
б) | (* + 2) = | (7* + 12); | -б (* + 2) = ^ (7* + 12) б; 5 (* + 2) = 7* + 12;
5х +10 = 7х +12; 5х - 7х = 1 2 -1 0 ; -2 х = 2; х = 2 : (-2); х = -1 .
в) 0,4(6х - 1) = 0,1(12х + 5); 2,4х - 0,4 = 1,2х + 0,5; 2,4х - 1,2х = 0,5 + 0,4;
1,2х = 0,9; х = 0,9 : 1,2; х = 0,75.
г) 0,5(7х + 8) = 1,5(7х + 8); 0,5(7х + 8) : 0,5 = 1,5(7х + 8) : 0,5;
7х + 8= 3(7х + 8); 7х + 8= 21х + 24; 7х - 21х = 2 4 - 8 ; -1 4 х = 16;
х = 16 : ("14); х = - ~ ; х = -1 у .
д) 5* —— ——(3* + 4);5 *-3 - —•3 = —(3* + 4)-3;1 5 * - 2 = 3 * + 4;
3 3 3 3
15х —Зх = 4 + 2; 12х = 6; х = 6:12; х = 0 ,5 .
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

11. е) !/-|(2|,-5) = 1 ^ - 2 г,; у 4 - | ( 2 * - 5 ) - 4 = | . 4 - 2 у 4 ;
4у - 3(21/ - 5) = 5 - 8*/; 4у - 6у +15 = 5 - 8у; ~2у + 8у = 5 -1 5 ;
6у = - 10; у = - 10: 6; у = у = - 1~ .
66. а) 2,5(у + 6) = у + 1,5(1/ -10); 2,5у + 15 = у + 1.5* - 15;
2,5у - у - 1,5|/ .= -1 5 - 15; 0 = -3 0 .
Так как равенство неверно, то уравнение решений не имеет,
б) 0,75(4 - *) - 0,5* = 5(0,05* + 3); 3 - 0,75* - 0,5* = 0,25* + 15;
-1 ,6 * = 12; * = 12 : (-1,5); * = - 8.
„ ч 3* + 7 х - 3 5*+ 2 3* + 7 0 х - 3 0 5* + 2 0
67 . а ) ------------------- = ----------; —*о ------------о ---------- о;
4 2 8 4 2 8
2(3* + 7) - 4(* - 3) = 5* + 2; б* + 14 - 4* +12 = 5* + 2; 2* - 5* = 2 - 26;
-3 * = -2 4 ; * - -2 4 : (-3); * = 8.
_ч 5* - 4 7 - * 3* +1 5* - 4 _ 7 - * _ 3* +1 _
б) ---------= --------+ —- — ; ----------- 6= --------- 6+ -----------6;
. 3 2 6 3 2 6
2(5* - 4) = 3(7 - *) + 3* + 1; 10* - 8« 2 1 - 3* + 3* + 1; 10* = 22+ 8;
10* = 30; * = 30 : 10; * = 3.
68. а) 8 ^ . 1 0 _ Ь % . 1 0 = 6 £ ± 1 7
5 2 10 5 2 10
2(8 - 3у) - 5(1 - 2у) = Ъу + 17; 16 - 6у - 5 + 10у = 6у + 17; 4у - Ьу = 17 - 11;
- 2у = 6; у = 6 : ( - 2); у = -3 .
б) 1 ^ 4 * = 1 ^ 2 * _ * ± 3 2 - 4 * 1- 2* £ + 3
5 3 4 5 3 4
12(2 - 4*) = 20(1 -2 * ) -1 5 (* + 3); 24 - 48* = 20 - 40* - 15* - 45;
-4 8 * + 55* = -2 5 - 24; 7* = -4 9 ; *.= -4 9 : 7; * = -7 .
6 9 . Обозначим число, которое надо вычесть, через х. Если вычесть от 135 это
число, получим 135 - *, а если от 83 вычесть это число, получим 83 - *.
Учитывая, что первая разность в 3 раза больше второй, составим уравнение:
135 - * = 3(83 - *); 135 - * = 249 - 3*; - * + 3* = 249 - 135;
2* = 114; * = 114 : 2; * = 57. Ответ: надо вычесть число 57.
70. Обозначим число, которое надо прибавить, как *. Если прибавить его
к 207, получим 207 + *, а если прибавить его к 33, получим 33 + *. Учи-'
тывая, что первая сумма в 4 раза больше второй, составим уравнение:
207 + * = 4(33 + *); 207 + * = 132 + 4*; * - 4* = 132 - 207;
—3* = —75; * = —75 : (—3); * = 25. П роверка. Если к 207 прибавить 25, полу­
чим 232. Если к 33 прибавить 25, получим 58. Найдем частное 232 : 58 —4,
удовлетворяющее условию задачи. Ответ: надо прибавить число 25..
71. Обозначим одно из чисел через * , тогда второе число 120 - *. После деле-
*
ния первого числа на 5 получим —, а после деления второго числа на 3 по­
лучим ——. По условию задачи эти частные равны. Составим уравнение:
3
х 120- * * . „ 120- * п
— = -------- ;~ •15 =*-- 15; 3* = 5(120 - *); 8* = 600 - 5*;
о о о 3
3* + 5* = 600; * = 600 : 8; * = 75. Первое число * = 75, второе число
120 - * = 120 —75; 120 - * = 45. Ответ: числа 75 и 45.
72. Обозначим меньшее из чисел через *, тогда большее число будет * + 12.
0,7 меньшего числа — 0,7*, 0,3 большего — 0,3(* + 12) и по условию
задачи они равны. Составим уравнение:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

12. 0,7* = 0,3(д: + 12); 0,7* = 0,3* + 3,6; 0,7х ~ 0,3л: = 3,6; 0,4* = 3,6;
* = 3,6 : 0,4; х = 9. Меньшее число равняется 9, большее х + 12 = 9 + 12;
х + 12 = 21. Ответ: 9 и 21.
73. Обозначим первое из чисел через *, тогда второе число будет 425 - х.
20 % первого числа — 0,2*, а 30 % второго — 0,3(425 - *), и по условию
задачи они равны. Составим уравнение: 0,2* = 0,3(425 - х);
0,2* = 127,5 - 0,3*; 0,2* + 0,3* = 127,5; 0,5* = 127,5; * = 1 2 7 ,5 :0 ,5 ; * = 255.
Первое число 255, второе число — 425 —* —425 - 255; 425 —* = 170 , то
есть второе число 170. Ответ: числа 255 и 170.
74. Обозначим массу угля на втором складе как * т, тогда масса угля на
первом складе составляет 2* т. После того, как на первый склад привезут
еще 84 т угля, на нем будет (2* + 84) т; после того, как на второй склад
привезут еще 140 т угля, на нем станет (* + 140) т. По условию задачи
угля на первом и втором складе станет поровну. Составим уравнение:
2х + 84 = * + 140; 2х - х - 140 - 84; * = 56. На втором складе 56 т угля.
На первом складе 2х = 2 •56; * = 112, то есть 112 т угля.
Ответ: на первом складе 112 т, на втором — 56 т угля.
75. Обозначимколичествобензинаво втором баке как * л, тогдав первом — 2х л.
Если из первого бака отольют 17 л бензина, в нем станет (2* - 17) л; если
во второй бак дольют 17 л, в нем станет (* + 17) л, и в двух баках бензина
станет поровну. Составим уравнение: 2 * —17 = * + 17;
2* - * = 17 + 17; * = 34. Во втором баке 34 л, а в первом — 2* = 2 *34 = 68,
то есть 68л. Ответ: в первом баке — 68л, во втором — 34 л бензина.
76*. Чтобы определить значение числа а, при котором будут равносильны­
ми данные уравнения, найдем корень уравнения, которое не содержит
а, заменим найденным значением * во втором уравнении и решим его
относительно о.
а) Решим уравнение 2(х - 1) = 4 - * ; 2х - 2 = 4 - *; 2* + * = 4 + 2;
3* = 6; * = 6 : 3; * = 2.
Решим уравнение ах = * + а, заменив * числом 2. а •2 = 2 + а; 2а - а = 2; а *=2.
Ответ: при а = 2 уравнения равносильны.
б) Решим уравнение *2= 0; * = 0.
Решим уравнение (1 - а)х = *, заменив * числом 0. (1 - а) * 0 = 0; 0 = 0.
Равенство верно при любом значении а.
Ответ: уравнения равносильны при любом а.
77*. Найдем значение а, составив уравнение, учитывая, что по условию при
* = -1 значение выражения равняется 4.
—1+ а) , к 3(—1+ а) 3 (—1+ а)
----------- + 0,5*(-1) + 3 = 4; -------- ^ -0 ,5 = 4 - 3 ; —^-------- ^= 1 + 0,5;
2 2 2
3(-1 + д) 3 3
= 1,5; -1 + а = —: —; -1 + а = 1; а = 1 + 1; а = 2.
2 2 2
Найдем значение выражения при а = 2 и * = 5:
3(5+ 2) + 0 ,5-6 + 3 = — + 2 ,5 + 3 = 10,5 + 5,5 = 16; Ответ-. 16.
2 2
78*. Найдем значение /п, составив уравнение, учитывая, что по условию при
2
* = 1— значение выражения равняется 16:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

13. тп—4
= 1 4 -1 5 ;
т
= - 1:
т - 4
(-3) = -1 *(-3); т - 4 = 3;
т = 3 + 4; т = 7. Найдем значение выражения при т = 7 и х = -
9
Ответ: 0,6.
7 9 . Ответ:
13 28 37
410 66 62
75 84 99
а) 80 2 б) 1024 2 в) 1001
40 2 512 2 91
20 2 256 2 13
10 2 128 2 1
5 5 64 2
1 32 2
16 2
8 2
4 2
2 2
1
11
7
13
81
Ответ: а) 80 = 24* 5; б), 1024 = 210; в) 1001 = 1 1 - 7 - 1 8 .
а 02
+11§ 2,
5
ит вет : а; ои = • о; о), =
(
1 Я а 92 Л4
4,3* — + 11* 2,25 :2 ,75 = 9,1
43 Ь )
1) 4,3
43
1 * - А = А = 0,3;
10 43 10
2) 11—-2,25 = — -2—= 29*® ' ® 261
5 5 4 5-Х а
3) 0,3 + 26,1 = 26,4;
26,4 «640“*‘
4 )2 6 ,4 :2 ,7 5 =
Ответ: 9,6.
10
48
2,75 ОГ7ГГ21*),
26,1;
9,6.
82. а) Полусумма чисел т и п :
«л
т + п
; б) полуразность чисел 2х и Зг:
2х —3г
2 ' ' 2
83. Определим, на сколько число 40 больше 32— 40 - 32 - 8.
Определим, на сколько процентов число 40 больше числа 32 — 8: 32 = 0,25,
то есть на 25 % . Определим, на сколько процентов число 32 меньше 40 —
8 : 40 = 0,2, то есть на 20 %.
Ответ: 40 больше 32 на 25 %; 32 меньше 40 на 20 %.
§ 3. Линейные уравнения
87 . а) 2 - Зх = 5 - 7х; 7х - Зх = 5 - 2; 4х = 3. б) 0 = 7х - 5; -7 х = -5 .
г)
1
—х -
3
х - 4
в 1
2 8
1 1
6 - ~ х ; —# + —д
2 3 2
К
1
і
= 1; ------ •2 =
2
6; - * = 6
1 * 2 ; х —4 = 2;аг = 2 + 4;ае = 6.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

14. Чтобы привести уравнение к линейному уравнению вида ах = Ъ9 надо:
избавиться от знаменателей, если они есть; раскрыть скобки, если они
есть; перенести члены с переменными в левую часть, а числа — в пра­
вую; привести подобные члены.
88. Приведем уравнение к линейному:
а) 2х + х - 7х + 3 = 8; б) у - 5у = 8 - у; в) Зх + 2(х + 7) = 2х;
-Ах = 8 - 3 ; - 4у + у = 8; Зх + 2х + 14 = 2х;
—Ах = 5. -3 у = 8. Зх +- 2х —2х = —14;
Зх = -1 4 .
г) 4(2 + х) - х = Зх +9; д) —с + 31(2 - с) = 32с; е) 0,7 = 2(х + 3,5) - 2х;
8 +•4х - х - Зх = 9; -с + 62 - 31с = 32с; 0,7 = 2х + 7 —2х;
Ох = 9 - 8; - с - 31с - 32с = -6 2 ; Ох = 7 —0,7;
Ох = 1. Ох = 6,3.
89. Чтобыопределить, сколько решений имеет уравнение, надо свести его к виду
ах —Ь. Если а ф 0, уравнение имеет одно решение; если а = 0; Ь - 0, уравнение
имеет множество решений; если а = 0и Ь* 0, уравнение не имеет решений.
а) 2х - 3 = х + 7; 2х - х = 7 + 3; х = 10. Ответ: одно решение.
б) Зх + 7 = Зх - 9; Зх - Зх = -9 - 7; Ох - -1 6 . Ответ: решений нет.
в) 2(3х - 1) = 3(2х + 1); 6х - 2 = 6х + 3; 6х - 6х = 3 + 2; 0 = 5.
Ответ: решений нет.
Решим уравнения 90—96. Смотри объяснение к упражнениям 8—10.
90. а) 32х = -1 6 ; х = -1 6 : 32; х - -0 ,5 .
б) -1 5 г = 0,5; г = 0,5 : (-15); 2= — — ; г = - — .
150 30
в) х + 4х = 5х; 5х - 5х = 0; 0 = 0. Равенство верно, поэтому х — любое число.
г) -0,5у = -0 ,5 ; у = -0 ,5 : (-0,5); у = 1.
д) 6х = 8+ 6х; 6х —6х = 8; 0 = 8. Равенство неверно; решений нет.
е) х - 4х = 5х; -Зх - 5х = 0; - 8х = 0; х = 0 : (-8); х = 0.
91 . а) Ох = 35; 0 = 35. Равенство неверно; решений нет.
б) Оу = 13 —13; 0 = 0. Равенство верно; у — любое число.
в) 2х = 3 + 2х; 0 = 3. Равенство неверно; решений нет.
3 2
92. а) 0,52 = 6+ —г; - г - —г = 6; —2= 6; 2= 6: —; 2= 36.
3 2 3 6 6 .
б) 0,2х + 5 = —х; —х ——х = -5; 0 = -5 . Равенство неверно; решений нет.
5 5 5
5 8
в ) —х + 7 = 0,6х; —х - 0 ,6 х =-7 ; —х - —х = -7 ;— х = -7 ; х = -105.
3 3 3 5 15
93. а) 4 - Зх = 8(1 — х);4 - Зх =8—8х; -З х + 8х = 8- 4; 5х = 4; х = —.
5
б) 2 - 5у = 5(1 - 2у); 2 - = 5 - 10у; - Ьу + Му = 5 - 2; 5# = 3; у = |.
в) х = 3(х + 1) - 2х; х = Зх + 3 - 2х; х = х + 3 ; х - х = 3 ; 0 = 3.
Равенство неверно; решений нет.
г) 2(5 - 8х) = -4(4х + 3); 10 - 16х = -1 6 х - 12; -16х + 16х = -1 2 - 10;
0 = -2 2 . Равенство неверно; решений нет.
94. а) 8(9 - 2х) = 5(2 - Зх); 72 - 16х = 10 - 15х; -16х 4- 15х = 10 - 72;
-х = -6 2 ; х = 62.
б) 5(2+ 3) = 8(10 - 2); 52 + 15 = 80 - 82; 52 + 82= 80 —15; 13г = 65;
2= 65 : 13; 2= 5.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

15. в) 2(* - 3) = 3(2* - 1); 2х - 6= 6* - 3; 2* - 6* = -3 + 6;
-4 * = 3; х = 3 : (-4); х = -0 ,7 5 .
г) 4(5 ~ х) = -5 * + 2; 20 - 4х = -5 * .+ 2; -4 х + 5* = 2 - 20; х = -1 8 .
9 5 . а) у —1,08 = 0,2(5 + у); у - 1,08 = 1 + 0,2у; у - 0,2у = 1 + 1,08;
0,8у = 2,08; у = 2,08 : 0,8; у = 2,6.
б) 0,3(1 - с) = с + 0,04; 0,3 - 0,3с = с + 0,04; -с - 0,3с = 0,04 - 0,3;
-1 ,3 с = -0 ,2 6 ; с = 0,26 : 1,3; с = 0,2.
в) 3 - 5* = 0,3(2* + 1); 3 - 5* = 0,6* + 0,3; -5 * - 0,6* = 0,3 - 3;
27
-5 ,6 * = -2 ,7 ; * - -2 ,7 : (-5,6); * =
56
г) 1 - 3(* - 5) = 7(3 - 2*); 1 - 3* + 15 = 21 - 14*; -3 * + 14* = 21
11* = 5; * = 5 : 11; * = — .
11
2
, 1 1 3 1 3 1 5 1 I f 5^
96. а) — * — = - х ; - - * — * = - ; — * = - ; * = - : — ;
2 3 4 2 4 3 4 3 3 { 4 J
1 - 1 5 ;
* =
4^
15
б) = %t - 0 ,6 t = -
3 5 3 5
в а
2 3 1 1 1
—t — t = —; — t -
3 5 5 15 5
3;
4 4
в) - 0,82+ 1= ~ z; — z
' 5 5
- z = - l ;
5
8
, - и =
( - 5)- -! ■
97. Решим уравнение, пользуясь для вычислений микрокалькулятором:
а) 235* = 408; б) 18,7у = 9,7; в) -3 2 ,4г = 58,8;
* = 408 : 235; у=9,7 : 18,7; 2 = -5 8 ,8 : 32,4;
* «в 1,73617; у«0,51872; 2* -1,81481;
* * 1,736. ( у * 0,519. 2 1,815.
98. Найдем корни уравнений:
а) 492* + 317 = 923 —
с точностью до тысячных.
492* = 923 - 317;
492* = 606; * = 606 : 492;
* = 1,2317073; * * 1,232.
б) 2,382 - 5,87 = 3,41 —
с точностью до стотысячных.
2.382 = 3,41 + 5,87;
2.382 = 9,28; 2 = 9,28 : 2,38;
2 = 3,8991597; 2 * 3,89916.
Решим уравнения 99—103. Смотри объяснение к упражнениям 8—10.
99. а) 3(* + 4) + 6(11 - *) = 9; 3* + 12 + 66 - 6* = 9;
3* - 6* = 9 - 12 - 66; -3 * = -6 9 ; * = 69 : 3; * = 23.
б) 8(1 - *) + 5(* - 2) = 2; 8 - 8* + 5* - 10 = 2; -8 * + 5* = 2 - 8 + 10;
“3* = 4; 4 : 3 ; * = - 1-
3
в) 7(ж - 5) - 3(2* - 6) = 10; 7* - 35 - 6* + 18 = 10; * = 10 + 35 - 18; * = 27.
г) 5(3 - 2*) - (12 + 7*) = 0; 15 - 10* - 12 - 7* = 0; -1 0 * - 1х = 12 - 15;
-1 7 х = -3 ; х = -3 : (-17); х = — .
17
100. а) 7(4 - t) + 3(t - 5) = 9t; 28 - 7t + 3t - 15 = 91; - 7 1 + 3t - 9« = 15 - 28;
-1 3 t = -1 3 ; * = 13 : 13; t = 1.
в) 42 - 1,2(2 - 62) = 1 - 52; 42 - 2,4 + 62= 1 - 5z; 102+ 52 = 1 + 2,4;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

16. 1Ъг = 3,4; г = 3,4 : 15; г - 2=
б) 3(х + 1,5) + 2(3 + х) = ~5; Зх + 4,5 + 6 + 2х = -5 ; 5х = -5 - 6- 4,5;
5* = -1 5 ,5 ; * = -15,5 : 5; х = -3 ,1 .
г) 2,5х - 1,7(5 - 2х) = Зх; 2,5х —8,5 + 3,4х = Зх; 5,9х - Зх = 8,5;
85 27
2,9х = 8,5; х = 8,5 : 2,9; х = — ; х = 2-— .
29 29
101. а) 8 + 3(х - 5) + х = 2(3 + 2х); 8 4- Зх - 15 + х = 6+ 4х;
4х —•4х = 6 + 7; 0 = 13. Ответ: уравнение не имеет решений.
б) 2 4- 2(4 4- г) = Зг 4- 8; г 4- 8 + 2г = Зг 4- 8; г 4- 2г - Зг = 8 —8; О= О.
Ответ: уравнение имеет множество решений.
_ 1 2х + х - 4х _ 1
2 4 У _/ ' 2 4 2 ' 2 4 Х ~ 2 * 4 ~ 2
, 1 1 / л X X 1 X X
в) - х + —( х - 2) = х; —+ -------- = х; —+ -----
2-±.
2 2*
1 1 1 А О О
— х = - ; —х = —*4; —х = 2; х = -2 .
4 2 2
1 ^1 Ч 1 2 2
г) —+ 21 —п + 11 = 3п; —+ —п+ 2 = Зп; —п -З п
2 УЗ ) 2 3 3
2 п -9 п - 4 - 1 7 5 5 3 15 ^ 1
---------- = ----------; — п = — ; л = ------ ; п = — ; п = 1— .
3 2 3 2 2 7 14 14
102. а) ^ (4 * -5 ) + - ( 2 * + 1) = * + 3; - 2 ( 4 * - 5 ) + --2 ( 2 * + 1) = (* + 3)-2;
2 2 2 2
' 4 х - 5 + 3(2х +1) = 2х + 6; 4 х - 5 + 6х + 3 = 2х + 6; 1 0 х - 2х = 6+ 5 - 3 ;
8х = 8; х = 8: 8; х = 1. Ответ: х = 1.
б) | (5 -3 * ) + |(2 + 9*) = 2 * -1 ; 3(5 - 3*) + 1 3(2 + 9*) = (2х -1 )-3 ;
2 (5 -З х ) + 2 + 9х = б х -3 ; 1 0 -6 х + 2 + 9х = б х -3 ; ~3х = -15;
х = —1 5 : (—3); х = 5. Ответ: х = 3.
в) —(6+ 7 * ) - 2 * = —(4 + 3*) + 3; --5 (б + 7 * )- 2 * - 5 = - - 5 ( 4 + 3*) + 3-5;
5 5 5 5
3(6 + 7х) - 1 0 * = 2(4 + 3*) +15; 18 + 21* -1 0 * = 8+ 6* +15;
2 1 * - 1 0 * - 6* = 15 + 8 -1 8 ; 5* = 5; * = 5 :5 ; * = 1. Ответ,'. * = 1.
г) 2 + ^ (8* + 1) = 5* + | (4 * -1 ); 2 -4 + ^ (8* + 1)-4 = 5 * -4 + | (4 * -1 )-4 ;
8 + 8 х + 1 = 20* + 3 (4 * -1 ); 8* + 9 = 20* + 12* - 3;
8х - 20х - 12х = -3 - 9; -2 4 х = -1 2 ; х = -1 2 : (-24); х = 0,5;
Ответ: х = 0,5.
103. а) 3(2х + 3) - 5(7 - 4х) - 2(5х + 4) = - 2; 6х + 9- 35 + 20х - 10х - 8= -2 ;
6х +. 20х - 10х = -2 - 9 + 35 + 8; 16х = 32; х = 32 : 16; х = 2.
Ответ: х = 2.
б) 8(4 - Зх) + 7(х - 3) + 3(9 + 7х) - 10; 32 - 24х + 7х - 21+ 27 + 21х = 10;
-2 4 х + 7х + 21х = 10 - 32 + 21 - 27; 4х = -28; х = -2 8 : 4; х = “ 7.
Ответ: х = -7 .
в) 6(х + 2) + 3(3х + 7) = 4(5 + 4х) - 7; 6х + 12 + 9х + 21 = 20 + 16х - 7;
6х + 9х - 1 6 х = 20 - 7 - 12 - 21; - х = -2 0 ; х = 20.
Ответ: х = 20.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

17. г) 5(12 - *) - 11(4* - 5) = 9(9 - 5*) - 26; 60 - 5* - 44* + 55 = 81 - 45* - 26;
-5 * —44* + 45* = 81 - 26 - 60 —55; —4* = -6 0 ; * = -6 0 : (—4); * = 15.
Ответ: х = 15.
Решим задачи, составив к ним уравнения.
104. Решение. Обозначим первое число через *. Тогда вторым числом будет
(х - 6). Если первое умножить на 5, то будет 5*, а второе умножить на 4,
то получим 4(* - 6). По условию задачи составим уравнение:
5* - 4(* - 6) = 40; 5* - 4* + 24 = 40; * = 40 - 24; * = 16. Первое число 16,
тогда вторым числом будет 16 - 6= 10. Ответ: 16 и 10.
105. Решение, Обозначим первое число через *. Так как второе число в 6 раз
больше, то оно будет составлять 6*. Исходя из условия задачи, (6* - 37)
должно равняться (* + 73). Значит, получаем уравнение: 6* - 37 = х + 73;
6* - * = 73 + 37; 5х = 110; * = 110 : 5; * = 22.
Первое число 22, тогда вторым числом будет 22 * 6= 132.
Ответ: 22 и 132.
106- а) Обозначим одно из чисел через *, тогда второе число (155 - *). По
условию задачи разность этих чисел равняется 91.
* - (155 - *) = 91; * - 155 + * = 91; 2* = 91 + 155; 2* = 246;
* = 246 : 2; х = 123. Одно число 123. Второе число 155 - х = 155 - 123;
155 —* = 32. Ответ: 123 и 32.
б) Обозначим меньшее число через * , тогда большее число * + 47. Полусум-
* + * + 47
ма этих чисел ---------------, что по условию задачи равняется 46. Составим
2
х + х + 47 2* + 47 2 *+ 47
уравнение: -------------- = 46; = 4 6 ; ------------2 = 46 *2; 2* + 47 = 92;
2 2 2
2* = 92 - 47; 2* = 45; х = 45 : 2; * = 22,5.
Меньшее число 22,5; большее число * + 47 = 22,5 + 47; * + 47 = 69,5.
Ответ: 22,5 и 69,5.
107. Обозначим число, которое надо найти, через *, тогда его третья Часть - *.
1 3
По условию числобольше своей третьей частина —.
Составим уравнение: * - —* = —; * •3 ——* •3 = —*3; 3* - * = 1; 2* = 1;
3 3 3 3
х = 1 : 2; * = і . Ответ: число —.
2 2
108. а) Сумма чисел х и 15 — * + 15, а их разность — * - 15. Составим урав­
нение, учитывая, что сумма чисел в два раза больше их разности:
* + 15 = 2(* - 15); * + 15 = 2* - 30; * —2* = -3 0 - 15; —* = —45; * = 45.
Ответ: х = 45.
б) Сумма чисел * и 1,5 — * + 1,5, а их произведение — 1,5*. Составим
уравнение, учитывая, что сумма чисел равняется их произведению:
* + 1,5 = 1,5*; х - 1,5х = —1,5; —0,5* = -1 ,5 ; * = -1 ,5 : (-0,5); * = 3.
Ответ: * = 3. . . , .
т - 1 4 /71+ 14
109. а) Полуразность чисел т и 1 4 --------------, их полусумма--------------- . Соста-
2 2
вим уравнение, учитывая, что полуразность составляет 0,2полусуммы:
т - 1 4 л л т + 14 т - 1 4 л л ^ ггс+14 л
—------ = 0 ,2 -— — ; ------------ 2 =0 ,2 ------------- 2; т - 14 = 0 ,2 (т + 14);
2 2 2 2
т - 14 = 0 ,2 т + 2,8; т - 0,2т = 2,8 + 14; 0 ,8 т = 16,8; т = 16,8 : 0,8;
т = 21. Ответ: т = 21.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

18. б) Полусумма чисел т и 14 — т-+1- , их разность — пг - 14. Соста-
2
вим уравнение, учитывая, что полусумма чисел составляет 120 % их
разности, то есть в 1,2 раза больше разности. ~ + = 1 ,2 (т -1 4 );
_ , |4 2
— *2 = 1 ,2 (т -1 4 ) •2; т + 14 = 2 ,4 (т - 14); т + 14 = 2 ,4 т - 33,6;
2
т - 2 ,4 т = -33,6 - 14; -1 ,4 т = -47,6; т = -47,6 : (-1,4); т =34. Ответ: 34.
110. Решение. Обозначим через * то, что дал первый жертвователь. Тогда по
условию задачи имеем: второй дал 2х; третий — 3 * 2х, что равняется 6*;
четвертый — 4 •6*, что равняется 24*; всего они дали * + 2х + 6х + 24х, что
составляет 132. Составляем и решаем уравнение: * + 2х + 6х + 24* = 132;
33* = 132; х = 132 : 33; * = 4. Ответ: первый жертвователь дал 4.
111. Решение. Обозначим количество гусей через х. Тогда полстолько будет
* *
составлять — гусей, четвертую часть будет составлять — гусей. Исходя
X X -
из условия задачи, составим уравнение: * + * + —+ —+ 1= 100;
2 4
2х + —+ —+ 1 = 100; 4| 2ж+ —+ —+ 1 1= 100• 4; 2х-4 + - - 4 + - - 4 + 4 = 400;
2 4 { 2 4 ) 2 4
8* + 2* + х + 4 = 400; 1Ъ: = 400 - 4; И х = 396; х = 396 : 11; х = 36.
П роверка: 36 + 36 + 36 • — + 36 • —+ 1 = 7 2 + 1 8 + 9 + 1 = 100, удовле-
2 4
творяет условию задачи. Ответ: летело 36 гусей.
112. Решение. Пусть голова весит * г. Тогда туловище весит (* + 150) г, а его
* + 150 „
половина----------- г. По условию задачи голова весит столько, сколько хвост
п 1СП ж+ 150
и половина туловища. Составим уравнение: * = 150 + — - — = *;
* 2 = 150 2 + * + 1 -° 2; 2* = 300 + * + 150; 2* - * = 450; * = 450.
2
Головавесит 450 г , тогдатуловище весит * +150 = 450 +150; * +150 = 600 (г).
Значит, вся рыба весит 600 + 450 + 150 = 1200 (г), или 1 кг 200 г.
Ответ: рыба весит 1 кг 200 г.
113*. Чтобы доказать, что заданные уравнения при любых значениях а имеют
единственный корень, надо привести уравнение к виду линейного уравне­
ния и показать, что множитель перед * отличный от нуля.
а) (о2+ 3)х = 5 — линейное уравнение. Множитель а2 + 3 отличный от
нуля, так как а2 — неотрицательное, а а2 + 3 — положительное. Поэтому
уравнение имеет единственный корень.
б) (а2 + 1)* = а — линейное уравнение. Множитель а2+ 1 отличный от нуля,
так как а2 — неотрицательное, а2+ 1— положительное. Поэтому уравнение
имеет единственный корень.
в) Приведем уравнение а2* = -2 * к виду линейного уравнения: а2* = —2х;
а2х + 2* = 0; (а2 + 2)* = 0. Множитель а 2+ 2 отличный от нуля, так как
а2 — число неотрицательное, а2+ 2 — положительное. Поэтому уравнение
имеет единственный корень.
г) Приведем уравнение 4 - 5* = а2х к линейному: 4 - 5* = а2*; -5 * - а2х = -4 ;
5* + а 2х = 4; (5 + а2)* = 4. Множитель (5 + а2) отличный от нуля, так как
а2 — число неотрицательное, 5 + а2 — число положительное. Поэтому
уравнение имеет единственный корень.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

19. 114*. Все заданные уравнения — линейные. Поэтому:
1) Чтобы уравнение имело единственный корень, необходимо, чтобы мно­
житель неред х не равнялся нулю:
а) уравнение kx = 8имеет единственный корень при любом kyкроме k = О;
б) уравнение (к + 3)* = 5 имеет единственный корень при любом к> кроме
того, при котором k + 3 = О, то есть к = -3 ;
в) уравнение kx —к имеет единственный корень при любом кукроме к = 0;
г) уравнение (2- к)х = (2- К) имеет единственный корень при любом к,
кроме того, при котором 2- к = 0, - k = - 2, к = 2, то есть кроме к - 2.
2) Чтобы уравнение не имело корней, необходимо, чтобы множитель перед
х равнялся нулю, а число, которое находится в правой части уравнения,
не равнялось нулю.
а) уравнение kx = 8 не имеет корней, если к = 0;
б) уравнение (к + 3)* = 5 не имеет корней, если к + 3 = 0, тоесть к = -3 ;
в) уравнение kx = к всегда имеет корни;
г) уравнение (2—k)x - (2- k) всегда имеет корни.
3) Чтобы линейное уравнение имело множество корней, необходимо, чтобы
и множитель перед х, и число, которое находится в правой части уравне­
ния, равнялись нулю.
а) уравнение kx = 8не может иметь множество корней;
б) уравнение (k + 3)* = 5 не может иметь множество корней;
в) уравнение kx - k имеет множество корней, если k - 0;
г) уравнение (2- к)х = (2—k) имеет множество корней, если 2—&= 0,
- k = - 2, k = 2, то есть при к = 2.
115*. X) Примеры уравнений, которые имеют один корень:
о« I о
а) 5* —4 + 2* = х + 2; б) 2(1,5* - 7) - Зх = *; в) =1 .
5
Если эти уравнение привести к линейным, множитель перед х не будет
равняться нулю.
2) Примеры уравнений, которые имеют множество корней:
Q y I О
а) Ьх - 4 + 2х = -4 + 7х; б) 2(1,5* - 7) - 3* * -1 4 ; в) --------= 0,6* + 0 ,4 .
5
Если эти уравнение привести к линейным, и множитель перед х> и число,
которое находится в правой части уравнения, будут равняться нулю.
3) Примеры уравнений, которые не имеют корней:
Зх + 2
а) 5* - 4 + 2х = 7х; б) 2(1,5* - 7) - 3* = 0; в) = 0 ,6 * .
5
Если эти уравнение привести к линейным, множитель перед * будет равнять­
ся нулю, а число, которое находится в правой части, будет отличнымот нуля.
116. а) Квадрат суммы чисел * и у: (* + у)2;
б) сумма квадратов чисел * и у: *2+ у2;
в) разность кубов чисел а и Ь: а3- Ьв;
г) куб разности чисел а и Ь: (а - Ь)3;
д) сумма кубов чисел а и Ь: а3 + Ь3;
е) куб суммы чисел а и Ь: (а + b f.
117. а) При а = 0,2, 5а3= 5 * (0,2)3= 5 * 0,008 = 0,04;
б) при * = -2 , 2*2- *4- 5 = 2* (-2 )2- (-2 )4- 5 ^ 2 - 4 - 1 6 - 5 =
= 8 - 21 = -13;
в) при а = 0,2, а3+ За2= (0,2)3+ 3 * (0,2)2= 0,008 + 3 •0,04 =
= 0,008 + 0,12= 0,128;
г) при а = -1 ,2 , За4- а2= 3 * (~1,2)4- (-1 ,2 )2= 3 * 2,0736 - 1,44 =
- 6,2208 - 1,44 - 4,7808;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

20. д) при х =: 2,5 и у = 3, 1 - (х - у)3 = 1 - (2,5 - З)3= 1 - (-0,5)э =
= 1 + 0,125 = 1,125.
118. Найдем сумму 10 + 11 + 12 + ... + 97 + 98 + 99.
Сумма первого слагаемого и последнего, сумма второго и предпоследнего
слагаемых, и так далее, является одинаковой и равняется: 10 + 99 = 109.
Всего сумма содержит 90 слагаемых, тогда пар слагаемый 90 : 2, и каж­
дая из них равняется 109. Тогда 10 + 11 + 12 + ... + 97 + 98 4- 99 =
- 109 •45 = 4905. Ответ: 4905.
119- Чтобы найти проценты от числа, надо проценты свести к десятичной
дроби, и умножить дробь на заданное число. Учтите, что 1% — 0,01.
а) 20 % от 350: 350 *0,2 = 70. Ответ: 70.
б) 30 % от 5600: 5600 * 0,3 = 1680. Ответ: 1680.
в) 12 % от 0,75: 0,75 * 0,12 = 0,09. Ответ: 0,09.
г) 125 % от 1,4: 1,4 * 1,25 = 1,75. Ответ: 1,75.
д) 15 % от 124 грн: 124 грн - 0,15 = 18,6 грн. Ответ: 18,6 грн.
е) 48 % от 3,5 м: 3,5 м - 0,48 = 1,68 м. Ответ: 1,68 м.
§ 4. Решение задач с помощью уравнений
Чтобы решить задачу с помощью уравнений, надо:
1) неизвестное или одно из неизвестных в задаче обозначить переменной
и записать условие задачи в виде уравнения;
2) решить составленное уравнение;
3) ответить на вопросы, поставленные в задаче.
125- Решение. Так как разность чисел составляет 1,6, то одно число мень­
ше другого на 1,6. Если одно из задуманных чисел обозначим через х, то
второе число будет составлять (# - 1,6). Их сумма равняется 13,6, значит,
можно составить уравнение:
х + (х - 1,6) = 13,6; 2х = 13,6 + 1,6; 2х = 15,2; х = 15,2 : 2; х = 7,6.
Одно число 7,6, тогда второе число 7,6 —1,6 = 6.
Ответ: искомые числа 6 и 7,6.
126. Решение.
1) Из рисунка 19 учебника ясно: в правую окружность нужно вписать
такое число, которое будет равняться сумме 36 и числа, которое надо
вписать в левую окружность, а также будет равняться числу, кото­
рое вписано в левую окружность, помноженному на 3. Исходя из этого
и обозначив число, которое вписано в левую окружность, через х, имеем
х + 36 —3#; х - Зх - —36; 2х = 36; х = 36 : 2; х = 18. Тогда число, которое
вписано в правую окружность, — 3 * 18 = 54.
2) Из рисунка 20 учебника ясно, что в окружности необходимо вписать
два числа, сумма которых равняется 100, а частное составляет 5.
Пусть делителем будет х. Тогда, исходя из того, что частное составляет 5, де­
лимое будет в пять раз больше, то есть 5*. Их сумма будет составлять Ьх + дг,
что равняется 100. Получаем уравнение: 5х + х = 100; 6х ~ 100; х =
50 * 50 к 250 _
х = — — делитель, тогдаделимое будет 5 ------. Выделив целуючасть
3 3 3
ОЛ1 „_2
в обоих числах, получим: 83 — и 16 —.
3 3
1 2
Ответ: 1) искомые числа 18 и 54; 2) искомые числа 8 3 — и 16 —.
3 3
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

21. 127. Решение. Пусть одно число х, тогда второе число в 2 раза больше (отно­
шение 1 : 2), что составляет 2*. По условию задачи составим уравнение:
х + 2 * = 105; Зх =105; х —35. Одно число 35, тогда второе число 2х = 2 *35;
2х = 70. Ответ: искомые числа 35 и 70.
128. Реш ение. Пусть искомое число будет х. Его половина составляет —,
2
* „
а треть — —. По условию задачи составим уравнение:
3
- - - = 0,5; ^ — ^ = 0,5; Зх - 2х = 0 , 5 - 6 ; * = 3.
2 3 6
П роверка: пусть найденное число 3. Его половина 3 : 2, а его третья часть
3 : 3. Разность половины числа и третьей части: 3 : 2 —3 : 3 = 1,5 —1 = 0,5,
удовлетворяющее условию задачи. Ответ: искомое число 3.
129. Реш ение. Пусть сыну х лет. Тогда, исходя из условия задачи, отцу
5* лет, что на 32 года больше, чем сыну, значит, 5х —х = 32; 4* = 32;
х = 32 : 4; х = 8. Сыну 8лет, тогда отцу 5 *8= 40 (лет). Ответ: 8и 40 лет.
130. Реш ение. Пусть площадь большей части поля будет х га, тогда площадь
меньшей части — (ас —130) га. Получаем уравнение: х + х —130 = 430;
2х = 430 + 130; 2х = 560; х = 560 : 2; х = 280. 280 га — площадь большей
части поля, тогда меньшая часть будет 280 - 130 - 150 (га).
Ответ: 150 га, 280 га.
131. Решение. Обозначим более короткую часть веревки через х м, тогда
более длинная часть будет Зх м. Так как длина веревки 84 м, получаем
уравнение: х + Зх = 84; 4* = 84; х = 84 : 4; х = 21. Более короткая часть
веревки — 21 м, тогда более длинная часть — 3 •21 = 63 (м).
Ответ: 21 м и 63 м.
132. Обозначим длину меньшей части веревки как х. Вторая часть на 50 %
длиннее, то есть составляет 150 % от х или 1,5*. Так как сумма частей
веревки 25 м, составим уравнение: * + 1,5* = 25; 2,5* = 25;
х = 25 : 2,5; * = 10. Тогда 1,5* = 15.
Проверка: одна часть 10 м, вторая 15 м, что в сумме составляет 10+ 15 = 25 м.
Вторая часть длиннее на 15 м - 10 м = 5 м. Найдем, на сколько процен­
тов вторая часть длиннее первой: 5 м : 10 м = 0,5, что составляет 50 %.
Условия задачи выполнены. Ответ: 10 м и 15 м.
133. Решение. Пусть бригада должна была за 5 дней изготовить * деталей.
*
Каждый день бригада изготовляла - деталей, что на 12 деталей больше
х х х 5 х _4.зс
нормы, составляющей — деталей. Значит, = 12; ----------- = 12;
5 4 5 20
* = 12 ■20; * = 240. Ответ: 240 деталей.
134. Решение. Пусть более длинная сторона прямоугольника — * см, тог­
да более короткая сторона будет (* - 12) см. Периметр прямоугольника
равняется удвоенной сумме длин двух его сторон и по условию задачи
составляет 118 см. То есть 2 ■(* + * - 12) = 118; * + * - 12 = 59;
2* = 59 + 12; 2* - 71; х = 71 : 2; * = 35,5. Более длинная сторона состав­
ляет 35,5 см, тогда более короткая сторона — 35,5 - 12 = 23,5 (см).
Ответ: 23,5 см и 35,5 см.
135. Решение. Обозначим через * га площадь, которую вспахал третий тра­
кторист, тогда по условию задачи второй вспахал (* + 9) га, а первый —
(* + 9 + 6) га, что вместе составляет 72 га. Получаем уравнение:
* + (* + 9) + (* + 9 + 6) = 72; 3* + 24 = 72; 3* = 72 - 24; 3* = 48;
* = 48 : 3; * = 16.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

22. Третий тракторист вспахал 16 га, тогда второй тракторист вспахал
16 + 9 = 25 (га), а первый — 25 4- 6= 31 (га).
Ответ: первый — 31 га, второй — 25 га, третий — 16 га.
136. Решение. Если количество учеников в первом классе обозначить через х,
то во втором классе будет (х 4- 3) учеников, а в третьем — (х —2) учеников.
Так как в трех классах было 79 учеников, можно составить уравнение:
х + (х + 3) + (х - 2) = 79; Зх + 1 = 79; Зх = 79 - 1; Зх = 78;
х = 78 : 3; х = 26. В первом классе 26 учеников, тогда во втором классе
26 4- 3 = 29 (учеников), а в третьем — 2 6 - 2 - 2 4 (ученика).
Ответ: в первом — 26 учеников, во втором — 29 учеников, а в треть­
ем — 24 ученика.
137- Решение. Пусть в первой корзине — х кг яблок, тогда во второй —
(х + 12) кг, а в третьей — 2х кг яблок. По условию задачи составим урав­
нение: х + (х + 12) 4- 2х = 56; 4х = 56 - 12; 4х = 44; х = 44 : 4; х = 11.
В первой корзине 11 кг яблок, тогда во второй — 11 4- 12 = 23 (кг), а в
третьей — 11 * 2 = 22 (кг). Ответ: в первой — 11 кг, во второй — 23 кг,
в третьей — 22 кг.
138. Купили два рулона ткани, в одном из которых на 10 м ткани больше,
чем во втором. Сколько метров ткани в каждом рулоне, если известно,
что всего купили 50 м ткани?
Решение. Пусть в меньшем рулоне х м, тогда в большем — (х 4- 10) м тка­
ни. Так как всего купили 50 м ткани, составим уравнение: х 4* х + 1 0 = 50;
2х + 10 = 50; 2х = 50 - 10; 2х = 40; х = 40 : 2; х = 20. Тогда: х + 10 = 30.
Ответ: 20 м и 30 м.
139. Решение. Пусть площадь наименьшего участка будет х га, тогда площадь
второго будет составлять 1,5х га, а площадь третьего — (х + 1,5х) га. Исхо­
дя из условия задачи, получаем уравнение: х 4- 1,5х + (х + 1,5х) = 860;
5х = 860; х = 860 : 5; х = 172. Площадь первого участка 172 га, тогда
площадь второго участка составляет 1,5 * 172 = 258 (га), а третьего —
172 4- 258 = 430 (га). Ответ: 172 га, 258 га, 430 га.
х
140. Решение. Пусть в букете было х лотосов. Шиве принесли в жертву — цвет-
о
X X X
ков, Вишну , Солнцу , Бхаване------, а 6лотосов отдали учителю,
5 6 4
X X X X _ X X X X _
значит, получаем уравнение: х = —+ —4 —+ —+ 6; х ---------------------- = 6;
* 3 5 6 4 3 5 6 4
60х —20х —12х - 10х - 15х с Зх с х
-----------------------------------------= 6; — = 6; — = 6; х = 6■20; х = 120.
60 60 20
Ответ: в букете было 120 лотосов.
141. Решение. Пусть у Пифагора было х учеников, из которых математику изу-
X X X
чали —, музыку — —, молчали — — и было 3 женщины. Значит, получа-
х х х л х х х 0 2 8 х - 1 4 х - 7 х - 4 х 0
ем уравнение: х = —+ —+ —+ 3; х -----------------= 3 ; -----------------------------= 3;
к 2 4 7 2 4 7 28
Зх
—г = 3; х = 28. Ответ: 28 учеников.
28
142. Решение. Пусть через х лет отец будет в 3 раза старше сына. Тогда в это
время сыну будет (10 4- х) лет, а отцу будет 3(10 4- х) или (40 4- х) лет,
отсюда: 3(10 4- х) = 40 + х; 30 + Зх = 40 4- х; Зх - х = 40 - 30; 2х - 10;
х = 10 : 2; х = 5. Ответ: через 5 лет.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

23. 143. Пусть сейчас Галке * лет, тогда Сороке — 2* лет. В позапрошлом
году Галке было {х - 2) лет, а Сороке — (2* - 2) лет. Так как Соро­
ка в позапрошлом году была старше Галки втрое, составим уравнение:
2х - 2 = 3(* - 2), откуда; 2х - 2 = Зле - 6; 2х - 3* = -6 + 2; - х = -4 ; х = 4.
Тогда 2х = 2 * 4 = 8. Ответ: Сороке 8лет.
144. Решение. Обозначим расстояние между пристанями через х км. Так
как по течению катер плывет со скоростью 20 4- 2 = 22 (км/ч.), а против
течения — со скоростью 20 - 2 = 18 (км/ч.), то по течению катер плыл
X X
— часов,а противтечения — часов. Поусловиюзадачиполучаемуравнение:
22 18 •
х х 9* +11* 20 к 10 2 л 99
— + — = 5; -------------= 5; -----х = 5; — * = 5; — * = 1; х = — ; * = 49,5.
22 18 198 198 99 99 2
Ответ: 49,5 км‘.
145. Решение. Обозначим расстояние между пристанями через * км. Так как
по течению скорость катера 15 + 2 = 17 (км/ч.), а против течения 15 - 2 =
* X
= 13 (км/ч.), то по течению катер плывет — часов, а против течения —
17 13
часов. По условию задачи получаем уравнение:
х х 1 1 7 * -1 3 * 1 221 ««со е ^ Л„
----------- = —; ---------------= —; х ----- ; * = 27,625. Ответ: 27,625 км.
13 17 2 221 2 8
146. Решение. Пусть расстояние между станциями будет * км. Двигаясь со
скоростью 70 км/ч., состав преодолеет расстояние за — часов, а со ско-
х
ростыо 60 км/ч. — за — часов. Исходя из условия задачи, имеем:
* * 1 7 * - 6 * 1 420
-----= —; ------------------- =—; х ------;х = 210. Ответ: 210 км.
60 70 2 420 2 2
147. Решение. Пусть скорость пассажирского состава * км/ч., тогда скорость
товарного (* - 20) км/ч. За 3 часа пассажирский состав пройдет 3* км,
а товарный за 4 часа — 4 *(* - 20) км. По условию задачи получаем урав­
нение: 3* 4 * (* “ 20) = 10; 3* - 4* + 80 = 10; - * = 10 - 80; - * = -7 0 ;
* = 70. Скорость пассажирского состава — 70 км/ч., тогда скорость товар­
ного 70 —20 = 50 (км/ч.).
Ответ: 70 км/ч., 50 км/ч.
148. Решение. Обозначим скорость велосипедиста на грунтовой дороге как
* км/ч., тогда его скорость на асфальтированной дороге — (* + 4) км/ч.
По грунтовой дороге велосипедист проехал 2* км, а по асфальтированной —
1 км. По условию задачи получаем уравнение:
2* + (* + 4) = 28; 3* = 28 - 4; 3* = 24; * = 24 : 3; * = 8.
8км/ч. — скорость велосипедиста на грунтовой дороге, тогда на асфаль­
тированной дороге его скорость будет составлять 4 + 8 = 12 (км/ч.).
Ответ: скорость на асфальтированной дороге — 12 км/ч., а на грунто­
вой — 8 км/ч.
149. Решение. Обозначим расстояние от станции до турбазы через * км.
х х
До турбазы туристы шли — часов, а назад часов, что на 1 ч. мень-
4 5 .
* * , 5* - 4 *
ше, значит, = 1; ----------- = 1;зс = 20.
4 5 20
Ответ: расстояние от станции до турбазы 20 км.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

24. 150- Пусть искомое число х. Если к нему прибавить 4, получим (* + 4); если
к нему прибавить 19, получим (* + 19). По условию первая сумма отно­
сится ко второй как 8 : 1 1 . Составим уравнение: (* + 4) : (х + 19) = 8 : 1 1 ,
откуда: (яг + 4) * 11 = (* + 19) •8; 11* + 44 = 8* + 152; 11* - 8* = 152 - 44;
Зле= 108; * = 108 : 3; * = 36. Ответ: 36.
151. Пусть большее из чисел Хутогда меньшее — (100 —х). Так как при деле­
нии большего числа на меньшее получим в частном 4 и в остатке 5, составим
уравнение, помня, что делимое равняется сумме делителя, умноженного на
частное, и остатка: * = (100 - *) *4 + 5, откуда: * = 400 - 4* + 5; * + 4* ~ 405;
5* = 405; * = 405 : 5; * = 81. Тогда 100 - * = 100 - 81 = 19.
Ответ: 81 и 19.
152. Пусть л — коэффициент пропорциональности, тогда количество работ­
ников первого деха — 8п работников, а второго — 5л работников. Так как
количество работников первого цеха превышает количество работников
второго на 12, составим уравнение: 8л - 5л = 12, откуда: Зл = 12; л = 1-2 :3 ;
л = 4. Тогда: 8л = 8 •4 = 32; 5л = 5 * 4 = 20.
Ответ: работников первого цеха 32, второго — 20.
153. Пусть * — коэффициент пропорциональности, тогда в I цехе — 3* ра­
ботников, во II цехе — 2* работников. Если из I цеха перейдут во II цех
8 работников, то в I цехе станет (3* - 8) работников, а во II цехе — (2* + 8)
работников. Так как после перехода отношение количества работников
станет 5 : 6, составим уравнение: •(3* - 8) : (2* + 8) = 5 : 6, отку
(3* - 8) * 6 = (2* + 8) * 5; 18* - 48 =10* + 40; 18* - 10* = 40 + 48;
8* = 88; * = 88 : 8; * = 11. Тогда 3* - 8 = 3 • 11 - 8; 3* - 8= 2
а 2* + 8= 2 * 11 + 8; 2* + 8= 30.
Ответ: в I цехе будет 25 работников, а во И цехе — 30 работников.
154. Пусть * — количество лет к моменту, когда мать втрое старше доче­
ри. Тогда матери в-это время (38 + *) лет, а дочери (12 + *) лет. Соста­
вим уравнение: 38 + * = (12 + *) * 3, откуда: 38 + * = 36 + 3*; * —3* =
= 36 - 38; -2 * = -2 ; * = -2 : (-2); * = 1.
Ответ: через год мать станет в 3 раза старше дочери.
Если * — количество лет к моменту, когда мать вдвое старше дочери,
тогда составим уравнение: 38 + * = (12 + *) * 2, откуда: 38 + * = 24 + 2*;
* - 2 * = 24 - 38; —* = -14; х = 14.
Ответ: через 14 лет мать будет в 2 раза старше дочери.
155- Пусть сыну * лет, тогда матери — * + 20 лет. Так как их года со­
относятся, как 7 : 2, составим уравнение: (* + 20) : * = 7 : 2, откуда:
(* + 20) •2 = * •7; 2* + 40 = 7*; 2* - 7* = -4 0 ; -5 * = -4 0 ; * = -4 0 : (-5);
* = 8. Тогда * + 20 = 8 + 20; * + 20 = 28. Ответ: матери 28 лет.
156. Пусть в позапрошлом году дочери было * лет, а матери — 5* лет. В сле­
дующем году дочери будет (* + 3) лет, а матери (5* + 3) лет. Так как дочь
в следующем году будет младше матери в 4 раза, составим уравнение:
5* + 3 = (* + 3) *4, откуда 5* + 3 = 4* + 12; 5* - 4* = 12 - 3; * = 9. Тогда
5* = 5 *9; 5* = 45. Если в позапрошлом году дочери * лет, а матери 5* лет,
то в этом году дочери (* + 2) лет, что составляет * + 2 = 9 + 2 ; * 4 - 2 = 11,
а матери (5* + 2) лет, что составляет 5* + 2 = 45 + 2; 5* + 2 = 47 лет.
Ответ: дочери 11 лет, а матери 47 лет.
157. Пусть первая цифра числа * , тогда вторая — (8- *), а само число —
(* • 10 + (8 - *)). Если цифры поменять местами, то получим число
((8- *) *10 + *), что на 18 больше, чем первое число. Составим уравнение:
(8- *) *10+ * - (* *10+ (8- *)) = 18, откуда: 80 - 10* + * - (10* + 8- *) =
= 18; 80 - 9 * - 10* - 8 + * = 18; -9 * - 10* + * = 18 - 80 + 8; -1 8 * =
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

25. = -5 4 ; * = -5 4 : (-18); х = 3. Тогда первая цифра числа * = 3, а вторая —
8 - ас = 8 —3; 8 “ ас = 5. Ответ: число 35.
158. Пусть данное число х. Если приписать справа к нему цифру 9, то пос­
ледняя цифра числа переместится в разряд десятков, а цифра 9 — в разряд
единиц, поэтому число можно записать так: х *.10 + 9. Если к этому числу
прибавить удвоенное число х, то получим х •10 + 9 + 2*, что по условию со­
ставляет 633. Составим уравнение: х *10 + 9 + 2* = 633, откуда: 10* + 2х =
= 633 - 9; 12* = 624; * = 624 : 12; * = 52. Ответ: 52.
159- Пусть данное трехзначное число — *. Если слева к нему дописать цифру
8, то цифра 8 будет занимать место единиц тысяч, поэтому полученное
число,можно записать так: 8000 + *. По условию задачи, если к образова­
вшемуся числу прибавить 619, то сумма будет в 40 раз больше, чем дан­
ное трехзначное число. Составим уравнение: 8000 + * + 619 = 40*, откуда
8619 + * = 40*; * - 40* = -8619; -3 9 * = -8619; * = -8619 : (-39); * = 221.
П роверка. Припишем к найденному числу слева цифру 8, получим 8221,
прибавим к нему число 619: 8221 + 619 = 8840. Найдем частное числа
8840 и найденного числа 221: 8840 : 221 = 40, что удовлетворяет условию
задачи. Ответ: 221.
160. Пусть заданное двухзначное число — *. Если справа и слева дописать к
нему цифру 4, то получим четырехзначное число, на месте единиц тысяч
и единиц стоит цифра 4, поэтому полученное число можно записать в виде
4000 + * * 10 + 4. Известно, что это число будет в 54 раза больше числа *.
Составим уравнение 4000 + * •10 + 4 = 54*, откуда: 4004 + 10* = 54*;
10* —54* = -4004; -4 4 * = —4004; * = -4004 : (-44); * = 91.
Ответ: число 91.
161. Пусть в первом ящике * кг яблок. Тогда во втором (112 - *) кг.
30 % яблок первого ящика составляет 0,3л: кг, если это количество пе­
реложить из первого ящика во второй, то в первом станет (* - 0,3*) кг,
а во втором — (112 - * + 0,3*) кг. Так как во втором ящике стало
в 3 раза больше яблок, чем в первом, составим уравнение: 112 —* + 0,3* =
= (* - 0,3*) * 3, откуда: 112 - 0 ,7 * = 0,7 * * 3; 112 - 0,7 * = 2,1*;
-0 ,7 * - 2,1* = -112; -2 ,8 * = -1 1 2 ; * = -1 1 2 : (-2,8); * = 40. Тогда 112 - х =
= 112 - 40; 112 —* = 72.
П роверка. Если в первом ящике 40 кг яблок, то во втором 72 кг. Если из
первого ящика взять, а во второй прибавить 30 % яблок первого ящика,
то получим в первом: 40 - 0,3 •40 - 40 —12 = 28 килограммов яблок, а во
втором 72 + 0,3 * 40 = 72 + 12 = 84 килограммов яблок. Найдем отноше­
ние количества яблок второго ящика к первому: 84 : 28 = 3, удовлетворяет
условию задачи. Ответ: 40 кг и 72 кг.
162. Пусть * грн — стоимость дисков. Если цену поднять на 25 %, то она будет
равняться 1,25* грн. После снижения этой цены на 25 %, новая стоимость
составляет 75 % от предыдущей, то есть: (0,75 *1,25*) грн, что по условию
задачи равняется 24 грн. Составим уравнение: 0,75 *1,25* = 24, откуда:
3 1 3 5 15 15
—-1 —* = 2 4 ; ------ * = 24; — * = 2 4 ; 16* = 24 •16; 15* = 384;
4 4 4 4 16 16
* = 384 : 15;* = 25,6. Ответ: начальнаястоимость 25,6 грн.
163. Пусть коэффициент пропорциональности *, тогда скорость катера в сто­
ячей воде 25* км/ч., а течения — 2* км/ч. Скорость катера по течению —
(25* + 2*) км/ч., а против течения — (25* - 2*) км/ч. По течению катер дви-
5 5
гался 3 ч. 50 мин, то есть 3 — часа, и за это время прошел 3 —(25* + 2*) км.
6 6
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

26. Чтобы найти время, за которое катер преодолеет это расстояние, двигаясь
против течения, надо расстояние разделить на скорость против течения
3 - (25* + 2 * ): (25* - 2*) = ( — •2 7 * 1 :2 3 * = — •27 : 23 = — = - = 4,5.
6 ^ 6 ^ 6 6 2
Ответ: 4,5 часа.
164. Пусть * км/ч. — скорость поезда, тогда расстояние между А и В, кото­
рое он преодолевает за 3 часа, равно 3* км. Если бы скорость увеличилась
на 10 км/ч., то есть стала (* + 10) км/ч., то такое же расстояние поезд
преодолел бы на полчаса быстрее, то есть за (3 - 0,5) = 2,5 часа. Это рас­
стояние можно записать как 2,5 * (* -+ 10). Составим уравнение:
3* = 2,5 *(х + 10), откуда 3* = 2,5* + 25; 3* - 2,5* = 25; 0,5* = 25; * = 50.
Тогда расстояние между А и В: 3* = 3 * 50; 3* = 150. Ответ: 150 км.
165. Пусть время, за которое теплоход планировал пройти расстояние, * ча­
сов, тогда расстояние между К и Р — 32* км. На первую часть расстояния
(к месту шторма), равную 216 км, теплоход потратил 216 : 32 часа, то есть
6.75 часа, а на вторую часть, которая равняется (32* - 216) км, раз­
вивая скорость (32 - 5) км/ч., то есть 27 км/ч., теплоход потратил
(32* —216): 27 часов. На весь путь потрачено 6,75 + (32* - 216): 27 часов,
что на 25 минут, то есть — часа, больше, чем запланировано. Составим
60
3 2 * -2 1 6 25 3 2 * -2 1 6 5
уравнение: 6,75 + ----- = х + -— , откуда 6,75 ч---------------- = * ;
27 60 27 12
ООу_ 216
6.75 -108 + — 108 = *-108 + — 108; 729 + 4(32* - 216)=108* + 45;
27 12
729 + 128* - 864 = 108* +- 45; 128* - 108* = 45 - 729 + 864; 20* = 180;
* = 180 : 20; * = 9. Тогда расстояние между К и Р 32* = 32 * 9; 32* = 288.
Ответ: 288 км.
166- Пусть скорость одной машины (* + Ю) км/ч. х км/ч.
* км/ч., тогда другой’— (* + 10) — Р ' < ■
км/ч. За 3 часа первая проехала 3* •-------------------------'-----------------•
км, а вторая — 3 (* + 10) км, что 450 км за 3 часа
в сумме составляет 450 км. Составим уравнение: 3* + 3(* + 10) = 450,
откуда: 3* + 3* -+ 30 = 450; 6* = 450 - 30; 6* = 420; * = 420 : 6; * = 70.
Тогда первая проехала 3* = 3 * 70; 3* = 210 километров, а вторая —
3 (* + 10) = 3(70 + 10) = 3 *80 = 240 километров.
П роверка. Вместе машины преодолели 240 + 210 = 450 километров.
Скорость одной 70 км/ч., другой (70 +- 10) км/ч. = 80 км/ч. Скорость
сближения — (70 + 80) км/ч. Вместе машины преодолели 450 км за —
450 : (70 + 80) = 450 : 150 = 3 (ч.). Условие задачи удовлетворено.
Ответ: первая машина проехала 210 км, вторая — 240 км.
167. Пусть расстояние, которое проехал х км (210 - *) км
ДО встречи первый автомобиль, — * КМ, ______
тогда второй проехал — (210 - х) км. А ‘ ^
Известно, что первый проехал до ветре-
чи на 30 км больше, чем второй. Соста- км
вим уравнение: * - ( 210 - *) = 30, откуда * - 210 + * - 30; 2* = 30 + 210;
2* = 240; * = 240 : 2; * = 120. Тогда первый проехал до встречи 120 км
за 1,5 часа, то есть его скорость равняется: 120 : 1,5 = 80 (км/ч.). Вто­
рой проехал до встречи 210 —* = 210 - 120; 210 - * = 90 километров за
1,5 часа, то есть его скорость равняется: 90 : 1,5 = 60 (км/ч.).
Ответ: 60 км/ч. и 80 км/ч.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

27. 168- Пусть скорость первого велосипедиста * км/ч. Скорость, с которой ве­
лосипедисты приближаются, находим, учитывая, что они преодолели рас­
стояние 36 км эа 1,5 часа:
36 : 1,5 = 24 (км/ч.). Бели второй вело­
сипедист задержится на полчаса, то пер­
вый преодолеет эа это время расстояние
0,5* км, а оставшийся путь они преодо­
леют эа 1,25 часа с общей скоростью 24 км/ч., и он будет составлять
24 * 1,25 = 30 (км). Всего велосипедисты проедут 36 км, поэтому уравне­
ние имеет вид: 0.5* + 30 = 36, откуда: 0,5* = 36 —30; 0,5* = 6; * = 6: 0,5;
х - 12. Скорость первого велосипедиста 12 км/ч., а если их общая скорость
24 км/ч,, то скорость второго: 24 - 12 = 12 (км/ч.).
Ответ: 12 км/ч. х
169. Пусть расстояниемежду-АиВ х км. — —ч. ч*
Тогда время, за которое вертолет пре-
одолел его со скоростью 250 км/ч., — Г . ~ ^
* 1 о
часов, а время, за которое верто- 5— ч. 1 • 12— ч
250 2 х ч. 4 '
лет преодолел это расстояние со ско- ^
ростью 200 км/ч., — часов. Составим схему движения вертолета по
1» зс 1 ос 3
времени, и по ней составим уравнение: 5 —н------- к—+ ------= 12 —, откуда:
. 2 250 2 200 4
* * 3 1 1 4* + 5* 3 9* 3 9 27
+ -— = 12— 5 ------- ; = 12— 6; = 6- ; * = — ;
250 200 4 2 2 1000 4 1000 4 1000 4
27 9 27 1000
* - — : ------- ; * = --------------; * = 750.
4 1000 4 9
Расстояние между А и В — 750 км. Ответ: 750 км.
170. Пусть скорость автобуса * кмч. и к моменту, когда автомобиль его дог­
нал, автобус двигался 1ч. 20минут, то есть 1— часа, преодолев расстояние
і 3
1—* км. Автомобиль догнал автобус за 1 ч., преодолев то же расстояние,
3 1 4
которое равняется 80 км. Составим уравнение: 1 - х - 80, откуда: —* = 80;
4 4 3 3
* = 8 0 : —; * = 8 0 — ; * = 60.
3 4
Ответ: скорость автобуса 60 км/ч.
171 *. Пусть первая партия товара стоит * грн, тогда вторая — (25000 - *) грн.
Первая принесла 25 % прибыли, что составляет 0,25* грн, а вторая —
50 % прибыли, что составляет 0,5(25000 —*) грн. Так как обе партии то­
вара принесли прибыль 40 %, то есть 0,4 *25000 грн, составим уравнение:
0,25* + 0,5(25000 - *) = 0,4 •25000, откуда: 0,25* + 12500 - 0,5* = 10000;
0,25* - 0,5* = 10000 - 12500; -0 ,2 5 * = -2500; * = -2500 : (-0,25); * = 10000.
Первая партия стоит 10000 грн, а вторая — 25000 —* = 25000 - 10000;
25000 - * = 15000, то есть 15000 грн. Ответ: 10000 грн и 15000 гря.
172*. Масса меди в слитке составляет 45 % , то есть равняется (0,45 * 15) кг.
Пусть к слитку надо прибавить * кг серебра, тогда общая масса слитка будет
(15 + *) кг, а масса меди будет составлять 30 % этогослитка и будетравняться
0,3(15 + х) кг.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

28. Учитывая, что масса меди не изменилась, составим уравнение:
0,3(15 + *) = 0,45 - 15, откуда: 4,5 + 0,3 х = 6,75; 0,3* - 6,75 - 4,5;
.. 0,3* = 2,25; * = 2,25 : 0,3; * = 7,5. Ответ: надо прибавить 7,5 кг серебра.
*
173*. Пусть в руде было * кг железа, тогда оно составило часть руды.
В примесях содержится 12 % железа, то есть 0,12 •400 кг, что составляет
48 кг. Когда из 1 т руды извлекли 400 кг примесей, масса руды стала 600 кг,
, * - 4 8 т
а железа (* - 48) кг и оно стало составлять — ■— часть руды. Так как со-
600
держание железа повысилось на 20% , то есть доля железа увеличилась на
10 6
ЛО * - 48 х * - 4 8 х
0,2, составим уравнение:-------------------- = 0,2; откуда:--------------------- = 0, 2;
Р 600 1000 600 1000
1 0 ( * - 4 8 ) - 6 * 1 0 ( * - 4 8 ) - 6 * Л
— *-------- }---------= 0,2; — 1-------1 6000 = 0,2 •6000; 10* - 480 - 6* =
6000 6000
= 1200; 4* = 1200 + 480; 4* = 1680; * = 1680 : 4; * = 420. Тогда в руде оста­
лось * - 48 = 420 - 48; * - 48 = 372 килограмма руды. Ответ: 372 кг.
174. Вычислим:
1) |-2,7[ + 2,4 = 2,7 + 2,4 = 5,1; 2) -2 ,4 + |-2,3| = -2 ,4 + 2,3 = -ОД;
3) |-10,5| : 7 - 3,2 = 10,5 : 7 - 3,2 = 1,5 - 3,2 = -1 ,7 ;
4) 4,8 - |3,2| : |-0,8| = 4,8 - 3,2 : 0,8 = 4,8 - 4 = 0,8;
5) : ——1,22= —•- - 1 ,4 4 = 3 —1,44 = 1,56;
2 2 1
6) |2,5|: ]—0,5|2- 200 = 2,5 : 0,52- 200 = 2,5 : 0,25 - 200 = 10 - 200 = -190.
175. На первом месте телефонного номера могут стоять только цифры 1, 2,
3, 4, 5, 6, 7, 8, 9, то есть 9 цифр и 9 возможностей набора, но правиль­
ная только одна, поэтому вероятность с первого раза набрать правильный
номер —. Ответ: —.
9 9
В упражнениях 176—177 раскроем скобки и упростим выражение.
1 7 6 .1 ) 2(а - 3 ) + 6= 2а - 6+ 6= 2а; 2)—3 (*-5 )+ 6 *= -3 *+ 1 5 + 6 *= 3 *+ 1 5 ;
3) * - 3(2 + *) + 7 = * - 6 - 3 * + 7 = - 2 * + 1;
4) -(а + 5) + 2 а - 4 = - а - 5 + 2а - 4 = а - 9.
1 7 7 .1 ) (2с - 1) - (Зс - 2) = 2с - 1 - Зс + 2 = -с + 1;
2) -(1 - 2а) + 3(1 - а) = -1 + 2а + 3 - За = -а + 2;
3) *2- 2(8+ *) + 16 = * 2- 16 - 2* + 16 = *2- 2*;
4) *2—2* + 2(2 —*) = *2—2* + 4 —2* = *2- 4* + 4.
178. Чтобы найти число по его процентам, надо это число разделить на дробь,
соответствующую количеству процентов (1% « 0,01).
1) 20 % числа — это 344, тогда число: 344 : 0,2 = 1720.
2) 125 % числа — это 4800, тогда число: 4800 : 1,25 = 3840.
3) 2,5 % числа — это 640, тогда число: 640 : 0,025 = 25600.
Ответ: 1) 1720; 2) 3840; 3) 2560.
Задания д ля самостоятельной работы
Прирешенииуравненийсмотри объяснение к упражнениям8—10 и 125—173.
Вариант 1
1. Решим уравнения:
а) 5* - 3 = 2* + 12; 5* - 2* = 12 + 3; 3* = 15; * = 15 : 3;* = 5.
б) 0>5у + 3(у - 2) = 2у; 0,5у + Зу - 6= 2у; 0,5у + Зу - 2у = 6;1,5у = 6;
у = 6 : 1,5; у = 4.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

29. 2. Решение. Пусть дочь будет младше матери вдвое через * лет. В это время
ей будет (12 + х) лет, а матери — (35 + *) лет. Получаем уравнение:
2(12 + дс) = 35 + ж; 24 + 2* = 35 + *; 2* - * = 35 - 24; х = 11.
Ответ: через 11 лет.
3 . Уравнение |*|= а не имеет решений, когда а отрицательное число.
Вариант 2
1. Решим уравнения:
а) 2 - 3* - 7* - 8; -7 х - Зх = -2 - 8; -1 0 * = -1 0 ; * = 10 : 10; * = 1.
б) 2г - 0,5(z - 1) + г; 2z = 0,5z - 0,5 + z; 2z - l,5z = -0 ,5 ; 0,5z = -0 ,5 ;
2= -0 ,5 : 0,5; z = -1 .
2. Решение. Пусть x лет прошло с тех пор, когда отец был старше сына в 5 раз.
Тогда отцу было (42 - *) лет, а сыну (10 - *) лет, откуда получаем урав­
нение: 42 - х = 5(10 - *); - * = 50 - 5* —42; —х + 5дс = 8; 4* = 8;
* = 8 : 4; * = 2. Ответ: 2 года назад.
3 . Выполним преобразование уравнения |*| + а = 0: |*| = - а . Уравнение не .
имеет решений, когда (-а) — число отрицательное, то есть когда число
а — положительное.
Вариант 3
1. Решим уравнение:
а) 2* - 4 - 3 —5jc; 2* + 5* = 3 + 4; 7* = 7; * = 1.
б) 3 - 0,7(1 - 2л) = бл; 3 - 0,7 + 1,4л = 6л; 1,4л - 6л = -3 + 0,7;
-4,6л - -2 ,3 ; п - 2,3 : 4,6; л = 0,5.
2. Решение. Очевидно, что ( 1 7 : 7 ) меньше трех, то есть сейчас сестра младше
брата менее, чем в 3 раза. Так как частное количества лет двоих людей с
каждым следующим годом только уменьшается, то в три раза младше она
была раньше. Пусть это было * лет назад. Тогда сестре было(7 - *) лет, а бра­
ту — (17 - *) лет. Получаем уравнение: 17 - * = 3(7 - *); - * = 21 - 3* - 17;
3* - * = 4; 2* = 4; * = 4 : 2; * = 2. Ответ: 2 года назад.
3. Уравнение (а + 1)* = 15 не имеет решений, когда а + 1 = 0, то есть а = —1.
Вариант 4
1. Решим уравнение:
а) * + 12 = 9 - 2*; * + 2* = 9 - 12; 3* = -3 ; * = - 3 : 3 ; * = -1 .
б) с - 0,2(с - 3) = 5с; с - 0,2с + 0,6 = 5с; 0,8с - 5с = -0 ,6 ;
-4,2с = -0 ,6 ; с = 0,6 : 4,2; с = —.
7
2. Решение. Очевидно, что (14 : 5) больше двух, то есть сейчас брат младше
сестры больше, чем в 2 раза. Так как отношение количества лет дво­
их людей з каждым следующим годом только уменьшается, то в 2 раза
младше он будет потом. Пусть это будет через * лет. Тогда сестре будет
(14 + *) лет, а брату — (5 + *) лет. Получаем уравнение: 2(5 + *) = 14 + *;
10 + 2* —* = 14; * = 14 - 10; * = 4. Ответ: через 4 года.
3. Уравнение ах = -8 не имеет решений, когда а = 0.
Готовимся к тематическому оцениванию
Тестовые задания № 1
1. Правильный ответ: в) -2 * = 0.
2. Правильный ответ: в) 100 : х = 5.
Решение. Проверим, является ли корнем уравнения число 5, заменив пе­
ременную числом 5:
а) 2* = 10; 2 * 5 = 10; 10 = 10, равенство верно, 5 — корень уравнения;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

30. б) х —5 = О; 5 —5 = 0; 0 = 0, равенство верно, 5 — корень уравнения;
в) 100 : х = 5; 100 : 5 = 5; 20 = 5, равенство неверно, 5 — не является кор-
нем уравнения;
г) 0 * х = 0; 0 •5 = 0; 0 = О, равенство верно, 5 — корень уравнения.
3. Правильный ответ: г) О : х = 10.
Не существует такого числа, при делении на которое числа 0 получим 10.
4
4. Правильный ответ: б) — .
3 4
Решим уравнение Зх + 5 = 1. Зх = 1 —5; Зх = - 4; х = -4 : 3; х = -----.
3
5. Правильный ответ: в) х2= 0.
а) уравнение х = х + 5 равносильно уравнению х - х = 5, 0 = 5, которое
не имеет корней;
б) х= 4 имеет 2 корня;
в) х2= 0 имеет один корень;
г) х{х - 1) = 0 имеет 2корня.
6. Правильный ответ: а) —5,5. Решим уравнение 5х + 13 = 3* + 2.
5* - Зх = 2 - 13; 2х = -1 1 ; х = -1 1 : 2; х = -5 ,5 .
7. Правильный ответ: в) один. Заменим уравнение 2(2- яг)= х - 2 равносиль­
ным: 4 - 2х = х —2; ~2х - х = —2 —4; -З х = - 6. Данное линейное уравнение
имеет единственный корень.
8. Правильный ответ: в) -1 0 : 5 = х. Найдем корень уравнения 5х = -1 0 ;
х = -1 0 : 5; х = —2. Проверим, какое из уравнений удовлетворяет это число:
а) 5х - 10 = 0; 5 * (-2) - 10 = 0; -1 0 - 10 = 0; -2 0 = 0, равенство неверно,
2не является корнем уравнения;
б) Юле = -5 ; Ю(-2) = -5 ; -2 0 = -5 , равенство неверно, -2 не является кор­
нем уравнения;
в) -1 0 : 5 = х; -1 0 : 5 = -2 ; -2 = -2 , равенство верно, -2 является корнем
уравнения;
г) 5(х + 10) = 0; 5(-2 4* 10) = 0; 5 * 8 = 0; 40 = 0, равенство неверно,
-2не является корнем уравнения.
9. Правильный ответ: в) 0.
10. Правильный ответ: а) 1. Уравнение имеет множество корней, если а - 1 = 0
и 1- а = 0, то есть в = 1.
Контрольная работа № 1
1. Решим уравнение:
а) 15 - х = 10; - х = 10 - 15; ~х = -5 ; х = 5.
б) -0 ,4 х = 2; х = 2 : (-0,4); х = -5 .
в) 2(х + 3) - 5 = 11; 2х + 6- 5 = И ; 2х = 11 - 6+ 5; 2х = 10; * = 10 :2; * = 5.
Так как уравнения а) и в) имеют одинаковые корни, то этиуравнения
равносильны.
Ответ: а) х = 5; б) х = -5 ; в) х = 5. Равносильные уравнения а) и в).
2. Проверим, каким уравнениям удовлетворяет число -1 :
а) Ъх = 0; 5 * 1 = 0; 5 = 0, равенство неверно, -1 не удовлетворяет уравнению;
б) х(х + 1)(2х - 1) = 0; -1 •(-1+ 1)(2•( - 1) - 1) = 0; 0= 0, равенство вер­
но, —1удовлетворяет уравнению;
в) х2 + 1= 2х; ( - 1)2+ 1= 2- ( - 1); 2= - 2, равенство неверно, -1 не удов­
летворяет уравнению.
Проверим, каким уравнениям удовлетворяет число 0:
а) Ъх = 0; 5 •0 = 0; 0 = 0; равенство верно, 0 удовлетворяет уравнению;
б) х(х + 1)(2х - 1) = 0; 0 * (0+ 1)(2* 0 - 1) = 0; 0 = 0, равенство верно,
0удовлетворяет уравнению;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

31. в) *2+ 1 = 2x1 О2+ 1 = 2 *О; 1 = О, равенство неверно, 0 не удовлетворяет
уравнению.
Проверим, каким уравнениям удовлетворяет число 1:
а) 5* = О; 5 * 1 = 0; 5 = О, равенство неверно, 1 не удовлетворяет уравнению;
б) * (* + 1)(2* - 1) = 0; 1•(1+ 1)(2•1- 1) = 0; 2= 0, равенство неверно,
1не удовлетворяет уравнению;
в) х* + 1= 2х; I2+1 = 2*1; 2= 2, равенство верно, 1удовлетворяет уравнению.
Ответ: -1 удовлетворяет уравнению б), 0 удовлетворяет уравнению а)
и б), 1удовлетворяет уравнению в).
3. Составим уравнение, которое имеет: а) один корень: 7х = 18; б) два корня:
(х - 1)(.г + 7,5) = 0; в) множество корней: Ох =*О.
4. Решим задачу. Пусть второй ученик собрал * кг ягод, тогда первый —
(х + 5) кг ягод. Если вместе они собрали 29 кг ягод, составим уравнение:
х + (х + 5) = 29, откуда: х + х + 5 = 29; 2* = 29 - 5; 2х = 24; х = 24 : 2;
х = 12. Второй учениксобрал 12 кг ягод, а первый — * + 5~ 12 + 5 ; * + 5 = 17,
то есть 17 кг ягод. Ответ: 17 кг и 12 кг.
5. Решим уравнение, заменив его равносильным:
10у + 42 = Чу - 3{у - 2); 10# + 42 = Чу - Зу + 6; 10у - Чу + Зу =6 - 42;
6у = —36; у = -3 6 : 6; у = - 6.
2х х 2х х
6. Найдем корни уравнений:------------=3 ; ------1 4 --------14 = 3 -14; 4х - х = 42;
Зх = 42; х = 42 : 3; х = 14. 7 14 7 14
7. Найдем корни уравнений, упростив уравнение:
* + 3 Ь + х х + 3 Ъ+ х х
------------------= х + 4 ; ---------1 0 ------------ 10 = (х + 4) *10;
2 5 2 5 1 1
Цх + 3) - 2(5 + х) = 10* + 40; 5* + 15 - 10 2х = 10* + 40;
3* - 10* = 40 - 15 + 10; -7 * = 35; * = 35 : (-7); * = -5 .
8. Решим задачу. Пусть скорость лодки в стоячей воде * км/ч., тогда ее ско­
рость по течению — (* + 3,5) км/ч., а против течения — (* - 3,5) км/ч.
За 2,4 часа по течению реки лодка прошла 2,4(* + 3,5) км, а за 3,2 часа
против течения — 3,2(* - 3,5) км, что на 13,2 км меньше, чем путь по
течению. Составим уравнение: 2,4(* + 3,5) - 3,2(* - 3,5) = 13,2, откуда:
2,4* + 8,4 - 3,2* + 11,2 = 13,2; 2,4* - 3,2* = 13,2 - 8,4 - 11,2;
-0 ,8 * = -6 ,4 ; * = -6 ,4 : (-0,8); * = 8.
Ответ: 8 км/ч. — скорость лодки в стоячей воде.
9 . Найдем корни уравнений: |1 - 3*| + 2 =5; |1 - 3*] = 5 - 2; (1 - 3*] = 3;
1. 1- 3* = 3; -3 * = 3 - 1 ; -З х = 2; * = 2 : (-3); * = - —;
3
4 1
2. 1 —3* = -3 ; -3 * = -3 -1 ; -3 * = -4 ; * = -4 : (-3); х = —; * = 1—.
2 1 3 3
Ответ: — , 1—.
3 3
10. Найдем все значения а , при которых корень уравнения а * = 5 + 2* явля­
ется целым числом. Найдем выражение для *: ах - 2* = 5; * (а - 2) = 5;
5 5
* = -------. Частное ------- будет целым числом, если а - 2 равняется чи-
а —2 а - 2
слам, на которые 5 делится нацело:
а - 2= - 1; а = -1 + 2; о = 1.
а - 2 - -5 ; а = -5 + 2; а = -3 .
а - 2 = 1 ;а = 1 + 2 ;а = 3.
а - 2 = 5 ;а = 5 + 2 ;а = 7.
Ответ: -3 , 1, 3, 7.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

32. Раздел II. ЦЕЛЫЕ ВЫРАЖЕНИЯ
§ 5. Выражения с переменными
184. а) - •- + 2,5 = — + 2,5 = 0,3 + 2,5 = 2,8.
5 4 10
о 21
б) 2 ,7 - — -7 = 2 ,7 ---- - = 2 ,7 -2 ,1 = 0,6.
10 10
. _ 1 2 5 7 10 7 1 6
в) 2 ------------= ---------- = --------- — — = 2.
9 3 5 6 3 30 3 3 3
185. а) 30,5 : 0,5 - 1976 : 32,5 = 61 - 60,8 = 0,2.
б) 3,85 5^ + 6 9 ,2 5 :2 7 ,7 = — — + 2,5 = — — + 2,5 =
7 100 7 20 7
= + 2,5 = — + 2,5 = 19,8 + 2,5 = 22,3.
10 10
1 8 6 .а) (1 ,7 5 : —- 1 —1-16 = ( 1—•— 1- 16 =
Н 3 8) { 4 2 8 )
= Г 2 1 - 1 3 Ь 6 = 8 . 16 = 1. 16= 16.
^4 2 8^ 1/8 ) 8
б) Г5 —11—: 2,5 1: 0,0625 = Гб —— I — |:
Ч 8 ) { 8 10)
<5_ ^ w y i o o o o f м у
I, 8 2 5 ) 625 ^ 4 ) .
625
10000
20z M .16= ! . 1 6 = 4.
4 4
187. а) для выражений 2 и с: б) для выражений 2х и с - х:
- сумма - 2 + с; - сумма - 2х + с - х;
- разность - 2- с; - разность - 2х - ( с -х);
- произведение —2с; - произведение —2х(с —х);
- частное - 2 : с. - частное - 2х : (с - х).
188. Запишем выражения:
а) сумма чисел а и х записывается как а 4- х;
б) произведение чисел k и п записывается как кп;
в) полупроизведение чисел c u d записывается как —c d ;
2
г) полусумма чисел х и у записывается как —(х + у);
2
д) полуразность чисел с и 5 записывается как —(а - 5);
2
е) удвоенное произведение а и х записывается как 2ах.
Чтобы найти числовое значение выражения с переменной при некото­
ром значении переменной, нужно это значение подставить в выражение
и выполнить действия.
189. а) 0,5* - 3, если * = 10: 0,5 •10 - 3 = 5 - 3 = 2.
б) * + 9,7, если * = -10: -1 0 + 9,7 = -0 ,3 .
в) *(* 4- 2), если х = 0,5: 0,5(0,5 4- 2) = 0,5 * 2,5 = 1,25.
г) 3*(5 - х), если * = -2 ,5 : 3(-2,5)(5 - (-2,5)) = -7,5(5 4- 2,5) =
= -7 ,5 * 7,5 = -56,25.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

33. 190- а) а +с - 3, если а = 2 и с = 7,5: 2 + 7*5 - 3 = 9,5 - 3 = 6,5.
б) 2х —3z + 1, если лс= 1, z = —: 2 * 1 —3* — + 1 = 2 —1 + 1 = 2 .
3 3
в) 2ху(х - у), если х = 2, у = 5: 2 * 2 •5(2 - 5) = 20 * (-3) = -60.
г) 3а(х + у -4), если а = —ух = 7 , у = 5: 3 • — (7 + 5 -4 ) = 1 2 - 4 = 8.
3 3
191.
192.
I
Чтобы найти значение х, для которого числовые значения выражений
равняются друг другу, надо поставить между этими выражениями знак
равенства и полученное уравнение решить.
193. а) 2х + 5х и 2(х + 5); 2х + Ъх = 2(х + 5); 2х + 5* = 2х + 10;
7х - 2х = 10; 5х = 10; х = 10 : 5; х = 2.
Ответ: при х = 2.
б) 1 + 3(ас - 5) и (1 + 3*) - 5*; 1 + 3(х - 5) = (1 + Зх) - 5*;
1 + За: - 15 = 1 + 3* - 5*; 3* + 2х = 1 + 15 - 1; 5* = 15; х = 15 : 5; х = 3.
Ответ: при х = 3.
п -2 -1 0 1 2 3 4 .5
5 - 2 п 9 7 5 3 1 -1 -3 -5
а 3 4 5 6 7 8 9
п 0 1 -1 2 -2 3 -3
2а + 5п 6 13 5 22 4 31 3
I
Число в виде выражения записывается так: число единиц плюс число
десятков, умноженное на 10, плюс число сотен, умноженное на 100,
плюс число тысяч, умноженное на 1000, и т. д. Обычно выражение за­
писывается в порядке убывания разряда числа.
194. а) а десятков и 6единиц. б) 5 десятков и Ь единиц.
Ответ: 10а + 6. Ответ: 50 + Ъ.
в) т десятков п единиц. г) а сотен и с единиц.
Ответ: Ю т + п. Ответ: 100а + с.
195. Найдем для выражений:
а) 65 * 27 и 35 * 27:
* сумму: 65 * 27 + 35 * 27 = 27(65 + 35) = 27 * 100 = 2700;
разность: 65 * 27 - 35 •27 = 27(65 - 35) = 27 * 30 = 810;
б) 3,6 * 103и 2,4 * 103:
сумму: 3,6 •103+ 2,4 * 103= 10э (3,6 + 2,4) = 1000 * 6= 6000;
разность: 3,6 * 103- 2,4 •103= 108(3,6 - 2,4) = 1000 •1,2 = 1200.
196. Запишем в виде числового выражения:
а) удвоенное произведение чисел 74 и 0,5: 2 * 74 *0,5;
б) полуразность чисел 38 и 7,6: —(38 —7,6);
2
в) произведение суммы чисел 35 и 12 на их разность: (35 + 12)(35 - 12).
Найдем значения выражений 197—200:
197. а) 2,37 + 4,23 - 13,7 * 0, 1 = 2,37 + 4,23 - 1,37 = 6,6- 1,37 = 5,23;
б) 8,21 * 3,14 - 8,11 * 3,14 = 3,14(8,21 - 8Д1) = 3,14 * ОД = 0,314;
в) (2,75 - 0,65 : 2,6) *4 - 1 = (2,75 - 0,25) *4 - 1 = 2,5 *4 - 1 = 10 - 1 = 9;
г) 5 - (0,8 + 15,15 : 7,5) = 5 - (0,8 + 2,02) = 5 - 2,82 = 2,18.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

34. 198. а) 3,18 - (0,13 + 4,27 : 1,4) = 3,18 - (0,13 + 3,05) = 3,18 - 3,18 = О;
б) 5,9 - (6,3 : 3,5 - 5,6) = 5,9 - (1,8 - 5,6) = 5,9 - (-3,8) = 5,9 + 3,8 = 9,7;
в)
г(6 (3 (2Л
1 1 „о2- + — + 12-
5 10 5
V )
/<4 (2 >
2 3 1
—------- 1-----
I 5
10 20
j
: — = (— + — + 12— 1-15 = 12— -15 =
15 V30 30 30) 30
373 373 1
— -15 = — = 186-
30 2 2
„ 2 3 8-6 + 1 5 3
1- + - = ---------------- + —
3 4 20 3 4
У ■ /’ 3 1 3 4 ,- Г - Г - ..+ _ ==_ + _ = _ ==1(
X 4 4 4 4
ч (л Л 2 ( 4 А _ 1 3 ( Л _ 1 , 1
199. а) ! 1 ---- |: —+ — 1 - 5 = h — I-5 = — 1 = — .
{ S ) 3 ) 3 2 ( 5 ) 2 2
200. а) (7,344 : 0,36 + 16 - : 5 - 0,5 •0,2) •0,08 = (20,4 + 16,25 : 5 - 0,1) •0,08 =
4
= (20,4 + 3,25 - 0,1) *0,08 = 23,55 * 0,08 = 1,884;
1 2 21 2
б) (0,02 * 0 , 5 + 7,9 0 4 : 0 , 3 8 - 2 1 : 1 0 - ) * - =(0,01 + 2 0 , 8 - 2 1 : — )• - =
2 9 2 9
= (0,01 + 2 0 , 8 - 21 - — )■- = (0 ,0 1 + 2 0 ,8 -2 )-- = 1 8 , 8 1 - - =2,09-2 = 4,18.
21 9 9 9
а -2 0 3 5 5 6 10 -10
Ъ 1 3 0 7 -2 2 7 - 7
2а(а - Ь) 12 0 18 -20 70 48 60 60
201.
202.
* 5 10 11 20 0 -2 - 2 !
3
—2—
3
3* + 8 23 38 41 68 8 2 1 0
203. Составим по условию уравнение и решим его:
а) 3(* + 1) - 7 = 2х - 9; 3* + 3 - 7 = 2* - 9; 3* - 2* = -9 - 3 + 7; * = -5 .
б) 8 - 2(3 - *) = 5 - 3(3 - 2*); 8 - 6 + 2х = 5 - 9 + 6*;
2х - 6* = 5 - 9 —8 + 6; -4 * = - 6; х = -6 : (-4); х = 1,5.
в) 0,5* + 2(7 - *) = 1,5* - 5(* + 2); 0,5* + 14 - 2* = 1,5* - 5* - 10;
0,5* - 2* - 1,5* + 5* = -1 0 - 14; 2* = -2 4 ; * = -2 4 : 2; * = -1 2 .
2 7
г) —* -----+ 5 = *
3 9
*/о ^ 2 7 * 1- ( 2 - 6 * ) ; —* -----+ 5 =* ------+ *;
6V ' 3 9 3
2 1 7 _ Д 4 в ^1 5
—х - х - х - — + 5; -1 —* = 5; - 1 —* = - 4 —; *
3 3 9 3 9 3 9
* =
41
9 :( з) * -
1:Н >
41 0 1 41 5
—з — ; * = —■; * = 3 —
э0 4 12 12
204. Запишем число:
а) а единиц, Ь десятков и с сотен: 100с + 106 + а;
б) а единиц, с сотен и сI тысяч: 1000<2+ 100с + а;
1 1в) а единиц, л десятых и т сотых: а + — л +-------т;
10 100
, 1 1г) с десятков, а единиц, л десятых и т сотых: 10с + а + ^ о П+ 100т '
205. Составим формулу числа:
а) число, кратное 5, можноразложить на множители, один из которых 5: 5л;
б) число, кратное 5 и четное, можно разложить на множители, среди ко­
торых 5 и 2: 2 * 5 * л = Юл;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

35. в) число, кратное 5 и нечетное, можно разложить на два множителя, один
из которых 5, а второй — нечетное число (2п 4- 1): 5(2п + 1);
г) число, кратное 5 и 3 одновременно, можно разложить на множители,
среди которых 5 и 3: 3 * 5л = 15л.
206. Определим периметры многоугольников, которые являются замкнуты­
ми ломаными:
С
В
Е
С
а К
К
В
В
Е
а М
Р =А М 4-АВ 4- ВС 4- СВ 4- ВЕ 4- ЕЖ+ д а 4-
4- КС 4 КЬ 4- ЬМ = А М 4- (АВ 4- ЬМ ) +
+ (ВС + £>£ + д а + КЬ) 4- (СВ + + КС) =
= А + 2Ь + в + (с + с) = 2а + 2Ь + 2с = 2(о
+ &4- с);
Р = АК 4- АВ + ВС + ВС + ВЕ + ЕЕ 4-
4- д а + <Ж =АК 4- (АВ 4- ВС + ЕР) +
+ СК +•(ВС 4- £>15 + да) = а + &+ &4-а = 2а4'2Ь = 2(а 4- Ь);
Р = АМ + АВ + ВС + ВС + ВЕ + ЕЕ + ЕС + КС + КЬ + ЬМ = А М +
+ (АВ 4- ВС 4- ЕР 4- КС) + (ВС + ВЕ 4- д а 4- 1Щ + Ш = а+ &+ а 4 Ь =
—2а 4- 26 = 2(а 4- 6).
207. Найдем значение выражения, упростив его в случае необходимости,
если х - у = 12:
а) | (*~ У ) = | 12 = 4;
б) 4у - 4х = —4(я - у) = -4 *12 = -48;
В) У - 6 - * = - ( * - у ) - в —12—6 -18
9 9
- 2;
4(лг + у ) - 8у = 4ж+ 4у- 8{ / = 4 * -4 у = 4 ( * - у ) = 4 - 0 * = 16 = 1
15 15 15 15 5 5 '
208. Найдем значение выражения, упростив его в случае необходимости,
если а = —5, Ъ - с = 4.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

36. 209. Запишем число, которое состоит из а сотен, 6 десятков и с единиц:
100а + 106 + с. Число, записанное этими ж цифрами» но в обратном порядке,
состоит из с сотен, 6десятков и а единиц: 100с + 106 + а. Запишем сумму
этих чисел: 100а + 106 + с + 100с + 106 + а = 101а + 206 + 101с.
210. Решим уравнение:
а) (2* + 3) + (4* - 8) = 37; 2х + 3 + 4х - 8= 37; 6* - 5 = 37; 6* = 37 + 5;
6* = 42; х = 42 : 6; х = 7.
б) 5 - Зг - (3 - 4г) = 42; 5 - Зг - 3 + 4г = 42; 2 4- г = 42; г = 42 - 2; г = 40.
в) 0,7 + х - (-0,7 + 4х) = -3 7 ; 0,7 4- х 4- 0,7 - 4х = -3 7 ; 1,4 - 3* = -37;
-З х = -3 7 - 1,4; -3 * = -38,4; х = -3 8 ,4 : (-3); х = 12,8.
г) -7 ,2 - (3,6 - 4,5*) = 2,7*; -7 ,2 - 3,6 4- 4,5* = 2,7х; -1 0 ,8 4- 4,5* = 2,7*;
4,5* - 2,7* = 10,8; 1,8* = 10,8; * = 10,8 : 1,8; * = 6.
211. Решим задачу:
Обозначим количество жителей первого села через *, тогда во втором селе
2х, а в третьем (2* - 40) жителей. Учитывая, что в трех селах 1200 жи­
телей, составим уравнение: * + 2* + 2* - 40 = 1200, откуда:
5* - 40 = 1200; 5* = 1200 + 40; 5* = 1240; * = 1240 : 5;
* = 248, тогда 2* = 2 * 248 = 496, 2* - 40 = 496 - 40 = 456.
Ответ: в первом селе 248 жителей, во втором — 496, в третьем 456 жи­
телей.
212. Решим уравнение. Обозначим первое число через *, тогда второе —
(* + 1). третье — (* 4- 2). Если эти числа выражают длину сторон тре­
угольника, то его периметр — (* + * + 1 4 - * +2) см, что равняется 30 см.
Составим уравнение: * + * + 1 + * + 2 = 30, откуда: 3* + 3 =30; 3* = 30 - 3;
3* = 27; * = 27 : 3; * = 9. Тогда * + 1 = 9 + 1 = 10, * + 2 = 9 + 2 = 11.
Ответ: 9 см, 10 см, 11 см.
213. Запишем все делители числа и найдем их сумму:
а) 8: 1, 2, 4, 8; 1 + 2 + 4 + 8= 15;
б) 18: 1, 2, 3, 6, 9, 18; 1 + 2 + 3 + 6 + 9 + 18 = 39;
в) 28: 1, 2, 4, 7, 14, 28; 1 + 2 + 4 + 7 + 14 + 28 = 56;
г) 38: 1, 2, 19, 38; 1 + 2 + 19 + 38 = 60.
§ 6. Тождественные выражения
Чтобы доказать тождественность выражений, надо доказать, что их чис-
ловые значения равны при любых значениях переменных.
216. а) р 2р и р 3; р 2р = р 1+г = р 3. Ответ: да.
б) * + х2+ * э+ *4и х5; эти выражения равны только при * = 0. Ответ: нет.
в ) а - с и с ~ а ; а - с = -(с - а). Ответ: нет.
г) -а 2и (—а)2. Ответ: нет.
д) ах + ах + ах и За*; а * .+ а* + а* = За*; За* = За*. Ответ: да.
е) * —2а и -2 а + *; * - 2а = -2 а + * . Ответ: да.
217. Сравнимсоответствующиечисловые значения выражений *2и * при* = - 1 ,
* = 0 и * = 1. При * = -1 , *2= 1 ф х; при х = 0, *2= 0 - *; при * = 1, *2= 1 = *.
Но при любых других значениях * эти выражения не равняются друг дру­
гу, поэтому не являются тождественными.
Ответ: х2 и * не тождественные.
218. Запишем утверждение в виде тождества:
а) а + (—а) = 0 — сумма взаимно противоположных чисел равняется 0;
б) а *— =1 — произведение взаимно обратных чисел равняется 1(а ф 0);
а
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

37. в) а • Ъ = ( - а) * (—Ь) — произведение двух чисел равняется произведению
противоположных им чисел.
Упростим выражения 219—220.
2 1 9 . а) 2с + Зс - 5 = 5с - 5; б) 3* - 4* + * = О; в) 12л - 17 - 2л = Юл - 17;
г) 19с —Зс + 8= 16с 4- 8; д) 63 —23р + 32р = 63 - 9р; е) 4* + 65 —10* = - 6*.
220. а) —4ас + За - 7а = -4 ас - 4а; б) 9 - 23* + 40* = 9 4- 17*;
в) -4 - 12 4- 8ас = —16 4- 8ас.
Докажем тождества 221—223. См. пример стр. 53 учебника.
221 - а) 5* + 3* 4- х = 9х: левая часть — 5* 4- 3* 4- * = 9*; правая часть — 9*;
9* = 9*, тождество доказано.
б) Ьх - 3* - * = *: левая часть — 5* - 3* - * = *; правая часть — *;
* = * , тождество доказано.
в) т 4- 2т 4- 3т = 6т : левая часть — т 4- 2т 4- 3т - 6т:
правая часть — 6т; 6т = 6т , тождество доказано.
222. а) 2* 4- 3* = * 4- 4*: левая часть — 2* 4- 3* = 5*;
правая часть — * 4- 4* = 5*; 5* = 5*, тождество доказано.
б) - а 4- 7а = 7а —а: левая часть — - а + 7а = 6а;
правая часть — 7а ~ а = 6а; 6а - 6а, тождество доказано.
в) 5 —2 а - 3 = 2 “ 2а; левая часть — 5 - 2 а - 3 = 2 - 2а;
правая часть — 2- 2а; 2—2а = 2—2а, тождество доказано.
2 2 3 . а) 7* —5* 4- х = 3*: левая часть — 7* - 5* 4- * = 3*;
правая часть — 3*; 3* = 3*, тождество доказано.
б) 5л: - 9* = 2* - 6*; левая часть — 5* - 9* = -4 * ;
правая часть — 2* - 6* = —4*; -4 * = —4*, тождество доказано.
в) а = 2а 4- 4а -5а: левая часть — а; правая часть — 2а 4- 4а - 5а = а,
а = а, тождество доказано.
225. Составим все возможные тождества из выражений:
-р •Р = -р2; - р - р = р - (-р); -р р = -(-р)2; -р •р = (-1)р2;
-р ■(~р) = р2; -р ■(-р) = (~р)2; -р •(-р) = |-р12;
р2=р •р ; р 2= (-р)(-р); р2= |-р|2;
-р2= - р - р ; -р2= -(-р )2; -р2=р(-р); -р2= -|-р|2; -р2= (-Цр2; -р2=(-1Х-Р)2;
-(~р)2= -р2; -(-р)2= -р •р; -(-р)2= р(-р); -(-р)2= -|-р12;
(-1)2 •р2=р2; <-1)2-р2= (-1)2 р -р; (-1)2-р2= (-1)2•(-р)(-р);
(-1)2 ■р2= (-1)2 •|-р|2; (-1)2•р2= И2-
Упростим выражения 226—228:
226. а) 19* - 4(* 4- 5) = 19* - 4* - 20 = 15* - 20;
б) 7(2 - 3*) 4- 21 = 14 - 21 4- 21 = 35 - 21*;
в) 2,5 4- 5(а - 1,5) = 2,5 4- 5а - 7,5 = 5а - 5;
г) 0,1* 4- 3(1 - *) = 0,1* 4- 3 - 3* = 3 - 2,9*;
д) ~3(21/ + 1) + 4 = - 6у - 3 4 - 4 = “6у 4- 1;
е) -2 - (7а - 5) = -2 - 7а + 5 = 3 - 7а.
227. а) 35 + 7(* - 7) = 35 4- 7* - 49 = 7* - 14;
б) 2(с - 3) - 5(2 - 4с) = 2с - 6- 10 + 20с = 22с - 16;
в) —(9 —2х) 4 4* = -9 4 2* 4 4* = -9 4 6*;
г) -4 + 4(5 - *) = -4 4- 20 - 4* = 16 - 4*;
д) -2 (* 4- 5) 4- 3(* - 7) = -2 * -1 0 + 3* - 21 = * - 31;
е) -1 3 - 3(5 - 6*) = -1 3 - 15 + 18* = -2 8 4- 18*;
228. а) 12(* 4- 2) - (2* - 4) = 12* 4- 24 - 2* 4- 4 = 10* + 28;
б) 1,5(5 - 2*) + 5(1,1 + *) = 7,5 - 3* 4- 5,5 + 5* = 13 + 2*;
в) —3(а - 2) 4- 7(2а - 1) = -З а + 64- 14а - 7 = 11а - 1;
г) 0,2(* + 2) - 3(2* - 0,4) = 0,2* 4- 0,4 - 6* + 1,2 = 1,6 - 5,8*.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

38. Докажем тождества 229—230:
229. а) Зс —3(с - 1) = 3: левая часть — Зс - 3(с —1) = Зс —Зс 4- 3 = 3;
правая часть — 3; 3 = 3, тождество доказано;
б) 2ху + 2(3 - ху) ~ 6: левая часть — 2ху 4- 2(3 - ху) = 2ху + 6- 2ху = 6;
правая часть — 6; 6= 6, тождество доказано;
и) 15* = 9 - 3(3 - 5л:): левая часть — 15л:;
правая часть — 9 - 3(3 - 5*) = 9 - 9 4- 15л: = 15 х; 15* = 15л:, тождество
доказано;
г) 1 —2л: = 5 - 2(* 4- 2): левая часть — 1 - 2х;
правая часть — 5 - 2(* 4- 2) = 5 - 2л: - 4 = 1 - 2л:; 1 - 2х = 1 - 2*, тож­
дество доказано.
230- а) 8х = 64- 2(4х - 3): левая часть — 8л:;
правая часть — 64- 2(4* - 3) = 6+ 8* -6= 8л:; 8л:= 8л:, тождество доказано;
б) 5(2* + у) = 10(* + у) - Ьу: левая часть — 5(2* 4- у) = 10* + 5у;
правая часть — 10(* + у) - Ьу = 10* 4- 10у - Ьу = 10* 4- 5у; 10* + Ьу =
= 10* + 5у, тождество доказано;
в) 7 - 12* - (-7 + 12*): левая часть — 7;
правая часть — 12* - (-7 4- 12*) = 12* + 7 - 12* = 7; 7 = 7, тождество
доказано;
г) Зс - 3(1 + с - *) = 3* - 3:
левая часть — Зс - 3(1 4- с - *) = Зс - 3 - Зс 4- 3* = 3* - 3;
правая часть — 3* - 3; 3* - 3 = 3* - 3, тождество доказано.
231. Упростим выражение и найдем его значение, заменив переменную за­
данным числовым значением:
а) 12(а —3) + 3(а 4* 12), если а = 0,2.
12(а - 3) + 3(а + 12) = 12а - + За + М = 15а.
если о = 0,2, 15а = 15 *0,2 = 3. Ответ: 3.
б) *2(2 - *) - 2(*2- 3), если х = - 0,3.
х2(2 —х ) - 2(х2- 3) = 2- зс3—,23с2 + 6= -х» + 6, если х = - 0,3, ~х3+ 6=
= -(-0 ,3 )8+ 6= -(-0,027) + 6= 0,027 + 6= 6,027. Ответ-. 6,027.
232. Решение. Если * = а - 6, то 2* + 3* = 5* принимает вид:
2(а - 6) + 3(а - Ъ) = 5(а - 6); 2а - 2Ь + За - ЗЬ = 5а ~ 56;
5* = 5(а - 6) = 5а - 56; 5а - 56 = 5а ~ 56. Ответ: да.
Упростим выражение 233—235:
233. а) 2* 4- 4 + 2(* 4- 4) + 4(* - 8) = 2* 4- 4 + 2* 4- 8 + 4* - 32 = 8* - 20;
б) -(5а - с-+ 2) + З а - с + 2 = -5 а 4* / - X 4- За - / + =
- -5 а 4* За = -2 а ;
в) 0,5(а + 6+ с) - 0,5(а - 6+ с) - 0,5(а 4- 6- с) =
= 4- ^ 6 4- 4- 0,56 - $ А с - 0,5а - + 0,5с =
= 0,56 - 0,5а + 0,5с.
234. а) 5(12« - 23*) - 8(6* - 13а) = 60а - 115* - 48* + 104а = 164а - 163*;
б) - 6(ас - 4) + 3(7 —2ас) = -бас + 24 + 21 - бас = -12ас + 45;
235. а) 2(хг - 3) - 4(17 - 4х2) = 2х‘ - 6- 68 + 16х2= 18зс2 - 74;
б) 4(хг - 3) - х(4х - 5) = - 12 - 0 1 + 5х = -1 2 + 5х;
в) с(3 - 2 с) + 3(с - 2с2) = Зс - 2с2+ Зс - 6с2= 6с - 8с2;
г) 2у —3 —2(а + у —1) = —3 —2а - ^ + 2= —1—2а.
236. а) 2(х - 3) - 5(х - 4) = 14 - Зх:
левая часть — 2(* —3) - 5(* —4) = 2* —6 - 5* 4* 20 = 14 - 3*;
правая часть — 14 - 3*; 14 - 3* = 14 - 3*, тождество доказано.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

39. б) 3(2а - 1) - 2(3а - 1) = - 1:
левая часть — 3(2о - 1) - 2(3а - 1) = - 3 - + 2 - —1;
правая часть — - 1; —1= —1, тождество доказано.
в) 5(0,5 + 2х) - 5(1,1 - *) = 15* - 3: левая часть — 5(0,5 + 2х) 7 5(1,1 - *) =
= 2,5 + 10* - 5,5 + 5* = -3 + 15*; правая часть — 15* - 3 = -3 + 15*;
- 3 + 15* = -3 + 15*, тождество доказано.
г) 9(* -1 ) - 3(2* - 3) = 3*:
левая часть — 9(* -1) - 3(2* - 3) = 9* - 0 - 6* - 0 = 3*;
правая часть — 3*; 3* = 3*, тождество доказано.
237« а) 9* - 4(* + 5) - 1 = 7(* -3 ) - 2*:
левая часть — 9* - 4(* + 5) - 1 = 9* - 4* - 20 - 1 = 5* - 21;
правая часть — 7(* - 3) - 2* = 7* - 21 - 2* = 5* - 21; 5* - 21 = 5* - 21,
тождество доказано.
б) —2(2а + 5) = 5(2а —9) —7(2а —5): левая часть — —2(2а + 5) = —4а - 10;
правая часть — 5(2а - 9) - 7(2а - 5) = 10а - 45 - 14а + 35 = -4 а - 10;
—4а —10= —4а —10, тождество доказано.
238. а) 3(а + с + *) —2(а + с - *) - (а - с + *) = 2(с + 2*):
левая часть — 3(а + с + *) - 2(а + с - *) - (а - с + *) - За + Зс + 3* - 2а -
- 2с + 2 х - а + с - х = 2с + 4*; правая часть — 2(с + 2*) = 2с 4- 4*;
2с + 4 * = 2с + 4*, тождество доказано.
б) 2* + 2= 2(*2+ х + 1) - (х2- * + 1) - (*2+ * - 1):
левая часть — 2* + 2; правая часть — 2(*2+ * + 1) —(*2—* + 1) - (*2+
+ * - .1) = 2*2+ 2* + 2- * 2+ X - Х - * 2~ Х + X = 2* + 2;
2* + 2= 2х + 2, тождество доказано.
в) п - (1- (п —(1- п))) = 3п - 2:
левая часть — п —(1—(л - (1—л))) = п —(1—(п —1+ л)) = л —(1—(2л -
- 1)) = л - (1- 2л + 1)) = л —(2—2л) = л —2+ 2л = Зл —2;
правая часть — Зл - 2; Зл - 2= Зл - 2, тождество доказано.
239. Проверим тождественность выражений:
а) 1 - (1- (1- с)) = 1- ( X - X + с) = 1- с, поэтому выражения тожде­
ственны;
б) 0,5(* + у) - 0,5(х - у) - у = %&х + 0,5у - ]3<5* + 0,5у - у = у - у = 0,
поэтому выражения тождественны;
в) а —Ь + 1 —2{Ь + 1 ) = а - д + 1 - 2Ь —2 = а —ЗЬ —1;
2(а - Ь - 1) - (а + Ь - 1) = 2а - 2Ъ - 2 —а - Ъ+ 1 * а - ЗЬ - 1;
а —ЗЬ - 1 ~ а - ЗЬ —1, поэтому выражения тождественны.
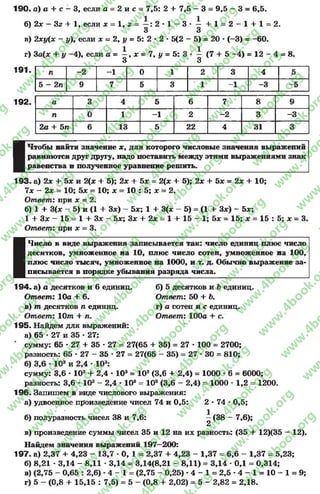
240. Заполним таблицу и определим тождественность выражения
*5- 5*3+ 5* и *.
В Заполним таблицу аналогично упражнению 191, подставляя числовые
Ия значения х в выражение *5—5** + 5*.
* -2 -1 0 1 2
* 5 - 5*3 + 5* -2 Г1 0 1 2
*5- 5*3+ 5* и * : принимают одинаковые значения при * = -2 , * = -1 ,
* = О, * = 1, * = 2, но при * = 3, принимают разные значения *5- 5*3+ 5* =
= 35—5 * 3 а + 5 * 3 = 123; 123 ф 3. Выражения тождественны, если * при­
нимает значения —2, —1, О, 1, 2, то есть данные числа являются решения­
ми уравнения. Значит, при любых других значениях * эти выражения не
равны, то есть не тождественны. Ответ: не тождественные.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

40. 241. Составим тождества'из заданных выражений:
а) ас(-*), а*(-с), с*(-а); ас{-~х) = ах(~с); ас(-х) = с*(-а); а*(-с) - сх(-а);
б) асх, а(-с)(-х), (-а)(-с)*, (~а)(~х)с;
асх ~ а(-с)(-*); асх = (-а)(~с)*; асх = (-а)(-л;)с.
242. Заполним таблицу:
* -2 -1 0 1 2 3 4 5
2(*2- 4) + 6 6 0 —2 0 6 16 30 48
2*2—2 6 0 -2 0 6 16 30 48
Выражения тождественны, так как их значения равны для всех значений х:
2(х2 —4) + 6= 2х2 —8 + 6= 2х2 - 2; 2хг —2 = 2х2 - 2.
243. Заполним таблицу:
а 0 1 2 3 4 5 100 100000
а + 1 1 2 3 4 5 6 101 100001
а + 1| 1 2 3 4 5 6 101 100 001
Равенства не являются тождеством, так как есть значения а, при которых
значения выражений не равны, например:
о = - 1, тогда м + 1= И 1+ 1= 1+ 1= 2, |a + 1|= |-1+ 1|= |01= О; 2* 0.
244. Проверим, является ли равенство тождеством:
а) х + 3|= х + 3 не является тождеством, так как есть значения *, при
которых значения выражений не равны, например х = —4:
х + 3) = |—4 -+ 3|= |-1| = 1; х + 3 = - 4 + 3 = -1 ; 1 * -1 .
б) х24- 5|= х2+ 5 является тождеством, так как х2+ 5 > 0и х2+ 5|> 0всегда
и их значения равны для всех значений *.
в) |a —b * Ь - а - (а - Ь)2 является тождеством, так как: если а > Ь9 то
а - b= а - b, b - а ~ а - Ь, а - Ъ- b - а - (а - Ъ)(а - b) = (а - Ь)г;
если а < Ь, то |а - Ь|= Ь - a, |b- а|= b - а, |а - Ь•[5 - а= (Ь - а)(Ь - а) =
= (6—а)2 = (а - Ь)2.
г) |* —у= х - у не является тождеством, так как:
если х > у, то |л: - = х - у; если х < у9 то х - i/|= у —х ф х - у.
д) а + b= |а|+ |Ь|не является тождеством, так как существуют значения
а и &, при которых |а + Ъф а+ |Ь|, например: а = —2, fc = 1.
|а + &|= |-2+ 1|- |-1|= 1; а+ Ь= |-2|+ |1|= 2+ 1= 3; 1ф 3.
е) |*|- у= |(/|- |*|не является тождеством, так как существуют значения
* и у, при которых 1*1- У ф Ы - 1* 1, например: * = 2, у = 1.
|2|- |1|= 2- 1= 1; Ы - |*|- |1|- |2|= 1-2 = - 1; 1* - 1.
245. Заменим в тождестве *2- 2 = 2(*2- 1) - *2переменную * выражением:
а) * = с + 3; (с + З)2- 2= 2((с + З)2- 1) - (с + З)2;
(с + З)2- 2= 2(с + З)2- 2 - (с + З)2; (с + З)2- 2= (с +З)2- 2.
Равенство выполняется.
б) х = ас - 1; (ас - I)2- 2 = 2((ае - I)2- 1) - (ас - I)2;
(ас - I )2- 2= 2(ас - I )2- 2- (ас - I)2; (ас - I)2- 2=(ас - I )2- 2.
Равенство выполняется.
в) * + 5; (* + 5)2- 2 = 2((* + 5)2- 1) - (* + 5)2;
(* + 5)2- 2 = 2(* + б)2- 2 - (* + 5)2; (* + 5)2- 2 = (* + 5)2- 2.
Равенство выполняется.
246. Заменим в тождестве 5* + 3* = 8* переменную * выражением а 2—ас + с2:
5(а2- ас + с2) + 3(а2- ас + с2) = 5а2- бас + 5с2+ За2- Зас + Зс2=
= 8а2- 8ас + 8с2;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

41. 8(а2- ас + с2) = 8а2- Sac + 8с2; 8а2- 8ас + 8с2= 8а2- 8ас + 8с2.
Равенство является тождеством.
247- Длина а см, ширина на с см менше, то есть
(а - с) (см. рис.) Р = 2(а + (а - с)); ( _ .
Р = 2(а + а - с); Р = 2(2а - с) см. V }
248. Длина основания а см, а боковая сторона
(а + 2) (см. рис.) ° см
Р = а + 2(а + 2); Р = а + 2а + 4; Я = За + 4 см.
249. Решим задачу. Обозначим массу муки, отсыпанной ^а 4. 2) См
из второго мешка, через х кг, тогда из первого отсы-
.пали Зх кг. В первом мешке осталось (80 - Зх) кг, а во
втором (60 - х) кг. Учитывая, что во втором мешке а см
осталось вдвое больше, чем в первом, составим уравнение:
60 - х = 2(80 - Зх), откуда: 60 —х = 160 - 6х; - х + 6х - 160 - 60;
5х = 100; х = 100 : б; х = 20, тогда Зх = 3 •20; Зле = 60.
Из первого мешка отсыпали 60 кг, а из второго — 20 кг.
250. Найдем координаты вершин треугольника: Л (-1; 4), В(3; 0), С(-4; -2).
Координаты середины АВ: х = (-1 + 3) : 2; х = 2 : 2; х = 1; у = (4 + 0) : 2;
у ~ 4 : 2; у = 2; (1; 2).
Координаты серединыАС: х = (-1 - 4) : 2; х = -5 : 2; х = -2 ,5 ; у = (4 -2 ) : 2;
у = 2 : 2; # = 1; (-2,5; 1).
Координаты середины ВС: х = (3 —4) : 2; х = -1 : 2; х = -0 ,5 ; г/ = (0 - 2) : 2;
= -2 : 2; у = -1 ; (-0,5; -1).
251. Решим уравнение:
а) 31(2 - х) = 93; 2 - лс = 93 : 31; 2 - я = 3; -х = 3 - 2; - х = 1; х = -1 .
б) 15(1 - 2х) = 45; 1 - 2х = 45 : 15; 1 - 2* = 3; -2 х = 3 - 1; -2 х = 2;
х - 2 : ( - 2); х = - 1.
в) 8,5(3 - 4х) = 17; 3 - 4х = 17 : 8,5; 3 - 4* = 2;-4 х = 2 - 3;-4 * = -1 ;
х = -1 : (-4); х = 0,25.
г) 4,7(3 - 5х) = 94; 3 - 5х = 94 : 4,7; 3 - 5х = 20; -5 * =2 0 - 3 ;
-5 х = 17; х = 17 : (-5); х = -3 ,4 .
д) 44 = 4(2 + Зх); 4(2 + Зх) = 44; 2 + Зх = 44 : 4; 2 + Зх = 11; Зх - 11 - 2;
Зх = 9; х = 9 : 3; х = 3.
е) 26 = 2(10 - Зх); 2(10 - Зх) = 26; 10 - Зх = 13; -З х = 13 - 10;
-З х = 3; х = 3 : (-3); х = -1 .
§ 7. Выражения со степенями
2 57. Вычислим:
а) 52, 2 103, 100э, 252. 52= 5 •5 = 25; 25= 2 * 2 * 2 * 2 * 2 = 32;
103= 10* 10 * 10 = 1000; 1003= 100 * 100 •100= 1000 000;
252 = 25 - 25 = 625. Отпеет: 25; 32; 1000; 1 000 000.
б) (0,2)3, (0,3)2, (0,04)3; (0,2)3= 0,2 *0,2 *0,2 = 0,008; (0,3)2= 0,3 •0,3 = 0,09;
(0,04)а = 0,04 * 0,04 * 0,04 = 0,000064. Ответ: 0,008; 0,09; 0,000064.
в) 1,22, 2,32, ЗД3, 1,0072; 1,22= 1,2 •1,2 = 1,44; 2,32- 2,3 * 2,3 = 5,29;
3,13= 3,1 * 3,1 * 3,1 = 29,791; 1,0072= 1,007 * 1,007 = 1,014049.
Ответ: 1,44; 5,29; 29,791; 1,014049.
т )(-2)(-1гуЛ -2)ъ; (—2)4=(-2)*(-2)*(—2)*(-2) = 16;(-13)2=(-13)*(—13)=169;
(~2)5= (-2) - (-2) *(-2) * (-2) •(-2) = -3 2 . Ответ: 16; 169; -32.
Д) (-3)4, ~(34), -3 (-0,5)2, -0 ,5 2, (-1)150, (-1 )105;
(-3)4 = ( - 3) . ( - 3) . (~3) . (-3) = 81; -(З4) = - ( 3 * 3 * 3 3 ) = -8 1 ;
-З 4= -(3 * 3 * 3 •3) = -8 1 ; (-0 ,5 )2= (-0,5) *(-0,5) = 0,25;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

42. -0,52= -(0,5 •0,5) = -0,25; (-1 )150= 1; (-1 )105= -1 .
Ответ: 81; -81; -8 1 ; 0,25; -0 ,2 5 ; 1; -1 .
258. Вычислим:
а) I2+ 22+ З2+ 42+ 52+ 62= 1 + 4 + 9 + 16 + 25 + 36 = 91.
б) З2- 42+ 52- 62+ Т = 9 - 16 + 25 - 36 + 49 = 81.
в) (-2 )2+ (-2 )3+ (-2 )4+ (—2)5+ (—2)6= 4 - 8 + 16 - 32 + 64 = 44.
259. Вычислим:
а) (0,3)3* 104= 0,027 * 10000 = 270;
б) 11,2 : 102= 11,2: 100= 0,112;
в) 2400 * (0,1)4= 2400 * 0,0001 = 0,24;
г) (-0 Д )5 : (0,01)2 = -0,00001 : 0,0001 = -0 ,1 ;
д) - 0,24* ( - 1)15= -0,0016 •( - 1) = 0,0016;
е) (-1 )12: (0,5)3= 1 : 0,125 - 8.
260. Вычислим:
а) 2 - 62 = 2 •36 = 72. б) ^ 2 -^ 1 = ^ -| ) = - | .
в) 5 - ( - 1 = 5 — = - = 1 - . г) —З2 •2 = -9 ■2 = -18.
^5^ 25 5 5
д) (5,6 - 4,5)3 : 0,1 = (1.1)э - 10 = 1,331 - 10 = 13,31.
261. Решение. Количество людей 7, тогда кошек 7 •7 = 72, мышей 72* 7 = 73,
колосков 73- 7 = 74, мерок ячменя 74* 7 = 75. Имеем ряд чисел 7, 49, 343,
2401, 16807, сумма которых равняется 7 + 49 + 343 + 2401 +16807 = 19607.
Ответ: 7; 49; 343; 2401; 16807; их сумма 19607.
262. Для выполнения этого упражнения найдем значения правой и ле­
вой частей выражения и сравним их»
I
а) З2+ 42= 52; 9 + 16 = 25; 25 = 25. Ответ: да.
б) 152 + 162 = 172; 225 + 256 = 481; 172 = 289; 481 * 289. Ответ: нет.
в) 35я+ 362= 372; 1225 + 1296 = 2521; 372= 1369; 2521 ф 1369.
Ответ: нет.
г) З3+ З2= 62; 27 + 9 = 36; 36 = 36. Ответ: да.
д) 43+ 62= 102; 64 + 36 = 100; 100 = 100. Ответ: да.
е) 972- 962 = 97 + 96; 9409 - 9216 = 193; 193 = 193. Ответ: да.
263. Докажем, что:
а) 102+ I I 2+ 122= 132+ 142; 100 + 121 + 144 = 169 + 196; 365 - 365.
б) I3+ 23+ З3+ .. + 93= 452;
1 + 8 + 27 + 64 + 125 + 216 + 343 + 512 + 729 = 2025; 2025 = 2025.
264. Площадь квадрата со стороной а считается по формуле 5 = а2.
а) 3 см. Решение. 8 = З2= 9 (см2). Ответ: 5 = 9 см2.
б) 10 м. Решение. 5 - 102= 100 (м2). Ответ: 5 = 100 м2.
в) 8,5 км. Решение. 5 = 8,52= 72,25 (км2). Ответ: & = 72,25 км2.
265. Представим число в виде степени с показателем, большим единицы,
и наименьшей по модулю основой:
а) 125 = 53; б) -3 2 = (-2)6; в) 2401 = 74; г) 243 = З5; д) 0,729 = (0,9)3;
. Л ч 8 ( 2V . „ 46 1296 ( б'4
е) 0,4096 = (0,8)4; е ) —I— ; е) 2
27 ^ 3 ) 625 625 ^5
266. Найдем значение выражения:
а) (-7 )2- (-1) 9* З4- 49 - (-1) * 81 = 49 + 81 = 130;
б) (0,02+ 0,28)4 * 105= 0,34* 100000= 0,0081 * 100000= 810;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

43. в) 63 —Г4- —^ -6^ = 6 3 - (| 1 •— =6 3 - -6^ . '^ 5 = 6 3 - 1 6 = 47;
I, 5 ) 4 U J 4
г) (-1)24 : f i l + (-3)5 = 1 : ^ - 243 = 1-64 - 243 = -179;
д) (5,6 - 4,5)э : 0,1 = (1,1)а ■10 = 1,331 - 10 = 13,31.
е) (0,3* + 0,4г) - 0,52= 0,09 + 0,16 - 0,25 = 0,25 - 0,25 = 0.
2 6 7 . Найдем значение выражения, заменив переменную заданным ей зна­
чением:
а) За4- 2а2, если а = -3 :
3 •(-3 )4- 2* (-3 )2= 3 *81 - 2 •9 = 243 - 18 = 225;
б) 5с3- 2с2+ с, если с = 0,5:
5(0,5)8- 2(0,б)2+ 0,5 = 5 •0,125 - 2 - 0,25 + 0,5 = 0,625 - fk £ + = 0,625;
в) п? + (л —З)2, если п - —2:
( - 2)8+ (-2 - З)2= -8 + (-5 )2= -8 + 25 = 17;
г) (2т —I )2: т если т = -ОД:
(2 *(-0Д ) - I )2: (-0Д )4= (-0 ,2 - I )2: 0,0001= (~1,2)2•10000 =
= 1,44 * 10000 = 14400.
Решим уравнение (268—269):
268. а) бх4= 5; х4= 5 : 5; х4= 1; х = -1 , х = 1.
б) 4х2= х2; 4л:2- хг = 0; Зх2= О; х2= 0; х = О.
в) 16(х + 5)2= О; (х + 5)2= О; х + 5 = О; х = -5 .
г) -2х 8 = 2; х3= 2 : (-2); х3 = —1; х = - 1.
2 6 9 . а) х9 + 1= О; х8= - 1; х = - 1. б) хь -1 = 0; х* =1; х = 1,х = - 1.
в) 2х 7 = 2; х7 = 2: 2; х7 = 1; * = 1. г) х3- 6= 2;х8= 2 + 6;х8=8; х = 2.
Запишем в стандартном виде числа 270-271.
270. А - а •10°, где 1< а < 10, п — натуральное число.
Скорость света — 300000 км/с = 3 * 105км/с.
Масса Земли — 6000000000000000000000 т = 6 * 1021т.
Масса Луны — 73500000000000000000 т = 7,35 * 1019т.
Объем Земли — 1083000000000 км3= 1,083 * 1012км8.
27 1 . а) 20 ООО= 2 * 104; б) 7 530 000 = 7,53- 106; в) 10 500 000 = 1,05 * 107;
г) 909 900 000 = 9,099 * 108; д) 33 000 = 3,3 * 104; е) 105 = 1,05 * 102;
е) 1 000 000 000 = 1* 109; з) 12 345,67 - 1,234567 •104.
272. Запишем числа стандартного вида в обычном виде. Для этого в первом
множителе перенесем запятую вправо на столько знаков, сколько нулей
содержит второй множитель (равняется показателю степени числа 10).
а) 5,2 •104= 52000; б) 1,31 * Ю8= 1310; в)7,1 •105= 710000;
г) 4,44 •102* 444; д) 2, 05 •104= 20500; е) ЗД25 - 10е = 3125000;
ж) 9 * 109= 9000000000; з) 6,75 •105= 675000.
2 73. Проверим, правильное ли равенство:
а) 22+ 22+ 62+ 102= 122
левая часть — 22+ 22+ 62+ 102= 4 + 4 + 36 + 100 = 144;
правая часть — 122= 144; 144 = 144, равенство верно;
б )22+ 42+ 62+ 132 = 1 5 2
левая часть — 22+ 42+ 62+ 132 = 4 + 16 + 36 + 169 = 225;
правая часть — 152= 225; 225 = 225, равенство верно;
в) 22+ 62+ 82+ 252 = 272
левая часть — 22+ 62+ 82+ 252 = 4 + 36 + 64 + 625 = 729;
правая часть — 272= 729; 729 = 729, равенство верно;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

44. г) 1а + 23 + За + 4а = (1 + 2 + 3.+ 4)2
левая часть — I3+ 28+ З3+ 4® = 1 + 8 + 27 + 64 = 100;
правая часть — (1 + 2 + 3 + 4)2 = 102 = 100; 100 = 100, равенство верно.
274.-Вычислим значения выражений, выполнив возведение в степень:
а) 3,24 - 102 = 3,24 •100 = 324;
б) (З4+ 19)6 = (81 + 19)5= 1005= 10 ООО000 000;
в) (0,875 + 0,53)10 = (0,875 + 0, 125)10 = 1,0= 1;
г) (-0,3)* •103 = 0,0081 •1000 = 8,1;
е) (44 - З6 - 13)12 = (256 - 243 - 13)12 = О12= 0.
_ч ( 2 ) г f 3 f = 9 1 .
UJ UJ 27 16 6 ’
275. Упростим выражение:
а) (35 - 25)4 = (35 - 32)4 = З4 = 81; б) 4000 •0,23 = 4000 - 0,008 = 32;
в) (0,33- 0,0 1 7)6 = (0,027 - 0,017)° = 0,01е = 0,000000000001;
г) (-1 Д )3 : 0,11 = -1,331 : 0,11 = - 1 3 3 , 1 1 1 = -1 2 ,1 ;
д) (27 - 53 - 4)15 = (128 - 125 - 4)15 = (-1 )15 = - 1 ;
276. Найдем значение выражений:
а) (4х2- у2)2 : (2х - у)2, если х = 0,6, у = - 0,2.
(4 * 0,62- (-0,2)2)2 : (2 •0,6 - (-0 ,2))2= (4 •0,36 - 0,04)2 : (1,2 + 0,2)2=
- (1,44 - 0,04)2 : (1,4)2= (1,4)2: (1,4)2= 1,96 : 1,96 = 1.
б) 2х5 + (# + 2у)3 + I/2, если х = -2 , у = 3.
2 •(—2)Б+ (-2 + 2 •З)3+ З2= 2* (-32) + (-2 + 6)3+ 9 * -6 4 + 4а + 9 =
= -6 4 + 64 + 9 = 9.
в) ((1+ Ъ)2 - (а - I )2)3- (а + Ь)2, если а = 1,1, Ь = 0,1.
((1 + ОД)2- (1Д - I)2)8- (1,1 + ОД)2= (1Д2- ОД2)3- 1,22=
= (1,21 - 0,01)3- 1,44 = 1,23- 1,44 = 1.728 - 1,44 = 0,288.
г) (2т - п)2 - (4 т 2+ п2 - 4тп), если т - 1,3, п = 2,5.
(2 •1,3 - 2,5)2- (4 * 1,32+ 2,52- 4 » 1,3 * 2,5) = (2,6 - 2,5)2- (4 •1,69 +
+ 6,25 - 10 * 1,3) = ОД2- (6,76 + 6,25 - 13) = 0,01 - ОД = -0,09.
277. Залолним таблицу:
X -4 “3 -2 -1 0 1 2 3 4
2х2 32 18 8 2 0 2 8 18 . 3 2
X -4 -3 —2 -1 0 1 2 3 4
(2 x f 64 36 16 4 0 4 16 36 64
278. Составим таблицу значений выражения х4 —Зх3 + 2х2,
X -3 -2 -1 0 1 2 3 4
Xі - Зх3+ 2*2 180 48 6 0 0 0 18 96
279. Вычислим, пользуясь калькулятором:
а) 3,45= 454,35424; б) 5,754+ 57 = 1093,1289625 + 57 = 1150,1289625;
в) 47,2 •2,843 = 47,2 * 22,907304 - 1081,2247488; г) 3,7 + 2,74=
= 3,7 + 53,1441 = 56,8441.
280. Вычислим и сравним значения выражений:
а) З2+ 52= 9 + 25 = 34; (3 + 5)2= 82= 64;
34 < 64, поэтому З2+ 52< (3 + 5)2;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

45. б) 102- 62= 100 - 36 = 64; (10 - 6)2= 42= 16;
64 > 16, поэтому ДО2- 62> (10 - 6)2.
2 8 2 . Составим числовое выражение и найдем его значение:
„ „ „ е /'2 + 3 + 4 + бУ!
а) квадрат полусуммы чисел 2, 3, 4 и 5: I I;
0 _ . _ 224 З2+*42+ 52
полусумма квадратов чисел 2, 3, 4 и 5: --------------------.
2
.2 .л» 4+ 9+ 16 + 25 54Г2 + 3 + 4 + 5 У _ 2г + Зг+ 4г+ 5г = ^141 _
Ответ: на 22. - Л Л .3
( 2 + 3 + 4 + 5^
б) куб полусуммы чисел 2, 3, 4 и 5: I I ;
- о о >. с 28 + З8+ 43+ 53полусумма кубов чисел 2, 3, 4 и о:
7г ~ — = 4 9 - 2 7 = 22.
2
2
^2 + 3 + 4 + 5^3 23+З3+ 43+ 53 8+ 27 + 64 + 125
224
= 78- — = 343 - 1 1 2 = 231. Ответ: на 231.
2
283. Решение. Пользуясь доказанным в задаче 107 равенством
1024- I I 24- 122= 132 + 142, запишем данную дробь в таком виде:
132 + 142 + 132+ 142 2(132 + 142) 2(1694196) 2-365 0 Ответ•9
365 ” 365 " 365 365
284. Найдем значения выражений и выясним, какое имеет наибольшее зна­
чение, какое — наименьшее:
ч 72+ 32 49 + 9 58 7 + 3 10 _
а) = ---------- = — = 29; —— = — = 5;
2 2 2 2 2
М
2 49 9 58 ЛА1
— + —= — = 1 4 -
4 4 4 2
72+ З2 7 + 3 „
Ответ: наибольшее значение---------------= 29 , наименьшее — = 5 .
2 2
7 1 -5 1 = 49 - 25 = 24 ( 7 - 5 Ї (2Л
2 2 2 ^ 2 ^ ^2^
Г ї у _ Г * у жі » _ М . м . б .
Ь ) Ы 4 4 4 72_52
Ответ: наибольшее значение — ----------= 12, наименьшее — I-— - I —1
2 1 - і
51+31 = 125 + 27 = 152 (б + зУ = Л * =
2 2 2 М , 2 ) У2)
е н а т - “ * ? - 8
_ , 53+3* __
Ответ: наибольшее значение--------------- = 76,
2
гь
наименьшее
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

46. 285. Докажем, что уравнения не имеют корней:
а) х4 + 3 = 0; х4——3; четная степень числа не может принимать отрица­
тельные значения. Ответ: корней нет.
£
б) Зх2 + 8 = 0; Зх2 = —8; х2 = ——; квадрат любого числа принимает неот­
рицательные значения. Ответ: корней нет.
в) (у - З)2+ X = 0; (у - З)2= - 1; квадрат любого числа принимает неотри­
цательные значения. Ответ: корней нет,
*
Решим уравнения 286—287.
286. а) (х - 5)а = 1; х - 5 = 1; х = 1 + 5; х = 6.
б) (х2 + I )2= 0; х2 +-1= 0; х2 = - 1; уравнение не имеет решений, так как
квадрат любого числа не может принимать отрицательные значения.
в) (х2 + I )3= 8; х2 + 1= 2; х2 = 2—1; х2 = 1; х = - 1; х = 1.
г) (2х - З)5= 1; 2х - 3 = 1; 2х = 1 + 3; 2х = 4; х = 4: 2; х = 2.
д) (8- Зг)3 = -1 ; 8 - Зг = -1 ; - Зг = -1 - 8; -З г = -9 ; г - -9 : (-3); 2= 3.
е) (х4 + З)2= 1;
1) х4 + 3 = -1 ; х4 = -1 - 3; х4 = -4 ;
2) х4 + 3 = 1; х4= 1- 3; х4 = - 2.
Уравнение корней не имеет, так как четная степень любого числа не мо­
жет принимать отрицательные значения.
287- а) 2(1,2- 1) = 0; у2- 1 = 0; у2 = 1; у = -1 ; у = 1;
б) ЗСг4 - 1) = О; г4- 1 = О; г4 = 1; г = -1 ; г = 1.
в) 0,5(*э + 2) = 1; х2 + 2 * 1 : 0,5; хг + 2 - 2; х* = 2 - 2; х* = 0; ж= 0.
г) 0,2(1 + г8) = 0,4; 1 + 23= 0,4 : 0,2; 1 + г3= 2; г3= 2 - 1; г3= 1; 2= 1.
д) (ас + 2)3= - 1; х + 2= —1; х = -1 - 2; х = -3 .
е) (5 —у)7 + 2 = 1; (5 - у)7 + 2 = 1; (5 - уУ = 1- 2; (5 - уУ = -1 ;
5 - у = -1 ; -у = -1 - 5; -у = - 6; у = 6.
288. Запишем в стандартном виде числа:
а) 287 287 000 = 2,87287 •108; 17 530 000 = 1,753 * 107; 220 500 ='
= 2,205 •Ю5; 90,99 = 9,099 * 10;
б) 0,0003 = 3 * 10~4; 0,235 = 2,35 •101; 0,05 = 5 - 10 2;
0,0000000041 = 4,1 * 10-9;
в) - = 0,5 = 5 •10-*; — = 0,05 = 5•10 г; — = 0,005 = 5 •10-8;
2 20 200
Ч 73
0,0006 = 6 * 10~4; — —— = 0,000146 = 1,46 * 10~4;
5000 500000
999
= 0,000000999 = 9,99 * 10"7.
1000000000
289. Запишем в обычном виде числа, поданные в стандартном:
а) 1,2 * 108= 1,2 •1000 = 1200; 3,47 * 105= 347000; 7,3 * 104= 73000;
14,23 * 105= 1423000;
б) 2 * 10-4= 0,0002; 1,1 * 10~3= 0,0011; 9 •10“5= 0,00009;
6,75 - 10-6= 0,00000675.
290*. а) 1012+ 2 делится на 3, так как: запись числа 1012состоит из 1 и 12
нулей. Если к нему прибавить 2, то запись будет состоять из 1 на первом
месте, 11 нулей и цифры 2 на последнем месте. Сумма цифр этого числа —
3 делится на 3, тогда по свойству делимости на 3, 1012+ 2делится на 3.
б) 1 + ДО10+ 10100. Запись этого числа состоит из цифры 1 на первом месте,
цифры 1 на 91-м месте, цифры 1 на последнем месте и нулей на остальных
местах. Сумма цифр этого числа 3, тогда по свойству делимости на 3 —
1+ 1010+ 10100делится на 3.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

47. в) 1015+ 8. Запись этого числа состоит из цифры 1 на первом месте, циф­
ры 8на последнем месте и нулей на остальных местах. Сумма цифр этого
числа 9, тогда по свойству делимости на 9 число 101Б+ 8делится на 9.
г) 1010- 1. Запись числа ДО10состоит из цифры 1 на первом месте и 10
нулей. Если из числа вычесть 1, то запись будет состоять из десяти цифр
9. Сумма цифр этого числа равняется 9 - 10 = 90. Так как сумма цифр де­
лится на 9, то число делится на 9.
291*. Докажем, что значение данных дробей является натуральним числом
для любого п:
6” 1
а) ---------. Любая степень числа 6заканчивается цифрой 6. Если из числа
5
6" вычесть 1, то запись разности будет заканчиваться цифрой 5; по свой­
ству делимости чисел на 5 такое число делится на 5, поэтому дробь — на­
туральное число.
10я+ 5
б) ----------. Запись числа 10я+ 5 состоит из цифры 1 на первом месте, циф-
3
ры 5 на последнем и нулей на остальных местах. Сумма цифр этого числа
равняется 6. Это число делится на 3, поэтому по свойству делимости на 3
10й+5 в
число ---------- делится на 3, поэтому значение дроби число натуральное.
3
10й-1
в) --------- . Запись числа 10* состоит из цифры 1 на первом месте и п нулей
9
на остальных местах. Если из него вычесть 1, то запись разности будет состо­
ять из п цифр 9. Сумма цифр этого числа 9п, что делится на 9. По свойству
делимости на 9 такое число делится на 9, поэтому значение дроби — число
натуральное.
34,‘ + 4
г) --------- . Степень З4”можно заменить тг-ной степенью числа 81 (З4= 81).
5
Записи всех степеней числа 81 заканчивается цифрой 1. Если к этому
числу прибавить 4, то запись суммы будет заканчиваться цифрой 5. Тог­
да число 34п+ 4 делится на 5 по свойству делимости чисел на 5, поэтому
значение заданной дроби — число натуральное. Замечание. Все числители
заданных дробей являются натуральными числами.
293. Проверим, тождественны ли выражения:
а) 2а + а + а = 4а, что равняется выражению 4а; выражения тожде­
ственны.
б) х + х + х = 3*, что не равняется выражению х8; выражения не тож­
дественны.
в) - 2(а - Ь) = -2 а + 2Ь = 2Ь - 2а, что равняется выражению 2Ъ - 2а; вы­
ражения тождественны.
г) 5 + 5 + 5х = 10 + 5*, что не равняется 15*; выражения не тождест­
венны.
д) Зу + 2у + у - 6 = 6# - 6, что не равняется у; выражения не тожде­
ственны.
е) а3—а не равняется а2; выражения не тождественны.
294- Определим, при каком условии пропорция правильна. Для этого составим
уравнение, применяя основное свойство дроби, и решим его:
а) 3 : * = х : 27; * *х = 3 * 27; х2 = 81; х = -9 ; * = 9
О твет: при * - -9 , х - 9.
б) у : 4 = 16 : у2; у *у2= 4 * 16; у - у2 = 4 * 42; у = 4
Ответ: при у = 4.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

48. 295. Пусть за 1 год из меньшей трубы вытекает х л воды, тогда за сутки, то есть
24 часа, из нее вытекает 24# л воды — такой объем воды вмещает бассейн.
За четверть суток, то есть за 6часов ( 2 4 : 4 = 6(ч.)), из меньшей трубы выте­
чет 6х л воды, тогда 24.x - 6х = 18х литров воды вытечет из большей трубы.
Значит, из большей трубы за 6часов вытечет 18х л воды, а за 1 ч. 1 8 х : 6=
Зх литров воды. Большая труба наполнит бассейн объемом 24х л за 2 4х: Зх ~
= 8часов. Ответ: за 8часов.
296. Пусть длина основания равнобедренного треугольника х см,-тогда бо­
ковой стороны — (х + 3) см. Составим и решим уравнение, учитывая, что
периметр равнобедренного треугольника равняется:
а) Р - 54 см
х + 2(х + 3) = 54; х + 2х + 6= 54; Зх + 6= 54; Зх = 54 —6; Зх = 48;
х = 48 : 3; х = 16. Тогда х + 3 = 16 + 3 = 19.
Ответ: основание — 16 см, боковая сторона — 19 см.
б) Р = 6см
х + 2(х + 3) = 6; х + 2х + 6= 6; Зх + 6= 6; Зх = 6 - 6; Зх = О;
х = О : 3; х = 0. Задача решений не имеет, потому что не существует тре­
угольника со стороной 0см.
в) Р = а см.
х + 2(х + 3) = а; х + 2х + 6= а; Зх + 6= а; Зх = а - 6; х = (а - 6) : 3;
0—6 л —6 Л 0—6
х = -------. Тогда х + 3 = -------- + 3. Ответ: основание — ------- см, боко-
3 * 3 3
а —6 _ _
вая сторона — ( ------- + 3) см. Замечание: данная задача имеет решение,
если а > 6. ®
§ 6. Свойства степеней
312. Определим, имеют ли уравнения решение:
а) х2х 4= - 1; х2+4 = —1; х® = -1 . Решений нет, потому что четная степень
числа не может быть отрицательной. Ответ: нет.
б) хъхъ - -1 ; х8+е = - 1; х9= -1 . х = —1. Ответ: да.
в) х7* 0 = О. Ответ: да.
г) О* х8= 1 — решений нет. Ответ: нет.
313. Решим уравнение:
а) хвх7~ 1; х15= 1; х.= 1. б) ~ - 1; у9= - 1; у ~ - 1.
в) х2х2= 1; х4= 1; х = - 1, х = 1. г) г*г2г%= - 1; г3+2+8= - 1; г - - 1.
314. Найдем сумму, разность, произведение и частное чисел:
а) 2,4 •10*+ 3 * 105= 240000 4- 300000 = 540000 — сумма;
2.4 •105- 3 * 105= 240000 - 300000 = -60 0 0 0 — разность;
2.4 * 10б* 3 •105= 2,4 * 3 * 105+5= 7,2 * 1010= 72000000000 — произве­
дение;
2.4 * 105: (3 * 105) = (2,4 : 3)(10б•105) = 0,8 •1 - 0,8 — частное.
б) 1,5 •107+ 5 * 107= 15000000 + 50000000 = 65000000 — сумма;
1,5- Ю7- 5 * 107= 15000000 - 50000000 = -35000000 — разность;
1.5 *107•5 - 107= 1,5 *5 - 107*107=7,5 *107+7= 7,5 *1014= 750000000000000 —
произведение;
1.5 •107: (5 * 107)= (1,5 : 5)(107: 107) = 0,3 * 1 = 0,3.
в) 6,4 •104+ (3,2 * 104) = 64000 + 32000 = 96000 — сумма;
6.4 * 104- (3,2 * 104) = 64000 - 32000 = 32000 — разность;
6.4 - 104•(3,2 •104) = 6,4 * 3,2 * 104* 104= 20,48 •10® = 2048000000 —
произведение;
6.4 •104 : (3,2 * 104) = (6,4 : 3,2ХЮ4 : 104) = 2 * 1 = 2 — частное.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

49. 3 1 5 . Выполним действия:
а) 2,5 - 105 + 3,3 •105= (2,5 + 3,3) - 105= 5,8 •10® = 580 ООО;
б) 7,7 •107 - 5 •107= (7,7 - 5) •107= 2,7 •107= 27 ОООООО;
в) 6,4 •104: (3,2 ■104) = (6,4 : 3.2Х104•104) = 2 •10е = 200 ОООООО;
г) 6,4 •10® •2 •10® = 6,4 •2 -10® •10®= 12,8 •10®+®= 12,8 •ДО®= 12 800 ООО.
3 1 6 . а) 0,512• 21®= 0,512- 2“ •2=(0,5 •2)“ - 2 = 1“ ■2 = 1- 2 = 2;
б) ОД21•1020= ОД20- 1020•ОД = (ОД •10)20■ОД = I 20•ОД = 1 •ОД = ОД;
в) 0,241 •(-0 ,5 )40 = 0,240 - 0,540 ■0,2 = (0,2 - 0,5)40 •0,2 = (ОД)40 •0,2 =
= 1- 1040•2•10-1= 2•10-41;
г) 527•0,2®° = 527•0,227•0,2® = (5 •0.2)27•0,2® = I27•0,008 = 1 •0,008 = 0,008;
д) (-0.25)15- 416= -(0,25)1S•4 = - I 15•4 = -1 •4 = -4 ;
е) 481■0,25 = 4®° •0,2530 •4 = (4 •0,25)®° •4 = I 30- 4 = 1 •4 = 4.
.12
5 ( 7 V» 49
7 Ь )) 25
„ 4 9 =1 49 = 49
25 25 25
16 ✓-чів / л15 - / л15
в 7“ ( Л ) - 7 “ ( і ) І - ( 7 І ) І . i l - і ;
f i f .f І Ї ‘ . Г! Г .f « Г . § , Гі . » Г . Î , . Î , , . Î , і .
M ,3j V2) W 2 2 ) 2 2 2 2
3 1 8 . a) 520 •0,2“ = 52 •5“ •0,2“ = 25 •(5 •0,2)“ = 25 - 1“ = 25 - 1 = 25;
б) 0,04“ •25” = 0,04 •0,04” •25й = 0,04 •(0,04 •25)11 = 0,04 •l 11=
= 0,04 •1 = 0,04;
в) (-2 ,5 )17- (0,4)“ = (-2,5)17•(0,4)17- (0.4)2= -(2 ,5 •0,4)17•0,16 =
= - 1 ” •0,16 = -1 •0,16 = -0 ,1 6 ;
г) 1026- ОД2®= 1026•0Д26•0,12= (10 - 0Д)26•0,01 = l 25•0,01 = 1 •0,01 = 0,01;
д) ' •(-8)37 = - ^ j •835 ' 82 = " ( f ' 8 ] ' 64 = “lS6 •64 = -1 -64 = -64;
е) (—1,25)22 - (-0 .8 )23= -(1,25)22 - (0.8)22•0,8 = -(1,25 * 0,8)22•0,8 =
= - l 22 •0,8 = -1 •0,8 = -0 ,8 .
Представим в виде выражения в степени произведение, воспользовавшись
основными свойствами степени 319—321.
3 1 9 . а) а5*(о2)7= а5•а2 7= а5+14= а19;
б) (х2)3*(х3)4= Xі *3*х3'4 = х6*12■=х 1В;
в) У * (і/5)2* Уе = У У5"2* У6 = У1hl0+6 = У17у
г) (Ь3*Ь5)2 = (Ь 3+5)2= Ь* 2 = Ь1Ъ;
д) (х * л:8)3*х3 = (#9)3* л:3= х9’3+3= дс30;
е) (—а2)3* (а3)5= —а 2‘ 3*а35= —а6+15= —а21;
ж) ( - y f * (”|/4)5= і/6* (-у 4'б) = -у в+20= -у 2Ь;
з) ((—jc)3)2* (—х)4= (~х)3'2•Xа = (-a:)6*дс4= дс6*х4= дс6+4= дс10. .
и) (—а4)3*((—а)3)5= - а 4’3*(—а)3*5= —а 12 *(—а3*5) = —а 12•(-о 15) = а 12+15= с27.
320. а) а6хе = (а*)6; б) (- Ь)7у7= (~ЬуУ; в) a3b3c3= (abc)3; г)( - 1)9т 9= ( - т ) 9;
д) 32*5 = 25*5= (2х)ь; е) 0,0081 Ь2 = 0,092 * Ь2= (0,09 Ь)2 ;
е)(|) î*>è*v "(ï)* v = ( i 4,) ;
з) ioooo f ^ T = io4f ^ T = f — Т .
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

50. 321. а) 5е- 125 = 56•53= 56*3= 59; б) 36 •6В= 6В- 62= 68*2= 6“ ;
в) 210 •64 = 210 •2 6= 210+6= 216; г) 0,001 •ОД5= ОД3 •ОД5 = ОД8*5 = ОД8;
д) <-0,3)16 •(-0,027) = (-0,3)15 - (-0,3)8 = (-0,3)15+8•=(-0,3)18= 0,318;
е) 0,4 ■0,16 = 0,4 •0,4* = 0,4’ +2 = 0,4а; ж) 0,25 •0,125 = 0,52 ■0,5®=
= 0,5г+3 = 0,55;
9.7 Я Г З '3 " " 2 '~ '8+2
з)
с ю к/lJ .*J к * ;
4+3
(-»г?) - (!) ■(-1) - -(! Г - ( - 1)
322. Решим уравнение, упростив левую его часть:
а) Ззс2•ас5+ 3 = О; Зх> + 3 = О; Зх7 = -3 ; х7 = -3 : 3; х7 = - 1 ; х = -1 .
б) -2 у 4 •у7= 2; -2 у 11 = 2; у11 = 2 : ( - 2); у11 = - 1; у = - 1.
в) 0,5л:3•х* + 1 = 1,5; 0,5л:11+ 1 = 1,5; 0,5хи = 1,5 - I; 0,5л:11= 0,5;
х11= 0,5 : 0,5; х11= 1; х = 1.
г) - у 4-у1+ 2 = 2 - ; - у 11+ 2 = 2 - ; —у11 = 2- - 2; ^-у11 = - ;
3 3 3 3 3 3 3 3
= уп = 1; у = 1.
323. а) хв •* = х 15; основание степени — х, показатель степени: 15 - 6= 9.
х6- х9= х 15.
б) а10** *а = а17; основание степени — а, показательстепени:
17 - 10 - 1 - 6. с10*с6•а = о17.
в) (* у = хъ; вместо звездочки надо подставить хп, где п = 20 : 5 = 4, то
есть х 4. (х4)5= х20
г) ( * у = -а 21; вместо звездочки надо подставить -а п, где п = 21 : 7 = 3, то
есть - а 3; (-а 3)7= - а 21.
324. Найдем значение переменной, пользуясь утверждением: если равны две
степени с одинаковыми основаниями, то показатели их степеней равны:
а) 5а- 54= 55+г; 57= 55+г; 7 = 5 + 2; 5 + 2= 7; 2= 7 - 5;2= 2.
б) 3х •З5= (32У; Зх+5= 32х; х 4- 5 = 2х; х - 2х = -5 ; - х = »5; х = 5.
в) ((43)х)4 = 4х * 422; 43 •*-4 = 4*+22. 412* = 4** 22. 12х =х + 22;
12х - х = 22; И х = 22; х = 22 : 11; х = 2;
г) (6х)4= (6Э)Х; 64х = 63х; 4х = Зх; 4х - Зх = 0; х = 0.
д) (7е)8= 712х; 74в= 712х; 48 = 12х; х = 48 : 12; х = 4.
е) (25)х * 22= (23)х *(2х)4; 25х * 22= 23х * 24х; 25х+2= 23*+4х; 5х + 2 = Зх + 4х;
5х - 7х = - 2; -2 х = -2 ; х = -2 : ( - 2); х = 1.*
325. Решим уравнение:
а) (2х)5= -3 2 ; 25* х5= -3 2 ; 32х5 = -3 2 ; х 5= -3 2 : 32; х5= -1 ; х = 1.
б) (Зх)4= 81; З4* х4= 81; 81х4= 81; х4= 81 : 81; х4= 1; х = - 1, х = 1.
в) 12х5х3= 0; 12х5х3= 0; х®= 0; х = 0.
г) (х® *х4)3= —1; (х13)3= - 1; х30= - 1; х = - 1.
д) (х7*х 11)5= 1; (х18)5= 1; х90= 1; х = - 1, х = 1.
е) (4(х + 2)2)8= 0; 48(х + 2),в = 0; (х + 2)16= 0 : 48; (х + 2)1в= 0;
х + 2= 0; х = - 2.
326. Найдем сумму, разность, произведение и частное чисел:
а) сумма 3 * 10~7+ 2 - 10“7= (3 + 2) * 10~7= 5 * 10~7;
разность 3 * 10“7- 2 * 10~7= (3 - 2) * 10 17= 1* 107;
произведение 3 * 10“7* 2* 10~7= 3 * 2 * 10-7* 10“7= 6 •10“7“7= 6 * 10-14;
частное 3 * 10~7: (2 * 10 7) = 3 : 2 - (10~7: 10“7) = 1,5 * 1 = 1,5.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

51. б) сумма 4,5 - 10“ + 3 - 10® = 4,5 •10 •10® + 3 •10® = 45 •10® + 3 •10» =
= (45 + 3) -10®= 48 - 10® = 4,8•10“ ;
разность 4.5 •10“ - 3 •10® = 45 - 10® - 3 10® = (45 -3 ) •10® = 42 •10® =
= 42 •10® = 4,2 •10“ ;
произведение 4,5 •10“ •3 •10®= 4,5 •3 •10“ •10®= 13,5 •10“ +®= 13,5 •10“ =
= 1,35 •1020;
частное 4,5 •10“ : (3 •10®) = 4,5 : 3 •(10“ : 10®) = 1,5 ■10 = 15.
в) сумма -6 •10“ + 1,2•10“ = -6 0 •10“ + 1,2•10“ = (-60 + 1,2) •10“ =
= -5 8 ,8 •10“ ;
разность -6 •10“ - 1,2•10“ = -6 0 •10“ - 1,2•10“ = (-60 - 1,2) •10“ =
= -61,2 - 10“ ;
произведение -6•10“ •1,2 •10“ = -6•1,2•10“ •10“ = -7,2 •10“ +“ = -7,2 •1025;
частное -6 •10“ : (1,2 •10“ ) = -6 : 1,2 -(10“ : 10“ ) = -5 •10 = -50.
г) сумма 2,8 •10“ + 7 - 1020= 2,8 •10“ + 70 •10“ = (2,8 + 70) •10“ =
= 72,8 •10“ ;
разность 2,8 • 10“ - 7 • 1020= 2,8 • 10“ - 70 • 10“ = (2,8 -7 0 ) • 10“ =
= -6 7 ,2 •10“ ;
произведение 2,8 •10“ •7 •1020= 2,8 - 7 •10“ •10го= 19,6 •10“ +20= 19,6 - 103®;
частное 2,8 •10“ : (7 •1020) = 2,8 : 7 •(10“ : 1020) = 0,4 •10*.
32 7 . а) сумма 1,4 •10* + 7 •10 е = (1,4 + 7) ■10 е = 8,4 •10*;
разность 1,4 •10* - 7 •10е= (1,4 - 7) •10* = -5 ,6 •10*;
произведение 1,4 •10* •7 - 1 0 * = 1,4 •7 •10* •10*= 9,8 •1 0 * * = 9,8 •10““ ;
частное 1,4 •10* : (7 •10*) = 1,4 : 7 - (10* : 10 * ) = 0,2 •1 = 0,2.
б) сумма 3,5 •10 4+ 5 •10 4= (3,5 + 5) •10*= 8,5 •10* ;
разность 3,5 •10* - 5 ■10* = (3,5 - 5) •10*= -1,5 •10* ;
произведение 3,5 •10* •5 •10* = 3,5 - 5 •1 0 *-1 0 *= 17,5 •1 0 ** = 17,5 ■10* ;
частное 3,5 - 10* : (5 •10*) = 3,5 : 5 •(10* : 10*)= 0,7 •1 = 0,7.
3 2 8 . Выполним действия, применив свойства степени:
а) 2,5 •104+ 3,3 - 105= 2,5 •104+ 33 •104= (2,5 + 33) •104= 35,5 •104=
= 355000;
б) 7,7 • 107- 5 •105= 770 - 105- 5 - 10® = (770 - 5) • 106= 765 - 105=
= 76500000;
в) 6,4 •105: (3,2 •104) = 6,4 : 3,2 •(105: 104) = 2 •10 = 20;
г) 5,5 • 107+ 8,3 • 10е = 55 - 10® + 8,3 - 10® = (55 + 8,3) • 10® = 63,3 • 10® =
= 63300000;
д) 7,7 - 104- 7,1 •10е= 7,7 - 104- 710 - 104= (7,7 - 710) •104= -702,3 •104=
=-7023000;
е) 6,4 • 10* - 2 • 10я = 6,4 - 2 • 10* - 10“ = 12,8 • 10 * * 3= 12,8 •10° =
= 12,8 •1 = 12,8.
329. Докажем тождество, пользуясь тождеством (аЬ)" = а" Ьп:
а) (хугУ = хп•уп •г”,
левая часть — (хуг)п= ((д:у)г)п= (хуУ •г* = х" •у" ■г“ ;
правая часть — х" - ;/" •г"; х" - у" ■г* = х" ■у" ■г”, тождество доказано;
б) (хугЬ)" = х" •у" •г" •Р1,
левая часть — (хг/г()" = ((х!/)(2())" = {хуУ •(г*)” = х" ■у" ■г™■
правая часть — хп•уп■г п• хя•у* •г" • = х" ■у* ■г" • тождество до­
казано.
330. Докажем тождество, пользуясь свойствами степени а" • а" = а ш* "
и (атУ = ат"г
о) ата"ак= а т+п+*
левая часть — атапак= ат+п•о* = а.т+" *А;
правая часть — а т* *+*; ат* "+* = а” +“+*, тождество доказано;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4bo
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

52. б) ((ап)т )* = аптк; левая часть — ((ап)т )А= (апт)к = апт*;
правая часть — апт*; а”т* = апт*, тождество доказано;
332. Проверим, Является ли тождеством равенство:
а) Зх + 5 = 3(* + 5); левая часть — Зх + 5;
правая часть — 3(* + 5) = 3* + 15, Зх + 5 Ф 3* + 15, равенство не явля­
ется тождеством;
б) 3(х -4 ) = Зх - 12; левая часть — 3(* - 4) = 3* - 12; правая часть —
Зх - 12, Зх —12 —3* —12, равенство является тождеством;
в) (2а - Ъ)2= (р - 2а)2; левая часть — (2а -Ь)2 = ( -(- 2а + Ъ))2= (-(Ь - 2а))2=
= {Ь —2а)2; правая часть — (Ь - 2а)2, (Ь ~ 2а)2= (Ь - 2а)2, равенство явля­
ется тождеством;
г) (2х - 3|/)а = (Зу ~2х)а; левая часть — (2х - Зу)8 = (-(-2 * + Зу))3 =
= (-(31/ - 2*))3- -(3 у - 2х)3; правая часть — (3у ~2*)3; —(Зу - 2х)3ф(3у -2х)3,
равенство не является тождеством;
д) (а + Ь) •О= а + Ъ; левая часть — (а + Ь) * О= О;
правая часть — а + Ь; 0 ф а + Ь, равенство не является тождеством;
в) у(х - х) = 0; левая часть — у(х -х ) = у •0 = 0;
правая часть — О; 0 = 0, равенство является тождеством.
333. Пусть с первого.склада вывезли х т угля, тогда на нем стало (2200 - х) т.
Со второго склада вывезли 5* т и на нем стало (2800 - 5*) т. Составляем
уравнение: (2200 - х) = (2800 - 5х); 4 х =600; х = 150, тогда 5* = 5 •150 = 750.
Ответ: из первого вывезли 150 т, со второго 750 т
§ 9. Одночлены
336. Определим одночлены стандартного вида.
Одночленом стандартного вида называется одночлен, который содержит
один числовой множитель, который стоит на первом месте, и степени
разных переменных. Поэтому выбираем одночлены, которые подходят
под это определение.
а) 3тп2тА; б) -Зхуг5; в) ЗаЪ •7с; г) - с ; д) 2х (- — );
2 2у
Ответ: одночлены стандартного вида: б) -Зхуг5; г) ^ с .
337. Запишем одночлены в стандартном виде и подчеркнем их коэффициенты:
I
Надо привести данные одночлены к виду, указанному в объяснении
к упражнению 336.
а) 2а * ЗЬ = 6ab; б) 12а* * а2= 12ад+2 •х = 12а8*;
в) -5cz * сг = -5 с 1+1z1+1= -5 c 2z2; г) 0,3а * 2а&2= 0,6а1♦1Ь2 = 0.6а2Ь2;
1
д) —тп ■3п2 = 1 * шп1+2 - тп3; е) (-2 ab) ■(-3) = 6ab;
3
е) а2 * ЗЬс*а3 = За2+3Ьс = За5Ьс; з)-3 *(~~Ь)ху = 15ху;
ж)—х * * 2 *1—* 8= —* ^ xi +2+з _ i
3 2 3 2 2
з) 2,5 * ах •(-0,4)х2 = 2,5 *(-0,4) •а * * * * 2 = -1 *а*3 = -а * 3
338. Найдем коэффициенты данных одночленов:
а) 2па3. Ответ: 2. б) ху2г9. Ответ: 1.
2 2 '
в) -a b 8c. Ответ: (-1). г) —а2* 3. Ответ: —.
3 3
д) -2ху * З*2 = -6 * 1+2у = -6 х2у. Ответ: (-6).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

53. 3 3 9 . Вычислим значение одночленов при данных значениях переменных:
а) 2а4Ь, если о = -1 ; Ь = 5; 2а4Ь = 2{-у * 5 = 2 * 1 * 5 = 1,0. •
б) - х 2у если X = 0,2, у = -3 ; - х 2у3= -0 ,2 2 •(-3)8 = -0 ,0 4 •(-27) = 1,08.
в) -0,5хс3, если х - -0 ,2 , с = — ;
2
-0,5хс'< = -0 ,5 - (-0,2) -(-- )> = -0 ,5 •(-0,2) - (-0,125) = -0,0125.
2
Умножим одночлены 340—341.
Одночлены умножаются таким способом: сначала умножаются коэффи­
циенты одночленов и произведение записывается коэффициентом ново­
го одночлена (произведение данных одночленов); после коэффициента
записываются все переменные умножаемых одночленов, со степенями,
которые равняются сумме степеней соответствующих переменных.
3 4 0 . а) 2аЪ и 3а?с; 2аЬ * 3а2с = 6а1 +2Ьс = 6а3Ьс;
б) 0,3ху2 и | х2у; 0,3ху* х2у = ОД*1+V +2 = 0 ,1 * У ;
в) —am 2 и Зт3р; —am2 * 3т3р = -З т 2+Зр а = —Зт5ра;
г) 0>2ху и 0,2xj/ * (-5jci/) = -1* х1+lyl +1= - х 2у2;
д) abed и -а&2сэ; a&cd *(~ab2c3) = - a 1+lb1+2cl +3d = - a 2bPcAd;
ч , 2 3 2 3 5 3
е) 1—а х и —z; 1—ад;* —z = —а х — г - ахг.
3 5 3 5 3 5
3 4 1 . а) За3, 2a2z и 6az3; За3’ 2a2z ' баг3= 36а3+2+1г 1+3= 36a6z4;
б) 2у, —Зу2 и у3; 2у{-3у2) *у3= -6 у 1+2+3 = - 6i/6;
2 5_4 5 __3 2 5 4 I 5 __ЯI 2 5+1 4+3 2 я 7
3 4 2 . Возведем в квадрат и в куб одночлены:
а) 2ах; (2ах)г = 4а гхг; (2ах)я = 23 •а?х3 = 8а8ж3;
б) -З а2; (-За2)2= 9а2 2 = 9а4; (-За2)®= (-3 )3 : а2 3 = -27а6;
в) 5Ьс2; (5Ьс2)2= 52 •Ь2с2 2 = 25Ь2с4; (56с2)3= 53 •63с2'3 = 125Ь3с6;
г) 0,2*®т; (0,2я3го)2= 0,04зс3 2пг1 2= 0,04лс6пг2;
(О .г^ т)3 = 0,28 •ж3‘Зт 8 = 0,008*9т 3;
д) - i x V ; = i * 5V 2 = ±
2 ( 2 J 4 4
Н Л ' ) ' - Н ) ‘ Л ” - - 5 Л "
- Л 4:
- | Л Л ( - § * ■ ) . ( - ! )
2 ^ Лчг
2-2 3-2 ^*4 6а х * = - о х ;
9
3 Q
23 .3 3 ° 6 9
а х а х .
27
Упростим выражения, данные в упражнениях 343—44.
343. а) (3ах2)9 = 27аэх2 3 = 27а3х6; б) (х3у3)2= х3 2уЭ 2 =
в) (-2аЬ)8 = -8 а 1"Ч>1 8= -8 а аЬ3; г) -Зхуг ♦2xi/2= -6 x l +Ч/а+2 = -6 x 2i/5;
д) (-2а2Ь)3= -8 а 2'3&3= -8 а 6Ь3.
3 4 4 . a) 2a(3mc)2 = 2a * 9т2с2 = 18am2c2;
6) | с2(-2же)3 = | с2•(-8) * V = - с 2+V = - c V ;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

54. в) - а 3 •(-Зад:)1= - а3■(-3 )4•а4*4= - 81 а3*4*1= 54а7х4;
3 3 3
г) (-2а2)3а3= —8а2'аа3 ——8а6+3 = —8а9;
Д) -0,7и3Г-^1/3) = -0,7уа— и3'2 = ——— —и3*6 = — —у9;
У { 7 У ) 49 10 49 70
( 1 „3 ( 11 _4 _24 Я _ 1 _4+3_8 _ 1 _7 В
е ) П И ] р Г з ) р ? р ~ ы р 9 “ Н Р 9 ‘
345. а) 2 а -5 * Г -1 | а ^ = 2 -| -1 ^а •а* = -2•—а •х = а *;
5 5
с8•с •* = -2 с9*1х = - 2с4*;б) 5с3 - ( - | ) сх = 5 -[- | ],
в) -4а *3аху ^ *21/j - -4 •3 •^- ^ а *а ** -у -* 2у = 9а1+1•* 1+2*у1+1 = 9а2* У ;
г) 0,8*^2*(-=-5|/) = 0,8 * (-5)* *у *у * 2^= -4 * *I/1+1*г = -4 хугг ;
д) ^ас3(-6с2) = ^ *(-6) а -с3-с2 = -4 а •с3+2 = -4ас5;
е) -5 а223 - ^ 2^= —5 ■ ^ а 2^3-г —За2г3+1 = За2г4.
346. а) - х у - — ху = - —•— * х у - у = - —х2у2;
7 10 ) 7 10 2 У
б) ( ——а с * 1 - а * 31 = 1 а - а * с - * * 3 = —а2с*4;
4 4 Д б ) 4 { Ь ) 5
в) -З а*2 •2а *(-5 * 3) = - 3 * 2 * (-5)а - а * * 2 * д^ = 30а2 * *2+3 = 30а2* 5;
г) -2 сгг * Зг * (-5 сг) = - 2 * 3 * (—5)с * с * гъ * 2*2= 30с2г8+1+1 = 30с2гб;
4* с с с * * - 2г = 2съхг2ш
347. Вычислим значение многочлена:
а) 0,5а5, если а = 2: 0,5 * 25= 0,5 * 32 = 16;
б) 2с2* 8, если с = 1,5, * = -10: 2 * 1,52* (-1 0 )3= -2 * 2,25 * 1000 = -4500;
в) - 8* 25, если * = 0,1, г = -2 : -8 * 0,1 * (-2 )5= -0 ,8 •(-32) = 25,6;
.2
г) - —а 2с4 , если а = —, с = -3 : ( —1 •(-3)4 = - —•—*81 = — = 13,5;
3 2 3 ^2^ ^ 7 3 4 2
д) • (£ *» ) ,
3 О 1
если * = 3, у = —
У 2
1— 3 6 * У 2•— * У = — 36 -— х?*ум = — хУ = 1— ж у ;
27 " 27 27 27 81 81
е) ■(-0 ,2ху)* ■(50{/эг)2, если л: = 0,2, у = 10, 2= —0,06:
^ . (_о, 2)4* У -2500 •у32 г2 = ^ •0,0016 •2500 •х лу**е22 = 0,0625.*У V
348. Умножим одночлены:
а) - ахуг * 2аг2* (-3 *) = 2 » 3 * а * а * * * * * у * г 1+2= 6а2х2угэ;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

55. б) 5а2* Зху9 * ( - ^ )аху* = 5 - 3 •(- ^ ) * а2•а * х *х •у9 *у9 =
= -10а2+Іх2у2+8= ~10а2х2у^;
в )- 2 - аЬ2 •( - - а Ь 2) *3&2= ( - - ) * За - а *Ь2 *Ь2•Ь2- За2д2+2+2= За2Ь*;
3 7 3 7
2 5
г) - 1 —ап2т •(-Зал2) - (-0 ,2а) = - — * (-3) * (-0,2) а •а •а ■т - п2 - п2 ~
= -1 - а9тп2+2= -а^тп*.
а а8 а3
а6 а4 а2
а5 1 а7
350. Возведем в куб одночлен:
а) (Зсх)8= 38с8х8= 27сV ; б) (2а2/л)3= 28а2*9т9 = 8а6т 8;
в) І0,Ьаху3)3 = (0,5)8а8х У ‘8= 0Д25а3х3у9;
г) (——аЬ2с9)9 = (——Уа3^2'8с8'3—— — а3Ьвсе;
З 3 27
1 Я 97
д) ( - 1—с2«2/?)8= (— )3*с23‘ П2 3 *р = -------с ^ р ;
2 2 8
9 19 1
е) ( - 2—ал2с8)3- ( У*а3п2 дс3 3 ---------- а3пес9.
5 5 125
351. Возведем в четвертую степень одночлен:
в) (2ал)4= 2*а4п4 = 16а4л4; б) (Зх2)4= 34х 24= 8ІХ8;
в) (ОДах2)4= (0Д)4а4х24= О.ОООІа^;
г) ( -0,1ас2)4= (- 0,1)4а4е24= 0,0001а4с8;
д) (- —х2у)4 = (- —Ух24у4 - — хву4;
З 3 81
1 о аі
е) ( - 1 —аЬ2с)4 = Є -)4* а4* 62‘4- с4= — а4Ьвс4.
2 2 16
Упростим выражение 352^354.
352. а) (2ас8)4- 24а4с84= 16а4с12; б) (-ах8)4= а4х84= а4х12;
в) (-Зал2)5= (-3)5а5л26= -243абл10;
г) (-ОЛху2)9 = ( - 0,2)8х8і/28- -0,008х3^6;
д) (~ ~ аху2)4 = (~§)*я4х4у 24= ^ а4х4ув.
о о 81
353. а) х 5* (2ах2)8= х5* 28а8х28= 8а3*х5* х6= 8а8хи;
б) За2* (2а2с) = 3 * 2а2*а2*с = 6а4с;
в) - х 2* (Зх3#)3= - х 2•З8•х 3'8* у9 = —27х2 *х® * у9 - -2 7 х п|/3;
г) а * (2сх2)2= а * 22*с2* х22= 4ас2х4;
д) с8- (Зсх2)2= с3* З2*с2* х22= 9с3+2*х 4= 9с5х4;
е) (-2 а 2х)2-і а = (-2 )2*—* а2*2х2•а = 4 ♦—а4*а •х2= 2абх2.
2 2 2
354. а) (2ах2)2•(ах)3= 22*а2* х2"2♦а8х8= 4а2+3- х4^8='4а5х7;
,3 чЗ
б)(3пг8)2-^іпга;1 = 9л2г32• ■пл■гл у? = 9 і _ . п™ ■X8•гв+3= - п У г';
27 З
в) (-2* У )2•(-багу2)3 V 2•(-б)3^ 2’8= 4 •(-125)*4*8-|/®+в« -5 0 0 *У 2;
к3 Г ~ 2 /■ „ 8 / л 2 л „
5
4 - і М . р А І = И л . . . » * . *
4 3 ; и ^ І з^ Ы 27 25
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

56. д) Зх2 * (-5 хду4)2~ Зх2 * (-5 )2•дс3'2#4*2= 3 * 25х2+йу* = 1Ьх?у*;
е) (-а 6Ь3)7* 6а3Ь4 = - 6а6 7*а8* Ъ* 7* Ь4= - 6а42+3621+4= - 6а4бЬ25;
е) 0,5тп 4* ( - 2 т )6- 0,5 •(-2)5т * т 5* п4 = 0,5 *(-3 2 )т 1+5л4~ - 1 6 т 6п4;
з) (-ОД*2*/)4* ЮООдсу2= (-0Д )4* ЮООх2У •х у2 =
= 0,0001 * ЮООж®- л: * у4* 2 = 0,1х9у
355. Покажем, что уравнение не имеет корней.
а) х4 •хъ + 3= 0; х4+8= -3 ; х12 = -3 ; четная степень числа не принимает
отрицательные значения, поэтому уравнение не имеет корней.
б) 2х7 ■х5= -3 1 ; 2х7+5 = -3 1 ; х12= - 3 1 : 2; х 12= -1 5 і ; четная степень числа
2
не принимает отрицательные значения, поэтому уравнение не имеет корней.
в) - 8у4 * у* = 64; -8 у 4+8= 64; у12 = 64 : ( - 8); у12 = - 8; четная степень чис­
ла не принимает отрицательные значения, поэтому уравнение не имеет
корней.
356. Решим уравнение.
а) (х8)4* х •х2 = - 1; х8'4•х1+2= - 1; х 12+8= - 1; х15= - 1; х = - 1.
б) (-х 2)8•х5*(х3)3= —1; -х 2'8*х* *х9= - 1; - х в+5+9= - 1; - х*>=- 1; х20= І; х = 1.
в) (0,2х7•*6)2+ 1,4 = (1,2)2; 0,04(х7+6)2+ 1,4 = 1,44;
0,04х13 2= 1,44 - 1,4; 0,04х26= 0,04; я28= 0,04 : 0,04; ж26= 1; х = 1, х = - І .
^ - 4 | / 1 2 ^ ^ 5 - а 4 Ь ^ ^ ^ 1 6 + 4 ^ 1
г) —(—дс) * х4 + ( —У*~ —; х5 3*х4Ч = —; ----дг1б+4 = —- —;
3 3 9 3 9 9 3 9 9
2 і« 6 .9 6 2 19 6 2 1е
— х19 = —; х19= —: (— ); дс1е ----- : —; х19 ~ - 1; х ~ - 1.
3 9 9 3 9 3
е) хА' хъ - 8хв; х4* 5= 8х8; х9= 8хв; (л:8)3= (2дс2)3; х3= 2х2; х = 0, х = 2.
д) г2 * г 4~ г2 - г3; г2+4= 22+3; г6= г6; г = О, г = 1.
е) *8•х 5- х *а:2; х8= х8; х = 0, х = 1.
357. Представим выражение в виде квадрата одночлена:
а) 16а4Ь2 = (4а2Ь)2; б) 0 ,3 6 х У 2 = (0,б*4/ ) 2; в) 0,01а18Ь2с10= (0,1а9Ьс5)2;
г) 361 т впао= (19т эп16)2; д) — а26Ь14= ( | а1аЬ7)2;
25 5
е) ^ х1Ьу22г^ = ( ^ х8!/11^2)2.
358. Представим выражение в виде куба одночлена:
а) - 8аб= (-2а2)3; б) 27х*у15= (Зх3*/5)8; в) -0,001а3Ь12= (-ОДаЬ4)8;
г) 0,064х18і/27= (0,4хV )3; Д) — — о9Ь6с8= ( ^ а3Ь2с)8;
125 5
е) 1 €00 ОООу21*30= (100г/7х10)8.
359. Чтобы найти одночлен, которым надо заменить звездочку так, чтобы
образовалось правильное равенство, нужно: произведение разделить на
известный множитель:
а) * = НОДхУ : ( - ( | * У І = : = {** ■х“)(уВ : У*) =
= - — - 3 - і у « = - — уг;
10 10
б) * = 4а5д7: ( - 8а262) = - —(а5 : а?)(Ь7 : Ь2) ~ ~ —а8Ь5;
8 2
в) * = 6а2Ь3: (0,6о2&) = (6: 0,6)(о2: аг)(Ьг : Ь) = 1 0 •1 - 62= 10Ь2;.
г) * = -т 5п6 : (5т2п?) = (-1 : 5)(т 5: т 2)(л® : п3) = - —т 5_2?г63= - і т 3п3.
5 5
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

57. 3 6 0 . Найдем значение выражения, если 3асу = 7:
а) 1,8* У = 0,6(3*У ) = 0,6 •7 = 4,2;
б) 5 * У = I (3 *У ) = | •7 = ^ = 1 1 § ;
О О О О
в) - 9 * У = ~ (ЗзсV)2= - 7 2= -4 9 ;
ч „ 3 6в 45 1 „ „ е в 5 /„ , аЧэ 5 _8 5 -£ 4 # " 245 2
г) б -ж у = -----------21х у = — (З х У ) = — •7В= — = ------ = 8 1 - .
' 7 # 7 27 * 2 1 ' ' 21 3 3
3 6 1 . Найдем значение выражения, если 2Ь2с = 5, (а2Ь)2 = 2:
а) (-2а2&2с)3•(3аЬ2)2= -^ а 23#2*8*:3•9а2&2'2= -9 *2*а*+2Ьв+*св= -9 - 23*а8Ь10с3=
= -9 (2 366е3)(а8Ь4) - -9(262с)э * ((а26)2)2= - 9 •58♦22= -9 * 125 •4 = -4500.
б) (~0,5а2Ь4)2* (2а2Ьс)3* а2Ъ = 0,25а4&8 •8а6Ъ3с* * а2Ь =
= 0,25 •8а4+6+2* Ьв+3+1 *с3= 0,25 * 28а12*?12с3= 0,25 * 2*Ьйс3•а12Ь6=
= 0,25(2Ь2с)3 *(а2Ь)6= 0,25 * 53*((а26)2)3= 0,25 * 125 * 23- 0,25 •125 * 8=
= 0,25 * 1000 = 250.
3 6 1 . Найдем:
а) сумму длин всех ребер куба, периметр грани которого на 18 см меньше
этой суммы. Пусть длина ребра х см, тогда периметр грани — 4х см, сумма
длин всех ребер (у куба 12ребер) — 12л: см. Составим уравнение:
12л: —4х = 18, откуда: 8х = 18; х = 18 : 8; х = 2,25, тогда 12л: = 12 •2,25 = 27.
Ответ: сумма длин всех ребер куба 27 см.
б) площадь поверхности и объем этого куба. Из предыдущей задачи из­
вестно, что длина ребра куба 2,25 см. 5 пов кува= 6а2, где а — длина ребра,
тогда 5 поциубп= 6- 2,252 = 30,375 (см2).
^куба = гДе а ~ Длина ребра, тогда: Гкува= 2,25а = 11,39065 (см3).
Ответ: площадь поверхности — 30,375 см2; объем — 11,39065 см2.
363. Обозначим количество яблонь через х д., тогда вишен было (х + 64) д.
Всего деревьев в саду было (х + х + 64) д. Учитывая, что яблони составля­
ли 40 % всех деревьев, составим и решим уравнение х = 0,4(л: + х + 64),
откуда: х = 0,4(2л: + 64); х = 0,8л: + 25,6; х - 0,8дс = 25,6; 0,2* = 25,6;
х = 25,6 : 0,2; х = 128, тогда х + 64 = 128 + 64; х + 64 = 192, х + х + 64 =
= 128 + 192 = 320.
Ответ: яблонь — 128, вишен — 192, всего деревьев — 320.
3 6 4 . Решим уравнение:
а) 2л: - 3(л: + 1) = 0; 2х - Зл: - 3 = 0; - х = 3; х = -3 .
б) 2л: 4- 3 = 3(х 4- 1) - х; 2х + 3 = Зл: + 3 - х; 2х + 3 = 2х + 3;
2л: - 2х = 3 —3; 0= 0, равенство верно, х — любое число.
в) 7(2л: - 5) + 3 = 45; 14л: - 35 + 3 = 45; 14л: - 32 = 45; 14л: = 45 + 32;
77 11 1
14л: = 77; х = — ; х - — ; х = 5 —.
14 2 2
г) 9(л: + 2) - Зл: = 6(л: + 3); 9л: + 18 - Зх = 6л: + 18; 6л: - 6л: = 18 - 18;
0= 0, равенство верно, х — любое число.
Задания д ля самостоятельной работы
Вариант 1
1. Вычислим:
*>Н ) Ч - § ) Н И - Э В Н -
б) 1,7* - 8 •0,53= 1,7 •1,7 - 8•0,5 •0,5 •0,5 = 2,89 - 1= 1,89.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

58. 2- Возведем в квадрат выражение О,За*3.
(0,3а*8)2- 0,09а2* 3 2= 0,09а2*6.
3- Упростим данное выражение (~2ас2)2* (0,5а2*)3= 4ас22*0,125а2 3*3=
= 0,5а2+€с4*3= 0,5аес4* 8.
4. Докажем тождество 4(7* - 1) + 3* = 28* - 4 + 3* = 31* - 4:
левая часть: 4(7* - 1) + 3* = 31* - 4;
правая часть: 31* ~ 4; 31* - 4 = 31* - 4, тождество доказано.
5. Запишем число 27500000000 в стандартном виде: 27500000000 = 2,75 *1010.
Вариант 2
1. Вычислим:
б) 2,12- 8* 0,54= 2,1 * 2,1 - 8 * 0,5 •0,5 * 0,5 * 0,5 = 4,41 - 0,5 = 3,91.
2. Возведем в квадрат одночлен —5с23. (—5сг8)2= 25c2z9'2 —25c2z6.
3 . Упростим выражение (3am2)3 .
(3am2f ■ = 27а*т2* -1 зА п " = 12e*m**V = 12a W V .
4. Докажем тождество 5 - * + 3(3* - 4) = 8* - 7:
левая часть: 5 —* + 3(3х —4) = 5 - х + 9х - 12 = 8х —7;
правая часть: 8* - 7; 8* - 7 = 8* - 7, тождество доказано.
5. Запишем число 17770000000 в стандартном виде: 1,777 •1010.
Вариант 3
1. Вычислим:
б) 3,72- 4 •0,5а = 3,7 * 3,7 - 4 * 0,5 *0,5 * 0,5 = 13,69 - 0,5 = 13,19.
2. Возведем в куб одночлен -1,2ас2. (-1,2ас2)8= -1,728а8с2'8= -1,728а3св.
3 . Упростим выражение (-0,5ac2)2(4a2*)8.
(-0,5ac2)2(4a2*)3= 0,25a2c2 2* 64a2'3*3= 16a2+ec4*3= 16a8c4* 8.
4. Докажем тождество 5* - 2(* - 4) = 3x + 8:
левая часть: 5* - 2(* - 4) = 5* —2* + 8 = 3* + 8;
правая часть: 3* + 8; 3* 4- 8= 3* + 8, тождество доказано.
5. Запишемчисло 350000000000 в стандартномвиде: 350000000000 = 3,5 - 10".
Вариант 4
1. Вычислим:
б) 2,32- 27 = 2,3 •2,3 - 27 - i = 5,29 - 3 = 2,29.
2. Возведем в куб одночлен -0 ,8 х2у. (-0 ,8 х2уУ = -0,512х2'3у3= -0,512 х*у9.
3. Упростим выражение (-0 ,4 *3)2*(-10а*2)3.
(—0,4*8)2* ( - 10а*2)3= 0,16*2 8( - 1000)а3*28= -160а3* 6+6= -160а3* 12.
4. Докажем тождество 9* - 2(2* + 6) = 5* ~ 12:
левая часть: 9* - 4* - 12 = 5* - 12;
правая часть: 5* —12; 5* —12 = 5* —12, тождество доказано.
5. Запишемчисло 98 790000000 в стандартном виде: 98 790000000 = 9,879 - 1010.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

59. Тестовые задания № 2
1. Ответ: в), так как 0,032 = 0,03 •0,03 = 0,0009.
2. Ответ: б), так как (5л:2)4= 54* л:24= 62бл*;
3. Ответ: в), так как а(-х)(-х) = а (-х)2- ах2;
4- Ответ: г), так как ат- а32: а16= а82"16= а16; т = 16;
5. Ответ: г), так как (с3У= с12; с3р = с12; 3р = 12; р = 12 : 3; р = 4;
6. Ответ: б), так как х ■л:8= —1; х4= -1 , что невозможно;
7. Ответг б), так как 9(х - 3) - 2(3л: + 5) - йх - 37;
9л: - 27 —6—10 « йх - 37; Зл: - 37 = йх - 37; Зл: - 37 = йх - 37; <2= 3;
8. Ответ: а);
9 . Ответ: в);
10. Ответ: в), так как х4 - Зл:2+ 4 = 24- 3 * 22+ 4 = 16 - 12 + 4 = 8.
Контрольная работа № 2
1. Возведем в степень: а) 53= 125; б) (0,2)4= 0,0016; в) (-1 )5= —1.
2. Найдем значение выражения:
а) 0,5а8- 3,9, если а = 2: 0,5 * 28- 3,9 = 0,5 * 8 - 3,9 = 4 - 3,9 = 0,1; *
б) З т 2- 82, если т = -5 : 3 •(-5 )2- 82 = 3 * 25 - 82 = 75 - 82 = - 7.
3« Представим выражение в виде одночлена стандартного вида:
а) 6ху * 0,5ад? = 6 * 0,5а * х * х •у = 3ах2у; б) а2* 4а2* х = 4а2а2х = 4а4х.
4. Возведем одночлен к квадрату и кубу:
а) —а9Ь2с5; (—ааЬ2с6)2—аа'2Ь2'2с5'2= аеЬ4с10; (—а3Ь2с5)8= а3' ЪЬ2'8сб*8= адЬ6с15.
5. Вычислим:
б) 2,42- 1,62= 5,76 - 2,56 = 3,2;
154 (3 5)4 З4-54 У ^ З 3
38-55 З^б5 3®•5® х■ ■5 5 '
в. Упростим выражение:
а) ^ а Ь аj •(-6а2ь) = ^ -(-б)аа2Ь8&= -3 а9Ь* ;
б) (-0 ,2 т 2п)2*(-Ьтп2) =(-0,2)2*(-5 )т 2+2п2тп2= 0,04 -(-5 )т 4- Ап2+2= Ч),2т*п4.
7- Решим уравнение:
- а) 2х2 ‘ х = 2; 2л:2+1= 2; 2х3= 2; л:3= 2 : 2; л:8= 1; х = 1.
б) 4л:3* дс2= 0; 4л:3+2= 0; 4л:5= 0; хь = 0; х = 0.
в) Зл:4+ 6= 0; Зх4= - 6; л^ = -6 : 3; х4- —2, .четная степень числа не может
принимать отрицательные значения, поэтому решений нет.
8. Найдем сумму, разность, произведение и частное чисел:
сумма: 2,5 •1010+ 1,25 * 108= 2,5 •102* 10е + 1,25 •108=
= 250 •108+ 1,25 * 108= (250 + 1,25) •10е= 251,25 * 108= 25125000000;
разность: 2,5 * 1010- 1,25 * 108* 2,5 * 102* 108- 1,25 - 108=
= 250 •108- 1,25 » 108= (250 - 1,25) * 108= 248,75 * 108= 24875000000;
произведение: 2,5 * 10,с* 1,25 * 108= 2,5 * 1,25 * 101С* 108=
= 3,125 •1010+8= 3,125 * 1018;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

60. частное: 2,5 •1010: (1,25 * 108) = (2,5 : 1,25) *(1010: 10е) = 2 * 10108=
= 2■102= 200.
9 . а) х - у= у - х; левая часть: х - у= |-(~* + #)|= -(у - х) = у - х;
правая часть: |у - х; у - х - |у - *|, равенство является тождеством.
б) |*2|+ 1 = х2 + 1|. Так как х2 > 0, а х2 + 1 > 0, то х2+ 1 = х2 + 1|, ра­
венство является тождеством.
74п- 1
10. Докажем, что — являетоя натуральним числом при любом п:
Число (74л- 1 ) — натуральное. 74" = (74)п= 2401”, тогда при любом п запись
числа 2401" заканчивается цифрой 1, а значит запись числа (2401л- 1)
заканчивается цифрой 0. Тогда по свойству делимости на 10 число
74" —1
(74л- 1) делится на 10, а
10
§10. Многочлены
3 6 9 . Найдем сумму одночленов:
а) 3* и Ьх.
Ответ: Зх + Ьх.
в) 2и х.
Ответ: 2 + х.
д) - а 2 и а 2.
Ответ: ~а2 + а2= 0.
ж) 2а и 3Ь.
Ответ: 2а + 3Ъ.
и) 3с и - 2у.
Ответ: Зс - 2у
л) - 4 * и 2х; -4 * + 2х = -2х.
Ответ: - 2х.
натуральное число.
б) 2аЬс2и 3abc2.
Ответ: 2аЪс2 + 3abc2 = 5abc2.
г) 7ас и За*.
Ответ: la c + За*,
е) 14х2у и -бас2.
Ответ: 14х2у - бас2,
з) -а и а2; -а + а2- а2- а.
Ответ: а2 - а
к) -0 ,5 и 0,5*.
Ответ: 0,5* - 0,5.
м) g3и - - д3;
,3 +
Я
Ответ
(-И
3? -Ç 2 ,
-----------= —о .
3 3*
3 7 0 . Найдем разность одночленов:
а) 2а и 3*.
Ответ: 2а - 3*.
в) -4 р и 2р;
-4р - 2р. - -6р.
Ответ: -6р.
д) -З а2* и - 8а2*;
-З а2* - ( - 8а2*) =
= -За2* + 8а2* = 5а2*. Ответ: 5а2*.
Приведем подобные члены.
37 1 . а) 4*2+ * - 5*2- 1 2 = - х 2 + * - 12;
б) - 6a.fr + 2а2+ Ь2 -а Ъ = - la b + 2а2+ Ь2;
в) 8а - 10а£> -+ За = 11а - ЮаЬ;
г) -0 ,5 *2- у2 + 2,2*2+ 0,8у= 1,7*2- у2 + 0,8у;
д) 2а2Ь - Ь2а + la b 2= 2а2Ь - аЬ2 + la b 2 = 2а2Ь + баб2;
б) -т и 5с.
Ответ: -га - 5с.
г) -4 ,7 * и 5.
Ответ: -4 ,7 * - 5.
е) а и -а ;
а - (-а) « а + а = 2а
Ответ: 2а.
е) ! V - 1 **„ - 1 і V + 2* У = g .-1 і ) V + [2 - 1 1A = - 1 V + 1 1
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

61. 3 7 2 . а) 4х2 + 2 х - 7х2- 9х3- 2х = -9 х 3- Зх2;
б) За* - 12 4- 13а2 + 5 - а2+ 8а4= 11а44- 12а2- 7;
в) 2 7 т 5 - 1 7 т 3 - 7 + Ю т3- 3 0 т 5= - 3 т 5- 7т 3- 7;
г) ул - 2у3 4- 2 + 5у3- 2у - 14 4- 7^ = ву44- Зу3- 2у - 12.
37 3 . Запишем в стандартном виде данные многочлены:
I
Приведем данные многочлены к такому многочлену, который соответс­
твует такому определению: многочленом стандартного вида называется
многочлен, членами которого являются одночлены стандартного вида,
среди которых нет подобных членов.
а) а - Ъ + За 4- 2Ь2= 2Ь2 + 4а - Ь; .
б) 7х - у2 4- Ъху - 2х * Зу = - у2 + 7х 4- Ъху - 6ху = - у2 —ху + 7х;
в) 37 - г3+ 3* - 3523= -36гэ + Зг 4- 37;
г) х + х 2+ х3—2х2—х = х3- х2;
ч’ 1 1 о 1 1д) —а + —а * 3 с -а с = —а + ас —ас = —а ;
’ 2 3 2 2
е) -105р 4- 15д + Юр * 10,5 = -105р 4- 15д + 105р = 15д.
37 4 . Запишем многочлены в порядке убывания степени с основанием х:
а) Зх4- 5х2- х3- 2х= Зх4- х 3- 5х2- 2х;
б) 1 —х2- рх - дх3= -£ х 3- х2- рх 4- 1;
в) ах 4* 6х24- сх34- с^х4= <*х44- сх34- Ьх24- ах;
г) 1 - X4+ Зх34- 2х24- X = - X44- Зх34- 2х24- X 4- 1.
37 5 . Вычислим значение многочлена при данном значении переменной:
а) х2—5х 4- 6, если х = 2; 22- 5 * 2 4 - 6 = 4 - 1 0 + 6= О.
б) 0,7х2+ 0,3х2, если х = 0,5; 0,7х24- 0,3х2= х2= (0,5)2= 0,25.
п) 2,8а - 1,8а2, если а = - 0,2;
2,8 •( 0,2) - 1,8(-0,2)2= -0,56 - 1,8 * 0,04 = -0,56 - 0,072 = -0,632.
376. Вычислим значение многочлена при данном значении переменной:
а) т 3- п2уесли т = 2, п = -3 ; 23- (-3 )2= 8 - 9 = —1.
б) ^ 4- 2*2- 4, если в = 2,3, £ = 0,5;
2,3 4- 2 * 0,52- 4 = 2,3 4- 2 * 0,25 - 4 = 2,3 4 0,5 - 4 = -1 ,2 .
3 7 7 . Решение. Как видно из рисунка, пло­
щадь фигуры равняется разности площа­
дей прямоугольникаи четырех квадратов
5 = «8пр—4£>кв. Площадь прямоугольника
равняется произведению его сторон, то
есть 5 пр= аЬ, а 5 кв = с2, потому что по
условию задачи каждое из четырех от­
верстий — квадрат со стороной с. Значит, 5 = аЪ —4с2. Ответ: аЬ - 4с2.
37 8 . Упорядочим многочлены по убывающим степеням а:
а) За2- За 4- 5 —а34- а4. Ответ: а4- а34- За2—За 4- 5;
б) 1 4- а 4- а2- аэ - а5. Ответ: —а5- а34- а24- а 4- 1;
в) 5а5- 5 4- 2а 4- а3- За2. Ответ: 5а54- а3- За24- 2а - 5;
г) 2ас - 3а2с 4- с2- а3. Ответ: -а 3—За2с 4- 2ас 4- с2.
379. Вычислим значение многочлена при данном значении переменной:
а) х 3- Зх24- Зх - 1, если х = 1,2
1,2» - 3 * 1,2» + 3 * 1,2 - 1 = 1,728 - 3 * 1,44 4- 3,6 - 1 = 1,728 - 4,32 4-
+ 3,6 - 1 = 0,008.
б) 2с3—5с2—с 4-7, если с = —2,1
2 *(-2 Д )3- 5 *(-2 Д )2- (-2,1) + 7 = -2 * 9,261 - 5 *4,41 4- 2,1 4- 7=
= -18,522 - 22,05 + 2,1 4- 7 = -31,472.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

62. в) 3а2 - 2ах - х2, если а = -0 ,4 и х = 1,2
3 - (-0 ,4 )2- 2 * (-0,4) * 1,2 - 1,22= 3 - 0,16 + 0,96 - 1,44 =
-- -0,48 4- 0,96 —1;44 = 0.
г) 0,25п2 4- 0 ,5 т - т 2, если п = 4,8 и т = 2,4
0,25 *4,82+ 0,5 •2,4 - 2,42= 0,25 и 23,04 + 1 ,2 - 5,76 = 5,76 4- 1,2 - 5,76
Запишем многочлены в стандартном виде 380—381.
380. а) х3- 2х2+ Зх - 5х2= х3- 7х2+ Зх;
б) 4х - 2х * Зу - Зу - Ьху = 4х - 6ху - 3у - 5ху = -И х у 4- 4х - 3у;
в) 2,3 —ас + а2с ~ 1,3 = а2с - ас 4- 1;
1,2.
г) 2 4- с3- 2с3+ с3 * 5 2 - с2 4- с3 2с34- 5с3= 4с3—с2 4-2.
4- 5 (—2)а4
л _
-4а5:а = 6а5—10а5
2Х3 4- 2х3 - X і - - х 4 4- 4х3;
За - 7а * 4а44 а54 а = За - 28а5 + а54- а =
х8 с5= 2х4—вх4—х5=
За64- а = 8аб 4- 12а5- 5а —9 —За64 а -
9х2- 4х54- 7 - 2Х3 =
х84- 6х2+ 10 +
д) 2а2* За34- 5а4*(—2а) = 6а2
с) х - 2х + 2х *х2- х2*х2
с) За - 7а(—2а2)24* а54- а
- -27а5 4* 4а;
з) (2х3)х 4- х(-2х)34- х9(-х 2) = 2х4+ х * (-2 )3
- -х 5—6х 4.
381. а) (2а2)3+ 4 - За5- 5а - 9
= 5а64- 12а5- 4а - 9;
б) х2+ 2Х3 - (Зх)2- 4х2*х 34- 7 - 2Х3 = х2+ 2х3
= -4 х 5- 8х24- 7;
в) (-5х) •2х —(х4)24- 6х24- 10 4- х3* Зх5—Зх5= -1 0 х 2
4- Зх8- Зх5= 2х» - Зх5- 4х2+ 10.
382. Запишем в виде многочлена число, которое имеет:
а) а тысяч, Ъсотен, 0 десятков и с единиц. Ответ: 1000а + 100Ъ 4- с;
б) а десятков тысяч, Ъ сотен, с десятков и 0 единиц.
Ответ: 10000а 4 1006 4- 10с.
383. Запишем число в виде двучлена:
а) делитель — т ; частное — 43; остаток — 2. Ощвет: 43т + 2.
б) делитель — т ; частное — 5; остаток — г. Ответ: 5 т + г.
Запишем в виде многочленов ответы к задачам 384—391.
384. В одном мешке а кг, во втором — (а 4- 6) кг, в двух мешках —
(а + а 4- Ь) кг. Ответ: а 4 а 4 Ь = 2 а 4 Ь .
385. Стоимость картошки т грн., капусты — п грн. 8 кг картошки стоят
8т грн., а 4 кг капусты — 4п грн. Покупка стоит
(8т 4- 4п) грн. Ответ: 8т 4- 4п.
386. Ребро куба За. Объем куба V= (За)3= 27а3. От куба
отрезали один прямоугольный параллелепипед с
размерами а, 2а, а и объемом а •2а- а - 2а8и второй
прямоугольный параллелепипед с размерами За, а,
а и объемом За •а - а = За3. Объем многогранника,
который остался: 27а3 - 2а3- За3= 22а3.
Боковая поверхность многогранника состоит из 2-х
квадратов с размерами За, За и каждый площа­
дью (За)2= 9а2. Поверхность, которую видно сверху, составляет полную
грань куба площадью 9а2. Площадь передней грани 7а2, а задней — 8а2.
Поверхность, которую видно справа, составляет полную грань куба пло­
щадью 9а2. Площадь поверхности многогранника 4 * 9а2+ 7а24- 8а2=
- 36а2 + 15а2 = 51а2. Ответ: объем — 22а3, площадь — 51а2.
387. Если книга стоит а грн., то 3 книги — За грн. Если 10 тетрадейстоят т грн.,
то 5 тетрадей — ~т грн. Вся покупка стоит За + —т грн. Ответ: За + —т .
2 2 2
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

63. 388. Если масса мешка пшеницы а кг, то т мешков — ат кг; если масса
мешка гречки Ъкг, то п мешков — Ьп кг; масса 1 мешка сахара — 50 кг.
Масса всего груза ат + Ьп + 50 кг. Ответ: ат + Ьп + 50.
389. Е]сли скорость одного поезда иукм/ч., а второго — и2км/ч., то скорость
их сближения — (и, + 1>2) км/ч. За полчаса, то есть 0,5 часа они прибли­
зятся на 0,5(и1+ 1>2) км. Ответ: 0,5(1^ + и2).
390. Велосипедист, который выехал из города, ехал 1 ч. (0,5 ч. + 0,5 ч.) со
скоростью км/ч., и проехал (1 - v1) км = км до встречи. Велосипедист,
который выехал из села, двигался 0,5 часа со скоростью и2км/ч. и проехал
(0,5у2) км до встречи. Тогда расстояние между городом и селом (и, + 0,5и2)
км. Ответ: 1^ + 0,5и2.
391. Если скорость автомобиля V, км/ч., то
за 1,5 часа он проехал (1,5^) км к момен­
ту, когда он догнал мотоцикл (автомобиль
выехал из города.А). Мотоцикл за 1,5 часа
проехал к месту, где его догнал автомо­
биль, (1,51>2) км, выехав из города В. Рас­
стояние АВ равняется (1 ,5 ^ - 1,5и2) км. Ответ: 1 ,5 ^ - 1,5и2.
392. Определим периметры фигур, изображенных на рисунке:
с
I?! км/ч.
►
В
V2км/ч.
►
2а
* 1
1а і
1
•
»
»___ 1._ - «
а
2а
с а
.
Периметр фигуры равняется пери­
метру квадрата со стороной а + с.
Р - 4(а + с). Ответ: 4(о + с).
а а
а
Периметр фигуры равняется пери­
метру квадрата со стороной За.
Р - 4 * За = 12а. Ответ: 12а.
393. Определим площади фигур, изображенных на ри­
сунке: фигуру получили из прямоугольника разме­
рами а + с + а = 2а + с и Ь вырезанием 2-х прямо­
угольников размерами с и т . Площадь всего прямо­
угольника (2а + с)Ь9а вырезанных — 2тс. Площадь
фигуры: (2а + с)Ь - 2тс.
Ответ: (2а + с)Ь - 2тс.
Фигуру получили из прямоугольника размерами
(а + Ь + а) и (а + Ъ + а), то есть квадрата со стороной
2а + Ъ вырезанием 2-х прямоугольников: одного разме­
рами а и Ь9 второго — размерами (а + Ь) и а. Площадь
всего квадрата (2а + Ь)2 и вырезанных прямоугольни­
ков — аЬ и а(а + Ь). Площадь фигуры:
(2а + Ь)2 - аЬ - а(а + Ъ).
Ответ: (2а + Ь)2 - аЬ - а(а + Ь).
Фигуру получили из прямоугольника размерами Ъ
и с площадью (Ьс) вырезанием 2-х прямоугольников
размерами а и т , площадь которых 2ат . Площадь
фигуры: Ьс - 2ат.
Ответ: Ьс —2ат.
394. Упростим выражение:
а) —44ху2 + 16у + х2у + ЬОху2 —16у —7х 2у - 6ху2 - Ьх2у;
б) 8- а2Ь2 - 4Ь2 + 23аб+ Ъа2Ь2 - 30 + 4а6= 27ав + 4а2&2- 4Ь2 - 22;
т
т
а Ь
Ь
а
а а
т
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

64. в) 9а2- 2а*3+ а4 - а2*34- а*3- а44- 5а*8= 4а*8- а2*9+ 9а2;
г) -Ю аЬс 4- 2аЬ 4- 2Ъс 4- 2ас - 7аЬс - бас = -17аЬс - 4ас + 2аЬ 4- 2Ьс.
395. Вычислим значение многочлена при данном значении переменной, упро­
стив выражение в случае необходимости.
п) 9*2- 4*2 15 —*54- 7*2- 8* 5, если * = -7 ;
9*2- 4*24- 15 - *54- 7*2- 8* б= - 9 *54- 12*24 15;
9 *(-7 )5+ 12 «(—7)2+ 15 = 151263 4- 588 4- 15 = 151866;
б) 2у10 - Юу3 - 3у10 - у4 + у10 + 6у если у = -5 ;
2у10 - 10^3- 3у10 - у4 + у10 + 6у3 = -у 4 - 4у*.
(~5)4- 4 * (-5 )3= -625 + 4 •125 = -625 + 500 = -125;
в) - 6а3Ь2 + а2Ь3 - ЮаЬ + 5а362- а2Ьэ, если а = 10, Ь = 0,9;
-6 а3Ь2 + а2Ь3 - ЮаЬ + 5а9Ь2- а2Ь3= -а эЬ2- ЮаЬ.
-103* 0,92- 10 * 10 •0,9 = -1000 •0,81 - 90 = -810 - 90 = -900.
396. Вычислим:
а) 22= 4; 23= 8; 24= 16; 25= 32; 2е= 64; 27«1 2 8 ; 2®= 256; 2®= 512; 210= 1024;
б) (-1)2= 1; (-1)3= -1 ; (-1)4 = 1, ... (-1)2" = 1; (-1)2л+1= -1 ;
в) 102= 100; 103= 1000; 104= 10000; 10Б= 100000; 106= 1000000;
107= 10000000; 108= 100000000;
г) ОД2= 0,01; ОД3= 0,001; ОД4= 0,0001; ОД5= 0,00001; 0,22= 0,04;
0,33= 0,027; 0,44= 0,0256.
397. Запишем выражения, сложенные из выражений 3* и 5у:
а) разность квадратов: (З*)2- (5у)2= 9*2—25у2;
б) квадрат разности: (3* —5у)2;
в) сумма квадратов: (З*)2+ (5г/)2= 9*2+ 25у2;
г) квадрат суммы: (3* + 5«/)2.
398. Реш ение. Работник заплатил за путевку 360 грн., что составляет
100 % - 90 % = 10 % стоимости путевки или ОД часть стоимости. Найдем
стоимость путевки: 360 : ОД = 360 •10 = 3600 (грн.). Ответ: 3600 грн.
§ 1 1 . Слож ение и вычитание м ногочленов
Найдем сумму и разность выражений 399-400.
401. Сложим многочлены:
а) (За24- 8а - 5) 4- (-5а2+ 2а + 4) = За24- 8а - 5 - 5а2+ 2а + 4 = - 2а2+ 10а - 1;
б) (12*3- 7*) + (4*2+ 3* - 2) = 12*э- 7* + 4*24- 3* - 2 = 12*94- 4*2- 4* - 2;
в) (-7а8£>+ 5аЬ2- аЪ) + (За2*?- 4аЬ 4- 2а*Ь) = -7 а 3Ь + 5аЬ2- аЪ + 3агЬ - 4аЪ 4-
+ 2а36 = -5 а3Ь + 5аЬ2+ 3а2Ь - 5аЬ;
г) (6а2- 462 + с2+ 2аЪ - 36с) + (-1 0 с2- 6а2- ас) = £ < / - 4Ь2 + с2+
+ 2аЬ - 3Ьс -Ю с2- £ < / - ас = -4№ - 9с2+ 2аЪ - 3Ъс - ас.
402. а) (2хъ - х 2- З х + 7 ) - (х3- З х + 17) = 2з? - х 2- /Яс + 7 - х я+ & с - 1 7 =
= х3 —х2 - 10;
б) (4хб4- * - 2*9- 7) - (*5- *24- 3* - 2) = 4*54- * - 2*3- 7 - *54- *2- 3* + 2 =
= З*5- 2*34- *2- 2* - 5;
в) (8а2с - 7ас2- а + с) - (7а2с2 - а 4 42) = 8а2с - 7ас2- / 4 с - 7а2с2- 16 =
- -1 а2с2- 8а2с - 7ас24- с - 16.
Для упрощения выражения необходимо раскрыть скобки и привести I
подобные члены, используя правила умножения, деления, сложения I
и вычитания выражений и свойства степени. В
Упростим выражения 403—404.
403. а) 7*2- 2* + (5 + 11* - 6* 2) = 7*2- 2* + 5 4- 11* - 6*2= *2+ 9* 4- 5;
б) 8а6 +■ 7Ь - (4аЬ 4- 7Ь - 3) = 8аЬ 4- 7Ь - 4аЬ - 7Ь 4- 3 = 4аЬ 4- 3;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

65. в) 1 —л + л2—(Зп2- 2л + 5) - 7л = 1 - л + л2—Зл2+ 2л - 5 - 7л =
= -2л 2- 6л - 4;
г) х2у + ху2 - (Зх2у - 2ху2- 7) + 2х2і/ = х 2у + ху2 —Зх2у + 2ху2 + 7 + 2х2у -
—Зху2 + 7.
404. а) 2а2+ За - 4 + (5а2- а + 7) = 2а2+ За —4+ 5а2- а + 7 = 7а2+ 2а + '3;
б) бх3+ 8х - 5 - (4л:2+ 8х —5) = бх3+ $ ґх - 4х2- +$ = бх3- 4х2;
в) Зг4 - 2г3 + 122- 5 - (324 - 22- 5) =
= - 2г3+ 12г - X - & + 2г + / = - 2гэ + 14г;
д) (2х + у) + (Зх - 4і/) - (5х + Зу - 1) = 2х + у + Зх - 4і/ - 5х - Зу + 1 =
= ~6у + 1;
е) 8ас —(За2—2с2+ 2ас) —(4а2+ 2с2) = 8ас —За2+ —2ас —4а2- ^ =
= -7 а 2+ бас.
Вычислим значение выражений 405—406, упростив их:
405. Вычислим значения выражений при данном значении переменной:
а) с3—2с24- Зс - 4 - (с3—Зс2—5) = р —2с2+ Зс —4 ■*- р + Зс2+ 5 —
= с2+ Зс +1; если с = 2, с2 + З с + 1 = 22 + 3 * 2 + 1 = 4 + 6 + 1 = 11.
б) 4хг - (-2а:3+ 4а:2- 5) = + 2а:3- 0 і + 5 = 2х3+ 5;
если х = —3. 2ДС3+ 5 = 2 - (-3 )3+ 5= 2 - (-27) + 5 = -5 4 + 5 = -4 9 .
в) 2р —(1- р2- р3) - (2р + р2- р 3) =
= у/р - 1 + ^ + р3- ^ ^ + р3= 2р3- 1;
2 о э , о Г2 ? і о 8 27 16 27 11если р = —, 2р3- 1= 2 — -1 = 2-------------= ----------- = ------- .
и 3 27 27 27 27 27
4 0 6 . а) л-3- За:2+ Зх - 1 -(За: - За:2) = а:3- + &с - 1 - &с + =
= х 3—1;
если х = 3, х3 - 1 = З3- 1 = 27 - 1 = 26.
б) 5а* - 2а3 - (4а4- 2о3+ 1) = 5а4- > / - 4а4 + - 1= а4- 1;
если а = -2 , а4- 1 = (-2 )4- 1 = 16 - 1 = 15.
в) а2- 2а6+ 62- (а - Ь - 3) = а2- 2аЬ + Ь2- а + Ъ+ 3;
если а = 5, Ь= 4, а2- 2аЬ + Ь2 - а + Ь + 3 = 52- 2 * 5 * 4 + 42- 5 + 4 + 3 =
= 25 - 40 + 16 - 5 + 4 + 3 = 3.
г) 2 + ху - х2- (у2- 2ху + 4) = 2 + ху - х2- у2+ 2ху - 4 = Зхі/ - х2- у2- 2;
если X = 0,2, у = -0 ,5 , Зху - х2- у2- 2 = 3 *0,2 *(-0,5) - 0,22- (-0 ,5 )2- 2 =
= -0 ,3 - 0,04 - 0,25 - 2 = -2 ,5 9 .
Составим уравнение по условию 407—408 и решим его:
407« х2- 8х + 9 = х2+ 6х + 4; ^ - 8х - ^ - 6х = 4 - 9; -1 4 х = -5;
X = - 5 : (-14); х = — .
14
408. Ї2—2* + 1 = і2+ 5 + 2; / - 2* - / = 5 + 2 - 1; -2« = 6; і = 6 : ( - 2);
* = -3 .
Решим уравнение 409—410.
409* а) 4х - 5 - (7х + 8) = 2; 4х - 5 - 7х —8= 2; -З х = 2 + 5 + 8; -З х = 15;
х = 15 : (-3); х = -5 .
б) 92 + 17 - (42 - 5) = 38; 92 + 17 - 42+ 5= 38; 52 = 38 - 17 - 5;
52 —16; 2= 16 : 5; г = 3,2.
в) 24 - (х2+ 8х - 17) = 5 - 5х - х2; 24 - х2- 8х + 17 = 5 - 5х - х2;
- ? ? —8х + 5х + ^ = 5 - 2 4 - 1 7 ; -З х = -3 6 ; х = -3 6 : (-3); х = 12.
г) 19 - (Зх2- 2х) - (6х - х 2) = 7 - 2х2; 19 - Зх2+ 2х - 6х + х2= 7 - 2х2;
-Зх2+ 2х - 6х + х2+ 2х2= 7 - 19; -4 х = -1 2 ; х = -1 2 : (-4); х = 3.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

66. 410, а) (5х2+ а;3- 7) —(2л:3- 5 + 4х2) = -(1 + х3); 5х2+ х3—7 - 2х? + 5 - 4х2=
-1 - х3; 5х2 + х3 - 2х3—4х2 + х3= -'1 + 7 —5; х2= 1; х = —1, х = 1.
Г») (х3- 2х4 + 7) - (Зх3+ 3 - 5х4) = 6+ Зх4; х3 - 2х4 + 7 - Зх3- 3 + бх4=
6 + Зх4; х3 - 2х4 - Зхэ +. 5х4- Зх4= 6 - 7 + 3; -2 х 3= 2; х3 = 2 : (-2);
дг:‘ = —1; х = - 1.
п) 0,5# - (4,3# + 2,7) + 0,3# = 46,3; 0,5# —4,3у - 2,7 + 0,3# = 46,3;
0,5# - 4,3у + 0,3# = 46,3 + 2,7; -3,51/ = 49; у = 49 : (-3,5); у = -1 4 .
г) ^* + - + ( - + -* 1 = 2 -3 * ; + - + - + = 2 -3 * ;
3 5 ,5 3 ; 3 5 5 3
1 2 л л 2 3 „ , , 1* + —£+ 3* = 2 ----------; 4* = 1; £ = 1 : 4 ; t -
3 3 5 5 4
д) -2 ,5 х - (3,7 - 4,3х) = 1,7; -2 ,5 х - 3,7 + 4,3х = 1,7;
2,5х + 4,3х = 1,7 + 3,7; 1,8# = 5,4; х = 5,4 : 1,8; х = 3.
, 2 (2 3 0 2 2
е ) — 2 = - --------2 + — 2 + 8; — 2 = —
5 5 / 5 5 5
! = Н >
3 0 2 3 0 2
+ 2 + —2 + 8; —г - г — 2 = 8 — ;
5 5 5 5
-1 „ 3 „ 3 ( , 1 ] 38 6 385 38 0 1
-1 —2 = 7 —; 2= 7 —: - 1 —1; 2= ----------- ; 2= ----------- ; 2= ------- ; 2= - 6—.
5 5 5 ^ 5 / 5 5 5 6 6 3
411. Найдем сумму многочленов:
а) (л3 +3л2+ Зп + 1) + (3 - Зл - л2- 2п2+ л4) = п3+ Зл2+ + 1 +
+ 3 - - л2- 2п2+ л4= п* + л3= 4;
б) (-бди/ - 4х2+ у2) + {у3 - Зх2+ 5х# —у2 - 2) =
= - 4х2+ } / + у9 - Зх2+ ^>х1/ - ^ —2 - у3 ~7х2- 2;
в) (0,7с4- 2,8с2+ 7) + (2,8с2- 0,7с4-7 ) =
= + У + = 0;
г) (1*г -!* +1г) +(^*Е"1*+х*_1о) =
= - зсг - ^ ж+ 12+ ^ л;2- - х + а:1- 10= х2 - х + х*+ 2;
3_ 3 ^ • 3__ ^
д) (0.8*3+ 1,2х2 - 3) + (4,5л:2- х - 0,3) + (0,2зе3- 1,2а:2+ 3,3) = -
= 0 ,8а:3+ ЛЛ*? - 3 + 4,5а:2- х - 0,3 + 0,2*3- Я х* + 3,3 = у? + 4,5а:2- х.
412. Найдем разность многочленов:
а) (2х2+ Зх + 1) - (х3+ Зх) = 2х2+ &с + 1 - х3- = - х э + 2х2+ 1;
б) (9т 3+ 2т + 5) - (4т3 - т + 6) = 9тэ + 2т + 5 - 4т3 + т - 6=
= 5т3 + 3т - 1;
в) ( ^ а + Ь2) —(За - —Ь? - а2) = —а + Ь‘ - З а + —№+ а2= а? + 1 —1?1- 2 —а;
2 2 2 2 2 2
г) (-2хс2) - (0,25хс2 - 2х2) = -2 х с2- 0,25хс2 + 2х2= 2х2- 2,25хс2;
д) (-4а3Ь + За2Ь2) - (За3- Ь3 + За2Ь2- 4аЬ2) =
= -4 а 3Ь + —За3+ Ь3 — $ £ 1 ? + 4аЬ3=—4а3Ь - За3+ Ь3+ 4аЬ3;
е) ( - § * * - § а ^ ) - ( 2± * г, - * 2* - 2 | ^ )
2 3 2 0 1 2 «1 2 «1 2 2 2
—х у х у - 2 —ху + хгу + 2 —у = 2 —у + —х #-Зх#.
3 5 3 — 2 2 5
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

67. Упростим выражение 413—415.
4 1 3 . а) 1 - а + За2+ 4а8+ (-а 2—За3) - 1 —а + За2+ 4а3—а2—За3=
= а3+ 2а2- 0+ 1;
б) х —2ху + 3ху2+ (4ху3+ 2ху - Зх) = х — + Зху2+ 4xt/3+ - Зх =
= 4ху9 + Зху2 - 2х;
в) (2аг ~ 3zz) + (-а г - г2) + (-5 аг) = 2аг - Згг - аг - г1 - 5аг = -4 аг - 4z2;
г) 0,7а - 0,7а2- 0,7 - (5,7а2- 4,7а - 1,7) = 0,7а - 0,7а2- 0,7 - 5,7а2+
+ 4,7а + 1,7 = -6,4а2+ 5,4а + 1;
д) - 4 т 2- ( т —пг) + (З т + 4 т 2) - 2 п2= - - т + п2+ З т + - 2л2=
~ - п2 + 2т;
414- а) Збсх2+ 18с2х - (13с2х - 16сх2~ х) = Збсх2+ 18с2х - 13с2х + 16сх2+ х =
= 52сх2 + 5с2х + х;
б) —г3 + Зтг - 2 - (2 + г —Зтг) —- г 9 + 3тг - 2 —2 —г + Зтг =
= - 29+ 6mz - г - 4;
в) 2 —az1
3
(2 2 0 1 2 , 5 Л П1 2 2 2 Л1 2 , 5 *
—а г - 2—аг - 1—2 I= 2—а2 — а г + 2 —аг + 1—2
U 6 6 J _3___ 3 6 6
/ 2
2i +2i
3 6
аг
^ 2 4 v Я j 1 9 ^ о
—а 2 = 1 —2 + 4 —а2 — а г;
г ) х2 — л: + с - ( х 2 + с ) - (Зс - 5 - х) =
= ^ ^ ^ - / - З с + 5 + X = -Зс + 5;
ч «1 «1д) 2 —а л - 3 - а т
2 2
q l 01 1 д
5ал = 2 —ал - 3 —am ал + 5 - 1 —ал =
2 2 2 2
(_ 1 1 _1 _ 1 0 1
= 2 -----------1— ал - 3 —am + 5 = -а л - 3 —am + 5.
2 2 2) 2 2 2
41 5 . а) —ах2 — а 2х - 2ах2 - а2х + —а2х
1 1 2 4 * 9
—аде - 1 —а де;
2 3
б) 0 ,3 т 2л - 1,7тл 2- 0,2т л 2- 1 ,3 т 2л = - т 2л - 1,9тл 2
3 2
в ) —а + —аде
4 3
г) 2—ах2с + 1
2
( 1 3 1 3 2 з
— ах — а + 5 = —а + —ах
( , 3 4 J 4' 3_
ах3+ i a x 8 + —а —5 = а + ах9- 5;
3 4
1 а -(.
4 2 5 2
сх + —ах с
,3
I, 2 2,1 I 3 3,1 I, 2 2^ I 3 3 ]
= 0•ах2с + О•х2с = 0+ 0= 0.
4 1 6 . РАВСОи. = 2р, АВ - а, АР = с, = Ь. Найдем стороны ВС, £2) и £Ю.
Решение. Достроим прямоугольник АВСК.
С К = А В ~ а.К В = :Е Р = Ь .гГогд& П С ~ С К -К В ;
ИС ~ а - Ь. Обозначим длину Е Б как х, тогда
РК=х,АК=АР+РК9АК=с + х,ВС=АК=с+х.
Периметр прямоугольника: Р = 2(а + (с + х)),
что по условию равняется 2р. Составим урав­
нение: 2(а + (с + х)) = 2р, откуда: а + с + х =
= 2р : 2; а + с + х = р ;х = р - а - с .
н
ах2с + 1—х2с
4 2 5 2
—сх — ах с
а
В
К
D
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

68. Тогда: ££> = р - а - с, ВС = с 4- х; ВС = с + р —а - с; ВС - р - а.
Ответ: ВС = р —а, Е В = р —а —с, ВС = а —Ь,
417. Докажем, что выражение принимает положительное значение для лю­
бых значений переменной, упростив выражение:
а) (*э + Зх2 - За:) 4- (*6+ 4*3- 7*) - (5*а - 10* - 5) = *9+ Зх2 - Зх + *« 4-
+ 4*э - 7х —5*3+ 10* + 5 - *® + Зх2 + 5. Значения выражений * е и З*2
неотрицательные, тогда * в4 З*24-6 — положительные.
Ответ: выражение принимает положительное значение.
б) -((2*8)2- 7*9) - (5(х3)2 - (*8)3- 5) 4- (10(*2)3- (2*3)8) = -(4 *в - 7*9) -
(5*в - *9- 5) 4- (10*в - 8* 9) = -4 * в 4- 7*9- 5*в + *9+ 5 4- 10*® - 8*9-
= х6 4- 5. *6> 0, тогда * в4- 5 > 0.
Ответ: выражение принимает положительное значение.
418. Докажем, что выражение принимает отрицательное значение при любых
значениях переменной, упростив выражение:
а) (б*6+ З*8- 1) - (**■+ 4*® - 8*3) —(** 4- б*44- I I * 3) = 5*5+ З*3- 1 - х8- 4хг>4-
+ 8 *3 - хь- б*4 - I I * 3= - * 8 - б*4 - 1 = -(*® + Б*4 + 1).
х8 + б*4> 0, так как четные степени любого числа принимают только не­
отрицательные значения, а дс8-Ь б*4+ 1 > 0. Тогда - (*® + б*4+ 1) < 0.
Ответ: выражение принимает отрицательное значение.
б) (4 - (З*6)3) - ((З*5)2- (2*3)6) - ((*2)5+ 9 + б*15) = (4 - 27*15) - (9*10-
- 32*15) - (*104- 9 4- 5*15) = 4 - 27*15- 9*10+ 32*15- *10- 9 - б*15= -1 0 *10- 5 =
- “(10*104- б). Четная степень любого числа принимает только неотрица­
тельные значения, тогда 10*10> 0, а 10*104- 5 > 0. Тогда противоположное
число —(10*104- б) < 0, то есть принимает отрицательное значение.
Ответ: выражение принимает отрицательное значение.
419. Найдем многочлен, которым можно заменить звездочку, чтобы образо­
валось тождество:
а) * - (8а8- 2а24- 7) = 3 - а2. Найдем неизвестное уменьшаемое, для этого:
* = 3 - а 2 4- (8а3- 2а2+ 7) « 3 - а24- 8а3- 2а24- 7 = 8а3- За2+ 10.
Ответ: 8а8—За24- 10.
б) * + (3* 4- 8) = -З *2+ 2* -1 5 . Найдем неизвестное слагаемое, для этого:
* = -З *24- 2* - 15 - (3* 4- 8) = -З *2+ 2* - 15 - 3* - 8= - З*2 - * - 23.
Ответ: -З *2- * - 23.
в) (2ху - I I *2+ 10у2) - * = 5*2+ 4у2 - 6.
Найдем неизвестное вычитаемое, для этого: * = (2ху - I I *24- Юг/2) - (5*24-
4- 4у2 —6) = 2ху —I I *24- 10у2 - 5*2—4у2 4- 6= бу2 - 16*2 4- 2ху 4* 6.
Ответ: 6у2 - 16*2 + 2ху + 6.
420. Составим схему к условию:
а) (2а3- а 2 - а + 3) + * = За8- 5а2- а 4- 7. Так как неизвестно слагаемое,
то: * = За3- 5а2- а + 7 - (2а3~ а2- а + 3) - За3- 5а2- / + 7 - 2а3+ а2+
+ 4 - 3 = а3- 4а2+ 4. Ответ: а* - 4а2 + 4.
б) (2а3- а2- а + 3) + * = а2- 6а 4- 13.
* = а2- 6а + 13 - (2а8- а2- а + 3) = а2- 6а + 13 - 2а34- а2+ а - 3 =
= -2 а 3 + 2а2 -5 а 4- 10. Ответ: - 2а3 4* 2а2-5 а 4- 10.
421 *Составим схему к условию:
а) * 4- (5*2—* + 17) = *3- 8*24- 3* + 9. Так как неизвестно слагаемое, то:
* = *8- 8*24- 3* + 9 —-(б*2- * + 17) = *3- 8*2+ 3* + 9 - 5*2+ * - 17 =
= *3—13*2 + 4* - 8. Ответ: *3- 13*2 4- 4* - 8.
б) * 4- (5*2- * + 17) = - 6*24- 4* - 23.
* = - 6*2+ 4* - 23 - (5*2- * 4- 17) = - 6*2+ 4* - 23 - 5*24- * - 17 =
= - I I *2+ 5* - 40. Ответ: - I I *24- 5* —40.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

69. 422. Составим схему к условию:
а) * —(9с2- 6с 4- 2) = 5с3—8с2- 6с - 8. Так как неизвестно уменьшаемое, то:
* = 5с3- 8с2- 6с - 8+ (9с2- 6с 4- 2) = 5са - 8с2- 6с - 8 + 9с2- 6с + 2 =
= 5с3+ с2- 12с - 6. Omeemz 5с3+ с2- 12с - 6.
б) * —(9с2- 6с + 2) —а3 - с2 4 с 4- 2:
* = а3- с 2+ с + 2 + (9с2- 6с + 2) = а3- с2 + с 4- 2 + 9с2- 6с + 2 =
= а34 8с2- 5с + 4. Ответ: а34- 8с2—5с + 4.
423. Составим схему к условию:
а) (6і/3 —у2 4- Зу —1) —* = у3 4- 3у2 + 3у + 1. Так как неизвестно вычита­
емое, то: * = 6у3 - у2 4- Зу -1 - (у3 4- 3у2 4- Зу 4* 1) = 6у3 - у2 + 34 - 1 -
- у 3 - Зу1- 0 - 1 = 5у3 - 4 у 2 - 2. Ответ: 5у3- 4у2- 2.
б) (6у3- у2 + 3 y - l ) - * = 2yi + 3ys + 3 y - 2.
* = 6уэ - у2 + Зу - 1 - (2у4 4- Зу2 + Зу - 2) = 6у3 - у2 + 3^ - 1 - 2у* - Зу2 -
- 0 + 2 = -2 у л +. 6іі3 - 4у2 + 1. Ответ: -2у' + 6у3 - 4у2 + 1.
424. Докажем тождество:
а) (За24- 2Ь2 4- с2) - (Зс24- 2а2- Ь2) + (~ЗЬ2+ 2с2- о2) = О. Приведем ле­
вую часть уравнения к правой: За24- 262 + с2- Зс2—2а24 Ъ2 - 3Ъ2 4:
4- 2с2—а2 - За2 —За2 + ЗЬ2—ЗЬ24- Зс2—Зс2= О, что равняется правой ча­
сти. Тождество доказано.
б) —г2 —(х24- (у2- (х2 4- у24- z2) 4- z2) 4- у2) - х2= —х2—у2 - г2. Приведем ле­
вую часть уравнения к правой: —г2—(х24- (у2- (х24- у24**г2) 4- г2) 4- у2) —х2=
= - г 2 - ( ^ ^ ^ - j / —f + f + yz) - x 2= —г2- у2 - х2= —х2—у2 - z2,
что равняется правой части. Тождество доказано.
в) ab 4- Ьс + ас - (abc + ab - (abc —bc —(abc + ас))) = —abc. Приведем ле­
вую часть равенства: ab 4- Ьс 4- ас - (abc 4- ab —( р&с —Ьс — р&с - ас)) =
= ab + Ьс + ас - (abc 4 ab + Ьс + ас) = ^ + &с —abc — ^ —
- —abc, что равняется правой части. Тождество доказано.
г) а3 - (Ь3 - (a2b - ab2)) - (-(-(a 2b - ab2) + 63) - о3) = 2а2. Приведем левую
часть равенства: а3—(63- а2Ь 4- аЬ2) —(~(—а2Ь 4- ab2 + 63) —а3) = а3—Ь3 4-
4- а2Ь - ab2- (а2Ь - ab2- Ь3- а3) = а3- - /ЛГ 4 4) / + а3=
= 2а2, что равняется правой части. Тождество доказано.
425. Упростим выражение, разложив на множители. Если хотя бы один из
множителей произведения делится на заданное число, то все произведение
делится на это число.
а) (7п + 21) - (10 - 4л) = 7п + 21 - 10 4- 4п = 11л + 11 = 11(л 4- 1) — чи­
сло делится на 11. Ответ: кратное 11.
б) 8л2+ 7п —4 - (Зл24 12п - 19) = 8а2+ 7п - 4 - За2- 12л 4- 19 =
= 5п2 - 5п 4- 15 = 5(д2- п + 3) — число делится на 5. Ответ: кратное 5.
в) (12л - 5) - (5л - 9) = 12л - 5 —5 л + 9 = 7 л + 4 — число при делении на
7 дает в остатке 4. Ответ: при делении на 7 имеем остаток 4.
426*. Представим в виде многочлена число:
a) abc = 100а + 10Ь + с; б) хух = ЮОде + 10і/ 4- х;
в) abc 4 ас = 100а 4- 10Ь + с 4 10а + с = 110а + 10Ь + 2с;
г) хуг - х у ~ ЮОх + 10у + 2- (10х 4 у) = 100* 4 10у 4- z- Юле ~у =
= 90лс 4- 9у 4- г;
д) abc 4 bca = 100а + 10Ь + с + ЮОЬ 4- 10с + а = 101а 4- 1106 4- 11с;
е) хуг —гху —100х + Юу + г —(100г + Юх 4•у ) -
~ ЮОде + 10у + г - 100z - Юзе - у = 90де —99z 4- 9у.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

70. 427*. Докажем кратность суммы или разности чисел данному числу, пред-
•тавив его в виде многочлена:
n) ab + Ьс + са —10а + 6+ 105 + с + 10с 4- а = 11а + lift + 11с =
11 * (а + 6+ с). Сумма чисел делится на 11 (кратна 11).
Г») сумма чисел х у г, yzx и г х у :
xyz + yzx + zxy ~ 100* + 10# + z + 100# + 10z + * + 100z + 10* + у =
111* + 111# + l l l z = 111 *(* + # + z).
Сумма чисел делится на 111 (кратна 111).
її) разность чисел а06 и 60а:
aOb - 60a = 100a + b - (1005 + a) = 100a + b - 1006 - a = 99a - 996 =
99 •(a - 6). Разность чисел делится на 99 (кратна 99).
і*) разность чисел (аб + ас нь6с) —(са + сб + 6а) =
10а + 6+ 10а + с + 106 + с - (10с + а + 10с + 6+ 106 + а) =
20а + 116 + 2с 10с - а —10с - 6- 106 - а = 18а - 18с = 18(а - с).
Разность чисел делится на 18 (кратна 18).
4 2 Л2
+ - = 1+ —= 1- ;
9 9 9
/ 4 ^
1 1
. 1 ( 3 2 ( 2 Г л 2
4 3 0 . « ) - + ^ - ] - + ^ — 1- -
= 1 —!-(-3 )- — Д = - - - 8~ — -4 = -3 -1 3 = -16.
' 1 4 2) 8 4 4 8 4
/
431. а) 6 - (-0,2) : 0,4 + 0,8 - 2,4 : 6= 6- (-0,5) + 0,8 - 0,4 =
=6+ 0,5 + 0,8 - 0,4 = 7,3 - 0,4 = 6,9;
б) - 2 - —6 :(-1 ,5 ) + (3 ,2 -0 ,2 -в )2= - 2 § - ( - 4 ) + (3 ,2 -1 ,2 )2=
5 5
= -2 —+ 4 + 22= - 2 —+ 4 + 4 = 8—2 —= 5 —,
5 5 5 5
432. Решим задачу:
1) 30 •- =10 (ц) — количество пшеницы, собранной с ^ га;
3 3
1 2
2) 1—— = — (га) — площадь второй части поля;
3 3
т гл 2 ЮО ^ 1 ^ С. ~ 23) 50 * — = ----- = 33 — (ц) — количество пшеницы, собранной с — га;
3 3 3 3
4) 10 + 33 — = 4 3 — (ц) — количество пшеницы, собранной с 1 га.
3 3
5) 43 ^ : 1 = 43 ^ (ц) — среднее количество пшеницы, собранной с поля в 1 га.
Ответ: 4 3 — ц.
3
§ 12. Умножение многочлена на одночлен
Перемножим выражения 436—438.
436- а) За + с и 2а; (За + с) * 2а = 6а2+'2ас;
6) 8* - у и 3*#; (8* - #) * Зху = 24* 2# —З*#2;
в) х2 - * и 2* ; (*2- *) * 2* = 2*3- 2* 2;
г) т3 + 3т и т2; (т3 + 3т) * т2 = т5 + Зт3;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

71. д) 2о + 3 и 4а; (2а + 3) * 4а = 8а2+ 12а;
е) Зх - у и 2ху; (Зле - у) * 2ху = 6x2i/ - 2jC£/2.
4 3 7 . a) Sac - 1 и 2ас2; (8ас - 1) * 2ас2= 16а2с3 - 2ас2;
б) ban - т и алш; (бал - т ) •атл = 6а2т л - ат 2п;
в) а2—2с и 0,5с2; (а2- 2с) * 0,5с2= 0,5а2с2- с3;
г) 4с3- ас и 0tБас2; (4с3- ас) * 0,5ас2= 2ас5- 0,5а2с3;
д) - х - 3у2 и 5х*у; (-х - 3у2) •5Х*у - - 5 хьу -1Бхлу3;
е) 0,5а - ху2 и -2 а 2; (0,5а - ху2) - (-2а2) = -а 3+ 2а2ху2.
43 8 . а) х 3+ Зх - 1 и х2; (х3+ 3* - 1) •х2* л:5+ Зх9- х2;
б) х2 + тх + т 2и -Зт х; (х2 + т л + т 2) *(-З т х ) = - 3 т х 3- 3т2х2 - 3т 8х;
в) 2 —а + а2и -^ а б 2; ( 2 - а 4 а2)- Г -^ а 6 21 = -аб2+ —а 2Ь2 - —аъЪ2;
2 у 2 у 2 2
г) 1^ х - х2- ^ и -9xi/2; ^1^ х - х2 - ^ j * (-9xi/2) = -15х2у2+9x3i/2 4- бху2.
■
Чтобы подать в виде многочлена данные выражения,надораскрыть
скобки по правилам умножения выражений»___________________________
43 9 . а) (х + 1) х2= х94- х2; б) а2(Ь - с) = а2Ь - а2с; в) (л2- л)пв = лб- л4;
г) (2а + 3d) *ОД = 0,2а + 0,3d; д) (-а + ас)с2= -а с 2+ ас8;
е) -2а(а2- 1) = -2 а 34- 2а.
Упростим выражения 440—441.
■
Для решения упражнений 440—441 используется способ, приведенный
в объяснении к упражнениям 403—405.________________________________
440. а) 2а3(4а2+ За) - 6а4= 8а5+ 6а4- 6а4= 8а5;
б) 7х2- 2х(3х - у) = 7х2- 6х2+ 2ху = xs + 2xi/.
в) 2х(х - 1) —х2= 2х2- 2х - х2= х2—2х;
г) (3 - а)а2- За2= За2- а3- За2= - а3;
д) (т - п) тп + 2п2т = т2п - тп2 + 2п2т ~ т2п + тп2;
е) (z 2) * (-32) = -32 2+ 62;
е) -З с3+ (с - 1)с2= -Зс3+ с3- с2= - 2с3- с2;
з) 2р - (р2 + 2)р = 2р - р3 - 2 р - -р 3.
4 4 1 . Тождественны ли выражения:
а) (а - х) * а и а2- ах; (а - х) •а = а2- ах. Ответ: да.
б) (х - |/)х2и х3- х2!/; (х - г/)х2= х8- х2#. Ответ: да.
в) (2р2+ q)q и </24- 2p2q; (2р2+ g)g = 2p2g + g2= g24- 2p2q. Ответ: да.
г) (m —л - 1)лт и т2п —п2т; (т —п —1)тп = т2п —т п 2- тп. Ответ: нет.
4 4 2 . Вычислим значения выражений при данных значениях переменных:
а) (Ь2- 4)6- 634- 36, если 6= -2 ,7 ;
(Ь2- 4)6 - 63+ 36 = 63- 46 - 63 + 36 = ~Ь; Ъ= -(-2,7) = 2,7.
б) (а2 - 1)а - (а - 1)а2, если а = 0,8;
(а2- 1)а - (а - 1)а2= а3- а - а3+ а2= а2- а = 0,82- 0,8 = 0,64 - 0,8 = -0,16.
в) с 4- с24- с3- с(1 4- с), если с = 0,5;
С4- С24- с3“ с(1 4* с) = с 4- с24- с3—с —с2= с3= 0,53= ОД25.
г) (х - у)х + (х - у)у, если X * 2, I/ = 3;
(х - ^/)х + (х - у)у = х 2- XI/ 4- х|/ - у2= х2- I/2= 22- З2= 4 - 9 = -5 .
Смотрите объяснение к упражнениям 8 —10.
4 43. а) 2(х - 3) 4- 5(х - 2) = 12; 2х - 6+ 5х - 10 = 12; 7х = 12 4- 6 + 10;
7х = 28; х = 28 : 7; х = 4.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

72. Г») 3(1 - ж) —2(3 - х) = 5; 3 - 3* - 6 + 2х = 5; - х = 5 - 3 + 6; - х = 8; х = - 8.
и) Зг - 7(2г + 4) = 18; 32 - 142 - 28 = 18; -112= 18 + 28; - 112 = 46;
46 . 2
л ---------; 2 = - 4 — .
11 11
г) 2 + 3у - 7(5 - у) = 15; 2 + 3# - 35 + 7у = 15; 10# = 1 5 + 3 5 - 2 ;
10«/ = 48; у = 48 : 10; # = 4,8.
444. а) 22- 15(1 - 2г) = 72; 22- 15 + 302 = 72; 322 - 72 = 15; 252 = 15;
2 - — ; 2 = 0,6.
25
Г>) 8с - (3 - 7с) = 9с + 2; 8с - 3 + 7с - 9с = 2; 6с = 2 + 3; 6с « 5; с =
|») 1 - 8(3 - 2у) = 2(1 - у); 1 - 24 + 16# = 2 - 2#; 16# + 2# = 2 + 24 - 1;
25 , 7
18*/ = 25; # = — . # = 1— .
* 18 " 18
г) Зг - (2- 5) •4 = (1 ~ 5г) •3; Зг - 4г + 20 = 3 - 15г;
г + 15г = 3 - 20; 14г = -1 7 ; г = - — ; г = - 1 — .
14 14
445. а) х2 - 3* + 1 = х(х + 2); х2 - 3* + 1 = х2 + 2х;
х2 - х2 - Зх - 2х = - 1; -5л; = -1 ; л: = ^ .
5
б) 3* - г2 = *(2 - О; з* - *2= 2* - «2; 3* - I2 - 2# + *2= 0; * = 0.
Перемножим выражения 446—447.
446. а) За:2- 4л: + 5 и 2л^; (За:2- 4л: + 5) г 2л:3= бас6- 8ж4+ 10а:8;
б) 0,5*3- 1,2*2+ %- 0,2и 10*2; (0,5*3- 1,2*2+ * - 0,2) * Ш 2=
- Ыъ - 1 2 * 4 + 10*8 - 2*2;
п) 5у3- 7#2+ # - 9 и 5#л:; (5#3- 7#2+ у - 9) •5#* = 25#Ъс- 35#3лс+ 5#2ат- 45#а:;
г) - 24- —г9 - 2г + — и -15#г2;
3 5 5
( г* - § г 8 - 2 г + § 1 *(- 1 5 # 2 2) = -5#2® + 6 # 2 6 + 3 0 # 2 3 - 9 # 2 2.
V3 5 Ь )
447. а) 2ас3и За2- 4ас + 5с - а; 2ас3(3а2—4ас + 5с - а) =
- 6а3сэ —8а2с4 + Ю ас4 —2а2сэ;
б) -2пл: и -Зл^ - 5я:2гс + х - 4п2; -2пх{-3х* - 5х2п + х - 4гс2) =
= бпа:4+ 10п2а:3- 2/га:2+ 8п8а:;
в) 0,4я2с и 5а8- 10а2с + 7с2- 20; 0,4д2с(5я3- 10а2с + 7с2- 20) =
- 2а5с - 4а4с2+ 2,8а2сэ - 8а2с;
2 2
г) — ху2 и 6а:4- Зх2у - л:#2- 9х#; - —ху2(Ьхл - За:2# г ху2 - 9ху) =
3 3
= -4л:5#2+ 2л:8#8+ ^ л:2#4+ 6л:2#3.
448. Представим выражение в виде многочлена:
п) (2ах + 3) * а2х? = 2а3а^ + За2* 8;
б) (-0,7с#2- 22) •2с32= —1,4с4#2г - 2с328;
(1 2 2 3 1 2
в) 0,3тг2 •—п ---2 = --- №—п —
и 3 J 10 3
г) - 2^ж3# *|бх#2+ ^ х2j = -
3 2з 1 а 1 4--------П2 ■2 = ---- П 2 -----П2 ;
10 3 10 5
^ .8,, л „,.2 7 а 3 о Ад 6
а: # *6а:# ~ - х * у - - х г = -14а:У - аГ#.
о!сл
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

73. 4 5 6 . a) —(Зх - 2) —i (9 - 2х) = —х; х - —- 3 + —х = —х;
3 V } З у ' 2 3 3 2
2 1 0 2 1 2 9 + 2 Зх + 2*2х 11 Зх + 4х 11*
х + —х — х = 3 + —; —х + —х - ; --------------= — ; — = — ;
3 2 3 2 3 3 6 3 6 3
7 11 11 6 22 0 1
х ~ — ; х --------; х - — ; х = 3 —.
6 3 3 7 7 7
б) - ( 8 - z ) - ~ ( 5 - 4 z ) = - z + 3; - - - z - - + - z = * z + 3;
6V 7 3 V } 2 6 6 3 3 2
1 4 1 0 8 5 - z + 8 z - 3 z 1 8 - 8 + 10 4z 20 ,
— Z + -Z — z - 3 ------ + - ; = -------------------- ; — = — ; 4z = 20;
6 3 2 6 3 6 6 6 6
2- 20 : 4; z -Ъ .
в) 0 ,5 (9 * + 7 ) - ^ * - ^ * | = Зб|; 4,б* + 3 , 5 - х + ^ * = 3б|;
1 36-7 + 2 . _
3,5x + —x = ----- 3,5; умножив обе части на 7, получим:
7 * 3,5х + х = 36 * 7 + 2 - 3,5 *7;24,5* + х = 254 - 24,5;
25,5* = 229,5; х = 2295 : 255; х = 9.
х о 1 1 7 1 , . Л 1 1 7 1 17
г) 2 у у + —- — (у +17); 2 у у + —= — у ------ ;
4 2 4 5 ; .4 2 4 5 5
1 1 1 0 7 17 —Ьу —Юу + 4у - 4 0 - 3 5 - 6 8
— У — У + —У = - 2 -----------■; — ----------------= --------------------;
4 2 5 4 5 20 20
-11*/= -143; I/= - 14 3 : (-11); у = 13.
4 5 7 . Упростив выражение, докажем, что оно при любых значениях перемен­
ной принимает одно и то же значение:
а) 2(в3+ 6) + 5а(3а - а2) - За2(5 - а) = 2а3+ 12 + - 5а3- Vtstf + За3=12.
Значение выражения не зависит от а и выражение принимает значение
12для любого а .
б) 2jc3(8 - 5х) - 8х(2хг + х3) + 6(3х4 - 4) = - 10х4 - - 8х4+
+ 18х4 - 24 = -2 4 . Значение выражения -2 4 при любом х.
в) 6x(2i/2- (5х + у) •3|/) + Зху{2у + ЗОх) = 6x(2i/2- 15ху - Зг/2) + 6ху2 +
+ 90х2# = Х2ху2 - - 18ху2 + 6ху2 + 9№?у - 0.
Значение выражения 0 при любом х.
г) ЗаЬ + 6(2л2+ аЪ + 5) —9аЬ - 12а2 = ЗаЪ + + 6ab + 30 - 9аЬ —
- - 30. Значение выражения 30 при любом х.
I
Задачи решим е помощью уравнений. Общее объяснение такого способа
дано к упражнениям 125—173.
458. Решение. Пусть в хозяйстве стало х коров, всего коров и телок стало 305' +
+ 90 + 15, то есть 410. Тогда телок стало (410 - х), что в 4 раза больше,
чем коров, то есть равняется 4х. Значит, получаем уравнение: 4х = 410 - х;
5х = 410; х = 410 : 5; х = 82. Ответ: в хозяйстве стало 82 коровы.
4 5 9 . Решение. Обозначим одно число через х, тогда другое будет (60 - х).
Умножив одно из них на 2, а другое на 7, будем иметь, например, 2х
и 7(60 - х). Так как сумма полученных произведений равняется 70, то
составим уравнение:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

74. 2* + 7(60 - *) = 70; 2х + 420 - 7* = 70; -5 * = 70 - 420;
-5х - -350; х = 350 : 5; х = 70.
70 — одно число, тогда второе число 60 - 70 = -1 0 . Ответ: 70 и -10.
460. Обозначим через х количество купленных тетрадей, тргда количество блок­
нотов — (35 - х) штук. За все тетради заплатили 0,6* грн., а за блокноты —
1,3(35 - х) грн., что вместе составляет 31,5 грн. Составим уравнение:
0,6* + 1,3(35 - *)= 31,5 откуда: 0,6* + 45,5 - 1,3*= 31,5; —0,7* = 31,5 - 45,5;
0,7* = -14; -0 ,7 * = -14; х = -1 4 : (-0,7); * = 20, тогда 35 - * = 35 - 20;
35 - * = 15. Ответ: тетрадей — 20 штук, блокнотов — 15 штук.
461. Пусть одна сторона прямоугольника * см, тогда вторая — 4* см, а пло­
щадь — 4*2см2. Если меньшую сторону увеличить на 3 см, ее длина будет
+ 3) см, а площадь прямоугольника 4*(* + 3) см2, что на 24 см2больше
площади данного прямоугольника. Составим уравнение:
х{х + 3) = 4*2+ 24, откуда: 4*2+ 12* - 4*2= 24; 12* = 24; х = 2, тогда
4* = 4 * 2; 4 * = 8. Ответ: стороны 2 см и 8 см.
462. Пусть длина меньшей стороны прямоугольника * см, тогда большей
’Ах см, а его площадь — 3* ** = З*2(см2). Если большую сторону уменьшить
на 5 см, то она будет составлять (3* - 5) см, а площадь прямоугольника
х(3* —5) см2, что на 200 см2меньше площади данного. Составим уравнение:
Зх2 - х(3х - 5) = 200, откуда: З*2- З*2+ 5* = 200; 5* = 200; * = 200 : 5;
х = 40, тогда Зх = 40 * 3; 3* = 120. Ответ: стороны 40 см и 120 см.
463. Пусть меньшее число * , тогда большее — 6* , а их произведе­
ние * * 6* = 6х2. Если меньшее число увеличить на 5, то оно составит
(* + 5), а произведение чисел — 6*(* + 5), что на 75 больше исходного.
Составим уравнение: 6х(х + 5) —6*2= 75, откуда: б*2+ 30*—б*2= 75; 30*= 75;
* = 75 : 30; * = 2,5, тогда 6* = 6•2,5; 6* = 15. Ответ: 2,5 и 15.
464. Решение. Пусть сыну сейчас * лет, тогда отцу сейчас 4* лет. Три года
назад сыну было (* - 3) лет, а отцу (4* - 3) лет, или 5(* - 3), так как тогда
отец был старше сына в 5 раз. Значит, получаем уравнение: 5(* - 3) = 4* - 3;
5* —15 = 4 * - 3; 5* - 4* = —3 + 15; * = 12. Значит, сыну сейчас 12 лет,
тогда отцу сейчас 4 * 12 = 48 (лет). Ответ: сыну 12 лет, отцу 48 лет.
465. Решение. Пусть ученику сейчас * лет. 10 лет назад ему было (* - 10), а
через 10 лет ему будет (* 4- 10) лет или 5(* - 10), потому что он был в 5 раз
младше, чем будет через 10 лет. Значит, получаем уравнение:
5(* - 10) = ж + 10; 5* - 50 = ж+ 10; Ьх - а: = 10+ 50; 4* = 60; * = 15.
Ответ: 15 лет.
466- Решение. Обозначим через * количество дней, через которое в первой
бочке бензина станет в 3 раза больше, чем во второй. В это время из другой
бочки возьмут 10* л и в ней останется (57 - 10*) л, а из первой бочки возь­
мут 12* л и в ней останется (99 —12*) л, или 3(57 - 10*) л, так как в ней
будет в 3 раза больше бензина, чем во второй. Значит, получаем уравнение:
99 - 12* = 3(57 - 10*); 99 - 12* = 171 - 30*; 30* - 12* = 171 - 99;
18х = 72; * = 72 : 18; * = 4. Ответ: через 4 дня.
467. Решение. Пусть надо перелить * г кислоты. Тогда после переливания во
второй емкости станет (12 + х) г, а в первой емкости останется (84 - *) г,
или 2(12 + *), так как в первой будет кислоты в 2раза больше, чем во
второй, отсюда 2(12 + *) = 84 - х; 24 + 2* + * = 84; Зх = 84 —24; * = 60 : 3;
х - 20. Ответ: 20 г.
468. Воспользуемся правилами умножения многочлена на одночлен:
и) -4дс2(* - *) = 2*3+ 12*4
2*3= -4 *2*(-0,5*); 12хл= -4 *2•(-3 * 2). Тогда: -4 * 2(-0,5* - Зх2) = 2*3+ 12 х4;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

75. б) 5ас(* + * - * ) = 50а2с - 15ас2 - ас
50а2с = 5ас * 10а; -15ас2= бас * (~3с); -а с = бас *(— )
1 5
Тогда: 5ас(10а - З с ) = 50а2с - 15ас2 - ас;
5
в) (—х2 + *)(-6ж) = * + 42жб, откуда: б*3- бж * * = * + 42ж5
42а:6 = -баг * (-7л:4). Тогда: (~х2 - 7ж4)(-6ж) = бж8+ 42л;5;
г) (* + 0,25ху - *) * 4х2у = 2х2у2 + * + 20х2уэ
4х2у * * + хгу2 - 4х2у •* = 2х2у2 + * + 20х2у9
2хгу2 = 4х2у *0,5у; 20ж2уа= —4ж2у •(-5i/2).
Тогда: (0,5г/ + 0,25а:у - 5у2) •4х2у = 2х2у2+ х3у2 + 20х2у2;
д) (2 т 3- 9 т ) * * = Ю т6- *
Ют® = 2 т 3* 5 т 3; 9 т •5га3- 4 5 т 4. Тогда: (2 т 3- 9 т ) - 5 т 3= Ю т6- 4 5 т 4
е) * •(* —ху3 + 4у4) = 12х2у* - 4х?у4 + *
-4 х эу4 = - ху3 * 4х2у; 12х2уд = 4х2у * 3у2; 4х2у * 4I/4= 16лг2|/5
Тогда: 4х2у(3у2 - хуъ + 4ул) = 12х2уъ - 4жэу4+ 16ac2i/5.
469. Упростим выражение и найдем его значение при данном значении пере­
менной:
а) -4ж(ж2—ас- 3) + 2ж(2ж2+ ас- 5) = — - 4х2+ 12ас + + 2ас2- 10* =
= - 2ж2+ 2ж.
Если х = -3 ; то -2ж2+ 2х = -2 •(-3)2+ 2 - (-3) = -2 •9 - 6= -1 8 - 6= -24;
б) За(4а2- За) - 6(4 + 2а3) - 5а(2 - 5а) = - 9а2- 24 - - 10а + 25а2
= 16а2 - 10а - 24.
Если а = - , то 16а2 - 1 0 а - 2 4 = 16 ■[-] - 1 0 - - - 2 4 = 1 6 ~ - 5 - 2 4 =
2 U J 2 4
= 4 - 5 - 24 = -2 5 ;
в) (5а(а - 46) + 12а6) •26 + 16а6 = (5а2- 20а6 + 12а6) - 26 + 16а62=
= (5а2- 8а6) •26 + 16а62= 10а!6 - yèurff + )&<£& = 10а26.
Если а = 3, Ь = 1,2, то 10а26 = 10 ■З2* 1,2 = 108;
г) ^ х(6у(3х + 2у) - 8ху) - 5х2у = ^ х(18ху + 12у2 - 8ху) - 5х2у =
Л £
= i ж(10жу + 12г/2) - 5ж21/ = ^ ^ у + 6ху2 - ^х*у = бжу2.
Если ас= - —, у = 11, то бжу2= 6 *( ) * I I 2= -121.
6 6
§13. Умножение многочленов
4 7 6 . Умножим многочлены:
а )а + & и т - д : ( а + Ъ)(т -п ) = а т - ап + Ът - 6п;
б) X - у п х + у: (х - у)(х + у) = X •X + X •у ~ у •х - у •у = X2+ $ - ~-у2=
= х2 - у2;
в) 2а —1 и а - 2: (2а - 1)(а - 2 ) = 2 а * а - 2 а * 2 - 1 - а - 1 * (-2) = 2а2- 4а - а +
4- 2 = 2а2- 5а + 2;
г) с •+ аж и а + ж: (с + аж)(а + ж) = с * а + с*ж + а«аж + аж-ж =
= ас + же + а2ж+ аж2;
д) 1—с и а + с2: (1- сХа + с2) = 1*а + 1*с2- с * а - с * с 2=а+ с2- а с - с 3;
е) -û + 1 и 2а - 3: (-а + 1)(2а - 3) = -а •2а - а *(-3) + 1* 2а + 1 * (-3) =
= -2 а 2+ За + 2а - 3 = -2 а 2+ 5а - 3.
Представим в виде многочлена 477—480.
4 7 7 . а) (а - Ь)(с + d) = ас + ad - bc - bd;
б) (ж - 2)(ж - 3) = ж2- Зж - 2ж + 6= ж2- 5ж + 6;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

76. в) (2х - 3)(а —Ь) = 2ха - 2хЬ - За + 3Ь;
г) (а2- Ь)(а - Ь2) =. а3- а2Ь2 - Ьа + 63.
478. а) (1 - 2хг)(1 + 2л;г) = 1 + - раїг - 4х2г2= 1 - 4л:2г2;
б) (0,5 + с2)(0,5 + с2) = 0,25 + 0,5с2+ 0,5с2+ с4=0,25 + с2+ с4;
в) (а2+ Ь)(а2+ 6) = а4+ а26+ а2&+ Ь2= а4+ 2а2Ь + 62;
* (і н й н
—х2+ х + х + 4 = —х2 + 2л: + 4 .
4 ~ ~ 4
479. а) (2х + 3)(3л: - 2) = 6л:2- 4х + 9х - 6= 6л:2+ 5л: - 6;
б) (5а - 4)(3а - 2) = 15а2 - 10а - 12а + 8= 15а2 - 22а + 8;
в) (7с —1)(5 - 6с) = 35с - 42с2 —5 + 6с = 41с - 42с2 - 5;
г) (-2 п + 3)(3п - 2) = - 6п2+ 4п + 9л - 6= - 6п2+ 13п —6.
480. а) (-а - Ь)(с + сі) - -а с - а<1 - Ъс - М;
б) (-2 + с)(-3 + с) = 6- 2с - Зс + с2= 6 - 5с + с2;
в) (л;2- х + 1)(л: + 1) = л;3+ ^ - £ + /( + 1= л:3+ 1;
г) (р - 1)(р2+ р + 1)'= р* + р -1 = р8- 1;
д) (с + г - </)(1- cq) = с - с2^ + г ~ сцг - д +~сд2;
е) (0,5л - 1,3X0,5л + 1,3) = 0.25л2+ %&5х - - 1,69 = 0,25 л2- 1,69.
Чтобы проверить тождественность выражений, надо раскрыть скобки
в первом выражении по правилам умножения выражений и сравнить ре­
зультат со вторымвыражением. Бели они равны при любых значениях пе­
ременных, тоданные выражения тождественноравныили тождественные.
481. а) (а - Ь)(а + 6) и а2- Ь2
(а —Ь)(а + Ь) = а2+ аЬ —аЪ —Ь2 = а2 - Ь2. Ответ: да.
б) (л: + а)(х + а) и х2 + 2ха + а2;
(х + а)(х + а) = л:2+ ах + ах + а2= л:2+ 2л:а + а2. Ответ: да.
в) (с2+ с - 1)(с - 1) и с3- 1;
[с1 + с - 1)(с - 1) = с3- с2+ с2- с - с + 1 * с3- 2с + 1. Ответ: нет.
г) с2+ 1и (с + 1)(с2- с + 1);
(с + 1)(с2- с + 1) = с3- с2+ с + с2- с + 1 = с3+ 1. Ответ: нет.
482. Для упрощения выражения смотрите объяснение к упражнениям 403-404.
а) (х - 1)(л:2- 2л; 4- 2) = х3 - 2х2 + 2х - х2 -V2х - 2 = хъ - Зх2+ 4л: - 2;
б) (1+ а)(а2 - а + 1) = ^ - /^ +1+ а3- + /^ = а3 + 1;
в) ( т 4- п)(т2—тп 4* п2) = т? - т2п + тпг 4- пт2 —тп2 4- пэ = т 3+•па;
г) (т - 1)(т + 1 )4 -1 = т2+ р{-/?1 - / + Х = т2;
д) (а + 2)(а - 5) + За = а2- 5а + 2а - 10 + За = а2- 10;
е) (л: - 4)(д: + 5) + 20 = л:2+ 5л: - 4х - ^ + ?б_ = л:2+ х;
ж) (л - 2)(п - 2) + 4п = п2 - 2п -2п + 4 + 4п = п2 + 4;
з) 4аЬ - (а + 2Ь)(а + 2Ь) = 4аЬ - (а2+ 2аЬ + 2аЬ + 4£>2) =
= 4а6 - (а2+ 4а6 + 462) = ^ - а2- ^ - 462= -а 2- 4Ъ
Вычислим значения выражений при данных значениях переменной. Для
:>тогосначала упростимданное выражение (см. предыдущее упражнение),
а потом в выражение-результат подставим значение переменной.
483. а) (а + Ь)(а - Ь) + Ь2, если а = 0,6 и Ь = 0,237;
(а + Ь)(а - Ь) + 62= а2- аЪ + а& - Ь2 + Ь2 = а2= 0,62= 0,36.
б) (л: + у)(х + у) - л;2- у2, если л: = 0,2 и у = 5;
(х + |/)(л: + #) - л:2- у2= л:2+ ху + ху + у2 - х2 - у2 = 2ху = 2* 0,2‘ 5 = 2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

77. в) (а2- 6)(а2+ 6) - а4, если 6= 0,2 и а = 3,27;
(а2- 6)(а2+ 6) - а4= а4+ а26- а2Ъ - Ъ2 - а4= - 62= -0 ,2 2= -0,04.
г) -*2+ у4 + (дс - у2)(* + у2) , если * = 5 и у = -7 ;
- * 2 + у4 + (дг - */2)(* + у2) = - х 2 + у4 + * 2 + ху2 - ху2 - у4 = О.
484. Для упрощениявыражениясмотрите объяснение купражнениям 403—404.
а) 3*(* - 6) + (2*2+ 14) = З*2- 18* + 2х2 + 14 * 5*2- 18* + 14;
б) (а - 3)с + 3(с - с2) - а с - ^ - Зс2= ас - 3с2;
в) (За + 6)(а - 6) - (2а2- Ь2) = За2- Заб + аЪ - Ъ2 - 2а2+. 62= а2- 2а6;
г) (а - 3)(а + 3) - 9 а2= а2+ X ~ ^ - 9 - 9 а2= - 8а2- 9.
485. а) (а - 6) (а - 3) + 2а(1 - а) ~ а 2 - За - аЬ + ЗЬ + 2а ~ 2а2 =
= -а 2- а - аЬ + 36;
б)(1 -аЬ )(1 + а&) + а2Ы2= 1 + ріб - <£ - = 1;
в) (х —у){х + у) - х(х - 3) = х 2 + ху - ху - у2 - Xі+ Зх = Зх —у2.
г) (с1 1)(с2+ 1) - с4+ 1= / Ч / - / - 1 - / _ +1 = 0.
I
Чтобы подать в виде многочлена данные выражения, надо представить
квадрат двучлена в виде произведения, раскрыть скобки по правилам
умножения выражений.
486. а) (а + 6)2= (а + 6)(а + 6) = а24- аЬ + аЪ + 62= а2+ 2а6 -I- 62;
б) (* - у)2 = (* - у)(х - у) = х2 -х у - ху + у2= *2- 2*у + у2;
в) (2а - х)2 = (2а - *)(2а - *) = 4а2- 2а* - 2а* + ж2= 4а2- 4а* + * 2;
г) (За + 2)2= (За + 2)(3а + 2) = 9а2+ ба + 6а + 4 = 9а2+ 12а + 4.
487. а) (6 + I)2 + 26(36 - 1) =(6+ 1)(6 +1)+ 662 - 26= 62 + 6+ Ь + 1 +
+ 662 - 26 = 762 + 1;
б) бху + 3(дс - у)2 —бху + 3(*- у)(х - у)=бху +З*2— Зху —3ху +3у2 =
= З*2+ Зу2.
Решим уравнение 488, пользуясь объяснением к упражнениям 8—10.
488. а) (* - 1) - (* - 3) = * 2; *2-3 * - * + 3 = * 2; *2- 3*
3
4 *
х - х г = -3 ;
-4 * = -3 ; х -
б) (у + 2)(у -
-3 у = 10; у -
в) (2* + 1)(*
-9 * = 5; * =
5) = У2;У2 - 5 у + 2 у - 10 у2; у2 - у2 з у = 10;
10
-3
5) = 2* 2; 2*2-
5
9 '
г) Зг2= (1 - 2}(1 - Зг); Зг2= 1
10* + * - 5 = 2*2; 2*2- 2*2- 9дс = 5;
Зг - г + Зя2; Зг2- Зг2+ 4г = 1; = 1; г =
а
489. Решение. Пользуясь правилом умножения многочленов, (а + 6)(с + й) =
= ас + ай + Ъс + 6<2, что и надо было доказать.
Из рис. 41 видно* что площадь большого пря­
моугольника со сторонами (а + 6) и (с + <0,
которая равняется Бвел= (а + 6)(с + й), состо­
ит из площадей четырех прямоугольников со
сторонами а и <2, 6 и й, а и с, 6 и с, площа­
ди которых равняются соответственно ^ = ай,
50=Ьс1,£3=ас, 5^=6с. Значит, 8^ = 8, + 5„+ 50+ 5,
то есть (а + 6)(с + с?) = ас + а<1. + 6с + 6*£, что и надо было доказать
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

78. Ответ: более общим является доказательство с использованием правила
умножения многочленов, так как доказательство с использованием рисун­
ка справедливо только для положительных а, Ь, с и й.
490- Решение. Из рисунка видно, что площадь большого прямоугольника со
п
т
а dсторонами (т + п) и (а + Ь + с), ко­
торая равняется = (/zi+ п)(а + Ь+ с),
состоит из площадей шести прямо­
угольников со сторонами а и л, а и
т , 6и л, 6и т , с. и п, с и т , площа­
ди которых соответственно равняют-
ся = а * л, S2= а •т, S3 = Ь * га,
S4= Ь •77г, S5= с *п, S6= с * 771. Значит, S6ojj = Sj + S2+ S3+ S4 + S5 + S6, то
есть имеем тождество (а + Ь + с)(т + п) = ат + ап + Ът + Ьп + cm + сп.
Ответ: (с + 6+ c)(m + h) - ат + ап + bm + bn + cm + сп.
491. а) 2а(5 - а) - 5(2а + а2) + 2а2= &а — - )Я а - 5а2 + = - 5 а2;
б) (х —#)(х + 7) - (х + у)(х + 7) + 7у = х2+ 7х - ху - 7у - (ху + 7у + х2 +
+ 7х) + 7у = ^_ + ^ - x y - ^ - x y - 7 y - ^ _ - ^ + J ^ = 2ху - 7;
в) -(а 2- 3)(3 + а *)~ (х + З)2+ 6* = -(За2+ а4-"$Г- За2) - (х + 3)(х +3)+
+ 6x = - J î d * - a 4 + 9 + - (х2 + Зх + Зх + 9) + 6х =
= - а 1 + 9 —(х2+ 6х + 9) + 6х = - а 4+ 0 - х 2— —0 + & £ = - а 4- х г
Предоставим в виде многочлена 492—495.
492. а) (а2- 2а + 2Ха - 1) = а2*а - а2•1 - 2а *а - 2а •(-1) + 2*а + 2 *(-1) =
= а3—а2- 2а2+ 2а + 2а - 2 = а3—За2+ 4а - 2;
б) (0,1х - 1,2ÿXOtlx + 1,2#) = ОДх *ОДх + ОДх *1,2у - 1,2у *ОДх - 1,2у *1,2# =
= 0,01х2+ 0 *Ш у - Ог Ш у - 1,44у2= 0,01jc2- l,44j/2;
в) (2,5с + 7zX7z - 2,5с) = - 6,25с2 + 49z2- lJiVSgz = 49z2- 6,25с2;
г) (-0,3а - 1,2Ь)(-0,За + 1,2Ь) = 0,9а2- - 1,44Ь2=
= 0,9а2- 1,44Ь2.
493.а)(ж2+ Зх2+ 2Х х-5)= х 4- 5 х 2+ Зх2-1 5 х 2+ 2 х -1 0 = х 4-2 х 2-1 5 х 2+ 2 х -1 0 ;
б) (х + 1)(х8- х2 + х - 1) = х * £ + ,* * '- У '+ /-1 = ж4- 1;
в) (4а2- 2аЬ + fc2X2a + fc) = 8а3+ 4 g ^ - Arfü - Зоб*'+ +Ь2= 8а2+ fca;
27 2;
494. a) (x2+ 2jc2j/- 5xj/2- 3j/2)(5jc - 4j/)= 5x4- 4x2y +10x3ÿ - 8xV - 25x2y2+
+ 20x#3- 15xi/3 + 12yA= бх4+ 6x8i/ - SSx2y2 +5xi/3+ 12y4;
б) (a3 + 3a2c - Зас2+ 4с3)(2а + Зс) = 2а4+ За3с + 6аас + 9а2с2- 6а2с2- 9ас3+
+ 8ас3+ 12с4= 2а4+ 9а3с + За2с2—ас3+ 12с4;
в) (4а2- За + IX«2+ 2а + 1) = 4а4+ 8а3+ 4а2- За3- 6а2- За + а2+ 2а + 1 =
= 4а4+ 5а3—а2- а + 1;
г) (2х2 - 5х + IX *2 - 2х - 1) = 2Х4 - 4х3
4- х2—2х —1 = 2х4 - 9х3 + 9х2 + Зх - 1.
1.
2х2- 5х3+ 10х2+ 5х +
ч f l 1 , 1 V l 1 ^ 1 ^4 9 5 -а) —а + —Ь + —с —а — Ь + —с
U 3 2 Д З 2 4 )
1 2 I ^ 1 1 *— а — аЪл ас н— аЬ
12 8 16 9
1и 1 ь 1—Ь + — Ьс + —ас
6 12 6
1«. 1 2—Ьс + —с
4 8
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

79. CTtw
Hto
+
в
н
+
Ö
оS»/
+
о03
II
Я
ю
О)
і/"Ч
0м
1
е
+
мW '
о4
+
м
о«
II
I
і3
«
I
і
4
00
IX '>
I V 1 4і
к
+
К
+
м
I
II
Н
$
+
СО
н
+
о
<с
to IСП
со I СП
«с
II
н*
tS5 1М
*3w
♦-*і
м . fcol м
ьо 1м
к +
м to
1 to 1M
м
to 1н* +
to
to 1м
н M
<с to 1M
+ к
н* 1
to 1м to
X to 1H*
+ <C
to +
to 1H*. I-*
H*
to 1І—
<§
II
II
to Iн*
I
о>
и
to Iм
>1"
3
16
&
II
ЬОI н»
лNi
I
wg
w
w
w
.4
ok.org
w
w
w
.4book
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
rg
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4b
ook.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4bo
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book
w
.4book.org
w
w
w
.4
ook.org
wrg

80. öl H- 1(0 1 н -
чг
ю
1
1 <С!
І
5 1 -
1
05 1 К*
* і
N
to
н
м
to H»(N>
+
00I!-»(«
1 Г
to
Vi
N
0>Iи*
<Cto
+
II-*
H
«с
+
to
&
05IM
00
•<1IM
to IN-
Ö
+
^ IH*
00IM
в
Ci
to
?•
CO
Оз I h*
o-
00IM
Ciw
I
s 1 >,
00IНЧ®
I .
COІм<»
Ч У
о
cr
+
to
o> 1-4te
+
COIh*(®
-N
to
rfbI M(ee
4 ✓
о*
Гі
w
w
w
.4
rg
w
w
w
.4book
ook.org
w
w
w
.4book.org
w
.4book.org
w
w
w
.4book.org
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4b
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4bo
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
book.org
w
w
w
.4book.org
w
w
w
.4book.org
.org
w
w
w
.4book.org
w
w
w
.4book.o
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
ook.org

81. в) (с —5)(с + 2) 4- Зс 4- 10 = с2 + 2с —5с — jKf + Зс + 10 = с2;
г) (х2 - J/)(X - J/2) - У3 + xy = Х%- x V + = X* - Хгуг.
4 9 7 .а )(1 - 2х)(4х2+ 2х + 1) + вх3= + + ^ + ^ = 1;
б) (9 - 6о + 4а2)(2а + 3) - 8а3= ===
^Л «^ '+ 27->2бг' -Л 8^ + ^ + >2йа' - ^ = 2 7 ;
в) (2а + 3*)(4а2- 6а* + 9л:2) - 27л:3=
= 8a3 - yZcfx + УЫ & + № fx - - ЗЯх? = 8аэ;
г) (3 - с2)(с4- Зс2+ 9) + с« - 27 =
= 3 ^ - ^ + ^ f - ;/ + 3 £ - ^ + ;/ - ^ = 6c4 - 1 8 c 2.
498. a) 0,01a4- (0.1а2+ IXO.la2- 1) =
= 0,01а4- (0,01a4- j W ^ + ^M^r - l ) = ^ 0lSr - p r01or + l = l ;
б) 0,008х3 - (0,2х - 1)(0,04х2 + 0,2х + 1) = 0,008х3 - (0,008х8 +
+ 0.04*2+ 0,2х - 0,04х2 - 0,2х - 1 ) = 0,008х3 - 0,008х3 +1 = 1;
499. Докажем тождество:
а) (л: + а)(х + 6) = л:2+ (а + b)x 4- ab. Левая часть: (х 4- а)(х+ Ъ) - х2 + Ъх
+ ах 4- аЪ; правая часть: х2 + (а + b)x + аЪ = х2 + ах 4- Ъх 4- аЪ;
л:24- ал; 4- fex 4- ab - х2 4 ах + Ьх + аЬ, тождество доказано;
б) (л: - у)(х + у) = х2- у2. Левая часть: (х - «/)(* + у) = л:24- ^ -у 2-
= х2 —у2; правая часть: х2 - у2; х2 —у2= х2 - у2чтождество доказано.
500- а) (2х - 3у)2= (2л: - Зу)(2х - 3#)*= 4х* - бху - бху + 9у2- 4Х2 - 12ху + 9у2;
б) (Зас 4 Ь2)2= (Зас + &2)(3ас 4- Ь2) = 9а2с24 3аЪ2с 4- За*2с + Ь* =
= 9а2с2+ 6аЬ2с 4 ЬА;
в) (2а - I )3= (2а - 1)(2а - 1)(2а - 1) = 8а3- 4а2- 8а24- 4а + 2а - 1 =
= 8а3-12а24- 6а - 1.
501. a) (a - 1)(а + 1Ха2+ 1) + 1 =(а2+/ - /{ -1)(а2+ 1) + 1=
= (а2- 1Ка2+ 1) + 1= а4+ + X = а4;
б) (2а - З)2+ 12а = (2а - ЗХ2а - 3) + 12а = 4а2- 6а - 6а + 9 + 12а = 4а2+ 9;
в) с * - ( с - 1)(с + 1Х<?2+ 1) = с4- (с2+ / - / - I X с2+ 1 ) =
= с4- (с2- 1)(с2+ 1) = с4 - (с4+ / - / - 1) = / - / +1 = 1;
г) (а - Ъ)3 - 3а 2Ь = (а - 6)(а - Ь)(а - Ь) - 3а2Ь =
= (а2- ab - аЬ + Ь2)(а - Ь) -3 a2b = (а2- 2ai> + 62)(а —£>) —3а2Ь =
= а3- а2Ь - 2а2Ь + 2аЬг + аЬ2 - Ь 3 ~ За2Ь = а3 - 6а2Ъ + ЗаЬ2- Ь3.
502. а) (х + 5)(х2- 2х - 3) - (5х + х2)(х - 2) + 3(х + 5) =
= х3- 2*2- + Ьх2 - 10х - ^ - (5х2- , 10х + х3- 2х2) + + 0 =
= ^ + Зх2- ,Шс - 5х2+ ,183с - + 2х2= 0;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4bo
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

82. Значение выражения равняется О при любом х, то есть от значения х не
зависит.
б) (Zx2 - З х + 6Х* + 4) - (х2 + 4х + ЗХ2х - 3 ) = 2х3 + 8х2- Зхг - 12х + 6х +
+ 24 - (2зг* - Зх2 + 8хг - 12а; + 6х - 9) = 2*3+ 5х2 - 6х +
+ 24 - (2х? + 5хг -6 х - 9) = + + 2 4 - + & е + 9 = 33;
Значение выражения равняется 33 при любом ж, то есть от значения х
не зависит.
в) (2х - 4)(3х + 2) - (2ж - 3)(4х + 2) + 2х2 = 6х2 + 4х - 12х - 8 - (8ж2+
+ 4х - 12ж - 6) + 2х2 = 6х2 - 8ж - 8 - (8х2 - 8* - 6) + 2ж2=
= 6х 2—JStfT—8- 8х2+ ßtic + 6+ 2л:2= -2 . Значение выражения равняется
-2 при любом х, то есть от значения х не зависит.
г) (ж- 3)(зс + 3)(х2+ 9) - (* + l)(jc - l)ix 2 + 1) = (х2+ &с -& с - 9)(хЕ+ 9) -
- (х2 - / + / - 1)(хг + 1) = (je2- 9)(де2+ 9) - (лг2- 1)(х2 + 1) =
= JC4 + - 81 - (а:4+ У - 1) = У ' - 8 1 - У ' + 1= -80.
Значение выражения равняется -8 0 при любом ж, то есть от значения х
не зависит.
Решим уравнение 503—507. Смотри объяснение к упражнениям 8—10.
503. а) (х - 1)(ж + 5) = (х - 2)(х + 3); ж2+ 5ж - ж- 5 = ж2+ Зж- 2ж - 6;
+ 4х - ^ - Зж + 2л: = -6 + 5; Зх = -1 ; х = -1 : 3; ж= —^ .
б) (2х + 3)(ж - 7) = (х + 3)(2ж + 1); 2л:2- 14л: + Зл: - 21 = 2л:2+ х + 6х + 3;
- l l x - ^ / - X - 6х = 3 + 21; —18л: = 24; х = 24 : (-18);
24 4 .1
х = ------; х —— ; х = -1—.
18 3 3
в) (3z2- IXz - 1) = 3z2(z - 1) + 5z + 7; 3z3- 3z2- z + 1 = 3z3- 3z2+ 5z + 7;
—г - 5z = 7 - 1; —6z = 6; z = 6 : (—6); z = —1.
r) (y - 2)(*/2+ 2y + 4) = г/(г/2- 4); у3+ ^ ^ ~ 8 = y3 ~4y;
j / - + 4y = 8; 4y = 8; у = 8: 4; у = 2.
504. а) (0,1 - х)(ж + 0,1) = 2х(0,5 - 0,5х); + 0,01 - ж2- = х - ж2;
^ - х = - 0,01; -ж = - 0,01; ж= 0,01.
б) (у - 0,2)(у2+ 0,2у + 0,04) = у(у2- 8);
у3 + £ ^ + £ ^ - £ ^ ^ £ ^ - 0 , 0 0 8 = у3- 8у;
ß / ~ j / + 8у = 0,008; 8у = 0,008; у = 0,008 : 8; у = 0,001.
в) (i* +2)(i**- *+4)" M s * ~ 2);
|ат3- +^ + i / - Х + 8= i ж3- 1* 2;
+|а:2= - 8; |а:2= - 8; агг = - 8: | ; а:2= -1 6 ;
Квадрат любого числа принимает только неотрицательные значения,
поэтому уравнение решений не имеет.
Г)-(i* +i ) ( i H ) +2H i * j :
_ ( 1 ж2_ 2 . 3 , + 3 . 2 ^ + 2 1 = 4 J 4 ^ _ / + / _ 9 V 2 1
9 3 2 2 3 4 ) 4 9 {9 4) 44 9
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

83. 2 2
505. а) (2л: + I )2- 2(х - 1)(2х + 3); (2х + 1)(2х + 1) = 2(х - 1)(2* + 3);
4х2 + 2х + 2х + 1 = 2(2х2 + Зх - 2х - 3); 4х2 + 4х + 1 = 4л:2+ 2л: —6;
^ + 4х - - 2л: = -6 - 1; 2х = -7 ; х = -7 : 2; х = -3 ,5 .
б) (3z - 2)2= 9(z - 2)(z + 3); (3z - 2)(3z - 2) = 9(z2+ 3z - 2z - 6);
9z2- 6z —6z + 4 = 9z2 + 9z —54; - 12г - —9z = —54 - 4;
~21z = -5 8 ; z = -5 8 : (-21); z = — ; z = 2 — .
21 21
в) (1 - 2 y f = 2(# - 2)(2y - 3); (1 - 2y)(l - 2#)= 2(2#2- 3# - 4# + 6);
1 - 2y - 2y + 4y2= 4#2- 14# + 12; -4# - + 14# = 1 2 - 1 ;
10# =11 ; # = 11 : 10; # = 1, 1.
г) (л: - l )3= л:2(л: - 3) + 5; (л: - 1)(л: - 1)(лг - 1) = х* - Зх2 + 5;
(л: - 1)(л:2- л : - л : + 1) = л:э —Зл;2+ 5; (х - 1)(х2 —2х + 1) = х3 —Зх2 + 5;
хз _ 2х2 + х —х2 + 2х —1 = х3 - Зх2 + 5; ?£* ~ + Зх —^ = 5 + 1;
Зл: = 6; х = 6 : 3; х = 2.
506. а) (л:2- х + 1)(л:2+ х + 1) = х4 + л:2+ х;
х 4 + jt? + ^ ^ - ^ + л:2+ ^ +1 = л:4+ х 2+ л:;
л:4+ х2 + 1= хА+ х2 + х; ^ ^ —х - - 1; —х = - 1; х = 1.
б) С*3+ л;2+ х + 1)(л; - 1) = хА+ Юл:;
хА- + ^ - / £ + / £ - 1 = х4 + Юл:; х4 - 1= х* + Юзе;
~ ~ IOjc = 1; -IOjc = 1; х = 1 : ( - 10); х = - 0,1.
507. а) 0,5с2- (0,5с - 1)(с + 2) = 1; 0,5с2- 0,5с2- с + с + 2 = 1 ; 2 * 1 .
Ответ: нет решений.
б) -(# + 2)(0,3# - 1) = 1 - 0,3#2; -0 ,3 #2+ # - 0,6# + 2 + 0,3#2= 1;
0,4# = 1 - 2 ; 0,4# = -1 ; # = - 1 : 0,4 = -2,5; # = -2 ,5 .
1 2 х х 1 2 1 1 1- ; х + -----------------х = — ; — ф — .
3 3 3 9 3 9 3в)М ) Ы Н
Ответ: нет решений.
. 2 2 / л(2 2 22 2 _ 2г) - х - (х + 1) - х + 2 ; - х - —х + 2л: + - х + 2;
5 1 Я 5 ) 5 5 5
2 , 2 2 _ 2« о 2 _ Юл: + 2л:
- д г х - 2х — х = 2; - 2л: — х = 2; --------------- = 2;
5 5 5 5 5
12 о о Г 5 1 5 5л: = 2; х - 2 1------- = ----- ; х= ----- .
5 I, 12) 6 6
I
Задачи решим с помощью уравнений. Общее объяснение такого способа
дано к упражнениям 125—173.
508. Решение. Обозначим искомое число через х. Увеличив каждый из четырех
множителей на х9получим произведение(11 + л;)*(44 + л:) и (16 + х) *(32 + х).
Так как по условию задачи полученные произведения равны, то получаем
уравнение; (11 + х) *(44 + х) = (16 + л:) •(32 + л:);
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

84. 484 + liar + 44* + *2= 512 +Д 6* + 32a: + x2;
11* - 16* + 44* - 32* + *2- *2= 512 - 484; 7* = 28; ж= 28 : 7; * = 4.
Ответ: 4.
509. Решение. Пусть таким числом будет *. Уменьшив каждый из четырех мно­
жителей на *, получим произведения (25 - *) •(51 - *) и (31 —*) *(40 - *),
Так как по условию задачи новые произведения равны, то получаем урав­
нение: (25 - *) *(51 - *) = (31 - *) *(40 - *);
1275 - 25* - 51* + *2= 1240 - 31* - 40* + * 2;
-2 5 * - 51* + 31* + 40* + *2- *2= 1240 - 1275; -5 * = -3 5 ; * = 7.
Ответ: х = 7.
510- Фигура состоит из полукруга радиусом г и пря­
моугольника, длины сторон которого Зг и (г + г), то
есть Зг й 2г. Тогда площадь фигуры S = £ поду1фуга +
+ ЯВДя,оу_ - Учитывая, что площадь круга счита­
ется по формуле SKp= nr2, S _ . = О.блг2. Площадь
прямоугольника считается по формуле ^праыоутольннка=
= abугде а и Ь — стороны прямоугольника, откуда S
моугольника= ЗГ ' 2Г = Т°ГДа S = + бг2= (0,5lt +
+ 6)r®(м2). Периметр фигуры состоит из длины полу­
круга и 3-х сторон прямоугольника: двух сторон дли­
ной Зг и одной — длиной 2г. Р = 0,5Скруга+ 2 *Зг + 2г;
Р = 0,5 * 2пг + 6г + 2г; Р = nr + Sr; P = ( n + 8)г (м).
Ответ: (я + 8)г (м), (0,5л: + 6)r* (м2).
511. Вычислим:
Л f - 2
а)
N )
З2- ( 1 - 3 ) -1 ,5 s
Н ) (И Г •
= 1,52- 9 - 4 -1,5* = -1 3 - ^<2^ = -13;
6)
3
1 1 1
2 + 6 2
f 2 8>
2 1
3 2 ♦ e r
ч >
4 - 3 + 1 4 - 3 1
+ —
6 9
2
6
12
1 1 2 - 3 + 4
в)
16
г)
И
9 36
(2 2
) А -
1 1
) 3 2~ 4
16
к
3 =
j
- 2;
t +J 1
17 2 7 ) -(1
13
36
16
3 4 Г 2 - 1 У
4 3 ^ ( 4 )
+ - - 3 = 1
16
- | + - - з
+ +
17 27
П = - * + А
17) 7 17
3 5__ 1_ _
27 7 17 27
3 3 6
7 7 ~ 7'
5Т2. Найдем неизвестный член пропорции, воспользовавшись основным свой­
ством пропорции: если пропорция а : Ь= с : й правильная, то а •й = Ь *с.
а) 2 : * = 7 : 10; х * 7 = 2 * 10; * = 20 : 7; х
20 _6
— ; * = 2—.
7 . 7
б) 1 : 4 = 3 : (* + 2); 1 •(* +2) = 4•3;* .+ 2 = 12; * » 12 - 2; * = 10.
в) 6 : 5 = 0,9 :3*;6 * 3 * = 0,9 *5;18* =4,5; * = 4,5 : 18; * = 0,25.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

85. 513. а) 36а6= (6а5) - (6а8) или 36а8 = (2а2) •(18а6);
б) 30х4ув = (30*4) •у9или 3 0 * У = (15ху2) ■(2х3у7);
в) -1 8 а “ 65= (~9а5Ь2) ■(2а5Ь8) или -1 8 а ,0Ь6 = (-18а10) •Ь5;
г) 100х51/я= (5ху3) ■(20ДС4) или 100х5{/8= (Юзе2) •(Юзе3}/8);
д) ^ т 2пе = (6ш2) ( ^ п в) или = ^ т ] '( тпв);
е) - | х У = ( - ^ 4) «/4 или - | * у = ( - * ^ ) .( | д у 1.
Задания д ля самостоятельной работы
1. Для вычисления значения выражения при данном значении пере-
менной, подставляем значение переменной в выражение и выполняем
действия.
2. Для упрощения выражения необходимо раскрыть скобки и привести
подобные члены, используя правила умножения, деления, сложения и
вычитания выражений и свойства степени.
3. Уравнение решается с использованием способов, приведенных в объ­
яснении к упражнениям 8—10.
ш
3
I
ш
X
о
в:
£
10
О
Вариант 1
1. Вычислим значение выражения Зх2 - х + 2, если х = -1 ,3 .
Зх2 - х 4- 2 = (~1,3)2- 3 - (-1,3) 4- 2 = 1,69 *3 + 1,3 + 2 = 5,07 4- 3,3 = 8,37.
2. Найдем сумму, разность и произведение многочленов: а2+ а - 3 и а2- 2.
Сумма: (а2+ а —3) + (а2- 2) = 2а2+ а —5;
разность: (с24- а - 3) - (а2- 2) = а —1;
произведение: (а2+ а - 3) ■(а2- 2) = а4—2а2 4- а® —2а—За2 46=
= а4+ а9 - 5а2- 2а + 6. Ответ: 2а2 4- а - 5 — сумма;а - 1 — разно
а44 а3—5а2—2а 4- 6 — произведение.
3. Упростим выражение: (3 4- дс)(3 - х) 4- х2 = 9 - Зх +. Зх - х2 4- х2 - 9.
4. Решим уравнение: (х - Ь)(х 4- 1) = х2 - 13;
х2 4 х - Ъх - 5 - х2= -1 3 ; -4 х = -1 3 4- 5; -4 х = - 8; # = 8 : 4; х = 2.
Вариант 2
1. Вычислим значение выражения а2- За 4- 1, если а = -1 ,6 .
а2—За 4- 1 = (-1 .6 )2- 3 *(-1,6) + 1 = 2,56 + 4,8 4- 1 = 8,36.
2. Найдем сумму, разность и произведение многочленов п2 - п - 2 и п2 - 1:
Сумма: (п2—п —2) 4- (и2—1) = 2га2—п —3;
разность: (а2- га - 2) - (га2- 1) = га2- га - 2- га2+ 1= -га - 1;
произведение: (га2- га - 2) * (га2—1) = га4—га2- га34- га - 2га2+ 2 = га4- га3-
- Зга24 га + 2. Ответ: 2га2—га —3 — сумма; -га - 1 — разность;
га4- га3- Зга2+ га 4- 2 — произведение.
3. Упростим выражение: 25 —(5 —с)(5 4- с) = 25 - 25 —5с + 5с 4- с2= с2.
4. Решим уравнение: (х —2)(х + 4) = х2; х2 4- 4х —2х - 8—х2= 0; 2х = 8;
х - 8 : 2; х = 4.
Вариант 3
1. Вычислим значение выражения с2- 2с 4- 3, если с = -1 ,2 :
с2- 2с 4- 3 = (—1,2)2- 2 •(-1,2) + 3 = 1,44 4- 2,4 + 3 = 6,84.
2. Найдем сумму, разность и произведение многочленов 2а2- а - 1 и а24- 2:
сумма: (2а2—а - 1) 4- (а24- 2) = За2- а 4-1;
разность: (2а2- а - 1) - (а2+ 2) = а2- а - 3;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

86. произведение: (2а2- а — 1) * (а24- 2) = 2а4+ 4а2- а3- 2а —а2—2 =
= 2а4 - а 3 + За2 - 2а - 2. Ответ: За2- а 4- 1 — сумма; а2- а - 3 — раз­
ность; 2а4—а3 4- За2- 2а - 2 — произведение.
3. Упростим выражение: р2 - (2 + р)(2 - р) = р2 - 4 4- 2р - 2р + р2= 2р2- 4.
4- Решим уравнение: х2 4- 3 = (х - 1)(лг 4- 3); х2 4- 3 = х2 4- Зх —х —3;
х2 —х 2 - Зх 4- х = -3 - 3; —2х = —6; х = 6 : 2; х = 3.
Вариант 4
1. Вычислим значение выражения г2- 2г 4- 3, если 2= -2 ,1 :
г2- 2г 4- 3 = (-2 Д )2- 2 * (-2,1) 4- 3 = 4,41 + 4,2 + 3 = 11,61.
2 . Найдем сумму, разность и произведение многочленов с2 4- 2с + 1 и с2 4- 3:
сумма: (с24- 2с 4- 1) 4- (с24- 3) = 2с24- 2с 4- 4;
разность: (с2+ 2с + 1) —(с24* 3) = 2с —2;
произведение: (с2+ 2с + 1)(с24- 3) = с44- Зс2+ 2с34- 6с + с24- 3 = с44- 2с34-
4- 4с24- 6с 4- 3. Ответ: 2с2 + 2с 4- 4 — сумма; 2с —2 — разность;
с44- 2с34- 4с2+ 6с + 3 — произведение.
3 . Упростим выражение: х2—с24- (с - эс)(с 4- ж) = х2—с24- с24- хс —хс —х2= О.
4 . Решим уравнение: х{х - 3) = х2 —5* 4- 4;
ж2- Зл: - х2 + Ъх = 4; 2* = 4; ж= 4 : 2; л: = 2.
Тестовые задания № 3
1. Ответ: 6) х2 4- у2 — многочлен.
2. Ответ: в) - х8- х2; Зх2- 1 - - 4х2- 7 + &с - х34*8= - х 2- х 3= -х 3- х2.
3. Ответ: а) 8.
4. Ответ: б) -9 а 4- 165;
(2а + 35) 4- (75 - За) - (8а - 65) = 2а 4- 35 + 75 - За - 8а + 65 = -9 а 4- 165.
5. Ответ: г) х2 - 1. (х - 1 )0 + 1) = х2 4- ^ - / - 1 = х2 - 1.
6. Ответ: в) 0,008. Упростим выражение 0,6л:34- 0,4л:3= х3.
Если х = 0,2, то "л:3= (0,2)3= 0,008.
7- Ответ: б) —1. Составим уравнение и решим его:
Ьх? - 9х + 17 —(5*3+ 4х + 17) = 13; ^ - 9* + у ( - - 4* ~ у ( = 13;
-1 3 * = 13; * = 1 3 : (-13); х = -1 .
8. Ответ: а) 8т 4- г.
9. Ответ: в) 1.
х(х 4- 1) - х(х - 2) = 3; ^ 4- х - ^ + 2л; = 3; Зл: = 3; х = 3 : 3; х = 1.
10- Ответ: в) 2а2—а3. Найдем разность суммы и известного слагаемого:
а24- 3 - (а3- а24- 3) = а24- 0 - а3 + а2 - $ = 2а2- а3.
Контрольная работа № 3
1- Вычислим значение выражения Зл:2- 2х - 6,42 при заданных значениях х.
Если х = 3, Зх2 - 2х - 6,42 = 3 * З2- 2 * 3 - 6,42 =3 * 9 - 6 - 6,42 =
= 27 - 12,42 = 14,58. Если л; = -1 ,2 , Зл:2- 2л: - 6,42 = 3 -(-1 ,2 )2- 2 *(-1,2) -
- 6,42 = 3 - 1,44 4- 2,4 - 6,42 = 6,72 - 6,42 = 0,3.
2- Запишем многочлен в стандартном виде:
а24 - 2 а 4 - 2 - а 4 - 5 + За2= 4а24- а + 7.
3. Найдем сумму и разность многочленов:
а) п2 —2п - 1 и п2 4- 3:
сумма: п2 —2л - 1 4- п2 4- 3 = 2п2 - 2п 4- 2;
разность: ^ - 2п -1 - ^ - 3 = 2п - 4;
б) Зх2 - 2ху + у2 и 5л:24- 2ху - 2у:
сумма: Зл;2- ^ у 4- у2 + 5л:2+ %Жу - 2у = 8х2 4 у2 - 2у;
разность: Зх2- 2ху + у2 —5л:2—2ху 4- 2у = —2л:2+ у2 - 4ху 4- 2г/.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

87. 4. Найдем корни уравнений у2 + 3 = у(у + 1).
у2 + 3 = у(у + 1); у2 + 3 = у2 + у; / - / - у = -3 ; -у = -3 ; у = 3.
5. Перемножим выражения:
а) 2х2 и х + у: 2х2(х + у) = 2дс34- 2де2*/;
б) а —26 и а2 + 2аЬ + 462: (а —26)(а2 + 2аЬ + 4Ьг) =
= а3+ 2а26 + 4аЬ2- 2а26 - 4а62- 8Ь3 = а3- 8Ь3.
6. Упростим выражение:
а) Ьхх - 3) + 15л:2= 5х3 - ХЯх* + у вэ? = 5х3;
б) За(а2- а + 2) + За3 - 6а2= За3- За2+ 6а + За3- 6а2= 6а3- 9а2+ 6а;
в) (2х - 1)(1 + 2х) - 4х! = &с + 0 ? - 1 - & с - = 1.
7. Решим уравнение:
а) (х ~ 2)(х + 3) = х2 - х; х2 + Зх - 2х - 6= х2 - х;
х2 + х - 6= х 2 - х; ^ + х - + х - 6; 2х - 6; х = 6 : 2; х = 3.
б) (3у - 4Ху + 1) = у(3у + 1): 3J/2+ Зу - 4у - 4 = 3у2 + у;
р / ~ У - $ # ~ У = 4; -2 у = 4; у = 4 : (-2); у = -2 .
8. Обозначим скорость лодки в стоячей воде как х км/ч., тогда скорость
по течению — (х + 3) км/ч-, а против течения — (х - 3) км/ч. Лодка
по течению проходит за 3 часа расстояние между А и В,что составляет
3(* + 3) км, и 4(х - 3) км за 4 часа против течения.
Составим уравнение:
3(х + 3) = 4(х - 3), откуда:
Зх + 9 = 4х - 12; Зх - 4х = -1 2 - 9; —х = —21; х = 21.
Тогда 3(х + 3) = 3(21 + 3); 3(лс + 3) = 3 * 24; 3(х + 3) = 72,тоесть рассто­
яние между А и В — 72 км.
9- Докажем, что выражение ЗаЬ + 6((2а + 6)а + 5) —3а{36 + 4а) при любых
значениях переменных принимает одно и то же значение:
Sab + 6((2а + Ь)а + 5) - За(ЗЬ + 4а) = Заб + 6(2а2+ ab + 5) - 9аЬ- 12а2=
= ЗаЬ + )2fif + баб + 30 - 9а6 - = 30.
Значение выражения от значений переменных не зависит.
10- Докажем, что (ab + ас + Ьс) - (са + cb + Ьа) кратно 18:
(ab + ас + Ьс) - (са + сЬ + Ьа) =
—10а + Ь + 10а + с + 106 + с —(10с + а + 10с + 6+ 106 + а) =
= 20а + 111»+ 2с - (20с + 2а + 116) = 20а + УХб + 2с - 20с - 2а- =
= 18а - 18с = 18(а - с).
Так как один из множителей произведения делится на 18, то произведе­
ние делится на 18, то есть данное число кратно 18.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

88. Раздел III. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ
НА МНОЖИТЕЛИ
т
§14. Вынесение общего множителя за скобки
527. Решение. Площадь большого прямоугольника со сторонами т и (а + Ъ+ с)
равняется 5 бол= (а + й + с)т . Она с о с т о и т 1 а , Ь , с
из площадей трех прямоугольников со
сторонами а и т , Ь и т , с и т . Их пло­
щади равняются соответственно £>ая?= а/71,
Б. = ЪтПуБ = с т . То есть 5. = 5 + £>. +бот 7 сш бол. ат Ьт
+ 5 ст или (а + 5 + с )т = а т + Ьт + Ьс.
Ответ': площадь большого прямоуголь­
ника равняется сумме площадей прямо­
угольников, из которых он состоит.
5 2 8 . а) (х - 3)х = 0;
х - 3 =-0;
х 1= 0; х2= 3.
Ответ
в) Зг(г + 4) = 0;
Зг = 0; 2+ 4 = 0 ;
г2= -4.г, = О;
Ответ: г 1= 0; г2 = -А.
д) х2 —12х = 0;
х(х - 12) = 0;
х = 0; или дс —12= 0;
* = 12.
Ответ: 0 или 12.
529. а) 2ж2- 2* = 0;
2х(дс - 1) = 0;
2х = 0; хг = 0;
х - 1= 0; х2 = 1.
Ответ: х1~ 0; х2 = 1.
в) 4у2= 8у;
4у2- 8у = 0; 4у(у - 2) = 0;
4у = 0; у г = 0;
у - 2= 0; у2= 2.
Ответ: ух = 0; у2= 2.
б) у(5 - у) = 0;
5 - у = 0;
Ух = 0; у2= 5.
Ответ: ух= 0; у2= 5.
г) 2лг(5 - 2дс) = 0;
2 * = 0, или 5 - 2х = 0;
дс = 0, -2дг= -5 ;
* = 2,5;
Ответ: 0 или 2,5.
е) Ах2 + х = 0;
дс(4дс + 1 ) = 0 ;
дс= 0 или АХ + 1 = 0; Ах = -1 ;
ж = -0 ,2 5 .
Ответ: 0 или —0,25.
б) Зг2 - г = 0;
г (Зг - 1) = 0;
г х= 0;
Зг - 1= 0;
Ответ: г л= 0; 2,
г) 12дс2- 6* = 0;
6ж(2ж- 1) = 0;
6ж= 0; или 2дс - 1= 0;
дс= 0; 2дс - 1= 0;
1
х = —.
2
Ответ: 0 или —.
2
д) Юдт2+ дс = 0;
*(10+ 1) = 0;
х = 0; или Юдс + 1= 0;
Юдс = -1 ; х = -ОД;
Ответ: 0 или -ОД.
е) 5х2 х = 0;
2
х = 0; или 5 * ----- = 0;
2
* = ОД;
Ответ': 0 или ОД.
5х = —;
2
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4bo
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

89. ж) 1,8дс2= Sx;
1,8л:2- Sx = О;
Зх(0,6х - 1) = О;
1
x —0: или х
з) х
X
л.
х2= 0;
0,6*
5
* = 5 ;
10
6
х(1 - х) = О;
х = Ô; или 1- х = 0; -дс = —1;
дс= 1.
Ответ: Оили 1.
лг= 1
Ответ: Оили 1—,
3
и) 1,5# = 5дс2;
1,5* - 5л:2= О;
5дс(0,3 - х) = 0;
5дс = О; или 0,3 - х = О;
дс= 0; -дс = -0 ,3 ;
дс= 0,3.
Ответ: 0 или 0,3.
530. Разложите на множители многочлен.
а) За26+ 2аЬ - 5а = а(ЗаЬ 4- 2Ъ - 5);
б) 7дс#3+ 8х2у2 - 9у* = #2(7 дс# + 8л:2- 9#2);
в) 5ас2- ас3- За2с = ас(5с - с 2- За); г) 8аг* - Таг3 - 4аг2- аг2(8г2- 7 г - 4).
531. а) 4а2- 5аЬ 4- а = а(4а - ЪЬ 4- 1);
б) Здс2 4- 8л:2# - х2~ л:2 (3 4* 8# - 1); в) -7т 2 - т 2г 4- т 2 -т 2(7 4- z - 1);
г) 10х4у* X2= л:2(л:4+ 10х2у2 4- 1).
532. а ) 4 а 2Ь3с4 - 5 atfc2 = ab3cz(4ac2 —5 ); б) 9 x?yz* + 7хАуггъ= x3yz 3(9 2 4- 7ху);
в) 1 8 а 3с2дс — 9 а с 2л:3 = 9 а с 2х (2 а 2 — л:2); г ) 1Ьтп2у 4- 4 5 т2п* = 1 5 тп2(у 4- 3 тп).
533. a) 15а3т х 4 4- 20o W - 25а4тдс = 5а2тдс (Зал:3 4- 4тл:2 - 5а2);
б) 32x*y3z - 8x3yz 3 4- 16дс2#324= 8x2yz (4л:2#2 - xz2 4- 2#2z3);
534. а) а 34- За2дс - Зал:2- а44- 2а = а(а24- Зал: —Sx2- а34- 2);
б) Зл:3- 2àx2 4- 4а2лс 4- ах ~ x* = x(Sx2 - 2ах 4- 4а2+ а - дс3).
535. а) 0,8ал^ 4- 0,2а2л^ 4- 0,4аэл:5+ 0,6а4дгв= 0,2ах3(4 4- ах 4- 2а2х 2 4- За3#3);
б) 1,2а2Ь3с4—0,6а3Ь3с44- 1,8а463с4= 0,6а263с4(2 - а 4- За2);
в ) 10,5Ь2с44- 1,5b9c2d2- 20b5c*d = 5fc2c2(2,lc24 0,3bd2- 463cd).
536. a) 144л:20#18 4- 36л:18#10= 36*16#1О(4л:2#0 4- 1);
б) 169а23Ь20 - 49а20Ь18= а20618(169а3Ь2 - 49);
в ) 529а15 т 36- 46а17Ь30= 23а15(23т 35 - 2а2Ь30);
г) 576п20л:31 4- 240п17* 32= 48п,7л:31(12п3 4- 5л:).
§15. Способ группировки
557. х(а 4- 1) 4- #(а 4- 1) = (а 4* 1)(дс 4- #);
а) т (3 - х) - т(3 ~ л:) = (3 - х)(т - т ) = (3 - л:) - О;
б) с 4- # 4- а(с 4- #) = (с 4- #)(1 4- а);
в ) а(х - #) —х 4- #) = а(дс - #) - (дс - #) = (дс - #)(а - 1).
558. а) х 4- # 4- а(лс 4 #) = (л: 4- #)(1 4- а);
б) х(а - Ь ) 4 - а - 6 = ( а - Ь)(дс 4- 1);
в) 2а 4- с(а - Ь) - 2Ь = с(а - 6) 4- 2(а - Ь) = (а - Ь)(с 4- 2);
г) 5л: - z(x + #) 4- 5# = 5(дс 4- #) - z(x 4 #) = (дс 4 #)(5 - 2);
д) ах - а#4- Ь(# - л:) = а(х - #) 4- Ь(х - #) = (дс - #)(а + Ъ);
е) п(дс 4- #) - тдс - ту - п(х 4- #) - т(х 4- #) = (дс 4- #)(а - т );
е) (* 4- #)2 - 4* - 4# = (л: 4- #)2 - 4(дс 4- #) = (дс 4- #)(л: + # - 4);
э) Здс 4 6# —(дс 4- 2#)2= 3(* 4- 2#) - (дс 4- 2#)2= (дс 4- 2#)(3 - (дс 4- 2#)) =
= (л: 4- 2#)(3 - х - 2#).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

90. 5 5 9 . а) а(х + у + z) + b(x + y + z) = (x-ry + z)(a + b);
б) a(z - x + l) + z - x + l = ( z - x + l)(a + 1);
в) т(а - b - с) + п(а - & - с ) = ( а - Ь - c)(m + л);
г) л(а - Ь + с )* -с + Ь - с = п{а - b + c) —(a —b + c) = (a —b + с)(л - 1).
5 6 0 . а) а(х + 3) + Ь(х + 3) + с(х + 3) = (* + 3)(а + b + с);
б) т (с - 2) - л(а - 2) + 2(а - 2) = (а - z)(m - л + 2);
в) дс(а2 —5) + у(а2 - 5) + а2 —5 = (а2 —5)(* + у + 1);
г) т х - т у + п(ж - у) + л: - у = т{х - i/) + п{х - у) + (а: - у) = '
—(jc —i/)(m + л + 1).
5 6 1 . а) ах - ш/ + Ъх - Ьу = а(* - у) + Ь(* - у) = (ж - у)(а + Ь);
или ах —ау + Ьх - Ьу = х(а + b) - у(а + Ь) = (а + Ь)(х —у);
б) са - сх + па - пх = с(а —х) + п{а - * ) = (а - *)(с + л);
или са —сх + па —пх = а(е + л) - *(с + л) = (с + л)(а —ж);
в) Û2 - 22 + ас - с2 = г(а —2) + с(а - 2) = (а - 2)(2 + с);
или az - z2 + ас ~ cz = a(z + с) - 2(2 + с) = (2 + е)(а - 2);
г) 5а - 10 + ас - 2с = 5(а - 2) + с(а - 2) = (а - 2)(5 + с)
или 5а - 10 + ас - 2с = а(5 + с) - 2(5 + е) = (5 + с)(а - 2).
562. а) 2а* - Ьх + Юау - 56i/ = *(2а - f>) + 5у(2а - Ь) = (2а - 6)(* +Ьу);
б) 10 ах - 4ау + 5сх - 2су = 2а(5* - 2у) + с(5* - 2у) = (5* - 2у)(2а + с);
в) Smp + mq - Зпр - nq = т(3р + g) - л(3р + g) = (3р + q)(m - л);
г) ас + bc + а2 + аЪ = с(а + Ь) + а(а + 6) = (а + 6)(с + а).
563. а) х 2 + ах + ху + ау = * (* + а) + |/(* + а) = (* + а)(* + у);
б) За3 + 12а2 - а - 4 = За2(а + 4) - (а + 4) = (За2 - Ща + 4);
в) а2 - ал - За + Зл = а(а - л) - 3(а - л) = (а - лХа —3);
r)ÿ8- Зу5+ Зу3- 9 = jftp3- 3 ) + Щу3- 3 ) = (у3- 3X*/5+ 3) (ошибкав условии);
д) 4 *2 —4*2 - 5 * + 52 = 4 *(* —2) - 5(* —2) = (дс - 2)(4* —5);
е) a3 -f а2 + а + 1 = а2(а + 1) + (а + 1) = (а + 1)(а2 + 1);
ж) 5а2 —5а* —8а + 8 * = 5а(а —*) - 8(а —*) = (а —*)(5а —8);
з) * 5 + * э - * 2 - 1 = * 8( * 2 + 1) - ( * 2 + 1) = ( * 2 + 1 )(*3 - 1).
567. а) 223 - З22 +22 - 3 = 0; б) х3 - Ьх2 + 2х - 10 = 0;
z2z - 3) + 22- 3 = 0
(2 2 - 3 )(2 2 + 1 ) = О;
или г22 - 3 = 0;
22= 3;
3
Z = 2;
2= 1,5.
2+ 1 О;
22= —1:
О
так как 22> О,
а —1< О,
то уравнение 22+ 1
не имеет решений
Ответ: * = 1,5
в) у3+ Зу2+ Ьу + 15 = 0;
|/% + 3 ) + 5 ( у + 3) = 0;
(У + 3)0/2+ 5) = О;
у + 3 = О; або у2 + 5 = О;
У = -3 . у2= -5 ;
так как у2> О,
а —5 < О, то уравнение
у2 + 5= Оне имеет ре­
шений.
Ответ: у = -3 .
* 2(* - 5) + 2(* - 5) = О;
(* - 5)(*2+ 2) = О;
* - 5 = 0; або *2+ 2= О.
* = 5. *2= -2 ;
так как * 2> О,
а -2 < О, то уравнение
*2+ 2= Оне имеет ре­
шений.
Ответ', х = 5.
г) З*3+ 9*2+ * + 3 = О;
3*2(* + 3) + * + 3 = О;
(* + 3)(3*2+ 1) = О;
х + 3 = О; или Зле2+ 1 = 0;
* = -3 . 3*2= —1;
*2= — ; так как х?> О,
а — < О, то уравне-
3
ние 3jc2+ 1 = Оне име-
Ответ:
ет решении.
* = - 3.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

91. 568. а) 4а2 - 4аг - За + 3z = 4а(а - г) - 3(а - z) = (а - z)(4a - 3);
б) Зх2 - Зху + Sy2 - 3ху = 3(х2- ху - ху + у2) = 3(х(х - у) - i/(x - #)) =
= 3(х - i/)(x - у) = 3(х - і/)2;
в) а 4- а2 - а3 - а4 = а(1 + а —а2 —а3) = а(1 4 а —а2(1 4 а)) =
= а(1 4- а)(1 —а2);
г) а3 4- а26 - а2с - abc = а(а24-аб —ас - 6с) = а(а(а 4- 6) - с(а 4- 6)) =
- а(а + 6)(а - с).
569. а) а2 - ab - 4а 4- 46 = a(a- 6) - 4(а - 6) = (а - Ь)(а - 4);
б) ах + 3 4- Зх 4* а = ах 4- а 4- Зле + 3 = а(х + 1) + 3(х + 1) = (х + 1)(а 4- 3);
в) ас 4- Ъ—Ьс - а = ас —Ъс —а 4 6 = с(а —6) - (а - 6) = (а —6)(с —1);
г) 3т - Ьх 4* тх —ЗЬ = З т 4- тх —ЗЬ —Ьх = т (3 4- х) —6(3 4- х) =
= (3 + х )(т —6).
570. а) ах + ау —аг 4- пх + пу —пг = а(х + у —г) 4- п(х + у —г) =
= (X + # - z)(a + п);
б ) a 4 - 6 - 2 - a x - 6 x + 2a; = a 4 6 - 2 - х(а 4 6 - 2 ) = ( а + 6 - 2)(1 - х);
в) 2ах 4- сх - бах2 - Зсх2 + 2ас + с2 = х(2а + с) ~ Зх2(2а 4- с) + с(2а 4 с) =
= (2а + с)(х - Зх2 + с)
или 2ах + сх - бах2- Зсх2 + 2ас + с2= 2ах —бах2 4- 2ас + сх —Зсх2 + с2=
= 2а(х —Зх2 4- с) 4- с(х - Зх2 4- с) = (х - Зх2 4- с)(2а + с);
г) X 2 4- 2х - са —2с - сх + ах = х2 + 2х 4- ах - сх —2с —са =
= х(х -f 2 4- а) - с(х 4 2 + а) = ( х 4 2 4 - а)(х - с).
571« a) az2 —6z2 - 6 z 4 - a z - a 4 - 6 = z2(a —6) 4- z(a - b) —(а —b) =
= (a - 6)(z2+ z - 1)
или az2 —dz2 - 6z 4 az —a 4- 6 = az2 + az —a - 6z2 —dz 4- b = a{z2 + z - 1)
- 6(z2 4- z —1) = (z2 4- z - lXa - 6);
б) a + b + ax2 + 6x2 - 6x —ax = a 4- ax2 —ax + 6 4- bx2 —bx =
- a (l + X 2 - x) + b(l 4- x2 - x) = (1 4- x2 - x)(a + 6);
в) ax2 4- bx2 4- ax —cx2 4- 6x - cx = ax2 4- bx2 - cx2 + ax + 6x —cx =
= x2(a 4- b - c) 4- x(a + b - c) = (a + b - c)(x2 + x) = x(x -4- l)(a + b - c);
r) ax2 + bx2 - bx - ax - cx2 - cx = x(ax 4- bx 4- cx - a - b ~~c) =
= x(x(a + 6 + c ) - ( a + H e ) ) = x(a 4- b + c)(x - 1).
572. a) 2am 4- 3mx —Im - 2ас - Зсх + 7 с = m(2a + Зх —7) - c(2a + Зх —7) =
= (2a + Зх - 7)(m - с);
б) 4ax2 - ax + 5a —4bx2 + bx - 5b= a(4x2 —x + 5)- b(4x2 —x + 5) =
= (4x2 - x + 5)(a - &);
в) 9c3x2 + 2c3x - c8 + 9x2 + 2x - 1 = c3(9x2 + 2x - 1) + 9x2 + 2x - 1 =
= (9x2 + 2x - l)(c2 + 1);
r) 4a6c2—4ac + 46 + abc2x —aex + 6x = 4(a6c2 —ac + b) 4- x(abc2 —ac + b) =
= (abc2 - ac + 6X4 + x).
573. a) x4 - a4 + a3x - ax3 + c3x - ac3 = x4 - ax3 - a4 + a3x + c3x - ac3 =
= x3(x - a) + a3(x - a) + c3(x - a) = (x - aXx3 + a3 + c3);
б) a3 —a2 4- x3 - x2 + a2x 4 ax2= (a3 —a2 + a2x) + (x3 —x2 4- ax2) =
= a2(a - 1 4- x) 4 x2(x - l + a ) = ( x - l + a)(a2 4- x2);
в ) X3 + ü 3 + xy2 + x2y 4- X 2Z + |/2Z = (x3 4 x2y + x2z) + ( v 3 + XI/2 + ü2z) =
= * ^ Л + 5 + і^ г.+ * + * ) - ( * + у + *х * * + Л
г) a3 + a 4- a62 —a2b - b —б3= а(с? + 1 4- б2) —6{д2 4- 1 + б2) =
= (а2 4- 1 4- 62)(а - 6).
574. a) x3 4 х2у + х9у - хуг - ху2 - у3 - х2(х + у + ху) - у2(ху 4- х 4* у) =
= (х + у 4- ху)(х2 - у2);
б) X2- X 3 4- у - у3- ху - х2у2= X24- у2 - X 3 - ху - х2у2 - у* =
- (*2 + у) - хі*2 + у) - У2(х2 + #) = (х2 + у)(1 - x - у2);
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

92. в) 0,9а* + 1,2х2 - 1,2ас - 1,6сх = 0,3х(3а + 4х) - 0,4с(3а + 4х) =
= (За + 4*)(0,3дс - 0,4с) = 0,1(3а + 4*)(3* —4с);
v 3 2 1 12 2 2 4 ( 3 2 1225Л (1 4 ^
г) — ах у ------х + — а х у ау = — ах у л------а ху I- — х + — ау =
13 - 1 3 13 У 13 * (,13 13 ) 13 13 * )
3 1 / з 1Л
= — а^г/(* + lay) - — (ж+ 4ад) = I— — 1(* + 4ау) = -(З а х у -1 )(х + 4ау).
575. a) 15a2m* - 20am - 21a* + 28 = 5am(3a* - 4) - 7(3a* - 4) =
= (3a* - 4)(5am - 7);
П роверка: (3ax - 4)(5am - 7) = 3a* * Sam - 3a** 7 - 4 * Sam + 4 * 7 =
= 15a2m* - 21аж - 20am + 28;
6) a2+ lOaft - 20a - 0,1a - b + 2 = 10a(0,la + b - 2) - (0,1a + b - 2) =
= (10a - l)(0,la + b - 2);
П роверка: (10a - l)(0,la + b - 2) = 10a * 0,1a +
+ 10a * b - 10a * 2- 1*0,1a - l * b + l *2 = a2+ 10a& - 20a - 0,1a - b + 2;
576. а) 2е * 35+ 20* 33- 28•35- 2е * 33= 26* 33*(28* 3a + 2Э- 32- 1) =
= 26- 3a(28(32+ 1) - (32+ 1)) = 26- 3?(32+ 1)(23- 1) = 26•33* 10 * 7 =
= 2e * 3a *2 * 5 * 7 = 27•33* 5 •7.
420 = 42 * 10 = 6 * 7 •2 •5 = 2 •3 * 7 * 2 * 5 = 22* 3 * 5 • 7.
Так как данное выражение раскладывается на множители 27* З3* 5 * 7,
а число 420 = 22* З3♦5 * 7, то 27* 3 * 5 - 7 = (22•3 * 5 •7)(25* З2).Значит,
данное выражение делится на 420;
б) 5го * 7W+ 510* 7е - 5* * 7го - 5* • 7s делится на 1200.
Разложим на простые множители число 1200:
1200 = 12 * 100 = 3 *4 •4 •25 = 3 •22* 22* 52= 24* 3 * 52.
Преобразуем данное выражение в произведение простых чисел:
510* 710+ 510•78- 5е * 710- 53* 78= 5е •78(52* 72+ 52- 72- 1) =
= 58- 78(52(72+ 1) - (72+ 1)) = 58* 78(72+ 1)(52- 1) = 58* 78* 50 * 24 =
= 58* 78* 52*2 *3 *23= 24* 3 * 510- 78= (24* 3 * 52)(58* 78).
Так как один из множителей полученного произведения равняется
24* 3 * 5 = 1200, значит, данное выражение делится на 1200.
в) 211- З6- 27* 3е - 27* З4+ 211•З4делится на 150.
Разложим на простые множители число 150:
150 = 15 •10 = 3 - 5 * 2 * 5 = 2 * 3 * 52
Преобразуем данное выражение в произведение простых чисел:
2П * З6- 27* 3е - 27* З4+ 2й •З4= 27* 34(24»З2- З2- 1 + 2*) =
= 27- З4(З2(24- 1) + (24- 1)) = 27•З4(24- 1)(32+ 1) = 27* З4* 15 •10 =
= 27* З4* 3 - 5 * 2 * 5 = 28* З5- 52= (2 •3 •52)(27* З4).
Так как один из множителей полученного произведения равняется 2 *3 *5s5=
= 150, значит, данное выражение делится на 150_.
577. а) 300 = 3 * 10 •10 = 22* 3 * 52.
210* З12+ 28* 312+ 210* З10+ 28* З10= 28* 310(22* З2+ 32+ 22+ 1) =
= 28* З10(З2(22+ 1) + (22+ 1)) = 28* З10•(22+ 1)(32+ 1) = 28*З10* 5 * 10 =
= 2Э* З10* 52= (22* 3 * 52) * (27* З9).
Один из множителей полученного произведения равняется 22*3 *52- 300,
значит данное выражение делится на 300,
б) 510* З15- 58* З16+ 511* З12- 59- 313= 58* 312(52* З3- З4+ 53- 5 * 3) =
= 58* 312(3Э(52- 3) + 5(52- 3)) = 58* З12(52- ЗКЗ3+ 5) = 58* З12* 22 - 32 =
= 58•З12- 2* 11 * 25= 2е •З12•58* И .
Так как один из множителей полученного произведения равняется 11,
значит, данное выражение делится на 11.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

93. в) ~710* 2А0+ 79•214- 78* 210+ 77•214делится на 45.
„ 710. 2н>+ 79. 214 - 7е * 210+ 77* 2й - 77 * 210 (-7 3+ 72•24- 7 + 24) =
= 77•210(72(-7 + 24) + (-7 + 24)) = 77*210*(24- 7)(72+ 1) = 77* 210- 9 * 50 -
= 77•210* З2- 2 * 52« 2й * З2 * 52* 77= (З2* 5)(2П * 5 * 77) = 45 •2П •5 •77,
Один из множителей полученного произведения равняется 45, значит,
данное выражение делится на 45.
578. а) х2+ (а + Ь)х + аб = (х + а)(х + 6).
I способ: х2 + (а + Ъ)х + аб - х2 + ах + Ъх+ аб - х(х + а) 4- 6(х +• а) =
= (х + а)(х + 6).
I I способ: х2 + (а + Ь)х + аЬ - (х + а)(х *+ 6) -
= х2 4- ах + 6х + аб - х2 - хЪ - ах - аЬ = О;
Первым способом путем тождественных преобразований одно из выраже­
ний преобразовали к виду второго выражения.
Во втором способе показали, что разность двух выражений равняется нулю,
а это значит, что выражения тождественно равны.
б) х2—(а - Ь)х + аЬ = (х ~ а)(х - 6).
I способ: х2- (а - Ь)х + аЬ = х 2 - ах - Ъх 4- аЬ - х(х - а) - Ь(х - а) -
= (х - а)(х ~ Ь).
I I способ: х2- (а - Ъ)х 4- аб - (х - а)(х - 6) =
- х2—ах - Ъх + аб - х24- Ъх 4- ах —аЬ = О
в) х2+ (а - Ь)х - аЬ —(дс 4- а)(х - 6).
I способ: х2 4- (а - 6)х - аЪ = х2 4- ах - Ъх - аЪ ~ х(х + а) - 6(х 4- а) =
= (х + а)(х - Ъ).
I I способ: х2+ (а - Ъ)х - аЪ - (х 4- а)(х - Ъ) =
= х24- ах —Ъх - аЪ - х2+ хЪ —ах 4- аЪ —О
г) х2-(а - Ъ)х ~ аб = (х - а)(х + 6).
I способ: х2 -(а - Ь)х - аЪ - х2 - ах 4- Ъх - аЪ = х(х - а) 4- Ъ(х - а) =
= (х —а)(х 4- 6).
I I способ: х2-(а - Ъ)х - аб - (х - а)(х 4- 6) =
= х2- ах + Ъх - аЪ - х2- хЬ + ах + аЪ = О.
579*. а) х2+ (2 + 3)* + 2 ■3 = (* + 2)(х + 3).
Проверка: х2+ 5х + 6= л:2+ Зх + 2х + 6; х2+ Ьх + 6= х2+ 5л + 6.
б) х2+ 6* + 5 = х2+ (5 + 1)х + 5 * 1 = (х + 5)(дс + 1).
П роверка: (х ~+ 5)(х + 1 ) = х2 х + 5х + 5 = х2+ Ьх + 5.
в) #2 + 7# + 12 = у2 + (4 + 3)у + 4 * 3 = (у + 4)(у + 3).
П роверка: (у + 4)(г/ + 3) = #2+ Зл: + 4де + 12 = #2+ 7х + 12.
г) 22-I- 82 + 3 * 5 = г2+ (3 + 5)2 + 3 * 5 = (г + 3)(г + 5).
Проверка: г2+ 82 + 3 * 5 = (2 + 3)(2+ 5);
г2+ 82 + 15 = 22+ 52 + 32 + 15; г2+ 82 + 15 = г2+ 82 + 15.
д) х2+ Зх - 10 = х2+ (5 - 2)х - 5 * 2 = (х + 5)(я: - 2).
П роверка: (х + 5)(я - 2) = х2—2х -I- 5х - 10 = х2+ Зх - 10.
е) х2- х - 6= х2- (3 - 2) ~ 3 * 2= (х - 3)(х + 2).
П роверка: (х - ЗХ* + 2) = х2+ 2х - Зх - 6= х 2- х - 6.
ж) а2 -I- ЗаЪ + 2Ь2= а2+ (26 + Ъ)а + 26 * 6= (а + 26)(а + 6).
П роверка: (а + 26)(а + 6) = а2+ аб + 26а + 262 = а2+ Заб +•262.
з) 2х2- 7x1/ + 3у2- 2(х2- 3,5ху + 1,5|/2) = 2(х2- (3у + 0,5#)х + 3у *0,5*/) =
= 2(х - 3у)(х - 0,5у) = (х - 3у)(2х - у ) .
Проверка: 2(х - 3#)(х - 0,5#) = (х - 3#)(2х - у) = 2х2- ху - 6ух + З#2=
- 2х2- 7ху + З#2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

94. 580*. а) ж(ж + 7) - 2(х + 7) = 0;
(х + 7)(х - 2) = 0;
* + 7 = 0; или х - 2 = 0;
х = -7 ж= 2
Ответ: -7 или 2.
в) 2ж(ж2 + 4) - 8ж2 - 32 = 0;
2ж(ж2 + 4) - 8Хж2 + 4) = 0;
(х2 + 4)(2ж - 8) = 0;
х2 + 4 = 0; или
х2 = -4 .
Так как * 2 > 0,
а —4 < 0, то
уравнение
ж2 + 4 = О
2ж - 8 = О;
2х = 8;
ж= 4.
б) Зж(ж - 1,5) + 6(ж - 1,5) = О;
(Зж + 6)(ж - 1,5) - О;
Зж + 6 = О; или ж—1,5 = О;
Зж = -6 ; ж= 1,5;
ж= -2
Ответ: -2 или 1,5.
г) у* ~ Зу3 + у = 3;
у* - З у э + у - 3 = 0;
УЭ(У ~ 3) + (у - 3) = О;
(У - з)(у3 + 1) = О;
у - 3 = О; или у3 + 1 = О;
у = 3. у3 = -1 ;
у = -1 .
Ответ: -1 или 3.
не имеет корней.
Ответ: ж= 4.
581*. а) ж8 —5ж2 + ж= 5; б) 13z - 78
ж3 - 5ж2 + ж- 5 = 0;
ж2(ж - 5) + (ж - 5) = О;
(ж - 5) * (ж2 + 1) = О;
ж- 5 = О; или ж2 + 1 = О
ж= 5 ж2= 1.
Так как ж2 > О,
а —1 < 0 , то уравнение
ж2 + 1 = О
2z[z - 6) = 0;
13z(z - 6) - 2z(z - 6) = 0;
(z - 6)(13z - 2z) = 0;
(z - 6) * llz = 0;
z —6 = 0; или llz = 0;
z = 6. z = 0.
Ответ: Оили 6.
не имеет корней.
Ответ: 5.
в) z5 + z3 + z - 2Z4 2z2= 2:
+ 2з + г _ 2г* _ 2z2 - 2 = 0;
z(zA+ z2 + 1) - 2(z4 + z2 + 1) =
(z4 + z2 + l)(z - 2) = 0;
z4 + z2 + 1 = 0; или z - 2 = 0;
г) -X4 + 5ж3 + 6ж2 + ж2 + 5ж + 6 = О;
ж2(ж2 + 5ж + 6) + (ж2 + 5ж + 6) = 0;
0; (ж2 + 5ж + 6)(ж2 + 1) = 0;
(ж2+ (3 + 2)ж + 3 •2)(ж2 + 1) = 0;
(ж + 3)(ж + 2)(ж2 + 1) = О;
Так как z4 > О,
z2> 0 и 1 > О, то
2.
уравнение
z4 + z2 + 1
не имеет
ней.
Ответ: 2.
582. а) - 2 —+ —
8 3
= 0
кор-
ж+ 3 = О;
ж= -3
или ж + 2
ж= -2
Ответ: -3 или
или ж2 + 1 = О;
ж2 = -1
О; Так как ж2 > О,
а -1 < О, то урав­
нение ж2 + 1 = О
не имеет корней.
2.
б)
в) - 4 - +
4
~(*Н)
(-D-S
Н ) - (
3 1 - 8
* = з *
7
8-3
3-5
2 = . 2 3 - 1 6
24
24 + 3 - 1 6 1 11
24 " 24
5-7
= 3
1 4 - 1 5
35
35 + 14
35 35
л 3 Л4 —+ 5 —
4 2 )
9
г) 4 —+ f - l —1 = 4 —- 1
2 { 3) 2
3 - 2
-9 -1 0
д) —^ = 4,2 = -0 ,6 + 4,2
2-3 6
4 , 2 - 0 , 6 = 3,6;
е) 3 , Л 3 1 3 - 2
-- + (-0,5) = -------= --------
4 4 2 4
1
4
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

95. 583. а) - 1 + (-1,8) = - f| +1, в! = -(0 ,6 +1,8) = - 2 ,4 ;
fi) 0,7 + 1 - — 1 = 0 , 7 - — = 0 , 7 - 0 , 9 = -0 ,2 ;
10 J 10
9 - 1 0 , 3 0 + 9 - 1 0 29
2 ~ 3 Ö - = ~l 30 = ' 1i ö ;
20 + 9 29
30 3 0 ’
л) 2,05 + = 2,05 - ^ = 2,05 - 0,125 = 1,925;
с) 1,5 + (- | 1 = 1 , 5 - | = 1 , 5 - 0 , 8 = 0,7;
584. а) Если |а|< 6, и а < 6.
если |а|< 6, то а принимает значения из заштрихованной части координат­
ной прямой.
То есть -6 < а < Ь. Значит, а <Ь и данное _____ /^///////У/У УУУУУУ ^___>
утверждение правильное. -6 0 6
б) а < |б|, то а < 6.
I способ. Если а < |б|, то 6 принимает значения из заштрихованной части
координатной прямой. УУУУУУУУ /............. ,_______ /УУУУУу
ГЬ < -а , Га < -6, -а 0 а
> а ; [а > 6;
То есть
6 > а ; [а > 6;
Из неравенства а < -6 не следует, что а < |б|. Значит, данное утвержде-
ИМЙТТЛЖНЛние ложно.
2 < |—3|; 2 < 3 .
I
/(ля того, чтобы доказать, что утверждение ложно, достаточно привести
один пример, для которого утверждение не выполняется.
584. Если |а|< |б|, то а < 6.
Пусть а = 2, 6 = —3, тогда |2|< |-3|, но 2 < —3 — неравенство ложно.
Значит, данное утверждение ложно.
585. Сколько существует целых чисел, которые удовлетворяют неравенству
х< 5? Обозначьте их на координатной прямой.
-5 —4 -3 -2 -1 0 1 2 3 4 5
Четыре положительных целых числа, четыре отрицательных целых числа
и число нуль. Вместе — 9 чисел.
Ответ: 9.
§16. Квадрат двучлена
589. а) (а + с)2 = а2 + 2ас + с2;
б) (х + у)2= х2 + 2ху + с2;
в) (п + 2)2 = п2 + 2п •2 + 22= п2 + 4п + 4;
г) (т + З)2= т2 + 2т * 3 + З2= т2 + 6 т + 9;
д) (1 + аЬ)2 = I2 + 2 * 1 * аб + (аб)2 = 1 + 2аб + а2Ъ
е) (р + Зд)2 = р 2 + 2р * Зд + (Зд)2 = р 2 + 6рд + 9<72;
ж) (2х + 4)2= (2х)2 + 2 * 2х * 4 +42 =4х2 + 16 х + 16;
з) (За + Ь)2= (За)2 + 2 •За * 6 +Ь2= 9а2 +баб + б2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

96. 5 9 0 . а) (тп 4- 2)2 = т 2 + 2 т •2 4- 22= т 2 4- 4 т 4- 4;
б) (2а + б*)2 = (2а)2 4- 2 •2а * 5х 4- (бас)2 = 4а2 + 20а* 4- 25х2;
в) (3 4- а2)2 = З2 + 2 - 3 ■а2 + (а2)2= 9 4- 6а2 4- а4;
г) (х - I)2 = x2 - 2х * 1 4- I2 = X2 - 2х + 1;
д) (2с —а)2 = (2с)2 - 2 •2с •а 4- а2 = 4с2 —4ас 4- а2;
е) (б - ж2)2 = б2 - 2 •б •X 2 + (X 2) 2 = 25 - 10х2 + х4;
ж) (1 - ab)2 = I 2 - 2 •1 * ab + (ab)2 = 1 - 2 ab + a 2b2;
з) (cq - 2p)2 = (cq)2 - 2cq ■2p + (2p)2= c2p 2 - Acqp + 4p2.
591. a) (ax + 5) = (ах)2 + 2ax •5 + 52 = a2x2 4- 10ax 4- 25;
б) (a 4- c2)2= a2 4- 2ac2 4- (c2)2= a2 4- 2ac2 4- c4;
в) (n 4- 2a) = n2 + 2n •2a + (2a)2 = n2 + 4an 4- 4a2;
r) (3x 4- 2y)2= (3x)2 4- 2 * 3x •2y 4- (2y)2 = 9x2 + 12xy 4- 4t/2;
д) (5a + 3b)2 = (5a)2 + 2 •5a - Sb 4- (3b)2= 25a2 + 30ab + 9b2;
е) (1 + 2abc)2 = l 2 + 2 ■1 * 2abc + (2abc)2 = 1 4- 4abc 4- 4a2b2c2;
ж) (4n 4- 3c)2= (4n)2 4- 2 *4n * 3c + (3c)2 = 16n2 + 24nc 4- 9c2;
з) (-2 4- 5ac)2 = (бас - 2)2= (5ac)2 - 2 •5ac •2 4 22 = 25a2c2 - 20ac 4- 4.
592. a) (3c - 5)2 = (3c)2 - 2 •3c •5 + 52= 9c2 - 30c + 25;
б) (ab - 2c)2 = (ab)2 - 2ab «2c 4- (2c)2 = a2b2 - 4abc + 4c2;
в) (За - 7c)2 = (За)2 - 2 * За - 7c 4- (7c)2= 9a2 - 42ac + 49c2;
r) (a2 - x)2= (a2)2 - 2a2 •x + x2 = a4 - 2a2x 4- x2;
д) (За - с3)2= (За)2 - 2 •За •с8 4- (с8)2= 9а2—бас3 4- с6;
е) (2а2 - Зсх2)2 = (2а2)2 - 2 - 2а2 •Зсх2 4- (Зсх2)2 = 4а4 - 12а2сх2 + 9с2х4.
593. а) ( т 4- 2)(т + 2) = ( т 4- 2)2 = т 2 4- 4 т 4- 4;
б) (3 4- р)(3 4- р) = (3 4- р)2= 9 + 6р 4- р2;
в) (2а 4- Ь)(2а 4- Ь) = (2а + Ь)2= 4а2 4- 4аЬ 4- Ь2;
г) (5 4- с)(5 4- с) = (5 + с)2 = 25 4- 10с + с2;
5 9 4 . а) + = + = п 2 +2п + =Rz+n + | ;
б) (р 4- 0,1)(р 4- ОД) = (р + ОД)2 = р2 4- 2р * ОД + ОД2= р2 4- 0,2р + 0,01;
в) (2а3 4- 1)(2а3 4- 1) = (2аэ 4- I)2 = (2а3)2 4- 2 * 2а3 * 1 + I2 = 4а6 4- 4а3 4- 1;
г) (1 + ху)(1 4- ху) = (1 4- ху)2 = I2 + 2 •1 •ху 4- (ху)2 = 1 4 - 2ху 4- х2у2.
595. а) (Ь + сэ)2= Ь2 4- 2Ь •с3 + (с3)2= Ь2 4- 2Ьс3 4- с6;
б) (Ь + 4с2)2 = Ь2 4- 2Ь •4с2 + (4с2)2 = Ь2 4- 8Ьс2 + 16с4;
в) (2 т - ç6)2= (2 т )2 - 2 •2 т - ç5 4- (g5)2 = 4 т 2 - 4mg5 4- ç!0;
г) ^ с + 2aj = ^ cj + 2 ‘~ с - 2 а + (2a)2 = ^ с2+ 2ac + 4â2;
ч (2 3 Ÿ (2 Ÿ _ 2 З (3 f 4 2 _ 9 2 4 2 п П1 2
д) - т +-р = - т 42 - т - р + -р= - т +2тр + - р = -т +2тр +2 - р ;
U 2 ) U ) 3 2 U J 9 * V 9 ґ V
е) (4ç2 + 5р)2 = (4ç2)2 4- 2 •4ç2 •5р + (5р)2= 16ç4 + 40ç2p 4- 25p2.
596. а) (3a - 5) (3a - 5) = (3a - 5)2= (3a)2 - 2 •3a - 5 4- 52 = 9a2 - 30a 4- 25;
б) (4x2 - 3y)(4x2 - 3y) = (4x2 - 3y)2= (4x2)2 - 2 •4x2 •3y 4- (3y)2 =
= 16x4 - 24x2y 4 9y2;
в) (l,3 x 3 - 1X1.3x3 - 1) = (l,3 x 3 - l)2= (l,3 x 8)2 - 2 * l,3 x 3 -1 + 12 =
= 1,69х* - 2,6x3 + 1;
г) (2,5ac - x3)(2,5ac - x3) = (2»5ac - x8)2 = (2,5ac)2 - 2 •2,5ac •x3 + (x3)2=
= 6,25a2c2 - 5acx3 4- x6.
597. a) (a - b)2= (b - a)2;
(a - b)2= a2 - 2ab + b2= b2- 2ab + a2 = (b - a )2.
6) ( -a - b f = (a 4- b)2;
(-a - b)2 + (-(a + b))2= (—l)2(a 4 b f = 1 •(a + b)2 = (a 4- b)2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4bo
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

97. н) (а -Нб)2 —2аб = о2 + б2.
/ способ: (а + 6)2= а24- 2аб 4- 62; (о 4- б)2 = (а 4- 6)2.
// способ: (а + б)2 - 2аЬ = а2 4- 2аб 4- 62 —2аЬ = а2 + 62.
«•) (а + б)2 - (а - б)2= 4аб;
(а I Ь)2 - (а - 6)2= (а2 + 2аб + б2) - (а2 - 2аЬ + 62) =
« •■+■2аб 4- 62 - а2 4- 2о6 - 62 = 4аб.
598. а) 9 —6* + х2= З2 - 2 * 3 * х 4- х2= (3 - л:)2;
б) 4х2 4- 25#2 - 20ху = (2х)2 - 2 « 2х * 5#4- (5у)2= (4х - 5#)2;
и) ай4- 4а4Ь + 4Ъ2= (а4)2 4- 2 * а4 * 26 4- (26)2= .(а4 + 26)2; *
г) а262 4- 36с2 4- 12абс = (об)2 + 2 * об * 6с + (6с)2= (об + 6с)2;
д) 16т° + 2 4 т 3 + 9 = (4ma) + 2 * 4ma * 3 4- З2 4- (4m3 4- З)2;
«) 40а262 - 462 - 100а462 = —(462 - 40о262 4- 100а462) =
~((26)2 - 2 •26 * 10о2б + (10о26)2) = -(26 - 10а26)2.
599. а) 9о2 4- бос 4- с2 = (Зо)2 + 2 * Зо * с 4- с2 = (Зо 4- с)2;
б) х4 - 10х2 4- 25 = (х2)2 - 2 •х2 * 5 + 52 = (х2 - 5)2;
в) 4 т 2 4- 4 т + 1 = (2т)2 + 2 * 2 т * 1 + I 2 = (2 т 4- I)2;
г) 6« - 662 4- 9 = (б2)2 - 2 * б2 * 3 4- З2 = (б2 - З)2.
600. а) (х —З)2 - х(х - 6) = х2 —6х 4- 9 —х 2 4- 6х = 9;
б) (т 4- 5)2 - ( т - 5) = т 2 4-Ю т + 2 5 - т + 5 = т 2 +9 т 4-30;
п) 1 - (2а - I)2= 1 - (4а2 - 4а 4- 1) = 1 - 4а2 4- 4а - 1= 4а - 4а2;
г) 22 + 1 - (1 + z)2= z2 + 1 - (1 4- 2г + г2) = z2 + 1 - 1- 2г - г2= -2z.
601. a) (х - 2)2 + (х - 5)(х 4- 7) =
- х2 —4х 4- 4 4- х2 4- 7х - 5х - 35 4- 2х2 —2х - 31;*
б) 3(а - I)2 + 8а = 3(а2 - 2а 4- 1) 4- 8а = За2 - 6а 4- 34- 8а =За2 + 2а + 3;
в) #(# 4- 2х) - (х 4- у)2= у2 + 2ху - (х2 4- 2ху 4- у2) =
- у2 4- 2ху ~ х2 - 2ху - у2 - - х 2;
г) (6 + 4)2 - (6 - З)2 = (б2 + 86 4- 16) - (62 - 66 4- 9) =
= 62 4- 86 4- 16 - б2 4- 66 - 9 = 146 4- 7.
602. а) (х - 2)2= х2; х2 - 4х 4- 4 = х2; -4 х = -4 ; х = -4 : (-4); х = 1. О твет: 1.
ок ъ 5
б) (3у 4- 5)2= 9у2; 9у24- 30# 4- 25 = 9#2; 30# = 25; # = — ; # = —. Ответ: ~ .
в) (с - 7)2 = с2 - 7; с2 - 14с + 49 = с2 - 7; -14с = -7 ~ 49; -14с = -5 6 ;
с ----- ; с - 4. Ответ: 4.
-14
г) (6 - z)2- z2 4- 36; 36 - 12z 4- z2 = z2 4- 36; -12z = 0; z = 0. Ответ: 0.
д) 3(x - 2)2= 3; (x - 2)2= 1;
x - 2 = 1; или x —2 = —1 -
x - 3; x = 1
Ответ: 1 или 3.
е) (2x2- l)24- 2 = 0; (2x2- l)2= -2 . Так как (2x2 - 1)2> 0, a —2 < 0, to урав­
нение (2x2 - l)2 4- 2 = 0 не имеет корней. Ответ: нет корней.
603. а) (х + 7)2 4- х2= 0;
/ способ: Так как (х 4- 7)2> 0, и х2 > 0, при этом (х + 7)2ф х2, то
(х 4- 7)2 + х2 > 0. Значит, данное уравнение не имеет решений.
Ответ: нет решений.
/ / способ: (х 4- 7)24- х2= 0; (х 4- 7)2= —х2; (х 4- 7)2> 0 и х2> 0, значит —х2< 0.
Значит, данное уравнение имеет решения, если (х 4- 7)2 = 0; х 4- 7 = 0;
х = -7 и х2= 0; х = 0. Так как -7 ф 0, то уравнение не имеет решений.
Ответ: нет решений.
б) -3 (х - 5)2 = -3 ; (х - 5)2= -3 : (-3); (х - 5)2= 1;
х - 5 = 1 ;х = 6 или х - 5 = -1 ; х = 4. Ответ: 4 или 6.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

98. в) (* - 4У2= Sx + 16; х2 - Sx -4- 16 = 8* + 16; x2 - 8* - Sx = 0;
jc2 - 16x = 0; x(x - 16) = 0; x —0, или x - 16 = 0; x = 16.
Ответ: 0 или 16.
г) (5 - #)2 = 10# + 25; 25 - 10# 4- #2 = 10# + 25; #2 - 10# - 10# = 0;
#2 - 20# = 0; #(# - 20) = 0; # = 0, или # - 20 = 0; # = 20.
д) (1 - 2z f + 4z = 0; 1 - 4z + 4Z2 + 4z = 0; 4z2= -1 ; z2 =
4
Ответ: 0 или 20.
Так как z2 > 0, а - —< 0, то данное уравнение не имеет корней.
4
Ответ: нет корней.
е) (3 - 5х)2= 25х2; 9 - ЗОх + 25хг= 25х2; -3 0 * = -9 ; х = — ; х =
—30
х = 0,3. Ответ: 0,3.
6 0 4 . а) (х + 3у)2 = хг + 2х ■3у + (Зу)2= хг + 6ху + 9у1-,
б) (ш + 5аЬ)г = т 2 + 2 т - 5аЪ + (5аЬ)2= т2 + 10таЬ + 25а2Ь2;
в) (7 + а2)2 = 72 + 2 ■7 •а2 + (а2)2 = 49 + 14а2 + о4;
г) (2х + у3)2= (2х)2 + 2 •2х •у3 + (у3)2 = 4х2 + 4ху3 + у6;
д) (Зс2 + у)2= (Зс2)2 + 2 •Зс2- у + у2= 9с4 + 6с2у + у2;
е) (5х2 - у3)2= (5х2)2 - 2 - 5х2 •у3 + (у3)2 = 25Х4 - 10х2у® + у®.
605. а) (0,2с - р3)2= (0,2с)2 - 2 •0,2с •р3 + (р3)2= 0,04с2 - 0,4ср3 + р6;
б) (1,2 + 2q3f = 1,2s + 2 - 1,2 •2q3 + (2g3)2= 1,44 + 4,8?3 + 4g°;
в) (4x2 - 3y2)2= (4x2)2 - 2 •4x2 - Зуг + (Зу2)2= 16X4 - 24хгу2 + 9y4;
г ) (a2 — 8c5)2= (a2)2 - 2a2 • 8c5 + (8c5)2= a 4 — 16a2c5 + 64c10;
д) (—x + у3)2= (у3 —x)2= (у3)2 - 2y3x + x2 = у0 - 2y3x + x2.
6 0 6 .a) f | - 2 c 2l = f| + 2c2j + 2 -| -2 c2 +(2c2)2 = ^ + 2c2+ 4c4;
б) ^0,3x3 + ^ c j = f ^ c - 0 ,3 x 3j = ^ j -2• i c -0,Зх3 + (0,Зх3)г =
= — cx3 +0,09x6 = — -ОДбсх3 +0,09x°;
16 2 16
в) ^ c - 0 , 5 a 2j = (0,2c + 0,5a2)2 = (0,2c)2+ 2-0,2c-0,5a2+ (0,5a2)2
= 0 ,04c2 + 0 ,2a2c + 0 ,25a4;
Л (2 з , 1 V (2 3 3f (2 ,V „ 2 3 3 (3 f
r) —m - 1 —x = —m — x = —m - 2 —m —jc+ —x =
1,3 2 J {S 2) 3 ) 3 2 2 )
= —m6 - 2m3x + —я:2 = —m6 - 2m3x + 2 —x2.
9 4 9 4
607. a) x2 -fr 12л: + 36 = л:2 4- 2 * л; * 6 + 62= (л: 4- 6)2;
б) 121 - 22# + #2= l l 2 - 2 * 11 *у 4- #2 = (11 - #)2;
в) 9a2 - 30a6 + 25Ь2= (За)2 - 2 * За •56 + (56)2= (За - 5Ь)2;
г) 16m2 4- 16mn + 4п2 = (4 т )24- 2 * 4 т * 2п4- (2п)2= (4 т 4- 2п)2;
д) 0,25л:2 - л: 4- 1 = (0,5л:)2 - 2 * 0,5л: * 1 4- I2 + (0,5л: - I)2;
е) — а2 +а6 + 962 = ( - а | + 2 ~ а - З Ь + (ЗЬ)2 = [ i a + 3fc| .
36 6 ) 6 ^6 )
608. а) (* 4- Ь)2 = с2 4- 2сЬ 4- Ъ2; (с 4- Ь)2= с2 4- 2с6 4- Ь2;
б) (а 4- *)2 = а2 4- 2 а т 4- *; (а 4- т ) 2= а2 4- 2 а т 4- т 2;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

99. «I) (Зх - *)2 = 9*2 - * + 1; (Зх - I)2= 9х2 - 6х + 1;
г) (* —ЗЬх)2 = * - 6аЬх + *; (а - ЗЪх)2= а 2 - ЬаЬх + 9Ь2я2.
609. а) (а - 5)2 - а(а + 8), если а = 0,5;
(« - 5)2 - а(а + 8) = а2 - 10а + 25 —а2 - 8а = -18а + 25 =
-18 * 0,5 + 25 = -9 + 25 = 16.
6) (Зс + 0,5)2 - (3с - 0,5)2, если с = - ; (Зс + 0,5)2 - (Зс - 0,5)2 = 9с2 +
9
I 2 •3 •0,5 + 0,25 - 9с2 + 2 •Зс •0,5 —0,25 = 6с = 6 - = - = - .
9 9 3
и) (2х —5)2 —4х2 - 20х, если х —0,25;
(2х - 5)2 - 4 х г - 20х = 4х2 - 20х + 25 - 4х2 - 20х = -4 0 х +25 =
- -4 0 •0,25 + 25 = -40 - + 25 = -1 0 + 25 = 15.
4
610. а) (а + б)2 - (а - 3)(а + 3) + 10а = (а2 + 10а + 25) - (а2- 9) +10а =
-- а2 + 10а + 25 - а2 + 9 + 10а = 20а + 34;
б) (2с - I)2 - (2с + 7)(2с - 7) + 5с = (4с2 - 4с + 1) - (4с2- 49 ) + 5с =
- 4с2 —4с + 1 - 4с2 + 49 + 5 = с + 50;
в) (За - 2Ь)2 - (2а - ЗЬ)2 + 562 = (9а2 - 12аЬ + 4Ь2) - (4а2 - 1 2 аЬ + 9Ь2) +
н562 = 9а2 - 12оЬ + 462. - 4а2 + 12аЬ - 962 + 562= 5а2;
г) (4а2 + с)2 + (а2 - 4с)2 - 17а4= 16а4 + 8а2с + с2 + а4 - 8а2с +
+ 16с2 - 17а4 = 17с2.
611. а) 3(2* - уУ - 2(3* - уУ + б*2 = 3(4х2 - 4ху + у2) - 2(9*2 - 6ху + у2) +
Нблг2 = 12хг - 12ху + 3у2 - 18ж2 + 12ху - 2у2 + 6х2= у2;
б) 1,5(ас - 2л:2)2 - 2,5(х2 - 2ас)2 =
- 1,5(а2с2 —4асх2 + 4л"4) —2,5(лс4 —4х2ас + 4а2с2) =
= 1,5а2с2 —бас*2 + 6ж4 - 2,6х* + 10д:2ас —10а2с2= 4асх2 + 3,5х2- 8,5а2с2;
в) 11с2- {х2 + Зс)2 - (Зх2- с)2= 11с2 - (г4 + 6х2с + 9с2) - (9х4- 6 *2с + с2) =
= 11с2 —х* —6х3с —9с2 —9л:4 + 6х2с —с2 - с2 —Юде4;
612. а) (2а - 5)2 —(2а - 5)(2а + 5), если а = 1,5;
(2а - 5)2 - (2а - 5)(2а + 5) = 4а2 - 20а + 25 - 4а2 + 25 = 50 - 20а =
= 50 - 20 •1,5 = 50 - 30 = 20;
б) (6х —2)(6дс + 2) - (6л: - 2)2, если х = 0,5;
(6х - 2)(6х + 2) - (6х —2)2 = 36л:2 —4 —36л2 + 24л: — 4= 24х — 8 =
= 24 •0,5 - 8 = 12 - 8 = 4;
в) 2(х - I)2 + 3(5 - х)2 + 14х, если х = 2;
2(х - I)2 + 3(5 - х)2 + 14х = 2(х2 - 2х + 1) + 3(25 - 10х +х2) + 14х =
= 2х2 - 4х + 2 + 75 - ЗОх + Зх2 + 14х = 5х2 - 20х + 77 =
= 5 •22 - 20 •2 + 77 = 20 - 40 + 77 = 57;
г) 0,5(2с - З)2 + 0,75(с + 4)2, если с = 2;
0,5(2с - З)2 + 0,75(с + 4)2 = 0,5(4с2 - 12с + 9) + 0,75(с2 + 8с + 16) =
= 2с2 - 6с + 4,5 + 0,75с2 + 6с + 12 = 2,75с2 + 16,5 = 2,75 •22 + 16,5 =
= 11 + 16,5 = 27,5.
613. а) (а + Ь)2 + (а - Ь)2 = 2(а2 + Ь2);
(а + ЬУ + (а - Ь)2 = а2 + 2аЬ + Ь2 + а2 - 2а6 + Ь2= 2а2 + 2Ь2= 2(а2 + Ь2);
Тождество доказано.
б) (2а + ЬГ + (а - 2Ь)2= 5(а2 + Ь2);
(2а + ЬУ + (а - 2Ь)2= 4а2 + 4аЬ + б2 + а2 - 4а6 + 4Ь2= 5а2 + бЬ2= 5(а2 + Ь2).
Тождество доказано.
в) (За + ЬУ + (а - ЗЬУ = 10(а2 + 62);
(За + ЬУ + (а - ЗЬУ = 9а2+ 6аЬ + Ь2+ а 2- баб + 9М= 10а2 + ЮЬ2+ Ю(а2 + Щ.
Тождество доказано.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

100. 614. а) (* - 6)2 = *(* - 8); *2 - 12* + 36 = *2 - 8*; -1 2 * + 8* = -3 6 ;
-36
-4 * = -3 6 ; * = ------; * = 9. Ответ: 9.
—4
б) 2(3 - хУ = *(2* + 6); 2(9 - 6* + * 2) = 2*2+ 6*; 18 - 12* + 2*2= 2*2 6*;
—18
—12д: - 6х = —18; —18л: = -1 8 ; х = ------; х = 1.Ответ: 1.
-1 8
в) (2* + 5)2= 4*2 + 21; 4*2 + 20* + 25 = 4*2 + 21; 20* = 21 - 25;
4 1 л 1
20* = -4 ; * = ------ ; * = — . Ответ: — .
20 5 5
г) (1,2* - I)2= 1,44*2- 1,4; 1,44*2 - 2,4* + 1 = 1,44*2 - 1,4;
-2 ,4 * = -1 ,4 - 1; -2 ,4 * = -2 ,4 ; * = -2 ,4 ; (-2,4); * = 1.
Ответ: * = 1.
д) (3* + 8)2= (3* - 4)2; 9*2 + 48* + 64 = 9*2 - 24* + 16;
48 2 2
48* + 24* = 16 - 64; 72* = -4 8 ; * = ------ ; * =— ; Ответ: — ;
72 3 3
е) (6* - 5)2 = 9(2* + I)2; 36*2 - 60* + 25 = 9(4*2 + 4* + 1);
36*2 - 60* + 25 —36*2 + 36* + 9; -6 0 * - 36* = 9 —25; —96* = -1 6 ;
* = —— ; * = —. Ответ: —.
-9 6 6 6
615. а) (* - 5)2 - *(* + 3) = 12; * 2 - 10* + 25 - * 2 - 3* = 12; -1 3 * = 12 - 25;
-13л: = —13; * = 1. Ответ: 1.
б) (Зг + I)2 - 9г(е + 6) = —1; 9г2 + 6г + 1 - 9г2 - 54г = —1; ~48г = -1 - 1;
-2 1 1
-48г = -2 ; г = ------; 2= — . Ответ: — .
-4 8 24 24
в) (0Л у + З)2- (0,2у - З)2= 0,8; 0,04у2 + 1,2у + 9 - 0,04у2+ 192у - 9 = 0,8;
*
2,4у = 0,8; у = У = . Ответ:
2,4 о 3
Г2 (1 , ¥ * Л 4 2 4 , 4 2 1 4
г) —х - 1 = - * + 1 - * ~ 1 ; —* — * + 1 = —* — * + —* - 1 ;
и ) и Д З ) 9 3 3 3 3
4 1 4 _ , 7 _ л ( 7 } 2*3 6
— * + —* * = - 1 - 1 ; — * = -2; * = - 2 : — ; * = ; * = —.
3 3 3 3 ^ 3 У 7 7
0
Ответ:
7
616. а) * 2 + 10* + 25 = 0; (* + 5)2= 0; * 4- 5 = 0; * = -5 .
Ответ: —5.
б) 4Х2 - 12л; + 9 = 0; (2х - З)2 = 0 2х - 8 = 0; 2х = 3; х = х = 1,5.
Ответ: 1,5. ^
в) 1 + 16*2 - 8*2 = 0; 1 + 8*2 = 0; 8*2 = -1 ; * 2 = . Так как * 2 > 0,
1 8
а < 0, то данное уравнение не имеет решений.
8
Ответ: корней нет.
г) ^ * 2+1 + л: = 0; + 2 * ^ * 1 + 12 = 0; ^ * + 1^ = ®*
^ * +1 = 0; —* = -1; * = -1*2; * = -2.
2 2
Ответ: -2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

101. Л) * - 9 ~ — * 2 =0; - ( — * 2 - * + 9І = 0; ( - х ) - 2 - х -3 + 32 =0;
36 и « ; 1б ; в
( - * - з 1 =0; і х - 3 = 0; —х = 3; х - 3-6; х = 18.
и ; 6 6
Ответ: 18.
0) 2* + 25 + 0,04л:2= 0; (0,2*)2 + 2 •0,2 * »5 + 52= 0; (0,2* + 5)2= 0;
0,2* + 5 - 0 ; 0,2* - —5; * = —5 : 0,2; * = -2 5 . Ответ: -2 5 .
617. а) I I 2 = (10 + I)2= 102 + 2 « 10 * 1 + I 2 = 100 + 20 + 1 * 121;
Г>) 992= (100 - I)2= 1002- 2 •100 * 1 + I 2= 10000 - 200 + 1 = 9801;
.і) 1012= (100 + I)2= 1002 + 2 * 100 * 1 + I 2 = 10000 + 200 + 1 = 10201;
1) 2022 = (200 + 2)2 = 2002 + 2 * 200 •2 + 22 = 10000 + 800 + 4 = 40804;
д) 522 = (50 + 2)2= 502 + 2 * 20 * 2 + 22 = 2500 + 200 + 4 = 2704;
«) 612 = (60 + I)2- 602 + 2 * 60 * 1 + I2 = 3600 + 120 + 1 = 3721;
ж) 792 = (80 - I)2= 802 - 2 * 80 * 1 + I2= 6400 - 160 + 1 = 6241;
і) 812 = (80 + I)2= 802 + 2 •80 ♦ 1 + I2= 6400 + 160 + 1 = 6561.
618. Так как * 2 = (~*)2 (квадраты противоположных чисел равны), то
а - Ъ = а + Ъ; -Ь = Ъ; -2 Ъ~ О; Ь = О.
Ь = О, а — любое число.
или а - Ъ= -(с + 6); а - Ь = - а - Ь; 2а = О; а = 0;
а = О, Ь — любое число.
Ответ: при о = О, Ь — любое число, при Ь = О, а — любое число.
619. При достаточно малых значениях а значение а2< |а|.
Тогда (1 + а)2= 1 + 2а + а2 = 1 + 2с.
и) (1 + 0,001)2* 1 + 2 »0,001 = 1,002;
б) 1,0032= (1 + 0,003)2» 1 + 2 * 0,003 = 1,006;
в) 0,992= (1 - 0,01)2 « 1 - 2 * 0,01 = 0,98;
г) 0,9982 = (1 - 0,002)2« 1 - 2 - 0,002 = 0,996.
620*. а) Если с > 0 и Ь > 0, то (с + Ь)2 > а2 + Ь2.
(а + Ь)2 - а2 - Ь2 = а2 + 2а6 + Ь2 - а2 - Ь 2= 2аЬ.
Так как с > Ои Ъ > О, то 2аЬ > О. Значит, (с + Ь)2 > с2 + б2.
б) Если с и Ъ — произвольные числа, то (с + Ь)2 > 2аЪ.
(а + Ь)2 - 2аЪ + с2 + 2аЬ + Ъ2 - 2аЬ = с 2 + Ь2.
Так как с и Ь — произвольные числа, то с 2> Ои Ь2> 0, значит с2+ Ъ2> О.
Значит, для произвольных чисел с и Ь (с + Ь)2> 2аЬ.
в) Если сумма двух чисел делится на 2, то делится на 2 и сумма их ква­
дратов. Если сумма двух чисел делится на 2, то сумма этих чисел являет­
ся числом четным. Это возможно, если оба числа с и Ь или четные, или
оба числа с и &не четные.
Если с и Ь — четные числа, то с 2 и Ъ2 —четные числа, значит а2 + Ь2 —
число четное, а значит делится на 2.
Если с и Ь — нечетные числа, то а2и Ь2 — нечетные числа, значит а2+ Ь2 —
число четное, а значит делится на 2.
г) Пусть а, Ь, с, й данные натуральные числа, при этом а < Ъ < с < й
и с + сЕ= 6>+ с.
621. Докажем, что квадрат нечетного числа, уменьшенный на 1, делится
на 8. Если число нечетное, то при делении на 2 в остатке получим 1.
Значит в общем виде нечетное число можно записать в виде 2п + 1, где
п - 0; 1; 2; .... (2с + I)2 - 1 = 4с2 + 4п + 1 - 1 = 4с2 + 4п = 4с(л + 1).
Один из множителей с или п + 1 является числом четным, значит делится
на 2. Значит число 4с(с + 1) делится на 8.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

102. «е
ф
«4
а ь С
Если л = О, то 4л(л 4- 1) = О, а — делится на любое число.
Значит квадрат нечетного числа, уменьшенный на 1, делится на 8.
622. Докажите, что сумма квадратов трех последовательных целых чисел не
делится на 3. Пусть л - 1 , л и л + 1 — три последовательных целых числа.
Тогда (л - I)2 4- л2 + (л + I)2= л2 - 2л + 1 + п2 + л2 4- 2л 4- 1 = Зл2 + 2.
Зл2 — делится на 3, а 2 на 3 не делится, значит Зл2 + 2 на 3 не делится.
Значит, сумма квадратовтрех последовательных целых чисел на 3 неделится.
623. Докажем тождество (а + Ь + с)2 = а2 + Ь2 + с2 + 2аЪ + 2ас + 2Ьс.
I способ, (а + Ь 4- с)2 = (((а 4- Ь) + с)2=
= (а + Ь)2 + 2(а + Ь)с + с2= а2 4- 2аЬ + Ь2 4- 2ас 4- с
4- 2Ьс 4- с2= а2 4- Ь2 4- с2 4- 2аЬ 4- 2ас 4- 2Ъс.
I I способ. (а + Н с ) 2=(а + Ь+ с)(а 4- Ь + с) =
= а2 4- аЬ 4- ас + Ъа 4- Ь2 + Ьс 4- са 4- сЪ 4- с2=
= а2 4- Ь2 4- с2 4- 2аЬ 4- 2ас + 26с.
Стороны квадрата разделим на отрезки длиной а, Ь о,
и с. Через концы полученных отрезков, перпенди­
кулярно к сторонам данного квадрата проведем от­
резки, которые разделяют квадрат на 9 частей: три квадрата со сторонами
с, Ь и с; два прямоугольника со сторонами а и Ь; два прямоугольника со
сторонами а и с; два прямоугольника со сторонами Ь и с;
Площадь данного квадрата считается па формуле 5 = х2, где х — сторона
квадрата равняется (а 4- Ь + с)2. С другой стороны площадь фигуры рав­
няется сумме площадей его частей. Имеем площади квадратов: 5 1 = а2;
£ 2= Ь2; £ 3 = с2. Площади прямоугольников: 5 4 = аЬ; Б5 = ас; £ 6 = Ьс.
Значит площадь данного квадрата равняется
8 14- 5 2 + 4- 2вл 4- 23,. + 2£6 = а2 4 Ь2 4* с2 4- 2аЬ + 2ас 4 26с.
Имеем: (а + Ь + с)2= а2 4- 62 4- с2 4- 2аЬ + 2ас 4* 2Ьс.
6 2 4 . а) (х - у 4- 5)2= ж2 + у2 4- 52 - 2ху 4- 2х * 5 - 2у * 5 =
= х2 4- у2 4- 25 - 2я;у 4- 10ж —10у;
б) (х 4- 2у 4- Зг)2= ж2 4- (2у)2 + (Зг)2 4- 2ж * 2і/ 4- 2х • Ъг 4- 2
= х2 4- 4у2 4- 9г2 4- 4ху 4- 6x2 4- 12уг;
в) (х + у2 + г3 )2= ж2 4- (у2)2 4- (г3)2 + 2ху2 4- 2хг3 4- 2у2г 3=
= дс2 4- у4 4- г6 4- 2лту2 4- 2хг3 4- 2у2г3.
625. а) (хп4- I)2= (хп)2 4- 2хп * 1 + I2 = х2п 4- 2хп 4- 1;
б) (а2т- I)2= (а2т)2 - 2 «а 2т* 1 + I 2= а4т~ 2а2т4- 1;
в) (ап 4- ат)2 = (ал)2 4- 2апат4- (ат)2= а2п + 2ап'*т4- а 2т;
2у •3г
г) (хп1
Д)
х)2 = (ж”" *)2 4* 2хп~1* X 4- х2
^ 2
х2п '2 4- 2дсп4- дс2;
[| (у га+ / т)] = [| ] ((У")" + 2|Г|Г + (У2”)2) =
= + 2г/3" + у--) = і у2™+ і І/3™+ І і,“ ;
е) ( І (6" - 2Ь2)]2 = [ І ] " ((*■ )2 - 2 -6” -2Ь2 +.(2Ь2)2) =
1« V
-2п 4^«+2
1 6 4 7 16
626. Задача Ал-Кархи (XI в.).
Если а = т л , то покажите, что
4іі4) = — Ь2п- - Ь " <2+ - 6 4/ 1Я
1
4
всегда ква­
драты определенных выражении.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

103. ( т “ л V
2 /
т2- 2тл + п2 т2 —2тл + /г2+ 4тл
+ а = --------------------- нтл = -------------------------------
т2 + 2тп + л2 Ґ т + лV
_ Т ~ Н :4
2 т 2+ 2т л + п2 т2 + 2тп + п2- Атп/ т + /Л
- т - ) - а =
пг2 - 2тп + п2
тп =
( т - п V*
Г Г ;
л^ Г т + л^ ( т + л^ Ґ т - л ^
і 2 - } + а Л — ) Л — ) - а = Ь г )
Что и тр еб о вал о сь д о к а за т ь .
627. Задача Лагранжа. Проверьте тождество:
(Л2 + В2+ С2КА,2+ В,2+ С,2) - (А -Л, + В ■В, + С •С,)2=
(АВ, - А,В)2+ (АС, - А,С)2+ (ВС, - В,С)3;
Упростим левую часть равенства:
(Л2+ В2+ С2)(А,2+ В ,2+ С,2) - (А •А, + В •В, + С - С,)2=
А2А,2+ А2В,2+ А2С,2+ В2А,2+ В2В,2+ ВгС,2+ С2А,2+ С2В ,2+
і С2С,2- (А2А,2+ В2В,2+ С2С,2+ 2АА, •ВВ, + 2ЛА, - СС, + 2ВВ, •СС,) =
А2А,2+ А2В ,2+ А2С,2+ В2А,г + В2В,2+ В2С,2+ С2А,2+ С2В ,2+
і СгС,2- А2А,2- В2В ,2- С2С,2- 2АА, •ВВ, - 2АА, •СС, - 2ВВ, - СС, =
(А2•В,2- 2АА, •ВВ, + В2•А,2) + (А2С,2- 2АА, •СС, + С2■А,2) +
I (В2•С,2- 2ВВ, - СС, + С2•В ,2) = (А - В, - А, •В)2+ (А - С, - А, •С)2+
I (В •С, —В, •С)2. Значит, тождество верное.
628. Докажем формулу куба двучлена.
(« + Ь)3= (а + Ь)2(а + Ь) = (о2+ 2аЪ + Ь2)(а + Ь) =
а3 + а2Ь + 2а 2Ь + 2аЬ2 + Ь~а + Ь3= о3+ За2Ь + Заі>2+ Ь®.
(г» - Ь)3= (а - Ь)2(а - Ь) = (а2- 2аЬ + Ь2)(а — Ъ) =
а 3 - а 2Ь —2аЧ> + 2чЬ2 + Ь2а —Ь3= о3—За2Ь + За6г —63.
и) (х + З)3= л3+ 3 •х2 - 3 + 3 - х - З2+ Зэ = х3+ 9х2+ 27х + 27;
б) (4а + с)3= (4а)3+ 3 •(4а)2■с + 3 •4а - с2+ с3= 64а3+ 48а2с + 12ас2+ с3;
и) (І —ахУ = I 3 - 3 ■I 2 •(ах) + 3 •1•(ах)2—(ахУ = 1- Зах + За2х2- а3! 3.
г ) (то 2 + 2ас)3= ( т 2) 3 + 3 • ( т 2) 2 • 2ас + 3 • т 2 -.(2ас)2+ (2ас)3=
<71° + 6т4ас + 12т 2а2с2+ 8а3с3;
л) (х - у)3 = х3- 3х2у + 3ху2 - у3;
= — с3——с2х2+ с х - х 6.
27 3
П29. я) (х + 2У = х3+ Зх2•2 + Зх •22+ 23= х3+ 6х2+ 12х + 8;
б) (у - 2У = у3 - 3 ■у2 - 2+ 3 - у - 22- 23= у3- 6у2+ 12у - 8;
и) (2х - I )3= (2х)3- 3 •(2х)г •1+ 3 •2х •I2- I3= вх8- 12х2+ 6х - 1;
і) (Зх + I )8= (Зх)3+ 3 - (Зх)2- 1 + 3 •Зх •I2+ I3= 27х3 + 27х2 + 9x4- 1;
л) (т - 2пУ = то3—3 •т2■2п + 3т - (2в)2—(2п)8= т 3- 4т2п + 12тп - 8и3;
<•>(2а + ЗУ = (2а)3+ 3 •(2а)2•3 + 3 •2а •З2+ Зэ = 8а8+ 36а2 + 54а + 27.
030. а) а3- За2+ За - 1 = а3- 3 •а2- 1 + 3 •а •I2- I3= (а - I)3;
о) Ну3- 36у2 + 54у - 27 = (2уУ - 3 ■(2уУ •3 + 3 •2у ■З2- З3= (2у - ЗУ;
и) 27хг3+ 108х2+ 144х + 64 = (Зх)3+ 3 •(Зх)3- 4 + 3 - Зх •42+ 43= (Зх + 4)3;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

104. г) о9- 15свЬ + 75а362- 125Ь3= (а3)3- 3 - (а3)2- 56 + 3 •а3(56)2 - (56)3 =
= (а3- 5Ь)
6 3 1 . а) (а + 6)3= а9 + 63+ За6(а + 6).
(а + 6)3= а3+ За*6+ ЗаЬ2+ 63= а3 + 63+ 3а6(а + 6). Тождество доказано,
б) (а - 6)3= а3- 63+ 3а6(с - 6).
(а - 6)э = а3 - 3а26+ 3аб2- Ь3 = а3- 63+ За6(а - 6). Тождество доказано.
632. Пусть а ± 6делится на 3, где а и 6— натуральные числа.
Пусть а и 6натуральные числа, такие, что их сумма а + Ь [разность а - Ъ
делится на 3. Докажем, что и а3+ 63[а3—63] также делится на 3.
Разложим на множители:
а3 + 63= (а + Ь)(а2 - аЬ + 62), [а3- Ь3 = (а - 6)(а2+ аЬ + 62)].
Один из множителей полученного произведения равняется а + Ъ [а - Ь
и делится на 3, а значит, и произведение, а значит, и с3+ Ь3 [а3- 63] со­
ответственно также делится на 3.
633*. Пусть п - 1 , п и п + 1 — три последовательных натуральных числа, где
л = {2; 3; 4 ; тогда (л - I )34- п9+ (л + I )3— делится на 3. Докажем это.
(л —I )3+ п3+ (л + I )3= п3 —3л2+ Зл —1+ п3 + п3 + 3п2 + Зл + 1= Зл3+
+ 6л = З(л3+ 2л). В полученном произведении один из множителей равня­
ется 3, значит произведение делится на 3. Что и требовалось доказать.
6 3 4 . а) (2о + Зс)3= (2а)а + 3 *(2а)2* Зс + 3 * 2а - (Зс)2+ (Зс)3=
= 8а3+ 36а2с + 54ас2+ 27с3;
б) (аЬ + 0,1с)3= (аб)3+ 3 *(аб)2* 0,1с+ 3аЬ •(0,1с)2+ (0,1с)3=
= а3Ь3 + 0,3а262с + 0,03а6с2 + 0,001с3;
в) (0,2с3- I)3= (0,2с3)3- 3 •(0,2с3)2* 1+ 3 * 0,2с3* I 2- 13=
= 0,008с9 - 0,12с0+ 0,63- 1;
е) (~аЬ2с3 - а2)3= -(аЬ2с9 + а2)3= -((а62с3)3+ З(а62с3)2* а2+
+ 3 * аЬ2с3•(а2)2+ (а2)3) = - а 366с9- За464с6- 3а562с3- а®.
635*. а) (* - I )3= х2(х - 3 ) ; х э - 3 х 2 + 3 х - 1 = х3 - Зх2; Зх - 1= 0;
Зх = 1; х =
3
б) (х + I )3= х3 + Зх2 + 2; х* + Зх2 + Зх + 1 = х3 + Зхг + 2; Зх = 2 - 1;
Зх = 1; х = ~.
3
636*. а) (* - 2)3+ 6х2= (* - 2)(х2 + 2х + 4);
х3 - блг2+ 12* - 8 + 6*2= х? + 2х2+ Ах - 2х2- Ах - 8;
х3 + 12* - 8= х3 - 8; 12* = 0; х = 0.
Ответ: 0.
б) (х + 2)3- 6х2= (х + 2)(х2 - 2х + 4);
зс9 + 6х2 + 12дс + 8- 6х2 = х3 - 2х2 + Ах + 2х2- Ах + 8;
х9 + 12* + 8= х3 + 8; 12* = 0; * = 0.
Ответ: 0.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

105. Упражнения д ля повторения
037. а) (За2+ 2а + 7) + (а3- 2а2+ а - 3) = За2+ 2а + 7 + а3- 2а2+ а - 3 =
а* + а2+ За + 4;
б) (1 ,5 * —х2- от3) + (2,5л:4- 1,5л:3- 2 * + 3 ) = 1,5л: - * 2 - л;3 + 2,4л:4- 1,5л:3-
2х + 3 = 2,5лґ* - 2,5л:3 - л:2 - 0,5л: + 3.
039. Так как игровой кубик имеет шесть граней,то количество возможных
нприантов падения кубика — шесть 1, 2, 3, 4, 5 или 6.
и) четных чисел на гранях кубика три: 2; 4; 6.
Значит, вероятность того, что при падении игрового кубика выпадет чет-
3 1
ное число очков, равняется —= —.
б) нечетных чисел на гранях кубика три: 1; 3; 5.
Значит, вероятность того, что при падении игрового кубика выпадет не-
3 1
четное число очков, равняется —= —.
6 2
и) чисел, кратных трем, на гранях кубика два: 3 и 6.
Значит, вероятность того, что при падении игрового кубика выпадет число
2 1
очков, кратное трем, равняется —= —.
г) чисел, кратных 5, на гранях кубика одно: 5.
Значит, вероятность того, что при падении игрового кубика выпадет число
* 1очков, кратное 5, равняется — .
640. Если путь, пройдений автомобилем, составляет 300 км, его скорость —
300
о км/ч., а время — t ч., то v * t = 300. Значит, v = ------.
300
Коли t увеличить в 2 раза, то дробь ----- уменьшится в 2 раза. Значит,
£
значение і? уменьшится в 2 раза. Аналогично: если t увеличить в 3 раза, то
v уменьшится в 3 раза, если t увеличить в 4 раза, v уменьшится в 4 раза.
б 17. Разность квадратов
646. а) (2а)2- (5*3)2; б) (2а - 5л:3)2; в) (2а)2+ (5л;3)2; г) (2а + 5л^)2.
647. а) (2аЬ)2- (а - Ь)2; б) (2аЬ - (а - Ь))2.
648. а) (4а + 1)(4а - 1) = (4а)2- I 2= 16а2 - 1;
6) (2а - с)(2а + с) = (2а)2- с2= 4а* - с2;
н) (2d + x)(2d - л:) = (2d)2- л:2= 4d2' - л;2:
г) (а - с2)(а + с2) = а2—(с2)2= а2—с4;
д) (8л: - у2){8х + у2) = (8*)2- (у2)2 + 64*2 - уА;
р) (2а2+ ЗЬХ2а2- зЪ) = (2а2)2- (ЗЬ)2= 4а4- 9Ь2.
649. а) (Зр - q)(q + Зр) = (Зр)2- q2 = 9р2 ~ q2;
6) (т - 4c2)(m + 4с2) = т2 - (4с2)2= т2 - 16с4;
її) (л:2+ у2)(х2 - у2) = (х2)2 - (у2)2= л:4- у4;
г) (т2 - п2)(т2 + п2) = ( т 2)2- (а2)2= т 4~ п4;
д) (4а - Ь3)(4а + Ь3) = (4а)2- (б3)2= 16а2 - Ь6;
<*) (5 + аЬс)(5 - а&с) = 52- (аЬс)2= 25 —а2Ь2с2.
« » . „ ( l . - . j g , * . ) . ( § , J - r 4•х2 -1*
9 '
г,) ( г ^ ) ( | с + р ) = ( 1 с ) - р 2 = г г - р2!
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

106. в) (0,4а - *)(0,4а + х) = (0,4а)2- х2 - 0,16а2 - х2;
г) (1,5 - т 2)(1,5 + т2) = 1,52- ( т 2)2= 2,25 - т
651. а) 2(4* - 1)(4х + 2) = 2((4х)2- I2) = 2(16ж2 - 1) = 32х2 - 2;
б) k(m 2 - 2pt)(m2 + 2pt) = k((m2)2 - (2pt)2) = k{m4 - 4p2t2) = km4 - 4kp2tz;
в) (2q - czn)(2q + cAn) = (2q)2 - (c3n)2= 4q2 - c6/i2;
r) (0,5 + 2a)(0,5 - 2a) - 2c2= (0,52- (2a)2) - 2c2= (0,25 - 4a2) * 2c2=
- 0,5c2- 8a2c2.
652. a ) ^ - 46j •4a = | ^ aj - (4bfj •4a = ^ a 2- 16b2j •4a = ^a3- 64ab2
+ 2rcj-5m - j^ m ^ - {2 n f j •5m - - 4n2j •5m =6)
4
= —m3 —20mn2;
5
в) 7a2(l + 3a26)(l - 3a2b) = 7a2(l2- (3a2b)2) = 7a2(l - 9a4i>2) = 7a2- 63ae62;
r) -cq(c + 2q){c - 2q) = -cq(c2—(2q)z) = —cq(<? - 4(f) = -c 3g + 4eg3= 4CQ3- c3^.
653- a) (a - 2b)(a + 26) + 462= a2- (2b)2+ 462= a2- 462 + 462= a2;
б) (m2+ Sy)(m2 - 3y) - m4= (m2)2- (3y)2 - m4= m4- 9у2- m4= -9i/2;
в) c2—(c —l)(c + 1) = c2- (c2- 1) = c2- c2+ 1= 1;
r> [ a - —c2)(a + —c2l + —c4 = a2 - f —cl + - c 4 = a2 - - c * + - c 4 =
I 3 Д 3 J 3 U > / 3 9 3
2 1 4 , ® 4 _ а , ^ 4
= a ——с н— с = a -i— c .
9 9 9
6 5 4 . a) (x - 3)(x + 3)(x2 + 9) = (x2 - 9)(x2 + 9) = (x2)2 - 92 = x4 - 81;
б) (m + 5 )(m - 5)(m2 + 25) = (m2 - 25)(m2 + 25) = (m2)2 - 252= m4 - 625;
в) (4a2 + l)(2a + l)(2a - 1) = (4a2 + lM4a2 - 1) = (4a2)2 - l 2= 16a4 - 1;
r) (9j/2 - z2Mz + Hy)(3y - z) = (9y2- z2)(9y2 - z2) = (9у2 - г2)2=
= (9j/2)2 - 2 •9j/2 •z2 + (z2)2 = 81(/4 - 18j/2z2 + z4.
6 5 5 . а) (-дс - y) ■(~x + y) = -1 •(x + y) •(-1X * - y) = (x + y)(x - y) = x2 - yh
б) (-1 + 3a) •(-1 - 3a) = -1 - (1 - 3a) •(-1)(1 + 3a) = (1 - 3a)(l + 3a) = 1 - 9a2;
в) (-2a + 3b) ■(-2a - 36) = -1 ■(2a - 3b) •(-l)(2a +3b) =
= (2a - 36)(2a + 36) = 4a2 - 962;
r) (-c - 7)(7 - c) = -1 •(c + 7) - (-l)(c - 7) = (c + 7)(c - 7) = c2 - 49;
д) (-0 ,5 - 2^ )(-0,5 + 2JC1) = -1 •(0,5 + 2x4) •(-1)(0,5 - 2x*) =
= (0,5 + 2x4(0,5 - 2x4) = 0,25 - 4**;
е) (3,5 - xy) •(-дcy - 3,5) = -1 •(xy - 3,5) •(-l)(xj/ +3,5) =
= (xy - 3,5)(xy + 3,5) = x2y2 - 12,25.
656. a) (5m - *)(5m + *)= 25m2 - 9a2b2; 25m.2 - 9a262= (5m - 3a6)(5n + 3a6);
Ответ: 3a6.
б) (4a - *X* + 3x2) = 16a2 - Эх4; 16a2 - 9jc4= (4a - 3*2)(4a + 3x2).
Ответ: Зле2; 4a.
6 5 7 . а) x 2 —m2 = {x - mXx + m); 6) a2 - 9 = a2 —32= (a - 3)(a + 3);
в ) б2- с4= б2- (с2)2= (6- с^Ь + с2); г) 1 - 16z2= I2- (4z)2= (1 - 4zKl + 4z);
д) q2- р?п2= (q - ря)(? + рп); е) 0,04 - х2 - (0,2)2- х2- (0,2 - х){0,2+ х);
„ 1 2 4 • Y 2 Г 1 V 1 'I
ж) - а - т = 1 —a -m = 1—в -m - a + m|;
4 u ; u Д 2 j
з) -c 4 + 9a2 = (3a)2 - (c2)2 = (3a - c2)(3a + c2).
658. а) 352 - 152 = (35 - 15)(35 + 15) = 20 - 50 = 1000;
б) 432 - 272= (43 - 27)(43 + 27) = 16 •70 = 1120;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4bo
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

107. Il) I362- 642= (136 - 64)(136 + 64) = 72 * 200 = 14400;
r) 51,52- 49,52= (51,5 - 49,5)(51,5 + 49,5) = 2 * 101 = 202;
д) 21,8а - 1,32= (21,3 - 1,3)(21,3 + 1,3) = 20 * 22,6 = 452;
,, Ґ3 —■')2- f l —Y = Гз ——1—1 [ з —+ 1—1 = 2— 5 = —-5 = — = 11—.
I 3j і 3 з д 3 3j з з з з
059. а) 104 * 96 = (100 + 4)(100 - 4) = 1002 - 42= 10000 - 16 = 9984;
ft) 1007 * 993 = (1000 + 7)(1000 - 7) = 10002- 72= 1000000 - 49 = 999951;
її) 0,95 * 1,05 = (1 - 0»05)(1 + 0,005) = І 2 - 0,052= 1 - 0,0025 = 0,9975.
ООО. а) (2abc - Saz)(2abc + За2) = (2abc)2 - (За2)2= 4а2&2с2- 9а4;
6) (5дс3- ЗаЬс)(5дс3+ 3abc) = (5*3)2- (ЗаЬс)2= 25*6 - 9а2Ь2с2;
її) (4аЬ2+ 5ас)(4аЬ2—5ас) = (4аб2)2- (5ас)2= 16а2Ь4 - 25а2с2;
і*) (8jcz3+ 3z2)(3z2—8*z3) = (3z2)2- (8*z3)2= 9z4- 64*2z6.
661. n) (0,2ах —1,2а#ХО,2а* + 1,2а#) = (0,2a*)2—(1,2a#)2—0,04a2* 2- 1,44a2#2;
fi) (-За + 5*2#)(3a + 5*2#) = (5*2#)2- (3a)2= 25* 4#2- 9a2;
1,2 - 4
- V - l a V ;
4 c2;
( I 2 Л ( I Y (2 2 y 1
и) —a x az = —ax - ~ а г = —a ‘
12 3 ) {2 ) U ) 4
, Л 1 1 V I „1 Y (3 Y (7 Ÿ 9 2 49 2 „ 1 2 _
r) 1—a - 2 —с 1—a + 2 —с = —a - —с = —a с = 2 —a - 5
(2 3 2 3 J U J U ) 4 9 4 9 .
662. a) ( - 3x +#2X~3* - #2) = (-1X3* - y2) •(-1X3* + #2) = (3*)2- (#2)2= 9л:2- y*;
f»)(-0,5ас + 1,1с2)(-0,5ас - 1,1c2) = (-1)(0,5ас - 1,1c2) *(-l)(0,5ac + 1,1c2) =
(0,5ac)2- (1,1c2)2= 0,25a2c2 - 1,21c4;
ii) (~2a*2- За2*)(-2а*2+ За2*) = (-1)(2а*2+ За2*) * (-1)(2а*2- За2*) =
(2а*2)2—(За2*)2= 4а2*4- 9а4* 2;
= f —e c Y - f —e*Y = - a 2c3~ - a 4= 2 - а гс2- - а * .
U ) u ) 4 9 4 9
063. a) (0,5a - 0,4b)(0,5a - 0,4b) •2ab = (0,5a - 0,4b f ■2ab =
(0,25a2- 2 •0,5a •0,4£> + 0,16b2) •2ab = 0,5a3b -0 ,8 a 2b2+ 0,32ab3;
fi) I0x2y(0,2x + 2y)(-0,2x + 2y) = 10x2y((2y)2 - (0,2 x f) =
10*2#(4#2- 0,04*2) = 40*2#3 - 0,4*4#;
н) ( г ^ В * +И И **)=( ( Н - ( H )
= (~9xy) = 4xy3 - x 3y,
" ( l | a 2b + l ) [ 1 - 1| a 2b] (-4b) = f ls - ( | a 2b] -(-4b) =
= f1 - 1a V j•(-4b) = 9 a V - 4b.
004. a) (a - 2)(a + 2) (a2+ 4) = (a2- 4)(a2 + 4) = a1 - 16;
fi) (ab - c)(ab + c)(o2b2+ c2) = (a2b2- c2)(a2b2+ c2) = a4b4- c4;
n) (3r * + y)(3x2 —j/)(9a:4+ yz) = (9зе4- y2)(9ar4+ y2) = 81лс®- y1;
r) (16a4c2 + 9xr')(4a2c —3x3)(4a2c + 3jcs) = (16a4c2 + 9зс6)(16а4с2 —9xe) =
256a»c4 - від:12.
005. a) (2x2- l)(2ar2+ 1)(4*4+ 1) + 1 = (4x4- 1K4X4+ 1) + 1=
I6jcb- 1+ 1= 16ace;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

108. б) (ОД - 2с)(0Д + 2с)(0,01 + 4с2) + 16с4 = (0,01 - 4с2)(0,01+ 4с2) + 16с4 =
= 0,0001 - 16с4 + 16с4 = 0,0001;
в) 16а4 - (2а - с2)(2а + с2)(4а2+ с4) = 16а4 - (4а2- с4)(4а2+ с4) =
= 16а4 - (16а4 - св) = 16а4 - 16а4 + с8= с8;
= - — { — - 81а8*>41 = — + 81ав64 = 81а8Ь4.
16 Ц б ) 16 16
666. (2а*хг + Ь3) •М = 4а8*4- Ье;
(2а4*2+ Ь3) - М = (2а4*2)2- (Ь2)2;
(2а4*2+ Ь3) •М = (2а4*2- 63)( 2а4*2+ Ь3);
М = 2а4*2- Ъ3.
Ответ: 2а4х2- Ь3.
667. (0,1х21/ - 2ху2) *М = 0 ,0 1 * У - 4х2уА;
(0,1х2у - 2ху2) •М = (ОД*2*/)2- (2ху2)2;
ОДж2*/ —2*у2) •М = (0Д *21/ - 2ху2)(0,1х2У + 2*у2);
М = 0Д *2у + 2*у2.
Ответ: 0,1 х2у + 2*у2.
6 6 8 . а) 0,04*в - 1 = (0,2*8)2- I2= (0,2*8- 1)(0,2*3+ 1);
б) ~х2у4 + а6Ьв = (сэЬ4)2- {ху2)2 = (а3Ь* —ху2)(агЬъ + ху2);
в) а2Ь2с2 - 121*в= (аЬс)2 - (I I *3)2= (аЪс - 11х*)(аЬс + II * 3);
д) -6 4 + 3 6 т 4л2= (6т2п)2 —82= (6т 2п —8) (6т 2д + 8);
е) а2 - (Ь + с)2= (а - (Ь + с))(а + (Ъ + с)) = (а - Ь - с)(о + Ь + с).
669. а) 602 + 8992= 9012; 602 = 9012 - 8992; 602 = (901 - 899)(901 + 899);
602 = 2* 1800; 602 = 3600; 602= 602.
Значит, данное равенство верно.
б) 652 + 21122= 21133; 652 = 21132 - 21122;
652 = (2113 - 2112)(2113 + 2112); 652= 1 - 4225; 652 = 652.
Значит, данное равенство верно.
670. а) 102+ I I 2+ 122= 132 + 142; 102= 132 - 122+ 142 - I I 2;
102= (13 - 12)(13 + 12) + (14 - 11)(14 + 11);
102= 1 * 25 + 3 * 25; 102= 25 -4 ; 102= 102.
Значит, данное равенство верно.
б) 212+ 222+ 232 + 242= 252 + 262 + 272;
242 = Д72- 212+ 262 - 222+ 252 - 232;
242 = (27 - 1)(27 + 1) + (26 - 22)(26 + 22) + (25 - 23)(25 + 23);
242 = 6 * 48 + 4 •48 + 2 •48; 242= 48 *<6+ 4 + 2);
242= 24 ♦2 * 12; 242 = 242.
Значит, данное равенство верно.
671. 362 + 372+ 382 + 392+ 402= 412 + 422 + 432;
Найдем последние цифры обоих выражений:
последняя цифра
362 6
372 9
382 4
392 1
402 0
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

109. 6 + 9 + 4 + 1 + 0 = 20.
последняя цифра
412 1
422 4
432 • 9
Значит, последняя цифравыражения, которая стоит в левой части равенства,
равняется 0.
1 + 4 + 9 = 14. Значит, последняя цифра выражения, которая стоит в правой
части равенства, равняется 4. Так как 0 э* 4, то данное равенство неверно.
672. а) (л + 5)2- л2= л2+ Юл + 25 - п2= Юл + 25 = 5(2л + 5).
Один из множителей в произведении равняется 5, значит, произведение
делится на 5. Значит, (л + 5)2—л2делится на 5.
б) (л + 7)2—л2= л2+ 14л + 49 —л = 14л + 49 = 7(2л + 7).
Один из множителей в произведении равняется 7, значит, произведение
делится на 7. Значит, (л + 7)2- л2делится на 7.
в) (6л + I )2- 1 = 36л2 - 12л + 1 - 1 = 36л2 - 12л = 12(3л2- л).
Один из множителей в произведении равняется 12, значит, произведение
делится на 12. Значит, (6л + I)2 - 1 делится на 12.
673. Пусть ОВ = х см, тогда ОА = (х —3) см. Тогда площадь кольца равняется
пх2= тг{х —З)2= п(х2~ (х —З)2) (см2). Зная это, составляем и решаем урав­
нение. (При этом х < 3).
п(х2 ~ { х - З)2) = 18,84; *2- (х - 3)2= 18,84 : 3,14:
15
х0 - х 0 + %х - 9 = 6; 6# = 15; х = — ; х = 2,5.
2 2 6
ОВ = 2,5 см, тогда ОА = 2,5 - 3 = - 0,5 (см).
81
675. а) (9 - + 9) = - х 2+ 3*; 81 - х2= -ж2+ Зх; Зх = 81; х = — ; х = 27.
3
Ответ: 27.
б) z2 = 2z - (z + 3)(3 - z); г2= 2z - (9 - z2); z2= 2z - 9 + z2; 2z = 9;
9
г - —; z = 4,5. Ответ: 4,5.
9
9 1 1
в) 4jc2+ 9 - 4х2 + 81#; 81* = 9; х = — ; х - —. Ответ: —.
81 9 9
г) 9Ь2 - (2 - ЗЬ)(2 + ЗЬ) = -4 ; 9Ь2 - 4 + 9Ь2= -4 ; 18Ь2= 0; Ь2 = 0; Ь = 0.
Ответ: 0.
676. (р2+ I )2- (р2- I )2= ({р2 + 1) - (р2- 1))((Р2+ 1) + (Р2 - 1) =
= (р2 + 1 - р2 + 1)(р2+ 1 + р2 - 1) = 2 * 2р2= 4р2. Тождество доказано.
677. (2а2+ 2а + I )2- (2а2+ 2а)2= (2а + I)2,
(2а2+ 2а + I )2- (2а2+ 2а)2= ((2а2+ 2а + 1) - (2а2+ 2а))((2а2+ 2а + 1) +
+ (2а2+ 2а)) = (2а2+ 2а + 1- 2а2- 2а)(2а2+ 2а + 1+ 2а2+ 2а) =
= 1 *(4а2+ 4а + 1) = (2а + I)2. Тождество доказано.
678. Докажите, что каждое нечетное натуральное число, большее, чем 1, яв­
ляется разностью квадратов двух последовательных натуральных чисел.
Пусть л и л + 1 — два последовательных натуральных числа.
2л + 1 = 2л + 1 + л2—л2= (л2+ 2л + I2) - л2= (л + I )2—л2. Значит, каж­
дое нечетное натуральное число, большее* чем 1, является разностью двух
последовательных натуральных чисел, что и требовалось доказать.
679. Докажите, что сумма двух последовательных натуральных чисел рав­
няется разности их квадратов. Пусть л и л + 1 — последовательные нату­
ральные числа. Тогда л + (л + 1) = (л + I )2- л2;
2л + 1 = л2+ 2л + 1 - л2; 2л + 1 = 2л + 1. Утверждение доказано.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

110. 680. Докажите, что квадрат каждого четного натурального числа равняется
разности квадратов двух целых чисел. 2п — четное число.
Рассмотрим ряд натуральных чисел и рад их квадратов:
а 1 2 3 4 5 6 7 8 9
а 2 1 4 9 16 25 36 49 64 81
Наименьшее четное натуральное число 2; 22= 4.
При этом 22- 1 = 4 - 1 = 3 * 4 ; 32- 2 2= 9 - 4 = 5 * 4 ; 3 2- 1 2= 9 - 1 = 8 * 4 .
п - 1; п и п + 1 — последовательные целые числа.
(п - I)2; л2; (п 4- I)2— их квадраты.
п2 - (л - I )2= п2 - п2 4- 2п - 1 = 2п - 1 — разность второго и первого
является числом нечетным.
(п 4- I)2 - я2 = п2 + 2п 4- 1 - п2 = 2п 4 1 — разность третьего и второго
является числом нечетным.
(2п 4- 1) —(2п —1) 4- 2п + 1 —2п + 1 = 2. Значит, разность квадратов двух
последовательных чисел увеличивается для каждой следующей пары на
2 и является числом нечетным. Так как квадрат любого числа является
числом неотрицательным, то достаточно будет рассмотреть только нату­
ральные числа и число нуль. Квадрат четного натурального числа являет­
ся числом четным. Значит, нужно брать разность квадратов двух четных
или двух нечетных натуральных чисел.
Пусть т > к.
а) 2т и 2к — четные числа,
(2 т )2—(2к)2= 4 т 2- 4М2= 4 (т 2—к2) = 4( т - К)(т 4- Ь) — число четное.
б) 2т + 1и 2к + 1— нечетные числа,
(2т + I)2 - (2£ + I)2 = 4 т 24- 4 т + 1 - 4&2- Ак - 1 = 4 (т 2+ т - к2- к) =
= 4 ((т 2—к2) 4- (т —к)) = 4 ((т —к)(т 4- к) 4- (т - А)) = 4 (т - к)(т + Л+1)—
число четное. Значит, квадрат каждого четного числа равняется разности
квадратов двух целых чисел.
682. а) З24- 42= 9 4- 16 = 25 = 52. Ответ: 5 см.
б) 524- 122= 25 4- 144 = 169 = 132. Ответ: 13 см.
в) 724- 242 = 49 + 576 = 625 = 252. Ответ: 25 см.
683*. а) (1 - х)(1 + х)(1 4- х 2)(1 4- х8)(1 4- ж16) =
= (1 - х2)(1 4- х2)(1 4- х4)(1 4- х*)(1 4- х16) = (1 - х<)(1 + х4)(1 4- х8)(1 4- х8) =
= (1 - х®)(1 4- х8М1 + * 16) = (1 ~ * 16)(1 + * 1в) = 1 - X32;
б) (а - Ь)(а 4- Ь)(а2 4- Ь2)(а4 + ЪА)(а* 4- Ь*)(а16 4- &16) =
= (а2- Ь2)(а24- Ь2)(а44- ЪА)(а* 4- 68)(а16 + Ь16) =
= (с4 - ЪА)(а44- Ъ4)(а8 + Ьл)(а1* 4- Ь1в) = (а8 - Ь*)(ав + 68)(а16 4- Ь16) =
= (а16 - Ь16)(а16 4- д16) = а32 - Ь32.
684*. (2 + 1)(224- 1)(24+ 1)(284- 1)(2164 1 ) - 232=
Так как 2 —1 = 1, то
= (2 - 1)(2 4- 1)(224- 1)(244- 1)(284- 1)(2164 1 ) - 232=
= (22- 1)(224- 1)(244- 1)(284- 1)(216+ 1) - 232=
= (24- 1)(24+ 1)(2® + 1)(216+ 1) - 232= (28- 1)(284- 1)(21в+ 1) - 232=
= (216 - 1)(21в+ 1) - 232= 232 - 1 - 232= -1 .
685. (3 4- 2)(324- 22)(344- 24)(384- 28)(3164- 2 16) - З32 4- 232=
Так как 3 —2 = 1, то
= (3 - 2)(3 4- 2)(324- 22)(344- 24)(384- 28)(31в 4- 216) - З324- 232=
= (З2- 22)(324- 22)(344- 24)(384- 28)($16+ 216) - З324- 232=
= (З4- 24)(34+ 24)(384- 28)(316+ 216) - З32+ 232=
= (З8- 28)(384- 28)(3164- 216) - З324- 232= (З16- 2,6)(3164- 216) - З324- 232=
= З32- 232- З324- 232= 0.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

111. 686. а) (2х - 1)(2х + 1) = 9 + 4х(х + 5); 4х2 - 1 = 9 + 4х2+ 20л:;
20х = 9 + 1; -2 0 * = 10; х = х = Ответ: ——.
-20 * 2 2
б) (3z + 2)(3z - 2) = 7z + 9(z2- 2); 9z2- 4 = Iz + 9z2- 18; Iz = -4 + 18;
14
lz —— ; z = 2. Ответ: 2.
7
687. 8z2- (3z + 5)(3z - 5) = z(5 - z); 8z2- 9z2+ 25 = 5z - z2;
-z 2+ z2- 5z = —25; z = (-25) : (—5); z = 5. Ответ: 5.
688. x2- (1,2* - 3)(3 + 1,2л;) = 0,2x(l,5 - 2,2л;);
x2 —1,44л:2+ 9 = 0,3л; —0,44л:2; —0,44л;2+ 0,44л:2- 0,3л; = -9 ;
-0,3л: = -9 ; х = - 9 : (-0,3); х = 30. Ответ: 30.
689. (2,5# - 2)(2,5# + 2) - (1,5# + 3)(1,5# - 3) = 4#(# - 5);
6,25#2 - 4 - 2,25#2 + 9 = 4#2- 20#;4#2- 4#2+ 20# = 4 - 9;
5 1 1
20# = - 5 ; # = ------; # = — .Ответ: — .
* * 20 * 4 4
690. а) л: + 2х и 3*.
х + 2* = Зх. Так как Зх = Зх, то данные выражения тождественны.
б) 7а2—а 2 и 6а2. Так как 6а2= 6а2, то данные выражения тождественны.
в) За + а2и 4а3. Пусть а = 2, тогда 3 * 2 + 22= 6+ 4 = 10; 4 - 23= 4 *8= 32;
10 * 32. Так как 10 ф 32,то эти выражения не являются тождественными.
691. Пусть один из углов равняется х, тогда второй угол равняется х + 40°. Так
как углы смежные, то их сумма равняется 180°. Получаем уравнение:
х + х + 40 = 180; 2х - 180 + 40; 2х = 140; х = 70. Первый угол равняет­
ся 70°, второй угол равняется 70° + 40° = 110°. Ответ: 70° и 110°.
Задания д ля самостоятельной работы
Вариант 1
1. а) (х + З)2= х2 + 6х + 9; б) (а2- с)2= а4 - 2а2с + с2.
2. а) (ах + 62)2= а 2х2 + 2ахЬ2 + Ь4; б) (1 + 2с3)(1 - 2с3) = 1 - 4с6.
3. 12аЪ (2а + 3Ь)2= 12а& - 4а2- 12а& - 9Ь2= -4 а 2- 9*>2.
4. (х - З)2= (х - 5)(х + 4); х2- 6х + 9 = х2+ 4х - 5х - 20;
-2 9 4 4
- 6х —4х + 5х = -2 0 - 9; —5х = -2 9 ; х = ------; х = 5 —. Ответ: 5 —.
-5 5 5
Вариант 2
1. а) (т - 5)2= т2 - Ют + 25; б) (х2- z)2= х4- 2x2z + z2.
2. а) (сх + 2Ь)2 = с2х2 + 4cxb + 4Ь2; б) (2 + Зс)(2 - Зс) = 4 - 9с2.
3. ЗОхс —(Зх + 5с)2- ЗОхс - 9х2- ЗОхс - 25с2= -9 х 2- 25с2.
4. (х - 2)2= (х + 3)(х - 4); х2- 4х + 4 = х2- 4х + Зх 12; -З х = -1 2 - 4;
-З х = —16; х - ; х = 5 — Ответ: 5 —
-3 3. 3.
Вариант 3
1. а) (3 —#)2= 9 - 6# + #2;б) (а - х3)2=а2—2ахэ + х6.
2. а) (2х + аЬ)2 = 4х2+ 4хаЬ + а2Ь2; б) (1+ 4аХ1 - 4а) = 1- 16а2.
3- 24/ла - (4т + За)2= 24та - 1 6 т 2 - 24т а - 9а2= - 1 6 т 2 - 9а2.
4. (х + 2)2= (х —1)(х + 4); х2+ 4х + 4 = х2+ 4х —х —4; х = —4 - 4; X = - 8.
Ответ: —8.
Вариант 4
1. а) (7 - а)2= 49 - 14а + а2; б) (t - а)2 = t2 - 2t2a + а2.
2. a) (Зс - х#)2= 9с2- бсх# + х2#2; б) (3 + 5а)(3 - 5а) = 9 - 25а2;
3. 9а2Ь2 - (2 - Sab)2= 9а2Ъ2 - 4 + 12аЪ - 9а262= 12аЬ - 4;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

112. 4. (х - 4)2= [х - 5)(* + 2); х2 - 8* + 16 = х2 + 2х - 5х - 10;
-26 1 1
-8 х - 2х + 5* = -1 0 - 16; -5 х = -2 6 ; х = ------; х = 5 —. Ответ: 5 —,
-5 5 5
§1 8 . Использование формул сокращенного умножения
ЩИспользуйте формулу разности квадратов а2 —Ъ2= (а —6)<а + Ь),
6 9 4 . а) р2 - д2= (р - дКр + д); б) ж2- 16 = ж2- 42= (х - 4)(х 4- 4);
в) ж2- 9у2 = ж2 - (Зу)2= (ж - Зу)(* + 3у);
г) р 2 —х* - р2 - (X2)2= (р - а:2)(р -I- ж)2;
д) а2- с2*2= а2- (с*)2= (а - ас)(а + сдс);
е) 9а2- 4&2= (За)2- (26)2= (За - 2Ь)(За + 2Ь).
6 9 5 . а) 1 - р4= (1 - р2)(1 + р2); б) 25 - с6= (5 - с3Х5 + с3);
в) 0,01- ** = (0,1- *)(0,1+ *); г) 1 - ± с 2= Г| - |е]Г| + 1с );
д) -с 2+ 16 = 42- с2= (4 + с)(4 - с);
е) -1 + а 2Ь*с6 = (а62с3)2- V = (а62с3 - 1)(а62с8+ 1).
6 9 6 . а) 9ш2- 4*2= (3/те)2- (2л:)2= (З т - 2*)(3т + 2л:);
б) 49с - х* = (7с)2- (л;2)2= (7с - л:2)(7с + л:2);
в) х* - 4с* = (л:2)2- (2с2)2= (л;2- 2с2)(л;2+ 2с2);
г) 0,01л2- ув= (0,1л:)2- (у3)2= (0,1л; - у8)(0,1л: + у3).
д) а9 - 0,04 с4 = (а8)2- (0,2с2)2= (а3- 0,2с2)(а3+ 0,2с2);
е) 1- а264с6= I2- (а62с3)2= (1- а62с8)(1+ аЬ2с3).
6 9 7 . а) л:2+ Юл: + 25 = л:2+ 2 ■л: •5 + б2= (л:2+ б)2;
б) л:2- Юл; + 25 = (ж - б)2;
в) а 2 - 8ах +' 16л:2= а 2 - 2а ■4х + (4л:)2= (а - 4л:)2;
Г) с2+ 8сл: + 16х2= (с + 4л:)2. .
6 9 8 . а) с 2+ 2ат + т 2= (а + т )2= (а + т )(а + т );
б) л:2+ 4л: + 4 = л:2+ 2 •2л: + 22= (х + 2)2= (х + 2)(л: + 2);
в) а2+ 4аЬ + 4Ь2= (а + 2Ь)2= (а + 26)(а + 26).
6 9 9 . а) 1+ бзс + 9л:2= (1 + Зх)2= (1 + Зх)(1+ Зл:);
б) 1+ х + - я * = 1+ 2 - х + - х =|1 + !л :] ;
4 2 {2 ) { 2 ) ’
в) За2- баб + 362= 3(а2- 2а6 + 62) = 3(а - 6)2;
г) -л:2 + 2л: - 1 = -(л:2 - 2* + 1) = -<х - I)2.
7 0 0 . а) -4 с 2- 4с - 1= -(4с2+ 4с + 1) = -(2с + I)2;
б) а + 2аа: + ах2 = а(х2 + 2х + 1) = а(х + I)2;
в) 4с - с2 - 4 = -(с2- 4с + 4) = -(с - 2)2;
■
Используется формула разности квадратов а2—Ь2= (а —Ь)(а + 6), в ко­
торую вместо переменной подставляется выражение или число.
7 0 1 . а) (2а - I)2- 100 = (2а - I )2- 100 = (2а - 1 + 10)(2а - 1 - 10) =
= (2а + 9)(2а - 11);
б) 1 - (а - Ь)2= (1 - (а - Ь))(1 + (а - Ь)) = (1 - а + Ь)(1 + а - Ъ);
в) (х + с)2- 9х2с* = (х + с)2- (3хс2)2= (х + с - Зхс2)(х + с + Загс2);
г) (1 - х2)2 - 4х2= (1 - х2)2 - (2а:)2= (1 - х2 - 2х)(1 - х 2 + 2х).
7 0 2 . а) (3* - 5)2- 49а:2= (За: - 5)2- (7а;)2= (За: - 5 - 7а:)(3* - 5 + 7а:) =
= (-5 - 4ж)(10а: - 5) = (4а: + 5)(5 - 10а:) = 5(4а: + 5)(1 - 2а:).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

113. б) 4 - (ly - 5У = 22- (7у - 5)2= (2 - 7i/ + 5М2 + 7у - 5) =
- (7 - Ту)(Ту - 3) = 7(1 - 1/)(7(/ - 3);
в) (0,5 - За)2- 16а4 = (0,5 - За)2- (4а2)2= (0,5 - За - 4а2)(0,5 - За + 4а2);
г) 64л2- (1,5 - 2п)2= (8л)2- (1,5 - 2 л)2= (8л - 1,5 - 2а)) (8л + (1,5 - 2и)) =
- (8л - 1,5 + 2п)(8п + (1,5 - 2л) = (10п - 1,5) (6га + 1,5).
703. а) (Зх - 2 f - 9 = (Зх - 2)2- З2= (Зх - 2 - ЗХЗх - 2 + 3) = (Зх - 5ХЗх + 1);
б) 64 - (а - 4)2= 82- (а - 4)2= (8- а + 4X8 + а - 4) = (12- а)(4 + а);
в) 16х2 - (5х + I)2= (4х)2- (5х + I )2= (4х - 5х - 1)(4х +-5х + 1) =
= (-х - 1)(9х + 1) = -(х + 1)(9 х + 1);
г) 36х2 (3 - 2х)2= (6х)2- (3 - 2х)2= (6х - 3 + 2х)(6х + 3 - 2х) =
= (8х - ЗХ4х + 3);
д) 4(а + 26)2 - (а - 2fc)2= (2(а + 26))2 - (а - 2 b f =
= (2(а + 26) - (а - 26))(2(а + 26) + (а - 26)) =
= (2а + 46 - а + 26)(2а + 46 + а - 26) = (а + 66)(3а + 26);
е) (Зх + у)2- 9(3х - y f = (Зх + y f - (3(3х - y ) f = ((Зх + у) - 3(3х - у)ЩЗх +
+ у) + 3(3х - у)) = (Зх + у - 9х + 3у)(3х + у + 9х —3у) =
= (4у - 6х)(12х - 2у) = 2(2у - Зх) •2(6х - у) = 4(2у - Зх)(6х - у).
704. а) (5а + 7)2- (За + 6)2= ((5а + 7) - (За + 6))((5а + 7) + (За + 6)) =
= (5а + 7 - За - 6X5а + 7 + За + 6) = (2с + 1)(8а + 13);
б) (12п - 1f - (3 - 5п)2= ((12п - 1) - (3 - 5п))((12и - 1) + (3 - 5п)) =
= (12л - 1- 3 + 5лХ12л - 1+ 3 - 5л) = (17л - 4Х7л + 2);
в) (0,3х2- х + 2Y - 0,09х4= (0,3х2- х + 2 - 0,3х2)(0,3х2- х + 2 + О.Зх2) =
= (2—х)(0,6х2- х + 2);
г) 9(4а62- с)2- (2а62+ с)2= (12о62- Зс)2- (2а62+ с)2=
= (12а62- Зс - 2а62- с)(12а62- Зс + 2а62+ с) =
= (Юаб2- 4с)(14а62 - 2с) = 4(5а62- 2сХ7а62- с).
705. а) (3 + а)2+ 2(3 + а) + 1= (3 + а)2+ 2(3 + а) - 1 + I2= (3 + а + 1)2=
= (а + 4)2;
б) (5х - 7)2- 2(5х - 7) + 1 = (5х - 7 - I )2= (5х - 6) 2;
в) (х2- 4)2- 6(х2- 4) + 9= (х2- 4)2 - 2(х2- 4) •3 + З2= (х2- 4 - З)2=
= (х2- 7)2;
г) 4(а - 2с)2- 4(а - 2с) + 1 = (2(а - 2с))2- 2 - 2(а - 2с) + I 2=
= (2(а - 2с) - I )2= (2а - 4с - I)2.
7 0 6 . а) 81а4 - 1= (9а2)2- I 2= (9а2- 1)(9а2+ 1) = ((За)2- 12)(9а2+ 1) =
= (За - 1)(3а + 1)(9а2+ 1);
б) а(а2—х2). + 2(х2- а2) = а(а2- х2) - 2(о2—х2) = (а2—х2Ха - 2) =
= (а —хХа + х)(а - 2).
707. Первым действием в упражнении 707 (а—д) вынесите за скобки общий
множитель.
а) За2- 3 = 3(а2- 1) = 3(а - 1)(а + 1);
б) 7х2- 28 = 7(х - 2)(х + 2);
в) бх2- 20 = 5(х2- 4) = 5(х - 2)(х + 2);
г) 0,5 - 0,5с2= 0,5(1 - с2) = 0,5(1 - с)(1 + с);
д) а2л2- л2= л2(а2- 1) = л2(а - 1Ха + 1);
е) а1- с4= (а2)2- '(с2)2= (а2- с ^ а 2+ с2)= (а - сХа + с)(а2+ с2).
708. а) х 2- 9= О; х2- 32= О; (х - ЗХх + 3) = О; х - 3 = 0; х = 3;
или х + 3 = О; х = —3.
Ответ: х = 3; или х = —3.
К упражнению 705 применить формулы квадрата двучлена
(а ± 6)2= а2± 2а6+ б2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

114. б) 25у2 - 4 = 0; (5у)2 - 22 = 0; (5у - 2)(5у + 2) = 0;
2 2
Ьу - 2 = 0; 5у = 2; у = - ; или 5у + 2 = 0; 5у = -2 ; у =
5 5
2 2
Ответ: у = — или у = — .
5 5
в) ^ г2 ~ 25 = 0; + 5 - 51 = 0; ^ 2 - 5 = 0; *2 = 5; 2= 5 : ^ ;
4 ^2 Д 2 ; 2 2 2
2= 10; или —-2+ 5 = 0; —2= -5; х = -5 : —; 2= -10. Ответ: 10 или -10.
2 2 2
6 6
а = — ; а = —
7 7Г)§ ~ а2=0: (?“в)(?+о) =0: |“о=0: "
6 Л 6 ^ 6 6
или —+ о = 0; а = — . Ответ: — или — .
7 7 7 7
7 0 9 . а) х 2 - 6х + 9 = 0; (ж - З)2= 0; х - 3 = 0; х = 3.
б) 22 + 42 + 4 = 0; (2 + 2)2= 0 ; 2 + 2 = 0; 2 = -2 .
в) Ч у2 - 8 у + 16) = 0; 5(у2- 2у ■4 + 42) = 0; 5(у - 4)2= 0; у - 4 = 0; у = 4.
г ) | (* г - * 4 ) = 0; * * 'а-* '5 + (1 ) =0; ( * " ! ) =0: *
1 = 0; х ш !
2 2
710. а) с2+ 9 = 6с; с2- 6с + 9 = 0; (с - З)2= 0; с - 3 = 0; с = 3.
б) у2 + 4 = 4у; у2 - 4у + 4 = 0; (г/ - 2)2= 0; у - 2 = 0; у = 2.
в) 2л:2 + 2 - 4л: = 0; 2(х2 —2л; + 1) = 0; (х - I)2= 0; х —1 = 0; х = 1.
г) х - 1 = 0,25л:2; 0,25х2 - х + 1 = 0; (0,5л: - I)2 = 0; 0,5л: - 1 = 0;
0,5х = 1; х = 2.
711.а) Зх2 +2х + | = 0; з (з х 2+ 2х + |^ = 0; 9х2 + 6х + 1 = 0; (Зх + I)2= 0;
х + 1 = 0; Зх = —1; х = ——;
3
б) 4х2 + 9 = 6х; 4х2 - 6х + 9 = 0; (2х - З)2= 0; 2х - 3 = 0; 2х = 3;
3 ! *х = —; х = 1,5;
2
в) 2у2 + 2у + 0,5 = 0; 2(2у2+ 2у + 0,5) = 0 -2; 4у2+ 4у + 1 = 0; (2у + I)2= 0;
2у + 1 = 0; 2у = -1 ; у =
г ) 4х2 + 0,25 = 2х; 4х2- 2х + 0,25 = 0; (2х - 0,5)2= 0; 2х - 0,5 = 0; 2х = 0,5;
х = 0,5 : 2; х - 0,25.
712. а) х 2у2 - 81 = (ху - Щ ху + 9);
б) 0 ,0 4 т 2 - п* = (0,2т)2 - (п2)2 = (0 ,2 т - п2)(0,2т +п2);
в) ~ р 6 - 16а2
9
= ( ^ 3) -(4 а )2 = ( з Р Э- 4 а ] ( 1 р э + 4 а ];
г) -«А/6 + 0,0001 = 0.012- (а У )2= (0,01 - аУ )(0,01 + а У );
д) 0,0144 - х2у'° = 0,122- (ху5)2= (0,12 - *у5)(0,12 + ху5);
е) -1 + а,и068с4= (а564с2)2- I2= (а6Ь4с2- 1)(а564с2+ 1).
713. а) 1 - (о + Ь + с)2= (1 - (о + Ь + с))(1 + (а + 6+ с) =
= (1 —а - Ь —с)(1 + а + Ь + с);
б) (2х + у - З)2- 4у2= (2л: + I/ - 3 - 2у)(2х + у - 3 +' 2у) =
= (2х - у —3)(2х + 3у —3);
в) (5а2 —а + З)2 —25а4= (5а2 - а + 3 - 5а2)(5а2 - а + 3 + 5а2) =
= (3 - а)(10а2 + 3 - а);
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

115. г) (х2 - Зх + I)2 - 9х2= (х2- Sx + 1 - Зх)(х2 - Зх + 1 + Зх) =
- (х2 —6х 4- 1)(х2 + 1).
714. а) о4 - 2а2п + п2 = (о2)2 - 2а2п + п2.= (а2 - п)2,
б) с 2 + 2ап2 + и4= (а +га2)2;
и) с» —6с4у3 + 9i/6 = (с4)2 - 2с4•3у3 + (Зі/3)2= (с4 —Зі/3)2
г) 9с8 + 6с4х3 + ж« = (Зс4)2 + 2 •Зс4 ■х2 + (ж3)2= (Зс4 + х3)2.
715. а) (2п + З)2 - (п - I)2= (2п + 3 + п - 1)(2п + 3 - п + 1) = (Зп + 2)(п + 4);
б) (За + 2р)2 - (о + р)г = (За + 2р + а + р)(3а + 2р - а - р) =
= (4а + Зр)(2а + р);
в) 4(х - y f - (х + y f = (2х - 2у + х + у)(2х 2у - х - у) = (Зх - j/)(x - Зі/);
г) 9(р + q f - (р - ç)2= (Зр + 3ç + р - g)(3p + 3ç - р + ç) =
= (4р + 2q)(2p + 4ç) = 4(2р + ç) (р + 2g);
д) (х - 2)2 + 2(х - 2) + 1 = ((х - 2) + I)2 = (х - I)2;
е) (Зс - 2 f + 4(3с - 2) + 4 = (Зс - 2 + 2)2 = 9с2.
716. a) Xs - X4 - X + 1 = х4(х - 1) - (х - 1) = (х - 1)(х4 - 1) =
= (X - 1)((х2)2 - I 2) = (X - 1)(х2 - 1)(х2 + 1) = (х - 1)(х - 1)(х + 1)(х2 + 1);
6) с(с4 - 16) - с4 + 16 = с(с4 - 16) - (с4 - 16) = (с4 - 16)(с - 1) =
= ((с2)2 - 42)(с - 1) = (с2- 4)(с2 + 4)(с - 1) = (с - 2)(с - 2)(с2 + 4)(с - 1).
717. а) (5х + I)2 - (5х - З)2, если х = 0,7;
(5х + I)2 - (5х - З)2= (5х + 1 - 5х + 3)(5х + 1 + 5х - 3) = 4(10х - 2)=
= 8(5х - 1) = 8 - (5 •0,7 - 1) = 8 - 2,5 = 20;
б) (а —Ь)2 + 2(а —ЬуЬ+ Ь2, если а = 0,3;
(а - b f + 2(а - Ь)Ь + Ь2= ((а - Ь) + b f = (а - Ь + b f = а2 = 0,32 = 0,09;
в) 17а2 - 34ах + 17х2, если а = 3,7; х = 2,7;
17а2 - 34ах + 17х2= 17(а2- 2ах + х2) = 17(а - х)2 = 17 •(3,7 - 2,7)2 = 17.
718. a) 760 •5S0 - (3525 - 1) ■(352S + 1) = (7 •5)50 - ((3525)2 - I 2) =
= 3560 - 35s0 + 1 = 1;
б) 820■930 + (1 - 7215) ■(1 + 7215) = (8 •9)30 + (1 - (72)‘5)2= 7230 + 1 - 7230= 1.
719. a) 5a0 ■З30 - (1515- 1) ■(1515 + 1) = 1530 - 1530 + 1 = 1;
б) 724 ■824 - (1 - 5612) •(1 + 5612) = 5624 - 1 + 5624 = -1 ;
в) (3232 - 2) •(3232 + 2) - 864•4е4 = 32м - 4 - 32м = -4 ;
г) (3 + 54е) ■(3 - 54е) + б16 •916= 9 - 54і6 + 54“ = 9.
720. а) X2 - 22х + 121 = х2 - 2 ■х - 11 + I I 2= (х - I I ) 2 > 0;
б) - X 2 + 20х - 100 = -(х 2 - 2 • X • 10 + 102) = - ( X - 10)2£ 0;
в) X2 - Юх + 26 = X2 - 2 •X •5 + 52 - 52 + 26 = (х + 5)2 - 25+ 26 =
= (X - 5)2 + 1 > 0,
г) -X2 + 6х - 10 = -(х 2 - 6 •X + 10) = -(X2 - 2 •X - 3 + З2 - З2 + 10) =
= -((* - З)2- 9 + 10) = -((х - З)2 + 1) < 0.
Так как (х - З)2> 0 и 1 > 0, то (х - З)2 + 1 > 0.
729. a) 4j/2 —4у + 1 = 0; (2у - І)2= 0; 2у - 1 = 0; 2у = 1; у = і .
б) 9х2 + 12х + 4 = 0; (3* + 2)2= 0; Sx + 2 = 0; Sx = -2 ; х = - —.
З
в) 16г2 + 9 = 24г; 16г2 - 24г + 9 = 0; (4г —З)2= 0; 4х —3 = 0; 4х = 3; z = —;
4
г) 121 + 1,21х2= 24,2х; 121 - 24,2х + 1,21х2= 0;
(1,1х)2 - 2 •ІД х - 11 + I I 2 = 0; (11 - 1,1х)2= 0; ІД х = 1 1 ; х = ^ = 10.
730*. а) (х2 + X + 2)2 - (х2 + X - 2)2= 0;
((х2 + X + 2) —(х2+ X —2)Х(х2 + X + 2) + (х2 + X —2)) = 0;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

116. (*2 + * + 2 - х2 - х + 2)(*2 + х + 2 + * 2 + * - 2) = О;
4(2*2 + 2х) = 0; 8*(* + 1) = 0;
8* = 0 или х + 1 = 0;
х = 0; х = -1 .
Ответ: 0 или -1 .
б) (2у2 + 2у + I)2- (2у2 + 2 у - I)2 = 0;
С2у2 + 2у + 1 - 2у2 - 2у + 1)(2у2 4- 2у + 1 + 2у2 + 2у - 1) = 0;
2(4*/2 + 4у) = 0; 8у(|/ + 1) = 0;
8у = 0; или у + 1 = 0;
У ~ 0; у = -1.
Ответ: 0 или -1 .
731*. а) (х - 4)(*2 - 2х + 1) = 0; б) (2* + 1)(г2 - 6г + 9) = 0;
(* - 4)(* - I)2= 0; (22 + 1)(* - З)2= 0;
х —4 - 0; или (х - I)2= 0; 2г + 1 = 0; или г - 3 = 0;
х = 4; ж- 1 = 0; х = 1. 2г = -1 ; 2= 3.
Ответ: 1 или 4. 1
2 ~~~ 2* ^
Ответ: — или 3.
2
7 3 2 . а) (* - у)2= х2 - у2; б) (х + у)2= х2 + у2;
* 2 —2ху + у2= х2 —у2; * 2 + 2*у 4- у2= * 2 4- у2;
2у2 - 2*у = 0; 2у(у - *) = 0; 2*у = 0;
2у = 0; или г/ - л; ~ 0; * = 0 или у = 0.
£/ = 0; у ~ х. Ответ: при х = 0 или при у = 0.
Ответ: при у = 0 или при у = х.
7 3 3 . Пусть 2п —1 и 2п + 1 — два последовательных нечетных натуральных
числа, тогда (2п 4- I)2 - (2л - I)2 = 144; .
(2л 4- 1 - 2п + 1)(2л + 1 + 2п - 1) = 144; 2 •4п = 144; п = — ; п = 18.
2 •18 - 1 = 35; 2 - 18 + 1 = 37. Ответ: 35 и 37. 8
7 3 4 . Пусть первое число равняется *, тогда второе число равняется (34 - *).
Допустим, что первое число больше, тогда х2 - (34 - ж)2= 408.
х2 - (34 - х)2= 408; х2 - 1156 4- 68* - х2= 408; 68* = 408 + 1156;
68* = 1564; * = ^ * = 23.
68
Первое число — 23; 34 - 23 = 11 — второе число.
Ответ: 23 и 11.
7 3 5 . Пусть большее из двух чисел равняется *, тогда меньшее из чисел рав­
няется * - 21. Зная, что разность квадратов этих чисел равняется 1155,
составим и решим уравнение:
* 2 - (* - 21)2 = 1155; * 2 - * 2 + 42* - 441 = 1155; 42* = 1155 4- 441;
* = 1596 : 42; * = 38.
Большее из двух чисел равняется 38; 38 - 21 = 17 — меньшее из двух
чисел.
Ответ: 17 и 38.
I
К примерам а—г примените формулу а2 —Ь2= (о —ЪЦа + Ь), к примерам
д, е примените формулу (а ± Ь)2 = а? ± 2аЬ + Ь2.
736*. а) х2" - 1 = (х” - 1)(х" + 1); б) а*" - 4 = (а2'’ - 2Ха2р+ 2);
в) 9х2"" 2 - (Л = (Зх" +1 - у*”)(3хп* 1 + у3»);
г) а4"-2 - 49Ь2”'4= (а2""1 - 74>т‘2Ха2ю_| + 7Ьт~2);
д) а2" - 2с'’ + 1 = (С - I)2; е) х2п+е + 8х"+3 + 16 = (х"*3 + 4)2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

117. Упражнения д ля повторения
1 1 5 - 2 1 з
2 V6 г) 2737. а)
_________ 6 _ 2 6 _ 1 -3»6 3
5 + 1 5 + ? 7 2- 6 7 14 ’
6 3 6 6
1 1 6 21 + 14 + 36
б» 2 * 3 * 7 12 П- 7 497 5
’ 1 1 6 1 1 6 12 1 12 12'
2 3 7 2- 3 7
738. Отличников — 6, путевок — 2.
Первую путевку можно распределить одному из шести отличников, то есть
6 способами, а вторую — одному из пяти отличников, которые остались, то
есть 5 способами. Значит, 6 - 5 = 30 способов. Так как не имеет значения,
кому из двух учеников путевка будет вручена первому, а кому — второму,
то — = 15 способов. Ответг 15.
2
739. а) 139 - 13е - 137= 137•(122 - 12 - 1) - 137- (169 - 14) = 137 •155.
Так как 155 делится на 5, то произведение 137• 155 делитсяна 5, а число
13® - 13е - 137 кратно 5.
б) 23й - 2310 - 239 = 239 - (232 - 23 - 1) = 239 - (529 - 24) = 23е - 505 =
= 239 - 5 •101. Так как один из множителей произведения 101, то произ­
ведение делится на 101, а число 23й - 2310 - 23? кратно-КН.
740. а) 4 •10* и 2 107;
4 108 + 2 - 107= 107•(4 « 10 + 2) = 42 107= 4,2 - 10е;
4 * 10е —2 * 107 = 107- (4 - 10 - 2) = 38 •107 = 3,8 * 108;
(4 •108) - (2 - 107) = (4*2)* (10* * 107) = 8 - 1015;
(4 108) : (2 •107) = (4 : 2)- (108 : 107) = 2 •10;
б) 3,6 - 1019 и 2 - 1019;
3.6 1019 + 2 - 1019= 1019- (3,6 + 2) = 5,6 - 1019;
3.6 •1019- 2 •1019= 1019•(3,6 - 2) = 1,6 •1019;
(3,6 1019) * (2 - 1019) = (3,6 - 2) * (1019- 1019) = 7,2 - 1038;
(3,6 - 1019) : (2 * 1019) = (3,6 : 2) - (10" : Ю19) = 1,8.
§ 19. Разность и сумма кубов
745. а) (а —х)(а2 + ах + х2) - аа - хэ;
б) (Ь + 2)(Ъ2 - 2Ъ + 4) = (Ь + 2)(Ь2 - 2Ъ + 22) = Ь3 + 2Э= 60+ 8.
746. а) (1 + х)(1 - х + х2) = I3 + ж3= 1 + х3;
б) (а - с2)(а2 + ас2 + с4) = (а - с2)(а2 + ас2 + (с2)2) = а3 - (с2)3- а3 —св. .
747. а) (2а - п)(4а2 + 2ап + а2) = (2а - а)((2а)2 + 2а - п + п2) = (2а)3 - п3 -
= 8а3 - а3;
б) (1 + с + с2)(1 - с) = I3 - с3 = 1 - с3.
|Примените формулу а3± Ь3= (а + Ь){а2+ аЬ + Ь2)
748. а) а 3 - с3= (а - с)(а2 + ас + с2); б) х3 + 8 = (х + 2)(х2 - 2х + 4);
в) 1 —р 3= (1 - /?)(1 + р + р2); г) с3 - 64Х3 = (с - 4х)(с2 + 4хс +16х2);
д) /г6 —1 = (а2 —1)(л4 + п2 + 1); е) 27а3 + Ь3- (За + Ь)(9а2 - 3ab+ b2).
749. а) 125 - г3= (5 - г)(25 + 5г + г2);
б) 0,001 - а6 = (0,1 - а2)(0,01 + 0,1а2 + а4);
в) 27х6 - а3у3 = (Зх2- ау)(9х4 + Зх2а# + а2у2);
г) р3 + q3= (р + q)(p2 - pq + ç2); д) 8 - а3 = (2 - а)(4 + 2а +а2);
е) с3 + 8Х3= (с + 2х)(с2 - 2хс + 4х2).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

118. 750- а) 1 + а®= (1 + а2)(1 - а2 4- а4); б) а3 4 с6 = (а + с2)(а2 - ас2 + с4);
в) 27 4- а3Ь3= (3 4- а&)(9 - 3ab + а2Ь2); г) ^ - ж3 = ^ + Х+ **)*
д) р3х® 4- 1 = (рх2 + lXp2*4 - рх2 4- 1);
е) 27m3 + nG~ (3т 4- л2)(9 т 2 - 3т л 2 + л4).
751- а) а3с3 + 27х® = (ас + Зх2)(а2с2 - Засх2 + 9х4);
б) —с® 4- 27х2= 27Х3 - с6 = (3* - с2)(9х24- Зхс2 4- с4);
в) а6с9 - 27х3 = (а2с3 - 3х)(а4сб + Зха2с3 + 9х2);
г) а3 - ^ Ь3с6 = |а - ^ be2j^a2+ ^ аЬс2+ ^Ь2с4^;
д) - 23 - р3= -(я3 4- р3) = -(z + p)(z2 - zp + р2);
е) 0,008 + у329 = (0,2 4- у23)(0,04 - 0,2у23 + y2z6).
752- а) а3 4- 8 = (а 4- 2)(а2 - 2а 4- 4); б) 27 4- т э= (3 4- т )(9 - З т + т 2);
в) 64а2 + 27 = (4а + 3)(16а2 - 12а + 9); г) | + с3 = + c j f i - + с2j ;
v 8 э „ (2 V 4 2 2 Л ч 27 (3 ¥ 9 3 А
д) — х + 1= —х + 1 —х -----х 4 1 1; е) — + z = —+ z -------- z + z .
27 {З )9 3 ) 64 U ){1 6 4 )
753- a) a3b3 - 1 = (ab - l)(a2b2 + ab - 1); 6) 8x3 - a3 = (2x - a)(4x2 + 2xa 4- a2);
в) 64 + a3c3= (4 4- ac)(16 - 4ac 4- a2c2);
r) - f l V - c 3
8
^ ax - сj a2x24 i axe 4 c2j ;
я) ( й “3' *V ) =( i a" Ki/) ( ^ fl2+ a * y + *v)s
е) — - a3x3z3 = f —- axzV —+ —axz 4 a2x2z21.
27 U Д 9 3 J
754- a) x3- y®= x3- (y2)3= (x —i/2)(x24- xy2 4* y4);
б) а3 4- г6= a34- (г2)3= (a + z2)(a2 —azz 4- z4);
в) a6- z9= (a2)3- (z3)3= (a2- z3)(a4-f a2z34- г6);
г) 8a3- x6= (2a)3- (x2)3= (2a - x2)(4a24- 2ax2+ x4);
д) 27 - a3i/6= 33- (ay2)3 = (3 - ay2)(9 4- 3ay2+ a2y4);
е) - 8a9- 27c6 = -( 8a94- 27c6) = -((2a3)34- (3c2)3) =
= -(2a 3+ 3c2)(4ae - 6a3c2+ 9c4).
755- a) (a - 2)(a2+ 2a 4- 4) = a3- 23= a3- 8;
б) (x 4- m)(x2- xm + m2) = x34- m3; в) (x - a2)(x24- a2x 4- a4) = x3- a6;
r) (a4+ l)(a® - a4+ 1) = (a4)34- l 3= a124- 1.
756- a) (a2- m)(a44- a 2m 4- m2) = a® - m3;
5) (2x + 3)(4x2- 6x + 9) = (2X)3 + 33= 8x 3+ 27;
в) (Зс - л)(9с24- Зел + л2) = 27c3 - л3;
r) (5 + y3)(25 - 5у3+ у6) = 53+ (у3)3= 125 + у9.
757. а) (4+ 2х 4- х2)(2 - х) = 8 - х 3;
6) (25 - 10т 4- 4 т 2)(5 4- 2т) = (52- 5 * 2т +(2 т )2))5 + 2 т ) = 534- (2 т )3=
= 125 4- 8т 3;
в) (9х2- 15х + 25)(3х + 5) = ((Зх)2- Зх 5 + 52)(3х + 5) = (Зх)2+ 52=
= 27х3 + 125.
758. Найдем числовое значение выражения:
а )(х 4- 1)(х2- х + 1 ) - х3, еслих = 5,73; ( х 4- 1)(х2- х 4 - 1 ) - х 3= х3+ 1 - х 3=1;
б) (z - 2)(z2 4- 2z 4- 4) + 8, если z = 0,02;
(z - 2)(z2 4 2z 4 4) + 8= 23-8 + 8= z3;(0,02)8=0,000008.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

119. Решим уравнение 759—761.
При решении следующих уравнений сначала для раскрытия скобок ис­
пользуется формула разности кубов а3 — Ь3 = (а —Ь)(а2 + аЬ + Ь2) или
суммы кубов а3 + Ь3 = (а + Ь)(аг —аЬ + Ь2). Потом уравнение решается
но обычному алгоритму (см. упражнения 4 —6).
759. а) (х - 1)(х2 + х + 1) = х + х2;
х3 - 1 - х - х3 = О; -1 - х - 0; х + 1 = 0; х = -1 ;
б) (у + 2)(у 2 - 2у + 4) = I/3 + 2у;
у* + 8 - у3 - 2у = 0; 8 - 2у = 0 ; 8 = 2у у = 8 : 4; у = 4.
760. а) (х - 3)(х2 + Зх + 9) + х = х3;
х3 - 27 + х - х3 = 0; -2 7 + х = 0; х = 27;
б) (1 + у )(у 2 - у + 1) - у3 = 2у; 1 + у3 - у3 = 2у; 2у = 1; у =
761. а) (За - 2Х9а2 + 6а + 4) = (За - 2Х(За)2+ За ■2 + 22) = (За)3- 23= 27аэ - 8;
б) (5 + х2)(х4 - 5хг + 25) = (5 + х2)((х2)г - х2■5 + 52) = (ж2)3 + 53 = ж6 + 125;
в) (0,5а2 + Ь)(0,25а4 - 0,5а?Ь + Ь2) = (0,5а2 + п)((0,5а2)2 - 0,5о2 - Ь + Ь2) =
= (0,5а2)3 + Ь2= 0,125а6 + Ь3;
г) (4т —т 2)(т 4 + 4от3 + 1 6 т 2) = (4 т —т 2)((4т)2 + 4 т •т 2 + ( т 2)2) =
= (4 т )3 - ( т 2)3= 6 4 т 3 —т 6.
762. а) (а3 - 1)(а6 + а3 + 1) = (а3)3 - I 3 = а9 - 1;
б) ( т - 1)(т2 + 2 т + 1) = т э - 1;
в) (За - 26)(9а2 + 6аЬ + 4Ь2) = (За)3 - (2Ь)Я= 27й3 - 863;
г) (7х + Зу)(49х2 - 21x1/ + 9*/2) = (7*3) + (3{/3) = 343хэ + 27у3.
Используется формула суммы кубов а8 + Ья = (а + ЬХД2 —аЬ + Ь2)- Д
763. а) (а2 + 1Ха4 - а2 + 1) = а6 + 1;
б) (зс3 —2аХ#® + 2лсэа + 4а2) = х9 —8а3;
в) (3* + у)(9х? - Зху + уг) = 27х' + у3;
г) (2а + ЗЬ)(4а2 - 6аЬ + 9Ь2) = 8аэ + 27ЬК
764. а) (4а14 - 2а7Ь4 + Ьв)(2а7 + Ь4) = 8а21 + Ь12;
б) (16а2 - 4аЬ + Ь2)(4а + Ь) = 64а3 + Ьъ.
При решении следующих упражнений используются формулы разности
кубов а3 —Ь3 = (а —Ь)(а2 + аЬ + Ь2) или суммы кубов а3 + Ь3 = (а + Ь) х
х (а2 —аЬ + Ь2).
I
765. а ) (а8 - 2х)(а16 + 2а8х + 4х2) = (а® - 2х)((а8) + а8* 2х + (2х)2) =
= (а8)3 - (2х)3 = а24 - 8х3;
б) (х3 + #2)(х6 - х3у2 + у4) = (х3)3 + (у2)3 = х9 + #6;
в) (2а —ху)(4а2 + 2ах# + х2#2) = 8а3 —х3#3;
г) (ас2 + За)(9а2 - 3ас2л + а2с4) = а3с 6 + 27а3.
766. а ) (х3- 1)2(х6 + х3 + I)2= ((х3 - 1Клс®+ х3 + I))2= (х9 - I)2= х18 - 2х9 + 1;
б) (х4 4- 1)3(х8 - х4 + I)3 = ((х4 + 1)(х8 - х4 + I))3= (х12 + I)3 =
= (х12)3 + 3 •(х12)2•1 + 3 * X12* I 2 + I 3 = X36 + Зх24 + Зх12 +1.
767. а ) х 2 + с и х4 - х2с + с2; (х2 + с)(х4 - х 2с + с2) = х6 + с3;
б) р - ф и р 2 + рц1 + д4; (р - д2)(р2 + р^2 + д4) = р3 - д6;
в) х —0,2 и х2 + 0,2х + 0,04; (х - 0,2)(х2 + 0,2х + 0,04) = х3 —0,008.
768. а ) а3 - Ь и а6 + аъЪ + Ь2; (а3 - 6)(а6 + а3Ь + Ь2) = а9 - Ь3;
б) а5 + 2Ь и а10 - 2а56 + 4Ь2; (а5 + 2Ь)(а10 - 2аьЪ + 462) = а15 + 8Ь3;
в) х2 + у2 и х4 + у4 - х2у2; (х2 + #2)(х4 + у4 - х2#2) = хс + #с.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

120. 769. Разложим иа множители выражения:
а) (а + 2)2 - 8 = (а + 2)2 - 23 = ((а + 2) - 2)((а + 2)2 + 2(а + 2) + 22) =
= а(а2 + 4а + 4 + 2а + 4 + 4) = а(а2 + 6а + 12);
- б) 27 - (* + у)8= (3 - (х + г/))(9 + 3(х + у) + (х + у)2) =
= (3 - х - у)(9 + Зл: + 3у + х2 + 2ху + у2);
в) (г - I)3 + г2 = ((г - 1) + г)((г - I)2 - (г(г - 1) + г2)) =
= (2г - 1)(г2 - 22 + 1 - 22 + 2 + 22) = (2г - 1)(г2 - 2 + 1);
Г ) 64а3 - (а - I ) 3 = (4а - (а + 1))(16а2 + 4а(а - 1) + (а - I ) 2) =
= (За + 1)(16а2 + 4а2 - 4а + а2 - 2а + 1) = (За + 1)(21а2 - 6а + 1);
д) | а 3 + (1 + | а3] = ^ а + (1 + | а ) ] [ 1 а 2- | а ( 1 + | а ]]+
+ ^1 + —й| ) —(а 4-1) а^ ——а ——о " 4-1 4*а 4-—а | — (а + 1 ) о 2 + —д + 1 ^ )
е ) 1 - (х + 1)€ = (1 - (х + 1Г)(1 + (х + I ) 2 4- (ж + I ) 4 = (1 - ж2 - 2х - 1 )(1 +
+ х2 + 2х + 1 + (х + 1 )2(х + I ) 2) = ( - х2 - 2х){2 4- X2 + 2х 4- (х2 + 2х + 1 )(х 2 4-
4- 2 * 4- 1 )) = -л:(л: 4- 2 )(2 4- дс2 4- 2 * + я;4 + 2х3 + х2 4- 2хя + 4л:2 4-2дс + х24
+ 2 * + 1 ) = -х (х + 2 ) ( * 4 + 4л:8 + 7л:2 + 6 * + 3 ).
7 7 0 . а ) 8 - (а - 2 )3 = (2 - (а - 2 ))(2 2 4- 2 (а - 2 ) + (а - 2 )2) =
= (2 — а 4- 2 )(4 4- 2а - 4 4- а 2 - 4 а 4- 4 ) = (4 - а )(а 2 - 2 а 4- 4 );
б) (х + у)3 - у8= ((х + у) - у)((зс 4- у)2 4- (ж + у)у 4- у2) =
= (х 4- у - у)(л:2 4- 2 * у 4- у 2 4- ху 4- у 2 4- у 2) = л:(д:2 + Зжу + З у 2);
В) х3 - у 8 - X + у = (х3 - у 3) - (х - у ) - (ж - у)(х2 + ху + у2) - (ж - у ) =
= (х - У)(х2 4- ху + у 2 - 1 );
г) а? —Ьэ —а 2 —аЬ - Ьэ = (а3 - £>3) - (а2 4- аЪ 4- Ъ2) =
= (а - 6 )(а 2 + аЪ + Ь2) - (а 2 + аЬ 4- 6 2) = ( а 2 + аб + 62)(а - Ъ - 1 ).
771. а ) (ж + 3)(л:2 - Вх + 9 ) - х3 - х, если х = 2 ,5 ;
(х 4- 3)(ж 2 - Зх + 9 ) - х 3 - х = х3 - З3 - ж® - х = - 2 7 - ж = - 2 7 - 2 ,5 = - 2 9 ,5 ;
б) (2дт - Зу)(4д;2 + бху + 9 у 2) + 2 7 у 2, е сл и х = 1 ; у = 3 ,8 ;
(2л : - Зу)(4л:2 + бху + 9 у 2) + 2 7 у 2 = 8л:3 - 2 7 у 3 + 2 7 у 3 = 8л:3 = 8 * I 3 = 8 .
772. а ) (1 4- 2дс)(4л:2 - 2х + 1 ) - Зл;3, е сл и х = —;
5
(1 + 2ж)(4*2 - 2х + 1) - З*3= 1 + 8*2 - Зж3= 5*а + 1 =5 - + 1 = 1 ^ ;
б) 37х Л—(Ах —3)(16де2 + 12л: + 9), если х ——;
3
37л:3 - (4л: - 3)(16л:2 + 12л: + 9)= 37л:3 - 64л:3 + 27 = 27 - 27л:3=
= 2 7 (1 - х 3) = 2 7 ^ 1 - — ! = 2 7 ' ( 2 7 " 1> = ; 26;
{ 2 7 ) 2 7
в ) 5л:3 + (Зл: + 2у)(9л:2 - 6л:у + 4 у 2) + 1 9 у 3, е сл и х = ^ ; у = ^ ;
г) 2 8 у 3 + (5л: - у)(25дс2 + 5 ху + у 2) - 61дсэ, есл и х = у = 1 ^ ;
2 8 у 3 + (5л: - у )(25л :2 + 5л:у 4- у 2) - 61л:3 = 2 8 у 3 4- 1 2 5 * 8 - у3 - 61л:3 =
= 2 7 у 3 4* 6 4 х 8 = 27 *(^ 1 —1 + 6 4 * ( - 1 = 2 7 ' 1 2 5 4-- - 2 7 = 1 2 5 + 2 7 = 1 5 2 .
I, 3 ) 1 4 ) 2 7 6 4
773. а) д:9 - у3“ = (х3 - у")(жв + х3у" + у2“);
б) а3”*'3 + Ь21= (а“-1 + Ь7)(а2т-2 - ат167 + &м);
в) авге+ в — ^зе_3п» = (д2я+ 3 — с12~п)(а4п+ 6 4- а2п+ эс12~п 4- с 24”2”);
г ) л:12”-3 + 6 4 у 27 + 3п = (л;4"“1 4- 4 у в + п) ( * Вл~2 - 4 * 4п"1у 9 + п + 1 6 у 1В+ 2п).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

121. 774. Доказать тождество:
п) а3 - Ь3 —(а —Ь)(а2 + Ь2) = аЬ(а —Ь).
а* - Ь3 - (а - Ь)(а2 + Ь2) - (а - Ь)(а2 + аЬ + Ь2) - (а - Ь)(а2 + б2) =
- (а - 6)(а2 + аЬ + Ь2 —а2 - Ь2) = (а —6) * аЬ. Тождество доказано.
0) а° —Ьв = іа 2 - Ь2)(а2 - аЬ + Ь2)(а2 + аЬ + б2).
(а2- Ь2)(а2- аЬ + Ь2)(а2 + аб + б2) = (а - Ь)(а + Ь)(а2- аЬ + Ь2)(а2 + аЬ + б2) =
[(а - &)(а2 + аЬ + 62)][(а + Ь)(а2 - аЬ + б2)] = (а3 - Ь3)(а3 + Ь3) = а6 - д6.
Тождество доказано.
775. а) 3273 - 227а делится на 100;
3273 - 2273= (327 - 227)(3272 + 327 •227 + 2272) =
- 100 •(3272 + 327 * 227 + 2272). Один из множителей произведения равня­
ется 100, значит, данное выражение делится на 100.
б) 7373 + 2633 делится на 103;
7373 + 2633= (737 + 263) •(7372 - 737 263 + 2632) =
- 1000 * (7372 - 737 • 263 + 2632). Один из множителей произведения
1000 = 103, значит, данное выражение делится на 103.
в) 2 •(10013 + 27) делится на 2008;
2 (10013 +.27) = 2 * (1001 + 3)(10012 - 1001 ■3 + 9) =
= 2008 - (10012 —3003 + 9). Один из множителей произведения равняется
2008, значит, данное выражение делится на 2008. 1
776- а) (* + 1)(*2 - * + 1) = 5* + Xя; * э + 1 = 5* + * 3; 1 = 5х; х = —.
5
64
б) (г - 4X16 + 4г + г2) = г(г2 —4); г3 - 64 = г3 - 4г; 4г = 64; г = — ; 2= 16.
777. а) (х2 + IX *4 " х2 + 1) = 1; ** + 1 = 1; *« = 0; * = 0.
б) (*3 + 3)(*в - З*3+ 9) - 26 = 0; х9 + 27 - 26 = 0; х9 = -1 ; * = -1 .
778. а) (4*2 - 2х + 1)(2* + 1) = 2*(4*2 + 5); 8*3 + 1 = 8*3 + 10*; 10* = 1;
* = 0,1.
б) (*2 - 4)(*2 - 2* + 4) = *(*3 + 8); (* - 2Х* + 2)(*г - 2* + 4) = х(х? + 8);
(* - 2Х*3 + 8) - *(*8 + 8) = 0; (*а + 8)(* - 2 - *) = 0; -2(х* + 8) = 0;
*2+ 8 = 0; *3= -8; * = -2.
779. Пусть л и л + 1 — два последовательных натуральных числа, где л = {1;
2; 3;...}.
(л + 1)э - л8 = (л + 1 - л)((л + I)2 + (л + 1)л + л2) =
- 1 * (л2 + 2л + 1 + л2 + л + л2) = Зл2 + Зл + 1 = Зл(л + 1) +1.
Так как л и л + 1 последовательные натуральные числа, то одно из них
четное. Тогда Зл(л + 1) делится на 6, а Зл(л + 1) + 1 при делении на 6
дает в остатке 1.
Утверждение доказано.
780. Пусть 2л - 1 и 2л + 1 — два последовательных нечетных натуральных
числа, где л = {1; 2; 3; ...}.
(2л + I)3 - (2л - I)3 = ((2л + 1) - (2л - 1))((2л + I)2 + (2л + 1Х2л - 1) +
+ (2л + I)2) = (2л + 1 - 2л + 1)(4л2 + 4л + 1 + 4л2 - 1 + 4л2 - 4л + 1) =
= 2(12л2 + 1) = 24л2 + 2.
24л2 делится на 24, то 24л2 + 2 при делении на 24 дает в остатке 2.
Утверждение доказано.
781. Докажем, что три последние цифры числа 19933 + 73 являются
нулями.
Доказат ельст во. 19933 + 73 = (1993 + 7) ♦(19932 - 1993 - 7 + 72) =
= 2000 - (19932- 1993 •7 + 72), так как множитель 2000 имеет три послед­
ние цифры — нули, то в произведении три последние цифры тоже будут
нулями, что и надо было доказать.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

122. Р Л В с п = 2(АВ + АО)
^АВС£> —
Г82. Докажем, что если сумма двух натуральных чисел делится на некоторое
число, то сумма их кубов тоже делится на то же самое число.
Доказат ельст во. Пусть натуральными числами будут числа п и т . Запи­
шем формулу суммы кубов п3+ т3= (л + тп){п2—тп + т2). Так как (л 4- т)
делится на какое-то число, то (л3 + т3) делится на то же самое число, что
и надо было доказать.
783. Кредит — 500 ОООгрн. Процент — 20 % годовых. Время — 2 года.
1) 500 000 * 20 % = 500 000 •0,2 = 100 000 (грн.) — прибыли по кредиту
получит банк за год.
2) 2 * 100 000 = 200 000 (грн.) — прибыли по кредиту получит банк че­
рез 2 года.
3) 500 000 + 200 000 = 700 000 (грн.) — нужно вернуть банку через 2 года.
Ответ: 700 000 грн.; 200 000 грн.
784. А(1; 0); В(1; 3); С(5; 3); Х>(5; 0).
А1> = ВС = 5 - 1 = 4; АВ = ВС =
= 3 - 0 = 3.
2 - (3 + 4) = 14;
АО = 3 ■4 = 12.
785. Решим математические кроссворды.
Реш ение. 1) Обозначим для удобства
кружки буквами а, б и у. Пусть в круж­
ке а находится число х, тогда в кружке
б. будет число (х - 10), а в кружке у —
число (х - 10 - 5) = (х —15). Так как
сумма чисел из кружков а и у равняется 47, то со­
ставим уравнение:
х + X - 15 = 47; 2х = 47 + 15; 2х = 62; х = 31.
Число из кружка а равняется 31, тогда числом
из кружка б будет 31 —10 = 21, а из кружка у —
31 - 15 = 16.
Ответ: 31, 21, 16.
2) Обозначимдляудобствакружки буквами
а, б, у и г. Пусть в кружке а будет число х,
тогда в кружке б будет число (80 - х а в
кружке г находится число ((80 - х) + 30),
то есть (110 - х). Так как число в кружке
у можно записать и как ((110 —х) + 16)
и как 20х, то можно составить уравнение:
(110 - х) + 16 = 20х; 126 = 21х; х = 6.
Значит, в кружке а находится число 6
(80 —6) = 74, а в кружке у находится (126 -
ло (110 —6) = 104. Ответ: 6, 74, 120, 104.
3) Обозначим для удобства кружки буквами а, б,
у и г. Пусть в кружке а находится число х, тогда
в кружке б будет число (х + 8), а в кружке у — чис­
ло 2х. Так как число в кружке г можно записать и
как ((х + 8) - 3), и как (2х - 5), то можно составить
уравнение: х + 8 —3 = 2 х - 5 ; 2 х - х = 10; х = 10.
Значит, в кружке а находится число 10, тогда
в кружке б будет число (10 + 8) = 18, а в кружке
г — число (18 - 3) = 15, и в кружке у находится
число (2 * 10) = 20. Ответ: 10, 18, 15, 20.
т о г д а в к р у ж к е б —
6 ) = 1 2 0 , и в к р у ж к е г
ч и сл о
— ч и с-
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

123. 786. а) (35 - 25)17= (35 + 32)17= З17;
Г») (0,874 + 0,53)10= (0,875 + 0Д25)10= I 10 = 1;
и) (0,33 - 0,017)6= (0,027 - 0,017)6 = 0,016 = (ОД2)6
г) (3* + 19)5 = (81 + 19)5 = 100б;
А) (27 - 53 - 4)15= (128 - 125 - 4)15= (-1 )15 = -1 ;
с) (44 - З5 - 13)12= (256 - 243 - 13)12 = О12 = О.
ОД12;
§ 20. Использование разных способов разложения
многочленов на множители
Разложение на множители начинай из вынесения за скобки общего
множителя, если он есть.
790. а) ар2 - ах2= а(р2 - х2) = а(р - *)(/? + х);
б) с3 - ср2 = с(с2 - р2) = с(с - р)(с + р);
в) 2 - 8а2= 2(1 - 4а2) = 2(1 - 2а)1 + 2а);
г) 27л;2 - 75 = 3(9лг2 - 25) = 3(3л; - 5)(3* + 5);
д) 18с2х - 2х = 2л;(9с2 - 1) = 2л:(3с - 1)(3с + 1);
е) 100а4 - а2 = а^ЮОа2- 1) = а2(10а - 1)(10а + 1).
791. а) 5а - 5а3 - 5а(1 - а2) = 5а(1 - а)(1 +- а);
б) 49т4 - т2 - т2(49т2 —1) = т2(7т - l)(7m -I- 1);
в) 64х2у - 9х2у3 = х2у{64 - 9у2) = х2у(8 - Зу)(& + Зу);
II примере г) сначала используется формула разности квадратов
а 1 - Ь2 = (а —ЬКа + Ь), а потом полученные двучлены раскладываются
на множители по формуле разности кубов а3 - Ь3 = (а - Ь)(а2 + ab+ Ь2)
и суммы кубов а3 + Ъ3 = (а + Ь)(а2 - аЬ + Ь% В примерах б) (дважды)и
в) используется формула разности квадратов.
г) те - 272= (т 3- 27)(т3 + 27) = ( т - 3)(т2 + 3т+ 9)(т + 3)(т2 - 3тЛ- 9);
д) jc4 - 625 = (х2 + 25)(зс2 - 25) = (х2 + 25)(л; + 5)(л; - 5);
е) х4 - у%= (х2 - у3)(х2 + у3).
792. а) дга2 - хс2 = х(а2 —с2) - х(а - с)(а + с);
б) а3 —ап2 = а(а2 - п2) = а(а - п)(а + л);
в) 20л;2 - 5 = 5(4х2 - 1) = 5(2* - 1)(2х + 1);
г) 100т2 - 25л;2 = 25(4т2 - х2) = 25(2т —х)(2т + х);
д) Зл;3 - 27* = 3*(л:2 - 9) = Зх(х - 3)(х + 3);
е) 45а - 5а3 = 5а(9 - а2) = 5а(3 - а)(3 + а).
1‘азложиге на множители левую часть уравнения, если правая равняется
нулю и приравняйте к нулю каждый множитель отдельно.
793. Решите уравнение,
а) 5л;5 - х4= 0;
лг4(5л ; - 1 ) = 0 ;
хА= 0; или 5jc ~ 1 = 0;
х = 0; 5л; = 1; х =
5
б) х 4 + 6*3=
л:3(л; + 6)
0;
0;
л;3= 0; или х + 6 = 0;
х = 0;
Ответ:
х ~ - 6.
-6 или 0.
Ответ: 0 или
5
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

124. в) 10х6 —Зле5;
Юх6 - Зх5= О;
х3(10х —3) = О;
х5= 0; или Юле “ 3 = 0;
х = О; Юле = 3;
3
* “ ю ;
Ответ: 0 или 0,3.
г) Зле3 - 12лс = О;
Зх(х2 *■4) = 0;
Зх(х - 2)(х + 2) = 0;
Зле= О; или ле- 2 = О; или ле+ 2 = О;
х = 0,3.
х = О; ле= 2; х
Ответ: -2 , или О, или 2.
2.
д) Зле2 - 12х = О;
Зле(ле - 4) = 0;
Зле = О; или ле- 4 = О;
х = О; х = 4.
Ответ: Оили 4.
7 9 4 . а) х 4 - х2= О;
е) ле5= х3г
ле5 —ле3
ле3(ле2 -
х3(х
О;
1) = О;
1)(х + 1) = О;
б) х2
х2(х2 - 1) = О;
х2(х - IX * + 1) = 0;
ле2= О; или х - 1 = 0; или ле+ 1 = О;
х = О; ле= 1; лс= -1*
Ответ: -1 , или 0, или 1.
в) бх3 А _О;
х3(5 - х) = 0;
ле3= 0; или 5 - ле= О;
ле= 0; -ле = -5 ;
х = 5.
Ответ: 0 или 5.
лс3= О; или ле—1 = О; или ле+ 1 = О;
ле= 0; . ле= 1; х = -1 .
Ответ: -1 , или 0, или 1.
25х = О;
х(х2 - 25) = 0;
х(х - 5)(х + 5) = О;
х = 0; или х —5 = 0; или лс + 5 = О;
х = 5; х = -5 .
Ответ: -5 , или О, или 5.
г) ле3 - 0,04х2= О;
ле2(ле - 0,04) - О;
де2= О; или х —0,04 = О;
ле= 0; ле= 0,04«
Ответ: Оили 0,04.
7 9 5 . а) аде2 - 2але + а = а(лс2 - 2ле + 1) = а(х - I)2;
б) 20а3 - 20а2 + 5а = 5а(4а2 - 4а + 1) * 5а(2а - I)2;
в) 27а6 + За2 - 18а4 = За2(9а4 + 1 - 6а2) = 3а2(3а2 - I)2;
г) 45лс3 + 20ле - 60х2= 5х(9х2 - 12х + 4) = 5х(3х - 2)2;
д) тле2 + 4тх + 4 т = т(ле2 + 4ле + 4) = т(ле + 2)2;
е) р 2 + бхр2 + 9х2р2= р2(1 + 6х + 9х2) = р 2(1 + Зх)2.
7 9 6 . а) —4 т 2 + 4 т —1 = —(4 т 2 4- 4 т + 1) = - (2 т + I)2;
б) -а 2 - 6а - 9 = -(а 2 + 6а + 9) = -(а + З)2;
в) 5ле2 + 5у4 - Юле#2= 5(ле2 + у* - 2лсу2) = 5(ле- у2)2;
' г) 4але2 + а - 4але = а(4ле2 - 4х + 1) = а(2х —I)2;
д) 3 - 6а + За2 = 3(1 - 2а + а2) = 3(а - I)2;
е) 7а2 - 28а4 + 28а6 = 7а2(1 - 4а2 + 4а4) = 7а2(1- 2а2)2.
ш
X
Ш
X
О
о;
А
из
О
В следующих примерах для разложение на множители используется спо­
соб группировки. Кроме того, после группировки в примерах 797 (в, г)
и 798 (в, г) сначала используется формула квадрата суммы или разно­
сти, а потом формула разности квадратов.
Использованные формулы сокращенного умножения приведены в пре­
дыдущих объяснениях.
7 9 7 . а) ах4 - х4 + ах3 - х3 = ха - 1) + х3(а - 1) = (х4 + х?)(а - 1) =
= хэ(х + 1)(я - 1);
б) х3 - х2у + х2- ху = х2(х - у) + ле(х - у) = (х2 + хХ* - у) = х{х + 1)(х - у);
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

125. в) х2 - 2ах + а2 - тп2 = (х - а)2 - т2= (х - а - т)(х - а + т);
I') х2 + 2х + 1 —а2 = (дс + I)2 - а2 = (л: + 1 + а)( х + 1 - а).
798. а) 4аЪ + 126 - 4а - 12 = 46(а + 3) - 4(а + 3) = (а + 3)(46 - 4) =
= 4(а + 3)(6 - 1);
б) 10 + 0,6ху ~ 5у ~ 1,2* - (10 - 5у) - (1,2* - 0,6ху) =
, 5(2 - у) - 0,6*(2 - у) = (5 - 0,6*)(2 - у);
в) т2 - х2 —4х - 4 = т2 - (*2 + 4х + 4) = т2 - (х + 2)2 =
~ (т - * - 2)(т + * + 2);
г) х2 - у2 - 6* + 9 = {х1 - 6* + 9) - у2= (* - З)2 - у2= (* - 3 - у)(* - 3 + у).
Используется способ группировки в комбинации с формулой разно- Ц
«*ти квадратов в примерах 799—800 а) и б), формулой разности кубов в 1
примере 800 в) и формулой суммы кубов в примере 800 г). Использо-1
наиные формулы сокращенного умножения приведены в предыдущих I
объяснениях. ЭД
799. а) * - а + х2 - а2 = (х - а) + (* + а)(* - а) = (* - а)(* + а + 1);
б) а2 —Ь2 + а - 6 = (а + 6)(а - 6) 4- (а - 6) = (а - 6)(а + Ъ+ 1);
в) k + р + k2 - р 2= (k + р) + (k + р){к - р) = (k + p)(k - р + 1);
г) с2 - с - т? —т = (с2 - т2) - (с + т) = (с + т)(с —т) - (с + т)(с - т —1).
800. а) а - 62 + а2 - 6 = (а2 - Ь2) + (а - 6) = (а + 6)(а - 6) + (а - 6) =
= (а - 6)(а + 6 + 1);
б) с3 - 3d2 + Зс2 - cd2= с(с2 - d2) + 3(с2 - d2) = (с2 - d 2)(c + 3) =
= (с*+ 3)(с - d)(c + d);
в) хэ - а3 + * - а = (хэ - а3) + (* - а) = (* - а)(х2 + ха + а2) + (* - а) =
= (х - а)(х2 + а * + а2 + 1);
г) а + 6 - а3 - 63= (а + 6) - (а3 + 63) = (а + 6) - (а + 6)(а2 - аб + 62) =
= (а + 6)(1 - а2 + аб - 62).
801. Решение. Таким двучленом будет любой двучлен, каждый член которого
возведен в степень, показатель которой одновременно делится на 2 и на 3.
Например, двучлен (*® - if).
х° ~ у* = (я3)2- (у3)2= (дс8- ^ Х *3+ у3) = (* ~ у)(х2+ ху + у2Х* + */Х*2- **/ + у2);
*° - у6= (*2)3 - (у2)8= (*2- у2)(х* + * 2у2 + у*) = ( * - уХ* + iM*4 + * V + У4).
802» а) 0,001а + а4 = а(0,001 + а8) = а(0,1 + а)(0,01 - а * 0,1 + а2);
б) -1 - а6= -(1 + а6) = -(1 + а2)(1 - а2 + а4);
в) -8*/4 - 64у = -8у(у3 + 8) = ~8y(i/ + 2)(г/2 - 2у + 4);
г) 1 + свх9 = (1 + с2*)(1 - с2* + с4* 2);
д) 0,008а + а7= а(0,008 + а6) = а(0,2 + а2)(0,04 - 0,2а2 + а4);
е) 27 000 - у21= (30 - |/®)(900 + ЗОу9 + у1В).
803. а) х?у2 - дсу* = ху2(х2 - у?) = хух - у)(* + у);
б) 9а5с —а3с3 = а3с(9а2 —с2) = а3с(3а —с)(3а + с);
в) 25а4 - х2уА= (5а2 - *у2)(5а2 + ху2);
г) 0,25*2 - х*у* = дс2(0,25 - х2ул) = дг2(0,5 - дсу2)(0,5 + дг2у4);
д) 0,08а4 - 0,32а2= 0,08а2(а2 - 4) = 0,08а2(а - 2)(а + 2);
е) -8 + 2х* = 2(х4 - 4) = 2(*2- 2)(х2 + 2).
804. а) —х - 2*8 = i *(1 - 16*2) = —х(1 - 4*)(1 + 4*);
8 8 8
б) —а 4- —а2* 4 = — а4- — а2* 4 = — а2(16а2- 9эс4) = — а2(4а - 3*2)(4а + З*2);
3 8 24 24 24 24
в) =-ar! ^ o c4 - j /Jj = - * 2^|at2 - ÿ i!j^ | *2 +ÿ2j =
= хуг - 1 ,5 jc 2) ( 1 ,5 x 2 + I/*).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

126. I
Сначала за скобки выносится общий множитель, а лотом двучлен в скоб­
ках раскладывается на множители, в примере а) по формуле разности
кубов и по формуле разности квадратов в примерах б) и в).
1 27 4
80 5 . а) —х х
2 16 2
= - х ( 1 - 1,5х)(1 + 1,5* + 2,25х2);
2
1 Л 27 3А 1 ( л 3 V* 3 9 Л
- х 1 х = —х1 X II 14— л: 4—■X =
2 1 8 / 2 V 2 Д 2 4 )
8 18 2 и 9 ) 2 и 3 Д 2 3 )
ч 2 ^ 2 3 2 2 18 3 2 . (1 9 2 Л _ (1 3 V I 3 ^
в) —а - Х — а с -~ ~ а а с = 2 а — а с = 2а — I— а с --------ас ;
9 16 9 16 1,9 16 ) 1,3 4 Д З 4 )
. 3 2 3 2 3 о(
г) - X у + — X25=—х у + — .
7 14 7 V 2 ;
8 0 6 . а) 0,04ал:э - 0,4ах2 + ах - ах(0,04х2 - 0,4х 4- 1) = ах(0,2х - I)2;
б) 4а2х - 2ах2 + 0,25с5= х(4а2 - 2ах2 4- 0,25х4) = х(2а - 0,5л:2)2; .
в) 1,21лс4 4- 2,2пс3+ пс2= гсс2(1,21с2 4-2,2с 4- 1) =гсс2(1,1с 4- I)2;
г) 0,5а2л:2 4* 0,5а2 - а2х = О^Ьа^х24- 1 - 2х) =0,5а2(х - I)2.
8 0 7 . а) —ас2—ас + а = а —с2 - с + 1|- а —с - 1 | ;
4 и ) и )
б) тхл- тх2+ ~ т = т^хл- х2+ ^ j = т ^л;2 - ^^ ;
в) а2+ а3- ал- а5= а2(1 + а - а2—а3) = а2((1 + а) - а2( 1 4- а)) =
= а2(1 + а)(1 - а2) = а2(1 + а)(1 - а)(1 + а) = а2(1 + а)2(1 - а);
г) X2 - х3 4- х4 - X5= х2(1 - х 4- X2 - х3) = х2((1 - х) 4- х2(1 - *)) =
= х2(1 - х)(1 4- л:2).
808. а) ас2 4- Ьс + Ьс2 - ас - с(ас 4- Ь - Ъс - а) = с(с(а - Ъ) - (с - Ь)) =
= с(а - Ь)(с - 1);
б) а2Ь 4- За 4- Зад 4- а2= а(а6 4- а 4- ЗЬ 4- 3) = а(а(6 + 1) + 3(Ь 4- 1) =
= а{Ь 4- 1)(а 4- 3);
в) ах - а24- ах2- а3= а(х - а 4- х2- а2) = а((л; - а) 4- (х - а)(х 4- а)) =
= а(х - а)(1 4- х 4- а);
г) а3 - аЬ2- а2 - аЬ - а(а2 - Ь2- а - Ъ) = а((а - Ь)(а 4- Ь) - (а 4- Ь)) =
= а(а 4- ^)(а —Ъ —1).
8 0 9 . а) 2ал: —аху + 2ау —ау2= а(2х —ху Л- 2у —у2) = а(х(2 - #) 4- #(2 - */)) —
= а(2 - !/)(* 4- #);
б) Т1Х 4' сх 4- с3х 4- с2пх = х{п + с2п + с 4- с3) = х(п( 4- с2) 4- с(1 4- с2) =
= х{1 4- с2)(п 4' с);
в) хг - 2ху + у2 + х - у = (х - у)2 + (х - у) = (х - у)(х - у + 1);
г) 9а2 + 6а + 1 + За + 1 = (За + I)2 + (За + 1) = (За + 1)(3а + 1 +1) =
= (За 4- 1)(3а 4- 2).
8 1 0 . а) ас 4- Ьс - 2с —асх —Ьсх 4- 2сд: = с(а + Ь - 2) —сх(а + г.- 2) =
- (с —сх)(а 4- Ъ—2) = с(1 ~ х)(а + Ъ—2);
б) х3 4- 2л;2 - асх - 2сх - сх24- ах2 = л:2(л: 4- 2 + а) —сх{а + 2 4- х) =
= (л: 4- а 4- 2)(х2- сх) = х(х - с)(х 4- а + 2).
811. а) а2лг24- а2у2- 2ах2- 2ау24- л;24- у2= а2(х2+ у2) - 2а(л;2+ у2) 4- (х24- у2) =
= (х24- у2)(а2- 2а 4- 1) = (х2+ у2)(а - I)2;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

127. б) а гх 2 + a2y2 + ах2 + ay2 -І- x2 + у2 = a2(x2 +#2) + a(x2+ i/2) + (x24- y2) =
(x2 + #2)(fl2 + а + 1)-
Ü12, а) а2 - 2ac + c2 —x2 —2x —1 = (о2 - 2ac + c2) —(де2 + 2x 4- 1) =
(a - c)2 - (x 4- l)2= (а - с - x - l)(ö - с 4- x 4- 1);
f>) a4 - 2a2 4- 1 - a2 4- 2ac - c2= (a4 - 2a2 + 1) —(a2 —2öc + c2) =
(а2 - l)2 - (a - c)2= (a2- 1 - с 4- c)(a2 - 1 4- a - c).
11рсдставьте в виде суммы квадратов один или несколько членов многочлена.
013. а) а 2 4- Ь2 + 2а + 2Ъ + 2 = а2 4- 2а + 1 + Ь2 + 2Ь 4- 1 = (а 4- I)2 + (Ь + I)2;
Г>) х4 + у4 + 4х2 + 4у2 + 8 = х4 + 4х2 + 4 + у4 + 4у2 + 4 = (х + 2У* + (у + 2)2;
і*) 2дг2 4- 4х 4- 2 = х2 + 2х + 1 4- де24- 2х 4- 1 = (х + I)2 4- (х + I)2.
і*) 2х2 + 2х 4- 1 = х2 4- 2х + 1 4- х2 = (х 4-І)2 4- х2.
014. а) а 2Ь2 - 2аЬ - 6с - с2 - 8 = (а2Ь2 - 2аЬ + 1) - (с2 +6с + 9) =
(ab - I)2 - (с 4- З)2;
6) (а —Ь)(а 4- Ь) + 4(а - Ь) = а2 —Ь2 4- 4а —4Ь = а2 4- 4а 4- 4 —Ъ2 —4Ъ —4 =
(а + 2)2 - (6 4- 2)2;
и) а24- Зх2- 4ах 4- 2сх - с2= а2—4ах 4- 4х2- х24- 2сх - с2= (а - 2х)2- (х - c f;
г) а4 —5а2 - 2ах - х2 + 4 - а 4 - 4а2 + 4 - а2 - 2ах - х2= (а2 - 2)2- (а + х)2.
015. а) (8* + З)2 4- (б* + 4>2 + 4х = 64л:2 + 48л; + 9 4- 36л;2+48л; 4- 16 4- 4л: =
- 100л:2 + 100л: 4- 25 = (10х 4- 5)2;
б) (Зс2 + 4)2 + (4с2 4- З)2 + 2с2 = 9с4 4- 24с2 4- 16 + 16с4 +24с2 4- 9 + 2с2 =
- 25с4 + 50с2 4- 25 = (5с2 + 5)2.
016. Докажем, что при каждом значении х данные выражения принимают
только положительные значения:
а)(х4- 2)2+ 1. Так как (л:4- >Оприлюбомзначениих, а 1 > О,то(х + 2)2+1 > О
при любом значении х.
б) х24- (л; - З)2. Так как л:2> Ои (л: —З)2> Опри любых х, то х2 4- (л; - З)2> О.
При этом х2 + (х 4- З)2 - О, если л:2= Ои (л; + З)2= Одля одного и того же
значения де.
Xі = О; (х 4- З)2= О; х = О; х 4- 3 = О; х - -3 . Так как Оф -3 , то х2 4- (х + З)2О.
Таким образом имеем х2 + (х + З)2 > 0 для любого значения х.
в) (л; - I)2 + (х + 2)2.
(х - I)2 > 0 и (х + 2)2 > 0 при любом значении де, тогда (де — I)2 +
н(де + 2)3> 0. При этом (де- I)2+ (де+.2)3= О, если (де- I)2= Ои (х + 2 f = О
для одного и того ж значения де.
(де - І)2 = О; (де + 2)2= 0; де- 1 = О; де+ 2 = 0; де= 1; де= -2 .
Так как 1 * -2 , то (де - І)2 + (де + 2)2ФО.
Таким образом, имеем (де —І)2 + (де + 2)2 > 0 для любого значения де.
г) д:2—4де + 5.
де2 - 4х + 5 = де2 —4де + 4 + 1 = (де —2)2 + 1.
(х - 2)2> Одля любого значения деи 1 > О. Значит, (де - 2)3 + 1 > О, а зна­
чит, де2 - 4jc + 5 > Одля каждого значения х.
д) X2 —X + 1.
1 З
X - X + —+
4 4
(
11 3 ( 11 3
х — + —. де— > 0 для любого значения деи —> О.
V 4( 2 ) 4
( 1Л2 з
Значит, I х - —I + —> 0, а значит, и х 2 - х + 1 > 0 для каждого значе­
ния х .
«О9х2 - бде + 2.
9хг - 6х + 2 = 9х2 - 6х + 1 + 1 = (Зх - I)2 + 1.
(Зх - I)2 > О для любогозначения х и 1 >О. Значит, (Зх - I)2 + 1 > О,
а значит, и 9х2- 6х + 2 > 0 для каждого значения х.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

128. 8 1 7 . а) 6х - х2 - 10.
6* - х2 - 10 = - ( * 2 - 6х + 9 + 1) = -((* - З)2 + 1).
. (х —З)2 > 0 для любого значения х и 1 > 0. Значит, (х —З)2 + 1 > О,
а -((* - З)2 + 1) < 0. Значит, и 6х - х2 - 10 < 0 для любого значения х.
б ) х - х 2 - 1 .
х - х 2 ~1 = -(х 2 - х + 1)
3
для любого значения х и —> 0.
4
Значит
Значит, идс-де2 - 1 < 0 для любого значения х.
в) 2х - х2 - 2.
2х —х2 —2 - ~(х2 - 2х + 1 + 1) = -((* - I)2 + 1).
(х - I)2 > 0 для любого значения х и 1 > 0. Значит, (х - I)2 + 1 > 0,
а, -((х - I)2 + 1) < 0. Значит, и 2х - х2 - 2 < 0 для любого значения х,
818- а) х2+ 5. Так как х2> 0 для любого значения х, то наименьшее значение
х2= О при х = 0. Наименьшее значение х2 + 5 при х = 0.
б) (х - 2)2. Так как (х —2)2 > 0 для любого значения х, то наименьшее
значение (х ~ 2)г = 0.
Тогда (х - 2)2 = 0; х - 2 = 0; х = 2.
Значит, выражение (дс - 2)2 принимает наименьшее значение при х = 2.
в) (х - З)2+ 5. Так как (х - З)2> 0 для любого значения х9то наименьшее
значение (* - З)2= 0 при х - 3 = 0, х = 3.
Значит, выражение (х - З)2+ 5 принимает наименьшее значение при х = 3.
г) х2 - 6х + 9.
х2 —6* + 9 = (х- —З)2. Так как (х - З)2 > 0 для любого значения х, то на­
именьшее значение (х —З)2= 0. Отсюда х —3 = 0, х = 3. Значит, выраже-
•ние х 2—6х + 9 принимает наименьшее значение при х = 3.
д) х2 + Ах + 6.
х2 + Ах + 6 = х2 + Ах + 4 + 2 = (х + 2)2 + 2. Так как (х + 2)2 > 0 для
любого значения х, то наименьшее значение (дс + 2)2 = 0 при х + 2 = 0,
х = —2. Значит, выражение х2 + 4л: + 6 принимает наименьшее значение
при х = -2 .
е ) 4 л:2 - 4дс + 3 .
4л:2 —Ах + 3 = 4дс2 - 4л: + 1 + 2 = (2л: - I)2 + 2. Так как (2л: —I)2 > 0 для
любого значения ж, то наименьшее значение (2дс - I)2 = 0 при 2х - 1 = 0;
2л: = 1; х = Значит, выражение 4дс2 - 4л: + 3 принимает наименьшее
1
значение при х = —.
2
I
При нахождении числовых значений выражений в двух последних при­
мерах для упрощения расчетов используется формула квадрата разности
(а - ЬУ = а? - 2аЪ + Ь2.
8 1 9 . а) х{х + 3)г + (5 + хУ, если х = -4 ;
х(х + ЗУ + (5 + хУ = х(х2 + 6х + 9) + (125 + 75х + 15хг + х3) =
= х3 + 6х2 + 9х + 125 + 75х + 15х2 + х3 = 2х3 + 21х2 + 84* + 125 =
= 2(-4)3 + 21(-4)2 + 84(-9) + 125 = -512 + 336 - 336 + 125 = -387;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

129. б) (а - З)4 - (4 4- а)4, если а - -0 ,5 ;
(а - З)4 - (4 + а)4 = ((а - З)2 - ( 4 4- аУ)((а - З)2 4- (4 4- а)2) =
- (а2 —6а 4- 9 —16 —8а - а2)(а2 —6а 4- 9 4- 16 + 8а 4- а2) = (—14а —7)(2а2 4-
| 2а 4- 25) = (-14 * (-0,5) - 7) •(2 •(-0 ,5 )2 4- 2 - (-0,5) + 25) = 0;
п) (с 4- З)2 - 2{с + 3)(с - 2) + (с - 2)2, если с - 2,53;
(г + З)2- 2(с + 3)(с - 2) + (с - 2)2 = ((с + 3) - (с - 2))2=
(с 4- 3 - с 4- 2)2= 52= 25;
I*) (2г + I)2 - 4г(2г + 1) 4- 4г2, если г ~ 3,75;
(2г + I)2 - 42(22 + 1) + 4г2= ((22 4- 1) - 22)2= (22 + 1 - 2г)2= I 2 = 1.
820, Докажем тождество 7хд + 5ж2 - 6* + 3 = ((7л: + 5)л: - 6)х + 3.
7л:3 + 5х2 - 6х 4- 3 = (7л:2 + 5х - в)х + 3 = ((7л: + 5)л: - 6)л: + 3, что и надо
было доказать.
При доказательстве в примере а) используется вынесение множителя,
а и примере б) формула разности квадратов.
8 2 2 . а) Число 5 5 - 5 4 4- 5 3 делится на 2 1 ;
5&- 54+ 53= §з. (52_ 5+ 1) _ 58. 21, то есть это число делится на 21;
б) число 9 5 7 2 - 4 3 2 делится на 1000;
9 5 7 2 - 4 3 2 = ( 9 5 7 4- 4 3 ) • ( 9 5 7 - 4 3 ) = 1 0 0 0 * 9 1 4 , то есть это число делит­
ся на 1000.
При доказательстве в примере используется формула разности ква­
дратов.
823. а) (п 4* I)2 - (л - I)2 делится на 4;
(п 4- I)2 - (л - I)2= л2 + 2п 4- 1 - л2 4- 2л - 1 = 4л
или (л 4- I)2 - (л - I)2 = (л 4- 1 4- л - 1)(л 4- 1 - л + 1) = 2л * 2 = 4л,
то есть это число делится на 4;
б) (Зл 4- 2)2 - (Зл - 2)2 делится на 24;
(Зл + 2)2 - (Зл - 2)2 = 9л2 4- 12л 4- 4 - 9л2 + 12л - 4 = 24л
или (Зл 4- 2)2 —(Зл —2)2= (Зл + 2 4- Зл - 2)(3л 4- 2 —Зл 4- 2) = 6л * 4 = 24л,
то есть это число делится на 24;
в) (5л 4- З)2 - (5л - З)2 делится на 60;
(5л 4 З)2 - (5л - З)2 = 25л2 + 30л + 9 - 25л2 4- 30л - 9 = 60л
или (5л + З)2- (5л - З)2= (5л + 3 + 5л - ЗХ5л 4- 3 - 5л + 3) = Юл •6 = 60л,
то есть это число делится на 60.
824. Докажем, что разность квадратов двух нечетных чисел делится на 4.
Решение. Представим два нечетные числа как 2л + 1 и 2т + 1.
(2п 4- I)2- (2т 4- I)2= 4л2 + 4л 4- 1 - 4тп2 - 4т —1 = 4л24- 4л - 4 т 2- 4т -
- 4(пг + п - т2- т), то есть это число делится на 4, значит, разность квад­
ратов двух нечетных чисел делится на 4.
825. Докажем, что разность квадратов двух последовательных нечетных
чисел делится на 8.
Решение. Представим два последовательные нечетные числа как 2л - 1
и 2л + 1.
(2л 4 I)2 - (2л - I)2 = 4л2 4- 4л 4- 1 - 4л2 4- 4л - 1 = 8л, то есть это число
делится на 8, значит, разность квадратов двух последовательных нечет­
ных чисел делится на 8.
026. Докажем, что разность квадратов двух последовательных четных чисел
на 8 не делится.
Решение. Представим два последовательных четных числа как 2л и 2л 4- 2.
(2л 4* 2)2 —(2л)2= 4л2 4~8л 4- 4 - 4л2 = 8л + 4; так как 8л всегда делится
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

130. на 8, а 4 надело на 8 не делится, то их сумма на 8 не делится, значит, раз­
ность квадратов двух последовательных четных чисел на 8 не делится.
82 7 . Докажем, что квадрат нечетного числа при делении на 8 дает в остатке 1.
Решение. Пусть нечетное число 2л 4- 1. Его квадратом будет (2л + I)2 =
= 4л2 + 4л + 1 = 4л(л 4- 1) 4- 1. Так как число л(л 4- 1) является произ­
ведением двух последовательных чисел, то есть четного и нечетного, то
оно четное при любом л, поэтому делится на 2. Значит, число 4л(л 4- X)
делится на 8. (2л 4- I)2= 4л(л + 1) + 1, то есть при.делении (2л 4- 1)2 на
8 в остатке остается 1.
82 8 . а 2 + За + 2 = (а + 1)(а 4- 2);
(а 4- 1)(а + 2) = а2 4- 2а + а 4- 3 = а2 4- За 4- 2. Тождество доказано.
82 9 . х2 + х - 6 = (х + 3)(лг - 2);
(х 4* 3)(лг —2) = х2 - 2х 4- Зх - 6 = х2 4- х - 6. Тождество доказано.
8 3 0 . с2 - 7 с 4-12 = ( с - 3)(с - 4);
(с - 3)(с - 4) = с2 - 4с - Зс 4- 12 = с2 - 7с + 12. Тождество доказано.
83 1 . (а4 + 1)(а2 + 1)(а 4- 1)(а - 1) + 1 = а8;
(а4 4- 1)(а2 + 1)(а - 1)( а + 1) 4- 1 = (а4 4- 1)(а2 + 1)(а2 - 1) 4- 1 =
= (а4 4- 1)(а4 - 1) 4- 1 = с8 - 1 4-1 = а8. Тождество доказано.
8 3 2 . (а 4- I)4 = а4 4- 4а8 4- 6а2 4- 4а 4- 1;
а4 4- 4а3 4- 6а2 4- 4а 4- 1 = а4 4- а8 4- За8 4- За2 4- За2 4- За 4- а 4- 1 =
= а3(а + 1) 4- За2(а 4- 1) 4- За(а + 1) 4- (а 4- 1) = (а + 1)(а3 + За2 4- За +1) =
= (а 4- 1)(а 4- I)3 = (а 4-1)4. Тождество доказано.
8 3 3 . а) х + хл= 0; зс(1 4- я:2) = 0; х = 0 или 1 4- х2= 0; х2= —1 — не имеетре­
шений, так как х2 > 0, а -1 < 0. Ответ: х = 0.
б) 2г2 - 9г + 18 = 23; 2г2 - 9г + 18 = г3; 2г2 - 9г + 18 - г8 = 0;
(2г2 - г3) + (18 - 9г) = 0; г 2(2 - г) + 9(2 - г) = 0; (г2 + 9)(2 - г);
2 —г = 0; г = 2; или г2 4- 9 = 0; г2= -9 — не имеет решений, так как г2> 0,
а - 9 < 0. Ответ: 2= 2.
в) У3 - 2у2 - У + 2 = 0; уЦу - 2) - (у - 2) = 0; (у - 2)(у2 - 1) = 0;
(у - 2Ху - 1)(у + 1) = 0;
у - 2 = 0; или у —1 - 0; или у 4- 1 = 0;
у = 2; у = 1; у = -1 .
Ответ: 2, или 1, или -1 .
г ) х9 + х = З * 2 + 3 ; хъ + х - Зх2 - 3 = 0 ; х(х2 + 1 ) - 3(х2 + 1 ) = 0 ;
(* - 3)(х2 4- 1) = 0;
х - 3 = 0; или х2 4- 1 = 0;
х = 3; х2= —1 — не имеетрешений, так как х2 > 0, а -1 < 0.
Ответ: х = 3.
834. а) х 8 4- 2х2 - х = 2; х3 + 2х - х - 2 = 0; х2(х 4- 2) - (х 4- 2) = 0;
(х2 - 1)(д: 4- 2) = 0; (х - 1)(я: 4- 1)(л: + 2) = 0;
х —1 = 0; или х + 1 = 0; или х 4- 2 = 0;
х = 1; х = -1 ; х = -2 .
Ответ: —2 или -1 или 1.
б) у9 ~ 3у2 4-4у = 12; у2(у - 3) 4- Цу - 3)= 0; (у2 4- 4){у - 3) = 0;
у2 + 4 = 0; или у - 3 = 0;
у2- - 4 ; у = 3.
Так как у2 £ 0, а -4 < 0, уравнение решений неимеет. Ответ: 3.
в) 2дт3 - З*2 4- 4х = 6; 2*3 - Зл:2 4- 4х - 6 = 0; д:2(2д; - 3) 4- 2(2х - 3) = 0;
(2х - 3)(х2 + 2) = 0;
2х - 3 = 0 или х2 4- 2 = 0;
2х = 3 ; х2 - -2 .
х = 1,5. Так как х2> 0, а -2 < 0, тоуравнение решений не имеет.
Ответ: 1,5.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

131. I') 0,52Ъ+ г* + г + 2 = 0; 0,5гг + 2) + (г + 2) = 0; (2 + 2)(0,5г4 + 1) = 0;
г + 2 = 0 или 0,5г4 + 1 = 0;
2 = -2 ; 0,5г2= -1 ;
г2= —2.
Так как гг > 0, а -2 < 0, то уравнение решений не имеет.
Ответ: -2 .
835. а) х 2(ж - 3) + 2х(ж - 3) + ж- 3 = 0; (ж - 3)(ж2 + 2х + 1) = 0;
(х - 3)(ж + I)2= 0;
лг —3 = 0 или х + 1 = О;
х = 0; х = -1 .
Ответ: -1 или 3.
6) х2(2х + 1) - 4х(2х + 1) + 8ж + 4 = О; ж2(2ж + 1) - 4х(2х + 1) + 4(2ж + 1) = 0;
(2х + 1)(ж2 - 4х + 4) = О; (2х + 1)(х - 2)2 = О;
2х + 1 = Оили (х - 2)2= О;
2х = -1 ; х - 2 - О;
х = ——. х = 2.
2
Ответ: — или 2.
2
836. а) ж2(ж2 - 4х + 4) - 9(ж2 - 4х + 4) = 0; (ж2 - 9)(ж2 - 4х + 4) = О;
(х - 3)(х + 3)(* - 2)2= О;
х - 3 = Оили х + 3 = Оили (х - 2)2= О;
х = 3; х = -3 ; х - 2 = О; х = 2.
Ответ: -3 или 2 или 3.
6) х*(х2 - 6х + 9) - 4х(х2- 6х + 9) = О; (х3 - 4х)(х2 - 6х + 9) = О;
х{х2 - 4)(х - З)2= О; х{х - 2)(х + 2)(х - 3)а = 0;
х = 0; или х - 2 = 0; или х + 2 = О; или (х —З)2 = О;
х = 2; дс= -2 ; ж- 3 = О; х = 3.
Ответ: —2 или Оили 2 или 3.
037. а) 8о8 - 4а2 + 2а - 1 = О; 4а2(2а - 1) + (2а - 1) = О;
(4а2 + 1)(2а - 1) = О;
4а2 + 1 = 0 или 2а —1 = 0;
4а2= -1 ; 2а = 1;
1 1
а = — . а = —.
4 2
'Гак как а2 > О, а — < 0, то уравнение не имеет корней.
4
Ответ: —.
2
б) 8а3 —4а2 + 2а - 1 = 4а2 + 1; 8а3 - 4а2+ 2а - 1 - 4а2 - 1 = 0;
8аА- 8а2 + 2а - 2 = О; 8а2(а - 1) + 2(а - 1)= 0; 2 (4а2 + 1)(а- 1) = 0;
4а2 - 1 = 0 или а —1 = 0;
4а2 = —1; а = 1.
аг = —^ . Так как а2 > О, а - ^ < О, то уравнение не имеет корней.
Ответ: 1.
038. а) (х + 1)2+ (х - 1)2- 6 = ^|((лг +1) + (х- 1))j ;
хг + 2х +1 + хг- 2 х + 1 - 6 = +1 + х —1)^; 2яг2- 4 = •2х ;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

132. 2х2 - 4 = х2; 2х2 - х 2 - 4 = О; х2 - 4 = 0; (х - 2)(х + 2) = 0;
х —2 = 0 или * + 2 = 0;
х = 2; х - -2 .
Ответ: ~2 или 2.
б) (х + I)2 + (х - 2)2 - 84 = (х + 2)(х - 1);
х 2 +"2х + 1 + х2 - 2х + 1 - 84 = х2 - 1; х2 - 81 = 0; (х —9)(х + 9) = 0;
х - 9 = 0 или х + 9 = О;
х = О; х = -9 .
Ответ: - 9 или 9.
8 3 9 . Найдем, при каких значениях а:
а) значение выражения а? + За2 - а равняется 3.
а3 + За2 - а = 3; а3 + За2 - а - 3 = О; а2(а + 3) - (а+ 3) = О;
(а + 3)(а2 - 1) = О; (о + 3)(а - 1)(а + 1) = О;
а + 3 = Оили а —1 —0 или а + 1 = 0;
а = 3; а = 1; а - -1 .
Ответ: при -3 ; или -1 ; или 1.
б) значения выражений а3 - а2 и 4а —4 равны.
а3 - а2= 4а - 4; а8 - а2 - 4а + 4 = 0; а2(а - 1) - 4(а - 1) = 0;
(а2 - 4)(а - 1) = О; (а - 2)(а + 2)(а - 1) = О;
а - 2 = 0 или а + 2 = Оили а —1 = О;
а = 2; а = -2 ; а = 1.
Ответ: при -2 ; или 2; или 1.
8 4 0 . а) х2(х2 + 4х + 4) = (5х)2 + 100х + 100;
х2(х2 + 4х + 4) = 25(х2 + 4х + 4); х2(х2 + 4х + 4) —25(х2 + 4х+ 4) = О;
(х2 - 25)(х2 + 4х + 4) = О; (х - 5)(х + 5)(х + 2)2= О;
х - 5 = Оили х + 5 = 0 или (х + 2)2 = О;
х = 5; х = -5 ; х + 2 = О; х = -2 .
Ответ: -5 , или -2 , или 5.
б) 4Х4 - 12х3 + 9х2= 36х2 - 108х + 81; х2(4х2- 12х + 9) = 9(4х2- 12х + 9);
х2(2х - З)2 - 9(2х - З)2= 0; (2х - 3)2(х2 - 9) = О; (2х - 3)2(х - Щ х + 3) = 0;
(2х - З)2= Оили х - 3 = 0 или х + 3 * О;
2х - 3 = О; х = 3; х = -3 .
2х = 3; х = 1,5. Ответ: -3 , или 1,5, или 3.
8 4 1 . а) х 2(9х - 6х + 1) = (6х)2 - 24х + 4; х2(9х2 - 6х + 1) = 4((3х)2 - 6х + 1);
(х2 - 4)(9х2 - 6х + 1) = О; (х - 2)(х + 2)(3х - I)2= О;
х - 2 = Оили х + 2 = 0 или (Зх - I)2= О;
х = 2; х = -2 ; Зх - 1 = 0; Зх =1; х = —.
1 3
Ответ: -2 , или —, или 2.
и
б) 4х* + 56х3 + 196х2 = х2 + 14х + 49; 4х2(х2 + 14х + 49х2) = х2+ 14х + 49;
4х2(х + 7)2 - (х + 7)2= О; (х + 7)2(4х2 - 1) = О; (х + 7)2(2х - 1Х2х + 1) = 0;
(х + 7)2= ОИли 2х 1 = Оили 2х + 1 = 0;
х + 7 = 0; 2х = 1; 2х = -1 ;
Ответ: -7 , или — , или —.
2 2
842. а) а4 + 4Ь4 = а4 + 4а2Ь- + 4Ь* - 4а?Ъг = (а2 + 2Ъг)г - 4а2Ь2=
= (а2 + 2Ьг - 2аЬ)(а2 + 2Ь2 + 2аЬ);
б) Ж4 + X2 + 1 = X* + хг + 1 — X2 + х2 — X2 = х* + 2 х 2 + 1 - хг =
* = (ж2 + I)2 - хг = (ж2 + 1 —х)(ж2 + 1 + ж);
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

133. п) X54 X + 1 = X5- X24 X2 4 X 4 1 = х2(х3 - 1) 4 (X2 4 X 4 1) =
- х2(х - 1)(х2 4 х 4 1) + (л:24 х 4 1) = (х2 + х 4 1)(х2(х - 1) 4 1) =
-=(х24 х 4 1)(*8 - х2 4 1);
Задания д ля самостоятельной работы
При решении используются формулы разности квадратов (1) а2 - Ь2 =
(а - Ъ)(а 4 Ъ), квадрата суммы (2) (а 4 Ъ)2= а А4- 2аЪ 4 Ь2, квадрата разно­
сти (3) (а - = а2—2аЬ + Ь2, разности кубов (4) а3 ( а - Ъ)(а24 аЬ 4 Ь2}
и суммы кубов (5) а3 4 Ь3 = (а 4 Ь)(а2 —аЬ 4 62), а также вынесение об­
щего множителя за скобки (6).
Вариант 1
1. п) ж2 ~ 9с2= ( х - 3с)(х 4 3с); (1)
б) 27 4 а3 = (3 4 а)(9 - За 4 а2); (5)
и) х3— 2х2у 4 ху2 = х(х2 - 2ху 4 у2) = х(х — у)2; (6) и (3)
г) (2х 4 I)2 - 49 = (2х 4 I)2 - 72= (2х 4 1 - 7)(2х 4 1 4 7) =
- (2* - 6)(2х 4 8)= 2(х - 3) * 2(х 4 4) = 4(х - 3)(х 4 4).
2 . Докажем, что 710 - 79 4 7е = 7йделится на 43.
7ю- 79 4 7й= 7®•(72 —7 4 1) = 7®■43; полученное число делится на 43,
значит, и 710 - 79 + 7йделится на 43.
3. Решим уравнение (* 4 3)(х2 - Зх 4 9) = х8 - 3*; х3 4 З3 = х3 - 3*;
*3 - х3 4 Зх = -27; Зх = -27; х = -2 7 ; 3; х = -9 . (5)
Вариант 2 .
1. Разложим на множители многочлен:
а) а2 - 16с2= (а - 4с)(а 4 4с); (1)
б) 8с3 — 1 = (2с - 1)(4с2 4 2с 4 1); (4)
и) а4 — 2а3с 4 а2с2 = а2(а2 - 2ас 4 с2) = а2(а - с)2; (6) и (3)
I’) 64 - (3* - 2)2 = 82 - (3* - 2)2= (8 - Зх 4 2)(8 4 3* - 2) =
- (10 - Зх)(6 4 Зх) = 3(10 - 3х)(3 4 *). (1) и (6)
2 . Докажем, что число 79 + 7й+ V делится на 57.
7я4 78 4 V = 77* (72 4 7 4 1) = V •(49 4 7 4 1) = 77•57;
полученное число делится на 57, значит, и 79 4 78 4 77делится на 57.
3. Решим уравнение (х 4 З)2 - (х - 4)(х —2) = 5;
х'г 4 6х 4 9 - х2 4 2х 4 4х - 8 = 5; 12х = 5 4 8 —9;
12х = 4; х = — ; х = —. (2)
12 3
Вариант 3
1. и) т2 - 25х2 = (тп - 5х)(т 4 5х); (1)
б) 27п3 4 а3= (3п 4 а)(9м2 - Зпа 4 а2); (5)
и) т2п2 - 2тп 2 4 п2 = п2(т2 - 2т 4 1) = п2(т - I)2; (6) и (3)
г) 49 - (2 - 5х)2= 72 - (2 - 5х)2 = (7 - 2 45х)(7 4 2 - 5х) =
(5 4 5х)(9 - 5х) = 5(1 4 х)(9 - 5х). (1) и (6)
2 . Докажем, что число 89 4 88 4 87 делится на 73.
8» 4 8е 4 87 = 87* (82 4 8 4 1) = 87 ■(64 4 8 4 1) = 87 •73;
полученное число делится на 73, значит, и 89 4 8а 4 87 делится на 73.
3. Решим уравнение (х - 2)(х2 4 2х 4 4) = х3 4 2х;
хл - 8 - х3 - 2х = 0; -2 х = 8; х = -8 ; х = -4 . (4)
дг= 4.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

134. Бариант 4
1. Разложим на множители многочлен:
а) 64а2 - ж2= (8а - ж)(8а 4- ж); (1)
б) 1 - 64z3= (1 - 4z)(l + 4z 4- 16г2); (4)
в) х5 - 2х* + ж3= ж3(ж2 - 2х 4- 1) = ж3(ж - I)2; (6) и (3)
г) 36жг - (1 - ж)2= (бас)2 - (1 - ж2) = (6ж + 1 - ж)(6х - 1 4- х) =
= (5ж + 1)(7ж - 1). (1)
2. Докажем, что число 88 4- 87 - 86 делится на 7.
8е + 87 - 86= 86 - (82 4- 8 - 1) = 86•(64 + 8 - 1) = 86 - 71;
полученное число делится на 71, значит, и 8® 4- 87 —86 делится на 71.
3- Решим уравнение (ж + 1)(ж2 - х 4- 1) = х3 - 2х;
х3 + 1 - х3 + 2х; 2х = -1 ; х = (5)
2
Готовимся к тематическому оцениванию
Тестовые задания № 5
1. 42 + 4у* + (у2)2 = 16 4- 4у2 4- у2, (г)
2. х2 4- 4ж 4- 6 = (ж2 4- 4х 4- 4) 4- 2 = (ж 4- 2)2 4- 2.
(ж 4- 2)2 > О. Наименьшее значение (ж 4- 2)2 = О; ж4- 2 = О; ж= -2 . (в)
3. 550- З50 - (1525 - 1) * (1525 4- 1) = 1530 - ((1525)2 - 1) = 1550 - 1550 4- 1 = 1. (а)
4. а 2 —а •5с 4- (5с)2- а 2 - бас 4- 25с2. (б)
5. ж3 —27 = (ж —3)(ж2 + Зж 4- 9). (б)
43
Если 2 = 4, т о 27 = 8 - 27 = -19. (а)
8 v 9
7 . 4ж3 - 16ж = О; 4ж(ж2 - 4) = 0; 4ж(ж - 2)(ж 4- 2) = 0;
ж= О; или ж- 2 = О; или ж4* 2 = 0;
ж= 2; ж= -2 .
г) -3 .
8 . ж5 - ж4 - ж+ 1
ж5; -ж4; -ж; 1.
б) 4.
9. (16 - 4у2 4- у4)(у2 + 4) = (42 - 4 - у2 4- (#2)2)(|/2 4- 4) = 43 + (у2)3= 64 + у (б)
10. а3 - а.
а3 = а = а(а2 - 1) = а(а —. 2)(а 4- 1) = (а - 1)а(а 4- 1).
а ~ 1 ; а ; а 4 - 1 — три последовательных натуральных числа. Значит, одно из
них обязательно делится на 2 и одно из них обязательно делится на 3.
Значит, выражение делится на 2 •3 = 6.
6 )6 .
Контрольная работа № 5
1. а) ж2 - 16 = (ж - 4)(ж 4- 4); б) а3 4- с3= (а 4- с)(а2 - ас 4- с2).
2. а) ж2 - 25 = 0; (ж - 5)(ж 4- 5) = 0; (ж - 5)(ж 4- 5) = 0;
ж- 5 = 0; или ж 4- 5 = 0;
ж= 5; ж= -5 ;
Ответ: -5 или 5.
б) а2 - 6ж 4- 9 = 0; (а - З)3= 0; а - 3 = 0; а = 3.
Ответ: 3.
3. а) (а - 2)(а2 4- 2а 4: 4) = а3 —23= а3 —8;
б) (Зж 4- 1)(9ж2 - Зж 4- 1) = (Зж)3 + I 3= 27*э 4- 1.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

135. 4. (<| х)2 + 4ах = (а + * )2.
(« - л:)2 + 4ах = а2 —2а* + х2 + 4а* = а2 + 2а* + * 2 = (а + *)2.
Тождество доказано.
Г») 1000а9 - Ь3св = -(1000а° + 63св) = -(10а3 + 6с2ХЮ0а6 - 10а36с2 + Ь2с4).
С. 27р:*- (Зр - 1X9р2 + Зр + 1) + р + 2, если р = 0,897;
21рл - (Зр - 1)(9р2 + Зр + 1 ) + р + 2 = 27р8 - (27р3 - 1) + р + 2 =
27р3 - 27р3 + 1 + р + 2 = р + 3 = 0,897 + 3 = 3,897.
7. л) За5*3 - 24а2с6 = За2ф3 - 8св) = За2(а - 2с2)(а2 + 2ас2 + 4с4);
Г») 25*2 - 10ху + у2 - 36 = (5* - у)2 - 62= (5* - у - 6X5* - у + 6);
») 8а3 + 4а26 - 2аЬ2 - Ь 3= 4а2(2а 4* Ь) - Ь2(2а + 6) = (2а + Ь)(4а2 - Ь2) =
(2а + 6)(2а - Ь)(2а + 6) = (2а + 6)2(2а - Ь).
0. и) хй—4*3 = О; * 3(*2 - 4) = 0; * 3(* - 2)(* + 2) = О;
хя= О или * - 2 = 0 или * + 2 = 0;
х = О; * = 2; * = -2 .
Ответ'. —2, или О, или 2.
б) * 5 + З*4 + З*3 + * 2= О; * 2(*8 + З *2 + 3 * + 1) = О; * 2(* + I)2= О;
*2= О или (* + I)2= О;
х = О; * + 1 = 0;
Ответ: —1 или 0.
») х4 - Юх3 + 250х - 625 = 0; х4 - Юх3 + 25х2 + 250х - 625 = О;
х2(х2 - Юх + 25) - 25(х2 - Юх + 25) = О; (х2- 25Х*2 “ Юх + 25) = 0;
(х - 5)(х + 3)(х г- 5)2 = 0; (х - 5)3(* + 5) = 0;
(х - 5)э = 0 или * + 5 = 0;
х - 5 = О; х = -5 .
х = 5.
Ответ: —5 или 5.
9. 97* + 783 + 972 - 78* делится на 175.
97я+ 783+ 972- 782= (97 + 78) •(972- 97 * 78 + 782) + (97 - 78) - (97 + 78) =
- 175 •(972 - 97 - 78) + 782 + 19 = 175 •(972 - 97 - 78 + 78 + 19).
Один из множителей произведения равняется 175, значит, произведение
делится на 175, а значит, и 973 + 783+ 972 —782делится на 175.
10. а) а4 + 9Ь4 = (а2)2 + 2а2* ЗЬ2 +(3Ъг) - 2а2 •3Ь2= (а2 + 362)2=
б) уъ+ у + 1 = уъ~ ул + у2 + у + 1 = уЧу3“ 1) + (у2 + у + 1) -
уЧу “ 1){у2 + у + 1) + (у2 + у + 1) = (у2 + у + 1КуЧу - 1) + 1) =
(У2 + У + 1)(у3 - У2 + 1)-
Готовимся к тематическому оцениванию
Тестовые задания № 4
1.6)
2. н)
3. а)
4. (а + 2Ь)2 = а 2 + 4аЬ + 4Ь2.
5. г) х3 —Зх2 + Зх —1 = х3 —3 •х2* 1 + 3 *х •I2 —I3= (* - I)3.
6. 6) 0,25х2 + у2 - ху = (0,6х)2 - 2 •0,5х - у + у2= (0,5* - у)2 = (у - 0,5*)2.
7. в)
К. II) — + 0,008у3 = + 0 .2 » ) ^ - - ~ 0 , 2 у + 0,04^ 1
* = — 1 .
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

136. 8.в) (6* - 8)2 = (2(3* - 4))2 = 22(3х - 4)2= 4(3* - 4)2.
9 . б) (2а4 + Ь*) *М = 4а8 - Ь6;
(2а4 + Ь3) * М = (2а4 - 6э)(2а4 + 68);
М = 2а4 - Ь3.
10. а) ж2— 16* + 64 = 0; (х - 8)2= 0; х - 8 = 0; х = 8.
Контрольная работа № 4
1- а) 12а3 - 18а2= 6а2(2а - 3); б) 60а4Ь5+ 36а3*>6- 48авЬ2= 12о362(5аЬя+ ЗЬ4- 4).
2 . а) 5а + 5Ь + аЪ + Ь2= 5(а + Ъ) + Ъ(а + &) = (а + Ь)(5 + &);
б ) ж - Зх# - 21# + 7 = х(1 - 3 # ) + 7 ( - 3 # + 1) = (1 - 3 #)(х+ 7 );
3. а) х2 - 8* +-16 = х2 - 2 *х •4 + 42 = (х - 4)2,*
б) 9х2 + 6* + 1 = (Зх)2 + 2 * Зх * 1 + I2 = (Зх + I)2;
4 . а) 2аЬ + 2ас + хс + хЪ + 5с + ЬЪ = 2а{Ъ + е) + х(с + Ь)+5(с + Ь) =
= (с + Ь)(2а + х + 5);
б) 16х2 - 25 = (4л:)2 - 52= (4х - 5)(4х + 5);
в) (За + 2)2 - 36а2= (За + 2)2 - (6а)2 = (За + 2 - 6а)(3а + 2 + 6а) =
= (2 - За)(9а + 2);
5. а) 2л:# - 2х + 4# - х2, если # = 2,55; х = 5,1.
2ху —2х + 4# - х2= (2ху - х2) + (-2л: + 4#) = х(2# - 1) + 2(2# - 1) =
= (2# - 1)(х + 2) = (2 - 2,55 - 1)(5,1 + 2) = 4,1 •7,1 = 29,11.
6 . 27л? + 108л:2 + 144л: + 64 = (Зд:)3 + 3 * (Зд:)2 •4 + 3 •Зх * 42 + 43 = (Зх + 4)3
7. а) 9л:2 + 6л: + 1 = О; б) 48л:3 + 12л: = 0;
(Зл: + I)2= 0; 12х(4х2 + 1) = О;
Зх + 1 = 0; 12х = О; или 4х2 + 1 = 0 ;
З х = ~ }; * = 0. 4х2= -1 ; х2
X = ----. ^ ^
3 Так как х2 > О, а — < О, то уравнение
1 4
Ответ'. 4х2+ 1 = 0 решений не имеет.
Ответ: О.
8 .1 3 •З8 + 12 *З7+ 45 *З6- 54 *З5= 13 •З8 + 4 - 3 •З7 + 5 •9 *З6 - 2 *27 •Зб=
13 ♦З8 + 4 * З8 + 5 •3е - 2 * З8 = З8 (13 + 4 + 5 - 2) =
= З8 •20 = З3 - З5 •2 - 10 = (З5 * 2) * 270.
Один из множителей произведения равняется 270, значит, произведение де­
лится на 270. Значит, данное выражение делится на 270.
9- 2п - 1 и 2п + 1 — два последовательных нечетных числа.
(2л + I)2 - (2л - I)2= 4л2 + 4л + 1 - 4л2 + 4л - 1 = 8л.
Один из множителей произведения равняется 8, значит, произведение де­
лится на 8. Значит, разность квадратов двух непоследовательных нечет­
ных чисел делится на 8.
10. (б+ 1)(б2+ 1)(б4+ 1)(б' + 1)(би +1) —0,2-632 =
= - р - •(6 -1 ) (6 +1) (б2 +1) (б4 +1) (б8 +1) (б16+1) - 0,2 •б32 =
= - (6 -1 ) (б2 +1) (б4+1) (6е +1) (б16+1) - 0 ,2 ■б32 =
5
= 0,2(б4 - 1)(б4 + 1)(б” +1)(б1в+ 1 ) - 0 , 2 - 6 32 =
= 0,2 (6е- 1)(б8 +1)(б16+ 1) - 0,2 ■632 = 0,2 (6“ - 1) (б16+ 1) - 0,2 -632 =
= 0 ,2 - (б32- 1) - 0 ,2 - 632 = 0 ,2 - 632- 0 ,2 - 0 ,2 б32 = - 0 , 2.
Ответ: -0 ,2 .
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

137. Раздел IV. Функции
§ 21. Что такое функция
Нгли каждому значению переменной х из некоторого множества В от-
1н*члет единственное значение переменной в у то переменная в называ­
ется функцией от X.
II«‘ременная х называется аргументом данной функции, множество
/> — областью определения данной функции, а соответствие между х и
ч — функциональным соответствием. Аргумент — это независимая пе­
ременная, а функция — зависимая переменная._______________________
051. Ответ: Периметр квадрата считается по формуле Р = 4а, где а — сто­
рона квадрата, то есть периметр квадрата зависит от длины стороны и
лиляется функцией от длины стороны квадрата.
052. Ответ: Если объем куба находят по формуле V = а3, где а — длина ребра
куба, то V является функцией от а, а — аргумент функции.
053. Ответ: Если площадь круга находят по формуле 5 = яг2, где г — радиус
круга, то площадь круга 5 является функцией радиуса круга г. Область ее
определения — множество положительных действительных чисел, потому
что площадь и радиус — положительные величини.
054. Ответ: т ~ У р = 8,6У, то есть т = 8,6У — тут т является функцией
от V, а V — аргумент этой функции. Область определения — множество
положительных действительных чисел, потому что масса и объем — по­
ложительные величини.
055. Ответ: &= VI - 5 5 * ; переменная £ является функцией от ^
056. Ответ: Площадь прямоугольника 5 = 5*. 8 является функцией от х,
а х ‘— аргумент функции.
057. Ответ: Периметр равностороннего треугольника равняется Р = а + а + а -
- За, то есть Р = За — формула для определения периметра равносто­
роннего треугольника, в которой а — сторона треугольника. Значит, Р
является функцией от а.
058. Зависит ли диаметр окружности й от его радиуса г? Выразите эту зави­
симость формулой. Диаметр окружности считается по формуле й = 2 г, где
г — радиус окружности, то есть диаметр окружности зависит от его радиу­
са и является функцией от радиуса окружности. ^
059. Ответ: Так как а и р являются смежными углами,
то а + р = 180° или а = 180° - р. а является функцией
от Р; р — аргумент этой функции.
0 6 0 . Так как + ZB = 90°, то ZA = 9 0 ° — ZB,
а ZB = 9 0 ° - УА.
Мера угла А является функцией от угла В, мера ZB —
аргумент.
Мера угла В является функцией от угла А, мера ZA — ^
аргумент.
061. Найдем значение функции, если х равняется:
1; 0 ; -3 ; 7; 1 0 0 0 , а функция задана формулой
у = 2х + 5 . Если х = 1, то I/ = 2 * 1 + 5 = 7;
если х = 0 , то у = 2 •0 + 5 = 5 ;
если х = -3 , то у = 2 * (-3) + 5 = - 1 ;
если ж= 7, то I/ = 2 * 7 + 5 = 1 9 ;
если х = .1 0 0 0 , то у = 2 • 1 0 0 0 + 5 = 2 0 0 5 .
Т*к
г .
%
Ш:
'хг
р
'Оч.
1Д.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

138. 862. Функция задана формулой у = —. Заполним таблицу.
х
X -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
У -1
5 2
-2 -3 ~6 — 6 3 2 і і
2
і і
5
1
863. Составим таблицу значений функции т = 42 - Зп для первых десяти
натуральных значений переменной п.
п 1 2 3 4 5 6 7 8 9 10
ТП 39 36 33 30 27 24 21 18 15 12
864. Ответ: Это соответствие является функцией у = х2, где * — числа сле­
ва, область ее определения — натуральные числа от 1 до 6, область зна­
чений — числа 1; 4; 9; І6; 25; 36.
865. Это соответствие является функцией, потому
что каждому значению аргумента (1; 2; 3; 4) от­
вечает единственное значение переменной справа
натуральные числа 1;
(ь І . А. I )
Г 2 ’ 3 ’ 4 У
Область ее определения
2; 3; 4. 1 1 1
Область ее значений — числа 1; —; —; —
2 3 4
ратные числам из области определения.
об-
* > - Ь
откуда8 6 6 . Реш ение. Если у = 20, то
3
х = —*20 = 30. Ответ: х = 30.
2
867. Функция задана формулой у = 0,3х. Заполним таблицу:
* -1 0 -3 -1 0 4 5 50
У -3 -0 ,9 -0 ,3 0 1,2 1,5 15
868. у = х2 + 3.
* 1 2 3 4 5 6 7 8 9 10
У 4 7 12 19 28 39 52 67 84 103
869. а) у = Зх —7. Областью определения функции является множество всех
действительных чисел.
х
б) I/ = —-----; х + 5 Ф 0; х ф -5 . Областью определения функции является
* + 5
множество действительных чисел, кроме X = -5 .
в) у = 5лс2 - х + 3. Областью определения функции является множество
действительных чисел.
870. Решение. 5 грн. = 500 к. Так как на карандаши ученик истратил 60* к,,
то у него осталось (500 - 60х) к., что составляет у к. Составим уравнение,
которое выразит зависимость у от *: у = 500 - 60 х.
500 в 1
Ученик может купить минимум 0 и максимум = 8^ карандашей,
но карандаши продаются поштучно, то есть целыми, поэтому область
определения функции — целые числа от 1 к 8.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

139. 071. Так как масса товара т по 2,5 грн. за килограмм, то стоимость товара
= 2,5т . Если т = 18 кг, то г = 2,5 * 18 = 45 (грн.).
г 125
1'л:ли 2 = 125 грн., то т = ---- = -------= 50 (кг).
2,5 2,5
072. Так как нефть проходит по трубе со скоростью 12 т/ч., то за 3 часа по
трубе проходит 12 * 3 = 36 (т) нефти. За £ часов — 12# (т).
т = 12*, где /71 — нефть, которая проходит по трубе за #часов.
073. В одном часе 60 мин. Значит, в #часов 60£ минут, х = 60#, где £ — время
и часах, х — время в минутах.
£ 1 2 2.5 3 3,5 4 5 6 6,5 7
X 60 120 150 180 210 240 300 360 390 420
074. а) у ——2х; б) у = 5х; в) у ——х +12; г) у = ^
075. а) у = 8* - 5. 2 х + 4
х = -2 ; у = (-2) - 5 = -21; х = О; # = 8 - 0 - 5 = —5;
* = 1,5; у = 8 •1,5 - 5 = 7; х = 12; у = 8 - 12 - 5 = 91;
х = 25; у = 8 * 25 - 5 = 195.
б) у —- —+ 1;
- 8 ^ ч Лг - -8 ; у —-+ 1 = 5; х = —1; у — ь1 = 1—;
у -2 2 2
0 * * * 1 * 1дг= 0; */= - - + 1= 1; * = 1; у = - - + 1= - ;
20
х = 20; # = ----н1 = -9 .
* 2
876. а) у = Зх + 2;
у = 8; 8 = Зх + 2; Зх = 8 - 2; Зх = 6; х = 2. Ответ: 2.
у = 2; 2 = 3 х + 2; Зх = О; х = О. Ответ: О.
гх 46) у = — - ;
х - 3
4 4
I/ = -2 ; -2 = ------- ; -2 (х - 3) = 4; х - 3 = — ; х - 3 = —2; * = 1. Ответ: 1.
х - 3 -2
5 5
у = 2; 2 = ------- ; 2(х - 3 ) = 5 ; х - 3 = —; х - 3 = 2,5; х = 5,5. Ответ: 5,5.
х - 3 2
и) # = *(* + 6);
// = -9 ; х(х - 6) = -9 ; х2 + 6х + 9 = О; (х + З)2= О; х = -3 . Ответ: -3 .
у = О; х(х + 6) = 0; х = О; или х + 6 = О; х = -6 . Ответ: -6 или О.
077. Пусть угол при основании равнобедренного треугольника а , а при вер­
шине - р. Так как сумма углов треугольника равняется 180°, а углы при
основании равнобедренного треугольника равны, то
1СП° 14 А
и + а = 180°; 2а = 180 —р; а = ——; а = 90° - — — функция.
2 2
Область определения функции — это все возможные значения угла р, то есть
О< р < 180°.
078. Так как Я = 1>£, то если V = 70 км/ч., то 5 = 70# — зависимость пути 5,
пройденного автомобилем, от времени #.
£, ч. 1 2 3 4 5 6 7 8 9 10
Б, км 70 140 210 280 350 420 490 560 630 700
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

140. 8 7 9 .5 = 5 км/ч.; і>= 4 км/ч.; іх = 10 мин. = ^ ч = —ч .
20 1
и = 20мин. = — ч = —ч
2 60 3
30 1
#я= 30 мин. = — ч = —ч . 5. — ?
э 60 2 1
5, — расстояние до города, на котором будет турист через £ часов.
Б2 — расстояние, на которое турист приблизился к городу,
в = 81+ 5 2; = 5 - 5 2; 5 2= Ы; = 5 - 4Х — функция от времени.
1) Я, = 5 - 4 - 1 = 5 - 1 = 4 1 (км); 2) = 5 - 4 1 = 5 - 1 1 = (км);
О О О О О О
3) 53= 5 - 4 ^ = 5 - 2 = 3 (км). * = — = ^ = 1,25 (ч.) = 1 ч. 15 мин.
Область определения функции — значение £ от 0 ч. 0 мин. до 1 ч. 15 мин.
1 2
Ответ: 4 — км; 3 - км; 3 км.
3 3
8 8 0 . Было на складе — 600 т угля. Ежедневно привозили — по 40 т угля.
т — количество угля на складе. * — количество дней, в которые на склад
привозили уголь, т = 40* + 600 — функция от #.
60
8 8 1 . Составим таблицу значений функции у = -----7 для целых значений
ЛГ+ 1
аргумента х, если -5 < х < 5.
X -5 -4 -3 -2 -1 0 1 2 3 4 5
У -1 5 -20 -3 0 -6 0 — 60 30 20 15 12 10
8 8 2 .1 дюйм = 2,54 см. Пусть с1 — расстояние в дюймах, а Ь — расстояние
Ь
в сантиметрах, тогда Ь = 2,54с? и й = -------.
2,54
йу дюймов 1 2 3 4 5
Ь , см 2,54 5,08 7,62 10,16 12,7
Ь9 см 1 2 3 4 5
дюймов
-------- *
~ 0,39 * 0 , 7 9 * 1,18 * 1,57 * 1,97
883. Р — 4а; а - — .
4
С
884. С = 2яг; г = — .
2п
885. Найдем область определения функций, заданных формулой:
а) у = х; область определения — множество действительных чисел;
4
3
б) у = — ; х ф 0; область определения — множество действительных чй-
4х
сел, кроме х = 0;
д
в) у —------- ; 4 + х Ф 0; х ф -4 ; область определения — множество дей-
х + 4
ствительных чисел, кроме х ф -4 ;
г) у = -------- ;х(х- 3) Ф 0; х Ф 0; х Ф 3; область определения — множе-
х (х —3)
ство действительных чисел, кроме х = 0; х = 3;
д) у = х2; область определения — множество действительных чисел.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

141. 886. а) у = х(х + 5); область определения — множество действительных чисел,
б) у - (х2 + 6)(х + 8); область определения — множество действительных
чисел.
16
н) у = х + 5 ф 0; х ф —5; область определения — множество' дей-
х + 5
ствительных чисел, кроме X —0.
г) У ——— —■I 8х - 1 ф О; 8х ф 1; х ф —
8 х - Г 8
Область определения
X
д) у =
множество действительных чисел, кроме X
; х2 - 36 ф 0; (х - 6)(х + 6) ф 0; х - 6 ф 0;
1
8
х" - 3 6
и х + 6** 0; х ф 6;
х Ф -6 .
Область определения — множество действительных чисел, кроме х
2х
6.
е) у
-5 х
1 - 2 6 * 2 ’ 1
25х2ф 0; (1 - 5х)(1 + 5х) * 0; 1 - 5х ф 0; 1 + 5х ф 0;
Область определения — множество1; 5х = -1 ; х ф —; х Ф —
5 5
действительных чисел, кроме х = ± —.
о
887. Решение. Площадь данного квадрата равняется 10 * 10 = 100 (см)2, пло
щадь вырезанного круга считается по формуле
71х2. Как видно из рисунка, площадь образованной
фигуры равняется разности площадей квадрата и
круга, .тоесть выражается функцией от радиуса кру­
га XI &фиг= 100 —тех2. Площадь и радиус — положи­
тельные величини, то есть радиус круга должен быть
не большим половины длины стороны квадрата
10 см : 2 = б см. Значит, область определения функ­
ции — значения х, которые являются решением не­
равенства 0 < ж< 5.
888. а) Площадь прямоугольника равняется 7 - 10 = 70 (см2). Площадь вырезан­
ного круга считается по формуле 5 = ях2.
Значит 5фиг= 70 —ях2. Область определения — зна­
чения х, которые являются решениями неравенства
0 < х < 3,5, где х — радиус круга должен быть не
больше половины меньшей из сторон прямоуголь­
ника: 7 см : 2 = 3,5 см.
б) Площадь большей окружности равняется я •82=
= 64я (см2).
Площадь малой окружности равняется ях2.
= 6471 ~ п* 2- “ * 2)*
Область определения — значения х, которые являются
решениями неравенства 0 < х < 8.
889. а) у
■ { -
2х + 5, если х < 0 ;
2х + 5, если х > 0.
X -3 -2 -1 0 1 2 . 3
У -1 1 3 5 3 1 -1
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

142. б) у
х 2 + 3, если х < О;
—+ 3, если х > О.
2
JC -3 -2 -1 0 1 2 3
У 12 7 4 3 3,5 4 4,5
890*. а) у = -
-1, если х < -1;
1
—, если X > -1 .
X
* -3 -2 -1 0 1 2 3
У -1 -1 -1 -1
1 1
2 3
“(х + 1)2, если х < О;
х 2 + 2, если х > О.
-3 -2 -1 0 1 2 3
У ”4 -1 0 -1 3 6 11
891 *. Taie как конфет п и в красных обертках на 6 больше, чем в зеленых, то
п
конфет в красных обертках —+ 3 штук. Вероятность того, что произвольно
* * - 1+3взятая конфета будет в красной обертке, равняется —
п 2п
n 10 20 30 40 50 60 70 80
вероят­ 4 13 3 23 14 11 19 43
ность 5 20 5 40 25 20 35 80
Упражнения для повторения
892- а) (0,5а - 0,46X0,5а + 0,46) •2а6 = (0,25а2- 0Д662) * 2а6 = 0,5а36 - 0,32а63;
б) 10дс2у(0,2л: + 2у){-0,2х + 2у) = 10х2у(4у2- 0,04дг2) = 40х2уг - 0,4х*у;
В) ^ “ I ^ + 1 у) ' (~9хУ) = ~ | (-Эху) = ~х?у + 4ху* =
= 4ху3 - х3у,
9
г) + 1j f l - (-46) = f l - | a V j- (-46) = 9a V 46.
I i
893. А(5; 2); В(3; 2); С(0; 2); АД-1; 2); Н (-3; 2); Р(2; 2)
Все точки лежат на одной прямой, потому
что ординаты всех точек одинаковые и рав­
няются 2.
Середина отрезка АВ — точка (4; 2); ; ;
середина отрезка АС — точка (2,5; 2); _|
середина отрезка АМ — точка (2; 2);
середина отрезка АН — точка (1; 2);
середина отрезка АР — точка (3,5; 2).
8 94. а) 4(х - 3) + 2(5 - х) = 8;
4х —12 + 10 - 2х = 8; 2х - 2 = 8; 2х = 10; Г
х = 5. I I ! I
УЬ
Î5
I4
й т 39
| *2
i ! ‘ 1
Л °
г2'
i-з
I I -
А
t i t
■!>*
I i
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

143. 6) 7(5 - у) + 8(г/ - 3) = 18; 35 - Чу + 8у - 24 = 18; у + 11 = 18; у = 7.
и) 6(г + 2) —5(г - 2) = 20; 62+ 12 - 5г + 10= 20; г + 22= 20; г - —2.
г) 9(* - 4) - 8(5 + #) = -7 9 ; 9# - 36 - 40 - 8* = -7 9 ; #- 76 = -7 9 ; * = -3 .
Было Стало
I пол. X кн. (х - 3) кн.
II пол. (88 - х) кн. (88 - х + 3) кн.
11усть на первой полке х книг, тогда на второй полке было (88 - х) книг.
Нели с первой полки переложить на вторую 3 книги, то на первой станет
(х - 3) книг, а на второй — (88 - х + 3) книг = (91 - ж) книги. Зная, что
книг станет поровну, составим и решим уравнение: х - 3 = 91 - х;
х + х = 91 + 3; 2х = 94; х = 47. На первой полке было 47 книг;
88 - 47 = 41 (книжка) была на второй полке. Ответ: 47 книг и 41 книжка.
§ 22. График функции
696. Просклоняйте слово:
а) аргумент; б) функция; в) график.
Именительный: аргумент; функция; график;
Родительный: аргумента; функции; графика;
Дательный: аргументу; функции; графику;
Винительный: аргумент; функцию; график;
Творительный: аргументом; функцией; графиком;
Предложный: на аргументе; на функции; на графике.
897. а) да; б) нет; в) да; г) нет.
898. а) с 0 ч. до 11 ч. и с 23 ч. до 24 ч. температура была отрицательной;
с 11 ч. до 23 ч. температура была положительной;
б) £ = -3° в 2 часа и в 8 часов 30 мин.; £ = —1° в 10 часов и в 24 ч.; £ = 0°
в 11 ч. и в 23 ч.; £ = +2° в 13 ч. и в 19 ч.;
в) в 7 чЛ = - 4 °С; в 14 чЛ = +2,5 °0; в 21 чЛ = +1,3 °С;
г) температура снижалась с 0 ч. до 7 ч. и с 16 ч. до 24 ч.;
температура повышалась с 7 ч. до 13 ч. 20 мин.;
д) температура была постоянной с 13 ч. 20 мин. до 16 ч. и была +2,5 °С;
е) температура была ниже, чем -3 °С с 2 ч. до 8 ч. 30 мин.
899. Докажем, что график функции у = х2 + 1 не пересекает ось абсцисс.
Так как х2 > 0, а 1 > 0, то х2 + 1 > 1, а это означает, что ордината у может
принимать только положительные значения, не меньшие, чем 1. Значит,
все точки графика данной функции расположены на координатной плос­
кости над осью абсцисс. Это означает, что график функции у = х2 + 1 не
пересекает ось абсцисс.
900. Пересекает ли ось абсцисс график функции у = х2 —9?
Областью определения данной функции является множество действитель­
ных чисел.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

144. Пусть: а) х = О, тогда у = О2 - 9 = -9 ; -9 < 0;
б) х =■5, тогда у = 52 - 9 = 16; 16 > 0.
Значит, для данной функции нашли точку графика, которая на коорди­
натной плоскости расположена под осью абсцисс (точка (0; -9)) и нашли
точку графика, которая на координатной плоскости расположена над осью
абсцисс (точка (5; 16)). Тогда линия, которой изображается график фун­
кции, пересекает ось абсцисс. Значит, график функции у = х2 - 9 пере-
секает ось абсцисс.
901 - (0; 0) — координаты начала координат,
а) у = 0,5* —1; 0 = 0,5л; - 1; 0 ф - 1 .
Не проходит.
б) у = -2 ,5 л:2; 0 - -2 5 * О2; 0 = 0. Проходит.
в) у ~ 3л:;'0 - 3 * 0; 0 = 0. Проходит.
г) У - Рх + 2; 0 = р - 0 4- 2; 0 Ф 2.
Не проходит.
Д) У - 3 •Зл:; 0 = 3* 3 •0; 0 = 0. Проходит,
е) у - х - Зж2; 0 = 0 - 3 - О2; 0 = 0. Проходит.
9 0 2 . А(5; 4); В(3; 3); С(1; 0); В(7; 3); £ (-2 ; 5);
Е (-2 ; - 2).
(4; 3) — точка пересечения прямых АС и В В ;
(-2 ; 3) — точка пересечения прямых В В и Е Г;
(—2; —3) — точка пересечения прямых АС и ЕЕ.
903. а) Если х = -1 , то у - 2,5;
если х = 3, то у = 1,5;
б) если у = -1 , то х «к-2 ,8 ;
если х
если х
если у
0, то у
5, то у
0, то х
5;
0,8;
-2 ;
если у - 3, ТО Хх
если у - 4, то л;1
904.
-0,9 и х2
-0,6 и х„
1,4;
0,8.
905.
д: - 3 - 2 -1 0 1 2 3 4 5
У -1 ,8 -1,1 0 2 2 0 -0 ,9 0 1,3
X -1 -0 ,5 0 1 1,5 2 2,5 3 3,5
У -5 -4 -3 -1 0 1 2 3 4
906. а) Если х = -3 , то у = 3; если х = -1 , то у - -1,3; если х = 0, то у - -2 ;
если х = 1, то у = -2 ; если х = 4, то у = 2;
б) значение у положительные для значений л;, которые являются решени­
ями неравенств х < 2 и х > 3;
в) значение у отрицательные, если - 2 <■х < 3.
907. у = 2х - 1
а) А(5; 1); 1 - 2 •5 - 1; 1 ф 0. т. А не принадлежит графику функции.
б) В(—1; 3); 3 = 2 •(-1) —1; 3 ф -3 . т. В не принадлежит графику функ­
ции.
в) С(—1; -3 ); -3 = 2 - (-1) —1; -3 = -3 . т. С принадлежит графику функ­
ции.
г) В (3; 5); 5 = 2 •3 - 1; 5 = 5. т. В принадлежит графику функции.
908.А(5; -4 ); В(3; 3); С(1; 0); Х>(1; 7); £ (-2 ; 5)
а) у = 5л; 4- 2. Графику функции у = 5л: 4- 2 принадлежит т. В(1; 7);
б) у = -ж 4- 1. Графику функции у = -л? 4- 1 принадлежит т. А(5; —4) и т.
С(1; 0);
в) у = л:2 4- 1. Графику функции у = х1 4- 1 принадлежит т. Е (-2; 5);
г) у ~ Юл; - 3. Графику функции у = 10х - 3 принадлежит т. £>(1; 7).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

145. 909. у = - х ; 1 < X < 12.
2
X 1 2 3 4 5 6
У
1
2
1 1,5 2 2,5 3
X 7 8 9 10 11 12
У 3,5 4 4,5 5 5,5 6
910- а) у - 2х —1, если 0 < х < 7.
X 0 1 2 3 4 5 6 7
У -1 1 3 5 7 9 11
со
б) у - 0,5* + 3, если -6 < * < 6.
X -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
У 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5 5 5,5 6
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

146. 9 1 1 . а) у = —х +1, если -3 < х < 6.
3
2
* -3 -2 -1 0 1 2 3 4 5 6
У -1
1 1
1 l i 2 * 3 а 5
3 3 3 3 3 3
б) у = - * , если -5 < х ^ 4.
* -5 -4 -3 -2 -1 0 1 2 3 4
У 5 4 3 2 1 0 -1 -2 -3 -4
912. Решение. График функции I/ = 0,5* + 3, заданной на множестве нату­
ральных чисел, — множество точек, лежащих на прямой у = 0,5* + 3.
Абсциссы этих точек соответствуют натуральним значениям *.
Если * = 1, то у = 0,5 - 1 + 3 = 3,5; если * = 2,то у = 0,5 * 2+ 3 = 4;
если * = 3, то у = 0,5 •3 + 3 = 4,5; если * = 4,то у = 0,5 - 4 + 3 = 5;
если * = 5, то у = 0,5 -5 + 3 = 5,5; если * = 6,то у = 0,5 *6 + 3 = 6;
если * = 7, то у = 0,5 •7 + 3 = 6,5; если * = 8,то у = 0,5 - 8 + 3 = 7 .
9 1 3 . Решение. График функции у - 5 —*, заданной на множестве целых чи­
сел, — множество точек, лежащих на прямой у = 5 - *. Абсциссы этих
точек соответствуют целым значениям * .
Бели * = —7, то у = 5 + 7 = 12; если * = -6 , то у = 5 4- 6 = 11;
если * = - 5 , то у =з 5 + 5 = 10; если * = -4 , то у = 5 + 4 = 9;
если * = —3, то у = 5 + 3 = 8; если * = -2 , то у = 5 + 2 = 7;
если * = -1 , то у = 5 + 1 = 6; если * = 0, то у = 5 ;
если * = 1, то у = 5 - 1 = 4; если * = 2, то у = 5 - 2 = 3;
если * = 3, то у = 5 - 3 = 4; если * = 4, то у = 5 - 4 = 1;
если * = 5, то у = 5 - 5 = 0; если * = 6, то у = 5 - 6 = -X;
если * = 7 , т о 1/ = 5 - 7 = -2 .
9 1 4 . у = 1 —0,8*.
- -5 -3 0 3 5
S 2,4 1 -1,4 - 3
а) если * = 0, то I/ = 1;
если * = 1, то у - 0,2;
если * = -1 , то у = 1,8;
если * = 2, то у = -0 ,6 ;
если * = —2, то у = 2,5;
если * = 5, то у = -3 ;
б) если у = -7 , то * = 10;
если I/ = -5 , то * = 7,5;
если у = -3 , то * = 5;
если у = 1, то * = 0;
если у = 0, то * = 1,2;
если у = 2, то * = -1 ,4 ;
если г/ = 5, то * = —5;
в) значения у положительные
для * < 1,2;
г) значения у отрицательные для х > 1,2
л ._ * - 4
915. у —------- .
* -4 -2 0 2 4
У . -4 -3 -2 -1 0
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

147. а) если у = -3 , то х = -2 ;
если у = -2 , то х = О;
сели у ——1, то х = 2;
если # = О, то х = 4;
если у = 1, то х = 6;
если I/ = 2, то х = 8;
если у = 3, то х —10;
б) если х = -2 , то # = -3 ;
если х = О, то у = —3;
если х = 2, то у = —1;
если х =-4, тол у = О;
если х = 6, то у = 1;
если х = 8, то у - 2;
в) значения у положительные
для х > 4;
г) значения у отрицательные для
х < 4.
016« 1. а) Область определения функции: —4 < х < 9,3.
б) если х = -4 , то у = -2 ;
если х ~ —3, то у = О; если х = О, то у = 3; если х = 2, то у —2,2;
если х = 3, то у = 1,4; если х = 4, то # = О; если х = 6, то I/ = —1,3;
2. а) если у = -1 , то Xj = -3 ,6 ; х2= 5; х3 = 7;
если I/ = О, то х, - -3 ; х2= 4; хэ = 8; если у = 2, то Xj = —1,7; х2 = 2,4;
если у —4, то х = О;
б) функция принимает положительные значения, если —3 <
и 8 < х < 9,3;
в) функция возрастает, если -4 < х < Ои если 6 < х < 9,3;
г) функция убывает, если О< х < 6.
917. а) Пешеходы начали двигаться не одновременно: сначала вышел пеше­
ход а, а через 10 мин. начал двигаться пешеход Ь;
б) скорость каждого пешехода изменялась, то есть не была постоянной.
918. А(3; -2 )
а) у = Зх - 8; -2 = 3 - 3 - 8; - 2 * 1. Не проходит.
б) у = 2(х - 4); -2 = 2 * (3 - 4); -2 = -2 . Проходит.
в) у = 7(1 - 5х); -2 = 7 * (1 - 5 •3); -2 * —98. Не проходит.
г) у = Зх - 2; -2 = 3 •3 - 2; -2 * 7. Не проходит.
7
х < 4
1 7
д) г/ = 2 - * - 9 ; у = - * - 9 ;
е) г/ = ^(1 5*); -2 = —(1
-2 = —*3 - 9; -2 = -2 . Проходит.
3
5 •3); -2 = -2 . Проходит.
Ответ: б), д), е).
919. а) у = 0,5х + 4;
А(4; 6); 6 = 0,5 * 4 + 4; 6 = 6. Точка принадлежит графику функции.
В (-8; О); О= 0,5 - (-8) + 4; 0 = О. Точка принадлежит графику функции.
С(2; 5); 5 = 0,5 - 2 + 4; 5 = 5. Точка принадлежит графику функции,
б) у = —12х + 17;
А(1; 5); 5 = -1 2 •1 + 17; 5 = 5. Точка принадлежит графику функции.
В ^ ; 11^; 11 = -12 ^^ +17; 11 э* 21. Точка не принадлежит графику
функции.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

148. С(0,5; 11); 11 = -1 2 0,5 + 17; 11 = 11.
Точка принадлежит графику функции.
8 8
в) у - 4 ---- ; Л(1; -4 ); -4 =4 ------; - 4 = -4 . Точка принадлежит графику
х 1
функции. В
функции.
( ї ; °>
С (4 ;-2 ); -2 = 4 -
9 2 0 . а) у
8
g
0 = 4 — —; 0 ф —12. Точка не принадлежит графику
1/2
-2 ф 2. Точка не принадлежит графику функции.
А(7; 1); 1 ; 1 = 1. Точка принадлежит графику функции.
(* й !
7 - 6
В(6; О); 0 = - 1- ; 0 = Так как выражение i не имеет смысла, то точ­
ка не принадлежит графику функции.
1 1 1 1 т— = ---------- ; — ф — . Точка не принадлежит графику функции.
3 3 —6 3 3
б) у = х(х - 5 ) ;
А(0; - 5 ) ; - 5 = О*(0 - 5 ) ; —5 Ф О. Точка не принадлежит графику функции.
В ( 5 ; О); О= 5 * ( 5 - 5 ) ; О= О. Точка принадлежит графику функции.
С(0; О); О= 0 * (О - 5 ) ; О= О. Точка принадлежит графику функции.
в) у = (6 - х)2;
А(7; -1); -1 = (6 - 7)2; —1 * 1 . Точка не принадлежит графику функции.
В(8; 4); 4 = (6 - 8)2; 4 = 4. Точка принадлежит графику функции.
С(4; 4); 4 = (6 - 4)2; 4 = 4. Точка принадлежит графику функции.
9 2 t . а) у = х.
X - 3 - 2 0 1 3
У - 3 -2 0 1 3
б)
в)
X - 4 - 2 -1 0 2
У 3 1 0 -1 - 3
X - 2 -1 0 1 2
У - 3 0 1 0 - 3
г) у = X2.
X - 2 -1 0 1 2
У 4 1 0 1 4
9 2 2 . а) у = 1,3ж + 2, если -3 < х < 4.
X -3 -2 -1 0 1 2 3 4
У -1 ,9 -0 ,6 0,7 2 3,3 4,6 5,9 7,2
Область определения: -3 < х < 4; множество значений: -1,9 < у < 7,2.
7
Функция возрастающая; у > Опри - 1 — < х < 4
7 ^ 20 7
у < О; при —3 < х < - 1 — ; 1,3д: +.2 = 0; 1,3л: = -2 ; х -------; х = —1—;
* * 13 13 3
б) у = 4 - 2ху если -2 < х < 5.
X -2 -1 0 1 2 3 4 5
У 8 6 4 2 0 "2 тг4 -6
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

149. I -
a
-2
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

150. Область определения: -2 < х < 5; множество значений: -6 < у < 8.
Функция убывающая, у > Опри -2 < х < 2; у < О при 2 < х < 5.
923. а) у = — — если - 8 < х < 4.
2
. X -8 -6 -4 -2 0 2 4
У -1 0 1 2 3 4 5
Область определения: -8 < х < 4; множество значений; -1 < у < Ъ;
функция возрастающая; у > 0 при -6 < х < 4; у < Опри -8 < х < 6.
б) У = — х, если -5 < л: < 5.
5
л: *-5 -3 -1 0 1 3 5
У 1
3 1
0
1 3
-1
5 5 5 5
Область определения: “ 5 < ж< 5 ; множество значений: -1 < у < 1.
Функция убывающая, у > Опри - 5 < х > О; у < Опри 0 х < 5 .
924. а) у = 2х - 5 ;
X -1 0 1 2
У -7 -3 -1
возрастающая
б) # = 3 ~2х;
X -1 0 1 2
У 5 3 1 -1
убывающая
®) У ~ О,1л:;
X -5 0 5 10
У -0 ,5 0 0,5 1
возрастающая
925. а) у = - —+ 2х;
5
X -2 0 2 4
У -4,2
1
5
3,8 7,8 .
возрастающая
Зж—1
б) у = с ;
5
X -3 0 2 4
У -2
1
5
1 2,2
возрастающая
17 - х
в) у = — -— ;
ж -3 2 - 7
У 4 3 2
убывающая
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

151. 926. у —2(1 —х);
X -3 -2 -1 0 1 2 3
У 8 6 4 2 0 -2 -4
Если -3 < у < 7, то -2 ,5 < х < 2,5.
9 2 7 . у - 2х + т; А (-2; 5)
Если график функции у = 2х + т проходит через точку А (-2; 5), то коор­
динаты точки удовлетворяют уравнению у - 2х + т.
5 = 2 - (—2) + то; 5 = -4 + то; то = 5 + 4; то = 9. Ответ: т —9.
9 2 8 . у = kx + 2; В(3; 8)
Если график функции у = kx + 2 проходит через точку В(3; 8), то коорди­
наты точки удовлетворяют уравнению у = kx + 2.
9 = &•3 + 2; ЗДе= 8 - 2; Sk = 6; k = 2. Ответ: k = 2.
9 2 9 . у = х2 - т; 0(0; О)
О= О2 - т; т = О. Ответ: т = 0.
930. а) На газоне растет трава, которую регулярно косят (л; — время, # — вы­
сота травы). Ответ: рис. 77в.
б) Груша растет, потом ее срывают и высушивают (х — время, у — масса
груши). Ответ: рис. 75а.
в) Мяч падает с некоторой высоты на пол (х — время, у — высота мяча
над полом).
Ответ: рис. 756.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

152. Упражнения д ля повторения
9 3 1 . a) ab 4- Ьс 4 ас + с2= Ь(а + с) 4- с(а 4 с) = (а 4 с)(Ь 4 с);
б) 2х - ух 4 2t/ - у2= х(2 - у) 4 1/(2 - у) = (2 - у)(х + у);
в) 3 —6а 4- z —2аг = 3(1 —2а) 4 z(l - 2а) = (1 - 2а)(3 + г);
г) Юах - 5Ьх 4- 2ау ~ Ьу = 5х(2а - Ь) 4 у(2а - Ь) = (2а - Ь)(5х 4 у).
9 3 2 . (л2 4 I)2- (n2 - I)2= 4л2.
Докажем тождество:
(л2 4 I)2 - (л2 - I)2= (л2 4 1 - л2 + 1)(л2 4 1 4 л2 - 1) = 2 - 2л2 = 4л2.
Тождество доказано..
Квадрат каждого четного числа равняется разности квадратов некоторых
целых чисел. Доказательство смотри в № 680 учебника, взяв за л + 1
и л —1 целые числа.
93 3 . Пусть 10 % раствора взяли х г, тогда 4 % раствора взяли (800 - х) г.
Соли в 10 % растворе х •10 % = ОДх (г), в 4 % растворе — (800 —х) •4 % =
= 0,04(800 - х) (г), в 7 % растворе — 800 • 7 % = 800 ■0,7 = 56 (г). Так
как 7 % раствор получили, смешав 10 % и 4 % растворы, то получаем
уравнение ОДх 4 0,04(800 - х) = 56. ОДх + 32 - 0,04х = 56; 0,06* = 24;
х = 400.
800 —400 = 400. Ответ: 400 г 10 % раствора и 400 г 4 % раствора.
9 3 4 . а) (х + З)2 = х2 4 9х; х2 4 6х 4- 9 = х2 4 9х; х2 + 6х 4 9 « х2 4 9*;
6х = 0; х = 0. Ответ: 0.
б) (у. - 5)2= у(у + 2); у2 - Юу + 25 = у2 4 2у; -Юу - 2у = -2 5 ; -12у= -2 5 ;
—25 1 1
у = ------; у = 2 — . Ответ: 2 — .
* -1 2 12 12
в) (1 - г)2 = 3 4 г2; 1 - 2г 4 г2 = 3 + z2; -2 г = 3 —1; ~2г = 2;
2= 2 : (—2); z ——1. Ответ: -1 .
г) (7 - je) 2 - х2= 35; 49 - 14* 4 х2- х2= 35; -1 4 х = 35 - 49;
—14х = —14; х = -1 4 : (—14); х = 1. Ответ: 1.
§ 23. Линейная функция
(
Линейной функцией является функция вида у = kx + Ь, где х — аргу­
мент, й и Ъданные числа. График линейной функции — прямая, поэтому
для его построения на координатной плоскости необходимо обозначить
только две точки и через них провести прямую.
9 3 5 . Определим, линейная ли функция, заданная формулой.
а) у = 5х 4 0,2 — линейная; б) у = -3 ,5 х + 2 — линейная;
в) у = 3 - 2х — линейная; г) у = х 4*5 — линейная;
2х - 5 2 2
д) У = — -— ; у = - X - 1 - — линейная;
о 3 о
, 1 - 2 х 1
е) у = -------- ; I/ = — х — линеиная.
ÿ 2 2
936. а) у = 0,7х — прямая пропорциональность;
«ч х 1
б) у = —= —х — прямая пропорциональность;
3 3
2х - 1 2 1
в) у = -------- = —х - — — не являются прямой пропорциональностью;
3 3 3
г) z = 5 - 2t — не являются прямой пропорциональностью;
д) z = 7t2 — не являются прямой пропорциональностью;
е) z = —3< — прямая пропорциональность.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

153. 937. Решение. Линейная функция задана формулой у = 0,5л: + 3.
Если х = -2 , то у - 0,5 •(-2) + 3 = 2; если у = 3, то 3 = 0,5* + 3;
0,5* = 0; х = 0. Ответ: при х - - 2 у - 2 ; при у = 3 х = 0.
938. Прямая о: у = 2,5; прямая Ь: у = -3 .
939. Построим графики функций.
а) # = Зх - 2 — функция линейная, значит, ее график — прямая, для по­
строения которой достаточно двух точек;
если х - 0, то у = -2 ; если х = 1, то у = 1;
б) у = -0,6# — функция с прямой пропорциональностью, значит, ее гра­
фик — прямая, которая проходит через начало координат (0; 0).
Достаточно посчитать координаты одной точки.
Если х = 5, то у = -3 ;
в) у = 1 - 0,3л; — функция линейная, значит, ее график — прямая, для
построения которой достаточно двух точек;
если х = 0, то у = 1; если х = -5 , то у = 2,5;
г) у = —х + 1 — функция линейная, значит, ее график— прямая, для
3
построения которой достаточно двух точек;
если х = 0, то у —1; если х = 3, то у = 3;
е) у = Х+ ^ — функция линейная, значит, ее график — прямая, для по-
2
строения которой достаточно двух точек;
если х = —1, то у = 1; если х = 3, то у = 3;
е) у = - —— — функция линейная, значит, ее график— прямая, для
3
построения которой достаточно двух точек;
1 7 1
если х •=0, то у = —; если х = -2 , то у = —= 2 —.
3 3 3
940. а) у = 0,5л: — прямая пропорциональность.
Значит, график — прямая, которая проходит через начало координат.
Достаточно посчитать координаты одной точки, х = 4; у ~ 2.
б) у = 2(х + 1) = 2л: + .2 — линейная функция, график — прямая.
х = 0, у = 2; л: = -2 , у = -2 .
в) I/ =5 3 - 2л: — линейная функция, дс= 0, у = 3; л: = 2, у = —1.
л: —5 1 1
г) г/ = --------= —ж- 2 — — линейная функция, х = 1, у = -2 ; л: = 5, у = 0.
2 2 2
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

154. 9 4 1 . а) у = 2х - 3, если -1 < х < 4.
I/ = 2х - 3 — линейная функция, так
как —1 < х < 4, то график функции —
отрезок.
х = -1 , у = -5 ; х = 4, у = 5.
б) т = 2* + 3,
если - 3 < £ < 2.
т = 2£ + 3 — линейная функция,
так как —3 < £ < 2,
то график функции — отрезок.
£ = - 3 , то = -3 ;
£ = 2, т - 7.
в) у = —х + 1, если -3 < х < 6.
3
у = —х +1 — линейная функция.
3
Так как - 3 < х < 6, то график функции — отрезок,
х = -3 , у = О;
х = 6, у = 3.
в) У*
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

155. 942. а) у = 5х + 3, если -4 < х < 2. х - -4 , у = -1 7 ; ж= 2, I/ = 13.
6) у = 2 —хуесли —2 < х < 4. х = —2, у = 4; ж= 4, у = —2.
и) р = 0,8а + 2, если 2 < а < 5. а = 2, р = 3,6; а = 5, р = 6.
2 2
-1 = —-0 - 1 ; 1 = —*3-1; так как х = 9, -3 < 9 < 6, то т. С принадлежит
графику функции. -1 = -1 . 1 = 1. 5 = 5. т. А принадлежит графику функ­
ции, т. В принадлежит графику функции.
944« Определим, проходит ли график функции у = 2х —1 через точки.
а)А(3; 5)?
Подставим абсциссу точки А в уравнение функции: х = 3; у = 2 3 - 1 = 5.
Получили ординату точки А. Значит, график проходит через точку А.
б) В (-10; -5)?
Подставим абсциссу точки В в уравнение функции: у - 2 *(-10) - 1 = -21.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

156. Получили значение, отличное от ординаты точки В. Значит, график не
проходит через точку В.
в) С(100; 99)?
Подставим абсциссу точки С в уравнение функции: у - 2 * 100 - 1 = 199.
Получили значение, отличное от ординаты точки С. Значит, график не
проходит через точку С.
945« Построим графики функций.
а) у = Ох + 3; у = 3; прямая проходит через точку (0; 3) параллельно оси
абсцисс;
б) у = 0х ~ 2; у ~ 2; прямая проходит через точку (0; 2) параллельно оси.
абсцисс.
946. а) у = х; к = 1 > 0, значит, функция возрастающая;
х 1
б )у = — ; h = — < 0, значит, функция убывающая;
3 3
в) у - -х ; к - -1 < 0 , значит, функция убывающая;
г) у - 2х; к = 2 > 0, значит, функция возрастающая.
947.1 м2 — 180 г. то= 180s — линейная функция, которая является прямой
пропорциональностью.
948. Так как на рисунке изображены графики функции вида у = кх (k Ф0),
то для записи формулы каждой прямой достаточно определить к. Если
(х0; у0) — точка, принадлежащая прямой вида у = kx, то к Ус
*о
3 2 1 х
Прямая а: (1; 3); к ——- 3; у —Зле; прямая Ь: (4; 2); к = —- у - —;
1 4 2 2
прямая с: (-5 ; 1); А= у = - ^ ;
-5 5 5
2
прямая й: (-2 ; 2); к —— -= -1; у = -х .
2
949. Решение. Построим график функции у - -3# + 2.
Функция является линейной, поэтому ее графиком будет прямая, для-
построения которой достаточно двух точек: если х —1, то у = —1; если х
- 2, то у = -4 .
(|; •) -
Точки (0; 2) и |—; 0 | — точки пересечения графика а осями коорди­
нат.
•2
Значения функции положительные, если х < —, и отрицательные, если
2 3
jc > —. Эта функция убывающая, потому что при увеличении значения
3
аргумента значение функции уменьшается.
950. Не делая построение, найдем координаты точек пересечения графика
функции с осями координат.
Чтобы найти точки пересечения графика функции с осями координат,
необходимо но очереди приравнять к нулю аргумент и значение функ­
ции.
а) у = 4х + 8; если х = 0, то у = 8; если у = 0, то х = -2 ; (0; 8) — точка пе­
ресечения с осью у; (-2 ; 0) — точка пересечения с осью х;
б) у = - х + 3; если х = 0, то у = 3; если у = 0, то х = 3; (0; 3) — точка пе­
ресечения с осью у; (3; 0) — точка пересечения с осью х;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

157. в) у = 0,5 - 2х; если х = 0, то у = 0,5; если у = 0, то х = 0,25; (0; 0,5) — точ­
ка пересечения с осью у; (0,25; 0) — точка пересечения с осью х.
951 - Функции вида у = кх + Ъ — линейные, их графиками будут прямые.
Достаточно для каждой из функций посчитать координаты двух точек,
а) у = 2х + 1; х = 0, у = 2; х = -2 , у = -3 ; (0; 1), (-2 ; -3);
у = 0; 2х + 2 = 0; х = (0; -4 ), (4; 0);
А
(0; X) — точка пересечения прямой с осью у
■ В 1°)
точка пересече­
ния с осью х. у > 0 при х > — ; у < 0 при х < — ; к = 2 > 0, функция
возрастающая. 2 2
б) у = * - 4; * = 0, у = -4 ; х = 4, у = 0;
Точка пересечения с осью у (0; -4), точка пересечения с осью х (4; 0).
у > 0 при х > 4; у < О при х < 4; к = 1 > 0, функция возрастающая.
в) у - - х - 5; х = 0, # = -5 ; я:= 4, у =-3 . Точка пересеченияс осью у (0; -5),
2 1 1
точка пересечения с осью х (10;0). у = 0; —х - 5 = 0; —х = 5; х = 10;
2 2
> 0 при х > 10; у < 0 при х < 10; &= —> О, функция возрастающая.
2
г) у = 3 - ^ х; х = 0, у = 3; х = 3, у = 2; I/ = О; 3 - ^ х = 0; - ^ х = -3; х = 9.
о о о
Точка пересечения с осью у (0; 3), точка пересечения с осью х (9; 0).
у > 0 при х < 9; у < 0 при х > 9 ; &= - —< 0, функция убывающая.
3
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

158. 3 - 2 х 2
д) у = — =
3 —2х
х ~ О, у = 1; х = 3, у = —1; г/ —О; — - — = 0; 3 - 2х = 0; -2 х = -3 ; х = 1,5.
о
Точка пересечения с осью у (0; 1), точка пересечения с осью х (1,5; 0).
2
у > 0 при х < 1,5; у < 0 при х > 1,5; к = — < 0, функция убывающая.
4х —6 1 3 3
е) у —-------- = —х — ;
* 8 2 4
1 1 >. I 1 п 6 3х = ■—, у - — ; дс= 4, у = 1—; * = 0; г/ = ——= — ;
2 2 4 8 4
4дс —6
р = 0; — - — = 0; 4х - 6 = О; х = 1,5. Точка пересечения с осью у
точка пересечения с осью х (1,5; 0).
(* 4
у > 0 при х > 1,5; у < 0 при х < 1,5; к = —> О, функция возрастающая.
3
( И
ж) у = —( 7 * - 4) = 3,5* —2;
2 1
* = О, у = -2 ; дс= 2, у = 5; у = О: —(7л - 4) = О; 7дг - 4 = О; х =
2 7
Точка пересечения с осью у (О; ~2), точка пересечения с осью дс
4 4
у > 0 при л: > —; у < Опри дс«с —; £ = 3,5 > О,функция возрастающая.
з) у = 3(2 - х) = -З х + 6;
х = О, у = 6; х = 2, у = О;
Точка пересечения с осью у (О;6), точка пересечения с осью х (2; О).
у > 0 при х < 2; у < Опри х > 2; = -3 < О, функция убывающая.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

159. 952. Точка пересечения графика с осью х имеет координаты (х0; О), точка
пересечения графика с осью у имеет координаты (О; у0).
и) у = 1,7х - 3,4; х = 0: у = -3 ,4 ; у = О,: 1,7* - 3,4 = 0; 1,7* = 3,4; х = 2.
(О; -3,4) и (2; О)
Г>) у = 0,5(х - 4); х = 0: у —0,5(0 - 4) = -2 ; у = О; 0,5(х —4) = О; х - 4 = О;
х - 4. (О; -2 ) и (4; О)
и) у - 3,5л: — прямая пропорциональность, значит, прямая пересекает оси
кооринат в одной и той же точке,
г) У = -2 ,5 х + 1;
(О; 0) х = 0: у = 1; у = 0: -2 ,5 * + 1 = 0; -2 ,5 * = -1 ; х = 0,4. (О; 1) и (0,4; О)
Я) У = -~ г~ ;х = 0 у = - 1 ; у = 0: - = 0 ; х - 1 = 0 ; х = 1 ; (о*, - ^ 1 и (1; О)
4 4 4 4 /
3 —2х . 3 . „ Л 3 - 2 ж _ _ Л ^
о) у = — - — ; х = О: у = - = 1,5; у = О: — - — = 0; 3 - 2х = О; -2 * = -3 ;
* = 1 , 5 . (О; 1,5) и (1,5; 0)
х
953. а> у = —+1 и у = -х + 4; б ) у - х - 5 и у = 5 - х ;
2 х = 5; у = О; х = 5; у = О;
ж= О; у = 1; х = О; у = 4; х = О; у = —5; х = О; у = 5.
х = 2; у = 2; х = 4; у = О; (5; О) — точка пересечения
(2; 2) — точка пересечения прямых, прямых.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

160. в) у = 3* - 1 и у = - х - 1; г) I/ = х + 3 и */ = 2х + 6;
х = 0; у — 1; х = 0; у = -1 ; х = 0 ;у = 3; х = 0; у = 6;
х = 2; у = 5; дг= -3 ; г/ = 2; х = -3 ; у =0; х = -3 ; у = 0.
(0; -1 ) — точка пересечения прямых. (-3 ; О) — точка пересечения
прямых.
954. а) у = 2х + Ь;
Ъ = -3 : у = 2х - 3; х = О; у = -3 ; х = 2; у = 1.
6 = О: |/ = 2х; х = 2; у = 4;
6 = 1: у = 2х + 1; х = 0; у = 1; х = -2 ; у = -3 . Прямые параллельны,
б) у = йх + 3;
Л= -1 : у = -х + 3; х = О; у = 3; х = 3; у = О;
й = 1/ = ^ х + 3; х = 0; у = 3; х = -2 ; у= 2;
к = 1: у = х + 3; х = О; у = 3; х = -3 ; у =0;
Л= 2: у = 2х + 3; х = 0; у = 3; х = -3 ; у = -3 .
Прямые проходят через точку (О; 3).
У»
х 6
X 5
Х4
Л/
Г */
/ 7
1 1 X І 1 т г-|г-
^ 6 - 5 Н к4 - / ‘ 0 1 2 34 5 6 7 >
ту»
X / ~2 V
/ / -3
XV
X**
X *
—4 X
-5
955. у = кх - 2
а) М {-3; 4). Так как график функции у - кх —2 проходит через точку
М(—3; 4), то координаты точки М удовлетворяют уравнению у = кх —2.
4 = к * (-3) - 2; 3к = -6 ; к = -2 .
б) у = -З х + 1,5; &= -3 . Так как две прямые параллельны, то й = 3.
956. у = кх - 1 и у = рх + 5 пересекаются в точке Р(4;3), если координаты
точки Р удовлетворяют каждому из двух уравнений.
3 = к •4 - 1; 4* = 4; А= 1.
3 = р •4 4- 5; .4р = 3 - 5;
4р = -2 ; р = 1
Ответ: Дг
2
1; Р =
957. Уравнение вида у = 6 задает прямую,
проходящую через точку (0; 6) параллель­
но к оси абсцисс.
а) у = 2; б) у = -4 ; в) г/ = 3,5.
958. */-рх + Зиі/ = £ х - 3 — параллельные
прямые, если р = к.
Прямая а проходит через точку (-2 ; 0).
УІ
5
3,5
і
У = 3,5
2 г/= 2
, 0 1 1 1 1 1 "►
- З - 2 _ ! 1 2 X
|/ = 4
-5
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

161. О- р * (-2) + 3; 2р = 3; р = 1,5. Прямая Ь проходит через точку (2; 0).
0 - k * 2 - 3; 2k = 3; k = 1,5. 1,5 = 1,5.
959. Прямая а проходит через точки (-4 ; 0) и (О; -2).
1) Пусть у ~ kx + Ъ — уравнение прямой а.
Тогда: О= k •(-4) + с; Ъ- 4fe; Значит, —2 = 4fc; k ——^ .
2) Прямая 6 проходит через точки (—4; О) и (О; 4).
Пусть у = рх НЬс — уравнение прямой Ь.
Тогда 0 = 4р + с и 4 = 0р + с
с - 4р; ' с = 4. ^
Значит, 4 = 4р; р = 1. Ответ: прямая а: у = — ж—2; прямая&:# = ж+ 4.
2
960. (Решение аналогично решению № 959). у - kx + р
а) А(О; 1) и В(2; 2)
I = fe* О+ р; и 2 = А* 2 + р;
/?=1; р = 2 - 2k. Значит, 2 -2fe=l;-2fe=-l; k = —.# = —х + 1 —
уравнение прямой, проходящей через точки А и В .
б) К(1; -2 ) и Р(0; 5)
-2 = k - 1 + р; и 5 = ft •0 + р;
k - -2 - р; р - 5. Значит, Л= —2 - 5 = -7 .
# = -6 х + 5 — уравнение прямой, проходящей через точки К u Р.
961 *. а) у = х + 4; х = 0; # = 4; лг= —4; #= О; # = —ж+ 4;
б) # = 1 - 2лг; лег= О; у = 1; дг= 2; у =-3 . у = 1 + 2ж;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

162. в) У
г) {/ = -
9 6 2
Зх; х - 1; у = 3; у = —Зле;
х х
—; х = 3; у = —1. у - —.
3 3
Если # = Дгх + 6и*/ = рх + с — две прямые, симметричные относительно
оси ординат, то к = ~р и Ь = с.
I/ = 2х + 3; х = -4 ; у = -5 ; х = О; у = 3;
у = -2 х + 3; х = О; у - 3; х = 4; у = -5 .
# = -З х + 3; х = -2 ; # = 9; х = 1; у = 0;
# = х - 1; х = 1; # = О; х = 4; у = 3.
а) у =
б) у
=1
2х + 3, - 4 < х < О;
-2 х + 3. О< х < 4;
-2 < х < 1;
1 < х < 4;
Г~3х + 3,
I х 1,
963*. а) у = |х|
1) Строим график функции у X.
X 0 2
У 0 2
2) Так как # = |х|, то график функции у = х при ж> Осовпадает з графиком
функции у = |х|, а при х < Ографик функции у - х симметрично отобра­
жаем относительно оси х.
б){/=|* + 3|
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

163. 2) Так как у = х + 3|, то график функции у = х + 3 при х > -3 совпадает
с* графиком функции у = х + 3|, а при х < -3 график функции у = х + 3
симметрично отображаем относительно оси х.
») у = х+ 3
1) Строим график функции у = |х|(см. № 963(а)).
2) Так как каждое значение функции у - |х( + 3 на 3 больше соответ­
ствующих значений функции у = |д4 то график функции у = хдвигаем
вдоль оси у, на 3 единичных отрезка вверх. Получим график функции
у = х+ 3.
г) у = 2|х| - 1
1) Строим график функции у = |х|(см. № 963(а)).
2) Так как каждое значение функции у = 2|х[ в 2 раза больше соответ­
ствующих значений функции у = |х|, то получим график функции у = 2|х|
по принципу: если (2; 2) — точка графика функции у =|ж|, то (2 * 2; 2), то
есть (4; 2) — точка графика функции у = 2х.
3) График функции у = 2|х|- 1 получим, сместив график функции у = 2|ж|
па 1 единичный отрезок вдоль оси у вниз.
-2
-3
Количество еди­
ниц продукции
200 ед. 400 ед. 1000 ед. 1200 ед. 2000 ед.
Стоимость * 100 грн. ? ? ? 800 грн.
у, грнл
800
700
600
500 — — — .—_ —
400 -— — — *—
300
200 ----,
100
^ 0
200 400 600 800 1000 1200 1400 1600 1800 2000 *
Так как функция затрат линейная, то построим график — прямую, прохо­
дящую через точки (200; 100) и (2000; 800). По графику определяем:
на 400 единиц — « 180 грн.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

164. на 1000 единиц — « 410 грн.
на 1200 единиц — » 490 грн.
Ответ: » 180 грн.; * 410 грн.; » 490 грн.
965*. ух = 100 + 30* и у2 = 150 + 20* — линейные функции, графики кото­
рых — прямые, пересекающиеся (к1= 30; Л2= 20и 30 *20). Найдем точ­
ку пересечения графиков: 100 + 30* = 150 + 20*; 30* —20* = 150 —100;
10* = 5 0 ; * = 5 .
у = 100 + 30 * 5 = 100 + 150 = 250. (5; 250) — точка пересечения прямых.
Так как * — расстояниеперевозоквсотнях километров, а у 1и у2 — транспорт­
ные затраты в сотнях гривень, то на расстояние 5 ■100 = 500 (км) транспорт­
ные затраты обеими видами транспорта составляют 250 * 100 = 25 000 (грн.).
Если расстояние менше, чем 500 км, имеем:
X = 1; Ух= 100 + 30 •1 = 130; у2 = 150 + 20 - 1 = 170; 130 < 170; ух < у 2.
Если расстояние больше, чем 500 км, имеем:
* = 6: ух= 100 + 30 - 6 = 280; у2 = 150 + 20 •6 = 270; 280 > 270; уг > у2.
Ответ: на расстояние, меньшее 500 км, груз выгоднее перевозить первым
видом транспорта, а на расстояние, большее, чем 500 км, груз выгоднее
перевозить вторым видом транспорта.
На расстояние, равное 500 км, перевозка груза обеими видами транспор­
та стоит однаково.
966*. Если * — количество единиц проданного товара, то * > 0. Пусть у —
заработная плата продавца. Так как 2* + 50 = 100 % , то за продажу 40
и более единиц товара надбавка к зарплате составляет 20 %, значит,
{ ох + 50 о < х < 40*, - - ,
(2* + 50) •1,2, 40 < *-
у = 2* + 50; * = 0; у = 50; * = 40; у = 130;
у = (2* + 5) •1,2; * = 40; у = 156; * = 60; у - 204.
Упражнения д ля повторения
967. а) (2* + З)2= 4*2 + 3; 4*2 + 12* + 9 = 4*2 + 3; 12* = 3 - 9;
12* = -6 ; * = ;
2
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

165. б) (5 - 3уУ - 9#2= 55; 25 - 30у + 9#2
30
У// =
-3 0
-1 ;
9у* = 55; -30# = 55 - 25; -30# = 30;
4;н) (42 + 2)2 = 2(8^2+ 13); 16г2 + 16г + 4 = 16г2 + 26; 162 = 26
22 11 3
I02 = 22; 2 = — ; 2 = ^ -; 2 = 1 - ;
16 8 8
г) (4 - 5х)2= (3 + 5х)2; 16 - 40х+ 25х2= 9 +ЗОх + 25х2; -40х - ЗОх = 9 - 16;
-7
7Од; - -7 ; х = ------; х = 0,1.
-70
060. а) (2х + З)2 - 4(х2 + 7) = 71; 4х2 + 12х + 9 - 4х2 - 28 = 71;
12л = 71 - 9 + 28; 12* = 90; х = 90 : 12; х = — ; х = 7,5;
12
б) (5г - I)2 - 5г(4 + 5г) = 31; 25г2 - Юг + 1 - 20г - 25г2= 31;
302 = 3 1 - 1 ; 2 = — ; 2 = -1 ;
-30
») (0,2# - 2)2 + 0Д#<2 - 0,4#) = -2 ; 0,04#2 - 0,8# + 4 + 0,2# - 0,04#2= -2 ;
0,6# = -2 - 4; у - у = 10;
-0,6
•')
f l 2 ? ( I .V I Л 1 2 2
—х = —х - 1 —х + 1 ; —х ~ —
и 3) и Д 2 У 4 3
( - ! } «
Х +
2 _ 13
3 Х ~ 9
9
1
1 2 1 41; — х = —1 ----
3 - 9
х = - - — у х —2 —•
9 У 2 ) 6 6
069. Пусть со скоростью 10 км/ч. велосипедист едет х ч., тогда со скоростью
12 км/ч. он проехал бы то же самое расстояние за (х - 1) ч. При этом
х > 1. Получаем уравнение: 10х= 12(х - 1); 10х= 12х - 12; -2 х = -12; х = 6.
(5 часов нужно велосипедисту, чтобы проехать из одного села в другое со
скоростью 10 км/ч.
10 * 6 = 60 (км) — расстояние между селами. Ответ: 60 км.
070. Пусть расстояние от Жашкова до Умани составляет 1. Тогда скорость
1 -
мотоциклиста равняется - - 1 расстояния за ч., а скорость велосипедис-
1 1
та — — расстояния за ч. Так как велосипедист и мотоциклист выезжают
5
одновременно навстречу друг другу, то скорость, с которой они прибли­
жаются, равняется 1 + —= 1— расстояния за ч. Найдем время по формуле
1 = 8 IV. 5 5
1:1
6
(ч.) = 50 мин.
Задания д ля самостоятельной работы
вариант 1
1. у = х + 4.
2. // = 5 —х; х < 7; х — натуральное.
X 1 2 3 4 5 6
У 4 3 2 1 0 -1
3. // = 2х - 1 — линейная функция,
х = 0; у = -1 ;
х —3; # = 5.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

166. 2)
7
6
5
4
3
2
1
О
УЬ
1 2 3 4 7 *3 -2 -1
-1
-2
-3
-4
4 . а) |/ = * 2 - 3* + 2.
Область определения х — любое действительное число.
2
б) у —------ ; * + 3 * 0 ; * * —3.
* + 3
Область определения — множество действительных чисел, кроме * = -3.
Вариант 2
1. у = х —9.
2. у = 1 - *; * < 5; * — натуральное.
* 1 2 3 4
У 0 -1 -2 -3
3 . 1/ = 3* - 1;
* = 0; у = - 1 ; * = 2; у
2) уА
2
1
0
3 - 2 - 1
-2
- 3
- 4
4. а) у = * 2 - * + 3.
Область определения
3
б) у = —; * - 2 * 0 ; * * 2
множество действительных чисел.
х - 2
Область определения
Вариант 3
у = 3*.
множество действительных чисел, кроме * = 2.
2. |/ = 2 + * ; * — натуральное, * < 5.
* 1 2 3 4
У 3 4 5 6
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

167. Ах + 3
0; у - 3; х = -2 ; I/ = -5 .
У*
7
6 ш
5 •
4 •
3 •
2
1
0 1 1 ■ 1 1 1 | ►
3 -2 -1
-1
1 2 3 4 5 6 7 *
- 2
- 3
—4
4. а) у = 1 “ х2. Область определения — множество действительных чисел.
^ ; д: - 9 ^ О; х # 9. Область определенияб) у ■■ 0
х - 9
тпльных чисел, кроме X = 9.
множество деистви-
Париант 4
1.1/ = -X.
2. у = - 3 + х 9х натуральное, х < 8.
* 1 2 3 4 5 6 7 8
У -2 -1 0 1 2 3 4 5
3. у = ~2х + 3;
х - О; у = 3; х = 3; у 3.
2) УЬ
7
6
5
4
3
2
1
О
3 - 2 - 1
-1
-2
- 3
- 4
4. и) у = дс3 + 1
Область определения
Г») у
3 4 5 6 7 8 X
множество действительных чисел.
; х + 9 * О; х ф -9 .
х + 9
Область определения — множество действительных чисел, кроме X
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

168. Тестовые задания № 6
1 .г ) Я ( 4 ;4 ) .
2 . б) ( - 5 ; 0 ).
3 . г ) (0 ; 5).
4 . а) у = - + 3.
У 2
5. г) у = За:.
6. а) у - 2х + 4.
7. а) -4 .
8 . в) 0 и 2.
9. г) у = -3 .
Ю* у = -
в) -5 .
4 *(“0 ,2) 4-1 - 0 ,8 + 1 0,2
= -5 .
Контрольная работа № 6
1. у = 0,5* - 3.
а) л; = 4: у = 0,5 * 4 - 3 = —1.
8
б) у = 5: 0,5а; - 3 = 5 ; 0,5* = 5 + 3; 0,5л; = 8; х = ----; л: = 16.
0,5
2. у - 7х - 3.
А(1; 4) В(2; 10) С(3,5; 0,06) 1>(0; -3 )
4 = 7 1 - 3 ; 10 = 7- 3 - 3 ;
0,06 = 7 3,5 - 3; -3 = 7 - О- 3;
4 = 4. 1 0 * 11.
0,06 * 21,5. -3 = -3 .
График функции проходит через точки А и И.
3 •у = —2х + 3.
х - О; у = 3;
х = 2; у = -1 .
Область определения — множество дей­
ствительных чисел.
Область значений — множество действи­
тельных чисел.
Функция убывающая.
-2л; + 3 = 0;
- 2 л; = - 3 ;
л;= 1,5.
у > Опри х < 1,5; у < 0 при х > 1,5.
4 . у - -З х + 5.
х = О: у = -3 - О+ 5 = 5.
(0; 5) — точка пересечения прямой с
осью у.
-5
У О: 3* + 5 = 0; = -5 ; х = — ;
-3
х - 1
(*1= °) -
точка пересечения прямой с осью х.
5- Если одна сторона прямоугольника равняется х см, то вторая сторона —
2х см. А площадь 5 = х ■2х = 2л:2. 5 = 2х2.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

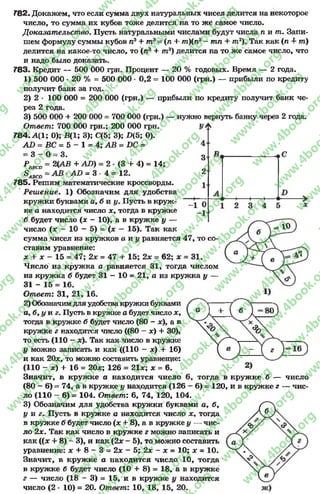
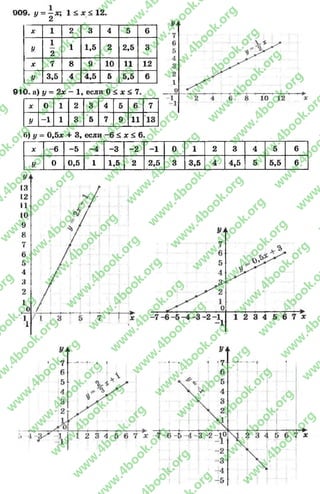
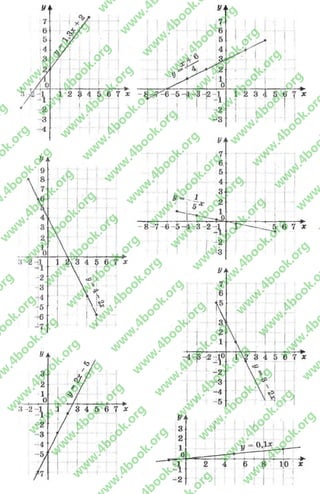
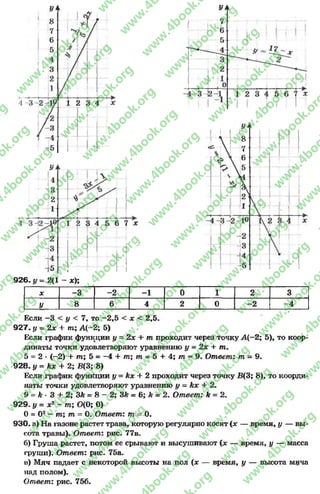
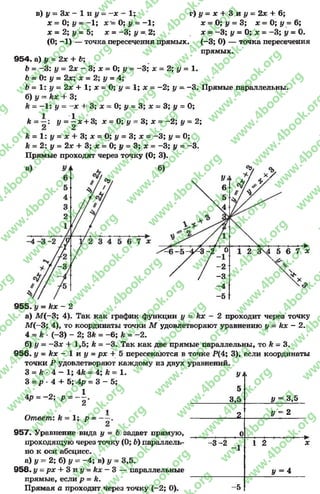
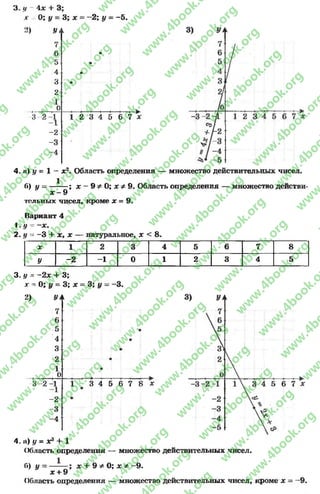
169. * 1 2 3 4 5
У 2 8 18 32 50
о
У
У
{ :
6. Тик как график линейной функции проходит через начало координат, то
;>то функция является прямой пропорциональностью и задается форму­
лой у = /г*.
Координаты точки А (-4; -6 ) удовлетворяют уравнению у —kx.
Имеем: -6 = k - (—4); fe= —6 : (-4 ); k = 1,5.
Ответ: у = 1,5*.
т 6
7* У - 2 g ;* + 5*
хг + 5* * О; х(х + 5 ) * 0 ; * # 0 и * + 5 * 0 ; * * -5 .
Ответ: область определения — множество действительных чисел, кроме
х - Ои * = —5.
В. Стоимость оборудования — 72 ОООгрн.
Годовая аммортизация — 3000 грн.
Тогда через * лет стоимость оборудования у выражается формулой:
72 ООО- 3000*.
2, * > 0;
2* - 2,* < 0.
У = х - 2;
у = - 2* - 2;
* = 5; у = 3;
х = 0 ;у = -2 ;
х = 0; у = -2 ;.
* = -2 ; у = 2.
10. При каком значении т графики функ­
цииу = 2|*|+ 1и у = т имеют одну общую
точку?
у - т — прямая параллельна оси * и про­
ходит через точку (0; т).
у = 2|*| + 1.
Так как |*|> 0 , то 2|*| > 0,
а 2х + 1 > 1.
При этом |*|= [-*].
Так как значения данной функции
для противоположных значений
аргумента равны, то,
если т > 1,
графики функций
у = 2|*| + 1 и у = т
имеют две точки пересечения.
Мели т < 1, то графики не пере­
секаются.
Если m = 1, то точка пересечения
графиков одна и имеет координа­
ты (0; 1).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

170. Раздел V. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 24. Уравнение с двумя переменными
■
Подставляем значение переменных в уравнение и проверяем правиль­
ность полученного равенства. _____________________________
9 7 5 . Определим* удовлетворяют ли значения х = 5 и у — -2 уравнению
Ъх —2у = 10.
5л: - 2# = 10; 5 * 5 —2 * (~2) = 10; 25 + 4 = 10; 29 ф 10, то есть данные
значения не удовлетворяют уравнению. Ответ: нет.
976. Найдем, какие из пар (3; 2), (4; -3), (—1; 4) являются решениями урав­
нений:
а) 2х + 1у = 20; пара (3; 2): 2 * 3 + 7 * 2 = 20; б + 14 = 20; 20 —20, то есть
пара (3; 2) является решением; пара (4; —3): 2 * 4 + 7 - (—3) = 20; 8 - 21 —20;
-1 3 * 20, то есть пара (4; -3 ) не является решением; пара (-1 ; 4): 2 -(-1) +
+ 7*4 = 20; -2 + 28 = 20; -26 Ф20, то есть пара (-1; 4) не является решением.
• Ответ: (3; 2).
б) -2* + Зг —0; пара (3; 2): -2 *(3) + 3 * 2 = 0; -6 + 6 = 0; 0 = 0, то есть
пара (3; 2) является решением; пара (4; —3): - 2 * 4 + 3* (-3) =*0; -8 - 9 = 0;
-1 7 Ф0, то есть пара (4; -3 ) не является решением; пара (—1; 4): -2 *(-1) +
+ 3 *4 —0; 2 + 12 = 0; 14 Ф0, то есть пара (-1; 4) не является решением.
Ответ: (3; 2).
в) х —4у = 16; пара (3; 2): 3 - 4 * 2 = 16; 3 - 8 = 16; -5 ф 16, то есть пара
(3; 2) не является решением; пара (4; —3): 4 - 4 * (-3) = 16; 4 + 12 = 16;
16 = 16, то есть пара (4; -3) является решением; пара (—1; 4): - 1 - 4 * 4 = 16;
-1 - 16 = 16; -1 7 Ф16, то есть пара (-1 ; 4) не является решением.
Ответ: (4; -3).
г) 5х - у —23; пара (3; 2): 5 * 3 - 2 = 23; 13 Ф23, то есть пара (3; 2) не
является решением; пара (4; —3): 5 * 4 - (-3) —23; 23 = 23, то есть пара
(4; -3 ) является решением; пара (—1; 4): 5 *(—1) - 4 = 23; -9 Ф23, то есть
пара (-1 ; 4) не является решением.
Ответ: (4; -3).
I
Чтобы найти решение уравнения с двумя переменными, нужно подста­
вить в уравнение произвольное значение одной переменной и, решив
полученное уравнение с одной переменной, найти соответствующее зна­
чение другой переменной. Метод решения уравнения с одной переменной
рассмотрен раньше (см. объяснение к упражнениям 8—10).
977. а) 2х + у = 7; пусть х = 0, тогда 2 * 0 + # = 7; # = 7; решение — (0; 7);
пусть х = 1, тогда 2 * 1 + # = 7 ; # = 7 - 2 ; # = 5; решение — (1; 5).
Ответ: (0; 7) и (1; 5).
б) 2х - Зг = 10; пусть х = 20, тогда 2 * 20 - Зг = 10; -З г = 10 - 40;
-Зг = -3 0 ; г = 30 : 3; г —10; решение — (20; 10);
пусть х —5, тогда 2 * 5 —Зг = 10; —Зг = 10 —10; —Зг = 0; г —0; решение
- (5; 0).
Ответ: (20; 10), (5; 0).
в) 4т + 5д = 21; пусть т = 9, тогда 4 * 9 + 5 п —21; 5л = 21 - 36;
5/I = —15; п = -1 5 : 5; п —-3 : решение — (9; -3);
пусть т —4, тогда 4 *4 + 5тг = 21; 5/г = 21 - 16;
5/1 —5; 71 = 5 : 5; п —1; решение — (4; 1).
Ответ: (9; -3 ), (4; 1).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

171. 078. а) х - у — 16.' Пусть х = 20, тогда 20 —# = 16; ~у —16 - 20, у = 4;
I»сушение (20; 4).
Пусть х = О, тогда О- у = 16; у = -1 6 ; решение (0; -16).
Пусть у = О, тогда л: - 0 = 16; л: = 16; решение (16; О).
0) 2х + у —3,5.11' ' У и>и*
Пусть л; = 2, тогда 2 * 2 + # = 3,5; # = 3,5 - 4, # = -0 ,5 ; решение (2; -0,5).
Пусть х = О, тогда 2 * 0 + # = 3,5; у = 3,5; решение (О; 3,5).
Пусть х = 1, тогда 2 * 1 + # = 3,5; # = 3,5 —2, # = 1,5; решение (1; 1,5).
а) 4а + 5Ъ —20.
Пусть а = 1, тогда 4 * 1 + 5Ь = 20; 56 = 16, 6 = 3,2; решение (1; 3,2).
Пусть 6 = 0, тогда 4а + 5 * О= 20; 4а = 20,' а = 5; решение (5; О).
Пусть 6 = 2« тогда 4а + 5 •2 —20; 4а = 10, а = 2,5; решение (2,5; 2).
г) 5т - 2п = -8 .
Пусть т = 2, тогда 5 * 2 - 2п = —8; —2а = -1 8 , п = 9; решение (2; 9).
Пусть то = О, тогда 5 * 0 - 2п —-8 ; - а —4; решение (О; 4).
Пусть п = -1 , тогда 5т - 2 *(—1) = -8 ; 5т = -1 0 , т = -2 ; решение (-2 ; -1).
1 3 1 3 ( 3^
д) - х - - # = 1. Пусть л: = О, тогда - * О- - # = 1; - # = 1 : ~ - к
5 4 5 4 ^ 4 )
у = - 1 —; решение (О; -1 —).
3 3
1 3 1
Пусть # = О, тогда —х * 0 = 1 ; - х = 1 : —, лг = 5; решение (5; -О).
5 4 5
1 3 3 3
Пусть х = 10, тогда - * 10 - “ # = 1; —- # = 1 —2, # = —1 : ( ——);
5 4 4 4
1 ' 1
I/ = 1 —; решение (10; —).
3 3
5 1 5 1 1
«) —а Л Ь —1. Пусть а —6, тогда — *6 + —6 = 1; —6 = 1 - 5 ,
6 4 6 4 4
Ь = -4 :; Ь = -1 6 ; решение (6;-16).
5 1 5
Пусть Ь —4, тогда —* а+— *4=1;—а = О; а = О; решение (О; 4).
6 4 6
5 1 5 1 1
Пусть Ъ—О, тогда — *а + — * 0 = 1 ; а = 1 : —; а = 1 —;решение (1—; 0).
979. Заменим звездочки числами так, чтобы пары (1; *), (2; *), (3; *), (*; 2),
(*; 0), (*; —5) удовлетворяли уравнению х + 3# = 10.
Пара (1; *): 1 + 3# = 10; 3# = 10 - 1; 3# = 9; # = 9 : 3; у = 3; пара (1; 3).
Пара (2; *): 2 + 3# = 10; 3# = 10 - 2; 3# = 8; # = ^ ; у = 2 ^ ; пара *
Пара (3; *): 3 + 3# = 10; 3# = 10 - 3; 3# = 7; # = | ; # = 2 ; пара (3;2^ 1.
Пара (*; 2): х + 3 * 2 = 10; х = 10 - 6; х = 4; пара (4; 2).
Пара (*; О): х + 3 * О= 10; х —10; пара (10; О).
Пара (*; —5): х + 3 * (-5) = 10; х = 10 + 15; х = 25; пара (25; -5 ).
Ответ-. (1; 3); Ь ;2 | ) ; ; (4; 2); (10; 0); (25; -5).
ООО. ах + Ьу —с — общий вид линейного уравнения с двумя переменны­
ми. Подставив в уравнение числа вместо а, Ъ и с, получим определенное
уравнение.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

172. а) (3; 2) — пара чисел удовлетворяет уравнению ах 4- Ьу = с. Пусть а —1,
6 — 1. Получим 1 * 3 4 1 - 2 = с; с - 5. Получаем уравнение: х 4 у = 5,
решением которого является пара (3; 2).
б) (-2 ; 5) Пусть о —2 и 6 = -1 . Получим: 2 * (-2) + (-1) •5 —с;
- 4 - 5 = с; с = —9. Получаем уравнение: 2х - у —-9
в) (-4 ; -1 ) Пусть а = -2 ; 6 = 5 . Получим: -2 *(-4) + 5 * (-1) = с;
8 - 5 = с; с —3. Получаем уравнение: —2х + 5у = 3.
1 2 1 2
г) ( —; —) Пусть а = 4;6 —5. Получим: 4 *— + 5 * — = с;
2 5 2 5
2 + 2 —с; с = 4. Получаем уравнение: 4х4 Ьу = 4.
9 8 1 . а) Зх 4 4у = 12; б) Ьх - у = 15;
. 12 -4|/ _ , 1 5 + ы
Зх = 12 - 41/; х = — — ^ ; 5х = 15 4 у; х = — —- ;
о о
х —4 — ~~У> Ау —12 “ Зх; х = 3 + ^ ; -у = 15 - 5х;
3 5
1 2 -З х „ 3 2/ = 5дс - 15.
У = ---- ;---- ; У = з - - а:.
4 4
в) х —2у —6; г ) 2х - Ьу = 1;
х = 6 + 2|/; 2х = 1 + 5?/;
-2# = 6 - х; 1 + 5|/ 1 , 5
я _ 6 - х . Х = - ё - ' Х ~ 2 + 2 У-
~2 -Ьу = 1 - 2х; у = ;
У - | - 3 . ^ = - 1 + 2
2 * 5 5
д) 10х - 15# = 0; 1 3
10х = 15^; е) - х + - у - О;
- - * ; х = 1,51/; 1 3 3 1
10 X — У1 х —— у
4 2 У 2
>
-15у —-10х;
-Ю х 2х -к= -би - 1/ = - ^ х *у — -------- ; у = — . * 0 У А
-15 3 2 4
1 3 1
У ~ ~ —х : у = - х.
4 2 6
982. Решение. Сумма х24- у2принимает неотрицательные значения при любых
х ту, поэтому она не может равняться отрицательному числу -5 . Значит,
уравнение не имеет решений.
983. а) х2 4- у4 ——1. Сумма х2 4- у4 принимает неотрицательные значения
при любых х и у, поэтому она не может равняться отрицательному числу
—1. Значит, уравнение не имеет решений.
Ответ: не имеет.
б) х2 —у2= -3 ; х2 и у2 принимают неотрицательные значения при любых
х и у, поэтому их разность может равняться отрицательному числу -3 при
условии, что х2 < у2, то есть при |х|< у. Например, пара (1; 2).
Ответ: имеет.
в) х2 4 3у2 —0; уравнение имеет одно решение (0; 0).
Ответ: имеет.
984. а) х2 4- у2 = 0; сумма х2 4- у2 принимает неотрицательные значения при
любых х и у, поэтому она равняется 0, только когда и х2 —0, и у2 = 0, то
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

173. есть при х —О и у = О. Значит, существует единственное решение (О; О).
Ответ: одно.
б) х2 + (у - 2)2 = О; сумма х2 + (у - 2)2 принимает неотрицательные зна­
чения при любых х и у9 поэтому она равняется 0, только когда и х2 = О,
и (у - 2)2 = О;
х2 = О; х —О; (у —2)2 = 0; у —2 —0; у = 2, то есть при д: = 0 и у ~ 2 . Зна­
чит, будет единственное решение (О; 2). Ответ: один.
в) х(лс2 + у2) = 0; при х = Опроизведение х(х2 + у2) всегда равняется 0, то
есть у может быть любым. Если х2 4- у2 —0, то х —0 и у —О.
Ответ: множество.
г) х2 + у2 = -2 ; сумма х2 + у2 принимает неотрицательные значения при
любых х и у, а -2 < 0, поэтому уравнение корней не имеет.
Ответ: не имеет.
985- а) х2 + (у - I)2 = 0. Так как х2 > 0 и (у - I)2 > О, то х2 + (у - I)2 = О,
если я2 = О; х —Ои {у - I)2 —0; у - 1 = О; у —1. Ответ: (О; 1).
б) (х + З)2 + у2 = О. Так как (л: + З)2> 0 и у2> О, то (х + З)2 + у2 = О* если
(дг + З)2 —0; х + 3 = О; х —-3 и у2 = 0; у = 0. Ответ: (—3; 0).
986. а) (х - З)2 + (у + I)4 = О. Так как (х —З)2> Ои (у + X)4> О,
то (х - З)2 + (у + I)4 - О, если (х - З)2 - О; х - 3 = 0; х - 3 и (у + I)4- 0;
у + 1 = О; у = -1 .
Ответ: (3; -1).
б) |л;|+ у2 = О. Так как х> 0 и у2 > О, то х+ у2 —О, если х—О; х О
и у2 = 0; у = О.
Ответ: (О; О).
в) (2л; + З)4 + у2 - О. Так как (2дг + З)4 > 0 и у2 > О, то (2х + З)4 + у2 « О,
если (2л: + З)4 —О; 2л; + 3 = О; 2л: = -3 ; х = -1 ,5 и у2 —О; у —О.
Ответ: (-1 ,5 ; О).
г) 4л;2 + |у - 1|= О. Так как л;2 > Ои |у - 1|> 0, то 4л:2 + |у - 1|= О, если
4х2 —0; л;2 = О; х —0 и |у - 1| = О; у - 1 = 0; у = 1.
Ответ: (О; 1).
987. Решение. ах + 5у = 1; так как л; —3, у = -4 — решения этого уравнения,
то их можно подставить в него:
а •3 + 5 * (-4) = 1; За - 20 = 1; За —21; а = 21 : 3; а —7.
988. ах + Ъу —с. Пусть а —1, тогда:
а) (2; 1) и (1; -1).
1 * 2 + 6 * 1 = с ;с = 6 + 2.
1 * 1 + 6* (-1) - с; с - ~6 + 1.
Имеем 6 +. 2 —-6 + 1;
26 = -1 ; 6 = -0 ,5 .
с = -0 ,5 + 2; с = 1,5.
л: - 0,5у = 1,5 |* 2;
2л; - у = 3.
Ответ: 2х - у = 3.
в) (5; О) и (-1 ; -3).
5 + 0 * 6 = с; с = 5.
1 —36 = с;
-1 - 36 - 5;
-3 6 = 6;
6 = -2 .
х - 2у —5.
Ответ: х - 2у —5.
б) (-3 ; 2) и (О; 4).
1 •(-3) + 26 = с; с = 26 -3 .
1 * 0 + 46 —с; с = 46.
46 = 26 - 3; 26 - -3;
6 = -1 ,5 .
с = 4 * (-1,5); с = -6.
л; - 1,5у = -6 |* 2;
2х - Зу ——12.
Ответ: 2х - Зу = -12.
г) (-2 ; 6) и (О; О).
1 *(-2) + 66 - с; с - 66 - 2.
0 * 1 + 0 * 6 = с ;£ = 0.
1_ •
3 ’
х + —у = О|* 3; Зл + у = 0.
66 - 2 - 0; 6 =
Ответ: Зл: + у —О.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

174. б) х2 + у2 + 2 = 2у.
х2 4 у2 - 2у + 1 4- 1 = О; х2 + (у - I)2= -1
Так как х2 4 (у - I)2 > О, а -1 < О,
то уравнение не имеет решений,
г) х - 1| 4 |*|4 у2 ** О.
|* - 1|> 0, |*|> Ои у2 > О, то
|* - 1| 4 |*|4- у2 > О.
989.
а) * 2 + (у - I)2 = -3 .
Так как * 2 4 (у - I ) 2 > О,
а —3 < О, то уравнение
не имеет решений.
в) 1*1 + у2 4 1 = О.
1*1 + У2 = -1 ;
Так как |*|+ у2 > О, а
-1 < О, то уравнение не
имеет решений.
990. (с; с)
а) 2* 4 3у —20;
2с + Зс = 20;
5с = 20;
с —4.
Ответ: с = 4.
в) * + 8у —9;
с 4- 8с = 9;
9с = 9;
с = 1.
Ответ: с = 1.
991. ( л ; - л )
а) 5* 4 4# = 3;
5 л 4 4 ( - л ) = 3;
л = 3;
Ответ: п —3.
в) * 2 + 4*/ = 0;
п2 4 4 (—л) = О;
п(п - 4) - О;
п —0, або п - 4 —0;
/1 = 4.
Ответ: и = 0, або л = 4.
992.
а) * 2 4 у 2 = л.
Так как * 2 + у2 > 0, то уравнение
имеет одно решение при л * 0.
Ответ: л = О.
в) |*|4 Ы = л 4 2.
Так как |*|+ |г/|> О,
то уравнение имеет одно реше­
ние при л 4 2 = 0;
п = —2.
Ответ: л —-2 .
При этом |* - 1| 4 I*] + г/2 = 0, если
|* - 1( —Ои |*|= Ои у2 = О.
* - 1 = О; * = 1. * = О; у = О.
То есть |* —1|и |*|одновременно не равны
нулю. Значит, |* - 1|4 |*|4* у2 ф О.
Ответ: уравнение не имеет решений.
б) Ьх - у —12;
5с - с - 12;
4с = 12;
с —3.
Ответ; с = 3.
г ) 7* - Зу = 20;
7с - Зс * 20;
4с = 20;
с = 5.
Ответ: с —5.
б) 9 * - у —70;
9л - (-л) = 70;
Юл = 70; п —7.
Ответ: п = 7.
г) * + Ы - 4;
п + (-п| = 4;
если -л > О,
то л 4- (-л) = 4; 0 = 4.
Решений нет.
Если -л < О,
то л - (—л) = 4; 2л = 4; л = 2.
Ответ: л = 2.
б) * 24 |у|= л - 1.
Так как * 2 4 -|#|> О,
то уравнение имеет одно решение
при п - 1 = О; л * 1.
Ответ: л = 1.
г ) (* - З)4 4 у4 —л4.
Так как ( * - 3 ) 44 ^ 4> 0 и для про­
тивоположных значений '
(* - З)4 - (3 - *)4
и у4 - (-у)4, то уравнение имеет
одно решение, если л4 = О,
л = О.
Ответ: л = О.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

175. 993.
a) 4jc2 + у= х2.
4х2 - х2 + у—О;
Зх2 + у= 0;
Так как Зх2 > 0 и |у|> 0, то
Зх2 + у—0, если
Зх2 = О, и у= О;
х = О, у = О.
Ответ: (О; О).
п) 10* - у—х2 + 25;
“Ы —х2 - 10х + 25;
“Ы = (* ~ 5)2;
Так как -у < О,
а (х - 5)2 > О, то уравнение име­
ет решения, если
-у ~ О и (* - 5)2 = О;
у = 0 и * - 5 = 0;
* = 5.
Ответ: (5; О).
994.
а) * 2 + у2 + 1 = 2*.
* 2 - 2* + 1 = - у2;
(* - I)2 = -у 2;
Так как (* - I)2 > 0, а —у2 < О, то
уравнение имеет решения, если
( * - 1 ) 2 = 0 и - у2 = О,
* - 1 = 0 ; у = О.
* — 1.
Ответ: (1; О).
в) х2 + 4i/2 + 1 = 4|/.
4|/2 - 4у + 1 = - * 2;
(2z/ - I)2 = - * 2;
Так как (2у - I)2> О, а - * 2< 0, то
уравнение имеет решения, если
(2у - I)2 = Ои -* 2 = О,
2у - 1 = О; * = 0.
У = 0,5.
Ответ: (О; 0,5).
995.
а) * 2 + у2 + 4 = -4 * .
* 2 + 4 * + 4 = -I/2;
(* + 2)2 = —у2; '
Так как (* + 2)2 > О, а - у2 < 0, то
уравнение имеет решения, если
(зс + 2)2 = 0 и - у 2 = 0,
* + 2 = 0; у = 0.
* —-2 .
Ответ: (-2 ; О).
б) |* - 2] - у* = |3* - б|.
х - 2 - у < = 3х - 2|;
-у 4 = 3|х - 2| - |д; - 2|;
- 2х - 2|;
Так как - у4 = < 0, а 2|д: - 2|>
О, то уравнение имеет решения,
если у4 —0 и 2|* —2| = 0;
у = 0 й х - 2 = 0 ; х = 2.
Ответ: (2; 0).
г) (у + 4| + |3* + 2| = О.
Так как у + 4( > 0 и |3* + 2|> 0, то
уравнение имеет решения, если
у + 4|= Ои |3х + 2| = О;
у + 4 = 0; 3* + 2 = О;
2
Ответ: ( — ; -4).
3
б) * 2 + у2 + 9 = 6*.
* 2 - 6* + 9 = - у2;
(х - З)2 = -у 2; '
Так как (* - З)2 > 0, а -у 2 < О, то
уравнение имеет решения, если
(* - З)2 = Ои - у2 = О,
* - 3 = 0 ; у = 0.
* = 3.
Ответ: (3; 0).
г) * 2 + 2* + у2 + 5 = 4у.
х2 + 2* + 1 + у2 —4у + 4 = 0.
(* + I)2 + (у - 2)2 = О;
Так как (* + I)2 > О,
а (у2 - 2) > О, то уравнение име­
ет решения, если
(* + I)2 = 0 и ( у - 2)2 = О,
* + 1 = 0; I/ -* 2 = 0.
* = -1 ; у = 2.
Ответ: (-1 ; 2).
б) * 2 + у2 + 9 = 6у.
у2 - 6у + 9 = - * 2;
(у - З)2 = —* 2;
Так как (у - З)2 > О, а - * 2 < О,
то уравнение имеет решения,
если
( у - З)2 = Ои - * 2 = О,
I/ - 3 = 0; * —О.
У = 3.
Ответ: (0; 3).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

176. в) 4л;2 + #2 + 2 = 2(2х - у); г)
4л:2 + #2+ 2 = 4л: - 2у2;
4х2 + 4л; + 1 + у2+ 2у + 1 = О;
(2л; - I)2 + (# + I)2 = О;
Так как (2л: - I)2> О,
и (у 4- I)2> О, то уравнение име­
ет решения, если
(2х - I)2 = 0, и (у + I)2 = О,
2л; - 1 = О; # + 1 = 0 ;
х = 0,5, у = -1 .
Ответ: (0,5; -1).
996« Так как х и у — натуральные числа,
1 < л ; < с и 1 < # < с .
а) х + 4у = 13. б)
Если у = 1, то х + 4 •1 = 13
х = 13 - 4; х = 9. (9; 1).
Если у —2, то х + 4 - 2 = 13
х = 13 - 8; х = 5. (5; 2).
Если у ~ 3, то х + 4 * 3 = 13
х = 13 - 12; х = 1. (1; 3).
Если у —4, то л; + 4 •4 = 13;
х = 13 —16; х = —*3.
- 3 — не натуральное.
Ответ: (9; 1); (5; 2); (1; 3).
в) Зл; + у —16. г)
Если х = 1, то 3 •1 + у = 16
у = 16 - 3; # = 13. (1; 13).
Если’л; = 2, то 3 •2 + # = 16
у — 16 - 6; # = 10. (2; 10).
Если х —3, то 3 * 3 + у = 16
# = 1 6 - 9 ; # = 7. (3; 7).
Если х = 4, то 3 •4 + у = 16
у = 16 - 12; # = 4. (4; 4).
Если л: = 5, то 3 * 5 + # = 16
# = 16 - 15; # = 1. (5; 1).
Если х = 6, то 3 * 6 + у = 16
# = 16 - 18; # = -2 .
-2 — не натуральное.
Ответ: (1; 1*3); (2; 10); (3; 7); (4;
4); (5; 1).
д) Зл: + 2# = 22. е)
Если х = 1, то 3 г 1 + 2# = 22;
2# = 19; # = 9,5.
9.5 - не натуральное.
Если х = 2, то 3 * 2 + 2# = 22;
2# = 16; # = 8. (2; 8).
Если х —3, то 3 •3 + 2# = 22;
2# = 22 - 9; 2# = 13; # = 6,5.
6.5 — не натуральное.
Если х = 4, то 3 * 4 + 2# = 22;
2# = 10; # = 5. (4; 5).
л:2 + #2 + 8 = 4(# - л:);
л;2 + #2+ 8 = 4# - 2л:;
х2+ 4л: + 4 + #2 - 4# + 4 = О;
(х + 2)2 + (# - 2)2 = О;
Так как (х + 2)2 > О
и (# —2)2> О, то уравнение име­
ет решения, если
(х + 2)2 = О, и (# - 2)2 = О,
х + 2 = О;. # - 2 = 0;
л; = -2 , # = 2.
О твет: (-2 ; 2).
то для уравнения вида ах + Ъу —с:
5л; + # = 14.
Если * = 1, то 5 - 1 + # = 14;
у = 14 - 5; у = 9. (1; 9).
Если л; = 2, то 5 * 2 + # = 14;
# = 14 - 10; # = 4. (2; 4).
Если л; = 3, то 5 * 3 + # = 14;
у = 14 - 15; # = -1 . (9; -1).
-1 — не натуральное.
Ответ: (1; 9); (2; 4).
л: + 12# = 37.
Если # = 1, то х + 12 * 1 = 37;
л: = 25; (25; 1).
Если # —2, то л; + 12 * 2 = 37
л: = 13. (13; 2).
Если у ~ 3, то х + 12 * 3 = 37
* - 1. (1; 3).
Если # = 4, то л: + 12 * 4 = 37
х - -11.
-11 — не натуральное.
Ответ: (25; 1); (13; 2); (1; 3).
4л; + 5# = 2 9.
Если # ** 1, то 4л: + 5 * 1 = 2 9 ;
4л: = 24 ; х = 6 ; (6 ; 1).
Если # = 2 , то 4л; + 5 * 2 = 2 9 ;
4х = 19; х — 4 ,7 5 .
4 ,7 5 — не натуральное.
Если # —3, то 4л: + 5 * 3 = 2 9 ;
4л; = 14; х = 3 ,5 .
3 ,5 — не натуральное.
Если # —4, то 4л: + 5 * 4 = 2 9;
4х —9 ; х = 2 ,2 5 .
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

177. 5 + 2у = 22; 2,25 — не натуральное.
Если у —5, то 4х + 5 * 5
4х = 4; х = 1. (1; 5).
4,75 — не натуральное.
Ответ: (6; 1); (1; 5).
29;
Если х —5, то 3
2у —7; у ~ 3,5.
3,5 — не натуральное.
Если х = 6, то 3 * 6 + 2у —22;
2у = 4; у - 2. (6; 2).
Если х = 7, то 3 * 7 + 2у = 22;
2у = 1; у = 0,5.
0,5 — не натуральное.
Ответ: (2; 8); (4; 5); (6; 2).
997. Так как х и у — целые неотрицательные числа, то для уравнения вида
ах2 + Ьі/2 —с: 0 < х < с и 0 < у < с
а) х2 + у2 = 2.
Если х —0, то 0 + у2 = 2;
у%= 2; уравнение не имеет це­
лых решений.
Если х = I, то I 2 + у2 = 2;
у2 = 1; у = 1 (1; 1).
Если х = 2, то 22 + у2 = 2;
У2 = ~4;
уравнение не имеет решений.
Ответ: (1; 1).
0 +
I 2 + у2
9;
=9
б) 2х2 + у2 = 9.
Если х = 0, то 2
# = 3; (0; 3).
Если х = 1, то 2
у2 = 7; целых решений нет.
Если х = 2, то 2 * 22 + у2 = 9
у* * 1; у = 1. (2; 1).
Если х = 3, то 2 * 3? + у2 = 9;
у2 = -9 ; уравнение не имеет решений.
Ответ: (0; 3); (2; 1).
998. Так как х и у — целые числа, то для уравнения вида ах2 + Ъу2 = с:
-с < х < с и —с < у < с.
б) * 2 + 3у2 = 32.а) * 2 + у2 = 3.
Если х = 0, то О2 + у2 = 3;
у2 = 3; целых решений нет.
Если х = ±1, то (±1)2+ у2= 3;
У2 = 2;
целых решений нет.
Если х —±2,
то (~2)2 + у2 = 3;
у2 ——1; решений нет.
Ответ: уравнение не имеет
целых решений.
999. 3* - 2у2 = 6.
а) (а; 3)
Зх - 2 •З2 = 6; Зх = 24; х * 8.
Ответ: а —8.
в) (а; 0)
Зх - 2 •О2 = 6;
Зх = 6;
х = 2.
Ответ: а = 2.
2.
Если у = 0, то х2 + 3 •О2 = 32;
х2 —32; целых решений нет.
Если у = ±1, то х2 + 3 *(±1)2 —32;
х2 = 29; целых решений нет.
Если у = ±2, то х2 + 3 •(±2)2 = 32;
х2 = 20; целых решений нет.
Если у = ±3, то х2 + 3 •(±3)2 = 32;
х2 ~ 5; целых решений нет.
Если у = ±4, то х2 + 3 *(±4)2 = 32;
х2 ~ -1 6 ; решений нет.
Ответ: уравнение не имеет целых
решений.
0; у2= 0; у = 0.
6) (2; а)
3 •2 - 2у2- 6; —2у2
Ответ: а = 0.
г) (8; а)
3 * 8 - 2у2 = 6;
~2у2 = -1 8 ; у2 = 9; у2 - 9 = 0;
(у - 3) (у + 3) = 0;
у —3 = 0, або у + 3 = 0
у = 3. у = ~3.
Ответ: а = - 3 або а = 3.
1000. 5х - ау
а) (2; 1)
5 * 2 - а * 1 = 2;
Ответ: а = 8.
-а = -8 ; а = 8.
б) <1; 2)
5 •1 - а •2 = 2;
Ответ: а = 1,5.
-2а -3; а = 1,5.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

178. (-5 ; 9)
5 * (-5) - 9а = 2;
-9 а =* 27;
а = 3«
Ответ: а ——3.
в) (4; 3) г)
5 •4 - а * 3 = 2;
-З а = -1 8 ;
а —6.
О твет: а = 6.
1001 - Если а и 6 — цифры двухзначного числа, то 10 *а 4- 1 *6 — данное число,
а 4- 6 — сумма цифр числа, при этом а € {1; 2; 3; 4; ...9}; 6 в {0; 1; 2; ,..9}
10а 4- 16 = 2(а 4- 6); 10а 4- 6 = 2а 4- 26; 8а —6 = 0.
Если а = 1, то 8 * 1 —6 = 0; 6 = 8.
Если а = 2, то 8 * 2 —6 = 0; 16 —6 = 0; 6 = 16.
16 — не цифра. О твет: 18.
1002.
а) 10а 4- 6 = 3(а + 6); б)
10а + Ь = За + 35;
7а - 26 = 0.
Так как 7а —26 = 0,
то а — четное.
Если а = 2, то 7 * 2 —26 = 0;
-2 6 - -1 4 ; 6 - 7 .
Если а = 4, то 7 * 4 - 26 —0;
4 —46 = 0.
6 - 46 = О.
-2 6 = -2 8 ; 6
Ответ: 27.
14.
г)
10а 4- 6 = 5(а + 6);
10а 4- 6 = 5а 4- 56; 5а - 46 =
При этом а — четное.
Если а = 2, то 5 * 2 - 46 = 0.
46 = 10; 6 - 2,5.
Если а = 4, то 5
46 = 20; 6 = 5.
Если а —6, то 5
46 = 30; 6 = 7,5.
Если а = 8, то 5
46 = 40; 6 = 10.
Ответ: 45.
10а 4- 6 = 8(а + 6);
10а + 6 = 8а + 86; 2а - 76 —0.
При этом 6 — четное.
Если 6 = 2, то 2а —7
2а = 14; а = 7.
Ответ: 72.
8 - 46 = 0.
2 = 0.
в) 10а + 6 = 6(а + 6);
10а 4- 6 = 6а 4* 66; 4а - 56 —0.
При этом 6 — четное.
Если 6 = 2, то 4а —5 * 2 = 0.
4а = 10; а = 2,5.
Если 6 = 4, то 4а - 5 * 4 = О.
4а = 20; а —5.
Если 6 = 6, то 4а - 5 - 6 = О.
4а = 30; а = 7,5.
Если 6 = 8, то 4а —5 * 8 —О.
4а —40; а = 10.
Ответ: 54. '
1003* 10а 4* 6 = 2,5(а + 6); 10а 4- 6 = 2,5а 4- 2,56; 7,5а —1,56.
Если а = 1, то 7,5 •1 = 1,56; 6 = 5 .
Если а == 2, то 7,5 * 2 = 1,56; 1,56 = 15;6 = 5 .
Ответ: 15.
1004.10а 4- 6 = 4(а + 6) и 10а 4- 6 = 2а6;10а 4- 6 = 4а 4- 46; 6а = 36; 2а
Если а = 1, то2 •1 = 6; 6 = 2. Если а —2, то 2 *2 —6; 6 = 4.
Если а = 3, то2 - 3 = 6; 6 = 6. Если а —4, то 2 *4 = 6; 6 = 8.
Если а = 5, то2 •5 = 6; 6 = 10.
Проверим, для каких из полученных чисел выполняется условие
10а 4- 6 = 2а6:
12: 12 = 2 * 1 - 2; 12 Ф4. 24: 24 = 2 •2 •4; 24Ф 16.
36: 36 - 2 * 3 * 6; 36 = 36. 48: 48 = 2 * 4 •8; 48Ф 64.
Ответ: 36.
1005. (10а 4- 6)(а 4- 6) = 370. Так как наибольшее значение а = 9 и 6 = 9 , то
наибольшее значение а + 6 = 9 + 9 = 18, наименьшее значение а = 1, 6 —О,
значит, наименьшее значение а 4- 6 = 1.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

179. При этом наименьшее значение 10а + Ъ —10, наибольшее — 99.
Разложим на множители число 370.
370 —2 •5 •37. Значит, если (10а + Ь)(а + Ь) = 370, то 37 - 10 = 74 - 5.
Проверим оба случая.
Если искомое число 37, то (10 - 3 + 7)(3 + 7) = 37 * 10 = 370.
Если искомое число 74, то (10 * 7 + 4)(7 + 4) = 74 * 11 = 814 Ф 370.
Ответ: 37.
1006. Реш ение. Пусть, чтобы проложить трубопровод, необходимо взять
дгтруб длиной 7 м и у труб длиной 8 м. Тогда трубами длиной 7 м проло-
лсат 7х м трубопровода, а трубами длиной 8 м — 8# м трубопровода. По­
лучаем уравнение 7х + 8# = 67; так как х к у целые и положительные, то
7х положительное, нацело делится на 7 и меньше 67, а 8# положительное,
нацело делится на 8 и меньше 67. Такими числами для 7х являются 63;
56; 49; 42; 35; 21; 14; 7; а для 8у — 64; 56; 48; 40; 32; 24; 16; 8.
Так как сумма равняется 67, то из этих чисел одновременно можно взять
только 35 и 32. Тогда 7х —35; х = 5; 8# —32; у = 4.
Ответ: надо взять 5 труб по 7 м и 4 трубы по 8 м.
1007. Пусть монет стоимостью 2 коп. у мальчика х штук и у штук монет
стоимостью 5 коп. Тогда у мальчика (2х + 5у) коп., что равняется 37 коп.
(при этом х и у натуральные числа).
Имеем 2* + 5у —37. Так как 2х — четное, а 37 — нечетное, то у — нечетное.
Если у = 1, то 2х + 5*1 = 37; 2х —32; х = 16.
Если у —3, то 2х + 5*3 — 37; 2х = 22; х = 11.
Если у = 5, то 2х + 5*5 — 37; 2х = 12; х = 6.
Если у = 7, то 2х + 5*7 = 37; 2х = 2; х = 1.
Ответ: без сдачи 37 коп. мальчик может заплатить так: 16 монет по 2 коп.
и 1 монета по 5 коп. или 11 монет по 2 коп. и 3 монеты по 5 коп.; или 6 мо­
нет по 2 коп. и 5 монет по 5 коп.; или 1 монета по 2 коп. и 7 монет по 5 коп.
1008. Пусть конфеты расфасованы в х коробок по 200 г и в у коробок по
300 г. Тогда всего расфасовано (200* + 300#) г конфет, что равняется
3 кг = 3000 г (при этом х н у — натуральные числа).
Имеем 200* + 300# = 3000.
2х + 3# = 30. При этом # — четное.
Если у = 2, то 2х + 3*2 = 30; 2х = 24; х = 12.
Если # —4, то 2х + 3*4 = 30; 2х = 18; х —9.
Если у —6, то 2х + 3-6 = 30; 2х = 12; х —6.
Если # = 8, то 2х + 3*8 = 30; 2х —6; х = 3.
Если # = 10, то 2х + 3 * 10 = 30; 2х = 0; х = 0.
Ответ: конфеты могут быть расфасованы такими способами:
12 коробок по 200 г и 2 коробки по 300 г.;
или 9 коробок по 200 г и 4 коробки по 300 г.;
или 6 коробок по 200 г и б коробок по 300 г.;
или 3 коробки по 200 г и 8 коробок по 300 г.
Упражнения д ля повторения
1010. а) 4а4 + 1 = (2а2 - 2а + 1)(2а2 + 2а + 1).
I способ. (2а2 - 2а + 1)(2а2 + 2а + 1) = 4а4 + 4а3 + 2а2 - 4а3 - 4а2 - 2а +
+ 2а2 + 2а + 1 = 4а4 + 1.
Тождество доказано.
II способ. (2а2 —2а + 1)(2а2 + 2а + 1) = ((2а2 + 1) - 2а)((2а + .1) + 2а) =
= (2а2+ I)2- (2а)2= (2а2)2+ 2 *2а2*1 + 1 - 4а4- 4а4+ 4а2+ 1 - 4а2- 4а4+ 1.
Тождество доказано.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

180. б) а4 + а2 + 1 = (а2 - а + 1)(а2 + а + 1).
/ способ, (а2 - а + 1)(а2 + а + 1) —а4 + а3 + а2 - а3 - о2 —а + а2 + а+1—
= а4 4- а2 + 1. Тождество доказано.
I I способ, (а2- а + 1)(а2+ а + 1) = ((а2+ 1) - а)((а2+ 1) + а) = (о2+ I)2 - а2=
= о4 + 2а2 + 1 “ а2 = а4 + а2 + 1. Тождество доказано.
1011 •Уравнение линейное относительно х. Линейное уравнение имеет мно­
жество корней, если коэффициент к равняется нулю и число, которое стоит
Га - 1 = 0,
I: <
[За - 3 = 0;
в правой части, равняется нулю. Тогда: л откуда а = 1.
Ответ: а = 1.
1012. Существуют ли такие значения а, при которых уравнение Зх + 4 = а
не имеет решений? *
а —4 а —4
3 * + 4 = а; Здг = а - 4 ; л: = --------. Так как выражение —— имеет смысл
3 3
для любого действительного значения, то данное уравнение имеет решение
при любом действительном значении а. Ответ: нет.
§ 25. График линейного уравнения с двумя переменными
Ю 18.А(-3; 2).
а) 5 * + 1 2у —9; б) 2х + 3 у = х; в) 5(х + 3) = 4(у - 2);
5 * ( - 3 ) + 12 * 2 = 9; 2х - х + Зу = О; 5 (-3 + 3) = 4(2 - 2);
- 1 5 + 2 4 = 9; х + Зу = О; 0 = 0.
9 = 9. - 3 + 3 •2 = 0; Точка А принадле-
Точка А 3 * 0 . жит графику урав-
принадлежит ТочкаА не принадлежит нения.
графику уравнения. графику уравнения.
1019. Реш ение.
. 8 - 3 * . 8 + 12
3 * 4 4у = 8 ; у = — -— ; * = - 4 ; у = —-— ; у = 5 ; ( - 4 ; 5) — точка А,.
4 4
* = - 2 ; I/ = ; у = 3 ,5 ; ( - 2 ; 3 ,5 ) — точка А.г.
£
* = 0; у = - ; у = 2; (0; 2) — точка А .
4
£ 0
* = 2; у = --------; у = 0,5; (2; 0,5) — точка А4.
х = 4; у = — — ; у = -1 ; (4; -1 ) — точка Д..
8 - 1 2
4
Обозначив полученные точки на плоскости, видим, что они лежат на од­
ной прямой.
■
Графиком любого уравнения первой степени с двумя переменными яв­
ляется прямая. Для построения графика такого уравнения достаточно
найти два его решения, и, обозначив на координатной плоскости соот­
ветствующие им точки, провести через них прямую.
1020. Решение. Достаточно найти два решения, которые и будут двумя точ­
ками, через которые можно провести прямую, которая будет графиком
уравнения, потому что график линейного уравнения с двумя переменны­
ми — это прямая.
а) * 4- у = 4; при * = 0: у —4; точкаА,(0; 4); при у = 0: * = 4; точкаА2(4; 0);
б) 2х + у = 6; при * = 0; у = 6; точкаА2(0; 6); при * = 3; у = 0; точкаА2(3; 0);
в) 3* + 2у —0; при * = 0; у = 0; точкаАД0; 0); при * = 2;у = -3 ; точкаАД2; -3).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

181. 1022. 7* - 2у = 12,5; х = 2,5.
7 * 2,5 - 2у = 12,5; 17,5 - 2# - 12,5; -2# = -5 ; у = 2,5.
Ответ: у —2,5.
1023. 5* + 4у = 16; у = 1,5.
5* + 4 * 1,5 = 16; 4х + 6 —16; Ах = 10; х = 2,5.
Ответ: х = 2,5.
1024. 0,6л: + у = 2,2.
а) х —-8 ; б) х = -3 ;
0,6 *(-8) + у = 2,2; у = 2,2 + 4,8; 0,6 •(-3) + у « 2,2; у = 2,2 + 1,8;
у = 7. у = 4.
Ответ: у = 7. Ответ: у = 4.
и) л: = 2; а) * —7;
0,6 * 2! + у —2,2; I/ = 2,2 - 1,2; 0,6 * 7 + у = 2,2; у = 2,2 - 4,2;
У - 1-
Ответ: у —1.
1 0 2 5 .11л: - 4# = 80.
а) у = -3 1 ;
11л: - 4 * (-31) = 80;
И * ^ 124 - 80; 11л: = -4 4 ; л: = -4 .
Ответ: х = -4 .
в) у = -3,5;
11л: - 4 * (-3,5) = 80;
11л: = 80 - 14; 11* = 66; х = 6.
Ответ: х —6.
1026. 2* + 5у = е*
а) А(3; 1).
2 •3 + 5 •1 = с ; с = 11.
Ответ: с —11.
в) С (-3; 4).
2 * (-3) + 5 * 4 = с; с = 14.
Ответ: с —14.
1027. ах - 4у —12.
а) М(10; 2).
а * 10 - 4 * 2 = 12;
10а —20; а = 2.
Ответ: а —2.
У = -2 .
Ответ: у —-2 .
б) у = -2 0 ;
11л: - 4 *(-20) = 80;
11л: = 80 - 80; 11л: = 0; * = 0.
Ответ: х = О.
а) у = 2;
11л: —4 * 2 = 80;
11л: —80 + 8; 11* = 88; * = 8.
Ответ: * = 8.
б) В (-5; 2).
2 * (-5) + 5 - 2 - с; с = 0.
Ответ: с = О.
а) Х>(—2; -1 ). .
2 * (-2) + 5 * (-1) = с; с = -9 .
Ответ: с = —9.
б) Щ - 1; -1).
а *(-1) - 4 * (-1) - 12;
-а = 8; а = -8 .
Ответ: а —-8 .
а) <2(6; 6).
а •6 —4 * 6 = 12;
6а = 36; а = 6.
Ответ: а = 6.
в) Р{2 ; -3).
а •2 - 4 * (-3) = 12;
2а = О; а = О.
Ответ: а —О.
1028. 6* + Ьу = О.
а) ЛГ(2; 3).
6 2 + 6 * 3 = 0;
36 = - 1 2 ; 6 = - 4 .
Ответ: Ь —- 4 .
в) Р (-4 ; 8).
6 * ( - 4 ) + 6 * 8 = 0;
86 = 2 4 ; 6 = 3.
Ответ: 6 = 3. Ответ: 6 = -9 .
1029. у = 1 ,5 * + с и 3* - 2у —4.
1 ,5 * - у —-с ; 3* - 2у = - 2 с . Значит, - 2 с = 4 ; с = - 2 .
Ответ: с = - 2 .
б) 0(0; О).
6 * 0 + 6 0 = 0;
О= О; 6 — любое действительное число.
Ответ: 6 — любое действительное число,
а) Я (-3; -2).
6 * (-3 ) + 6 *(-2) = О;
-2 6 - 18; 6 = -9 .
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

182. 1030.
а) Зх + 2у —6.
х —0; 3 •0 + 2у —6;
у 3. (0; 3).
у = О, Зх + 2 * О= 6;
х = 2. (2; О).
Построим график уравнения.
У*
7
6
5
.(0; 3)
2
0 ( 2 ; °) , ,
_ 2 - г
- 2
- 3
1 23 4 5 6 7 X
V
х
- 4
- 5
б) х + 5у = 10.
Если х = О; то 0 + Ьу = 10;
у = 2. (О; 12).
Если у = 0, то * + 5 * 0 = 10;
* = 10. (10; О).
*Построим график уравнения.
УА
(10; 0)
9 НГлг-
Если х = —2;
3 - (-2) + 2у = 6,
у = 6. (-2 ; 6).
Если х = 1,
3 * 1 + 2у = 6,
у = 1,5. (1; 1,5).
Ответ: (О; 3) — точка пересе­
чения с осью у; (2; 0) — точка
пересечения с осью х.
в) Зх - 2у = 6.
Если * = О;
3 - О—2у = 6;
у = —3. (О; —3).
Если у —О,
Зх —2 * О= 6;
* = 2. (2; О).
Построим график уравнения.
Если х = 1;
3 * 1 - 2у = 6
У = -1 ,5 .
Если х = 4,
3 •4 - 2у = 6
у = 3.
Ответ: (2; О) — точка пересе­
чения с осью х; (О; -3 ) — точ­
ка пересечения с осью у.
г) - х —5у = 10.
Если * = О; то -О - Ъу = 10;
у = -2 . (О; -2 ).
5;
10
Если *
5 + 5у
У - 1.
Если * = -5 ,
- 5 + 5у = 10;
У = 3.
Ответ: (10; О) — точка пересечения
с осью х; (О; 2) — точка пересечения
с осью I/.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

183. Если у = О,
то - х - 5 * 0 = 10:
* = - 10. ( - 10; 0).
Построим график
уравнения. Если х = 5;
- 5 - 5 у = 10; у —-3 .
Если х = -5 ,
-(-5 ) - 5# = 10;
у -= -1 .
Ответ: (-10; 0) — точ­
ка пересечения с осью х;
(0; -2 ) — точка пересе­
чения с осью у.
1031. Решение. * - у —3;
при л: = О; # = - 3 ; пр и у = О; л: = 3 .
График уравнения х - у = 3 проходит через точки А,(0; -3 ), А,(3; О).
3* + у = 1; при х —0, у = 1; при * = 2; # = 1 - 6 , у —-5 .
График уравнения Зл: + у = 1 проходит через точки ВД2; ~5), В2(0; 1).
Ответ: графики уравнений пересекаются в точке С(1; -2 ).
1032. Решение. 2х + Зу = 5; при у = 1; 2х —5 - 3; х = 1;
при # —-1 ; 2л: = 5 + 3; х = 8 : 2; я: = 4.
График уравнения 2х + Зу —5 проходит через точки АД1; 1), А2(4; -1).
2х + Зу = 10; при у —О; 2л: = 10; х = 10 : 2; х —5; при л: = 2; 3# = 10 - 4;
# = 6 : 3; у — 2. График уравнения 2л: + 3у — 10 проходит через точки
ВД2; -2), В2(5; О).
1033. Ьх ~ у = 7; при х —О; у —-7 ; при х = 1; -у = 7 - 5; у —-2 .
График уравнения 5л: - у = 7 проходит через точки АД1; ~2), А2(0; -7).
10* - 2 у —14; 2(5л: - 2у) = 14; 5л: - 2у —7. Упростив второе уравнение,
получили первое из них. Значит, график второго уравнение пройдет че­
рез те самые точки, что и график первого уравнения, то есть их графики
совпадают.
1034. а )* + # = 5ил:-
х + у = 5.
Если * = 5,
то у —О(5; О).
Если * = О,
то у —5 (О; 5).
УЬ
у —-1 . б) 2л: - у —6 и 4л; - Зу —12.
2х - у = 6
л: = 0 , 2 - 0 - # = 6
у = -6 (0; -6).
УЬ
7
6
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

184. х - у = -1
Если х = О, то у —1 (0; 1).
Если х —3, то у *=4 (3; 4).
Точка пересечения
графиков (2; 3).
в) 2х + Зу = - 9 и х + Зу = -6 .
2х + Зу = - 9 ;
х = 0;
2 * О+ Зу = - 9 ;
у = -3 (0; -3).
х = -3 ;
2 * (-3) + Зу = -9 ;
у = -1 (-3 ; -1).
х + 3у —-6 ;
х —О, 0 + Зу 88 -6 ;
у = -2 (О; -2).
х 3, 3 + Зу * ”6;
у = -3 (3; “3).
1035. а) 4х + 5у = 20 и -4 * + 5 у —20.
4х + 5у —20;
х = О;
4 * О+ 5у = 20;
у = 4 (О; 4).
х = 5;
4 * 5 + 5у = 20;
у - О(5; О).
-4 х + 5у —20;
х = О;
-4 * О+ 5у = 20;
у = 4 (О; 4).
х = —5;
-4 *(-5) + 5у - 20;
у - О (-5 ; 0).
х —3, 2 * 3 - у —6; у = О(3; О).
4х —Зу = 12; х * 0, 4 * О- Зу —12
у - - 4 (О; -4).
х = 3; 4 ♦3 - Зу = 12; у = О(3; О).
Точка пересечения графиков (3; О),
г) 4х —5у —Ои 2х - 5у —-1 0 .
4х - 5у = О;
х = О,
4 * О- 5у = О;
у - О(О; О).
х = 5;
4 •5 - 5у - О;
У - 4 (5; 4).
2х —5у = -1 0 ;
х —0, 2 * 0 —5у = -1 0 ;
у - 2 (О; 2).
х = -5» 2 * (-5) - 5 у —-10;
у = О(-5; 0).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

185. б) 2х + Зу = 6 и 2х - Зу = 6.
2х + Зу —6
х —О,
2 *О + Зг/ = 6
«/ = 2 (О; 2).
х * 3,
2 * 3 + 3у = 6
у - О(3; О).
2х - Зу = 6
х = О,
2 * О - 3# = 6
у = -2 (0; —2).
х —3,
2 ■3 - 3|/ - 6
У = О(3; О).
в) 5х - 2и = 10 и 10х - 4у = 20.
Ьх - 2у —10
х - 0, 5 * О- 2у - 10
у = -5 (О; -5 ).
х = 2, 5 •2 - 2у = 10
у - О(2; О).
10х - 41/ = 20
2(5х - 2у) = 2 * 10
5х - 2у = 10.
г) -З х + 2у —6 и -З х + 2у
—Зх + 2у = 6
х = О,
- 3 •0 + 2у = 6
у - 3 (О; 3).
х = -2 , -3 * (—2) + 21/ = (
^ = 0 (-2 ; О).
-З х + 2у = -6
х = О, -3 *О+ 2у —- 6
У = “3 (О; -3).
х —2, -3 •2 + 2у —-6
у = 0 (2; О).
Значит, график второго уравне­
ния совпадает з графиком пер­
вого уравнения.
1036. 5х + 6у —13. Докажем, что график уравнения не проходит через на­
чало координат (О; 0). Если график не проходит через точку (0; О), то ее
координаты не будут решением уравнения. 5 * 0 + 6 • О= 13; ОФ 13.
Ответ: да. График уравнения 5х + 6у = 13 не проходит через начало
координат.
1037. Если в уравнении ах + Ьу —с коэффициенты а —О; ЪФО, то уравнение
задает прямую, параллельную оси абсцисс. Эта прямая проходит через
точку
И )
и ординаты всех точек прямой равны.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

186. б) Зх + Оу = 9;
3 3 3
Значит, ординаты каждой точки графика неотрицательные.
1038.
а) Од: + 5у —10;
п 10а = О; у = — .
У —2. 5
Прямая параллельна оси х
и проходит через точку (О; 2).
9
3
6 = 0 ;* =
* = 3.
Прямая параллельна оси у
и проходит через точку (3; О).
У *
1
О
5 -4 -3 -2
05
=3>
О
+
н
со
1 2 4 5 *
У = о
У
о, у = О(О; 0);
3, у —3 (3; 3)*
0;
-1
- 2
-3
в) *
*
*
х
1039.
а) 2х + Оу = О
Ь —с —0 и 2х
х = 0.
Значит, уравнение задает ось у.
б) О* + Оу —О
а = Ъ = с —О
Значит, любому значенню * можно по­
ставить в соответствие любое значение
у. Значит, координаты любой точки координатной плоскости является
решением уравнения. Поэтому уравнение 0* + Оу = Озадает координат­
ную плоскость.
в) 0* + Оу = 13
а —Ъ —О; с ФО. Уравнение не имеет решений, а значит, не задает на ко­
ординатной плоскости ни одной точки.
1041. Для того, чтобы три разные прямые проходили через одну и ту же
точку, необходимо, чтобы соответствующие значения коэффициентов а уЬ
си
и с уравнений не были пропорциональными (если
а гх + Ьуу = сг и а2х + Ь2у = с2 совпадают).
а)А(4; 3).
1) 0 * * + у —3; 2) * + О•у = 4;
3) Пусть а = 3; Ъ —-4 , тогда уравнение имеет вид 3* - 4у
Найдем е: 3 * 4 —4 * 3 = с; с = 0. Имеем: 3* - 4у = 0.
= — , то прямые
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

187. б)А (-2; 4).
I) О* дс + i/ = 4; 2) х + О•y —-2 ;
3) Пусть a —2; b = 1, тогда уравнение имеет вид 2х + у = с.
Найдем с: 2 * (-2) + 4 = с; с = 0. Имеем: 2х + у = 0.
в) А(0; —3).
1) 0 * л: + у = -3 ;
2) Пусть а —1; Ъ = 2, тогда уравнение имеет вид л: + 2у = е.
Найдем с: 0 + 2 *(-3) = с; с —-6 . Имеем: x + 2i/ = -6 .
3) Пусть а = 2; 5 —3, тогда уравнение имеет вид 2х + Зу = с.
Найдем с: 2 * 0 + 3 - (-3) = с; с = ~9. Имеем: 2х + Зу = —9.
г) А(1; 0).
1)х + 0 * у = 1;2) Пусть а = 1; b = 1, тогда уравнение имеет вид х + у —с.
Найдем с: 1 + 0 = с; с = 1. Имеем: х + у —1.
3) Пусть а —2; b = -3 , тогда уравнение имеет вид 2х - Зу —с.
Найдем с: 2 * 1 + 3 *0 = с; с = 2. Имеем: 2х —Зу —2.
1042. Если прямая проходит через начало координат (О; О), то в уравнении
ах + Ьу = с, с = Ои уравнение имеет вид ах + Ьу = О.
а) Х (2; 2). Пусть а = 1; тогда уравнение имеет вид х + Ьу ** О.
Найдем 5: 2 + 25 —О; b = —1. Имеем: х - у —0.
б) У(—5; 2). Пусть а = -2 ; тогда уравнение прямой имеет вид -2 х + Ьу = О.
Найдем Ь: -2 *(—5) + Ь •2 = О; 6 = —5. Имеем: -2 х - 5|/ = О.
в) Д -4 ; -6 ). Пусть а = —; тогда уравнение прямой имеет вид —х + Ьу = О.
4 4
Найдем 5: — *(-4 ) + b - (—6) = О; -6 Ь = 1 ; Ь = - —. Имеем: —я: - —у = 0.
4 6 4 6
г) 7X3; -1). Пусть а = 2; тогда уравнение прямой имеет вид 2х + Ьу = О.
Найдем Ь: 2 * 3 + b *(-1) = О; -Ь = -6 ; Ъ = 6. Имеем: 2х + бу = О.
1043. а) А (-3; О) и В(0; 1). Пусть а = 1; тогда уравнение прямой имеет вид
х + Ьу = с. Найдем 5 и с:
-3 + 5 * 0 = с и 0 + 5 1 = с
с = -3 ; 6 = с.
Отсюда 5 = -3 . Получаем уравнение прямой дс - Зу = -3 .
б) М(4; О) и iV(0; 5). Пусть 5 = 1; тогда уравнение прямой имеет вид
ах + у —с. Найдем а и с:
û * 4 + 0 = c и а * 0 + 5 = с
4а = с; . g е = 5.
Отсюда а = —= — = 1,25. Получаем уравнение прямой 1,25* + у = 5.
4 4
в) Р(0; -3 ) и Q(3; 0). Пусть а = 2; тогда уравнение прямой имеет вид
2* + Ьу = с. Найдем 5 и с:
2 * 0 + 5 * (-3) = с и 2 * 3 + 5 * О= с
С и
Отсюда Ь ~= — —-2 . Получаем уравнение прямой 2х —2у —6.
3 3 «
г) С(0; -4 ) и Х>(—2; О). Пусть 5 = 1 ; тогда уравнение прямой имеет вид
ах - у = с. Найдем а и с:
а *О- (-4) = с и а - (-2) - О= с;
с = 4; -2 а = с;
с с 4
а —— . Отсюдаа = - —= — = -2 . Получаем уравнение прямой -2 х - у —4.
2 2 2
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

188. 1044. а) Прямая проходит через точки (-1 ; О) и (О; 2), пусть а — 1, тогда
уравнение прямой имеет вид х + Ьу = с.
Найдем Ь и с:
—1 + 6 * О= с и О + b * 2 —с
с — 1 Ъ - - ;
1 2 1
Отсюда Ъ = —= — . Получаем уравнение х - —у —-1 .
2 2 2
б) прямая Ъпроходит через точки (О; -4 ) и (4; 0), пусть а —1, тогда урав­
нение прямой имеет вид х + Ьу —с. Найдем б и с :
О+ Ь * (—4) = с и 4 + * 0 = с
Ь - - ^ ; с = 4.
4 4
Отсюда Ъ = — = -1 . Получаем уравнение я; - у —4.
4
в) прямая с проходит через точки (0; 2) и (2; 0), пусть а —1, тогда урав­
нение прямой имеет вид х + Ъу —с.
Найдем Ь и с:
О+ Ь -2 = с и 2 + b * О —с
6 = | ; с = 2.
2
Отсюда Ь = - = 1. Получаем уравнение дс + у = 2.
2
г) прямая d проходит через точки (-4 ; О) и (О; —2), пусть а —1, тогда урав­
нение прямой имеет вид х + Ьу = с. Найдем b и с:
—4 + Ь •О= с и О+ Ь * (—2) = с
с = -4 . 6 - - J ;
4
Отсюда 6 ------ = 2 . Получаем уравнение прямой х + 2у ——4.
CL. b. С.
1045. Если прямые + Ьгу = с1и а2х + Ь2у —с2параллельны, то — = ,
при этом возможно Oj = а2, —b2 и Cj * с2. 2
В таком случае уравнения двух паралельних прямих имеют вид ах + Ъу = с,
и а* + Ьу —с2.
2х - у = О. Уравнение прямой, параллельной данной прямой, имеет вид
2х —у ~ с.
а) Щ 4; 2). Найдем с: 2 * 4 —2 = с; с = 6.
Получаем уравнение прямой, проходящей через точку üC(4; 2) параллель­
но прямой 2х - у —0.
Ответ: 2х - у —6.
б) L(0; 5). Найдем с: 2 * 0 - 5 = с; с —-5 .
Получаем уравнение 2х - у = -5 .
в) М (-3; 0). Найдем с: 2 •(-3) - О= с; с = -6 .
Получаем уравнение 2х - у —-6 .
г) N(2; -1 ). Найдем с: 2 * 2 —(—1) —с; с = 5.
Ответ: 2х - у —5.
Для решения упражнений 1046—1048 воспользуемся определением
если а > О,
если а < О.
м К е
W " U
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

189. 1046.
а) |*|- у = О.
Если х > О,имеем * - у = О;
если х = 0, то у —О; (О; О);
если * = 3, то у = 3; (3; 3);
если * < О,имеем —х - у —О,
* + у = о,
если * = 0, то у —О; (0; О);
если * = -3 , то у = 3; (-3 ; 3).
-Ы - -х ; Ы = х.
Так как |(/|> 0, то уравнение имеет
решения для х £ 0.
у = х
если * = О, то у —О; (0; 0);
если * —2, то у = 2; (2; 2);
или -у = х,
У = -Х
если * = О, то у —0; (0; 0);
если х = 2, то у —-2 ; (2; -2).
б) х+ у = 0.
Если х > О, имеем х + у = О,
если * = О, то уг= О; (О; О);
если х = 3, то у —-3 ; (3; -3);
если х < О, имеем —х + у = 0,
если х = О, то у ==О; (О; 0);
если х —-3 , то у = -3 ; (-3 ; -3 ).
Ы= -ж ;
Так как |у|> О, то уравнение имеет
решения для * < О.
у = -X
если * = 0, то у —0; (О; 0);
если х = -2 , то у —2; (-2 ; 2);
или - у = -х ,
у * *-
если х = 0, то у = О; (О; 0);
если х —-2 , то у = 2; (-2 ; 2).
5 -4 ~3 х 1 2 3 4 5 х-5-4 -3 -2
О)
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

190. 1047- |* - 2|+ - 3) = 0. Так как х- 2> 0 и у- 3|> 0» то х - 2+ у- 3[ * О.
При условии
|* - 2| = О и у - 3| = О,
* - 2 = 0 и # - 3 = 0
х = 2 и у = 3.
(2; 3) — единственное решение уравнения. Значит, графиком уравнения
является одна точка К(2; 3). х - 2| = у - 3|; х - 2 —О; х —2.
Если * > 2, то х - 2 = х - 2; если * < 2, то х - 2) ==-(* - 2) = 2 —*.
у - 3 - О; у —3; если у > 3, то у - 3|= у - 3;
У•если у < 3, то у - 3| = -(# —3) = 3 —
I) * < 2 и # < 3
2 - х = 3 - у;
х ~ у = - 1;
если * = О, то у = 1; (О; 1);
если х = -2 , то у = -1 ; (-2 ; -1 ).
III) * > 2 и у < 3
х - 2 = 3 - у;
х + # = 5;
если * = 2, то у = 3; (2; 3);
если * = 3, то у = 2; (3; 2);
IV) * > 2 и у > 3 '
х - 2 = у - 3;
х - у = - 1;
если х = 2, то # = 3; (2; 3);
если * = 4, то # = 5; (4; 5).
Прямые * = 2 и # = 3 разбивают
.координатную плоскость на четыре -
части: I, II, III и IV, нумерация сов­
падает з рассмотренными случаями
для уравнения. Решениями уравне­
ния |* - 2| = |# - 3| являются коор­
динаты каждой из точек, лежащих
на графике. Значит, уравнение имеет
множество решений.
104В. а) у= 2 - х.
Так как у> О,
то уравнение имеет решения.
Если 2 —х > О
* < 2.
Ы = 2 - *
У = 2 - х;
если х = 2,
тоу = 0; (2; О);
если * = О,
то у = 2; (0; 2).
Или у = -{2 - х);
у = * - 2,
если х = 2,
то у = 0; (2; О);
если * = О,
то у = -2 ; (О; -2 ).
II) * < 2 и # > 3
2 ~ * = у - 3;
* + # = 5;
если * —О, то у = 5; (О; 5);
если * = -2 , то у —7; (-2 ; 7).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

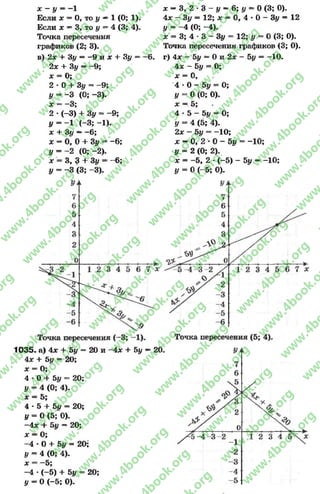
191. Ы = Зх - 4.
Тпк как |у|> О, то уравнение имеет ре­
шения.
Если Зх - 4 > О
х >
У = Зх - 4; у = Зх —4.
если х = 1 ^ , т о у = 0(1 —
3 У 3
если х —3, то у —5; (3; 5).
Или у = -(Зле - 4);
у = -3 * + 4
4
е с л и х — — , ТО у
О);
3
если х = 3, то у —-5 ; (3; -5).
и) ||/|+ |2 - х| = О.
Так как у> Ои |2 —х> О,
то ||/|+ |2- х] = О,
если |у|~ О, у —О.
и |2 - х| - О
2 - х = О, х = 2.
(2; О) — решение уравнения.
График уравнения — точка (2; О)
1049.
п) х2 - 9у2 —О; х2 —9у2; х2 = (3у)2.
Данное уравнение равносильно второму
ы - ы
I. х < Ои у < О; Зу < О*
имеем —х = —3у, х = Зу;
II. х < Ои у > О; Зу > О,
имеем —х —3у9 х = —Зу;
III. х > 0 и у < О; Зу < О,
имеем х = -Зу;
IV. х > Ои у > О; Зу > О,
имеем х = Зу.
Для I и IV случаев — прямая х —Зу = О.
Для II и Ш случаев — прямая х + Зу = О.
х - Зу = О.
если х = О, то у = О; (О; 0);
если х = 3, то у = 1; (3; 1).
х + Зу = О.
если х = 0,вто у = О; (О; 0);
ссли х = 3, то у = —1; (3; -1).
б) 4х2 - у2 = О;
4х2 = у2;
(2х)2 = у2.
Данное уравнение равносильно второму |2х| + |у|.
I. х < Ои у < 0, имеем —2х = -у , у = 2х;
II. х < Ои у > О, имеем —2х —Ууу ——2х;
УЬ
3
2
О
-3 -2
-1
-2
-3
1 2 3 х
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

192. III. х > 0 и у < 0, имеем 2х —-у ; у = —2х
IV. х > 0 и у > О,
имеем 2х —у; у —2х.
Для I и IV случаев — прямая 2х - у =
*Для II и III случаев — прямая 2х + у =
2х - у = О.
если х —О, то у —О(О; О);
если х —2, то у —4 (2; 4).
2* + у = О.
если х = О, то у = О(О; О);
если х = 2, то у = -4 (2; —4).
в) (# - 2)2 - (х + I)2.
Данное уравнение равносильно второму
|у - 2| + |х + 1|.
* + 1 = 0 у - 2 = 0
* = —1 у = 2.
I. * < -1 и у < 2,
-(у - 2) = -(х + 1); 2 - у = - х - 1;
* - у = -3 .
И. jc < -1 и у > 2
I/ - 2 = -(х + 1); * + у = 1.
III. х > -1 и у < 2,
“(У ~ 2) = * + 1; х + у = 1.
IV. х > “1 и у > 2
у - 2 = х + 1 ; * - у = -3 .
Для случаев I и IV — прямая х —у —-3 .
Если * = 1, то у = 4 (1; 4);
если * = О, то у = 3 (О; 3).
Для случаев II и III — прямая х + у = 1.
Если х —О, то у —1 (О; 1); если * = 2, то
У = ~~1 (2; -1).
Упражнения д ля повторения
1050. Так как S = v •t9где v — скорость, t — время, S —
а) через полчаса между автомобилями будет расстояние
расстояние, то:
350 120- -
2
350 - 60 = 290 (км).
б) через 2 часа между автомобилями будет расстояние
350 - 120 * 2 = 350 - 240 = 110 (км).
Ответ: а) 290 км, б) 110 км.
1051. Если 2,5 составляет 100 %, то 3,2 составляет * %.
9 0,1 00%
х _ О,* Л.™К = 128 % Значит> 3 2 от 2,5 больше на 128 % -1 0 0 % = 28 %
2,5
Ответ: на 28 %.
1052.
а) х2 = 64;
х2 - 64 = О;
(х - 8)(х + 8) - 0;
х —8 = О; або х + 8 = 0;
х = 8. х = -8 .
Ответ: -8 або 8.
б) (х - 2)2 = 25;
(х - 2)2 “ 25 = О;
(х - 2 - 5)(х - 2 + 5) = О;
(х - 7)(х + 3) = О;
х - 7 = О; або х + 3 = О;
х = 7. х = -3 .
Ответ: -3 або 7.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

193. § 26. Системы уравнений
Чтобы выяснить, является ли пара чисел (а; —Ь) решением системы,
надо подставить абсциссу (первое число) вместо х, а ординату (второе
число) вместо Бели оба уравнения превратятся в верное равенство,
шнчит эта пара чисел является решением системы уравнений.
1055. а)
Ответ: нет
б)
Ответ: да
?1*V JL•
х + у = 1,
[ 4 х - 3 у = 11;
при х 2 и. у —-1
в) Х
[2*
2у = 6;
при х = 2 и у = -1
и ;
у = 3,
[2 —1 = 1,
[2 + 2 * 6 .
[ 2 - 1 = 1,
18 + 3 = 11.
при х —2 и у
[2 + 1 = 3,
1 4 - 1 = 3.
х ~~у ——6.
л: = у - 6;
[2* + у = 3;
О твет: да.
1056. * + 2у = 0 и
х = -2у
Имеем -2у = у - 6; —Зу = —6; у —2;
д: - - 2 * 2 —-4 или х = 2 - 6 —-4 .
(-4; 2) — точка пересечения графиков данных уравнений.
Рассмотрим систему
Значит, пара (—4; 2) является решением системы.
1057. (-1 ; 3).
ас+ 2# = 0, Г-4 + 2 -2 = 0,
О
II
р
х ~ у = ~6; j- 4 - 2 = -6; 1-6 = -6
«)
Гх + у = 2,
|3х - у = -6;
б)
-1 + 3 = 2,
3 •(-1) - 3 = -6;
12= 2,
1-6 = -ß.
(-1 ; 3) — решение системы.
Зх - 2у = -9,
Зл: + 2у = -3;
3 *(-1) - 2 * 3 = -9,
3 *(-1) + 2 ♦3 = “3;
-9 = -9,
3 = -3 .
(-1 ; 3) — не решение системы.
1058. а) (3; 4).
{
[0 = 0,
[5 = 5.
Зх + у = 0,
х + 2у = 5;
(-1) + 3 = 0,
-1 + 2 3 = 5;
(-1 ; 3) — решение системы.
->{
в)
1 х - у = -4,
х -2 у = -7 ;
{:!:
[-4 = -4,
1 -7 = - 7.
I—1 —3 = —4,
2 3 = - 7 ;
(-1 ; 3) — решение системы.
Пусть
3 + 4
3 - 4
Га, = 1 1 ^ = 1,
|а2 = 1 і Ъг = -1;
—Сц Je, = 7, х
< имеем <
= С2* р2
тогда имеем систему
1х + у = с,,
{дс-у = с2;
найдем сх и
+ У= 7,
~У = -1
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

194. б) (2; -5 )
Пусть тогда имеем систему
[5х + 2у - сх
х+ у
найдем сг и с2.
-2 + 2 •(-5) = с,
12 + И )
в) (0; 3).
'2*
имеем
Пусть
|0 + 3 = с,, к = з. Г
имеем 4
|3•0 + 2 -3 = е2; к = в; 1
Ьх + 2у - 0,
[х + I/ = -3 .
х + у = сг,
тогда имеем систему <
|3х + 2у =
х + у = 3;
Зх + 2у —6.
найдем с1 и с.
'2*
Г) (-2 ; О)
Пусть тогда имеем систему
I
х + У=.Сі*
2х + 2у - сг;
найдем с1 и с2.
{
-2 + О= с.
-2 •(—2) + 2 •0 = с2;
к = -2 .
к = *
имеем
! * + {/ = -2,
[-2 * + 2у = 4.
1059
а)
Гх + у = 6,
Iх - у = 2.
X + у = 6
если х = 0, то у —6; (О; 6);
если а; = 3, то і/ = 3; (3; 3).
х - у = 2
если х —О, то у —-2 ; (О; —2);
если х =>2, то у = О; (2; О).
Ответ: (4; 2).
Гх + у = 7,
[х - у = 3.
х + у = 7
если х —3, то і/ —4; (3; 4);
если х —О, то у = 7; (О; 7).
х - у = 3
если х = 3, то у = О; (3; О);
если х —О, то у —-3 ; (О; -3).
Ответ: (5; 2).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

195. X - у = -2,
х + 3у - —10.
X - у = -2
если я: = 0, то I/ = 2; (О; 2);
если лг = -2 , то у —О; (-2 ; О).
х + Зу = —10
если х = -4 , то у = -2 ; (-4 ; -2 );
если х = -1 , то у = -3 ; (-1 ; -3).
Ответ: (-4 ; -2).
[2* +
|3х-
У = 4,
# = 1.
2дс + 1/ —4
если яг= 2, то у = О;(2; 0);
если х = О, то у —4; (О;4).
Зя: - у = 1
если х - 0, то у = -1 ; (О; -1);
если х = 2, то у = 5; (1; 5).
Ответ: (1; 2).
1060.
а)
х - у = 0, Гж- у = О,
[Зя: - у = 4. [4я: - у = 6.
х - # = О х - у = О
если х = 2, то у =2;(2; 2); если я; = 2, то у —2; (2; 2);
если я = -1 , то у=-1 ;(-1 ; -1 ). если я: = -1 , то у =-1 ; (-1 ; -1).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

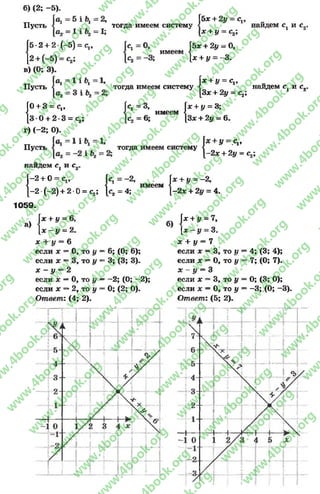
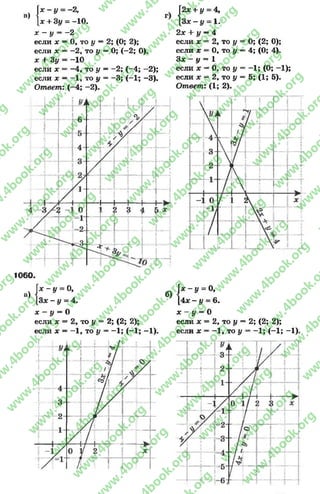
196. З* - у = 4
если х —1» то у = -1 ; (1; -1 );
если х = -1 , то у = -7 ; (-1 ; -7).
Ответ: (2; 2).
4* - у = 6
если * = 2, то у = 2; (2; 2);
если * = 0, то у —-6 ; (0; ~6).
Ответ: (2; 2).
I
Такие системы уравнений с двумя нерешенными решают графическим
способом. Для этого в одной системе координат строят графики урав­
нений системы. Координаты точек пересечения прямых являются ре­
шениями системы.
а)
Я Ж,
2 х -
| 3х-
б)
л.
{
х +
1061. Решим графически системы уравнений:
У - 2,
У = 5.
Построим графики уравнений.
2х - у = 2; у = 2х - 2;
если х —0, то у = -2 ;
если х —2, то у —2.
График проходит через точки (0; -2 ) и (2; 2).
Зх - у = 5; і/ = Зх - 5;
если х —0, то у —-5 ; если х = 2, то у = 1.
График проходит через точки (0; -5 ) и (2; 1).
Графики пересекаются в точке с координатами (3; 4),
которые являются решением системы. Ответ: (3; 4).
У = 4,
У = 2.
Построим графики уравнений,
х + у = 4; у = 4 - х;
если х = 0, то і/ —4;
если х = 2, то г/ —2.
График проходит через точки (0; 4) и (2; 2).
х ~ у = 2; у = х —2; если х = 0, то у = -2 ;
если х = 2, то і/ *=0.
График проходит через точки (0; —2) и (2; 0).
Графики пересекаются в точке с координатами
(3; 1), которые являются решением системы.
Ответ: (3; 1).
]4х - у = 5,
|_3х+ 2у = 12.
Построим графики уравнений.
4х - у = 5; у « 4х - 5;
если х = 0, то і/ —-5 ;
если х = 2, то у = 3.
График проходит через точки (0; -5 ) и (2; 3).
1 2 - З х
1062. а)
Зх + 2у = 12; у
если х —2, то у —3; если х = 4, то у —0.
График проходит через точки (2; 3) и (4; О).
Графики пересекаются в точке с координатами
(2; 3), которые и являются решением системы.
Ответ: (2; 3).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

197. Гб*+ 4# = 13,
[Ззс + 5# = 13.
Построим графики уравнений.
5л* + 4у = 13; у = 13— - Х ;
4
«ели д; = 1, то у —2;
если х —5, то у —-3 .
График проходит через точки
(1; 2), (5; -3).
3* + 5у = 13;.у = ^ Ц - ^ ;
5
если х .—1, то у —2;
если х - -4 , то у = 5.
График проходит через точки (1; 2) и (-4 ; 5).
Графики пересекаются в точке с координатами (1; 2), которые являются
решением системы. Ответ: (1; 2).
1 У - 6,
1063. а)
2л; +
2
4х + у 12.
2лг+ - у = 6; у = 2(6 2ж); у = 12 - 4х; 4х + у = 12.
б)
&
Получили уравнение, равносильное второму, тогда
графики уравнений совпадают, и координаты всех
точек графика будут решениями системы. Построим график уравнения
4л: + у = 12.
у —12 —4л;; при л: = 3; у = 0; при л: = 2; # = 4.
График проходит через точки (3; 0) и (2; 4).
Ответ: система имеет множество решений.
У = -2,
Зх ~3у - 6.
Построим графики уравнений
х ~ У —“2; у = * + 2; если л: = 0, то у = 2;
если л: = -2 , то у —0.
График проходит через точки (0; 2), (-2 ; 0).
Зх - Зу = 6; у = 3уо--? ;
о
если л; = 0, то у —-2 ; если х —1, то у = -1 .
График проходит через точки (0; —2) и (1; -1).
Графики не пересекаются, поэтому система
не имеет решений.
Ответ: решений нет.
5х - 2 у = -3,
2л: —Зу = 1.
5л: - 2у = - 3; если х ——1, то у —-1 ; (—1; -1);
если х = 1, то у —4; (1; 4).
2х - Зу = 1; если л: = 2, то у = 1; (2; 1);
если * = —1, то у ——1; (-1 ; —1).
Ответ: (-1 ; -1).
в)
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

198. Г)
Г-3* + by = 1,
[4х - у = 10.
-З х + 5у = 1;
если х —-2 , то у —-1 ; (-2 ; -1);
если х = 3* то у = 2; (3; 2).
4 л: - у — 1 0 ;
если х —2Уто у —-2 ; (2; -2);
если х = 4, то у = 6; (4; 6).
Ответ: (3; 2).
1064
а) { *
1&
; 8 ФЗ Ф2.
в)
+ 31, = 5,
8х + 9у = 10;
8 9 10
1 3 5
Значит, прямые пересекаются
и система имеет одно решение,
+ у ~ 8,
= 15;
х + у = 8,
Оде+ у - 15;
б)
f x - 4 y = 1,
[2* - 8у = 3;
1 1
— Ф—
2 3
I*
[У
г)
1 - 4 1 1
2 “ -8 ~ 3 5 2
Значит, прямые параллельны
и система не имеет решений.
f—лг+ 5у = 7,
[2х - 1 0 у = -14;
- 1 5 7
0 1 15 Л , , 7
—= - = — ; 0 * 1 * 1 - .
1 1 8 8
Значит, прямые пересекаются
и система имеет одно решение.
2 -1 0
1 _ _ 1
2 ~ 2
-14
1
2 '
Значит, прямые совпадают и сис­
тема имеет множество решений.
1065. Не строя графиков, докажем, что приведенные системы уравнений
не имеют решений.
[8* + 2у = 15,
а)
б)
Система не имеет решений, потому что 8* + 2у не может
8х + 2у - 35. одновременно равняться 15 и 35 при любых х и у.
1066
{
ГЗх-
[ З х -
Гбх + 10у = 36,
[Зх + Ъу - 18;
У
У
8,
16.
Система не имеет решений, потому что Зх - I/ не может
одновременно равняться 8 и 16 при любых х и у.
2(3* + 5{/) = 2-18,
[Зх + Ъу = 18;
Эти уравнения равносильны, значит, система имеет множество реше­
ний.
Ч :
Зх + 5у = 18,
Зх + 5у - 18.
Ъу = 1 8 - Зх; у
18 —Зх
Если х = 1, то у =
Если х = 6, то у =
5
1 8 - 3
5
1 8 - 3
- = у = 3 ; ( 1 ; 3 ) .
о
= 0 ; (6; 0).
Если х = -4 , то у =
18 - 3 •(-4) 18 + 12 30
= 6 ; (-4 ; 6).
5 5 5
Ответ: система имеет множество решений, три из них (1; 3), (6; О), (-4 ; 6).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

199. 1067.
|0,5х + у = 2,
[- 0 ,4х + у = 2.
0,5* + у = 2;
х = 0, у = 2; (0; 2);
* = 2, у = -1 ; (2; -1).
-0 ,4 * + у = 2;
* = 0, у = 2; (0; 2);
* = 5, у = 0; (~5; 0).
Ответ9. (0; 2).
б) Г1,5*-|, = 3,
[0,3х + у = -1,2.
1,5х - у = 3;
дс = 0, у = -3 ; (О; -3 );
х = 2, у = О; (2; О).
0,3* + у = -1 ,2 ;
* = -4 , у = О; (-4 ; О);
х = 6, у = -:3; (6; -3 ).
Ответ: (1; —1,5).
Г0,2х + 0,6у = 1,8,
|* - 0 ,5у = 2.
0,2* + 0,6у = 1,8;
* = О, у = 3; (0; 3);
* = 3, у = 2; (3; 2).
* - 0,5у = 2;
* = 2, у = О; (2; 0);
* = 0, у = -4 ; (0; -4).
Ответ: (3; 2).
|1,1* + у = 0,1,
[1,2* —у = 2,2.
1Д* + у = 0,1;
* = 1, у = -1 ; (1; -1 );
* = 6 , у = - 6 ,5 ; (6 ; - 6 ,5 ) .
1,2* - у = 2,2;
* - 1. у - -1 ; (1; -1 );
х = 6 , у = 5 ; (6 ; 5).
Ответ: (1; -1 ).
1 0 6 8 . 3* - 2у = - 6 ;
* + 2у = -2 ;
5 * + 2у = 22.
|3* - 2у = -6,
|* + 2у = -2 .
3* - 2у = -6 ;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

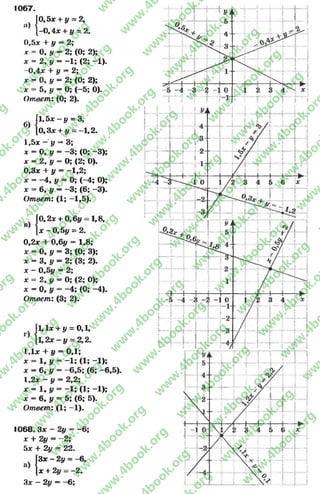
200. б)
в)
а)
5*
х = -2 , у = 0; (-2 ; 0);
х = 0, у = 3; (0; 3).
|3х - 2у = -6,
[5* + 2у = 22.
л: + 2у = -*2;
л: - - 2 , у - 0 ; ( - 2 ; 0);
х = 0, у = -1 ; (0; -1).
1л: + 2у = - 2 ,
[5л: + 2|/ = 22.
5л: + 2у — 2 2 ;
л: = 4 , у = 1; (4; 1);
л: = 2 , у = 6 ; (2; 6).
Ответ: а) (—2; 0);
б) (2; 6);
в) (6; -4 ).
1 0 6 9 .
Г5л: - 4у - 1,
[12л: + 22у = 33.
4у = 1;
л: = 1, у = 1; (1; 1);
л: 3, у 3,5,
(3 ; 3 ,5 ).
12л: + 22 у = 33 ;
х ~ 0 , у — 1 ,5 ;
(О; 1 ,5 );
х = 1 1 , у = -4 ,5 ;
(1 1 ; - 4 ,5 ) .
(1; 1) — приблизи­
тельное значение.
{Зх + 2у = 7,
[1 1 л: —20у = 55.
Зл: + 2у = 7;
л: = 1, у = 2; (1; 2);
х = 3, у 1; (3; -1).
11л: - 20у — 55 ;
дг = 5 , у = О; (5 ; О);
х = 3, у = -1 ,1 ; (3; -1,1).
Ответ: (3; -1 ) — приблизительное
значение.
1 0 7 0 - Подберем уравнения, которые
с указанными имеют:
1) множество решений:
а) -З х + у = -5 ; бдг - 4у —4;
15л: +• 1 2 у = 3 ; - 2 л : - 6у — 8 .
2) не имеют ни одного решения:
а) Зл; - у = 0; б) Зх - 2у = 5;
в) 5л: + 4у = 3; г) -л: - Зу —-8 .
3) единственное решение:
а) х + у —3; б) 2л: + Зу = 8; в) х + у —О; г) х - Зу = -4 .
б)
У к
6-
К-
к ......т - ~ г - -
// /
‘
о
4-
з-
>
ш :
: /
/ «
.1I—■■:
___1 _ /
Г Х л И
1
1
/ 1 1
Т г I
I I г 1 ъ
-1 1 2 5 <5 1Г *} 9 10 11 х
~2-
-з -
-4-
5
__
——^
{ !
1 ]_
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

201. 1071
•а ) { *
7 2
- Ф- ; а Ф 14.
а 4
1072
3* - # = 3, ^ Г7* + 2у = 11,
ау = 1; [а* + 4у - 22.
1) система имеет одно решение.
3 * -
а
2) система имеет множество решений.
З -1 3 1 1 _ 2 = И
а ” 4 ~ 22
Ьх + 2у = 7, [4л: + Ъу = 5,
З х - у = 5;
1) система не имеет решений.
6 2 7 4 8
3 -1
—Ф—
1 - а
_ - 1 = 3 . = 1
1 - о 1 ; ° 3
; а = 14.
2х + Ьу ——1.
5
2 ; 6 = - 6 2 = | ; Ь
6
4.
2) система имеет единственное решение
26 — .- ф — ; Ь ф
3 -1
4 8
—Ф—; Ь Ф4.
2 6
х - у = 1, 3 - # = 1, У = 2,
1073. а) •х + у —3; 3 + у = 3; - У = 0; 2 * 0
2* = 6; * = 3; X = 3.
Значит, система не имеет решений.
З х - у = 1, Зх —2 = 1, 3* = 3,
б) - * + У = 3; -* + 2 = 3;
К
1!
Л4
і
4і/ = 8; У = 2; # = 2;
* = 1,
* = 1;
У = 2.
Значит, система имеет решение.
2* + 7у - 39, 2* + 7 ( 3 * - 1 ) = 39, 23* = 46,
в) «3* - у = 1; у = 3* - 1 ; у - 3 * - 1 ; -
11* -А у = 1; 11* - 4(3* -1 ) = 1; —х = 3;
1 =
Значит, система не имеет решений.
1077. а) (х + 3)(* - 2) = х2 - 2х + 3* - 6 = * 2 + х - 6.
б) (а - 5)(а + 4) - а2 + 4а - 5а - 20 = а2 - а - 20.
п) —тп2 - л2.
15 + Зг - Ъг - г2
в) ( т + п)(т
г) (3 —г)(5 + г)
1078.100 * а + 10 * Ъ + с.
1079. ж * 7 = х + 30; 7* - х = 30; 6* = 30; *
Ответ: 5.
15 - 2г - г2.
12; * - ^ ж= 12;
6 6
12; х
12-6
1080. - = ;
6
1081. Пусть х кг
х кг олова.
Составим уравнение:
17х + 2х + х = 200; 20* = 200; * —10.
17 •10 = 170 (кг) меди; 2 •10 = 20 (кг) цинка; 1
Ответ: 170 кг, 20 кг, 10 кг.
одна часть, тогда меди берут 17* кг.
10
1.
= 2,
= 3* - 1 ; 2 Ф3.
= 3.
= 14,4.
, цинка — 2* кг,
10 (кг) олова.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

202. § 27. Способ подстановки
Способ подстановки, использующийся в упражнениях: одну из перемен­
ных выражаем через вторую из одного из уравнений системы. Потом
выраженную переменную подставляем во второе уравнение, что приво­
дит к образованию уравнения с одной переменной. Решив полученное
уравнение, находим первую переменную. Эту переменную подставляем
в любое из уравнений системы, после решения которого находим вто­
рую переменную.
1084.
а) 3 * - у = 8;
~у = -З х + 8;
у = Зх - 8.
в) 0,5л: - 0,3# = 1,5;
-0,3# = —0,5* + 1,5;
- 0 ,5л:+ 1,5
б ) 5 л: + 2 # = 7 ;
2 # = 7 — 5 л:; # =
# = 3 ,5 - 2 , 5 л:.
ч 1 л. 2 *г) - * + - у = 5;
7 - 5 л:
У =
-0 ,3 # = 5
5 * I 2 *# = - х - 5 ; # = 1 з ЛГ~ 5 *
У =
5 3
1*12 1
1 3
1086
а)
2 2*2
# = 7 ,5 — 0 ,7 5 л:.
3
2
*; У =
15
Г*- 2
[3* +
{з,
- 2 # = 5,
5# = 26;
= 2# + 5,
3(2#+ 5)+ 5# = 26;
3(2# + 5) + 5# = 26;
11# = 11;
У = 1-
* = 2 * 1 + 5 = 7.
Ответ: (7; 1).
б)
I
|3* +
Ь у =
# = 7* - 56,
3* + 4(7* —56)
1087.
а)
3* + 4# = 55,
7х - у = 56;
4# = 55,
7л:+ 56;
Зл; + 4(7* - 56) = 55;
Зл: + 28л: - 224 = 55;
31* = 279; * = 279 : 31; х = 9.
# = 7 * 9 - 56 - 7.
Ответ: (9; 7).
5 5 ;
|3* - # = 1, Г-
[3* + 8# = 19; [3
1088.
# = -3 * +1,
3* + 8# = 19;
1# = 3 * - 1 ,
[3* + 8 ( 3 * - 1 ) = 1 9 ;
3* + 24* - 8 = 19;
3* + 28* - 224 - 55;
27* = 27; * = 1;
# = 3 * 1 - 1 = 2. Ответ: (1; 2).
б)
а)
[3 * + 4г = 85,
|5* + 42 = 107;
42 = 8 5 - 3 * ,
5 * + ( 8 5 - 3 * ) = 107;
5 * + 8 5 - 3 * = 107;
б)
{
|3* + 2# = 27,
[* + 5# = 35;
3 5 -5 # ,
[3(35-5# )+ 2# = 27;
105 - 15# + 2# = 27;
-13# = -7 8 ; # = -7 8 : (-13);
у = 6.
* = 35 - 5 * 6 = 5. Ответ: (5; 6).
|5* + 72 = 101,
|7х - 2 = 55;
Г-2 = -7 * + 55,
15* + 72 = 101;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

203. 2* = 22; х = 11.
4г = 85 - 3 * 11.
42 = 85 - 33; 42 = 52;
52
2 4
Ответ: (11; 13).
13,
1089.
а)
!
1090.
15у - 8г = 29,
Зу + 2г = 13;
Зу = 13 - 22,
5 -Зу - 82= 29;
5 г (13 —22) - 82- 29;
65 - 102 - 82—29;
-182 = -3 6 ; 2 - -3 6 : (-18);
2 = 2;
Зу = 13 - 2 * 2; Зу = 9;
У —3.
Ответ: (3; 2).
а)
I
1091. а)
I;
{;
1092. а)
С
6
2 = 7 * - 5 5 ,
5л: + 7 (7х - 5 5 ) = 101;
5* + 49* - 385 = 101;
54* = 486; * = 486 : 54; * = 9;
2 = 7 * 9 —55 = 63 —53 = 8.
Ответ'. (9; 8).
б)
{
3* + 8* = 59,
6* + 5* = 107;
3* = 59 - 8£,
2 •3* + Ы = 107;
2 * (59 - 8*) + Ы = 107;
118 - Ш + 5# - 107;
-11* = 107 - 118;
-11* = -11; г = 1.
3* = 59 - 8 * 1; 3* = 51;
3* = 51 : 3; * = 17.
Ответ: (17; 1).
1093. а)
у - 22= 6,
у + 22= 10;
у = 6 + 22,
[6 + 2г + 2г = 10;
42 —4; 2 = 1;
тогда у = 6 + 2 = 8.
Ответ: (8; 1).
2/? + ^ = 11,
5р - 2д = 41;
<?= 11-2/?,
5р - 2(11 - 2р) = 41;
9р - 22 = 41; 9/> = 63;
р = 7; тогда д = 11 - 2 * 7;
<2>= -3 .
Ответ: (7; -3).
9* + 2у —4 = 0,
8* + у - 2 = О;
I/ = 2 - 8*,
9* + 2 (2 - 8х) - 4 = 0;
-7л: = 0; * = О;
тогда у —2 —8 * 0 ;
у = 2.
Ответ: (О; 2)
4* - Зу =
8 * - 6у
б)
30.
б)
2г + Зу = 216,
2 + у = 82;
2 = 82 - у,
2(82 - у) + Зу = 216;
164 - 2у + Зу = 216;
у —52; тогда 2= 82 - 52
Ответ: (52; 30).
16а - 36 = 4,
2а - Ь = 5;
6 = 2а - 5,
6а - 3 (2а - 5) = 4;
6а - 6а + 15 = 4; 15 * 4,
то есть система не имеет решений.
Ответ: решений нет.
{
б)
I
IV», л/.
|4* —Зу = 8, Г4* —Зу = 8, Г
[8* - 6у = 9; [2(4*- Зу)= 2 *4,5; [
5и + 71>+ 3 = О,
10а - V+ 6 = О;
11; = 10а + 6,
[5и + 7(10а + б) + 3 = 0;
75а + 45 = 0; и = -0 ,6 ;
тогда и = -0 ,6 *10 + 6;
V = 0.
Ответ: (-0,6; О).
4 * - Зу = 8,
4.5: 14* - Зу = 4 ,5 .
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

204. Система решений не имеет, так как (4л:
временно и 8, и 4,5.
Ответ: решений нет.
3#) не может равняться одно-
б)
Г0,5л:-# = 0,5, ГО,5 * - г / = 0,5, Г
х - 2 у = 1; [2(0,5 - у) - 0,5 *2; [
5х - у = 0 ,5 , Г л ;-2 # = 1,
5 - # ) = 0 ,5 * 2; x - 2 y = 1;
Первое уравнение системы равносильно второму, поэтому система имеет
множество решений.
Ответ: множество решений.
1094.
а)
|14ы-91> = 24, р
[7а - 2и = 17; [!
—9и = 24,
2и = 17;
2 * (2и + 17) - 9и
17« = 2и + 17,
2 *7а - 9и = 24;
■24;
4и + 34 - 9и = 24;
-51> = -1 0 ; V = 2.
7и = 2 * 2 + 17;
а = 3.
Ответ: (3; 2).
б)
5л: = 13 - 4#,
Зл: + 5# = 13;
1095.
а)
|5дс+ 4# = 13, Г
[Зл; + 5# = 13; [
Г* = 2 ,6 -0 ,8 # ,
[3 (2,6-0,8#) + 5# = 13;
7,8 - 2,4# + 5# = 13;
2,6# = 5,2; у = 2;
* = 2,6 - 0,8 -2 = 1.
Ответ: (1; 2).
За —56 —13,
2а + 7Ь = 81;
40,5-3,56,
Г2а =
[За-
81
56
76,
13;
б)
| 2а-
14а-
а
[ 3 ( 4 0 , 5 - 3 , 5б)-56 = 13;
121,5 - 10,56 - 56 - 13;
-15,56 = -108,5; 6 = 7;
а = 40,5 - 3,5 * 7 = 16.
Ответ: (16; 7).
-7 6 = 8,
96 = 19;
Га = 3,56+ 4,
[4(3,5256 + 4 ) - 9 6 = 19;
146 + 16 - 96 = 19;
56 = 3; 6 = 0,6.
а = 3,5 *0,6 + 4 = 6,1.
Ответ: (6,1; 0,6).
1096.
а)
16 х -
[8л;-
{
{
-4 # = 5,
3# = 2;
4# = б* - 5,
8л: - 3# = 2;
# = 1,5л: -1,25,
8л: - 3(1,5л; -1,25) = 2;
8л: - 4,5л: + 3,75 = 2;
3,5л: = -1,75;
х = -0 ,5 .
# = 1,5 * (-0,5) - 1,25.
# = ~2.
Ответ: (-0,5; -2).
б)
[12# + 15л; = 8, Г
[16# + 9л; = 7; [
7 16
х = ------ #,
9 9 *
9х - 7 -16# ,
12# + 15л: = 8;
12# +15
35
12# +
12#
80
# = 8;
2 6 - # = 8
3
11 - 1 4 - #
3 *
11 3 11 1
3-44 44 4
х = —
16 ±
9 *4
7*4 3
9
1
3
Ответ: (
1 1
3 ’ 4
- 3
СО|ьо
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

205. а)
1097.
4 (* + 2#) = 5* + 6,
3 (2х - у ) - 24у + 6;
4х + 8у = 5* + 6,
6* - 3# = 24у + 6;
= 6 -8 # ,
- 27# - 6;
* = 8 # -6 ,
6(8# —6) —27# = 6;
48# - 36 - 27# - 6;
21у = 42; у = 2;
X = 8 • 2 - 6 = 10.
Ответ: (10; 2).
б)
н16*
{:
- 3#) = 2х + 7,
+ 6#) = 9# +15;
5* - 15# = 2* + 7,
За; +18# = 9# +15;
ГЗ* —15# = 7, Г
[З* + 9# = 15; 1
3* = 15# + 7,
15# + 7 + 9# = 15;
24# = 8 ; у
Зх = 12; *
Зх = 15 - - + 7 ;
3 3
Ответ: (4; —).
3
1098.
а)
І 5 * - :
[3(2*
J 5 * -
[ 6 * -
{:
X =
2 = 4(* + 2#) —8,
#) + 6 = 24# +12;
- 2 = 4* + 8# - 8,
3# + 6 = 24# +12;
* = 8# - 6,
6 * -2 7 # = 6;
6(8# - 6) - 27# = 6;
48# - 36 - 27# = 6;
21# = 42;
У = 2;
* = 8 * 2 - 6 = 10.
Ответ: (10; 2)
4(* - 3z)
5(* + 2г)
1 8 -1 0 z
б)
I
2 * - 3 = 5 (х -
2 (3 * -1 ) = 4у
-Зх + 5# = 3
4# = -3:
#), |2* —
—5; [6* -
|-3* + 5# = 3, Г
[6* - 4# = -3; [
2 •(5# —3) - 4# = -3 ;
3 = 5 * - 5#,
2 = 4# - 5;
3* = 5# - 3,
2 -3* - 4# = -3;
10# - 6 - 4# = -3 ; 6# = 3; # « - ;
^ 1 о о 1 1
2 ~ ЗХ = -~2;Х = ~ 6
, 1 1ч
Ответ: ( - —; - —)*
6 2
1099 а |4(* —Зг) + 33z = 50, |4* - 12z + 33z = 50, Г
^ [5(* + 2z) - 3* = 18; [5* + 10z —3* = 18;
36 - 20z + 21z —50; z
Ответ: (-61; 14)
4* + 7 = 5(* -* )
3(* + 6*) - 9* = 15:
* - 9 - 5z; 4(9 - 5z) + 21z = 50;
14; тогда * = 9 - 5 * 14; *
[4* + 21z = 50,
2* + 10z = 18;
61.
6)
{;
• і-
L5; i
4* - 5* + 7 + 5*
3(* + 6*) - 9* = 15;
* = 7 + 5*; 3(7 + 5*) + 9t = 15;
21 + 15* + 9* = 15; 24* = -6 ; * —-0 ,2 5 ; тогда * = 7 + 5 •(-0,25); * = 5,75.
о, I*
>; ІЗ;
-5 * = 7,
З *+ 9* = 15;
Ответ: (5,75; -0,25).
1101.
а)
{
1 9 * -2 1 # = 17,
5* +14# = 24;
5* = 24 -14# ,
19* - 21# = 17;
б)
[8* —33# —19,
[12*+ 55# = 19; I
1
8* = 33#+ 19,
12* + 55# = 19;
* 4 —# + 2 —,
8 * 8
12(4| j, + 2|) + 55j/ = 19;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

206. 1* = 4 ,8 -2 ,8 у ,
1 1 9 (4 ,8 -2 ,81/)-21г/ = 17;
91,2 - 53,2у - 21у = 17;
-7 4 ,2у = -74,2;
У - 1',
х = 4,8 - 2,8 -1 = 2.
Ответ: (2; 1).
|Зж+ 1 = 5 (3 -2 у),
В) [4 (лс —X) = 2(8,5 —5у);
[Зж+1 = 15 —10у,
[4* —4 = 17 —10#;
|3* + 10# = 14,
4* +10# = 21;
Г10# = 14 - 3*,
[4* +14 - 3 * = 21;
х + 14 = 21; * = 7.
10# = 14 - 3 * 7;
10# = 14 - 21; # - -0 ,7 .
Ответ: (7; -0,7),
и + —(ы+ и- 3) = 14,
49,5# 4-28,5 + 55# = 19; 104,5 •# = - 9,5
У =
9,5 1
1 0 4 ,5 ’ У 1 1 ;
М . ( М + 1 9 - 2
8 1 11 ]
1-----—м>
8
Ответ: (2; - — ).
Гб(*-2#) = 7 -9 # , Гб* - 12# = 7 -9 # ,
[8л: + 3# = 5(2* + 1); [8л: + 3# = 10х + 5;
Гб* - 3# = 7, |2д
[-2л: + 3# = 5; [3-
2х = 3# - 5,
2х + 3# = 7;
1103. а)
3 6 ' ’ 6
3(3у - 5) - Ьу = 7; 9{/ - 15 - Ьу = 7;
6# = 22;# = у ; # = з | ;
11
2л: = 3 ■ — - 5;
3
2л: = 6;
ж= 3. 2
Ответ: (3; 3 —).
3
1 1 л лли + —и + —V- 1 = 14,
3 3
1 1 1 5
V и V= —;
3 6 6 6
, 1 11—и + —V= 15,
3 3
1 1 5
— и + —и - —;
6 6 6
—и + —и = 15, [4м+ и = 45,
3 3 1 *
- и + „ = 5; = *
и = 5 + 1/;4и + 5 + м = 45; 5и = 40; и = 8; тогда V = 5 + 8; и = 13.
Ответ: (8; 13).
|7(2* + #) - 5(3* + #) = 6, Г14* + 7# - 1 5 * - 5 # = 6, (2# - * = 6,
[3(* + 2#) - 2(* + 3#) = -6; [З* + 6# —2* - 6# = -6; [* = -6;
2# + 6 = 6; # = О.
Ответ: (-6 ; О).
1104. а)
^ {х + у ) - ^ ( х - у ) = 5,
^ ( * + !/) + | ( * - {/) = 6;
3 3
* + # - - * + - # = 15,
4 4
—+ ^ + * - # = 18;
4 4
Г* + 7# = 60,4 Х + 4 У 15’ х + 7у = 15- 4, „ . . .
5 3 , - б х - 3 у = 18 4; 1 5 *-З у = 72;
- * # = 18; 1 1 *
4 4
* = 60 - 7#; 5(60 - 7#) - 3# = 72; 300 - 35# - 3# = 72;
38# = 228; # = 6; тогда * = 60 - 42; * = 18.
Ответ: (18; 6).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4bo
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

207. б)
± ( у - 1 ) - | ( * + 1) = 2,
1 ( * + 3 )-| (у + 1) = -4;
™ ( у - 1 ) - у ( ж + 1) = 2 1 2 ,
~ ( х + 3 ) - у ( г/ + 1) = (-4 )1 2 ;
13у —3 —4х —4 —24, |3у 4дс —31, 31 + 4х
[Зх + 9 - 4у - 4 = -48; |3х - 4 у = -53; ^ 3
З х - 4 ^ 3 1 * 4* ^ = -5 3 ; З х -
124 16х
9х - 124 - 16* = -159; 7х = 35; х = 5; тогда у =
Ответ: (5; 17).
31 + 4 5
# = 1 7 .
1105. а)
х + # х - у
4 3
х + у , х - #
8 6
= 10,
= 5;
12( х ^ у _ ^ у 1 0 Л 2
ГЗдс+ 3# - 4х + 4# = 120, Г7# - х = 120,
[Зх + 3# + 4 х -4 # = 120; [ 7 * - # = 120;
х = -1 2 0 + 7#; 7(-120 + 7#) - у = 120; -8 4 0 + 49# - # = 120;
48# = 960; # = 20; х = -120 + 140; тогда х = 20.
Ответ: (20; 20).
х + 2# —6* +10#
б)
* + 2# _ Зх - 5#
1 1 1 / о *
х + —# = 7 — (х -2 # );
3 2 4 *
= 3,
4х + 6# + Зх - 6#
12
= 7;
7х
12
= 7;
12# - 5х
= 3,
[12# -5
[ х = 12;
- 5х = 12,
х
— = 1;
12
Ответ: (12; 6)
0,2а + 4Ь = -5 - 0 ,8а,
2,5а +
а = -5 - 4Ь,
тогда 12# - 60 = 12; 12# = 72; у = 6.
1106. а)
4 6 - 5 0,8а, Г0>2в + 0,8а + 46 = -5, |а + 46 = -5,
0,56 = 1 — 6; {2,50 + 0,56 + 0,56 = 1; |2,5а + 6 = 1;
а —-5 - 4(1 - 2,5а); а = -5 - 4 + 10а;|
[6 = 1 - 2 , 5а;
9а = 9; а = 1; тогда 5 = 1 - 2,5; Ъ = —1,5.
Ответ: (1; -1,5).
|0, З х - 2,8# = 0 ,7 (3 -# ), |0,3х -2,1# = 2,1
[1,2х +1,1# = 3 - 7,5#; [1,2х +18,6# = 3
|х -7 # = 7, Гх = 7 + 7#,
[4х + 62# = 10; [4 (7 + 7#) + 62# = 10;
90# = -18,
у = -0,2;
: 0,3
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4b
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4bo
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

208. * = 7 + 7 •(-0,2).
* = 5,6.
Ответ: (5,6; -0,2).
1107. Решение. Чтобы найти координаты точки пересечения графиков уравне­
ний, не делая построений, нужно решить систему, составленную из данных
уравнений. Решение системы будет координатами искомой точки.
+ # = 37,
а) * + # = 3 7 и д : - #
# = 5;
2у —32; # = 16; тогда * = 5 + 16; * = 21
Ответ: (21; 16).
2х —3у = 16,
б) 2д :-3# = 1 6 и * + 2# = 1 1 у
х = 5 + #; (5 + #) + # = 37;
* = 1 - 2#; 2(1 - 2#) - 3# = 16;
+ 2# = 1;
2 - 4# - 3# = 16; -7# = 14; # —-2 ; тогда * = 1 - 2 *(-2); * = 5.
Ответ: (5; -2).
2# = 8,
в) * + 2# —8 и х - 2#
2# = 2,5;
-4# ——5,5; # —1,375; тогда х » 8 - 2 •1,375; * —5,25.
Ответ: (5,25; 1,375).
[4* - 7# = 4,
* = 8 - 2#; 8 - 2# - 2# —2,5;
г) 4* - 7# = 4 и 20* + 3#
1 - 3 # . , Г -3 #
- 20* + 3# = 1;
* ; 4
_ . 1 - 3# _ л
7# = 4 ; — - 7# = 4 ;
20 20 ~ ' 5
1 - 3# - 35# = 20; -38# —19; # —-0 ,5 ;
тогда х - (1 - 3 •(-0,5)) •^ ; л: = 0,125.
Ответ: (0,125; -0,5).
1108.
1 1* + —# + —г —14,
3 * 3
1 1 о
# + —* + —2 = 8,
* 4 4
1 1
2 + -’- * + ■—# = 8;
5 5
3* + # + 2 - 42,
* + 3# + 2 = 32,
* + # + 52 = 40;
* = 42 - 3* - 2,
* + 4(42 - 3* - 2) + 2 =г32,
* + 42 - 3* - 2 + 52 = 40;
# = 42 - 3* - 2, # = 42 - 3* - 2,
1
к
со
1
II
*+168-12*-42 + 2 = 32, <-11* - 42 =-136, * = 2г +1,
- 2 * + 42 = -2 ; * - 22 = 1; -11(22+ 1)-32 = -136;
-222 - 11 - 32 = -136; -252 = -125; 2
*='= 2*5 + 1 = 11;
# = 42 - 3 * 11 - 5 = 4.
Ответ: (11; 4; 5).
125
25
; 2 = 5.
5* + 3# = 65, 2 = 2# -1 1 , 2 = 2 # - и ,
1109. 2 # - 2 = 11, 5* + 3# = 65, 5* + 3# = 65,
3 * + 42 = 57; Зд: + 4(2# —11) = 57; 3* + 8у = 101;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

209. 2 = 2 # - 11,
x = 1 3 -0 ,6 # ,
3(13-0,6#)-»-8# = 101;
39 - 1,8# + 8# = 101;
6,2# = 62; # = 10;
x = 13 - 0,6 * 10 = 7;
z - 2 * 10 - 11 = 9.
Ответ: (7; 10; 9).
Упражнения а л я повторения
1110. З#4 - 2 # 2'+ 5 + М = 5^ + #я- 2#2 + 8;
М = 5#4 + #э —2#2 + 8 - З#4 + 2#2 - 5; М = 2#4 + #8 + 3.
Ответ: 2#4 + #3 + 3.
1112. а) (2а —л)(4а2 + 2ап + п2) = 8а8 —п8; б) (1 + с + с2)(1 - с)
1113. а) (а3 - 1)(ое + а3 + 1) - а* - 1;
б) (т - 1)(т2 + 2т + 1) = т3 + 2 т 2 + т - т 2 - 2 т - 1 = т 3 + т2 - т - 1.
1114. а) (а2 + 1)(а4 - а2 + 1) - а6 + 1; б) (х8 - 2а)(х* + 2х»а + 4аг) = х»~ 8с3;
1115. a) 213 •0,513 = (2 * 0,5)13 - I 13 = 1; б) 0,518 •218 = (0,5 * 2)18 - I 18 = 1;
в) 257 * 0,047 = (25 * 0,04)7 = I 7 = 1; г) 5ЗЭ* 0,2ЭЗ= (5 •0,2)33 = I33 = 1.
1 - с3.
§ 28. Способ сложения
1120. а)
С
+ У
- у
7;
3;
б) [*-*
L-*
+ 2# = 18;
+ 3# = 2;
1121.а)
2х = 10; х = 5;
5 + # = 7; # = 2,
Ответ: (5; 2).
3* + 2# = 15;
7* - 2# = 5;
10* = 20;
3* + 2# = 15;
{
{
J* = 2; J* = 2;
13-2 + 2# = 15; {# = 4,
1123.
= 2;
2 +2# = 15;
Ответ: (2; 4,5).
- 2# = 5;
[3* + 5# = 26;
-Sx + 6# = -15;
[3* + 5# = 26;
11# = i l ; у —li
* - 2 - 1 = 5; х = 7.
Ответ: (7; 1).
5# = 20; # = 4;
х + 8 = 18; х = 10.
Ответ: (10; 4).
4х - 3# = 2;
Sx + 3# = 5;
7х = 7;
3* + 3#
x = 1;
б)
{;
[7х = 7; J3 1 +
|3х + 3# = 5; {* = 1;
3# = 5;
2
3
Ответ
У
■ > {*
t
б)
: ( 1; з )
[Зх + 4# = 55;
1 7 * -# = 56;
{
1124. а)
| З х-# = 1; |
[Зх + 8# = 19; [
9# = 18;
Зх + # = -1;
Зх + 8# = 19;
Зх + 4# = 55;
28х - 4# = 224;
31х = 279; х = 9;
7 * 9 —# = 56; у = 7.
Ответ: (9; 7).
(Зх + 2# = 27; |3х + 2# = 27;
[х + 5# = 35; [-Зх -1 5 # = -105;
13# - -7 8 ;
б)
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

210. 1125
1/ —2;
3 •х —2 —1;
х = 1.
Ответ: (1; 2).
Зх + 42 = 85;
5х + 42 = 107;
£ = 6;
х + 5 - 6
5.
35:
■а){;
X
б)
J-3 x - 4 z - -85;
[5х + 42 = 107;
{
2х = 22; х = 11;
3 * 11 + 4г = 85;
42 = 52; 2= 13.
Ответ: (11; 13).
15#-82 = 29;
3# + 22 = 13;
б)
15# —82= 29;
12# + 82= 52;
27# = 81; # = 3;
3* 3 + 22= 13; 2= 2
Ответ: (3; 2).
Ответ: (5; 6).
Г5х+7г = 101;
[7 х - г - 55;
|5х + 7г = 101;
[49х —72 = 385;
54х = 486; х = 9;
7 - 9 - 2 = 55;
2 = 8.
Ответ: (9; 8).
l3x + 8t = 59;
[бх + Ы = 107;
Г -6х-16* = -118;
[бх + 5* = 107;
- 11* = - 11; t = 1;
Зх + 8 * 1 = 59; х =
Ответ: (17; 1).
17.
1127
Jl4u - 9 v = 24; Г
[7а —2d = 17; 1
14м - 9v
7 u - 2 v
7и - 2 * 2 = 17; о
Ответ: (3; 2).
14u - 9t> = 24;
-14м + 4i>= -34:
-5у = - 10; v —2;
б)
|5х + 4# = 13;
[Зх + 5# = 13; |
5х + 4# =
Зх + 5#
Зх + 5 •2 = 13; х = 1.
Ответ: (1; 2).
15х + 12# = 39;
15х —25# = —65;
“*13# = -2 6 ; # = 2;
1128
■а) {3 о ~5г> = 13; |
[50 + 76 = 81;
21а-3 5 6 = 91;
25о + 356 = 405;
46а = 496; а =
496
46
а = 10— ;
46
а = 1 0 ^ ; 3 10 —
23 23
56 = 13; -56 = 1 3 -3 2
_8^
23
56
8
19— ;
23
Ь= ^ ; ь = з ^ .
23 5 23 23
Ответ
б)
: (l0 * f ; зЩ{ 23 2 3 ;
| 2 а -7 6 = 8; Г-4а
[4а - 96 = 19; [4а -
+146 = -16;
96 = 19;
- 76 = 8;
96 = 19;
2а = 12,2; а = 6,1.
Ответ: (6,1; 0,6).
1129. а) (6* ~ 4У = 5: 118Х ~ 12У = 16’
[8х - 3# = 2; [-32х +12# = -8;
6 *(-0,5) - 4# = 5;'# = - 2.
Ответ: (-0 ,5 ; —2).
56 = 3; 6= 0,6; 2а - 7 - 0,6 = 8;
14х = 7; х = 0,5;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

211. 6)
[12#+ 15* = 8;
[16# + 9* = 7;
4
(-3) {-
3 3 * = И ; зс = —; 16у + 9 —
3 3
48у + 60х = 32;
48</ - 27х = -21;
1
7; у - —.
у 4
Ответ
1130
■ & а
Г
’’ а) |
1131. а)
3(л —т)
5
Ответ:
3* - 8# = а;
4х + 8# = 20а;
7х = 21а; х —За;
4 ■За + 8# = 20а;
8у = 8а; у = а.
Ответ: (За; а).
{ Зх + 7# = т;
8х + 7у = л; [
б)
Г-5* -
1 5 * -
+ у = 10с,
2# = 10с;
-# = 20с; у = -20с;
5* - 2 •(-20с) = Юс;
5* = -30с; * = -6с.
Ответ: (-6с; -20с).
Зх - 7 у - -т ; п - т
5* = л - т ; * = —-----
8* + 7# = л; 5
+ 7у = т; 7у = т - 0,6л + 0 ,6 т ; 7# = 1 ,6 т - 0,6л; у
8 т —Зл( п - т 8 т —Зл^
5 ; 35 )'
б)
|3* —4# = к; Г
[5* —4# = р; 1
35
Зх + 4# = —Др;
5* - 4# = р;
2х = р - к; х —
р —к
- * - ^ + 4у
2 *
Ответ
2
З р -5й
У
Зр
8
( р - к Зр-ЬкЛ
8 }
1 1 3 2 .а ) ( 8г + 3е = 7; I|-4г - 5< = 7; 2
б)
{
8* + 3* = 7;
8г -1 0 * = 14;
-7* = 21; г = -3 ;
8г - 9 = 7; 8а = 16; г
Ответ: (2; -3 ).
2.
1
3 т - 2л = 2;
5т + 8л = 26;
Г12т - 8л = 8;
[5 т + 8л = 26;
1 7 т = 34; т = 2;
3 ■2 - 2л = 2; -2л = -4 ; /
Ответ: (2; 2).
в)
[3* - # = 11;
[5* + 6# = 26;
118* -6 # = 66;
[5* + 6# = 26;
23* = 92; * = 4;
4 * 3 —# = 11; # = 1 .
Ответ: (4; 1).
1133- Точку пересечения графиков найдем как решение системы:
а)
£
{:
2# = 1;
2* + у - 7;
- 2# = 1;
4* + 2# = 14;
б)
{
5* + 2# = 1;
4 * -7 # = 18;
+14# = 7;
14# = 36;
8 т - Зл
35
5к
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

212. 1134
Ьх = 15; х = 3;
2 * 3 + # = 7 ;# = 1.
Ответ: (3; 1).
-21# = 17; -2
14# = 24; ■3
42# = 34;
42# = 72;
53* = 106; х —2;
5 * 2 + 14# = 24; #
Ответ: (2; 1).
" а> {к9*.[5л; +
Г38л; -
[15л: +
43* —43; * = 1;
5 * 1 + 2 # = ! ;# = -2.
Ответ: (1; -2 ).
б)
8л: - 33# = 19; -5
12л:+ 55# = 19; 3
40л: -165# = 95
36л: +165# = 57
76л: = 152; х = 2
12 *2 + 55# = 19
55# = -5 ;
1
у = - п .
Ответ
1135.
[5л: - 2 = 4(х + 2#) - 8
[3(2л: - #) + 6 = 24# +
[-6л: + 48# = 36;
(2; ~п)
I
1 I
12; [
5* - 2 = 4л: + 8# - 8
6л: ~ 3# + 6 = 24# +
* Глг-е
12; [6л:-
8у = -6 ;
27у = 6;
(-6)
21у = 42; у = 2; х - 8 - 2 = -6 ; х
6* ~ 27У ~ 6: Ответ: (10; 6).
10;
б)
{:
|2х —3 = 5 (х -# ); |
[2(3л: - 1 ) = 4# - 5; [
2* —3
2(3л:
-6л: +10# = 6;
6л - 4# = -3;
2л: - 3 = 5л: - 5#; [-3л: + 5# = 3;
6л: - 2 = 4# —5
#; |~3л:
; [6* - 4# = -3 ;
6# = 3; # = —; 6л: —4* —= -3 ; 6л: = —1; х = ——
Ответ
1136. а)
' ( 6= 2)*
Юм + 7и = 51;
1 о2и — и = 2 —;
5 5
ГЮм+
[-Юм
7и = 51;
+ 2м = -24;
(-10) 9 „ = 27; V = 3;
Юм + 21 = 51; 10м = 30; и —3.
Ответ: (3; 3).
б)
1 1 п—х — # = 0;
4 5
(-3) Г 3 3 п— х + —у = 0;
4 5
3 2—х + —# = 10;
.4 5
3 2 1П
-х-— и —10;
.4 5
10 = 0; ж—8 = 0; зс = 8.
4 5
Ответ: (8; 10).
1р + 0 ,2д = 0,3; -(-4)
4р + 0 ,5д = 0 ,9;
# = Ю;
1137. а)
Го,
К
б)
&
7
17
Г—0 ,4р - 0 ,8 д = -1,2; Г8,4л: - 23,*
[0,4р + 0,8д = 0,9; [42,5л: + 23,
—О,Зд — 0,3;
2х -3 ,4 # = 12;
5л: +1,4# = 25;
—23,8# = 84;
8# = 425;
50,9л: = 509;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

213. £ = 1; ОДр + 0,2 = 0,3; * = 10; 12 - 3,4# = 12; -3,4# = О;
р = 1. # = 0.
Ответ: (1; 1). Ответ: (10; 0).
2а Ь
— + —= 10;
3 2
1138. а)
а Ь _
х + —= 5; 2
3 4« <
Ь г 1
а - —= 5;
2
( о - 1 = 5;
-~ = 15; а = 9; 9 - ^ = 5; - = 9 - 5 ; Ь = 8.
3 2 2
Ответ: (9; 8).
б)
— ——= 0; (-3)
3 34 4
7л 0
т - — = 2;
2
5л 4
= 2; л = ----
2 5
~т + л = 0;
7л
т - т = 2;
4 Л 4
т — = 0; т = —
5 5
1139- а)
[ 1 - 3 * 4 -2 #
12 Г
< 4 3
0,7 = 0,4# - 0,3*; •10 1
|3 —9* -1 6 -
[4 # -3 * = 7;
16 + 8# = 0;
[8# —9* = 13;| Г
[4# —3* = 7; |•(-2) |
8# - 9* = 13; _ „ 1 Л 1
- 3 * —-1 ; х = —; 8 # - 9 *—= 13;
(-2) 1-8#+ 6* = -14; 3 3
8# “ 3 = 13; # = 2.
Ответ:
( Ь 4
б)
2х - 1 9 - 5 т
6 8
2х = 1 ,5 т + 0,5;
0 I 24 [8* - 4 - 27 + 15 т = 0;
[2х - 1 ,5т = 0,5;
|8* + 15т = 31;
Ю [20л: —1 5 т = 5;
9 ^ 2 0 9 1К 18 3
* = —; * = 1 —; 2 ------1 ,5 т = 0,5; — -* —т = —;
7 7 7 7 2 2
90 С
29 = 2 1 т ; т = — = 1— -
21 21
28* = 36;
1 36 - 2 1т 7
~ 14 ’14
Ответ
1140. а)
* у _ 1 . -6 г
2 3 ' |3* -2 # = 6;
2* —1 3 # -1 5
-------- = —------+ - ;
[6* - 3 = 6# —2 + 5;
*о
2 3 6
(-2)
1-6* + 4^ 12; _ = _5; и = 3; Ззе - 3 •2 = 6; За: = 12; х = 4.
1 б * -6 у = 6;.
Ответ: (4; 3).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

214. б)
Х + у Х - у
2*
3
х + у Х - у
. 3
Т
4
I-7 х —35# = —336;
[7* + у = 132;
Ответ: (18; 6).
5# —2х
8; *6
11; 12
-34# = -204; у
Зх + 3# - 2х + 2# = 48
4х + 4# + Зле- 3# = 132
; х
2; [7
+ 5# = 48;
7х + у = 132;
( - 7)
1141. а)
6 ( * - 1 ) -
14*
0:
- у - 2 ;
б)
6; х +- 5 *6 = 48; х = 18.
2х + 1 ^ У 1 = 5;
2
Зх - 7# Л
5(х -1 ) + ---- :г-^ = 0;
12х —12 - 5# + 2х —0;
14л:-5 # = 10;
14дс - 5# = 12;
14*+ 5# = -10;
0 * 2 .
I
(-1)
Ответ: решений нет.
1142. а)
х + у х - у
2
х + у
3
х - у
2;
7;
Зле+ 3# - 2дс + 2# = 12;
бде+ 6# - л: + у = 42;
+ 5# = 12;
5* + 7# = 41
-5л: —25# =
{:
{
1144
-18# = -1 8 ; # = 1;
х + 5 * 1 = 12;
х = 7.
Ответ: (7; 1).
7л: - 3(л: + #) = 2Д;
2л: - 2(# - х) = 17,6;
—Здс—3# = 2,1;
2# + 2л: = 17,6;
|2,7л: —
[3,2л: -
Г-о,
15,2:
|0,6
115,1
|-0, Зл: - 3# = 2,1;
2л: - 2# = 17,6;
6л: + 6# = -4,2;
,6лс - 6# = 52,8;
(-2)
3
2
5# = 5;
Ьх -3 ,5 #
11л: -7 # = 10;
13л: + 7# = -10;
2х = 0; х = 0;
Г5,5лг —3,5-
[5л: —5 + 1,)
{*:
0;
2
(-2)
11 •0 - 7#
Ответ
5л: - 3
10
б)
: (* - 1?)-
+ 1/ = Ю;
л: - 5
7
* + #
{
4 9 2;
5л: - 3 + 7# = 70;
9* + 9# - 4х + 20
36
72;
(-5) '5л: + 7# = 73
; 5л:+ 9# = 52 (-1)
-60; Ьх + 7# = 73
; —Ьх —9# = —52;
-2# = 21; # = -1 0 ,5 ;
5* + 7 *(-10,5) = 73;
5л: = 146,5; х = 29,3.
Ответ: (29,3; —10,5).
1,5# - 0,2(2# - 2) = 31,2;
|,2г + 0 ,7(# - 2г) = 10,8;
В,1#+ 0,2г = 31,2;
3,82 + 0,7# = 10,8;
б)
{
31#+ 22 = 312; 19
7#+ 382 = 108; (-1)
589# + 382 = 5928;
7 # -3 8 2 = -108;
со1
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

215. 16,2дс = 48,6; х = 3;
0,6 •3 + 6# = -4 ,2 ;
6у = -6 ; у = -1 .
Ответ: (3; -1 ).
1145- а)
| * - 3 |
[ ь - * ,
= 12; - - я - 21/4-3* = 15!;
2
I * - 2!
1 = 2 . '
3 ’
2 2
—х - * + 2# = —;
3 3
|7х —4# = 24; I ГТ.
|-х + 6# = 2; |*7 [-
Ответ: (4; 1).
7л: - 4# = 24;
7л: + 42# = 14;
# = Ю;
3.82 + 0,7 * 10 = 10,8;
3.82 —3,8; 2 = 1.
Ответ: (10; 1).
2
3
38# = 38; # —1; - х + 6 •1 = 2; л: = 4.
б)
2 3 _
- = х - - у = у-Ъ
5 4
-(л :-3 # ) = Зл;-Ю;
20
{:
8л: -1 5 # - 20# =
3# —9дс = -30
-160; Г
? 1
8л: - 35# = -160;
8л: - 3# = -30;
-38#
Ответ
190; # = 5; 8л: - 35 - 5 = -160; 8л: = 15; л: = 1^ .
: ( * 1 ; 5)-
1146. а)
!
Г4(3х - 2) + 2(7 - 4л:) = 20 + 2(# - 3);
[5(2# + 3) + 2(6л: - #) = 3(5л: - 3) + 31;
0 - 6; |4л: - 2# = 8; (4л: -
= 3 1 - 9 ; [8# - З х = 7; [8 # -
- 2# = 8;
Зх = 7;
12л; - 8 +14 - 8л; - 2# = 20 -
10# +15 + 12* - 2# - 15л;
16х - 8# = 32;
8# - Зл: = 7;
х = 3; 4 •3 - 2# = 8; -2# = -4 ; # = 2. Ответ: (3; 2).13л: = 39;
б)
|5(л: ~ 2#) + 33 = 2(4л: - 3) - 2(3# - 5);
[2(3* - 5#) - 3(л: - 5) = 56 - 4(6 + 2#);
-Зх - 4# = -29;
Зх - 2 у = 17;
5л -1 0 # - 8л; + 6# = -33 - 6 +10;
6л -1 0 # - Зл: + 8# = -15 + 56 - 24;
- 6# = - 12;
у —2; Зх - 2 * 2 = 17; Зл: = 21; х —7. Ответ: (7; 2)
(х + З)2 - 2у
бх + 0 ,- 1 ) 2
6х —2у = 4:
у —Л, О.
1147. а)
1<
{:
, ил
х2+13; |:
у (у - 5): 1<
6х + 3# = -1;
х2 + 6л: + 9 - 2# = х2 +13;
6л: + #2 - 2# + 1 = #2 - 5#;
6л + 2# = -4;
6л; + 3# = -1;
5у = —5; # = -1 ; 6л + 3 *(-1) = -1 ; х = Ответ: -1^
б)
-1 0 х + (# + 4)2 = #2 + 18;
(2л: - 1)2 + 7# = 2л:(2л; + 3);
—Юле+ #2+ 8# +16 = #2+18;
4л:2-4 л :+ 1 + 7# = 4л:2 + 6л;;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

216. Г—Юх + 8# = 2;
1-10* + 7у = -1;
# = 3;
-Юл: + 7 * 3 = -1 ; -Юл: = -2 2 ; х —2,2-
О твет: (2,2; 3).
х(х + 3) + 9 = (х - #)(х + у) + #(# - 3);
26 + 3(2х - #) = 9х - 5(3х + 2у);
[х2 + Зх + 9 - х2 - у 2 + у2 - Зу;
[26 + 6х —Зу = 9х - 15х —10#;
1148. а)
-9; М )
-5 у = 10; # = -2 ; Зх + 3 •(-2) в -9 ; Зх = -3 ; х = -1 .
|3х + 3#
[12х + 7# = —26;
-12х -1 2 # = 36;
[12х + 7# - -26;
Ответ: (—1; -2 ).
1149. Прямые проходят соответственно через точки:
1) (-5 ; 0) и (0; 3); 2) (0; 4) и (4; 0); 3) (0; -2) и (2; 0);
ах Ъу —с — уравнение прямой.
2) Пусть а —1, тогда:1) Пусть а —1, тогда:
|1 •(—5) + 6 -0 = с; с = —5;
[ 1 0 + Ь-3 = с; с = ЗЬ;
с = —5;
ь — * .
5 3
Получаем уравнение: х — у - -5«
5
3) Пусть а —1, тогда:
{
1 *0 + Ь *4 =5с; 4Ь = с;
1 •4 + Ь*0 = с; [с = 4;
|с = 4;
[Ь = 1.
Получаем уравнение: х + # = 4.
Г 1 0 + М ~ 2) = с; Гс = -2&; Гс = 2;
< < Ползаем уравнение: х - # —2.
[1 *2 + 6 -О= с; [с = 2; = —1. *
х + # = 3; (-1)
♦г*
II
1
н
1
х + # = 3; X + у = 3; 2 = 3;
1150. а) «х + 2= 4; |# - 2 = 4; * - # = -1; «22 = 6; # = 2;
# + 2 = 5; # + 2 = 5; # + 2 = 5; # + 2 = 5;
•
*4
н
н----л
Ответ: (1; 2; 3).
х + # = 5; # + 2 = 3; 2# = 4; # = 2;
б) «х - 2= 2; «# - 2 = 1; 4
•»
00
II
N
+
=95
2 = 1;
# - 2 = 1; х + # = 5; X + # = 5; х = 3.
Ответ: (3; 2; 1).
2х + 3# = 11; 2х + 3# = 11; 8х = 8; х = 1;
1151. а) «Зх + 2# = 13; 2 «2х - 42 = -18; -3# = 11 - 2х; - 3# = 9; -
Зх + 42 = 29; 6х + 42 = 26; 22 = 13 - Зх; 2г = 10;
х = 1;
# = 3;
2 = 5.
Ответ: (1; 3; 5).
х + # - 2= 11;
б) ^ х -# + 2= 1;
у + г - х = 5;
2х = 12;
22 = 6;
2# = 16;
х = 6;
2 = 3; Ответ: (6; 8; 3).
# = 8.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

217. I t 52. а)
7x + 6y-tTz = 100;
x - 2y + z = 0;
Sx + у - 2z = 0;
10* + lOz = 100; [-100* = 300;
7 * - 3 z = 0; ilOOz = 700;
-11л: + 19z = 100; x - 2t + z = 0;
6)
x = 3;
z = 7;
3 —2у + 7 = 0;
2x —2z —St = 1;
x + 4z + 2t = 7;
3* - z + t = 0;
* = 3;
z = 7; Ответ: (3; 6; 7).
у = 5.
5* - 4* = 9;
13л: + 6* = 7;
x + 4z + 2t = 7;
41* = 41; * = 1; 6f = 7 —13; £ = 1; 1 + 4z + 2 •(-1) = 7; 4z = 8; z = 2.
Ответ: (1; 2; -1 ).
Упражнения д ля повторения
1 1 5 6 .1 ) Пусть п —2, п - 1, п9п + 1, п -4- 2 — последовательные натуральные
числа, тогда их сумма п —2 + п - 1 + л + п + 1 + л + 2=г5д делится на 5.
2) Пусть п ~ 1 ,п , и + 1 и д + 2 — последовательные натуральные числа,
тогда их сумма л - 1 + л + л + 1 + п + 2 = 4п + 2 = 2(п + 1).
Если п — нечетное, то п + 1 — четное. Значит, 2 *(п + 1) — делится на 4,
если п — нечетное, то 2 •(п + 1) на 4 не делится. Ответ: 1) сумма пяти
последовательных натуральных чисел делится на 5; 2) сумма четырех по­
следовательных натуральных чисел может делиться на 4.
1157. у = - ~ .
а) у = 12; — = 12; х - — ; б) у = -1 2 ; — = -12; х = —
1
х 2' х 2
§ 29. Решение задач сложением систем уравнений
1160. Реш ение. Пусть купили х м ткани одного вида, а другого — у м.
За ткань одного вида заплатили 40* грн, а за ткань другого вида —
30# грн. Всего купили 9 м, то есть х + у = 9. Так как заплатили 330 грн, то
40х + 30# = 330. Составим систему уравнений:
I х
І4І
+ # = 9,
40х + 30# 330;
(-30)
I
30* - 30# = -270,
40jc+ 30# = 330;
10* = 60;
х = 6; 6 + у = 9; # = 9 - 6; # = 3.
Ответ: 6 м по 40 грн за метр и 3 м по 30 грн за метр.
1161. Решение. Пусть сначала работало х маляров и # столяров. Так как
вместе их было 50, то * + # = 50. После того, как маляров стало в два раза
больше, то есть 2х, а столяров — в три раза больше, то есть 3#, всего их
стало 130, .поэтому 2* + 3у —130. Составим систему уравнений:
I х12.
+ # = 50,
2х + 3# = 130;
(-2)
{
2х - 2# = —100,
2х + 3# = 130;
У = 30;
* + 30 = 50; х = 50 - 30; * = 20.
Ответ: 20 маляров и 30 столяров.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

218. 1162. Решение. Обозначим собственную скорость лодки через х км/ч., а ско­
рость течения реки через # км/ч. Так как скорость лодки по течению 23
км/ч-, а против течения — 17 км/ч., то х + у = 23, а х —у = 17. Составим
систему уравнений:
Гх + у = 23,
—# = 17;
2х = 40;
х = 40 : 2; х = 20; 20 + у = 23; у = 23 - 20; у - 3 .
Ответ: скорость лодки 20 км/ч., скорость течения реки 3 км/ч.
1163« Реш ение. Пусть скорость состава будет х км/ч., а скорость автобу­
са — у км/ч. За 7 часов поездом туристы проехали 7х км, а автобусом за
4 часа они проехали 4# км. Так как всего туристы проехали 640 км, то
7дг + 4у —640.
х —у + 5, потому что скорость состава на 5 км/ч. больше скорости авто­
буса. Составим систему уравнений:
VIх + 4# = 640,
= у + 5;
7 (# + 5) + 4# = 640; 7у + 35 + 4у = 640; 11# = 605; # = 55;
* = 55 + 5; * = 60.
Ответ: скорость состава 60 км/ч., скорость автобуса 55 км/ч.
1164. Реш ение. Пусть скорость одного туриста будет * км/ч., а скорость
второго — # км/ч. До встречи один прошел 4х км, а другой — 4# км.
Вместе они прошли 38 км, то есть 4х +- 4# = 38. Так как первый прошел
на 2 км больше, чем второй, то 4х - 4# = 2. Составим систему уравнений:
4х + 4# = 38,
[4* - 4# - 2;
8* = 40;
* = 40 :8 ; х = 5; 4 -5 + 4# = 38; 4# = 38 - 20;
* = 1 8 :4 ; # = 4,5.
Ответ: 4,5 км/ч. и 5 км/ч.
1165. Пусть одно число равняется ж, а второе — #, тогда х + # = 35,5,
а х - # = 12,3 (х > #). Составляем систему уравнений:
2х - 48; х = 24; # = 35,5 - 24 = 11,5.
Ответ: 24 и 11,5.
1166. Пусть одно число равняется х, а второе — #, при этом х > #.
Тогда | (х + #) = 37,5, а | ( х -# ) = 7,5.
Составим систему уравнений:«
|(ж+і/) = 37,5;
|(зс-у) = 7,5;
Іх + # = 75; 2х
| х -# = 15; 12#
Ответ: 45 и 30.
х + у = 75; [2* = 90; |х = 45;
х - # = 15; |2# = 60; {# = 30.
|2* = 90; Г
|2і/ = 60;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

219. 1167. а) Пустьодно число равняется х, а второе — у, при этом х > у. Тогда
1 1 1
—(х + у) = у + 5 и —(х + у) = —(х - у) + 1.Составляем систему уравнений:
2 2 2
(х + у) = у + 5;
1
(х + у) = - ( х - у ) + 1;
); х - у = 10; Гу = 1;
Ї < Ответ: 11 и 1,
2; [2# = 2; |х = 11.
Гх + у = 2# + 10;
[х + у = х - у +
б) Пусть одно число равняется х, а второе — у, при этом х > у. Тогда
^ (х —у) = х —13 и ~ (х - у) = (х - у) —12. Составляем систему уравнений:
2 2
(х - у) = х - 13;
(х — = (х —у) —12;
|х - у = 2х - 26; 1х + у = 26;
[х —у = 2х —2у —24; { х - у = 24;
Г2х = 50; |х = 25;
|2у = 2; [у = 1.
Ответ: 25 и 1.
1168. Пусть одно число равняется х, а второе
1
- х = у;
Составляем систему уравнений:
%у = х
і і _і/, тогда - х - у и —у = х —5.
& о
5;
х - 2 у = 0;
1 *
х - - у = 5;
5 *
—У = 5;
3 *
I/ = 3; х * 6. Ответ: 6 и 3.
1169. Пусть одно число равняется х, а второе — у, тогда 2х
2х = у + 37;
у + 37 и
х - у - 2 . Составляем систему уравнений:
3
—х = 39; х
2
У- 2 ;
26; у = 15. Ответ: 26 и 15.
1170. Пусть одна часть числа равняется х, а вторая — у (х > у).
Тогда х + у = 7 5 и х = 3(х - у). Составляем систему уравнений:
7 5 - х ;
3(х —75 + х);
6х - х = 225; х —45; у = 75 —45 = 30. Ответ: 45 и 30.
1171. Пусть первое число равняется х, а второе — у (х > у). Тогда х + у =
# = 82;
Гх + у = 75; |у
1* = 3(х - у); |х
Гх +
Е 1 « - 5у + 4;
82 и х —5у + 4. Составляем систему уравнений:
5у + 4 + у = 82; 6у —78; у = 13; х —69.
Ответ: 69 и 13.
1172. Пусть первое число равняется х, а второе — у (х > у).
Тогда х —у = 61 и х = 6у + 1. Составим систему уравнений:
6у + 1 - у = 61; 5у = 60; у = 12; х = 73.
Ответ: 73 и 12.
1173. Пусть стоимость тетради х грн., а карандаша — у грн. Тогда за 3 тетра­
ди и 5 карандашей заплатили (Зх + 5у) грн., что равняется 3,95 грн. А за
4 тетради и 2 карандаша заплатили (4х +- 2у) грн., что равняется 2,7 грн.
1::
- у =01;
6# + 1;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

220. „ ГЗ* + 5# = 3,95; -(-2) Г
Составим систему уравнении: < 4
14* + 2# = 2,7; 5
-6* -1 0 # = -7 ,9 ;
120* +10# -1 3 ,5 ;
Составляем систему уравнений
t/ldJLV^XU. V IX V A V IU J J J J L V y ДА«
Г* + # = 65; 2x-72; x =
{зс-і/ = 7; |2j/ = 58; { y =
14* = 5,6; * = 0,4; 2# = 1,1; # = 0,55.
Ответ: тетрадь стоит 0,4 грн., карандаш стоит 0,55 грн.
1174. Пусть матери * лет, а дочери у лет. Тогда * - # = 2 4 и * = 3#.
# = 24;
3#;
3# - # = 24; # = 12; * —3 - 12 = 36.
Ответ: матери — 36 лет, дочери — 12 лет.
1175* Пусть на первой полке * книг, а на второй — # книг (* > #). Вместе
(* + #), или 65 книг. Зная, что на первой полке на 7 книг больше, состав­
ляем систему уравнений:
= 36;
29.
Ответ: на первой полке 36 кн., на второй — 29 кн.
1176- Пусть в 7-А классе * учеников, а в 7-Б — у учеников. Вместе * + #, или
72 ученика. Если бы из 7-А к 7-Б классу перешло 2 ученика, то учеников
в классах стало бы поровну. Зная это, составляем систему уравнений:
= 38;
34.
Ответ: в 7-А классе — 38 учеников, в 7-Б классе — 34 ученика.
1177. Пусть конь за день съедает * кг сена, а корова — # кг сена. Тогда
10 коней и 16 коров съедают за день 10* 4- 16# = 160 (кг) сена. Так как
5 коней получают на 5 кг сена больше, чем 7 коров, составляем систему
[10* +16# = 160;
-10* +14# = -10;
30# = 150; # —5; 5* - 7 - 5 = 5; * = 8.
Ответ: корове — 5 кг сена, коню — 8 кг сена.
1178. Пусть длина первой части — * м, а второй — # м. Тогда * + у —35 (м).
Первая часть на 50 % длиннее второй, значит, перваячасть составляет
(100 + 50) % = 150 % от второй, то есть больше в 1,5 раза.
» 1 W IU W U A . V & U J1 V JT ■ ЖщГЯ.1Ш 1 V 1V j l y V v l
{
* + у = 72; Г* + # = 72; 2х —76; J * =
* - 2 = у + 2; { * - # = 4; [2# = 68; [# =
V IV V IA V U U V iri-jr W a w . V V JU U w .
„ flO* +16# = 160; fl(
уравнении: < <
[5 * -7 # = 5; [-]
Составляем систему уравнений:
I* + у - 35;
I* = 1,5#;
1,5# н- у —35; # = 14; * = 14 * 1,5 = 21. Ответ: 21 м и 14 м.
1179. Пусть длина первойчасти — * м, а второй — у м (* < #).
Тогда * + у = 35 (м). Так какпервая часть на 33 —%меньше второй, то
3
1 2
первая часть составляет 100 % - 33 —% = 66 —% от второй.
3 3
Имеем х = у -^6б|% : 100 %|= у ■ •.100%) = | у.
Составляем систему уравнений:
* + # = 35;
2
х = з у;
2 35- 3 2
—* + у = 25; у = —-— ; у —21; * = —-21 = 14. Ответ: 14 м и 21 м.
3 5 3
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

221. 1180. Пусть большая часть поля имеет площадь х га, а меньшая — # га.
Тогда х + у =■200 (га). Зная, что первая часть больше второй на 5 га, со-
= 205;„ х + у = 200; 2х =
ставляєм систему уравнении: •{
1 * -# = 5; |2# =
х = 102,5; у - 97,5
Ответ: 102,5 га и 97,5 га
195;
1181. Пусть х га и ута — участки поля площадью 100 га. Тогда х = —у + 5.
х + у = 100;
Составляем систему уравнений: 1
Х= 2 У +
= 95; 1/ = 6з| ; * = 1 00-63^ ; * = 3 6 § .
О О О О
2 1
Ответ: 36 — га и 63 — га.
3 3
1182. Пусть х см и у см — стороны прямоугольника, тогда его периметр
равняется 2{х + у) см, или 168 см. Составляем систему уравнений:
|2(х + у) = 168; 1х + # = 84; |2х = 92;
х - у = 8; х - у = 8; [2у = 76;
х —46; у = 38. Ответ: 46 см и 38 см.
1183. а) Пусть х см и у см — стороны прямоугольника, тогда его периметр
равняется 2(х + у) см, или 126 см. Так как сторона х на 10 % больше, чем
сторона #, то сторона х составляет (100 + 10) % —1,1 от стороны у .
= 126;
Составляем систему уравнений
. |2(х + #) =
х = 1,1і/;
4,2# - 126; # = 30; 2(х + 30) - 126; х = 33.
Ответ: 33 см и 30 см.
б) Пусть х см и у см — стороны прямоугольника, тогда его периметр рав­
няется 2(х + у) см, или 126 см. Так как сторона х на 10 % меньше сторо­
ны #, то сторона х составляет (100 - 10) % = 0,9 от стороны у.
п = 126;
Составляем систему уравнении:
[2(х + у) =
|д: = 0,9#;
1260 630
38 ’ У ~ 19
630*9
= 29— ,
19 10 19
3
3,% —126; у = 3 3 - ,
33 — —
19 10
16 3
Ответ: 29 — см и 33 — см.
19 19
1184. Пусть основание равнобедренного треугольника равняется х см, а его
боковая сторона — # см. Тогда х - у —10 (см) и х + 2# = 82 (см).
+ 2# = 82
# = Ю;
3# = 72; # —24; х - 24 —10; х —34. Ответ: 34 см, 24 см и 24 см.
1185. Пусть основание равнобедренного треугольника равняется х см, а боко­
вая сторона — # см. Тогда периметр треугольника равняется (х + 2#) см,
или 62 см. Так как основание больше, чем боковая сторона на 10 % , то
оно составляет (100 + 10) % = 1,1 от боковой стороны.
Составляем систему уравнений:
{;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

222. Ix + 2# = 62;
[х = 1,1#;
Составляем систему уравнений
3,1# = 62; # —20; х = 1,1 *20; х = 22.
Ответ: 22 см, 20 см и 20 см.
1186. а) Пусть х и у — данные числа (х > #). Тогда х —# = 4 и х 2 —#2 = 44.
Составляем систему уравнений:
[ х - # = 4;
[4(х + #) = 44;
Гх - # = 1; |х —# = 4; Г:
[х2 - #2 = 44; 1(х - #)(х + #) =44;
Гх - # = 4; 2х = 15; Гх = 7,5; „ чк
< < < Ответ: 7,5 и 3,5.
[х + # = 11; 12# = 7; [# = 3,5.
б) Пусть х н у — данные числа (х > #). Тогда х + # = 4 и х 2 - # 2 = 60.
Составляем систему уравнений:
+ # = 12;
[12(х —#) = 60;
Гх + # = 12; Гх + # = 12; Гх
{х 2 - #2 = 60; |(х - #)(х + #) = 60; [15
Гх + v = 12; f2x = 17; fx = 8,5;
Г і 1 Ответ: 8,5 и 3,5.
[ х - # = 5; 12# = 7;[# = 3,5.
1187. а) Масса болта с двумя гайками равняется 250 г. Найдите массу болта
и массу гайки, если болт тяжелее гайки на 130 г.
[х + 2# = 250;
I:
3у = 120; у —40; х = 130 + 40; х = 170.
[х - # = 130;
Ответ: масса болта 170 г, масса гайки 40 г.
б) Яблоко легче груши на 50 г. Найдите массу яблока и массу груши, если
масса трех яблок такая же, как масса двух груш.
у = 50 + х; з х - 2 х = 100; х = 10, у = 50 + 100; у = 150.
[3* = 2(50 + х);
Ответ: яблоко весит 100 г, а груша — 150 г.
1188. Пусть х км/ч. — скорость первого велосипедиста, а # км/ч. — ско­
рость второго велосипедиста. За 0,5 часа движения они приблизятся на
(х + #) -0,5 см, что составляет 9 км. Зная, что скорость первого на 1,6 км/ч.
больше, составляем систему уравнений:
у ~ х - 50; fl
|3лс = 2у;
Г(х + #) •0,5 = 9; Гх + у = 18; 2х = 19,6; Гх = 9,8;
[ х - # = 1г6; [х - # = 1,6; [2# = 16,4; [# = 8,2.
Ответ: 9,8 км/ч. и 8,2 км/ч.
1189. Пусть скорость моторной лодки равняется х км/ч., а скорость течения
— # км/ч. Тогда по течению за 8 часов лодка проходит (х + #) - 8 км, а за
10 часов против течения — (х —#) - 10 км. Так как эти расстояния равны
и равняются 320 км, составляем систему уравнений:
|8 (х + #) = 320; Гх + у = 40; |2х = 72; Гх = 36;
[10(х - #) = 320; [х - # = 32; [2# = 8; |# = 4.
Ответ: скорость лодки — 36 км/ч., скорость течения —4 км/ч.
1190. Пусть скорость велосипедиста равняется х км/ч., а скорость мотоцик­
листа — у км/ч. Через 2 часа движения в одном направлении расстояние
между ними будет составлять 2(# - х) км, или 14 км, а через 3 часа дви­
жения в противоположных направлениях расстояние между ними будет
составлять 3(х + #) км, или 174 км.
Составляем систему уравнений:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

223. I2(у —х) = 14; Гу-ж = 7; 2у = 65; Гу -3 2 ,5 ;
|3(х + у) = 174; [у + * = 58; [2* = 51; [* = 25,5.
Ответ: скорость велосипедиста — 25,5 км/ч., скорость мотоциклиста —
32,5 км/ч.
1192. Пусть продуктивность первого мастера ху а второго — у. За 12 дней
два мастера сделают 12(дг + у), что составляет все задание. (Все задание
примем за 1). Если первый мастер будет работать 2 дня, а второй — 3 дня,
то вместе они сделают 2х + Зу, что составит 20 % = 0,2 всего задания.
Составляем систему уравнений:
2(х + у) = 1;
[2х + Зу = 0,2;
Г12* + 12у = 1;
(-4) 1-8ж -12у = -0 ,8 ;
4х = 0,2; х = — 2 - 0,05 + Зу = 0,2; Зу = ОД; у = — . За один день
20 30
первый мастер сделает — задания,а второй — — задания. 1 : — = 20
20 30 20
(дней) будет делать самостоятельно все задание первый мастер. 1 : = 30
(дней) будет делать самостоятельно все задание второй мастер.
Ответ: 20 дней и 30 дней.
1193. Пусть х и у — части бассейна, которые за 1 ч. наполняют через пер­
вую и вторую трубу соответственно, а емкость резервуара примем за 1.
За 1 ч. 20 мин. = 1— часа две трубы, открытые одновременно, наполнят
3
1 1
(х + у) -1—, или весь резервуар. За 10 мин. = — часа первая труба и за
3 6
1 1 1 2
12 мин. = —часа вторая трубазаполнит —х + —у, чтосоставляет —
5 6 5 15
резервуара. Составляем систему уравнений:
15 •
4 *
(ж+ іг) - і | - 1 ;
1 1 О
і
3
х + у = —;
9 4
(-5) 4
-5 х - 5 у = -
1 1 ^
6 * + 5 * = Тб:
*30 5х + 6у = 4; 5х + 6у = 4;
А 1 5 Л О 3 1
4 - — ; у = 4 - 3 - ; у = -
4 4 4
1 3 1
х + —= —; х -
4 4 2
1 : - = 4 (ч.)
4
будет наполняться резервуар через вторую трубу.
1: —= 2 (ч.) — будет наполняться резервуар через первую трубу.
2
Ответ: 4 часа; 2 часа.
1194. и, км/ч. ч. 5 , км
А —>В X 2 + 2,5 = 4,5
4-5* }з о
2,5у]В ^ А У 2,5
А В X 3 3x1
^30
5уВ А У 2 + 3 = 5
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

224. Пусть скорость первого туриста равняется * км /ч., а второго —
у км/ч. За 2 + 2,5 = 4,5 (ч.) первый и за 2,5 часа второй пройдут вместе
(4,5л; + 2,5у) км. За 3 часа первый и за 2 4- 3 —5 (ч.) второй вместе пройдут
(3* 4* 5у) км. Так как расстояния равны и равняются по 30 км, то состав-
„ [4,5л: + 2,5у = 30; •(-2) Г-9* - 5 у - -60;
ляем систему уравнении: < 4
[3* + 5# = 30; [3* + 5# = 30;
-6л: = -3 0 ; у —5; 3 * 5 + 5# —30; у —3.
Ответ: скорость первого туриста — 5 км/ч., второго — 3 км/ч.
1195. Пусть х и у — данные числа (х > у). Тогда х2- у2—275 и (х - у)2—121.
У2 = 275;
[(л: - у)2 = 121;
[11(* + #) =275;
Составляем систему уравнений:
■С
p - j / 2 = 275; Г(* -» )(* + У) = 275; Г
| * -у = 11; ] * - * / = 11; |
Г* + # = 25; І2* = 36; Г*
[ * - # = 11; [2# = 14; [#
I*2 —#2 = 275; {(* - #Х* + #) = 275; Г
или і і і
[ * - # = -11; [ * - # = -11; 1
* - # = 11;
= 18;
= 7.
-11(* + #) = 275;
* - # = -11;
I* + # = -25; [2* = -36; Г* = -18;
< Ответ: 18 и 7 или -1 8 и -7 .
1 * - # = -И ; 12# = -14; )# = -7 .
1196. Решение. Пусть на первой полке будет * книг, на второй — у книг.
Если половину книг со второй полки переложить на первую, то на первой
станет (* + 0,5#) книг, а на второй останется 0,5# книг, что в четыре раза
меньше, чем на первой, то есть 0,5# * 4 = * + 0,5#, или 2# = * + 0,5#.
Так как всего на двух полках 50 книг, то * + # = 50. Составим систему
уравнений:
- * = 0;І2# = * + 0,5#; І2#- 0,5# -
I* + # = 50; I* + # = 50;
2,5# = 50;
# = 20; * + 20 = 50; * = 30.
Ответ: на первой 30 книг, а на второй 20 книг.
1197. Реш ение. Обозначим количество детей через *, а количество столов —
через #. Если детей рассадить по двое за стол, то необходимо * столов,
* 2
что на 3 стола больше, чем их есть, значит # = 3. Если детей раеса-
2
*
дить по трое, то нужно — столов, что на 1 стол меньше, чем еоть, значит
о
х 1# - —= 1.
* 3
Составим систему уравнений:
х *
# — = 1;
3
* * . 3* - 2* . . Л 24 „ „ _
2 ~ 3 -6---- ! * = 4 6; х = 24; у - — = 1; {/ = 1 + 8; у = 9.
Ответ: 24 детей, 9 столов.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

225. 1198- Решение. Пусть было х воробьев и у столбиков. Из условия задачи
ясно, что воробьев на 2 больше, чем столбиков, то есть х - 2 = у. Если же
они сядут по двое, то займут на два столбика меньше, чем есть, значит
X
у = 2. Составим систему уравнений:
2
|* ~У = 2,
х _ ^- = 4; х = 8; 8 - у = 2 ;у = 8 - 2 ; у = 6 .•
у ~ 2 = 2: 2
Ответ: 8 воробьев и б столбиков.
1199. Решение. Пусть сейчас отцу х лет, а сыну — I/ лет. 8 лет назад отцу
было (х - 8) лет, а сыну — {у - 8) лет, что в 8 раз меньше, чем тогда
было отцу, то есть х - 8 — 8(у - 8). 5 лет назад отцу было (х - 5) лет,
а сыну — (у —5) лет, что в 5 раз меньше, чем тогда было отцу, то есть
х - 5 —5(у - 5). Составим систему уравнений:
+ 8у = 56,
5у = -20;
X
1
00
II
00
н
1
-у); |х —8 = 8# -6 4 ;
к
1
н
-56; (-і) (
| * -5 = 5{у--5); |х - 5 = 5# —25; к
1
II
-20; 1
3у = 36;
у = 36 : 3; у = 12; х - 5 * 12 - -2 0 ; х = -2 0 + 60 = 40.
Ответ: отцу 40 лет, сыну 12 лет.
1200. Пусть Антону х лет, а Насте у лет, тогда вместе им (х + у) = 17 (лет).
8 лет назад Антону было (х - 8) лет, что в 2 раза меньше, чем Насте сей­
час. Составляем систему уравнений:
Ы х - 8) = (2* - „ = 16; = _ _ _
х + у = 17; х + у = П-,
Ответ: Антону — 6 лет, Насте — 11 лет.
1201. Решение. Пусть осел нес х мешков, а мул — у мешков. Если мул возь­
мет один мешок у осла, то у него станет (у + 1) мешков, которые будут
весить в два раза больше, чем (х —1) мешков, оставшихся у осла, то есть
2(х - 1) = у + 1. Если осел возьмет один мешок у мула, то у него станет
(х + 1) мешков, вес которых будет равняться весу (у - 1) мешков, остав­
шихся у мула, то есть х + 1 —у - 1. Составим систему уравнений:
= -у + 1;
У + 1;
у жи ь ч о * I *
ІX +1 = у -1 ; .(-1) Г-х ~ 1 =
[2 (х -1 ) = у + 1; [2х - 2 =
х - 3 = 2;
х = 2 + 3 ;х = 5 ; 5 + 1 = у —1 ;# = 6 + 1 ;# = 7 .
Ответ: 5 мешков было у осла и 7 мешков — у мула.
1202. Решение. Пусть один вол стоит х таелей, а один баран — у таелей.
5 волов и 2 барана стоят 11 таелей, то есть 5х + 2у = 11, а 2 вола и 8 ба­
ронов — 8 таелей, то есть 2х + 8у —8. Составим систему уравнений:
5х + 2у = 11;
2х + 8у - 8;
2 |10х + 4# = 22,
(-0,5) 1-х - 4 у = -4;
9х = 18;
дг = 18 : 9; х = 2; -2 - 4у ~ -4 ; -4 у —-2 ; у = 0,5.
Значит, один вол стоит 2 таеля, а один баран стоит 0,5 таеля. 5 волов
будут стоить 5 * 2 = 10 таелей. За 10 таелей можно купит 10 : 0,5 =
20 баранов.
Ответ: 20.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

226. 1203. Решение. Пусть в клетке х фазанов и у кроликов. Так как вместе у них
35 голов, то всего животных тоже 35, то есть х + у = 35. У кролика 4 ноги,
то есть кроличих ног в клетке 4уг а у фазана две ноги, то есть в клетке
2х ног фазанов. Тогда 2х + 4у = 94, потому что по условию задачи всего
у них 94 ноги. Составим систему уравнений:
(-2) -2х - 2 у - —70,
[2* + 4у = 94;
у и п л . « Л
Гк + 3/ = 35; (-2) Г
[2л: + 4у - 94; [
2у = 24;
у = 24 : 2; у = 12; л: + 12 =* 35; х —35 - 12; х = 23.
Ответ: 23 фазана и 12 кроликов.
1 204. Пусть х м/с и у м/с — скорости движения по кругу первого и второго
тел соответственно (л: > у). Бели тела двигаются навстречу друг другу, то
за 4 с до встречи тела пройдут (л; + у) ■4 = 120 (м). Если тела двигаются
в одном направлении, то первое тело пройдет больше, чем второена це­
лый оборот, то есть на 120 м. За 10 с первое тело пройдет Юл: м, а вто­
рое — Юг/ м. Составляем систему уравнений:
{
(л; + у) 4 = 120
(л:- у ) 10 = 120
; 2х = 42; Г;
0; [2у = 18; [і
21;
Ответ: 21 м/с и 9 м/с.
х =
[У = 9.
1205. Пусть х м/с и у м/с — скорости движения по кругу первого и второго
тел (л: > у). За б с движения в одном направлении тела пройдут 6* и 6у м.
Так как х > у9то первое тело пройдет на 1 оборот больше. Имеем 6х~~6у =
90 (м). Так как скорость первого тела в 4 раза больше, чем скорость
. = 4у;
второго, составляем систему уравнении:
3у = 15; у = 5; х = 20.
Ответ: 20 м/с и 5 м/с.
1206. Пусть х — данное число, тогда х —4 - у + 2; х
или *-* Ж | / и и и V | Ж.V*АТА
х = 4у; х = 4у;
к л 1
|б(х - у) = 90; х - у = 15;
7 - г + 1; х = 11 •т + 6;
где У + 2 + Ш + 2 = —.
2
Составляем систему уравнений:
4 у + 2 = х;
7г +1 = х;
11т + 6 = х;
у + г + т + 2 = 0 ,5л:;
У =
г =
т =
4 ’
х —1 •
7 ’
* - 6
11
- 2 * - 1 л - 6 л
+ + + 2 = —;
4 7 11 2
77(л: - 2) + 44(л:
77л: - 154 + 44л:
Ответ: 50.
1207. у —кх р
а) А(1; 3) и В(3; 7)
1) + 28(х
44 + 28*
308
6) + 308 •2 - 154л;;
168 + 616 - 154л: = 0; -5л: = -250; х = 50.
I?:
к + р;
3к + р;
К(3; 2) и Р (-1; -2 )
Ї2 —Зх + р:
1-2 = -х + р;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

227. 2£ = 4; к = 2; 4* —4; * = 1;
р = 1; у = 2* + 1. р = -1 ; # = * - 1.
и) С(2; 4) и £>(5; -2 ) г) Е(1; 2) и F(3; 6)
|4 = 2к + Ь; Ї2 - к + Ь;
{ —2 = 56 + Ъ; [6 = Зк + Ь;
3к = -6 ; к = -2 ; 2к —4; к —2;
Ь = 8; у = —2х + 8. Ь —О; у = 2х.
1208. а) Прямая проходит через точку (-4 ; 0) параллельно оси у. х —-4 ;
б) прямая проходит через точку (О; 3) параллельно оси х. у = 3;
[О= 4к + р;
в) прямая проходит через точки (4; О) и (О; 2). <
± г [2 = ОА: + р;
р = 2; 4к = -2 ; к - - - ; # = - - * + 1 .
Л &
1209- а) Пусть х га и у га — части поля площадью 100 га (* > у). Так как
х больше у на п, составляем систему уравнений:
2х = 100+ п; п „ п
* = 50 + —; у —5 0 -----.
2у = 100- п; 2 У 2
1* + # = 100; Г
х~~у = п;
Ответ: ^50 - ^ j га и ^50 + ^ га.
б) Пусть * га и у га — части поля площадью а га (* > у), тогда * + у —а
и * - у —5 (га). Составляем систему уравнений:
| 2 ,.„ + у . .
[ * - # = 5; [2у = а -.5; 2 2
а; І2х ~ а
5; [2у = а
Ответ: I—+ 2,5| гаи [ ——2,5І
2 ) {2 ’ )
га.
1210. а) Так как число а поделили на части, пропорциональные числам 2,
3 и 5, то числоа состоитиз2 + 3 + 5 = 10 частей. Значит, наши части
2 с 3 5 1
равняются: — а ——; — а и — а - —а.
10 5 10 10 2
б) Так как число 1000 поделили начасти, пропорциональные числам И, р
и *, то число 1000состоит из (к + р + О частей. Значит, наши части рав-
1000/е ЮООр 1000*
няются: ------------ ; --------— ; -----------
£ + р + * £ + /? + * £ + />+ *
1211. Пусть за неделю шьют * моделей костюмов первого вида и у моделей
костюмов второго вида. Тогда на пошив костюмов израсходуют (2х + 3у) м,
что составляет а м за (4* + 5#) год, или за * часов. Составляем систему
[10* + 15# = 5а;Г2* + 3# = а; Г-4* —6# = -2а; Ги
[4*+ 5у - і; [4* + 5у = і; -
уравнении
у = —2а + і; і у —2а + *;
12* —15# = -3*;
у = ъа
-2 х —-3* + 5а; I * = 1,5* - 2,5а.
Ответ: 1,5* —2,5а — костюмов первого вида и 2а - * — второго.
1212. Пусть по плану за неделю добывают * т угля. Тогда шахта добыла сверх
рх Дг*
плана за первую неделю р % ~ (т) угля, а за вторую — к % = — — (т)
100 100
угля. Значит, сверх плана за две недели шахта добыла | + 7^ |= т (т)
угля.
Г рх кх
+ -—
1100 100 )
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

228. px kx
Имеем: -f— + — - = m;
100 100
x[p + k) = 100m; x = m .
p + k
Задания д ля самостоятельной работы
а)
В каждом варианте в задании 1(6) используется способ сложения
(см. объяснение к упражнениям 1116—1117). Для решения задач зада-
ния 2 см. объяснение к упражнениям § 29._____________________________
Вариант 1
1. Систему уравнений а) решим графически, б) — способом сложения.
]'2х - у = 4,
[х - у = 3.
Графики уравнений системы — прямые, поэтому для каждого уравнения
надо найти два решения, которые и будут точками, через которые прове­
дем эти прямые.
2х - у —4; у —4 - 2х; если х = 0, то у ~ -4 ; если х = 2, то у = 0.
Имеем точки (0; —4) и (2; 0).
х - у = 3; у = х + 3; если х — 0 , то у — -3 ; если х — 3, то у — 0 .
Имеем точки (0; -3 ) и (3; 0). Построив трафики, находим точку их пере­
сечения (1; —2). Ее координаты являются решением системы.
Ответ: (1; -2 ).
б)
1л; + 0,7 у —5,2,
2х + 096у = 7;
0,6 fl,86* + 0,4
(-0,7) [-3,64л;- 0
42у = 3,12,
42у = -4 ,9 ;
-1,78л: = -1,78;
х = 1; 3,1 +. 0,7у = 5,2; 0,7у = 5,2 - ЗД; 0,7у = 2,1; у = 2,1 : 0,7; у = 3.
Ответ: (1; 3).
2- Решение. Пусть площадь одной части х га, площадь второй — у га, тогда
половина площади второй части будет — га. Так как все поле 80 га, то
2
х + у —80. А так как площадь первой части на 2 га больше половины
площади другой, то х - ~ = 2. Составим систему уравнений:
2
х + у = 80,1 х + у = 80,
9 [ 2 х - у = 4; л; = 8 4 :3 ;л; =У - о о %х —у = 4; л; = 8 4 : 3 ; л: = 28;28 + # = 8 0 ;I/= 80 —28;у = 52.
л ; - - - 2 ; |•2 ---------------------- „
А Зх = 84;
Ответ: площадь одной части 28 га, а второй — 52 га.
а)
Вариант 2
1. Систему уравнений а) решим графически, б) — способом сложения.
4х - 2у = 6,
[х + у = 3.
Графики уравнений системы — прямые, поэтому необходимо для каждого
уравнения найти два решения, которые и будут точками, через которые
проведем эти прямые.
4 л: - 2у = 6; 2х - у —3;
у —2х —3; если х —0, то у ——3; если х —2, то у ~ 1.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

229. Имеем точки (О; —3) и (2; 1).
х + у = 3; у = 3 —х; если * —О, то у —3;
если х —3, то у —О. Имеем точки (О; 3) и (3; О).
Построив графики, находим точку их пересечения (2; 1). Ее координаты
являются решением системы.
Ответ: (2; 1).
б)
2,2х + 0,5# = 3,2,
[1,2* + 0,8у - 2,8;
8 ■ (17,6*+ 4# = 25,6,
(-5) 1 -6 * -4 # = -14;
11,6* = 11,6;
* - 1; 17,6 + 4# = 25,6; 4у = 25,6; у - 8 : 4; у = 2.
О твет: (1; 2).
Решение. Пусть площадь одной части * га, площадь другой — у га, тогда
половина площади второй части будет 0,5# га. Так как все поле 100 га, то
х + у —100. А так как площадь первой на 5 га меньше половины площади
+ # = 100,
второй, 0,5# —* = 5. Составим систему уравнений: Х
К 5у - * = 5;
1.5 у = 105;
# = 105 : 1,5; у = 70; 70 + * - 100; * = 100 - 70; * = 30.
Ответ: площадь одной части 30 га, а второй — 70 га.
а)
Вариант 3
Систему уравнений а) решим графически, б) — способом сложения.
х - 2 у = 3,
* + у = -3 .
Графики уравнений системы — прямые, поэтому необходимо для каждого
уравнения найти два решения, которые и будут точками, через которые
проведем эти прямые, * - 2# ~ 3; * = 3 +- 2у; если у —0, то * —3; если
у —-1 , то * = 1.
Имеем точки (1; -1 ) и (3; 0). * + у ——3; у = -3 - *;
если * = 0, то у = -3 ; если * —-3 , то у = 0.
Имеем точки (0; -3 ) и (-3; 0). Построив графики, находим точку их пере­
сечения (—1; -2), Ее координаты являются решением системы.
Ответ: (-1 ; -2).
30* + 6# = 90,
30* + 25,5у = -90;
|1,5* + 0,3і/ = 4,5, *20 Г
[2* -1 ,7 # = 6; (-15) I
31,5# = 0;
у = 0; 30* = 90; * = 90 : 30; * 3.
Ответ: (3; 0).
Решение. Пусть длина одной части * м, длина второй — ум , тогда половина
длины второй части будет 0,5# м. Так как весь провод имеет длину 40 м,
то * +* # —40. Учитывая, что длина первой части на 4 м больше половины
длины второй, имеем * - 0,5# = 4. Составим систему уравнений:
х + у = 40, + У = 40,
х - 0 ,5 у = 4; (-1) | -* + 0,5у = -4;
1, Ьу = 36;
у = 36 : 1,5; у = 24; 24 + * = 40; * —40 - 24; * = 16.
Ответ: одна часть провода имеет длину 16 м, а вторая 24 м.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

230. Вариант 4
1. Систему уравнений а) решим графически, б) — способом сложения.
а)
|3* - 2у = 7,
* + у = 4.
Графики уравнений системы — прямые, поэтому необходимо для каждого
уравнения найти два решения, которые и будут точками, через которые
7 + 2у , 0
проведем эти прямые. 3* - 2у —7; х = — — если у = 1, тох = 3; если
О
I/ = —2, то х = 1. Имеем точки (3; 1) и (1; —2).
ле + у —4; I/ = 4 - *; если х = О, то у = 4; если * = 4, то у—О.
Имеем точки (О; 4) и (4; О). Построив графики, находим точку их пересе­
чения (3; 1). Ее координаты являются решением системы.
Ответ: (3; 1).
|1,7* + у - 4,4, 0,8 Г1,36* + 0,8у = 3,52,
[3,5* - 0,8у = 6,2; [3,5* - 0,8у = 6,2;
4,86* = 9,72;
* = 9,72 : 4,86; х —2; 1,7 - 2 + у = 4,4; I/ = 4,4 - 3,4; у —1.
Ответ: (2; 1).
2- Решение. Пусть длина одной части а: м, длина второй — у м, тогда половина
длины второй части будет 0,5# м. Так как весь провод имеет длину 50 м,
то * + у —50. Учитывая, что длина первой на 1 м меньше половины длины
. _ . _ = 50,
второй, имеем 0,5у —х = 1. Составим систему уравнений: {
Л " * = 1;
|* + У=
10, Ь у -
м :
1,5у —51; у = 51 : 1,5; у = 34; 34 + * —50; * = 50 - 34; * = 16.
Ответ: одна часть провода 16 м, а вторая 34 м.
Тестовые задания N27
1. б) -1 . 2.а) 2* + у = 7; 3 . а )* 4 + уА= -5 .
4. г) * = 2. 5 . в) 1. 6 . а )(1 1 ;3 ).
7 . б) (5; 5).
2* - 3у - 16;
+ 2^ = 1; ( - 2)
2* —3у —16; —2* —4у = -2 ; —7у = 14; у = —2; * +2 •(—2) = 1; * = 5.
Ответ: (5; -2).
о 2. , 3 , 7 , ч
9. - = 1; - - = -1; - = 1.а) одна.
2 о 7
12 _ -8 _ 6 0 ’ 4 8 _ 4 ’ ° ~
Контрольная работа № 7
1. Г4* —Зу = —1;
[5* - 21/ = 4;
(3; 2) — не является решением системы; (2; 3) — является решением
системы.
[4 •3 —3 •2 = -1; ГбФ-1; Г 4 -2 -3 * 3 =-1; 1-1 = -1;
[ 5 - 3 - 2 2 = 4; |и ^ 4; [ 5 - 2 - 2 - 3 = 4; 14 = 4;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

231. (-1; -1 ) — не является решением системы; (3; О) — не является решени­
ем системы
14 (-1) - 3 •(-1) = -1; |
( - 1 ) - 2 (-1) = 4; 1
18* - Зу = 20;
|* + 2у = 12;
8* - Зу = 20;
X = 1, то у = -4 (1; -4 )
х 4- 2у = 12;
л; = 6, то у —3 (6; 3)
х * 4Тто у = 4 (4; 4).
1 = -1;
'3 * 4 ; I:
4 -3 —3 •О= —1; | 1 2 *-1 ;
5 3 - 2 0 = 4; [1 5 * 4 .
Г!/ = 1;
[|л:|+ у = 2;
|*|+ у = 2;
у = -|*| + 2.
Зу 20
I Ответ: (-1 ; 1), (1; 1),
Ответ: (4; 4).
| 5*-З у = -9; Гу = 2дг+ 2;
[2* —у = -2; [5* -3 (2 * + 2) = -9;
5* - 6 * - 6 = -9 ; - * = -3 ; * = 3 ;у = 2 * 3 + 2 ;у = 8.
Ответ: (3; 8).
153* - 2у 5* - 3у .
у + —- - * = 1;
5 3
2* - Зу 4* - Зу
-У = 1;
3 2
9* —6у + 25* —15у —15* = 15;
4* —6у - 1 2 * + 9у —6у = 6;
27
Зу = -8 * - 6;
1 9 * -7 -З у = 15;
75* 27; * =
75
72 - 450
11= 75 ’ У
|Зо —7Ь = 8;
16а - 56 —-2;
; [19* —21у = 15; [
[-8 * - Зу = 6; [
9 в _ Г 9 ^ А 1 Г72 Л
; * ------; Зу = - 8 - ---------- 6; у —— --------6 ;
25 у у 2Ь) У 3 1,25 )
378 к 1 г, ( 9» У = -5 — . Ответ: I - — ; - 5 — .
75 25 V 25 25^
(-2) [-6а +146 = -16;
■6а - 56 = -2;
96 = -1 8 ; 6
За - 7 ■(-2) —8; За —-6 ; а = -2 . Ответ: (-2 ; -2).
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

232. 2* + у = 7;
з * - ; = 6; ( 2ж + г= 9:
[3* - 2 = 6;
г - у = 2;
5* = 15; * = 3; 3 - 2 + 2= 9; 2= 3; 3 - # = 2; §/ = 1. Ответ: (3; 1; 3).
8« Пусть в сарае л; гусей и # кроликов, тогда голов х + у — 50, а ног
2* + 4# —160. Составляем систему уравнений:
+ у = 50;
2* + 4у - 160;
(-2) I-2 х ~ 2# = -100;
[2* + 4у - 160;
2у —60; у —30; х + 30 = 50; х —20. Ответ: 20 гусей и 30 кроликов.
9. Пусть на складе было х маберезовых и у м8сосновых дров. Тогда всего на
складе было (* + у) или 1500 м8дров. За месяц использовали 0,15# (т) со­
сновых и 0,2* (т) березовых дров, что составляет 0,15# + 0,2* или 270 м3.
Составляем систему уравнений:
= 1500 - у;
2(1500 - #) + 0,15# = 270;
300 - 0,2# + 0,15# = 270; -0,05# = -3 0 ; # *=600; * = 1500 - 600; * = 900.
Ответ: 900 м3 березовых и 600 м3 сосновых дров.
10. ах + Ьу = 13
М(5; 3); # (8; 3)
л.и о л / г и ш аVij.Tj.jp у
(* + # = 1500; х
}0 ,2 * + 0,15# = 270; |о,
5а - 36 = 13;
8а + 36 = 13;
13а = 26; а = 2; 5 * 2 - 36 — 13; -3 6 = 3; 6 = -1 . Ответ: а *> 2; 6 = -1 .
Задачи и упражнения д ля повторения
Уравнение
Решим уравнения 1213—1218. См. объяснение к упражнениям 8 —10.
1213. а) 7* + 15 + 15* + 8 - 10 = 9*;
7* + 15* - 9* = -1 5 - 8 + 10; 13* = -1 3 ; * =-1 3 : 13; * = -1 ;
б) 25 + 5# - 17 + 7# = 150 - 130#;
5# + 7# + 130# - 150 - 25 + 17; 142# - 142;# =142 : 142; # = 1.
1214. а) 7* - 39 - 2(* + 3) + 6 - 2х + 5;
7* - 39 = 2* + 6 + 6 - 2* + 5; 7* - 39 = 17; 7* «=17 +39; 7* —56;
* = 56 : 7; * =* 8;
б) 3(* - 5) = 5(* - 3) - 4(2 - 3*); 3* - 15 - 5* - 15 - 8 + 12*;
Зх - б х - 12* = -1 5 - 8 + 15; 4* = -8 ; * = - 8 : (-14); * = — ; * =
14 7
1215.а) | ( 2 * - 4 ) + | ( 4 * - 2 ) = * + 5; * - 2 + 2* - 1 = * + 5;
3* - 3 = * + 5; 2* = 8; * = 8 : 2; * = 4;
б) ~ (3* +1) + ~ (6* - 2) = * + 6; 2* + ^ + 2* - ^ = * + 6; 4* = * + 6;
3 о О и
4* - * = 6; 3* = 6; * —6 : 3; * = 2.
1216. а) 5(* - 3) + 7(3* + 6) = 2(* - 2) + 103; 5* - 15 + 21* + 42 - 2* - 4 + 103;
26* + 27 —2* + 99; 26* - 2* = 99 - 27; 24* = 72; * —72 : 24; * —3;
б) 8(# - 2) + 5(3# - 2) = 3(# - 5) + 69;
8# - 16 + 15# - 10 = 3# - 15 + 69; 23# - 26 = 3# + 54;
23# - 3# ~ 54 + 26; 20# = 80; # = 80 : 20; у = 4.
1217. а) 7(6* - 1) + 3(2* + 1) - 5(12* - 7) = 23;
42* - 7 + 6 * + 3 - 60* + 35 - 23; -1 2 * + 31 = 23;-1 2 * =2 3 - 31:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

233. 8 2
12х = —8; х = -8 : (-12); х = — ; * = - .
12 3
6) 5(8г - 1) + 8(7 - 4г) - 7(4г + 1) = 19; 402 - 5 + 56 - 32г - 28г - 7 = 19;
-20г + 44 = 19; -20г = 19 - 44; -20г = -2 5 ; г = -2 5 : (-20); г 1,25.
«218. а) ± (х - 3) + | (* - 4) = | (х - 5) + | (х —1);
± ( * - 3 ) 8 + ± ( * - 4 ) 8 = ^ ( * - 5 ) 8 + ^ ( * - 1 ) 8;
4 . 0 £, о
2(х - 3) + х - 4 = 4(х - 5 ) + х - 1 ; 2 х - 6 + х - 4 = 4х —20 + Х - 1 ;
Зх - 10 = 5х - 21; Зх - 5х —-2 1 + 10; -2 х = -1 1 ; х —-1 1 : (-2); х —5,5;
б) ^ ( 8 ~ х ) - ( 5 - 4 х ) = {х + в); ^ (8 —ле)-6 - ^(5 - 4дс)-6= ^(а: + 6)-6;
О О 2 0 О £>
8 - х - 2(5 - 4х) = 3(х + 6); 8 - х - 10 + 8х — Зх +18; 7х - Зх = 18 + 2;
4х = 20; х —20 : 4; х = 5.
1219. Покажем, что при любом значении а уравнение (а + 2)х - (а + 3)х ч* 5
имеет единственноерешение: х(а + 2 —(а + 3)) —5;
х(а + 2 - а - 3) = 5;х* (-1) = 5. Таккак множитель х не равен нулю, то
уравнение имеет единственный корень.
Найдем его: х •(-1) * 5; х = 5 * (-^1); х —-5 . Ответ: х —-5 .
1220- Определим, существуют ли значения а, прикоторых уравнение(а2+ 1) * 7
имеет множество корней. Это уравнение линейное, поэтому может иметь
множество корней, если множитель х равняется нулю, а число, которое
стоит в правой части уравнения, равняется нулю. Правая часть содержит
число 7, 7 - О, поэтому уравнение не может иметь множество корней.
Ответ: таких значений нет.
1221. Уравнение ах = 12 линейное и не имеет корней, если множитель х
равняется нулю, а число, которое содержится в правой части уравнения,
не равняется нулю. Множитель а может равняться нулю.
Ответ: при а = О.
1222. Приведем уравнение к линейному: (о - 2)х —х + 1; (а - 2)х - х —1;
х(а —2 —1) —1; х(а - 3) = 1. Чтобы уравнение не имело множителей, не­
обходимо, чтобы а —3 = 0, то есть а —3. Ответ: при а = 3.
Решим задачи 1223—1238. См. объяснение к упражнениям 125—173.
1223. Решение. Пусть количество купцов — х человек. Если каждый внесет
по 5 монет, то собранная сумма денег — 5* монет, что меньше стоимос­
ти барана на 45 монет, то есть стоимость барана (5* + 45) монет. Если
каждый купец внесет по 7 монет, то собранная сумма денег — 7х мо­
нет, что меньше стоимости барана на 3 монеты, то есть стоимость барана
(7х + 3) монет.
Составляем уравнение: 5* + 45 = 7х + 3, откуда: 5х —7х = 3 —45; —2х = -42;
х = -4 2 : (-2); х = 21.
Значит, купцов было 21. Тогда стоимость барана 5х + 45 = 5 * 21 + 45;
5х + 45 = 150, то есть 150 монет.
Ответ: 21 купцов; 150 монет.
1224. Решение. Пусть количество лет, которые прожил Диофант, — х лет,
1 1 1
оно состоит из лет детства — —х лет, юности — — х лет, еще —х лет,
еще 5 лет и количества лет, которые прожил его сын, что равняется поло­
вине жизни Диофанта — —х лет, а потом еще 4 года после смерти сына.
2
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

234. ( I 1 1
—X X ,
1з 5 )
Составляем уравнение:
1 1 1 * 1* = —* + — * + —* + 5 + —* +4,откуда:
6 12 7 2 У
1 1 1 1 2* + * + 6* 1
х = —х + -— х + —х + —х + 9; х —--------------- + —* + 9;
6 12 2 7 12 7
9 * 1 Л 3 1 Л 21*+ 4*
х - — + —* + 9; х = —х + —х + 9; х --—— + 9;
12 7 4 7 28
х —— х + 9; х - — х ~ 9 ; — х - 9 ; * = 9 : — ; * = 9 - — ; * = 84.
28 28 28 28 3
Ответ: Диофант жил 84 года.
1225. Решение. Пусть пчел всего *. Тогда на цветке кадамба — —х пчел,
5
на цветах силиндха — ^ * пчел, на цветах кутеля — 3 •|~ х - ~ х |, на
жасмине и панданусе — 1 пчела. Составимуравнение:
1 1 0 (1 1 ^ .
* = —* + —* + 3- —* — * +1, откуда:
5 3 1,3 5 )
3* + 5* _ 5 * - 3 * 8 6 . 14 ч
х ~ ----------- + 3 ----------- + 1; * = — хл------* + 1; х —— * + 1;
15 15 15 15 15
* - — * = 1;— * = 1; * = 1 : — ; * —1 * 15; * = 15.
15 15 15
Ответ: всего 15 пчел.
1226. Решение. Пусть меньшее число *, тогда, если их разность 5, то большее
число * +•5. Так как сумма этих чисел 10, составим уравнение:
* + * + 5 = 10; откуда: 2* = 10 —5; 2* = 5; * = 5 : 2; * = 2,5.
Меньшее число 2,5, а большее * + 5 = 2,5 + 5; * + 5 —7,5, то есть боль­
шее число 7,5. Ответ: 2,5 и 7,5.
1227. Решение. Пусть первая часть числа *, тогда вторая — (10 - *). Если
первую часть умножить на 5, получим 5*, а после деления результата на
5* 10 п
вторую часть — — -,что по условию равняется — . Составим уравне-
5* 10
ние: —----- = — . Решим, пользуясь основным свойством пропорции:
5* * 3 —10(10 - *); 15* = 100 - 10*;
15* +■ 10* = 100; 25* —100; * = 100 : 25; * = 4.
Тогда первая часть числа 4, а вторая — 10 - * = 10 - 4 = 6.
Ответ: 4 и 6.
1228. Решение. Пусть одежда стоит * флоринов. За 12 месяцев человек должен
был получить (* + 10) флоринов, то есть за 1 месяц — - + флоринов.
_ _ * + 10
За 7 месяцев работы его зарплата составляла-----------7 флоринов, что по
условию задачи равняется (* + 2) флоринов.
л * + 10 „ л * +10 л л „
Составим уравнение: ——— 7 - * + 2, откуда: ^ — 7 12= * *12 + 2 *12;
7(* + 10) = 12* + 24; 7* + 70 = 12* + 24; 7* - 12* = 24 - 70; -5 * = -46;
* =* -4 6 : (-5); * = 9,2, то есть одежда стоила 9,2 флоринов.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

235. 1229. Решение. Пусть у учителя х учеников. Если бы было еще столько —
1 1 1х учеников, и половина их — —*, и четверть их — —х и 1 ученик, то
2 4
эта сумма равнялась бы100. Составим уравнение:
1 1 2 1 3
х + х + —х + —х + 1 = 100, откуда:2* + —* + —* = 1 0 0 -1 ; 2* + —* = 99;
2 4 4 4 4
О О -а А
2 —* = 99; * = 9 9 :2 —; * = 9 9 : — ; * = 9 9 -----; * = 36.
4 4 4 11
Ответ: 36 учеников.
1230. Пусть у крестьянина было * овец. Если родится столько же ягнят, бу­
дет (* + *) овец. Если крестьянин купит 1 молодую овечку, у него будет
(2* + 1) овец. После еще трех покупок этого количества у крестьянина
станет 2* + 1 + 3(2* + 1), что по условию равняется 100. Составим урав­
нение: 2* + 1 + 3(2* + 1) —100, откуда: 2* + 1 + 6* + 3 = 100;
8дс + 4 = 100; 8* —100 - 4; 8* —96; * = 96 : 8; * = 12.
Ответ: крестьянин имеет 12 овец.
1231. Решение. Пусть младшему сыну * лет, тогда:
старшему — (* + (* + 2) + 6) лет
среднему — (* + 2) лет 58 лет
младшему — * лет.
Составим уравнение: * + * + 2 + 6 + * + 2 + * = 58, откуда:
4* + 10 —58; 4 * = 58 - 10; 4* = 48; * = 48 : 4; * = 12.
Тогда младшему сыну — 12 лет, среднему — * + 2 = 1 2 + 2; * + 2 = 14,
старшему — * + * + 2 + 6 = 12 + 1 2 + 2 + 6 ; * + * + 2 + 6 = 32.
Ответ: 32, 14, 12 лет.
1232. Решение. Пусть дневная норма мастерской — * деталей. За 20 дней
она должна была изготовить 20* деталей. Мастерская за день изготавли­
вала на 8 деталей больше, то есть (* + 8) деталей, поэтому сделала всю
работу за 18 дней. Это количество составляет 18(* + 8) или 20* деталей.
Составим уравнение:
20* = 18(* + 8), откуда: 20* = 18* + 144; 20* - 18* = 144;
2* = 144; * = 144: 2; * = 72. Тогда дневная норма мастерской 72 детали, а за
20 дней мастерская должна была изготовить 20* = 20 *72 —1440 деталей.
Ответ: 1440 деталей.
1233. Пусть дневная норма выпуска станков была * станков. Тогда за 15
дней необходимо было изготовить 15* станков. Завод выпускал на 2 стан­
ка в день больше, то есть (* + 2) станков. Завод работал на 2 дня меньше
запланированного строка, то есть 13 дней, и выпустил 13(* + 2) станков,
что на 6 станков больше заказа. Составим уравнение:
13(* + 2) - 15* = 6, откуда: 13* + 26 - 15* = 6; 13* - 15* * 6 - 26;
-2 * = -2 0 ; * = -2 0 : (-2); * = 10. Тогда запланированная дневная норма
10 станков, а весь заказ: 15* = 15 * 10; 15* —150.
Ответ: 150 станков.
1234. Решение. Пусть второй вытаскивал за 1 ч. * м3земли, тогда первый — (*
+ 40) м3. За 16 часов первый вытащил 16(* + 40) м3, а второй за 24 часа
— 24* мэ. Учитывая, что вместе они вытащили 8640 м3 земли, составим
уравнение: 16(* + 40) + 24* = 8640, откуда:
16* + 640 + 24* = 8640; 40* = 8640 - 640; 40* = 8000; * = 8000 :40; * = 200.
Тогда второй вытаскивал за 1 ч. 200 м3, а первый * + 40 = 200 + 40;
х + 40 —240, то есть 240 м3. Ответ: 240 м3, 200 м3.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

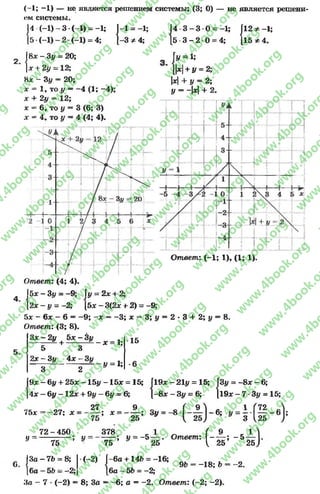
236. 1235. Решение. Пусть ежедневно планировалось засевать * га, а за 14 дней —
14* га. Но за день засевали на 4 га больше, то есть (* + 4) га, поэтому
закончили сев на 4 дня раньше, то есть за 10 дней провели сев, засеяв
10(* + 4) га. Составим уравнение: 14* —10(* + 4),
откуда: 14* = 10* + 40; 14* —10* = 40; 4* —40; * —40 : 4; * —10.
Тогда засеяли 14* = 14 * 10; 14* = 140. Ответ: 140 га.
1236. Решение. Пусть продуктивность первой землечерпалки — * м3, тог­
да второй — 1,5* м3. Их совместная продуктивность — (* + 1,5*) м3.
За 12 дней обе землечерпалки выкопали бы 12(* + 1,5*) м3, то есть
12 * 2,5* = 30* (м3). Тогда первая землечерпалка самостоятельно сделает
работу за — = 30 (дней), а вторая — - = 20 (дней).
* 1,5*
Ответ: 20 дней, 30 дней.
1237. Решение. Пусть расстояние между пристанями будет * км. Тогда соб­
ственную скорость теплохода можно записать т а к : ----- 2 I км/ч. при
( И
• ( И
движении по течению и |—+ 2 | км/ч. при движении против течения.
Получаем уравнение:
( - - 2 ) = ( - + 2 ); - + - = 2 + 2; 5* ~ '** = 4; * = 20; * = 80.
^4 ) ^5 ) 4 5 20
Ответ: 80 км.
1238. Решение. Пусть собственная скорость вертолета будет * км/ч. Тогда
расстояние между городами можно записать как 5,5(* + 10) км при попут­
ном ветре и как 6(* - 10) км при встречном. Получаем уравнение:
6(* - 10) = 5,5(* + 10); 6* - 60 = 5,5* + 55; 6* - 5,5* = 55 4- 60;
0,5* —115; * = 230. 230 км/ч. — собственная скорость вертолета. Тогда
расстояние между городами будет составлять 6(230 - 10) = 1320 км.
Ответ: 230 км/ч., 1320 км.
Найдем: значения выражений 1239—1240.
1239.а) Г 2 | - 2 | - 0 ,з ) :6 ;
і) 21 - 2 * = 2 « - 2 * Л ; 2) --0,3 = - - — = ^ — ^ = —
4 8 8 8 8 8 8 10 40 40
3 „ 3 1 3 1 1 Л 1
3) — : 6 = ------- ~ -------- —— . Ответ: — .
40 40 6 40 -6 80 80
1) 5 — -2 ,3 6 = 5 — - 2 — = 5 — - 2 — = 3;
25 25 100 25 25
2) 3 —+ 0,2 = 3,8 + 0,2 = 4; 3 ) 3 : 4 = 0,75.
5
Ответ: 0,75.
1240. а) 13 ^ : 1 - -0 ,7 5 ]: 1^ + 0,75;
V 4 4 ) 2
1) 3 | :1 7 = Т : 1 = Т Г т т = ^ 2 )3 - 0,75 = 2,25;4 4 4 4 4 5 4 -5
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

237. 3) 2 , 2 5 : 1 - = 2 ,2 5 :1 ,5 = 1,5; 4 )1 ,5 + 0,75 = 2,25.
2
Ответ: 2,25.
6) 1 2 , 5 - 2 i - f 4 , 1 2 8 - 3 | j : | ;
1) 4,128 - 3 - = 4,128 - 3,75 = 0,378; 2 )0 ,3 7 8 :^ = 0,378 : 0,4 = 0,945;
4 5
3) 1 2 ,5 -2 - = 12,5-2,25 = 28,125; 4)28,125 - 0,945 = 27,18.
4
Ответ: 27,18.
1241. Найдем значение выражения, заменив данным значением переменную:
„ л г 1 л ГIV ( IV « 1 .. 1 1 4 3а) 9х4 - 4х2, если * = —; 9 — “ 4 — =9* — - 4 * —= --------—“ х«
8 3 и ; и ; 81 9 9 9 9
Ответ: — .
9
б) 10а2 + 125а3, если а = -0 ,2 ;
10 * (-0,2)2 + 125 •(—0,2)3 - 10 * 0,04 + 125 * (-0,008) - 0,4 - 1 - -0 ,6 .
Ответ: -0 ,6 .
Выполним умножение многочленов 1242—1243.
1242. а) 5а2Ь -—аЬ3 *Зс4 = 5 •—•3 *а2+1+1 *Ь1+3 -с4 = 9а*Ъ*сА—9(аЬс)*;
5 5
б) - 8 * * (-2,5)&2 * 0,1а* - -8 *(-2,5) *ОДаЪ2х2у - 2 аЪ2х2у.
1243. а) 4рд2 •0,15рг2 * 5рдг « 4 * 0,15 * 5р1+1+У +1 •22+1 = 3р 3г3 = 3(д а)3;
5 2 I А I I I I АI I |Л1+1 ^2+2+1 .Л+1б) - 1 - а *
(-j “ v)■(-2f^ )= - у Н ) •( - Ї У " ■* zt2+l ’ у'
1 2 * 1*21 2 5 2 3 2 5 2
а х у - - - а х 5у2,
7*3*8 47 2
1244. Возведем в степень многочлены:
а) (2*3)5 = 32*15; б) (-ху)7 = ~ * У ;
в) (-За)4 - (—3)4а4 - 81а4; г) (0 ,5 т 2)3 = 0,53( т 2)3 = 0Д25т®.
1245. а) Зхп * 4х2ут= 12*”+2ут; б) —ап+1 *6ап~2 = —*6ап+1+л~2 = 4а2" 1.
3 3
Выполним действия сложения и вычитания многочленов*
1246. а) (п3 + т2п) + (т2п - пэ —4) —пв + т2п + т2п —п3 —4 = 2m2n
б) Q & - 2,6z2 + z3 + 2,3z3 + - 2 - 3,3z3 - 2,6z2 + z;
v 2 З 2 л 1 3 2 2 i ^ 2 З 2 2 З 2
в) — т х т x + 2 —m x m * - 1 —* = — т х т х ~
3 5 3 5 2 5 5
- 1- х 2+ ( 2—- —lm * = mz*z mz* - l —*z + 1—m*.
2 ( 3 3 ) 5 5 2 3
1247. a) 6*3 —2*5 + * - (8*3 -f З*5- 4*2) = 6*3 - 2*5 + * —8*3 —3*5 + 4*2 —
= -5 * 5 - 2*3 -f- 4*2 + *;
б) 3a2 + 2at> - b2- (2b2- 2a2) = 3a2 + 2ab - b2- 2b2 + 2a2 = 5a2- 3b2+ 2ab;
в) m2+ 5m - 1 2 - (3m4+ mz~ 12) = m2+ 5m - 1 2 - 3m4- m2+ 12 = -3m 4+ 5m;
r) - x 2y2 + 4* - 3x2y - 8 - (2 - 3xy2- x2y2 + y) —- x 2y2+ 4* - 3x2y - 8 - 2 +
+ 3xy2 + x2y2 —y = - 3 x2y + 3xy2 - y + 4* - 10.
1248. Преобразуем выражение в многочлен стандартного вида:
а) -1 2 * 2 - (-3 * 6 + 8 - 10*2) = -1 2 *2 + 3*в - 8 + 10*2 = З*6 - 2*2 - 8;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

238. б) 9m3- 5m + (m - 6m3- 2m4) = 9m3 - + Ш~~6m3 - 2m4= -2m 4+ 3m3- 4m;
в) (-4 xy 4- 7y2) —(-8JC2) 4-(6*# —lOx2—5) = -4хц + 7y2+ 8x2 4- 6*1/ - 10x2- 5 =
= 7y2 —2x2 4- 2xi/ —5;
г) -(3b2 + 4b2c) 4- (6b2- c2b 4- b2c) - (2b2 4- 5b2c) = -362 - 4b?c + 662 - c2b 4-
4- ЬЦс - 2b2 - 5b_ç = “8b2c - c2b 4- b2. .
1249- a) 3x(2x4 - 5x + 1) = 6x6 - 15x24- 3x;
б) -5 a 2(3a2 + 4a - 2) - -15û4 - 20a3 + 10a2;
в) (-a b 4- 2a2 - 3b2) •(-a 2b) = a3b2 - ?a4b + 3a2b3;
r) (4x2y - 3xi/2 4- 5) * 2xy = 8x3#2 - бх2#3 4- 10xi/;
д) -0,25(2m 2 - 4m + 6) —-0,5m 2 4- m - 1,5;
е) (—10n5 —6n3 + 2) * (—1,5m) = 15mn5 4- 9m/i3 - 3m.
1250. a) -12x3 - { - X + - X * - - ] = -2 x “ - Sx* + 9;
V6 3 4 )
б) lOx# * (-0 ,7 л* 4- 3,2y2 —x2y2) = - 7 x4y 4- 32xy3 - 10x?y9;
ч 3 2 Л 2 5 2 1 ^
в) — ax - 5 a x a x -ь—a| =
5 ^ 6 2 )
3 2 e* 2 3 £( 5^ 2 3 2 1
= — ax -5ax — ax • — a x - —a r - - a =
5 5 V 6y 5 2
= 3a2x4 + ~ a 3x3 - — a2x2;
2 10
r) 0,5i f * (-0,8x# 4- l,2 x 3 4- 7x2#) = 0,5 * (-0,8)#« * xy 4- 0,5 •1,2 ? y* * x3 4-
4- 0,5 * 7j/6 ? x 2# = -0,4x#7 4- О»бх3!/6 4- 3,5x2|/7.
1251. Преобразуем выражение в многочлен стандартного вида, для этого
раскроем скобки и упростим выражение:
а) (5х(х + 4) - х(6 - 2х2) = 5х2 + 20 - 6х + 2х3 = 2хэ 4- 5х2 - 6х + 20;
б) ~уЧ2у - 6) 4- 4у(у2 - у) =-2 у*+ 6у2 4- 4у* - 4у2 = 2yz + 2у2
в) 6a2b3 - b2(5a2b + b2- 1) = 6а2Ь3 - 5а2Ьэ - Ь4 4- Ьг = а2Ь3 - Ь4 4- Ь2;
г) Зх#(2 - 4х2у 4- ху2) - 7ху = 6ху - 1 2 х3#24- Зх2!/3- 7х# —-12х3г/24- Зх2#3- xt/.
1252. Докажем тождество:
а) х(у - г) + i/(z - х) - z(y - х).
Преобразуем левую часть: х{у —z) 4- y{z - х) = ху - xz + yz - ху *=yz - xz;
преобразуем правую часть: z{y —х) = yz —xz. Выражения в левой и правой
частях равны yz - xz = yz - xz, поэтому равенство является тождеством.
б) х(у 4- z - yz) - у{х + z - xz) = z(x - у).
x(i/ 4- z - #z) - у{х 4- z - xz) —х# 4- xz —xyz - ух - yz + xyz —xz - #z.
Левая часть: z(x —i/) = xz —yz. Выражения в левой и правой частях равны
xz - уz —xz —ух, поэтому равенство является тождеством.
в) ab(a 4- b 4- с) - b2(a - с) = Ьс(а 4- b 4- с) - Ь(с2 - а2).
ab(a 4-b 4-с) - Ь2(а - с) = а26 4-ab2 4-abc - ab2+ Ь2с = а2Ь 4-abc 4-b2c.
Левая часть: ab(a 4 Ь 4 с) - Ь2(а - с) —а 2Ь 4-ab2 4-abc - ab2 4-b2c = a2b 4-
4-abc 4-b2c. Правая часть: bc{a + b 4-c) - b(c2 - a2) = abc + b2c 4-bc2 - bc2 4-
4-a 2b — abc 4-b2c + a2b = a26 + abc 4 b2c.
Левая и правая части равны, поэтому равенство является тождеством.
г) ab(b + с) - bc(a 4* b) 4- ac(a + с) = a(b2 4- с2) 4- c(a2 - Ь2).
Левая часть: ab(b 4 с) - bc{a + b) 4- ac(a 4- с) ** ab2 4- abc —abc - b2c -l- a2c 4-
4- ac2= ab2—b2c 4*a2c + ac2. Правая часть: a(b2+ с2) + c(à2- b2) 4- c(a2- b2) =
= ab2 4- ac2 + a2c - b2c = ab2 - b2c 4- a2c + ac2.
Левая и правая части равны, поэтому равенство является тождеством.
1253. Умножим выражения, воспользовавшись формулами сокращенного
умножения:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

239. а) (-2 а - Ь) •(-2о + Ь) - (-2 а 2 - 1>2 = 4а2 - Ь2;
б) (-х 2 + у3) ■(х2 - у3) = (~х2)2 - (у3)2 = х 4 - уе;
в) (—abc + 1) •(abc + 1) = (1 —abc)(l + abc) = l z —(abc)2 = 1 —а2Ь2с2;
г) (-0.2*4- x ) - ( x - 0,2x4) = (-0.2X4- xX-0,2*4+ *) = (-0,2х*У - зс2- 0,04*» - ж2;
д) (а + b + с) •(о —b - с) = (а + (Ь + е)(а —(Ь + с)) = а2 —(Ъ + с)2;
е) (х + у - г) - (х - у + г) = (х + (у - г)(х ~ (у - г)) = х2 - (у - г)2.
1254. Умножим выражения, воспользовавшись формулами сокращенного
умножения, и представим произведение в виде многочлена:
а) (4 - *)(4 + *)(16 + л:2) = (16 - *2)(16 + х2) = 162 - (*2)2 = 256 - х4;
б) (а2- 5 ЬХа2+ 5ЬХа4+ 25b2) = (й4- 25Ь2Ка4+ 2562) = (о4)2-(2 5 V f = а8-62564;
в) (0,09х6 + xV K0.8x* - ху*Х0,3х3+ ху2) = (0,09*е + *V )((0,3jc3)2- (ху2)2)
= (0,09зс« + xVM 0,09x6 - * V ) = (0,09je6)2 - (*У )* - 0,0081х12 - * У ;
г) ( a V + i c 2J 0 c + с - a V j = ^a4b4 + c ^ ~ c 2 - a 4b4J =
8l8f i e 2 + a v j f ^ c 2 - a4«.4! = A C4 - 0вь
1255.а)(2*-ЗХ 2х+ЗХ 4*г+ 9) + 8 1 = (4 г!-9Х4ж2+ 9) + 81 = 16*4-8 1 + 8 1 = 16*4;
б) (5 + хб)(5 - аг5)(лс10+ 25) + х20 = (25 - * 10)(*10 + 25) + х20 =
= (25 - ж‘“)(25 + х10) + х20 = 625 - х20 + х 2° - 625;
в) 256а4 - (4а - Ь3)(4а + У»)(16а2 + Ь6) = 256а4 - (16а2 - 66)(16а2 + Ь6) =
= 256а4 - (256а4 - Ь12) - 256а4 - 256а4 + Ь12 = Ь12;
г) (0Д 1,2)4 + ( - * - 0,1у2)(-х + 0Ду2)(0,01^ + х2) = 0,0001у6 + ((-я)2 -
- (0,1у2)г)(0,01у4 + х2) = 0,0001у* + (х2 - 0,01у4)(х2 + 0,01 у4) =
= 0,0011/« + х4 - 0,001у® - х4.
1256. Представим двучлен в виде произведения, разложив его на множители
с помощью формул сокращенного умножения:
а) р2 - я2 = (р - <7)(р + Я); б) 25 - 0 ,2 5 т 2 = (5 - 0,5т)(5 + 0,5т );
в) 9х2 - а4 = (Зх - а 2)(3х + а2); г) 0,04*« - 1 = (0,2л3 - 1)(0,2*3 + 1);
д) ~х2ул + а6Ь8 = а€Ь8 - х2у4 —(аэЬ4 - ху2)(аэЬ4 + ху2);
е) а2Ь2с2 - 121л:6 = (абс - 11з^)(аЬс + 11л:3);
з) -6 4 + 3 6 т 4л2 = 36тлп2 - 64 —(6т2п —8)(6т2п + 8);
и) а2 - (6 + с)2 = (а - (Ь + с))(а + Ь + с) = (а - Ь - с)(а + Ь + с).
1257. Вычислим, воспользовавшись формулой разности квадратов:
а) 242 - 142 = (24 - 14) *(24 + 14) = 10 - 38 = 380;
б) 622 - 382 = (62 - 38) •(62 + 38) = 24 - 100 - 2400;
в) 982 - 972 - 982 - 972 = (98 - 97) * (98 + 97) = 195;
г) 52,52 - 48,52 - (52,5 - 48,5) *(52,5 + 48,5) = 4 * 101 = 404;
д) 14,32 - 4,32 - (14,3 - 4,3) •(14,3 + 4,3) = 10 •18,6 = 186;
е) 5,92 - 5,22 = (5,9 - 5,2) * (5,9 + 5,2) = 0,7 * 11,1 - 7,77;
•* Н Н 2й Ч ^ - 4 И Ф 2й ’ 55 “ ' “ т - 6 3 ! -
1258. Воспользуемся формулой квадрата двучлена:
а) (0,4с2- 5а5)2- 0,16а4- 2 *0,4 *5а2*аЪ + 25а2Ь2= 0,16а4- 4а?Ь + 25а2Ь2;
б) (6,5ху + ву2)2= 42,25*2у2+ 2 •6,5 *8ху *у2+ 64^ = 42,25х?у2+104ху* + 64у4;
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

240. в) (* V - l)2 = * У - 2x2y2 + 1;
r) (2 + aeb * f = 4 + 4aeb* + a l2b".
1259. a) (-X + i/2)2 = (-jc)2 —2xy2 + y* = x2 - 2xy2 + у*;
б) (-2 a 2 + 3y3f = (-2 o2)2 + 2 •(-2) -3 a V + (Зу3)2 = 4a4 - 12a2{/3 + 9{/e;
в) = f - | l - 2 -f - 1 J 3*5+ (3*5)2 = i + 2 *5+ 9 * 10;
r) ^ m 3 —0,2n = f-i/ n 3j - 2 - f — 0,2m 3n + (0,2ra)2 =
= —m® + 0 ,2msn + 0 ,04n2;
4
д) (-0,1*1/ + б)2= (5 - ОД*#)2= 25 - 2 •5 *ОД*# + 0,01*2#2= 25 - *# + 0,01*2#2;
е) (-6 * 2#- 0,5#)2= (-б*2#)2- 2 •(-6) *0,5*2# *#+ 0,25#2= 36*4#2+ 6 *2#2+ 0,25#2.
I I способ: (-6 * 2# —0,5#)2 = (—(6*2# + 0,5#))2 = (6*2# + 0,5#)2 = 36*4#2 +
+ 6*2#2 + 0,25#2.
1260. a) (3* - 5#)2 - 3*(3* - 10#) = 9*2 - 30*# + 25#2 - 9*2 + 30*# = 25#2;
б) 8a(b —2a) + (4a + b)2 —8ab —16a2 + 16a2 + 8ab + b2 = b2 + 16ab;
в) (4* + #)(3* + 4#) —(2# + 3*)2= 12*2 + 16*# + 3*# + 4#2- (4#2+ 12*# +
+ 9*2) = 12*24. iQxy + 4#2- 4#2- 12*#2- Э*2=3*2+ 19*# - 12*#2= 3x2+ 7*#;
r) (3c + 6b)2- (2a + 9b)(3a + 4b) = 9a2+ 36ab + 36b2- (6a2+ 8ab + 27ab +
+ 36b2) = 9a2+ 36ab + 36b2 - 6a2- 27ab - 8ab - 36b2 —3a2+ ab.
1261. Докажем, что значение выражения от * не зависит (1261-1262):
а) (2* - 5#)2 + 4*(5# - * ) = 4*2 - 20*# + 25#2 + 20*# - 4*2 = 25#2; значе­
ние выражения от * не зависит;
б) 3*(12* - 4#) - (6* - #)2= 36*2- 12*# - (36*2- 12*# + #2) = 36*2- 12*# -
- 36*2 + 12*# - #2 = -#2; значение выражения от * не зависит.
1262. а) (4* + 5#)2 - 8(2* - #)(* + 3#) = 1 6 * 2 + 40*# + 25#2 - 8(2*2 + 6*# -
- *# - З#2) — 16*2 + 40*# + 25#2 - lè * 2 - 40*# + 24#2 = 49#2; значение
выражения от * не зависит;
б) 4(* - 6#)(* - 3#) - (2* - 9#)2 = 4(*2 - 3*# - 6*# + 18#2) - (4*г - 36*# +
+ 81#2) = 4*2 - 36*# + 72#2 - 4*2 + 36*# - 81#2 —-9#2; значение выраже­
ния от * не зависит.
Воспользуемся формулой куба двучлена;
1263. а) (* + З)2 - * 3 + 3 * * 2 * 3 + 3 * * * З2 + Зэ - х3 + 9*2 + 27* + 27;
б) (# - 2)2 = #3 - З#2 •2 + 3# * 22 - 23 = #3- 6#2 + 12# - 8;
в) (2* — I)3 = 8*3—3 * 4*2 *1 + 3 - 2* * I 2 - I3 = 8*3 —12*2 + 6* - 1;
г) (3* + I)3 = 27*3 + 3 * 9*2 * 1 + 3 * 3* •I 2 + I3 - 27*3 + 27*2 + 9* +
д) (т —2п)3 = т3 —3т2 - 2п + 3т - 4п2 —8п3 —та ~ 6т2п + 1 2 т « 2 —8п3;
е) (2a + З)3 —8а3+ 3 •4а2 *3 + 3 * 2а * 9 + 27 = 8а3 + 36а2 + 54а + 27.
Разложим на множители многочлены.
1264. а) * э + * 2# + 2*2 + 2*# = * 2(* + #) + 2*(* + #) —*(* + #)(* + 2);
б) а3с2 —а2с2 + а3 - a2 = а2с2(а —1) + а2(а - 1) = а2(а —1)(с2 + 1);
в) 4*# + 12*2# - 4* - 12*2= 4*# - 4* + 12*2# - 12*2= 4*(# - 1 ) + 12*2(# - 1 ) —
= 4*(# - 1)(1 - 3*);
г) 6а2Ь - 18а2 - ЗаЬ + 9а = 6а2(Ь - 3) - За(Ь - 3) = За(Ь - 3)(2а - 1);
д) xyz - 4xz - 5*# + 20* = xz(y - 4) - 5*(# - 4) —* (# - 4)(z - 5);
е) 4ab + 3ac - abc - 12a —4ab - abc + 3ac - 12a = ab(4 - c) + 3a(c - 4) =
= a(4 - c)(b - 3).
1265. a) a2 - b2 - a + b —(a - b)(a + b) - (a - b) = (a - b)(a + b - 1);
6) * + # + * 2 - #2 = (* + #) + (* - #)(* + #) = (* + #)(1 + * —#);
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

241. в) 4а2 - 9 - 2а - 3 = (2а - 3)(2а + 3) - (2а + 3) = (2а + 3)(2а ~ 3 - 1) =
= (2а + 3)(2а - 4);
г) 5 —Зле + 25 —9х2 = (5 - 3*) 4- (5 - Зх)(5 + 3*) - (5 - Зх)(1 + 5 + Зх) =
- (5 - Зх)(6 + Зх).
1266. а) х2 - 2ху + у2 - z2 = (х - у)2 - г2 —(х - у - z)(x - у + z);
б) а1 + 2а + 1 - Ьг - (а + I)2 - Ь2 = (а + 1 - Ь)(а + 1 + 6);
в) х2 - у2 + 8у - 16 —х1 - (у2 - 8у + 16) = х2 - {у - 4)2 = (х - (у - 4))(х +
+ у ~ 4) = ( х - у + 4)(х + I/ - 4);
г) а г - Ъ 2~ 14Ь - 49 - а2 - (Ь2 + 146 + 49) - а2 - (Ь + 7)2- (а - (6 + 7))(а +
+ 6 + 7 ) = ( а - 6 - 7)(а + 6 + 7).
1267. а) аЬ2- 4а - Ъ* + 4b —ab2- Ь3- 4а + 46 = 62(а -~Ъ)~ 4(а - Ь) —(а - Ь)(Ь2 -
- 4) - (а - 6)(6 - 2)(Ь + 2);
б) х3 + х2# - 9х - 9у = х2(х + у) - 9(х + у) = (х + i/)(x2 - 9) = (х + у)(х -
- 3)(х + 3);
в) х 2а + За2 - а3 - Зх2 = х2а - а3 + За2 - Зх2= а(х2- а2) - 3(х2 - а2) = (х2-
- а2)(а - 3) = ( х а ) ( х + а)(а - 3);
г) х3 - 5Ь2 + 5х2- хЬ2 = х3 - xb2 + 5х2 - ЬЬ2 =х(х2 - b2) + 5(х2 - 62) —(х2 -
- Ь2)(х + 5) = (х - Ь)(х + 6)(х + 5).
1268. а) а2х2- 2аЪх2+ 2аЬ + Ь2х2- а2- Ь 2—а2х2- 2аЬх2+ Ь2х - (а2- 2аЬ + Ь2) —
- х2(а2 - 2аЬ + 62) - (а ~ 6)2 = х 2(а - Ь)2 - (а - 6)2 - (а - Ь)2(х2 - 1) -
= (а - Ь)2(х - 1)(х + 1);
б) а2х2 - 4Ь2х + 462 + 4а2 - 4а2х + Ь2х + Ь2х2 = а2х2 + 62х2 - 4Ь2х —4а2х +
+ 4а2 + 4Ъ2 = х2(а2 + Ь2) - 4х(а2 + Ь2) + 4(а2 + Ь2) = (а2 + 62)(х2 - 4х + 4) -
= (а2 + 62)(х - 2)2.
1269. а) а2- Ь2+ х2- у2+ 2ах + 2Ъу = а2 + 2ах + х2- Ь2+ 2Ьу - у2* (а + х)2-
- (Ь - у)2 ==(а + х - (6 - #))(а + х + Ь - #) = (а + х - Ь + j/)(a + х + Ъ - у);
б) х4 + у4 - х2 - у2 + 2х2у2 - 2ху —х4 + 2х2у2 + у* - х2 —2xi/ - у2 —(х2 +
+ у2)2 - (х2 + 2ху + у2) = (х2 + у2)2 - (х + у)2 —(х2 + у2 - (х + у))(х2 + у2 +
+ X + I/) = (х2 + у2 - х - у)(х2 + у2 + X + у).
Докажем равенства:
1270. а) 1452- 1442= 172. Левая часть: 1452- 1442= (145 - 144) *(145 + 144) -
= 1 * 289 = 289; правая часть: 172 —289. Левая часть равняется правой.
б) 2212 - 2202= 212. Левая часть: 2212- 2202= (221 - 220) •(221 + 220) =
= 441 * 1 ■=441; правая часть: 212 = 441. Левая часть равняется правой.
в) 3132- 3122= 242+ 72. Левая часть: 3132- 3122- (313 - 312)»(313 + 312) =
= 1 * 625 = 625; правая часть: 242 + 72 = 576 + 49 = 625. Левая часть ра­
вняется правой.
г) 8412 - 8402 = 402 + 92.
Левая часть: 8412 - 8402 = (841 - 840) * (841 + 840) = 1 * 1681 = 1681;
правая часть: 402 + 92 = 1600 + 81 = 1681. Левая часть равняется правой.
Используем формулу разности квадратов в упражнениях 1271—1272.
-J271 472 —412 _ (47 —41) -(47 + 41) _ 6 88
282 - 162 (2 8 -1 6 ) (28 + 16) 12 44 9
572 - 422 = (57 - 42) -(57 + 42) 15 -99 =
292 - 2 6 2 ” (2 9 -2 6 ) (29 + 26) ” 3 55 “ ’
512 - 122 (5 1 -1 2 ) (51 ч-12) 39-63 273.
902 - 92 (90 - 9) *(90 + 9) ~ 81 *99 891’
612 -1 1 2 _ (61 -1 1 ) (61 + 11) 50 72 5
362 - 242 ~ (36 - 24) *(36 + 24) ~ 12 60 "
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

242. 1272. а) 632*432- (2416- 5) •(2416+ 5) - (6 *4)32- (2432- 25) = 2432- 2432+ 25 = 25;
б) (5610- 7 ) * (56ю+ 7 ) - 7 20-820= 5620- 7 2-(7 *8 )20= 5620- 72- 5620= -7 2= -49;
в) 418 * 91в+ (4 - 369)(369 + 4) - (4 *9)18 + (4 - 369) *(4 + 369) = 3618+ 42 -
- 3618 = 42= 16,
Решим уравнение 1273—1274, приведя левую часть уравнения к произве­
дению множителей, а правую — к нулю.
1273. а) 5*5 - * 4 = 0; х*(5х - 1) = 0; откуда: х4 = 0; х = 0;
или 5х —1 = 0; 5х = 1; х * 1 : 5; х = —. Ответ: 0; —.
5 5
б) З*3 - 12* = 0; 3*(*2- 4) = 0; 3*(* - 2)(* + 2) - 0; откуда:
Зх —0; * —0; или * - 2 —0; * = 2; или х + 2 = 0; х = -2 . Ответ: -2 ; 0; 2.
в) 10*6 = З*5; 10*6 - З*5 = 0; * 5(10х - 3) = 0; откуда: * 5 = 0; * = 0;
или 10* - 3 = 0; 10* —3; * = 3 : 10; * = 0,3. Ответ: 0; 0*3.
1274. а) * 3 + 4*2 - * = 4; *3 + 4*2 - * —4 = 0; *2(* + 4) - (* + 4) = 0; (* +
+ 4)(*2 - 1) = 0; (* + 4)(* - 1)(* + 1) * 0; откуда:
* + 4 = 0; * —-4 ; или * - 1 = 0; * = 1; или * + 1 = 0 ; * = —1.
Ответ: -4 ; -1 ; 1.
б) х3 - З*2 + 2* = 6; х3 - Зх2 + 2* - 6 = 0; * 2(* - 3) + 2(* - 3) =0;
(* - 3)(*2 + 2) = 0; откуда: * - 3 = 0; * = 3. Замечание: * 2+ 2 > 0.
Ответ: * = 3.
в) 2*3 + * 2 —8* = 4; 2*3 + * 2 - 8* - 4 = 0; * 2(2* + 1) —4(2* + 1) = 0;
(2* + 1)(*2 - 4) —0; (2* + 1)(* - 2)(* + 2) = 0; откуда:
2* + 1 = 0; 2* * -1 ; * = - 1 : 2 ; * = -0 ,5 .
или * - 2 = 0; * = 2; или * + 2 * 0; * = -2 . Ответ: -2 ; -0 ,5 ; 2.
г) 12*3 - 8*2 - 3* = -2 ; 12*3 - 8*2 - 3* + 2 - 0; 4 *2(3* - 2) - (3* - 2) = 0;
(3* - 2)(4*2 - 1)= 0; (3* - 2)(2* - 1)(2* + 1) = 0; откуда:
3* —2 = 0; 3* =*2; или 2* - 1 = 0; 2* —1; или 2* + 1 = 0; 2* = —1;
2 1 1 Л 1 1 2
* = - ; * = —; * = - —. Ответ: ; —-
3 2 2 2 2 3
1275. Зададим формулой функцию: ^
а) у *= * + 4; б) у = * - 9; в) у = Зх; г) у = - * ;. д) у = - .
*
1276. Учитывая, что объем прямоугольного параллелепипеда считается по
72 12
формуле V = д&с, составим уравнение: Gab —72; откуда 6 = — ; 6 = —■.
^2 а
Ответ: b = — .
а
1277. Если первый угол равняется а, то второй — 2а. Учитывая, что сумма
углов треугольника 180°, составим уравнение, обозначив третий угол как
* градусов: а + 2а + * = 180; За + * = 180; * = 180 - За.
Ответ: х = 180 - За.
1278. Если на одну рубашку нужно 2,5 м ткани, то на * рубашек — 2,5* м.
Обозначим остаток ткани как у, запишем формулу для у: у = 200 - 2,5*.
Ответ: у = 200 - 2,5*.
24
1281. у - — —, для значений аргумента —6 < * < 6.
2 - х
Область определения : * Ф 2.
* -6 -5 -4 - 3 -2 -1 0 1 3 4 5 6
У 3 e i
7
4 4 —
5
6 8 12 24 -24 -1 2 -8 -6
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

243. 24
2 - (-6)
24
24
8
3;
24 24 э 3 24
2 - ( - 5 ) ~ 7 “ 7 ; 2 - ( - 4 )
24
- — = 4 - -
2 - ( —3) ~~ 5 “ 5 ; 2 - ( —2)
24
= 6:
24
24
6
24
24
2 - 0
24
2 - 4
24
2
12;
24
2 - 1 “
М = . 12; Л .
-2 2 - 5
24
— = 24;
1 2
2 - (—1)
24 24
= 4;
= 8;
24
= -8;
3 -1
24 24
= -24;
2 - 6 -4
= -6.
1284. Проанализируем график функции:
а) велосипедист выехал через 10 мин. после начала движения пешехода;
б) скорость изменялась;
в) скорость пешехода:
. 2000 , 200 , „ 2 _
I участок — и= м/мин = м/мин = 66 —м/мин;
30 3 3
II участок — пешеход сделал остановку;
5000 - 2000 , 3000 , ,
III участок — V = -------—-------м/мин = -------- м/мин = 150 м/мин;
20 20
скорость велосипедиста
3000
I участок — и
20
м/мин = 150 м/мин; II участок — остановка;
пт 5 0 0 0 -3 0 0 0 , 2000 , .
III участок — V= -------—-------м/мин = - м/мин = 100 м/мин;
г) пешеход останавливался на 10 минут; велосипедист останавливался на
5 минут;
д) расстояние между пешеходом и велосипедистом через 30 минут после
начала движения пешехода была 3000 м - 2000 м = 1000 м.
1285.
а) у = 5х; б ) у = 5 х - 1 ;
X 0 1
У 0 5
X 0 1
У -1 4
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

244. t - I "H
t 0 X
0 f ..7?.....
0 X
i f 4. X = â (в
9821
:xz - і = я (g
- 5- s - f -
— f---- 1 h
ixg = ft (a
*Z + I = «
1 - 4 -
2- 8- t' і
-j— (— ( _
X =Æ
z - 0 a
I 0 X
s - 0 a
T 0 X
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

245. Чтобы построить график, симметричный графику данной функции от­
носительно оси ординат, надо абсциссу точек, принадлежащих графику,
изменить на противоположную:
(О; 4) -> (О; 4) (О; 1) -+ (О; 1) (О;О) ->(0; 0) (0; 0) -> (0; 0)
(4; О) -» (-4 ; О) (1 ;-1 )-> ( - 1 ;- 1 ) (1; 3) -> (-1 ; 3) (3; -1 ) -> (-3 ; -1).
Чтобы задать формулой функцию, график которой симметричен данной
относительно оси ординат, надо переменную х заменить на противополож-
х
ную (-*): у = - х + 4; у = 1 + 2х; у —-В х; х = —..
и
1287. Чтобы задать формулой линейную функцию у = Их + 6, график которой
проходит через точкиЛ^х^ ук) и В(х2; у^), надо найти угловой коэффициент
X —X
к по формуле Дг= —1 Чтобы найти число Ъ в уравнении у = Их + 6,
У1-У 2
у и х заменим на соответствующие координаты одной из точек А и Б Д —
найденным значением.
а) А(3; 2) и В (-5; 4); к = 3 ~ (~5 ); * = ; к - -4 ;
2 = —4 * 3 + Ь; -6 = -1 2 - 2; -6 = -1 4 ; Ъ —14. Ответ: у —-4 х + 14.
б )А (-Д ;-6 )и В (1 ;6 ); Л= Л= ^ г ; к = -,
—О — О — О
б = —*1 + 6; -6 = ^ - 6 ; -6 = - 5 —; 6 = 5 —. Ответ: у - х + 5 ^ .
6 6 6 6 * 6 6
в) Л(—2; 1) и В(1; —2); Де=1~2 ~ ^ ; * = ^ ; * = 1;
1 —(“^) о
1 = 1* (-2) + 6; —6 = —2 —1; -6 = —3; 6 = 3. Ответ: у = х + 3.
гМ (-1: 5 )и В (3 ;-3 ); к = * = * = — ; б = -£ -(-1 > + *
. э — ( - о ) о 2 ^
-6 = —“ 5; -6 = - 4 —; 6 = 4 —. Ответ: у = - —х + 4 ^ .
2 2 2 * 2 2
1288. Чтобы построить график уравнения, надо из уравнения выразить у
через х и построить график линейной зависимости.
а) х + у —4; I/ = х - 4; б) 2х + у = 6; у = 6 - 2х;
X 0 3 -
У 6 0
X 0 4
У 4 0
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

246. в) —3 * + 2у —5;
2у = 5 + Зх; у =
X 1 -1
У 4 1
г) - х - Чу = 7;
выразим л: через £/:
- х = 7 + 7у; х = -7 - Чу.
Составим таблицу:
X 2 -1
У -3 2
Зх + 2у =5
X -7 0
У 0 -1
1291. Выразим в каждом из уравнений Зх - 2у —12 и 5х + Зу = 1 у через
х, составим таблицу значений х к у для построения графиков функций.
В одной системе координат построим графики функций, найдем коорди­
наты точек их пересечения. Проверим, удовлетворяют ли координаты
найденной точки каждому из данных уравнений.
Зх —2у = 12;
—2у — 12 - Зх;
у = (12 - Зх) : (-2);
# = - 6 + 1,5х;
X 4 0
У 0 -6
5х + Зу —1;
Зу = 1 - 5х;
1 - 5 х
9 - — ;
Обозначим точку пересечения прямых Л: -А(2; -3 ). Проверим, является ли
пара чисел (2; -3 ) решением данных уравнений:
1) 3х - 2 у —12;
левая часть: 3 * 2 - 2 * (-3) = 6 + 6 = 12; правая часть: 12.
Значит, 12 = 12, пара чисел является решением уравнения.
2) 5х + Зу = 1;
левая часть: 5 * 2 + 3 - (-3) = 10 - 9 = 1; правая часть: 1.
Значит, 1 —1, пара чисел является решением уравнения.
Решим системы уравнений 1292—1297.
См. объяснение к упражнениям 1082—1106 и 1116—1117.
1 2 Ю .» ( 2* + 1' “ 1Ч 5 М ° * + 5У = 60=
[Зх - Ьу = 5; | [ Зх - Ьу = 5;
13х = 65; х = 65 :13; х = 5.
Подставим х = 5 в уравнение 2х + у —12:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

247. б)
2 * 5 + 1/ = 12; 10 + у = 12; у = 12 - 10; у = 2.
Ответ: (5; 2).
ас-4 # = 11, Г* = 11 + 4у,
3* + 2у = 5; [З* + 2# = 5;
3 •(11 + 4у) + 2у —5; 33 + 12у + 2у = 5; 14у = 5
14у = -2 8 ; у = -2 8 ; 14; у = -2 .
Найдем х: х = 11 + 4 * (-2); * = 11 - 8; х = 3.
Ответ: (3; ~2).
12* - 8г = 10,
33;
| б * -4 г = 5, -2 Г
|4х - 1 ,5г = 1; (-3) [ -12* + 4,52 —-3;
- 3,52 = 7; 2 = 7 : (-3,5); 2 = -2 .
Найдем *: 4* - 1,5 *(-2) = 1; 4* + 3 = 1; 4* = 1 - 3; 4* = -2 ;
* = —2 : 4 ; * - — Ответ:
2 Н ! - 2)
- е
2* - 3у - -3,
3* = 18; * = 18 : 3; * = 6.
+ 3у = 21;
2 *6 —Зу = —3; 12 - Зу = -3 ; -3 у = -3 - 12; -Зу = -1 5 ; у = -1 5 : (-3); у = 5.
Ответ: (6; 5).
1293. а)
{
2* - 3(* - у) =
5 у - 2 (* - 2 у )
=7, 2х - 3* + Зу = 7, Г-* +
= 23; |5у - 2* + 4у = 23; |9у —
+ Зу = 7,
2* = 23;
Г-* = 7 -З у , Г*
|9у —2* = 23; [9|
7 + Зу,
2* = 23; |9у - 2* = 23;
9у - 2(-7 + Зу) = 23; 9у + 14 - 6у = 23; Зу = 23 - 14; Зу = 9; у = 9 : 3; у = 3.
Найдем * из уравнения * = -7 + Зу: * = -7 + 3 * 3; * = -7 + 9; * = 2.
Ответ: (2; 3).
б)
4у - 5(1/ - ж) = 8; |4{/ -
}2(3х - у ) + 7у = -14; [6а:-
- 5у +5х =
2у + 7у
= 8; Г
= -14; }
-у + 5* = 8;
6* + 5у = -14;
Г-у = 8 - 5*; Г
[б* + 5у - -14; [
у = -8 + 5*;
6* + 5у = -14;
14: 6* - 40 + 2Ъх = -1 4 : 31*6* + 5(-8 + 5*) =
26
* = — . Найдем у из уравнения у
31
-8 + 5*: у = -8 + 5 *——;
У 31
14 + 40; 31* = 26;
26
У
248 + 130
31
У =
118
31
у = -3 * > . Ответ
у 31
|0,5* + 0,3у = 8;
В) [1,2* - 0 ,5у = 7;
0,5 * 10 + 0,3у = 8;
5 + 0,3у = 8;
0,3у = 8 - 5 ;
0,3у = 3;
у = 3 : 0,3;
Ответ: (10; 10).
: ( * ; - . * 1
1,31 3 1 ;
Г 2,5* + 1,5у = 400,
|+3 ,6 * -1 ,5 у = 21;
6,1* = 61;
* = 6 1:6,1;
* = 10.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

248. г)
Г1,4х - 2 ,Ъу = 39; -4 Г 5,
1о, 8х - 1 ,3 у = 21; (-7) (+ -5 ,
1294. а)
Зу = 21;
1,4х - 2,5 - (-10) = 39;
1,4х + 25 - 39;
1,4л: - 39 - 25;
1,4л: = 14;
х — 10.
Ответ: (10; -10).
4
5
2
- 2,51/ = 39; 6* -101/ = 156;
,6л: + 9,11/ = -147;
- 0,91/ = 9;
у = 9 : (-0,9);
У = -ю .
х - у = 7;
х + —ы= 11;
3 5
~ х - I/ = 7;
5
10
х + у = 55;
^ х + — х ~ 62; — х = 62; х = 6 2 : ^ ; х=?15»
5 3 15 15
4
— 15 —г/ =-7; 12 - у —7; -у = 7 - 12; —у —-5 ; у = 5. Ответ: (15.; 5).
б)
[з 3
—х - 2= 15; . . . —
7 7
2 3
—х н— г = 14;
5 7
— х + —х = 14 + ,
49 5 7 245
_9_ 3 _ 45
4 9 Х 7 2 ~ 7
2 3 и
—х + —2 - 14;
5 7
45 45 + 98 98 + 45 143
х =
245
х =
143
: 143;
х
245 7
; 7х = 245; х = 35.
3 3
Найдем 2из уравнения —х - 2= 15: —*35 - г = 15;
15 - 2= 15; -2= 15 - 15; -2 = 0; 2= 0. Ответ: (35; 0).
х +I/
в)
+ х = 15;
„ у ~ х - л-—— = о;
3
5
{
х + у + Зх = 45; |4х +
5у - ( у - х ) = 30; [Ъу -
+ у = 45;
I/ + х = 30;
{
4х + у = 45; Гг/ = 45 —4х;
4у + х = 30; |4у + х = 30;
4 *(45 - 4х) + х = 30; 180 - 16х + х = 30; -1 5 х = 30 - 180;
-1 5 х = -150; х = -1 5 0 : (-15); х - 10.
Тогда у —45 —4 * 10; у = 45 —40; у —5.
О твет: (10; 5).
х - у
+ 1/ = 4;
1 / - * 9;
-2
•3
Гх ~ I/ + 2# = 8;
[Зх - (I/ - х) = 27;
+ = 8;
[Зх —у + х = 27
Г х + у = 8;
; | 4х - у - 27;
5х = 35; х = 35 : 5; х = 7.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

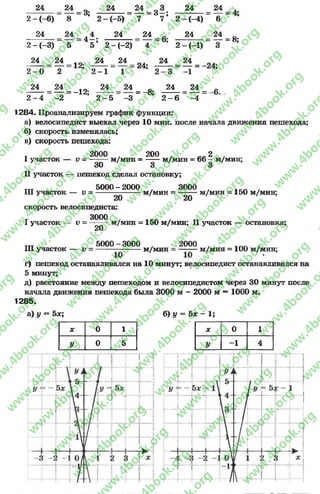
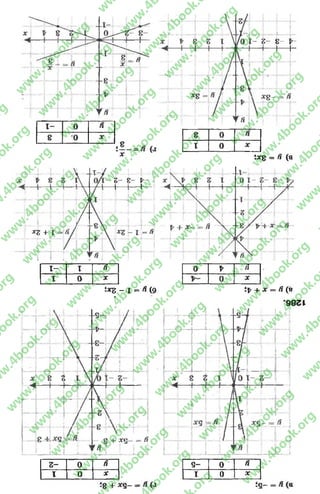
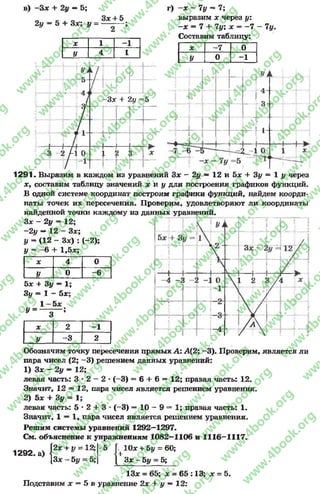
249. Найдем у из уравнения * + # = 8: # = 8 - * ; # = 8 —7; # = 1.
Ответ: (7; 1).
7 + х 2 х - у
1295. а)
20
14(7 + * )-5 (2 * - у) = 20(3у - 5);
[5# - 7 + 3(4* —3) = 6(20 - 5*);
[28 + 4* -.10* + 5# = 60# -1 0 0 ;
[5# - 7 + 12* - 9 = 120 - 30*; {
-6 * + 5# - 60# = -100 - 28;
5#+ 12*+ 30* = 120+ 16;
[-6 * - 55# = -128; I•7
[42* + 5# = 136; (
-42* - 385# = -896,
42*+ 5# = 136;
—380# ——760; # —-7 6 0 ; (-380); # 2, Найдем * из уравнения 42* + 5# = 136
42* + 5 - 2 - 136; 42* + 1 0 - 136; 42* = 136 - 10; 42* - 126;
* = 126 : 42; * = 3.
Ответ: (3; 2).
(* -# )(* + #) = 80;
+ # = 10;
( * - # ) • 10 = 80; * - # —80 : 10; * —# = 8.
Решим,равносильную систему уравнений:
X - # = 8;
У''*
хг - у2 = 80; кх
х + у = 10; ]*
{ * + # = 10;
2* = 18; 9 + # = 10;
* - 1 8 :2; у = 10 - 9;
* = 9. # = 1.
Ответ: (9; 1).
* + 4 (2 # -(* -5 )) = 36;
1296. а)
7 ^(# + 2*)
* + 4(2# - * + 5) = 36,
7^# + 2 * - i # j = 4*;
8# - 3* = 36 - 20, [8# - 3* = 16,
| » ) = 4 ч
|* + 8# - 4* + 20 = 36, Г8|
[7(0,8# + 2*) = 4*; [5,
|8# —3* = 16, |8# - 3* = 16;
1.10* = -5,6#; { * = 0,56#;
8# - 3(-0,56#) - 16; 8у + 1,68# - 16; 9,68# = 16;
16
Ю, Г;
; 16# + 14* = 4х; 114* - 4* = -5,6#;
У
9,68
-0 ,5 6
У
200
121
Ответ:
1600
968 ’ У
200
1 21’
112
; * = ------------.
121
1 200^1
’* 121 Г
б)
Г
-у = %
+ # = 8;
Рассмотрим 2 случая:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

250. х - у = Ь; 2 ) ( .
+ у = 1
2х = 13;
х —13 :2;
* = 6,5.
(6,5; 1,5)
Ответ: (6,5; 1,5); (1,5; 6,5).
5 + # Зх + 4у
6,5 + # = 8;
у = 8 - 6 , 5 ;
У= 1,5;
~У = - 5;
+ У = 8;
2х = 3;
* = 1,5;
1,5 + 1/ = 8;
у = 8 - 1 , 5 ;
у = 6,5.
(1,5; 6,5).
1297. а)
1
3
7х + 2
4
4х —3
= Зх +1:
+ — = 1 -З х ;
63 2
4(5 + у) - 3(3х + 4#) = 12(3х +
2(7х + 2) + 3(4х - 3) +11 = 6(1
-9 х —36х + 4х -12# = 12 —20;
26х + 18х = 6 - 4 + 9 - 1 1 ;
12
і); Г
- з ху, 1
ч
20 + 4# - 9х -12# = 36х +12;
14х + 4 + 12х - 9 + 11 = 6 —18х;
|-45х —8# = -8 ;
1* = 0;
Ответ; (0; 1).
■{
—45 -О—8# = -8
* = О:
- 4 5 * - 8 #
44х = О;
8# =
О:
= -8,-8, 4 5 х - 8 #
|х = О: 44;
; |#= - 8 :(-8), |#=1,
[х = 0; |х = О.
б)
7 + *
1
1
£
5 4
5 # - 7
н
1
со.
2 6
18 = -5х;
20
6
4(7 + х) - 5(2х - у ) - 60у = -100
3(5# - 7) - (3 - 4х) - 1 0 8 = -ЗОх
- 6 х - 55# = - 1 0 0 - 2 8 ,
4х + ЗОх +15# = 108 + 21 + 3;
-1 8 х -165# = -384;
374х + 165# = 1452;
28 + 4х - 10х + 5# - 60# = —100,
15# —2 1 - 3 + 4 х - 108 = -ЗОх;
Л
~6х - 55# = -128;
34х +15# = 132;
3
11
356х = 1068; х = 1068 :356; х = 3.
Найдем # из уравнения 34х + 15# —132:
34 * 3 + 15# = 132; 102 + 15# = 132; 15# = 132 - 102; 15# = 30;
# = 30 : 15; # = 2.
Ответ: (3; 2).
Решим задачи 1298—1306 сложением системы уравнений
1298. Пусть длина большей части веревки х м, а меньшей — у м. Их сумма
равняется х + # = 22. Так как первая часть на 20 % 22 м
длиннее второй, то есть составляет 120 % второй, то ее ^ ------------
длина в 1,2 раза больше, чем длина второй, то есть
х ~ 1,2#. Составим систему уравнений:
|х + # = 22;
1* = 1,2#;
* м У м
1,2# + у = 22; 2,2# = 22; у = 22 : 2,2; # = 10. * = 1,2 * 10; * = 12.
Тогда длина меньшей части 10 м, большей — 12 м.
Ответ: 10 м и 12 м.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

251. 1299. Если длину большей части обозначить за * м, а меньшей — за у м, то
х + у —22, а если меньшая часть короче большей на 20 % , то есть состав­
ляет 80 % большей, то у = 0,8*. Составим систему уравнений:
Jх + у = 22,
1# = 0,8*;
х + 0,8* = 22; 1,8* —22; * = — ; * _ 220 x _ Ü 5.; * = 12—,
1,8 18 9 9
Тогда, у = 22 - *; у = 2 2 - 1 2 ^ ; у - 9 ^ .
7 2
То есть, длинаменьшей части 9 —м, большей — 12—м.
7 2 9
Ответ: 9 — м, 12— м. *
9 9
1300. Пусть объем работы,который, делает первый мастер за 1 день, — *,
а второй — у. Вместе за 1 день они выполнят (* + у) за 1 день, а за
12 дней — всю работу 12(* + у). Если первый будет работать 4 дня, а вто­
рой — 6 дней, то они выполнят вместе 4 * + 6#, то есть 40 % , или 0,4 часть
всей работы, а именно 0,4 * 12(* + у) = 4,8(* + у). Составим уравнение:
4* + 6# = 4,8(* + у), откуда: 4* + 6у —4,8* + 4,8у;
4* - 4,8* = 4,8у ~ 6у; -0 ,8 * = -1,2у;
- 1,2 3 - 0,8 2
* = у; * = —у, а у = ------- *; у = —х.
-0 ,8 2 У -1 ,2 У 3
Чтобы найти, за сколько дней первый сделал бы всю работу, надо весь
объем работы разделить на объем работы, который делает первый мастер
2
за 1 день: 12(* + # ) : * . Заменим у на —*, тогда:
и
12(* + у ): х - 12| * + —*1 : * = 12* ( 1 + —1: * = 12-(l + ^ 1= 12 ■—= 20
(дней). V з ^ з ; К З ) з
Аналогично найдем количество дней, необходимых второму:
12(* + у ) : у = 12^| у + i/j : у = 12у +1 j : у = 1 2-1 = 30 (дней).
Ответ: 20 дней и 30 дней.
1301. Обозначим массу угля на первом складе за * т, а на втором — за у т.
Если на первом складе угля на 800 т больше, чем на втором, то * —у = 800.
Если из первого забрали 60 % угля, то на нем осталось 40 % , то есть 0,4* т;
если со второго забрали 50 % , то на нем осталось 50 % , то есть 0,5# т.
Учитывая, что на первом складе осталось на 200 т больше угля, чем на
втором, имеем: 0,4* - 0,5# = 200. Составим систему уравнений:
* —# = 800;[* - # = 800; Г
|о, 4х - 0 , 5 у = 200; -(-2) —0 ,8 * + # = —400;
0,2* = 400; х - 0 , 8 х = 800 - 400;
* = 400 : 0.2;
* = 2000.
2000 - # = 800; -у = 800 - 2000; -# = -1200; # = 1200.
На первом складе осталось 0,4* = 0,4 •2000; 0,4* = 800;
на втором — 0,5# = 0,5 * 1200 = 600.
Ответ: на первом — 800 т, на втором — 600 т.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

252. 1302. Пусть из первого сплава надо взять * т, а из второго — у т, чтобы
получить 400 т сплава, тогда х + у — 400. В первом куске содержится
0,1* т цинка, а во втором — 0,3у т, что составляет вместе (0,1* + 0,3#) т.
Это количество должно составлять 25 % , то есть 0,25 часть, всего сплава
и будет равняться 0,25 *400 т: 0,1* + 0,3# —0,25 *400. Составим систему
уравнений:
Г* + у - 400;
о,1* + 0,3# = 0,25-400;
Г*+ # = 400; -(-ОД)
[0,1* + 0,3# = 100;
Г -0 ,1 * - 0,1# = -40;
| 0,1* + 0,3# = 100;
0,2# = 60;
* = 60 : 0,2; у —300.
Тогда
* + 300 = 400;
* - 400 - 300;
* = 100.
Ответ: из первого сплава надо взять 100 т, из второго — 300 т.
1303. Пусть первого раствора взяли * г, а второго — у г, что вместе состав­
ляет 40 г: * + у —40.
Первый раствор будет содержать 0,1* г соли, а второй — 0,15# г соли, что
вместе будет (0,1* + 0,15#) г соли и будет составлять 12 %, то есть 0,12
часть раствора: 0,1* + 0,15# —0,12 *40.
Составим систему уравнений:
Г* + у = 40;
|0,1* + 0,15# = 0,12 40;
|х + # = 40;
[0,1* + 0,15# = 4,8;
(-0,1)
{
+ -0,1* —0,1#=—4,
0,1* + 0,15# = 4,8;
0,05# = 0,8;
# = 0,8 : 0,05; у —80 : 5; # = 16. Тогда: * = 40 - у; х = 40 - 16; * = 24.
Ответ: первого раствора взяли 24 г, а второго — 16 г.
1304. Пусть необходимо взять * первого сплава и # — второго сплава. В пер-
1 2 ъвом сплаве содержится одного металла — —*, а второго — —*. Во вто-
3 4 п,ром сплаве содержится одного металла — —#, а второго — —у. Тогда
(1 3 Л (2 4 )
в третьем первого металла — I—* + —# I, а второго — I—л: + у# I,
:: ^дс + | ^ :^ | д с + | И = 5 : 8 , откуда:
и эти
массы соотносятся так:
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

253. 0 Г1 3 ^ Л 2 4 А
8 —* + —у = 5 —* + —у ;
1,3 7 У) 13 7 )
8 24 10 20
—х л------у = — х + — у;
3 7 3 7 *
8 10 20 24
- — х - — У - — У1
3 3 7 * 7
— * = — у; * = — у
3 7 7 * !Н ) !
4 ( 3 } 6
х = ------ 1— ш; * = —у,
7 2) 7
Отношение (# : у) показывает, сколько частей определенного сплава надо
взять: х : у - —у : у; х : у —6 : 7.
Ответ: 6 частей первого сплава и 7 частей второго.
1305. Пусть масса первой детали х кг, второй — у кг, тогда третьей —
(250 - х - у) кг.
Если масса третьей детали на 10 кг больше, чем масса первой и второй, то
(250 —х - у) - (х + у) = 10.
Если масса второй и третьей на 110 кг больше массы первой, то
(у + 250 - х - у) - х = 110. Составим систему уравнений:
Г(250 - * —# ) - ( * + #) = 10; Г250 - х - у —х - у = 10;
(у + 250 —х —у) —х - 110; 1у + 250 - х - у —х ~ 110;
110
2 5 0 - 2х
2 5 0 - 2х
Г110 - 2 у = 10; Г-2у = 10 -1 1 0 ;
[250 - 2х = 110; -2х = 110 - 250;
Г-2# = -100; у = - 1 0 0 : (-2); [у = 50;
1-2* = -140; х = - 1 4 0 : (-2); * = 70.
Масса первой детали 70 кг, второй — 50 кг,
а третьей — 250 - * - у —250 - 70 - 50;
250 —х - у —30 (килограммов).
Ответ: 70 кг, 50 кг, 130 кг.
1306. Обозначим массу яблок в первом ящике за * кг, а во втором — за
у кг. Если в первом яблок на 2 кг больше, чем во втором,то * - у—2.
В третьем яблок на 4 кг больше, чем во втором, то есть{у + 4) кг, что
4 4
в 1 - раза меньше, чем в первом и втором вместе, то есть {х + у) :1 —.
Составим систему уравнений:
ся
11
а»
1
н
* - у = 2, х - у = 2,
4 "
# + 4 = (* + # ): 1 —; # + 4 = (* + # ) : у ; # + 4 = (* + #)
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org

254. X- у = 2; х - у = 2,
, 7 7
у + 4 = — х + ~7у;
* 11 г г
7
----- Х+ У
. 11
х - у = 2;
7 4 *------д: + — у ~ -4;
11 11*
11
* 4
х - у = 2,
+ 7
— х + у = -11;
4 *
7_
11
х — х = 2 - 1 1 ;
4
*3 3
х —1—х - -9 ; — х
4 4
= -9; * = - 9 : Г ~ 1 ; х = - 9 - Г - ^ 1 ; х = 12.
Тогда: 12 - у = 2; -у —2 - 12; -у = -1 0 ; у = 10.
у + 4 = 10 + 4; у + 4 = 14.
В первом ящике 12 кг яблок, во втором — 10 кг, в третьем — 14 кг.
Ответ: 12 кг, 10 кг, 14 кг.
rg
w
w
w
.4book.org
w
ook.org
w
w
w
.4book.org
w
w
w
.4
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.or
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4boo
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
w
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.org
w
w
.4book.org
w
w
w
.4book.org
w
w
w
.4book.o
book.org
w
w
w
.4book.org
w
w
w
.4b
.org
w
w
w
.4book.org
w
w
w
w
w
.4book.org