Учебно-методическое пособие по рациональным уравнениям предназначено для студентов 1-2 курсов и учителей, охватывает основные темы, такие как целые и дробно-рациональные уравнения, их решение и примеры задач. Пособие включает задачи различного уровня сложности и многообразие методов решения, включая графические методы и теоремы равносильности. Также рассматриваются особенности уравнений высших степеней и эффективные приемы для их решения.

1. КГУ Горно-металлургический колледж
Учебно-методическое пособие
«Рациональные уравнения»
г.Жезказган, 2015

2. Составитель:
Мишина Н.М., преподаватель математики КГУ «Горно-металлургический колледж»
Настоящий сборник создан как методическое пособие для студентов 1 -2 курсов по
математике. Учебный материал, включенный в сборник, охватывает один из самых крупных
разделов школьного курса математики «Рациональные уравнения».
Пособие призвано помочь учителям, работающим в старших классах для подготовки к
занятиям, а также может быть использован студентами 1-2 курсов для закрепления,
систематизации и расширения своих знаний по данному разделу школьного курса
математики. В сборник включены задачи различных уровней сложности.
В данном пособии рассматриваются практически большинство вопросов по данной
теме, рассматриваются основные положения теории, приводятся многочисленные примеры и
соответствующие задания с ответами.
К сожалению, охватить в одном сборнике все разнообразие задач по данной теме не
представляется возможным. Поэтому для подготовки к занятиям можно использовать задачи
из других источников.
Рассмотрено на заедании ПЦК естественно-математического цикла
Протокол № _________ «_______»______________2017 г.
Председатель ________________ Мишина Н.М.
Утверждено на заседании методического совета
Протокол № _________ «_______»______________2017 г.
Председатель ________________ Турегельдинова Р.К.

3. СОДЕРЖАНИЕ
1. Целые рациональные уравнения 3
1.1 Линейные уравнения 4
1.2 Методы решения квадратных уравнений 5
1.3 Уравнения высших степеней 7
упрощение и разложение на множители; 8
замена переменных; 10
решение симметрических и возвратных уравнений; 12
использование теоремы Безу; 15
метод неопределенных коэффициентов; 18
однородные уравнения; 20
графический метод решения. 22
1.4 Целые рациональные уравнения, содержащие знак модуля
23
1.5 Уравнения в целых числах 27
1.6 Рациональные уравнения с параметром 30
2. Дробно-рациональные уравнения
2.1 Равносильные переходы в дробно-рациональныхуравнениях
37
2.2 Замена в дробно-рациональныхуравнениях 38
2.3 Дробно-рациональные уравнения c модулем 39
2.4 Дробно-рациональные уравнения c параметром 40
3. Системы рациональных уравнений
3.1 Системы линейныхуравнений 41
3.2 Симметрические системы 47
3.3 Системы однородных уравнений 47
3.4 Системы уравнений с параметром 48
3.5 Графическое решение систем уравнений 49
4. Задачи на составление уравнений.
4.1 Задачи на проценты 51
4.2 Задачи на работу 54
4.3 Задачи на движение 56
4.4 Задачи на целочисленные значения 58
Список использованной литературы 59

4. Рациональные уравнения
Если обобщить известные нам способы решения рациональных уравнений, то мы
увидим, что в процессе решения сложного уравнения нам приходится шаг за шагом
заменять его более простым уравнением. В конце концов, мы получаем достаточно
простое уравнение и находим его корни.
В этот момент и возникает главный вопрос: совпадает ли множество корней
последнего уравнения с множеством корней исходного уравнения? Если все
преобразования были равносильными, т.е. каждое последующее уравнение было
равносильно предыдущему, то ответ на поставленный вопрос положителен, если же
равносильность хоть в каком то шаге нарушилась, то возможно вы потеряли корни
или получили посторонние.
Теоремы равносильности уравнений:
№
пп
Формулировка
Математическая
модель
1
Если какой-нибудь член уравнения перенести из
одной части уравнения в другую, с
противоположным знаком, то получится
уравнение равносильное данному.
f ( x ) = g ( x )
f ( x ) - g ( x )= 0
2
Если обе части уравнений возвести в одну и ту же
нечетную степень, то получится уравнение
равносильное данному.
f ( x ) = g ( x ) 
f 2n+1 ( x ) = g2n+1 ( x)
)
3
Если обе части уравнения f ( x ) = g ( x ) умножить
на одно и то же выражение h ( x ), которое:
а) имеет смысл всюду в области допустимых
значений уравнения f ( x ) = g ( x );
б) нигде в этой области не обращается в 0, то
получится уравнение f ( x )h ( x )= g ( x)h (x ),
равносильное данному.









;0)(
);(
);()(
xh
hDОДЗ
xgxf
f (x) h(x) = g(x) h(x).
рациональные
уравнения
целые
рациональные
дробные
рациональные

5. 4
Если обе части уравнения f ( x ) = g ( x )
неотрицательны в ОДЗ уравнения, то после
возведения его обеих частей в одну и туже четную
степень получится уравнение равносильное
данному.









;0)(
;0)(
);()(
xg
xf
xgxf
f 2n(x) = g 2n(x).
5
Уравнение h (f ( x )) = h (g ( x )) равносильно
уравнению f (x) = g(x), если:
а) функция h ( t ) – монотонна;
б)ОДЗ исходного уравнения совпадает с ОДЗ
полученного уравнения.






;)(
));(())((
монотоннаяth
xghxfh
f (x) = g(x), ОДЗ!
Раздел 1. Целые рациональные уравнения
Функция вида P(x) = а0хn + a1xn-1 + a2xn-2 + … + an-1 x + an, где n — натуральное,
a0, a1,., an —некоторые действительные числа, называется целой рациональной
функцией.
Уравнение вида P(x) = 0, где P(x) — целая рациональная функция, называется
целым рациональным уравнением.
1.1. Линейные уравнения
Линейное уравнение имеет вид : ax = b.
Если а = 0 и b = 0, то любое значение переменной х является решением.
Если а = 0 и b ≠ 0, то уравнение решений не имеет.
Если а ≠ 0, то решением является значение
b
x
a
 .
целые
рациональные
уравнения
1. линейные
уравнения
ax+b=0
2. квадратные
уравнения
ax2
+ bx + c = 0
3. уравнения
высших
степеней

6. 1.2. Методы решения квадратного уравнения
1. Формула корней квадратного уравнения ( )0D
ax2 +bx+c=0
при b=2k
02
 gpxx
;
2
42
2,1
a
acbb
x


a
ackk
x


2
2,1 ;
42
2
,1 2
g
pp
x 


2. Теорема, обратная теореме Виета
ax2 +bx+c=0 02
 gpxx








.21
21
a
c
xx
a
b
xx
gxx
pxx


21
21
3. Приём «коэффициентов»:
Если а+b+с=0 (или a+b=c) Если b = а + с
то .,1 21
a
c
xx  то .,1 21
a
c
xx


Примеры.
1. 09134 2
 xx
Решение: Так как 4+9=13, то 11 x . Чтобы найти х2, воспользуемся формулой
.
4
1
2
4
9
2 
a
c
x
Ответ:
4
9
,1 21  xx
2. 0619841978 2
 xx
Решение Так как 6+1978=1+9=13, то 11 x . Чтобы найти х2, воспользуемся формулой
.
4
1
2
4
9
2 
a
c
x
1978
6
;1 21  xx
квадратные
уравнения
1. Формула
корней
2. Теорема,
обратная
теореме Виета
3.
Специальные
приемы
02
 cbxax

7. Задания
Уровень А Уровень В Уровень С
1 х2+15х-16=0; 07114 2
 xx 0619841978 2
 xx
1 и -16
4
7
,1 21

 xx
1978
6
;1 21  xx
2 х2+23х-24=0; 0189 2
 xx 0208137345 2
 xx
1 и -24
9
1
;1 
345
208
;1
3 2х2+х-3=0 -5х2+0,6+4,4х=0 016691988319 2
 xx
1 и -1,5 1 и -0,12
.
319
1669
;1 21  xx
4 -2х2+1,7х+0,3=0;
4
1
х2+3
4
3
х -4=0 0391448839 2
 xx
1 и -0,15 1 и -16
839
391
;1 
5 5х2+х-6=0
3
1
х2+2
3
2
х-3=0 0220112009 2
 xx
1 и -1,2 1 и -9 -1 и -2/2009
4. Приём «переброски»
Примеры
1. 05112 2
 xx . «Перебрасываем» 2, умножив 5 на 2, получим
010112
 xx . Корни последнего уравнения 10 и 1 делим на 2.
Тогда корни исходного уравнения 5 и 0,5.
2. 01870376 22
 xxxx
Корни 9 и (-2). Делим числа 9 и ( -2) на 6:
6
2
,
6
9
21  xx . Ответ
3
1
;
2
3

5. Особые случаи
1.








a
x
ax
axaax 10)1(
2
1
22
Пример: 06376 2
 xx . Ответ:
6
1
6 21
 xx
2.








a
x
ax
axaax 10)1(
2
1
22
Пример:








15
1
15
01522615
2
1
2
x
x
xx

8. 3.








a
x
ax
axaax 10)1(
2
1
22
Пример: 01728817 2
 xx








17
1
17
2
1
x
x
4.








a
x
ax
axaax 10)1(
2
1
22
Пример:








10
1
10
0109910
2
1
2
x
x
xx
Данные приёмы решения заслуживают внимания, поскольку они не отражены в
школьных учебниках математики. Овладение данными приёмами поможет учащимся
экономить время и эффективно решать уравнения, а потребность в быстром решении
обусловлена применением тестовой системы ЕНТ.
1.3 Уравнения высших степеней
anxn + an-1xn-1 + … + a1x + a0 = 0 , an ≠ 0
Мы будем рассматривать, в основном, частные виды уравнений третьей и
четвертой степени, т.е. те, в которых коэффициенты специально подобраны.
Существуют общие формулы решения уравнений третьей степени (в XVI в.
итальянские алгебраисты Ферро, Тарталья, Кардано (метод Кардано) и ученик
Кардано Феррари (метод Феррари) решили в радикалах уравнения третьей и
четвертой степеней. Более того, все уравнения данной степени n (n ≤ 4) можно
"обслужить" одной общей формулой. При подстановке в нее коэффициентов
уравнения получим все корни – и действительные, и комплексные.
Итальянец Паоло Руффини и норвежский математик Нильс Хенрик Абель в
начале XIX в доказали, что общее уравнение степени n при n ≥ 5 неразрешимо в
радикалах (Теорема Абеля – Руффини).
Итак, рассмотрим решения уравнений высших степеней следующих видов:

9. Упрощение и разложение на множители.
Некоторые уравнения можно решить, не применяя особо сложных методов. Эти
уравнения упрощают до квадратных или линейных, либо упрощают и раскладывают
на множители, приводя их к виду f(x)∙g(x) = 0. Далее пользуются правилом, что:
произведение равно нулю тогда, и только тогда, когда равен нулю один из
его множителей, а другой при этом не теряет смысла.
Следовательно, решение уравнения f(x)∙g(x) = 0 сводится к решению
совокупности 




.0)(
,0)(
xg
xf
Рассмотрим этот метод на примерах:
1.      
22
3 2,1 6 5 0,7 5x x x x x      .
Решение: Преобразуем уравнение:
          
2
3 0,7 1 5 0,7 5 0 0,7 5 3 3 5 0x x x x x x x x x              
       
5,
0,7 5 2 2 0 0,7 5 1 0 0,7,
1.
x
x x x x x x x
x
 
            


Ответ: -5; -0,7; 1.
2. 4 3 2
3 12 4 0x x x x    .
Решение:
уравнения высших
степеней P(x)=0
уравнения третьей
степени
ax3+bx2+cx+d=0
уравнения четвертой
степени ax4+bx3+cx2
+dх+е=0
возвратные
ax4+bx3+cx2+kbx+k2a=0
симметрические
ax4+bx3+cx2+bx+a=0
однородные
u2(x)+u(x)v(x)+v2(x)=0

10.       4 3 2 3 2 2
3 12 4 0 3 12 4 0 3 1 4 3 1 0x x x x x x x x x x x x              
      2
0,
2,
3 1 4 0 3 1 2 2 0 1
,
3
2.
x
x
x x x x x x x
x
x

  

          
 


Ответ:-2;
1
3
 ; 0;2.
3. 3 2
2 7 7 2 0x x x    .
Решение: Преобразуем уравнение:
        3 2 3 2
2 2 7 7 0 2 1 7 1 0 2 1 1 7 1 0x x x x x x x x x x x                
     2 2
1 2 2 2 7 0 1 2 5 2 0x x x x x x x           
    
2,
1 2 2 0,5 0 1,
0,5.
x
x x x x
x
 
         

 
Ответ: -2; -1; -0,5.
4. 3
7 6 0x x  
Решение:    3 3 2
7 6 0 6 6 0 1 6 1 0x x x x x x x x             
           2
1 1 6 1 0 1 6 0 1 3 2 0x x x x x x x x x x                
3,
1,
2.
x
x
x
 
 


Ответ: -3; 1; 2.
Задания
Уровень А Уровень В
1       
2
0,4 2 2 5 2 2x x x x x           
22
50 0,16 1,5 2 3 5 2x x x x    
–0.4;2;3 0.4;1.5
2       2 2
2 3 4 3 12 4 9x x x x          2 2
2 5 3 3 2 1 6 9x x x x x x      
–4;-3;1.5 –3;-0.5
3 4 3 2
2 2 1 0x x x x     4 3
4 2 3 9 0x x x   
 1 5 /2  
4 4 3 2
4 7 7 7 4 0x x x x     4 3 2
9 3 14 2 4 0x x x x    
 3 5 / 2   1 7 /3  ;–2/3; 1
5 3 2
3 2 0x x x    3 2
2 1 0x x x   
–2;  1 5 / 2 0.5
6 3 2
5 5 3 0x x x    3 2
3 4 7 2 0x x x   

11. –3; 1 2  –1/3
Уровень С
8 2 3 4 5 6 7
1 0x x x x x x x        2 3 4 5 6 7
1 0x x x x x x x       
–1 1
9    2 2 2
3 1 3 2 9 20 30x x x x x x           2 2 2
1 6 3 4 120x x x x x x       
 3 25 4 30 / 2  ; 3 29 /2 –3;2;  1 19 2 145 / 2  
Замена переменных
Достаточно часто при решении уравнений высших степеней используется
метод замены переменных. Он заключается в том, что если уравнение имеет вид
P(Q(x)) = 0, где P и Q - многочлены, то замена y = Q(x) сводит его решение к
решению двух уравнений меньших степеней: P(y) = 0 и Q(x) = y. Метод замены
переменных применяется при решении различных уравнений, очень часто как
составная часть других методов.
ПРИМЕРЫ.
1. (x2 – 6x)2 – 2(x - 3)2 = 81.
Решение: Преобразуем исходное уравнение к виду(x2 – 6x)2 –2(x2 –6x+ 9)=81. Пусть x2
– 6x = t. Тогда исходное уравнение примет вид t2 – 2(t + 9) = 81. Отсюда t = -9 или t =
11. Следовательно, исходное уравнение равносильно совокупности 




.116
,96
2
2
xx
xx
В
итоге x = 3, x = 3 - 20 или x = 3 + 20
2.    
22 2
2 3 7 2 3 10x x x x    
Решение: Пусть 2
2 3x x t  , получим уравнение 2 2,
7 10 0
5.
t
t t
t

     
Получим
совокупность двух уравнений:
2 2
2 2
2,
0,52 3 2, 2 3 2 0,
2 3 5, 2 3 5 0, 2,5,
1.
x
xx x x x
x x x x x
x
 
                 
 
Ответ: -2,5; -
2; 0,5; 1.
3.   2 2
3 1 3 3 3x x x x     .
Решение: Пусть 2
3 1x x t   , тогда 2
3 1 2 2x x t     , получим уравнение:

12.   2 3,
2 3 2 3 0
1.
t
t t t t
t
 
         
Получим совокупность двух уравнений:
2 2
2 2
0,3 1 3, 3 4 0,
3.3 1 1, 3 0,
xx x x x
xx x x x
        
          
Первое уравнение имеет отрицательный дискриминант и не имеет
действительных корней. Ответ: 0; 3.
4. (x – 4)(x – 5)(x – 6)(x – 7) = 1680.
Решение.(x – 4)(x – 7)×(x – 5)(x – 6) =1680, т.е. (x2 – 11x + 28)(x2 – 11x + 30) = 1680.
Обозначим x2 – 11x + 28= t, тогда t(t + 2)=1680, t2 + 2t – 1680=0, t1 = – 42; t2 = 40.
Поэтому x2 – 11x + 28 = – 42; x2 – 11x + 70 = 0; D = 121 – 280 < 0, нет решений.
x2 – 11x + 28 = 40; x2 – 11x – 12 = 0; x1 = 12; x2 = – 1.
Ответ: x1 = 12; x2 = – 1.
5. (x + 3)4 + (x + 5)4 = 16.
Решение. Сделаем подстановку x = t – 4. Тогда получаем (t – 1)4 + (t
+ 1)4 = 16, т.е. t4 – 4t3 + 6t2 – 4t + 1 + t4 + 4t3 + 6t2 + 4t + 1 = 16,
т.е. 2t4+12t2 –14=0, или t4+6t2–7 = 0. Положим t2 = z , тогда z2+6z–7=0, z1=–7; z2 = 1.
С учётом t2 = z отбрасываем z1. Итак, z = 1,т.е. t2 = 1, отсюда t1 = –1; t2 = 1.
Следовательно, x1 = – 1 – 4 = – 5 и x2 = 1 – 4 = –3.
Ответ: x1 = – 5 и x2 = – 3.
Задания
Уровень А Уровень В
1    2
6 16 63 10 10x x x x         1/2 1/3 2/3 3/2 1/3 0x x x x     
8 6   5 97 /12  5 73 /12;
2    2
10 24 5 3 15 0x x x x             
2 23 2
1 25 5 5 1x x x x x     
 9 21 /2 2; 1; 5  
3   2 2
10 21 12 32 60x x x x    
2 2
( 1) ( 2) ( 1) ( 2) 12x x x x      
2;9 -1
4 3 2
2 3 6 0x x x    3 2
4 11 30 0x x x   
2; 3  -3; 2; 5
5    2 2
6 7 3 7 4 1x x x        
2
6 5 3 2 1 35x x x   
–1.5;-5/6
 5 21 /6 
6    2
64 112 49 4 3 1 4,5x x x x        2
4 3 2 1 4 7 3 34x x x x    
–1.25;-0.5
 3 17 /4
7    
4 4
2 2 626x x       
4 4
1 3 82x x   
3 –2;0
8
   
4 4
2 2 64x x       
4 4
3 1 3 2 17x x   
2 0;1/3

13. 9 (х2+х+2)(х2+2х+2)=2х2
  2 2 2
2 3 1 2 5 1 9x x x x x    
–2; -1
 3 7 / 2  ; 2 2 / 2
Уровень С
10    2 2 2
4 2 3 3 4x x x x x          2 2 2
2 2 12 3 10 60x x x x x x      
 1 17 /2  ; 1 15 2 17 / 2   -1;3; 1 12 21 
11    
5 5
5 2 243x x       
5 5
1 1 32x x x   
2;5 0; 1
12  
55
6 1056x x        
5 5
1 3 242 1x x x    
2;4 –2;-1;0
13      2
2 8 3 12 4x x x x x       2 2 2
15 54 5 6x x x x x    
 15 129 / 2  ;–6;-4  10 50 222 20 50 / 2   
 10 50 222 20 50 / 2   
Решение симметрических и возвратных уравнений.
Уравнения вида:a0x2n+1 + a1x2n + … + anxn+1 +λanxn + λ3an-1xn+1 + … + a0λ2n+1 = 0.
a0x2n + a1x2n-1 + … + an-1xn+1 +anxn + λ an-1xn-1 + λ2an-2xn-2 + … + λna0 = 0, 00 а , где λ –
некоторое число, отличное от нуля, называются возвратными уравнениями. При λ =
1 данные уравнения являются симметрическими уравнениями. Симметрическое
уравнение легко определить по его внешнему виду, в нём равны коэффициенты,
находящиеся на одинаковых местах с концов многочлена.
Примеры.
1. х4 + х3 – 10х2 + х + 1 = 0.
Решение: Это симметрическое уравнение четвёртой степени, х = 0 не является
решением, делим обе части на х2 и получаем 2
2
1 1
10 0x x
x x
     . Вводим замену
1
y x
x
  , получаем у2 + у − 12 = 0, откуда, возвращаясь к замене, получим
1
4x
x
  
или
1
3x
x
  . Данные уравнения равносильны уравнениям х2 + 4х + 1 = 0 и х2 − 3х + 1
= 0. Ответ: 2 3  ;
3 5
2

.
2. х4 − 10х3 + 120х + 144 = 0.
Решение: Это - возвратное уравнение четвёртой степени, у которого λ = −12, так
как его можно переписать в виде х4 − 10х3 + 0х2 – 10∙(−12)х+ (−12)2 = 0. Разделив обе
части уравнения на х2 (так как х = 0 не является решением исходного уравнения) и
сгруппировав члены, получим уравнение, равносильное данному:
2
2
144 12
10 0x x
x x
 
    
 
. Положив
12
y x
x
  , получим у2 − 10у + 24 = 0, откуда,

14. возвращаясь к замене, получим
12
6x
x
  или
12
4x
x
  , т.е. х2 − 6х − 12 = 0 или
2
4 12 0x x   . Ответ: −2; 6; 3 21 .
3. 4х4 – 8х3 + 3х2 – 8х + 4 = 0.
Решение: Это симметрическое уравнение четвёртой степени, х = 0 не является
решением, делим обе части на х2 и получаем 2
2
8 4
4 8 3 0x x
x x
     . Вводим замену
1
y x
x
  , получаем 4у2 − 8у − 5 = 0, откуда, возвращаясь к замене, получим
1 1
2
x
x
  
или
1 5
2
x
x
  . Данные уравнения равносильны уравнениям 2х2 + х + 2 = 0 и 2х2 − 5х +
2 = 0. Ответ: 0,5; 2,5.
Рассмотрим возвратные уравнения степени n>4.
Уравнение 2х5 + 6х4 – 2х3 + 4х2 – 48х – 64 = 0 является возвратным (λ = −2), и
уравнение 4х6 + 5х5 – 3х4 + 10х3 – 9х2 + 45х + 108 = 0 является возвратным (λ = 3), а
уравнение х5 + 2х4 + 3х3 + 3х2 + 2х + 1 = 0 является симметрическим (λ = 1).
Возвратное уравнение нечётной степени всегда имеет корень х = −λ.
Следовательно, выделив в левой части возвратного уравнения нечётной степени
множитель х + λ, получаем, что данное уравнение эквивалентно совокупности,
состоящей из уравнения х = −λ и возвратного уравнения чётной степени.
4. х5 + 2х4 + 3х3 + 3х2 + 2х + 1 = 0.
Решение: Это симметрическое уравнение пятой степени, значит в его левой
части можно выделить множитель х + 1, получаем (х + 1)(х4 + х3 + 2х2 + х + 1) = 0.
Решим уравнение х4 + х3 + 2х2 + х + 1 = 0. Это симметрическое уравнение четвёртой
степени, х = 0 не является решением, делим обе части на х2 и получаем
2
2
1 1
2 0x x
x x
     . Группируем 2
2
1 1
2 0x x
x x
   
       
   
и вводим замену
1
y x
x
  ,
получаем у2 + у = 0, откуда у = −1 или у = 0. Уравнения
1
0x
x
  ,
1
1x
x
   решений
не имеют. Ответ: −1.
5. х6 + х5 + х4 + 6х3 + х2 + х + 1 = 0.
Решение: Это симметрическое уравнение шестой степени. Делим обе части на х3,
вводим замену
1
y x
x
  , и получаем у3 + у2 − 2у − 8 = 0. Последнее уравнение
представляем в виде (у − 2)(у2 + 3у + 4) = 0, откуда
1
2x
x
  . Ответ: 1.
6. х6 − 5х4 − 5х2 + 1 = 0.

15. Решение: Это симметрическое уравнение шестой степени. Делим обе части на х3,
вводим замену
1
y x
x
  , и получаем у3 − 8у = 0, откуда
1
0x
x
  , или
1
2 2x
x
   ,
или
1
2 2x
x
  . Ответ: 2 1  ; 2 1 .
7. 2х8 − 9х7 + 20х6 – 33х5 + 46х4 – 66х3 + 80х2 – 72х + 32 = 0
Решение. Это - возвратное уравнение восьмой степени, у которого λ = 2, так как
его можно переписать в виде
2х8 − 9х7 + 20х6 – 33х5 + 46х4 – 33∙2х3 + 20∙22х2 – 9∙23х + 2∙24 = 0.
Разделив обе части уравнения на х4 (так как х = 0 не является решением
исходного уравнения) и сгруппировав члены, получим уравнение, равносильное
данному: 2(х4 + 4
16
х
) – 9(х3 + 3
8
х
) + 20(х2 + 2
4
х
) – 33(х +
х
2
) + 46 = 0
Положим у = х +
х

= х +
х
2
. Тогда х2 + 2
4
х
= у2 – 4; х3 + 3
8
х
= у3 – 6у; х4 + 4
16
х
= у4 –
8у2 + 8, и последнее уравнение примет вид 2у4 – 9у3 + 4у2 + 21у −18 = 0.
Используя метод отыскания рационального корня, получим корни этого
уравнения: у1 = 1, у2 = 2, у3 = 3, у4 =
2
3
 . Таким образом, данное уравнение
равносильно совокупности, состоящей из четырёх уравнений:
х +
х
2
= 1, х +
х
2
= 2, х +
х
2
= 3, х +
х
2
=
2
3
 .
Решая эту совокупность, найдём корни исходного уравнения – числа 1 и 2.
Задания
Уровень В Уровень С
1 х4 – 2х3 – 13х2 – 2х + 1 = 0. 78х6 – 133х5 + 133х-78 = 0.
3 5
2
 
;
5 21
2
 1 ;
2/3;1.5;
2 х4 +2х3 – 6х2 + 2х + 1 = 0. 68х8 – 257х6 – 257х2 +68 = 0.
1; 2 3  0.5; 2 
3 16х4 +4х3 – 8х2 – 4х + 1 = 0. 5 4 3 2
2 3 5 5 3 2 0x x x x x     
0.5 ; 1 17 /8  –2;-1;-0.5;1
4 4х4 –10х3 +8х2 -5х + 1 = 0. 5 3 2
5 5 1 0x x x   
–2;6;3 21 1; 3 5 / 2 
5 х4 − 3х3 − 8х2 + 12х + 16 = 0. 5 4 3 2
4 6 15 15 6 4 0x x x x x     
−2; −1; 2; 4 –1;  101 1 38 2 101 /8    ;
 101 1 38 2 101 /8  

16. 6 3х4 – 7х3 + 2х -3 = 0. 5 4 3 2
2 3 3 2 1 0x x x x x     
 1; 7 13 /6  –1
Использование теоремы Безу для решения уравнений высших степеней
Теорема о рациональных корнях многочлена:
Если несократимая дробь p/q является корнем многочлена P(x) = anxn + an-1xn-1 +
… + a1x + a0, an ≠ 0 с целыми коэффициентами, то ее числитель p является
делителем свободного члена a0 , а знаменатель q - делителем старшего
коэффициента an .
С помощью этой теоремы можно найти все рациональные корни уравнения с
целыми коэффициентами испытанием конечного числа "кандидатов".
ПРИМЕРЫ
1. x3 + 3x2 +x – 2 = 0
Старший коэффициент уравнения равен 1, "кандидатами" на корни будут делители
числа –2. Их всего четыре: 1, −1, 2 и −2. Проверка показывает, что корнем является
только одно из этих чисел: x0 = –2. Если один корень найден, можно понизить
степень уравнения. Согласно теореме Безу
Остаток от деления многочлена P(x) на двучлен x – c равен P(c), т. е. P(x) = (x−c) ∙
Q(x) + P(c).
Из теоремы непосредственно следует, что:
Если c - корень многочлена P(x), то многочлен делится на x – c , т. е. P(x) = ( x−c) ∙
Q(x), где Q(x) - многочлен степени, на 1 меньшей, чем P(x).
Продолжая наш пример, вынесем из многочлена P(x) = x3 + 3x2 +x – 2
множитель x – x0 = x + 2. Чтобы найти частное Q(x), можно выполнить деление
"уголком" или применить схему Горнера. Но есть и более простой способ. Он станет
понятен из примера:
P(x) = x3 + 3x2 +x – 2 = (x3 + 2x2) + (x2 + 2x) – (x + 2) = (x + 2) ∙ (x2 + x – 1). Теперь
остается решить квадратное уравнение x2 +x – 1 = 0. Его корни:
2
51
2,1

x
2.
3 2
4 6 0x x x    .
Решение: Нетрудно заметить, что среди делителей свободного члена:
1; 2; 3; 6    одним из корней уравнения является -1:
3 2
( 1) 4( 1) 1 6 0, 1 4 1 6 0, 0 0            . Значит левая часть - многочлен делится,
по теореме Безу, на x +1.
Применим схему Горнера или выполним деление в «столбик».

17. Как видим, рациональным будет применение схемы Горнера для деления
многочленов.
Корень 1 -4 1 6 _ х3-4х2+х+6 х+1
-1 1 -5 6 0 х3 +х2 х 2-5х+6
_ -5 х2+х+6
-5 х2-5х
_ 6х+6
6х+6
0
и получим       2
1 5 6 0 1 3 2 0x x x x x x         
1,
2,
3.
x
x
x
 
 


Ответ: -1; 2; 3.
3. x3 + 2x2 – x – 2 = 0
Решение: Корни отыскиваем среди чисел ±1, ±2. Подстановкой убеждаемся, что
х=1 является корнем. Делим на (х − 1),
Корень 1 2 -1 -2
1 1 3 2 0
получаем уравнение (х−1)(х2+3х+2) = 0, равносильное уравнению
(х−1)(х+1)(х+2) = 0. Ответ: ±1, −2.
4. x3 – 6x2 + 15x – 14 = 0
Решение: Корни отыскиваем среди чисел ±1, ±2, ±7. Подстановкой убеждаемся, что
х=2 является корнем. Делим на (х−2),
Корень 1 -6 15 -14
2 1 -4 7 0
получаем уравнение (х−2)(х2−4х+7)=0;уравнению (х2−4х+7)=0 корней не имеет.
Ответ: 2.
5. 6x4 – x3 – 7x2 + x + 1 = 0
Решение: Корни отыскиваем среди чисел
1 1 1
1, , ,
2 3 6
    . Проверяем, и убеждаемся,
что х=1 − корень. Делим на (х−1),
Корень 6 -1 -7 1 1
1 6 5 -2 -1 0
получаем уравнение (х−1)(6х3+5х2−2х−1)=0. Решаем уравнение 6х3+5х2−2х−1=0
аналогично исходному. Корнем является х=0,5. Получаем уравнение
(х−0,5)(6х2+8х+2)=0, решаем его. Ответ
1 1
1, ,
2 3
  .

18. 6. 2x4 + 7x3 – 12x2 – 38x + 21 = 0.
Решение: Корни отыскиваем среди чисел
1 3 7 21
1, 3, 7, 21, , , ,
2 2 2 2
        .
Проверяем, и убеждаемся, что х=−3 − корень. Делим на (х+3) по схеме Горнера
Корень 2 7 -12 -38 21
-3 2 1 -15 7 0
получаем уравнение (х+3)(2х3+х2−15х+7) = 0. Уравнение 2х3+х2−15х+7 = 0 решаем
аналогично исходному. Корнем является х=0,5. Получаем уравнение
(х−0,5)(2х2+2х−14)=0. Корнями уравнения 2х2+2х−14=0 являются числа
1 29
2
 
.
Ответ: −3; 0,5; 1 29
2
 
.
Задания
Уровень А Уровень В Уровень С
1 х3 − 3х + 2 = 0 4 3 2
2 9 3 9 5 0x x x x     3 2
30 89 82 24 0x x x   
1; −2 –5;0.5 –1.5;-0.8;-2/3
2 4х3 − 9х2 − х +6 = 0 4 3 2
6 5 14 14 3 0x x x x    
−0,75; 1; 2 –1.5;-1/3; 1 5 / 2
3 х4 + 2х3 − 6х2 − 7х + 10 = 0 3 2
6 11 6 0x x x   
−2; 1; 1 21
2
  –3;-2;-1
4 4 3 2
6 6 5 12 0x x x x     3 2
6 35 26 5 0x x x    3
7 2 5 0x x  
3;4; –5; -0.5;-1/3
 5; 5 13 /2 
5 4 3 2
9 29 39 18 0x x x x     3 2
30 31 10 1 0x x x    3
2 5 2 0x x  
–3;-2;-1 0.2;1/3;0.5 2; 1/ 2; 1 1/ 2;  
Метод неопределенных коэффициентов.
Если у многочлена с целыми коэффициентами рациональных корней не
оказалось, можно попробовать разложить его на множители меньшей степени с
целыми коэффициентами.
ПРИМЕРЫ
1. x4 – 2x2 – 8x – 3 = 0
Представим левую часть в виде произведения двух квадратных трехчленов с
неизвестными (неопределенными) коэффициентами:
x4 – 2x2 – 8x – 3 = (x2 + ax + b)∙(x2 + px + q)

19. Раскроем скобки в правой части и приведем подобные:
x4 – 2x2 – 8x – 3 = x4 + (a + p)x3 + (b + ap + q)x2 + (aq + bp)x + bq
Теперь, приравнивая коэффициенты при одинаковых степенях x в обеих частях,
получим систему уравнений











.3
,8
,2
,0
bq
bpaq
qapb
pa
Попытка решить эту систему в общем
виде вернула бы нас назад, к решению исходного уравнения. Но целые корни, если
они существуют, нетрудно найти и подбором. Не ограничивая общности, можно
считать, что b ≥ q, тогда последнее уравнение показывает, что надо рассмотреть лишь
два варианта: b = 3,q = -1 и b = 1, q = -3. Подставляя эти пары значений в остальные
уравнения, убеждаемся, что первая из них дает искомое разложение: x4 – 2x2 – 8x – 3
= (x2 + 2x + 3)∙(x2 - 2x - 1). Этот способ решения называется методом
неопределенных коэффициентов.
Решая далее исходное уравнение, получим
2
2
1 2,2 3 0,
2 1 0; 1 2.
хх х
х х х
     
 
     
Ответ: 21õ .
2. x4 - 4x3 - 10x2 + 37x – 14 = 0.
Решение: Рассуждая аналогично, получим
x4 - 4x3 - 10x2 + 37x – 14 = (x2 + ax + b)∙(x2 + px + q)
x4 - 4x3 - 10x2 + 37x – 14 = x4 + (a + p)x3 + (b + ap + q)x2 + (aq + bp)x + bq
4,
10,
37,
14.
a p
b ap q
aq bp
bq
  
    

 
  
последнее уравнение показывает, что надо рассмотреть лишь
четыре варианта: b = 14,q = -1; b = 7, q = -2; b = 2,q = -7 и b = 1, q = -14. Подставляя
эти пары значений в остальные уравнения, убеждаемся, что третья из них дает
искомое разложение:
x4 - 4x3 - 10x2 + 37x – 14 = (x2 – 5x + 2)∙(x2 + x – 7), следовательно, исходное
уравнение равносильно совокупности

20. 2
2
5 17
,
2
5 17
,
5 2 0, 2
7 0; 1 29
,
2
1 29
.
2
х
х
х х
х х
х
х
 


 
   

    


  


Ответ:
5 17 1 29
;
2 2
х х
  
  .
3. x4 – 22x2 – 5x + 2 = 0
Решение: x4 – 22x2 – 5x + 2 = (x2 + ax + b)∙(x2 + px + q)
x4 – 22x2 – 5x + 2 = x4 + (a + p)x3 + (b + ap + q)x2 + (aq + bp)x + bq











.2
,5
,22
,0
bq
bpaq
qapb
pa
Имеем для рассмотрения два варианта: b = 2,q = 1 и b = -1, q = -
2. Первая из них даёт искомое разложение: x4 – 22x2 – 5x + 2 = (x2 + 5x + 2)∙(x2 – 5x +
1). Далее переходим к совокупности и решаем её.
2
2
5 17
,
2
5 17
,
5 2 0, 2
5 1 0; 5 21
,
2
5 21
.
2
х
х
х х
х х
х
х
  


  
   

   


 


Ответ: 5 17 5 21
;
2 2
х х
  
  .
Задания
Уровень В Уровень С
1 х4-4х3-10х2+37х-14=0 x4 + 2x3 – 16x2 – 2x + 15 = 0
2
291
;
2
175  –5; –1; 1; 3
2 х4 – 8х +63 = 0 4 2
2 12 8 0x x x   
корней нет 1 3
3 4 3 2
2 3 4 1 0x x x x     4 3 2
3 14 19 8 1 0x x x x    
 3 5 / 2  ; 1 2 / 2  3 5 / 2   5 13 /2  ;
4 4 2
3 4 3 0x x x   
 1 13 /2

21. Однородные уравнения
Уравнение называется однородным, если каждое его слагаемое имеет одну и ту
же степень. Так второго порядка однородности относительно выражений f(x) и g(x)
будет уравнение вида af2(x) + bf(x)g(x) + cg2(x) = 0. Решается оно путём деления
обеих частей уравнения на g2(x), с предварительной проверкой того, являются ли
корни уравнения g(x) = 0 решением исходного уравнения, и последующей заменой
y
xg
xf

)(
)(
.
ПРИМЕРЫ.
1. (х2 + х + 4)2 + 8х(х2 + х + 4) + 15х2 = 0.
Так как х = 0 не является решением данного уравнения, то можно разделить обе
его части на х2, получим 015
4
8
4 222







 
х
хх
х
хх
. Введя замену y
х
хх

 42
и перейдя к квадратному уравнению у2 + 8у +15 = 0, получим










.3
4
;5
4
2
2
x
xx
x
xx
.
Откуда получаем 532,1 x , 23 x .
2. (х2 - х + 1)4 – 6х2(х2 - х + 1)2 + 5х4 =0.
Решение: Учитывая, что х = 0 не является решением, получим
22 2 2 2
2 2
( 1) ( 1)
6 5 0
х х х х
х х
      
     
   
, откуда, выполнив замену
2 2
2
( 1)х х
у
х
 
 ,
получим у2 − 6у + 5 = 0. Решаем последнее уравнение, возвращаемся к замене и
получаем
2 2
2
( 1)
1
х х
х
 
 или
2 2
2
( 1)
5
х х
х
 
 , откуда переходим к решению
совокупности
2
2
2
2
1 0,
2 1 0,
(1 5) 1 0,
(1 5) 1 0.
х
х х
х х
х х
  

  
    

    
Ответ: 1; 1 5 2 2 5
2
  
; 1 5 2 2 5
2
  
.
3. 2(х2 + х + 1)2 – 7(х − 1)2 = 13(х3 − 1).
Решение: Учитывая, что х = 1 решением не является, т.к. 18 ≠ 0, то делим обе
части уравнения на (х−1)2 и получаем уравнение
22 2
1 1
2 13 7 0
1 1
х х х х
х х
      
     
    
.

22. Введя замену
2
1
1
x x
y
x
 


и решая квадратное уравнение, получим
2
1 1
1 2
х х
х
 
 

или
2
1
7
1
x x
x
 


. Ответ: −1; −0,5; 2; 4.
4. (x - 1)4 + 9(x + 1)4 = 10(x2 - 1)2.
Решение. Если раскрыть все скобки и привести подобные члены, то получится
уравнение четвёртой степени. Попробуем другой путь: введём новые неизвестные U
и V: U = (x - 1)2, V = (x + 1)2. Уравнение примет вид однородного уравненияU2 + 9V2
= 10UV.Это уравнение однородное, и после деления на V2 оно становится
уравнением относительно неизвестного W: W = U / V = (x - 1)2 / (x + 1)2.
Решим вспомогательное уравнение W2-10W+9 = 0. Его корни W1=1, W2=9.
Осталось решить уравнения (x -1)2/(x+1)2 =1 и (x -1)2/(x +1)2 =9.
Из первого уравнения следует, что либо (x -1)/(x + 1)=1, либо (x -1)/(x + 1)=-1.
Из второго получаем, что либо (x - 1)/(x + 1) = 3, либо (x -1)/(x +1)=-3. Решая
получившиеся уравнения, видим, что первое из них не имеет корней, а
из трёх остальных получаем x1 = 0, x2 = - 2, x3 = -0,5.
Ответ: x1 = 0, x2 = - 2, x3 = -0,5.
5. 3(x2 – x + 1)2 – 5(x + 1)(x2 – x + 1) – 2(x + 1)2 = 0.
Решение. Решим уравнение как однородное. Разделим обе части уравнения на (x2 – x
+ 1): 3 – 5(x + 1) / (x2 – x + 1) – 2((x + 1) / (x2 – x + 1))2 = 0.
Пусть (x + 1)/(x2 – x + 1)=t, тогда 3–5t – 2t2 =0, т.е. t1=–3; t2=0,5.Следовательно:
(x + 1)/(x2 – x + 1) = 0,5 = 1/2; 2x + 2 = x2 – x +1; x2 – 3x – 1 = 0;
2
133
2,1

х
(x + 1)/(x2 – x + 1)=–3;x+1=–3x2+3x–3; 3x2–2x+4=0; D = 4–48<0, нет решений.
Ответ:
2
133
2,1

х
Задания
Уровень В Уровень С
1      
2 22 3
2 1 7 1 13 1 0x x x x          8 4 6 2 4
2 1 4 3 0x x x x x     
–1;-0.5;2;4
 3 5 / 2 
2      
22 3 2
7 4 4 6 8 2 4 0x x x x x           
4 22 2 2 4
1 6 1 5 0x x x x x x      

23. –10;1
 5 1 2 2 5 / 2  
3 (х2 − х)4 − 5(х2 − х)2х2 + 6х4 = 0. (х2 + х + 1)2 = х2(3х2 + х + 1).
0; 1 2 ; 1 3 . 2
7 ;
1 5
2

4 (2х - 1)2 + (2х - 1)(х + 2) – 2(х + 2)2 = 0. (3х2 + 7х − 2)2 + 5х2(3х2 + 7х − 2) −
24х4 = 0.
−0,75; 3. 7 137
22
 
Графический метод решения
Уравнения решаются не только аналитически, но и графически. Рассмотрим
графический способ решения на примере. Решить уравнение х5 + х − 2 = 0. Решим его
графически, для этого преобразуем уравнение к виду х5 = 2 − х, и построим графики
функций у = х5 и у = 2 − х.
Очевидно, что графики имеют только одну точку пересечения, абсцисса которой
приблизительно равна 1. Выполнив проверку, убеждаемся, что х = 1 является
единственным корнем исходного уравнения.
1.4 Целые рациональные уравнения, содержащие знак модуля.
При решении уравнений с модулем используется определение модуля и метод
интервалов. Напомним, что | f (x) | =[
f (x), если f (х) ≥ 0
– f (x), если f (x) < 0
.
Рассмотрим различные виды уравнений, содержащих знак модуля.
1. Уравнения вида | f(x)| = b, b R
При b<0 решений нет, при b=0 имеем f(x)=0, при b>0 уравнение | f(x)| =b равносильно
совокупности двух уравнений

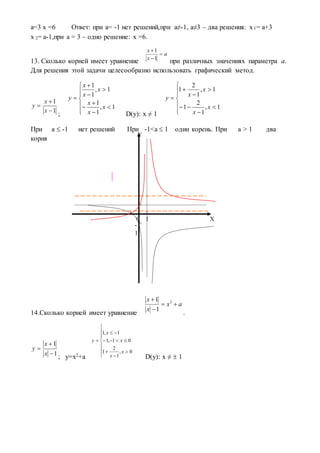
24. 2. Уравнение вида f(| x| )=g(x),
где f(x) и g(x) некоторые рациональные выражения. Уравнение равносильно
совокупности систем: и
3. Уравнение вида | f(x)| =g(x)
Уравнение равносильно совокупности систем: и
4. Уравнение вида | f1(x)| +| f2(x)| +…| fn(x)| =g(x)
Такие уравнения проще решать методом интервалов. Для этого находят сначала все точки, в
которых хотя бы одна из функций | f1(x)| +| f2(x)| +…| fn(x)| меняет знак. Эти точки делят
область допустимых значений уравнения на промежутки, на каждом из которых эти функции
сохраняют знак. Затем, используя определение модуля, переходят от данного уравнения к
совокупности систем, не содержащих знак модуля.
Примеры
1.|3x - 1| = |2x + 3|.
В силу сказанного выше из этого уравнения вытекает, что либо 3х - 1 = 2х + 3,
либо 3х - 1 = -(2х + 3). Корнем первого уравнения является число 4,
а второго — число -2 / 5. Итак, решение уравнения имеет вид х1 =4, х2 =-2 / 5.
2. |x| = |3 - 2x| - x - 1.
Решение. Выражение x обращается в нуль при x=0, а выражение 3-2x— при x =3/2.
Точки 0 и 3/2 разбивают числовую ось на промежутки (-∞;0),[0;3/2], (3/2; ∞).
1) При -∞ < x < 0 имеем x < 0 и 3 - 2x > 0.Поэтому на этом промежутке |x|=-x, |3 - 2x| = 3 -
2x и уравнение принимает вид -x = 3 - 2x - x - 1. Решая его, получаем, что x = 1. Но это
значение x не лежит на (-∞; 0), и потому на этом промежутке уравнение корней не имеет.
2) При 0 < x <3/ 2 имеем x > 0, 3 - 2x< 0, поэтому|x| = x, |3 - 2x| = 3 - 2x. И уравнение
принимает вид x =3 - 2x - x - 1. Решая его, находим x = 0,5. Так как это значение x
принадлежит промежутку [0; 3 / 2], то 1 / 2 является корнем заданного уравнения.
3) Наконец, на промежутке (3 / 2; +∞) имеем x > 0, 3 - 2x <0, а потому |x| = x, |3 - 2x| = -(3 -
2x) и уравнение принимает вид x = -(3 -2x) - x - 1, т.е. 0 = - 4. Значит, на этом промежутке
нет корней заданного уравнения. Мы получили, таким образом, что уравнение имеет лишь
один корень, а именно x= 0,5.
В некоторых случаях уравнение со знаком модуля имеет бесконечно много решений.
3. |8 - 5x| = |3 + x| + |5 -6x|.
Решение. Выражения (8 - 5x), (3 + x) и (5 - 6x) обращаются в нуль соответственно в
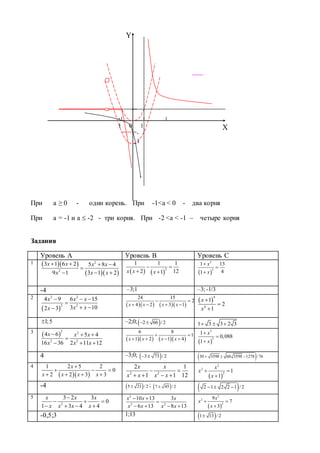
точках 8/5, -3, 5/6. Эти точки разбивают числовую ось на 4 промежутка. При этом, в

25. ходе решения, устанавливаем, что на промежутках (-∞;-3), (5/6; 8/5],(8/5; +∞)
уравнение корней не имеет, а на промежутке [-3; 5/6] оно обращается в тождество 8 -
5x = 3+x+5- 6x. Поэтому ответ имеет вид [-3; 5/6]. Ответ: [-3; 5/ 6].
Несколько сложнее решаются уравнения, в которых встречается знак модуля под
знаком модуля. Однако и в этом случае метод разбиения оси на промежутки
знакопостоянства позволяет решить уравнение.
4. |2x - 3 - |x + 2|| = 8x + 12.
Решение. Выражение (x + 2) обращается в нуль при x = -2.
1) Если x<-2, то (x+ 2)<0 и потому |x +2|= -(x + 2). Значит, на промежутке (-∞; - 2)
заданное уравнение принимает вид |2x-3 + (x+2)| = 8x+12, т.е. |3x-1|=8x+12. Но при x
< -2 имеем 3x - 1 < 0 и потому |3x - 1| = - (3x - 1). Получаем уравнение -(3x - 1) = 8x +
12,имеющее корень x = -1. Так как это число не лежит на промежутке (-∞; - 2),
то заданное уравнение не имеет на это промежутке корней.
2) Пусть теперь x> - 2. Тогда |x + 2| = x + 2, и мы получаем уравнение
|2x - 3 - (x + 2)| =8x + 12, т.е. |x - 5| = 8x + 12.Здесь надо рассмотреть два случая: x < 5
и x≥ 5. В первом случае | x - 5| = -(х - 5), и потому получаем уравнение
-(x - 5) = 8x + 12. Его корень равен -7 / 9. Поскольку -2<-7 / 9 < 5, то -7 / 9 является
корнем заданного уравнения. Если же x≥5, то |x - 5| = x - 5 и уравнение принимает
вид x - 5 = 8x + 12.Корнем полученного уравнения является число -17 / 7. Поскольку
оно не лежит на луче [5; +∞), оно не является корнем заданного уравнения. Итак,
решение имеет вид x= -7/9. Ответ: x = -7 / 9.
5.|1 – 2x| + |3x + 2| + |x| = 5.
Решение. Приравниваем к нулю выражения, стоящие под знаком модуля, отмечаем
на числовой оси полученные значения, исследуем уравнения в каждом из
полученных интервалов:
-2/3 0 0,5
1) если x < – 2/3, то 1– 2x > 0, 3x+2<0, x<0 и уравнение переписывается так:
1 – 2x – 3x – 2 – x = 5, т.е. – 6x = 6, x = – 1 Î(–∞; – 2/3).
2) если – 2 /3< x < 0, то 1–2x >0, 3x +2>0, x < 0 и поэтому имеем:
1 – 2x + 3x + 2 – x = 5, и т.к. 5> 0, то в промежутке [– 2 / 3; 0) корней нет.
3) если 0 <x < 0,5, то получаем: 1 – 2x + 3x + 2 + x = 5, т.е. 2x =2; x = 1 [0; 0,5).

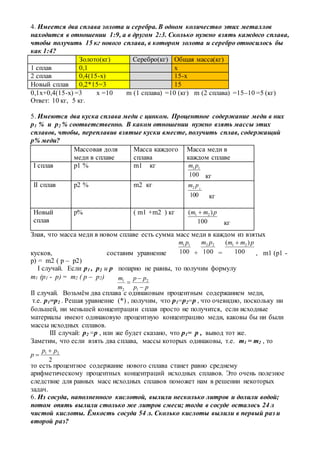
26. 4) если 0,5> x, то – 1+2x+3x+2+x=5, 6x=4, x =2/3∈(0,5;∞). Ответ:x1=– 1; x2 = 2 / 3.
6. | x | + | x – 1 | = 1.
Решение. x – 1= 0, x =1; х=0 получаем интервалы:
0 1
1) x ∈(-∞; 0), тогда – x – x +1 = 1; – 2x = 0; x = 0  (-∞; 0).
2) x∈ [0;1), тогда x –x+1= 1; 1=1—тождество, значит, x—любое число из [0; 1).
3) x ∈[1; ∞), тогда x + x – 1 = 1; 2x = 2; x = 1 ∈[1; ∞). Ответ: x ∈[0; 1].
7. Решить систему
Из второго уравнения выразим | у+1| и подставим в первое уравнение.
Получим систему:
Ответ: (4; 2), (4; -4)

27. Существует интересный метод графического решения уравнений, содержащих поз знаком модуля
простейшие функции. Под
Задания
Уровень А Уровень В Уровень С
1
-1;0;1
2 5 5
10 2 2x x x   
1/2 4
5
3 2 3 2 3x x x      4 3 2 4
2 3 1 1x x x x x     
-1 2;4 –2; 1
4 3 2 3
3 1 3 1x x x x     2 2
2 3 2 5x x x x     
–2;0;1 –2;0;1/2;4/3
5 2 2
8 5 5x x x    2 2
4 3 4 3x x x x    
0;1,25;4    ;0.75 1;3 U
6 2 1 1 2x x x      3 3
4 1 1x x x    5 5
10 2 2x x x   
–2;0;2; 2 ; 0;0.5 - 4
5 ;0;0.4

28. 1.5 Уравнения в целых числах
Диофантовы уравнения – алгебраические уравнения с целыми
коэффициентами или системы таких уравнений, у которых разыскиваются целые или
рациональные решения. Особенности их решения:
1) они сводятся к уравнениям или системам уравнений с целочисленными
коэффициентами. Как правило, эти системы неопределённые, т. е. число уравнений в
них меньше числа неизвестных;
2) решения требуется найти только целые, часто натуральные.
При решении уравнений в целых и натуральных числах можно условно
выделить следующие методы: способ перебора вариантов, метод остатков, алгоритм
Евклида, цепные дроби, метод разложения на множители, решение уравнений в
целых числах как квадратных относительно какой-либо переменной, метод остатков,
метод бесконечного спуска.
Способ перебора вариантов.
Задача: Допустим, в аквариуме живут осьминоги и морские звёзды. У осьминогов по
8 ног, а у морских звёзд – по 5. Всего конечностей насчитывается 39. Сколько в
аквариуме животных?
Решение: Пусть х - количество морских звёзд, у – количество осьминогов. Тогда у
всех осьминогов по 8у ног, а у всех звёзд 5х ног. Составим уравнение: 5х + 8у = 39.
Заметим, что количество животных не может выражаться нецелым или
отрицательным числами. Следовательно, если х – целое неотрицательное число, то и
у=(39 – 5х)/8 должно быть целым и неотрицательным, а, значит, нужно, чтобы
выражение 39 – 5х без остатка делилось на 8. Простой перебор вариантов показывает,
что это возможно только при х = 3, тогда у = 3.
Ответ: (3; 3)
Метод остатков
Покажем на примере решения линейного уравнения в целых числах
0152127  yx .Преобразуем отношение коэффициентов при неизвестных. Прежде
всего, выделим целую часть неправильной дроби
52
127
;
52
23
2
52
127
 . Правильную
дробь
52
23
заменим равной ей дробью
23
52
1
.Тогда получим
23
52
1
2
52
127
 . Проделаем такие
же преобразования с полученной в знаменателе неправильной дробью
23
52
. Теперь

29. исходная дробь примет вид:
6
23
1
2
1
2
52
127


.Повторяя те же рассуждения для дроби
6
23
получим
5
6
1
3
1
2
1
2
52
127


 .Выделяя целую часть неправильной дроби
5
6
, придем к
окончательному результату:
5
1
1
1
3
1
2
1
2
52
127




.Мы получили выражение, которое
называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой
цепной дроби - одну пятую, превратим получающуюся при этом новую цепную дробь
в простую и вычтем ее из исходной дроби
52
127
:
9
22
9
4
2
4
1
2
1
2
1
1
2
1
2 



 ,
952
1
952
11441143
9
22
52
127




 .
Приведем полученное выражение к общему знаменателю и отбросим его, тогда
0122529127  . Из сопоставления полученного равенства с уравнением
0152127  yx следует, что 9x , 22y будет решением этого уравнения и
согласно теореме все его решения будут содержаться в прогрессиях tx 529  ,
ty 12722   ,2,1,0 t .
В общем случае для нахождения решения уравнения 0 cybxa надо
разложить отношение коэффициентов при неизвестных в цепную дробь, отбросить ее
последнее звено и проделать выкладки, подобные тем, которые были проведены
выше.
Разложение на множители
1. 2х2-3ху-2у2=7
Решение. Разложим левую часть на множители 2х2+ху-4ху-2у2=х(2х+у)-
2у(2х+у)=(2х+у)(х-2у). Тогда уравнение имеет вид (2х+у)(х-2у)=7. Так как х и у
целые числа, то данное уравнение равносильно совокупности систем уравнений

30. 
































12
72
12
72
72
12
72
12
ух
ух
ух
ух
ух
ух
ух
ух
, решим

































1
3
6,2
8,1
1
3
6,2
8,1
у
х
у
х
у
х
у
х
.
Из полученных ответов выбираем только целые (-3;-1),(3;1).
2. у2-2у-2х(у-1)-8х2+6=0.
Решение. Выделим полный квадрат (у-1)2-2х(у-1)-8х2=-5.
Сделаем замену t=y-1, t2-2xt-8x2=-5. Разложим t2-4xt+2xt-8x2=-5, t(t-4x)+2x(t-
4x)=-5, (t-4x)(t+2x)=-5. Перейдем в совокупности систем

































52
14
12
54
52
14
12
54
xt
хt
xt
хt
xt
xt
xt
xt

































3
1
1
1
3
1
1
1
t
х
t
х
t
x
t
x
Получим соответствующие значения у=t+1.
Ответ:
 )4;1(),2;1(),2;1(),0;1( 
Решение уравнений в целых числах
как квадратных относительно какой-либо переменной.
Задача: Решите в целых числах 5х²+ 5у² + 8ху + 2у – 2у + 2 = 0.
Решение: Рассмотрим уравнение, как квадратное относительно х
5х²+(8у-2)х+5у²+2у+2=0,
х1,2= (1 –4у ±√(1 – 4у) ²-5(5у²+2у+2))/5 =(1 –4у ±√-9(у+1)²)/5.Данное уравнение имеет
решение тогда, когда дискриминант равен нулю, т.е. –9(у+1) = 0, отсюда у = -1. Если
у = -1, то х =1.Ответ: (1; -1)
Задания
Уровень А Уровень В Уровень С
1 2 2
3x y  2 2
5 4 11x xy y   2 2 2 2
2 5 0x y y x   
   2; 1 , 2; 1   m    2; 1 , 2; 9   m  2; 1 ,   2; 1 m
2 2 2
2 2x x y   2 2
3 2 3x xy y   2 2 2 2
5 4 2 11 0x y y x   
   3; 1 , 1; 1      1; 2 , 1;0    1; 3 ,   1; 3 m

31. 3  2 2
2 2 1 3 4x x x y y      2 2
9 3 2 11x xy y    2 2
2 1 0x xy x y y     
 3;1 , 1; 1 ,   1;1 ;  1; 4  
4 2 2 2 2
2 6 12 0x y y x    2
2 5 2 3 0xy x x y     2 2
2 2 3 2 7 0x xy x y y     
 2; 2 ,   2; 2 m    1;0 , 3;6    6;1 , 3; 2 ,      2;1 , 5; 2
5 2
1 0y xy x    2
5 2 5 0x xy x y     2 2
2 3 5 2 5 0x xy x y    
   1; 1 , 1;0 ,      5;2 , 5;3  17; 11 ,
     21;29 , 3;29 , 1; 11   
 1;2
6 2
3 3 6 3xy x x y    2 2 2 2
2 6 12 0x y y x    2 2
15 11 14 2 5 3 0x xy x y y     
 3;1    2; 2 , 2; 2   m        10; 23 , 3; 9 , 3; 5 , 0;3 ,     
       2;5 , 5;13 , 5;17 , 12;31
1.6 Рациональные уравнения с параметром
Иногда в уравнениях некоторые коэффициенты заданы не конкретными числовыми
значениями, а обозначены буквами. Такие буквы называются параметрами.
Предполагается, что эти параметры могут принимать любые числовые значения, т.е.
одно уравнения с параметрами задаёт множество уравнений (для всех возможных
значений параметров).
Например, линейное уравнение ax + b = c с неизвестным x можно рассматривать как
уравнение с параметрами a, b, и c. Его решением при a ¹ 0 является x = (c - b) / a. Если
a = 0, то получается “уравнение” b = c, и если действительно b = c, то корнями
данного уравнения являются все действительные числа. Если же b  c, при этом a = 0,
то данное уравнение корней не имеет.
Так, с параметрами учащиеся встречаются при введении некоторых понятий. Не
приводя подробных определений, рассмотрим случай в качестве примеров
следующие объекты:
функция прямая пропорциональность: y = kx (x и y-переменные; k-параметр,k  0);
линейная функция: y = kx + b (x и у — переменные, k и b —параметры);
линейное уравнение: ax + b = 0 (x — переменная; a и b —параметры);
уравнение первой степени: ax + b = 0 (x — переменная; a и b — параметры, a 0);
квадратное уравнение: ax2 + bx + c = 0 (x- переменная; a, b и c —параметры, a 0).
Решить уравнение с параметрами означает следующее:
исследовать, при каких значениях параметров уравнение имеет корни и сколько их
при разных значениях параметров.

32. Найти все выражения для корней и указать для каждого из них те значения
параметров, при которых это выражение действительно определяет корень уравнения.
Ответ к задаче “решить уравнение с параметрами” должен выглядеть следующим
образом: уравнение при таких- то значениях параметров имеет корни …, при таких-
то значениях параметров — корни …, при остальных значениях параметров
уравнение корней не имеет.
ПРИМЕРЫ
1. Решим уравнение px=6 с неизвестным x и параметром p.
Если p 0, то можно разделить обе части уравнения на p, и тогда мы находим корень
уравнения x = 6 /p. Если p = 0, то уравнение корней не имеет, потому что 0× x = 0 для
любого x. Ответ: при p 0 уравнение имеет единственный корень x = 6 / p; при p = 0
уравнение корней не имеет.
2. Решить уравнение ax = 1.
Решение. На первый взгляд представляется возможным сразу дать ответ: x = 1 / a.
Однако при a = 0 данное уравнение решений не имеет, и верный ответ выглядит так:
Ответ: Если a = 0, то нет решений; если a 0, то x = 1 / a.
3. Решить уравнение (a2 - 1)x = a + 1.
Решение. Нетрудно сообразить, что при решении этого уравнения достачно
рассмотреть такие случаи:
a = 1; тогда уравнение принимает вид 0x = 2 и не имеет решений;
a = - 1; получаем 0x = 0, и очевидно x — любое.
a  ± 1; имеем x = 1 / (a - 1).
Замечание. Существенным этапом решения задач с параметрамиявляетсязапись ответа. Особенно
это относится к тем примерам,где решение как бы “ветвится” в зависимостиот значений параметра.
В подобных случаях составление ответа — это сбор ранее полученных результатов. И здесь очень
важно не забыть отразить в ответе все этапы решения. В только что разобранном примере запись
ответа практически повторяет решение.
Ответ: Если a = - 1, то x — любое число; a = 1, то нет решений; если a ± 1, то x = 1 /
(a - 1).
3.При каких a уравнение ax2 - x + 3 = 0 имеет единственное решение?
Решение. Прежде всего обратим внимание на распространённую ошибку: считать
исходное уравнение квадратным. На самом деле это уравнение степени, не выше
второй. Пользуясь этим соображением, естественно начать решение, рассмотрев
случай, когда a = 0, то очевидно данное уравнение имеет единственное решение. Если
же a 0, то имеем дело с квадратным уравнением. Его дискриминант 1 - 12a
принимает значение, равное нулю, при a = 1 / 12.

33. Ответ: a = 0 или a = 1 / 12.
4.При каких a уравнение (a - 2)x2 + (4 - 2a)x + 3 = 0 имеет единственное решение?
Решение. Понятно, что надо начинать со случая a = 2. Но при a = 2 исходное
уравнение вообще не имеет решений. Если a 2, то данное уравнение — квадратное,
и, казалось бы, искомые значения параметра — это корни дискриминанта. Однако
дискриминант обращается в нуль при a = 2 или a = 5. Поскольку мы установили, что a
= 2 не подходит, то
Ответ: a = 5.
Вероятно, в двух последних примерах ничего сложного нет (тем более, ели они уже
решены). Однако, на наш взгляд, параметр в этих задачах проявляет своё “коварство”,
особенно для начинающих. Поэтому полезно рассмотреть ещё несколько примеров,
где параметр “расставляет ловушки”.
5.При каких значениях a уравнение ax2 + 4x + a + 3 = 0 имеет более одного корня?
Решение. При a = 0 уравнение имеет единственный корень, что не удовлетворяет
условию. При a 0 исходное уравнение, будучи квадратным, имеет два корня, если
его дискриминант 16 - 4a2 - 12a — положительный. Отсюда получаем - 4 < a < 1.
Однако в полученный промежуток (- 4; 1) входит число 0, которое, как мы уже
проверили, неприемлемо. Ответ: - 4 < a < 0 или 0 < a < 1.
6. При каких a уравнение a(a + 3)x2 + (2a + 6)x - 3a - 9 = 0 имеет более одного корня?
Решение. Стандартный шаг — начать со случаев a = 0 и a = - 3. При a = 0 уравнение
имеет единственное решение. Любопытно, что при a = - 3 решением уравнения
служит любое действительное число. При a = - 3 решением уравнения служит любое
действительное число. При a - 3 и a 0, разделив обе части данного уравнения на a +
3, получим квадратное уравнение ax2 + 2x - 3 = 0, дискриминант которого 4(1 + 3a)
положителен при a > - 1 / 3. Опыт предыдущих примеров подсказывает, что из
промежутка (- 1 / 3; +∞ ) надо исключить точку a = 0, а в ответ не забыть включить a =
- 3. Ответ: a = - 3 или - 1 / 3 < a < 0, или a > 0.
7. При каких значениях a уравнение (x2 - ax + 1) / (x + 3) = 0 имеет единственное
решение?
Решение. Данное уравнение равносильно системе
Наличие квадратного уравнения и условие единственности решения, естественно
приведут к поиску корней дискриминанта. Вместе с тем условие x - 3 должно
привлечь внимание. И “тонкий момент” заключается в том, что квадратное уравнение
системы может иметь два корня! Но обязательно только один из них должен
равняться - 3. Имеем D = a2 - 4, отсюда D = 0, если a = ± 2; x = - 3 — корень

34. уравнения x2 - ax + 1 = 0 при a = - 10 / 3, причём при таком значении a второй корень
квадратного уравнения отличен от - 3. Ответ: a = ± 2 или a = - 10 / 3.
8. Решить уравнение с параметром (a2 - 9)x = a2 + 2a - 3.
Решение. Уравнение имеет смысл при любых значениях параметра. Запишем
уравнение в виде: (a - 3)(a + 3)x = (a + 3)(a - 1).
Если a = - 3, то уравнение принимает вид: 0x = 0. Отсюда следует, что при x∈ R, т.е.
решением уравнения является любое действительное число. Если a  - 3, то
уравнение принимает вид: (a - 3)x = a - 1.При a = 3 имеем 0x = 2. Уравнение решения
не имеет. При a - 3 имеем x = (a - 1) / (a - 3). Уравнение имеет единственное
решение (например, x = 3 при a = 4, x = 3 / 5 при a= - 2 и т.д.)
Ответ: a = - 3, x∈ R ; a = 3, нет решений ; a  ± 3, x = (a - 1) / (a - 3).
Утверждения о расположении корней квадратного трехчлена
Пусть f(x)=ax2+bx+c имеет действительные корни x1 и x2, а M – какое-нибудь
действительное число, D=b2 -4ас
Утверждение 1. Для того чтобы оба корня квадратного трехчлена были
меньше, чем число M (т.е. лежали на числовой оси левее, чем точка M),
необходимо и достаточно выполнение следующих условий:
или
Утверждение 2. Для того чтобы один из корней квадратного трехчлена был
меньше, чем число M, а другой больше, чем число M (т.е. точка M лежала бы
между корнями), необходимо и достаточно выполнение условий:
или
Утверждение 3. Для того чтобы оба корня квадратного трехчлена были больше,

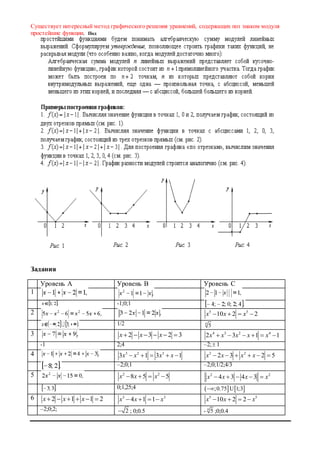
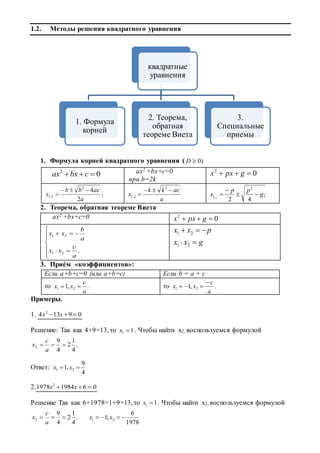
35. чем число M (т.е. лежали на числовой оси правее, чем точка M), необходимо и
достаточно выполнение условий:
или
Утверждение 4. Для того чтобы оба корня квадратного трехчлена были больше,
чем число M, но меньше, чем число N (M<N), т.е. лежали в интервале между M и
N, необходимо и достаточно:
Утверждение 5. Для того чтобы только больший корень квадратного трехчлена
лежал в интервале [M,N] (M < N), необходимо и достаточно:
или
при этом меньший корень лежит вне отрезка [M, N]).
Утверждение 6. Для того чтобы только меньший корень квадратного
трехчлена лежал в интервале [M, N], необходимо и достаточно:

36. или
(при этом больший корень лежит вне отрезка [M, N]).
Утверждение 7. Для того чтобы один из корней квадратного трехчлена был
меньше, чем M, а другой больше, чем N (M < N), т.е. отрезок [M, N] целиком
лежал внутри интервала между корнями, необходимо и достаточно:
или
Задания
1. При каких значениях а все корни уравнения
2 2
6 2 2 9 0x ax a a     удовлетворяют
неравенству 3x  ?    1 11/9;U
2. Найти наибольшее значение а , при котором оба корня уравнения
2
3 4 0x x a  
принадлежат интервалу  2/3;2 .  4
3. При каких значениях параметра a одиниз корней уравнения    2 2 2
1 1 5 0a a x a x a     
больше 3, а второй – меньше 3?
3 3 3 3
;
2 2
    
  
 
4. Решить 1 0x x a   при 0a   1 1 4 / 2x a    ;
при 0 1/4a     1,2 31 1 4 / 2, 1 1 4 / 2x a x a        ; при 1/4a   1 1 4 / 2x a   
2. ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
2.1 Равносильныепереходы в дробно-рациональныхуравнениях
Дробь равна 0






0)(
0)(
0
)(
)(
xQ
xP
xQ
xP

37.  Дробь равна нулю тогда и только тогда,когда ее числитель равен нулю, а знаменатель не
равен нулю.
Применение основного свойства пропорции Дробь равна 1









0)(
0)(
)()()()(
)(
)(
)(
)(
xF
xQ
xRxQxFxP
xF
xR
xQ
xP
Универсальный алгоритм решения дробно-рационального уравнения:
• Найти общий знаменатель дробей, входящих в уравнение;
• Умножить обе части уравнения на общий знаменатель;
• Решить получившееся целое уравнение;
• Исключить из его корней те, которые обращают в нуль общий знаменатель.
• Выполнить проверку и записать ответ.
ПРИМЕРЫ
1.
• Решение:
• ОДЗ:
Знаменатель при данных значениях
х не обращается в нуль,
следовательно 0 и 0,5–корни
уравнения.
0 +2 = 2 – не равно нулю
0,5+2=2,5
Ответ :0;0,5
2.
• Решение
• ОДЗ:
Исходное уравнение не
.1
3
4
2
1






x
x
x
x
.1
3
4
2
1






x
x
x
x
01
3
4
2
1






x
x
x
x
0
)3)(2(
)3)(2()2)(4()3)(1(



xx
xxxxxx
0
)3)(2(
)3)(2()2)(4()3)(1(



xx
xxxxxx
3
03


x
x
2
02


x
x






0)(
)()(
1
)(
)(
xQ
xQxP
xQ
xP
0
2
4
2 2




x
x
    0
2
422
2
2



x
xx
0
2
442
2
2



x
xx
5,0
2
1
0120
0)12(
02 2




x
xилиx
xx
xx
0
2
2
2
2



x
xx
2
02
2
2


x
x

38. имеет корней, так как
числитель равносильного
уравнения не имеет
корней.
Ответ: нет корней.
3.
x = -8 Ответ: -8.
2.2 Замена вдробно-рациональныхуравнениях
4.
2
2
9 3
5x x
x x
 
    
 
Решение. О.Д.З. уравнения: 0.x 
Введем замену:
3
;x y
x
 
тогда
2
2
2
3 9
6,x x
x x
 
    
  откуда
2 2
2
9
6.x y
x
  
С учетом замены получим уравнение:
2
5 6 0,y y   которое имеет два корня: 2y 
и 3.y  Возвращаясь к исходной переменной, получим совокупность двух уравнений:
3
2;
3
3.
x
x
x
x

 

  

2
2
2 3 0;
3 3 0.
x x
x x
   
 
  
Первое уравнение совокупности имеет два корня : 1x   и 3.x 
Дискриминант второго уравнения совокупности 21D  , следовательно, корни
уравнения
3±√21
2
.Ответ: {-1; 3;
3±√21
2
}.
5.
6
352
2
32
13
22



 хх
х
хх
х
3
1
189
3
65
72
22






xxxxx
x
0
3
1
)3)(6(
3
)1)(6(
72







xxxxx
x
0
)3)(1)(6(
24112



xxx
xx





0)3)(1)(6(
024112
xxx
xx






















3
1
6
3
8
x
x
x
x
x
0
)3)(2(
62384233 222



xx
xxxxxxxxx
0
)3)(2(
532



xx
xx
0209 D
0532
 xx

39. Решение. Разделим числитель и знаменатель дробей на x  0:
13 / (2x + 1 + 3 / x) + 2 / (2x – 5 +3 / x) = 6,обозначим 2x + 3 /x = t.
Получаем 13 / (t + 1) + 2 / (t – 5) = 6, т.е. 13t – 65 + 2t + 2 = 6t2 – 24t – 30, т.е.6t2 – 39t +
33 = 0, т.е. 2t2 – 13t + 11 = 0, t1 = 1; t2 = 5,5.Следовательно: 2x + 3 / x = 1; 2x2 – x + 3 =
0; D = 1 – 24 < 0 нет решений .
2x + 3 / x = 5,5; 4x2 – 11x + 6 = 0; x1 = 2; x2 = 0,75.Ответ: x1 = 2; x2 = 0,75.
6 .
81х2
(9+x)2+х2=40
Решение. Воспользуемся формулой: a2 + b2 = (a – b)2 + 2ab
(a - b)2 = a2 - 2ab + b2 , a2 + b2 = (a - b)2 + 2ab. Получаем:
(x – 9x / (9 + x))2 + 2x× 9x / (9 + x) = 40, или (x2 / (9 + x))2 + 18x2 / (9 + x) = 40.
Пусть: (x2 / (9 + x)) = t. Тогда t2 + 18t – 40 = 0, t1 = – 20; t2 = 2. Получаем два
уравнения: (x2 / (9 + x)) = 2; x2 – 2x – 18 = 0; x1,2 = 1 ± √19,
(x2 / (9 + x)) = – 20; x2 + 20x + 180 = 0; D = 400 – 720 < 0, нет решений .
Ответ: x1,2 = 1 ± √19.
2.3 Дробно-рациональные уравнения c модулем
При решении уравнений, содержащих переменную под знаком модуля, чаще всего
применяются следующие методы:
1) раскрытие модуля по определению:
2) метод разбиения на промежутки;
3) возведение обеих частей уравнения в квадрат.
6. Раскроем модуль по определению ОДЗ: х ≠ -1







),(
,0
),(
)(
xf
xf
xf
1
1
4
3 

 x
x
если f (x) >0
если f (x) =0
если f (x) <0

40. Ответ: -5:3.
7. ОДЗ: х ≠ 0
Для решения этого уравнения воспользуемся методом разбиения на промежутки.
Нанесем на числовую прямую значения х, при которых |х| =0 и |х+1| =0.
Числовая прямая при этом разобьется на промежутки:(-∞; -1], (-1; 0) (0;+ ∞).
Решим заданное уравнение на каждом из этих промежутков.
Ответ:
8. ОДЗ: х ≠ 0
Если , то уравнение решений не имеет, т.к. при любых значениях х.
Если , то обе части уравнения неотрицательны. Возведем обе части уравнения

























1
1
4
3
1
1
1
4
3
1
x
x
x
x
x
x




























0
1
5
1
0
1
6
1
2
2
x
xx
x
x
xx
x









































1
5
0
1
1
3
2
1
x
x
x
x
x
x
x
x







5
3
x
x
x
x
x
1
11







































x
x
x
x
x
x
x
x
x
x
x
x
1
2
0
1
2
01
1
1






































0
1
0
0
13
01
0
1
1
2
2
2
x
xx
x
x
xx
x
x
xx
x





















































0
2
51
0
0
2
53
01
0
2
51
1
x
x
x
x
x
x
x
x
x

















2
51
2
53
x
x
.
2
53
,
2
51 
x
x
3
2 
0
3

x
02 x
0
3

x
Х
-1 0

41. в квадрат.
х = 3 Ответ: +3.
9. ОДЗ: х ≠  3
Пользуясь определением раскроем сначала «внутренний» модуль, а затем решим
совокупность двух полученных систем.
или
1)
х – любое число из [0;3)
2) x >3
х – любое число из (3; +∞)
1) x<-3
x=0 0 (-∞; -3)
2) -3<x<0
x=0, 0  (-3;0)
Ответ: [0;3)  (3;+ ∞).
2.4 Решение дробно-рациональных уравнений с параметром
10.
x
x
3
2  





2
2 9
)2(
0
x
x
x








0
9)2(
0
2
22
x
xx
x








0
)32)(32(
0
2
22
x
xxxx
x

















0
0
032
032
2
2
x
x
xx
xx





















0
0
1
3
x
x
x
x
xx
x




3
1
9
3
2










xx
x
x
3
1
9
3
0
2 









xx
x
x
3
1
9
3
0
2
30  x
xx
x




3
1
9
3
2
xx 

 3
1
3
1
3
1
9
3
2




xx
x
3
1
3
1


 xx
xx
x





3
1
9
3
2
0
3
1
3
1



 xx
0
9
33
2



x
xx





3
0
x
x
xx
x




3
1
9
3
2
0
3
1
3
1



 xx
0
9
33
2



x
xx





3
0
x
x
xaxa
a
)2(
52
2
3





Х
0 3-3
Х
-3 0 3
Х
-3 0 3

42.  если а ≠ -3, а ≠ -2, то выясним, при каких значениях а х=0
, . если а = -3, то нет решения. при а = -3, а = -2, нет
решений. Ответ: при а ≠ -3, а ≠ -2,
11.
если , то выясним при каких m x=1
, нет решений
если m = 1, то х - любое число, х ≠ 1  если m = -1, m=0, то нет решений.
Ответ: при ,при m = 1, то х - любое число кроме 1,
при m = -1, m=0 нет решений.
12.
x² -2x(a+1)+(a2+2a-3)=0 D1=(a+1)2-(a2+2a-3)
D1= a2 +2a+1-a2-2a+3=4 x 1= a+3 x2= a-1 выясним, при каких а каждый из
корней принимает значение 2 x1= a+3=2 x2= a-1=2 а= -1





0)2(
5)2(2)3(
ax
axa








2
0
12)3(
a
x
aax
3
12



a
a
x
0
3
12



a
a
2
1
a
3
12



a
a
x
2
1
a
2
1
a
)1(
11



xm
m
m
m





0)1(
)1()1()1(2
xm
mxxm








1
0
1122
x
m
mxmxm








0
1
)1)(2()1( 2
m
x
mmmx
0,1  mm 1
2



m
m
x
1
1
2



m
m
0
1
1

m
0,1  mm 1
2



m
m
x
2
12
1
2





x
ax
a
x





0)2)(1(
)1)(12()2)(2(
xa
aaxxx








2
1
1224 22
x
a
axaaaxx








2
1
0)32()1(2 22
x
a
aaaxx








2
0
5423
a
x
axax

43. а=3 х =6 Ответ: при а= -1 нет решений,при а≠-1, a≠3 – два решения: x1= a+3
x 2= a-1,при a = 3 – одно решение: х =6.
13. Сколько корней имеет уравнение при различных значениях параметра а.
Для решения этой задачи целесообразно использовать графический метод.
; D(y): x ≠ 1
При a  -1 нет решений При -1<a  1 один корень. При a > 1 два
корня
14.Сколько корней имеет уравнение .
; y=x2+a D(y): x ≠  1
a
x
x



1
1
1
1



x
x
y














1,
1
1
1,
1
1
x
x
x
x
x
x
y













1,
1
2
1
1,
1
2
1
x
x
x
x
y
ax
x
x


 2
1
1
1
1



x
x
y 












0,
1
2
1
01,1
1,1
x
x
x
x
y
0
-
1
1
Y
X

44. При a ≥ 0 - один корень. При -1<a < 0 - два корня
При a = -1 и a  -2 - три корня. При -2 <a < -1 – четыре корня
Задания
Уровень А Уровень В Уровень С
1   
  
2
2
3 1 6 2 5 8 4
9 1 3 1 2
x x x x
x x x
   

      
2
1 1 1
2 121x x x
 
   
3
3
1 13
41
x
x



-4 –3;1 –3; -1/3
2
 
2 2
2 2
4 9 6 15
3 102 3
x x x
x xx
  

 
     
24 15
2
4 2 3 1x x x x
 
   
 
4
4
1
2
1
x
x



1; 5 –2;0; 2 66 /2  1 3 3 2 3  
3
 
2 2
2 2
4 6 5 4
16 36 2 11 12
x x x
x x x
  

  
     
6 8
1
1 2 1 4x x x x
 
   
 
5
5
1
0,088
1
x
x



4 –3;0;  3 73 / 2   30 3598 60 3598 1278 /76  
4
  
1 2 5 2
0
2 2 3 3
x
x x x x

  
    2 2
2 1
1 1 12
x x
x x x x
 
     
2
2
2
1
1
x
x
x
 

-4  5 21 / 2 ;  7 45 / 2
 2 1 2 2 1 / 2  
5
2
3 2 3
0
1 3 4 4
x x x
x x x x

  
   
2
2 2
10 13 3
6 13 8 13
x x x
x x x x
 

     
2
2
2
9
7
3
x
x
x
 

-0,5;3 1;13  1 13 / 2
Y
X0
-
1
1
-
1

45. 6  
2
2 11 61 3 2
6 4 12 2
xx x
x x x x

 
   
 
   
22
2 2
1 49
451 1
x x
x x
 

 
 
2
2
2
25
11
5
x
x
x
 

7 0.5;2; 9 65 /4   1 21 /2
7
2
2 3 1 1
3 2 1 2
x
x x x x

 
   
2
2
1 1
2 6x x
x x
 
    
 
 22 2
2
2 11 2 1 3
1 2 1 3 1
xx x x x
x x x x x
        
      
         
  2, 1x R x x     1; 2 3  0
8 2
2
5 9 3
10 21 2 3 5 7
x x x
x x x x
 
 
   
2
2
48 4
10
3 3
x x
x x
 
   
 
 22 2
2
2 42 1 2 4
2 1 2 4 4
xx x x x
x x x x x
        
      
         
  1.4, 1.5x R x x    0.5 ; 1 17 /8  0; 6 2 10 
9
 
2
23
5 1 2
3 2 2 1
x
x x x x

 
   
2
2
1 1
16 4 8 0x x
x x
      22 2
2
2 11 2 1 3
1 2 1 3 1
xx x x x
x x x x x
        
      
         
  1, 2x R x x    –2;6;3 21 ; 0;
   1 2 2 57 4 2 20 6 / 2 3 2 2    
10 2 2
2 2
2 2 2 1 7
2 3 2 2 6
x x x x
x x x x
   
 
   
3 7 3
7 3
x
x
x



1 2 3 4
4
1 2 3 4
x x x x
x x x x
   
   
   
–2;0  1; 7 13 /6   5 345 /10 
11 2 2
2 2
4 2 3 2 2
2
2 1 6 3 1
x x x x
x x x x
   
 
   
4 7 5
5 7
x
x
x
 


2 1 3 1 7
4
1 2 1
x x x
x x x
  
  
  
–1;0.5 –1 –1.25;5
12 2
2 2
1 35 56 25 3
5 8 5 20 32 28 4
x x
x x x x
 
 
   
5 133 78
133 78
x
x
x



2 2
4 4 2 6 1 2 9
4 2 1 3
x x x x x x
x x x x
     
  
   
–1;-0.6 1 ; 2/3;1.5; 0;  5 3 / 2 
3. Системы рациональных уравнений
Рассмотрим системы, состоящие из уравнений с двумя неизвестными. Если в одно из
них какое- нибудь неизвестное входит лишь в первой степени, то из этого уравнения
можно выразить это неизвестное через другое и подставить полученное выражение во
второе уравнение системы. Получится уравнение с одним неизвестным. Решая его,
находим значения этого неизвестного, а потом по ним находим значения оставшегося
неизвестного
3.1 Системы линейныхуравнений.
Уравнение вида a1x1 + a2 x2 + … + an xn = b,
где a1, b2, … ,an, b —некоторые постоянные, называется линейным уравнением с n
неизвестными x1, x2, …, xn.
Система уравнений называется линейной, если все уравнения, входящие в систему,
являются линейными. Если система из n неизвестных, то возможны следующие три
случая: система не имеет решений; система имеет ровно одно решение; система
имеет бесконечно много решений.
Примеры:. решить систему уравнений

46. 1.
Решение. Решить систему линейных уравнений можно способом подстановки,
который состоит в том, что какого-либо уравнения системы выражают одно
неизвестное через другие неизвестные, а затем подставляют значение этого
неизвестного в остальные уравнения.
Из первого уравнения выражаем: x= (8 – 3y) / 2. Подставляем это выражение во
второе уравнение и получаем систему уравнений
Из второго уравнения получаем y = 2. С учётом этого из первого уравнения x = 1.
Ответ: (1; 2).
2.
Решение. Система не имеет решений, так как два уравнения системы не могут
удовлетворяться одновременно (из первого уравнения x + y = 3, а из второго x + y =
3,5). Ответ: Решений нет.
3.
Решение. Система имеет бесконечно много решений, так как второе уравнение
получается из первого путём умножения на 2 (т.е. фактически есть всего одно
уравнение с двумя неизвестными). Ответ: Бесконечно много решений.
4.
Решение. При решении систем линейных уравнений удобно пользоваться методом
Гаусса, который состоит в преобразовании системы к треугольному виду.
Умножаем первое уравнение системы на – 2 и, складывая полученный результат со
вторым уравнением, получаем – 3y + 6z = – 3. Это уравнение можно переписать в
виде y – 2z = 1. Складывая первое уравнение с третьим, получаем 7y = 7, или y = 1.
Таким образом, система приобрела треугольный вид Подставляя y =
1 во второе уравнение, находим z = 0. Подставляя y =1 и z = 0 в первое уравнение,
находим x = 1.Ответ: (1; 1; 0).
5. При каких значениях параметра a система уравнений

47. имеет бесконечно много решений?
Решение. Из первого уравнения выражаем x: x = – (a / 2)y + a / 2 +1.
Подставляя это выражение во второе уравнение, получаем
(a + 1)( – (a / 2)y + a / 2 +1) + 2ay = 2a + 4.
Далее умножим обе части уравнения на 2 и упростим его:(a + 1)(a + 2 – ay) + 4ay = 4a
+ 8, 4ay – a(a + 1)y = 4(a + 2) – (a + 1)(a + 2), ya(4 – a – 1 ) = (a + 2)(4 – a – 1),
ya(3 – a) = (a + 2)(3 – a). Анализируя последнее уравнение, отметим, что при a = 3 оно
имеет вид 0y = 0, т.е. оно удовлетворяется при любых значениях y. Ответ: 3.
3.2 Системы уравнений второй степени.
В простейших случаях при решении систем уравнений второй степени удаётся
выразить одно неизвестное через другое и подставить это выражение во второе
уравнение.
При решении систем уравнений второй степени часто используется также способ
замены переменных.
6. Среди решений (x; y) системы найти то, для которого сумма (x + y)
максимальна. Вычислить значение этой суммы.
Решение. Из первого уравнения получаем y = 7 – 2x. Подставляя значение y во второе
уравнение, получаем систему уравнений
Квадратное уравнение – 2x2 + 7x – 6 = 0 имеет корни x1 = 2; x2 = 3 / 2. Из первого
уравнения получаем y1 = 3; y2 = 4.Решения имеют вид (2; 3) и (1,5; 4). Наибольшая
сумма x + y = 1,5 + 4 = 5,5.Ответ: 5,5.
3.3 Симметрическиесистемы
Напомним, что многочлен P (x, y) называется симметрическим, если P(x,y)=P(y,x).
При решении систем уравнений вида где P1 (x, y) и P2 (x, y) —
симметрические многочлены, полезной оказывается такая замена неизвестных:
x + y = U, xy = V. Напомним, что любой симметрический многочлен P (x, y) можно
представить как выражение от U и V.
7.
Решение. Обозначим a = x + y; b = xy. Получаем систему уравнений

48. Отсюда . Возвращаясь к переменным x и y, получаем
Решив эту систему:
y2 – 3y + 2 = 0, y1 = 1;x1 = 2; y2= 2; x2 = 1. Ответ: (2; 1) , (1; 2)
8.
Решение. Сначала введём неизвестные X и Y: X = 1 / x, Y = 1 / y,
а затем U и V: U = X + Y = 1 / x + 1 / y, V = XY = 1 / xy.
Получается система: из которой U = 5, V = 6. Далее решая систему
находим X1 = 2, Y1 = 3; X2 = 3, Y2 = 2, откуда получаем x1 = 1 / 2, y1 = 1 / 3;
x2 = 1 /3, y2 = 1 / 2. Можно сразу ввести неизвестные U = x + y, V = xy, получится
система приводящая к тем же решениям исходной системы.
Ответ: x1 = 1 / 2, y1 = 1 / 3; x2 = 1 /3, y2 = 1 / 2.
Системы неоднородных уравнений
9.
Решение. Ни одно из уравнений системы не является однородным. Но если умножить
первое уравнение на 7 и прибавить к нему почленно второе уравнение, умноженное
на 3, то получится уравнение 7y2 - 10xy + 3x2 = 0, являющееся следствием исходной
системы. Разделим обе части уравнения на x2 и решим уравнение 7U2 - 10U + 3 = 0
(здесь U = y / x, причём из второго уравнения системы следует, что x ≠ 0). Находим,
что y = x или y = 3x / 7. Подставляя это выражение во второе уравнение и, рассмотрев
оба случая, найдём решения:
x1 = 7, y1 = 3; x2 = - 7, y2 = - 3. Ответ: x1 = 7, y1 = 3; x2 = - 7, y2 = - 3.
Мы получили решения системы путём выведения из заданных уравнений
вспомогательного следствия. Такой способ решения систем в некоторых случаях
приводит к появлению “посторонних” корней — значений x и y, не удовлетворяющих
исходной системе. Поэтому найденные корни надо проверить, подставив их

49. исходную систему и убедившись, что уравнения системы обращаются в верные
числовые равенства.
3.5 Системы уравнений с параметрами
10. При каких значениях a система уравнений
имеет единственное решение?
Решение. Умножим второе уравнение на a и вычтем его из первого уравнения.
Получаем равносильную систему
Если a = 1, то - 3y + 0,5 = 0, т.е. y = 1 /6. Подставив это значение во второе уравнение,
находим единственное значение x. Система имеет единственное решение. Если a =
- 0,5, то система имеет единственное решение.
При остальных значениях a сведём систему к квадратному уравнению; из первого
уравнения системы находим y = ((1 - a)x +1,5 - a) / (2a +1), подставляем во второе
уравнение: x + ((2 - 2a)x + 3 -2a) / (2a + 1) + ((1 - a)x2 +1,5x - ax) / (2a +1) +1 = 0, т.е.
2ax + 3x - 2ax + 3-2a + x2 – ax2 +1,5x - ax + 2a +1 = 0, (1-a)x2+(4,5 - a)x +4 = 0.
Уравнение имеет единственное решение в том случае, когда дискриминант равен
нулю:(9 / 2 - a)2 - 4× 4(1 - a) = 0, т.е. a2 + 7a + 17 / 4 = 0, т.е. a = (- 7 ± 4√ 2) / 2.
Ответ: a = 1, a = - 1 / 2, a = (- 7 ± 4√2) / 2.
3.6 Графический способ решениясистем уравнений
Системы нелинейных уравнений с двумя неизвестными можно решать графически.
Для этого нужно начертить графики обоих уравнений и найти координаты точек их
пересечения. Нам уже известны графики следующих уравнений:
ax + by + c = 0 — прямая линия. xy = k — гипербола.
(x - a)2 + (y – b)2 = R2 — уравнение окружности с центром A(a, b) и радиусом R.
К этому виду приводятся с помощью выделения полных квадратов уравнения вида:
x2 + y2 - 2ax - 2by + c = 0. ax2 + bx + c = 0 — парабола y = ax2 c вершиной в точке
A(m, n), где m = - b / 2a, а n = (4ac - b2) / 4a.
11.
Решение. Найдём графически корни системы, выделяя полные квадраты, получаем:
x2 + y2 - 2x + 4y - 20 = (x2 - 2x +1) + (y2 + 4y + 4) - 1 - 4 - 20 = (x - 1)2 + (y + 2)2 - 25.

50. Значит, систему уравнений можно записать так:
Графиком первого уравнения является окружность с центром A(1; - 2) и радиусом 5.
А 2x - y = - 1 — уравнение прямой, проходящей через точки B(0; 1) и C(2; 5). Строим
окружность радиуса 5 с центром в точке A и проводим прямую через точки B и C.
Эти линии пересекаются в двух точках M(1; 3) и N(- 3; - 5). Значит решение системы
таково:
x1 = 1, y1 = 3; x2 = - 3, y2 = - 5.
Замечание: уравнение х2 - 8х + 15 = 0 можно вывести быстрее, используя теорему,
обратную теореме Виета: так как сумма чисел х и у равна 8, а их произведение равно
15, то эти числа являются корнями уравнения z2 - 8z + 15 = 0.
Задания
Уровень А Уровень В Уровень С
1 3 3
2 3 0
7 2 8 1
x y z
x y z
x y z
  

  
   
2 2
25
12
7
x y
y x
x y

 

  
2 2 2
3 3 3
1
1
1
x y z
x y z
x y z
  

  
   
 1;1;1  4;3    1;0;0 , 0;1;0 ,  0;0;1
2 3
3 3
2 3
x y z
x y z
x z
  

  
  
2 2
10
3
5
x y x y
x y x y
x y
 
 
 
  
18
20
8
xy yz
xz zy
yx xz
 

 
  
 ; ;3 2 ,a a a a R   2;1  1; 3; 5  
3 1
3 1
3 3 3
x y z
x y z
x y z
  

  
   
2 2
13
6
1
x y
y x
x xy y

 

   
1 1 1 11
6
2 3 4 29
6
3 4 5 8
3
x y z
x y z
x y z

  


  


  

 ;1 ;0 ,a a a R   3/ 11; 2/ 11 ,   2; 3   1;2;3
4 2
3 9 27 0
3 3 28
2
9
x y x xy
x y
x
    

  


2 2
2 2
2 0
3 7 3
x xy y
x xy y x y
   

     
2 2
2 2
2 2
( ) 1
( ) 1
( ) 4
x y z
y z x
z x y
   

  
   

51.  1;3     3; 3 , 13 157; 13 157 / 2    
, 1; 1
 1.25; 1.25; 2  
5 2
3 2 6 4 0
12 3 17
1
3 2
x y xy x
x y
x
    

  


2 2
2 2
3 5 2 0
5 6
x xy y
x xy y x y
   

    
2 2 2
2 3
2 0
2 4 3 0
x y x y
x x y
   

   
 1;2
 24/19; 36/19 , 
 1 3;1 3 , m  4;6
 1; 1
6 2
3 3 0
4 7
3
1
xy xy y
x y
y
    

 
 
2 2
2 2
2 3 3
2 2 6
x xy y
x xy y
   

  
 
 
3 3
2 2 2 2
13
468
x y xy x y
x y x y
    

 
 1;3  2; 1     2;3 , 3; 2 
7 1
5
2
2 3 2
x y
y x

  

   
1 2 1
3 1
x y
y x
    

   




2432
202415
yx
yx
 0,3;4,4  3; 2
8 2 10 2 0
2
2 12 1 0
y
y x
x x y

    

     
5 3 4
3 4 2 8
x y
y x
   

   




232
202415
yx
yx
   3;1 , 5/3;11/3  3;2
4. Решение задачна составление уравнений
4.1Задачи на проценты
1. Яблоки при сушке теряют 85% своей массы. Сколько надо взять свежих
яблок, чтобы получить 30 кг сушёных?
Вода
сушёные
яблоки
15% — 30кг
Решение: 30:15*100=200 (кг) Ответ: 200 кг.
2. В сплаве олова и меди медь составляет 85%. Сколько надо взять сплава,
чтобы в нём содержалось 4,5 кг олова?
Медь 85 %
Олово
15%—4,5 кг
Решение: 4,5:15*100=30 (кг) Ответ: 30 кг.
3. Сначала приготовили 25%-ый водный раствор поваренной соли. Затем одну
треть воды выпарили. Найти концентрацию получившегося раствора.
Решение. До выпаривания:
NaCl Н
2
О Н
2
О Н
2
О
25% 25% 25% 25%
После выпаривания:
NaCl Н
2
О Н
2
О
33
3
1 % 33
3
1 % 33
3
1 %
Сейчас соль стала составлять одну треть всего раствора или 33 3
1
%Ответ: 33 3
1
%

52. 4. Имеется два сплава золота и серебра. В одном количество этих металлов
находится в отношении 1:9, а в другом 2:3. Сколько нужно взять каждого сплава,
чтобы получить 15 кг нового сплава, в котором золота и серебро относилось бы
как 1:4?
Золото(кг) Серебро(кг) Общая масса(кг)
1 сплав 0,1 х
2 сплав 0,4(15-х) 15-х
Новый сплав 0,2*15=3 15
0,1х+0,4(15-х) =3 x =10 m (1 сплава) =10 (кг) m (2 сплава) =15–10 =5 (кг)
Ответ: 10 кг, 5 кг.
5. Имеются два куска сплава меди с цинком. Процентное содержание меди в них
p1 % и p2 % соответственно. В каком отношении нужно взять массы этих
сплавов, чтобы, переплавив взятые куски вместе, получить сплав, содержащий
p% меди?
Массовая доля
меди в сплаве
Масса каждого
сплава
Масса меди в
каждом сплаве
I сплав p1 % m1 кг
100
11 pm
кг
II сплав p2 % m2 кг
кг
Новый
сплав
p% ( m1 +m2 ) кг
100
)( 21 pmm 
кг
Зная, что масса меди в новом сплаве есть сумма масс меди в каждом из взятых
кусков, составим уравнение 100
11 pm
+ 100
22 pm
= 100
)( 21 pmm 
, m1 (p1 -
p) = m2 ( p – p2)
I случай. Если p1 , p2 и p попарно не равны, то получим формулу
m1 (p1 - p) = m2 ( p – p2)
II случай. Возьмём два сплава с одинаковым процентным содержанием меди,
т.е. p1=p2 . Решая уравнение (*) , получим, что p1=p2=p , что очевидно, поскольку ни
большей, ни меньшей концентрации сплав просто не получится, если исходные
материалы имеют одинаковую процентную концентрацию меди, каковы бы ни были
массы исходных сплавов.
III случай: p2 =p , или же будет сказано, что p1= p , вывод тот же.
Заметим, что если взять два сплава, массы которых одинаковы, т.е. m1 = m2 , то
то есть процентное содержание нового сплава станет равно среднему
арифметическому процентных концентраций исходных сплавов. Это очень полезное
следствие для равных масс исходных сплавов поможет нам в решении некоторых
задач.
6. Из сосуда, наполненного кислотой, вылили несколько литров и долили водой;
потом опять вылили столько же литров смеси; тогда в сосуде осталось 24 л
чистой кислоты. Ёмкость сосуда 54 л. Сколько кислоты вылили в первый раз и
второй раз?
100
22 pm
pp
pp
m
m



1
2
2
1
2
21 pp
p



53. Решение. Обратим внимание, что на втором шаге воду не доливали.
По условию задачи объём сосуда, наполненного кислотой, 54 л. Её концентрация
100%. Пусть вылили Х литров смеси, тогда в сосуде осталось (54-Х) литров 100%-ной
кислоты. В сосуд доливают Х л воды. По определению массовой доли кислоты надо
массу кислоты разделить на массу раствора: (54-Х)/54.
Опять выливают Х литров смеси, в сосуде остаётся (54-Х) л смеси с массовой долей
кислоты (54-Х)/54.
Чтобы найти массу кислоты в этой оставшейся смеси, надо массу раствора умножить
на массовую долю чистой кислоты в этом растворе. По условию масса чистой
кислоты в этом растворе стала 24л. Составим и решим уравнение:
(54-Х)* ((54-Х)/54) = 24, (54-Х)2 = 1296, зная, что Х меньше 54, получим
единственное решение Х = 18. В первый раз вылили 18 литров чистой кислоты. Но
во второй раз выливали 18 литров смеси, в ней чистой кислоты было 18* (54-18)/54 =
12 (л) Ответ: 18 л; 12л
1. Какое наибольшее число избирателей могло принять участие в выборах из двух
кандидатов на должность руководителя предприятия при условии, что пятнадцатая
часть избирателей проголосовала за обоих кандидатов сразу, 10% - только за первого
кандидата, 72% - только за второго, а недействительными признано не более 35
бюллетеней? 300.
2. Некоторый материал снижает свою прочность за один год на 20%. Каков общий
процент снижения прочности данного материала за два года? 36%.
3. С одного счета на другой перечислили 10% денег, затем еще 200 тенге и, наконец,
еще 20% от остатка. В результате количество денег на втором счете увеличилось на
9%. Сколько денег было вначале на первом счете, если на втором было 8000 тенге? 2
тыс. тенге.
4. В школьной газете сообщается, что процент учеников 7"Б" класса, повысивших в
первом полугодии успеваемость, заключен в пределах от 2,9% до 3,1%. Определить
минимально возможное число учеников в 7"Б" классе. 33
5. Длину кирпича уменьшили на 25%, ширину уменьшили на 20%, высоту увеличили
на 65%. Увеличился или уменьшился от этого объем кирпича и на сколько
процентов? Уменьшился на 1%.
6. Имеется два слитка, содержащие медь. Масса второго слитка на 3 кг больше массы
первого. Процентное содержание меди в первом слитке равно 10%, во втором – 40%.
После сплавления этих слитков получился слиток с содержанием меди 30%.
Определить массу полученного слитка. 9 кг
7. Имеются три слитка. Первый содержит 90% золота и 10% платины, второй - 20%
серебра и 80% платины, а третий - по 40% серебра и платины и 20% золота. Их
сплавили, и в полученном слитке содержание платины оказалось равно 20%. Какое
наименьшее и какое наибольшее процентное содержание серебра может быть в этом
новом слитке? 20/7%, 40/3%.

54. 8. От 10 литров 60%-го раствора кислоты в воде отлили некоторое количество
раствора и долили такое же количество чистой кислоты, после чего содержание
кислоты в растворе увеличилось до 80%. Найдите, сколько литров раствора было
отлито? 5л.
9. При проведении опроса среди населения выяснилось, что большая часть
опрошенных предпочитает отдыхать в Казахстане, а не за рубежом. Пять человек
затруднились сделать выбор. Среди любителей отдыха за рубежом 90%
предпочитают отдых в горах другим видам отдыха. Среди любителей отдыха в
Казахстане 56,25 % предпочитают отдых у моря, 31,25 % предпочитают отдых в
горах, а оставшиеся два человека предпочли отдых на даче. Сколько человек было
опрошено? 31.
10. Число А больше числа В в пять раз. На сколько процентов число В меньше числа
А? 75%
11. Число А меньше числа В на 40%. На сколько процентов число В больше числа А?
200/3%.
4.2 Задачи на работу
1. Заказ по выпуску машин завод должен был выполнить за 15 дней. Выпуская в
день на 2 машины больше, чем планировалось, завод уже за 2 дня до окончания
срока выпустил на 6 машин больше. Сколько машин в день должен был
выпускать завод по плану?
наименование производительность
машин в день
Время
дни
Работа
машины
по плану
15
х 15 х
фактически
2
1513
6

 хх 13 х+6
2
1513
6

 хх
х=150,
10
15

х
машин в день по плану.
11. Соревнуются три бригады. Первая и вторая бригады совместно изготовили в 6 раз
деталей больше, чем третья бригада, а первая и третья совместно в 2,5 раза больше,
чем вторая. Во сколько раз больше изготовила деталей бригада-победитель, чем
бригада, занявшая последнее место в соревновании?
Решение. Пусть первая бригада изготовила x деталей, вторая y деталей, а третья - z
деталей. По условию задачи: 




yzx
zyx
5,2
6
. Решение этой системы можно представить
в виде: zx 4 ; zy 2 . Отсюда видно, что больше всех деталей изготовила первая
бригада, а меньше всех – третья. Причем первая бригада изготовила деталей в 4 раза
больше, чем третья. Ответ: в 4 раза.

55. 12. Баржа была разгружена с помощью двух подъемных кранов за 15 ч, причем
второй кран приступил к работе на 7 ч позже первого. Известно, что второй кран,
работая один, может разгрузить баржу на 5 ч быстрее, чем первый. За сколько часов
смог бы разгрузить баржу каждый кран, работая отдельно? 25ч. и 20ч
13. Двое рабочих за смену изготовили вместе 72 детали. После того, как первый
рабочий увеличил производительность в 1,15 раза, а второй в 1,25 раза, они стали
изготавливать за смену 86 деталей. Сколько деталей изготавливает первый рабочий за
смену после повышения производительности труда? 46.
14. Три комбайна, работая вместе, убирают поле за 4 часа. Это же поле первый и
второй комбайны вместе убирают за 6 часов, а первый и третий вместе – за 8 часов.
Во сколько раз больше площадь, убираемая за час вторым комбайном, по сравнению
с площадью, убираемой за час третьим комбайном? В 1,5 раза.
15. На автозаводе расход металла на каждый автомобиль уменьшился на 80 кг. В
результате из 15960 кг металла изготовлено на 2 автомобиля больше, чем ранее
планировалось. Сколько металла теперь требуется на изготовление одного
автомобиля? 760 кг
16. Два насоса различной мощности, работая вместе, наполняют бассейн за 4 часа.
Для наполнения бассейна наполовину с помощью одного первого насоса требуется
времени на 4 часа больше, чем с помощью одного второго насоса для наполнения
бассейна на три четверти. За какое время можно наполнить бассейн каждым из
насосов в отдельности? 16ч. и 5ч.20м
17. В момент, когда два бассейна были пустыми, 7 труб одинаковой
производительности были подключены для заполнения первого бассейна. Когда
первый бассейн был заполнен на 1/4 его объема, три трубы переключили для
заполнения второго бассейна. Когда первый бассейн был заполнен на 1/2 его объема,
еще две трубы переключили для заполнения второго бассейна. После этого оба
бассейна заполнились доверху одновременно. Найти отношение объемов бассейнов.
23/16
18. В прошлом году объемы добычи угля на двух шахтах относились как 7:2. В этом
году объем добычи угля на первой шахте вырос на 10%, а на второй шахте
уменьшился на 8%. На сколько процентов увеличилась суммарная добыча угля на
двух шахтах в этом году? 6%.
19. Соревнуются три бригады. Первая и вторая бригады совместно изготовили в 6 раз
деталей больше, чем третья бригада, а первая и третья совместно в 2,5 раза больше,
чем вторая. Во сколько раз больше изготовила деталей бригада-победитель, чем
бригада, занявшая последнее место в соревновании? 4
4.3 Задачи на движение
Задача. Из пункта А в пункт В вышел пассажирский поезд. Одновременно с ним из
пункта В в пункт А отправился товарный поезд. Расстояние от места их встречи
до пункта В пассажирский поезд прошел за 1 час 48 минут, а товарный поезд

56. преодолел путь от места их встречи до пункта А за 3 часа 12 минут. Поезда шли с
постоянными скоростями. Сколько всего времени находился в пути товарный поезд?
Решение. Пусть С – точка встречи поездов, лежащая между А и В;
Vт – скорость товарного поезда; Vп – скорость пассажирского поезда;
t1= п
АС
V
- время, которое был в пути пассажирский поезд до встречи с товарным;
t2= т
ВС
V
- время, которое был в пути товарный поезд до встречи с пассажирским;
Очевидно, что t1=t2, т.е. п
АС
V
= т
ВС
V
. Так как расстояние СВ пассажирский поезд
прошел за 108 минут, то СВ=108* Vп, а расстояние АС товарный поезд прошел за 192
минуты, то АС=192* Vт. Подставив эти значения в уравнение (1), получаем
т п
т
192 V 108 V
Vп V
 

или
2
т
2
п
V 108 9
V 192 16
 

п
т
V 4
V 3

. Товарный поезд находился в пути t=
тV
ВС
+192=
п
т
108 V 4
192 108 192 144 192=
V 3

     
336минут=5часов 36минут.
Ответ: 5часов 36 минут
20. Велосипедист за каждую минуту проезжает на 500 м меньше, чем мотоциклист,
поэтому на путь в 120 км он затрачивает времени на 2 ч больше, чем мотоциклист.
Найти скорость движения велосипедиста. 30 км/ч.
21. Расстояние между двумя станциями пассажирский поезд проходит на 45 мин
скорее, чем товарный. Определить это расстояние, если известно, что скорость
пассажирского поезда равна 48 км/ч, а скорость товарного поезда - 36 км/ч. 108
км
22. Из двух городов, расстояние между которыми 150 км, одновременно выехали
навстречу друг другу велосипедист и мотоциклист. Скорость велосипедиста в 5 раз
меньше скорости мотоциклиста. Сколько километров проедет каждый из них до
встречи? 25 км, 125 км
23. В зимнем забеге на 400 м лыжнику удалось пробежать дистанцию со скоростью,
которая была на 1/3 м/с больше его прежнего результата. За счет этого он пробежал
дистанцию на 2 с быстрее, чем раньше. За какое время лыжник пробежал дистанцию
в 400 м? 48с
24. Из двух городов навстречу друг другу выезжают два велосипедиста и
встречаются через 6 ч. Известно, что первый из них проезжает расстояние между
городами на 5 ч быстрее второго. За сколько часов второй велосипедист может
проехать расстояние между городами? 15ч.
25. Кошка, гнавшаяся за мышкой вдоль длинного коридора, догнала ее через 5 секунд
после начала погони. Первоначальное расстояние между ними было 20 м. Если при

57. таком же начальном расстоянии мышка побежала бы не от кошки, а навстречу ей, то
была бы схвачена через 2 с. Полагая, что в том и в другом случае кошка и мышка
прилагали бы максимальные усилия, найти средние скорости каждой из них. 3 м/с
26. По сигналу дрессировщика два пони одновременно побежали равномерно вдоль
внешней окружности арены цирка в противоположных направлениях. Первый пони
бежал несколько быстрее второго и к моменту встречи пробежал на 5 м больше, чем
второй. Продолжая бег, первый пони подбежал к дрессировщику, остававшемуся на
том же месте, от которого начали бежать пони, через 9 с после встречи со вторым
пони, а второй – через 16 с после их встречи. Каков диаметр арены? 35/ м
27. Школьник должен был выйти из дома в 7:30, сесть в ожидавшую его машину и
доехать на ней до школы к определенному моменту. Однако он вышел из дома в 7:00
и побежал в противоположном направлении. Машина в 7:30 отправилась вслед за ним
и, нагнав его, доставила в школу с опозданием на 10 мин. Во сколько раз скорость
машины превосходит скорость бегущего школьника? В 7 раз
28. Между поселками А и В расстояние равно 4,35 км. Мотоциклист и велосипедист
отправились из этих поселков одновременно навстречу друг другу. Мотоциклист в
первую минуту проехал 450 м, а в каждую следующую минуту на 30 м меньше, чем в
предыдущую. Велосипедист первые шесть минут ехал со скоростью 60 м/мин, а затем
за каждую минуту проезжал на 10 м больше, чем за предыдущую. Какое расстояние
проехал велосипедист до встречи с мотоциклистом? 930 м
29. Из пункта А в пункт В выехал велосипедист. Через час из пункта А в пункт В
выехал мотоциклист, который прибыл в пункт В одновременно с велосипедистом.
Если бы они выехали одновременно из пунктов А и В навстречу друг другу, то они
встретились бы через 1,2 ч. Сколько времени провел в пути велосипедист? 3ч
4.4 Задачи на нахождение целочисленных значений
30. Если бы груз перевозили в вагонах вместимостью 80 т, то один ваго н оказался бы
загруженным не полностью. Если бы тот же груз перевозили в вагонах вместимостью
60 т, то понадобилось бы на 8 вагонов больше, и при этом все равно один вагон
остался бы не полностью загруженным. Наконец, если бы груз перевозили в вагонах
вместимостью 50 т, то понадобилось бы еще на 5 вагонов больше, но при этом все
вагоны были бы загружены полностью. Какова масса груза? 1750 т
31 В двух бригадах вместе 27 человек. Число членов первой бригады более чем в 2
раза превышает число членов второй бригады, уменьшенное на 12. Число членов
второй бригады более чем в 9 раз превышает число членов первой бригады,
уменьшенное на 10. Сколько человек в каждой бригаде? 11 и 16 чел.
32 В двух бригадах вместе не менее 27 человек. Число членов первой бригады более,
чем в три раза превышает число членов второй бригады, уменьшенное на 12. Число
членов второй бригады более, чем в 9 раз превышает число членов первой бригады,
уменьшенное на 11. Сколько человек в каждой бригаде? 12 и 15 чел.

58. 33 Рота солдат прибыла на парад в полном составе прямоугольным строем по 24
человека в ряд. По прибытии оказалось, что не все солдаты могут участвовать в
параде. Оставшийся для парада состав роты перестроили так, что рядов стало на 2
меньше прежнего, а число солдат в каждом ряду стало на 26 больше числа новых
рядов. Известно, что если бы все солдаты участвовали в параде, то роту можно было
бы построить так, чтобы число солдат в каждом ряду равнялось числу рядов. Сколько
солдат в роте? 144
34 Число двухкомнатных квартир в доме в 4 раза больше числа однокомнатных, а
число трехкомнатных кратно числу однокомнатных. Если число трехкомнатных
квартир увеличить в 5 раз, то их станет на 22 больше, чем двухкомнатных. Сколько
всего квартир в доме, если известно, что их не меньше 100? 132.

59. Используемая литература
 Сборник задач для поступающих в ВУЗы. Под редакцией М.И.Сканави. М.:
«Высшая школа». 2008г.
 Сборник задач по математике для поступающих в МГГУ. Под ред Редкозубова
С.А., М., издательство МГГУ, 2007.
 500 способов и методов решения задач по математике. А.Р.Рязановский. Для
школьников и поступающих в вузы. Дрофа. М.: 2001г.
 Уравнения и неравенства. Нестандартные методы решения. Учебно –
методическое пособие. 10 – 11 классы. С.Н.Олейник, М.К. Потапов,
П.И.Пасиченко. Москва. «Дрофа». 2001г.
 Г.Дорофеев, М.Потапов, Н.Розов. Математика для поступающих в вузы.
Дрофа.2002.
 Шарыгин И.Ф. Факультативный курс по математике. Решение задач: Учебное
пособие для 10 класса средней школы: М., “Просвещение”, 1994 г.
 Алгебра 9 класс. Н. Я. Виленкин. Москва, изд. “Просвещение”, 1995.
 Алгебра и математический анализ. 10 класс. Н. Я. Виленкин. Москва, изд.
“Просвещение”, 1997.
 Материалы с сайта «1сентября. Фестиваль педагогических идей»