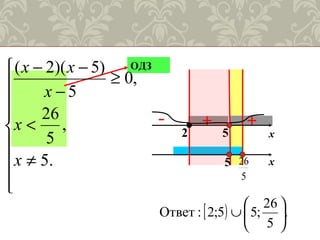
Документ описывает решение логарифмических неравенств, объясняя их определение и различия с показательными неравенствами. Также представлен алгоритм решения, включающий важные условия и ограничения, определяющие область допустимых значений. Приводятся примеры решений с разными значениями оснований логарифмов и их последствий для неравенств.




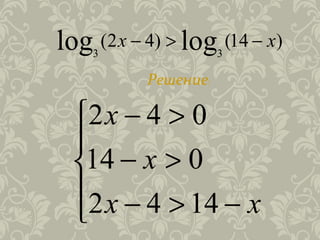











![;0
)98(log
)46(log
7,0
5
≥
+
+
x
x
−>
−>
≤
+
+
;
8
9
,
3
2
,0
88
36
х
х
х
х
x- 1
2
1
−
-+ +
x
x
8
1
1−
]
2
1
;
3
2
(:Ответ −−
>+
>+
≠+
≥
−+⋅−
−+⋅−
;098
046
,198
0
)198()17(0,
)146()15(
x
,х
x
,
х
х
3
2
−
Решим неравенство:](https://image.slidesharecdn.com/random-150128153034-conversion-gate02/85/slide-17-320.jpg)












![1
4
6
log 2
250
≤
− x
x,
−≠
≠
≠
<
≤
−−
⋅−
.2
,2
,0
,6
,0)
4
6
()125,0(
2
2
x
x
х
x
xх
x
( ] ( ) ( ) ( ).6;22;02;0-3;-:Ответ ∪∪∪−∞](https://image.slidesharecdn.com/random-150128153034-conversion-gate02/85/slide-31-320.jpg)

![;3
3
log
3
log 5
4
5 ≤
−
+
−
++
x
x
x
x
xx
−≠
−>
>
<
≤
−
+
;4
,5
;3
,0
,3
3
log3 5
x
x
x
х
x
x
x
( )
−≠
−>
>
<
≤
−−
−
⋅−+
;4
,5
;3
,0
,05
3
15
x
x
x
х
x
x
x
x
( ) [ ] ( ).;33;-1-5;-4-:Ответ ∞∪∪
.
3
log4
3
log4
3
log
то0
3
Т.к.
55
4
5
x
x
x
x
x
x
,
х
х
xxx
−
=
−
=
−
>
−
+++](https://image.slidesharecdn.com/random-150128153034-conversion-gate02/85/slide-33-320.jpg)
![;
7
1
log1
1
7
log 8
2
8
−
+
−≤
+
−
++
x
x
x
x
xx
;
1
7
log1
1
7
log2 88
+
−
+≤
+
−
++
x
x
x
x
xx
;01
1
7
log 8 ≤−
+
−
+
x
x
x
( )
−≠
−>
>
−<
≥
+
++
⋅+
;7
,8
;7
,1
,0
1
158
7
2
x
x
x
х
x
хx
x
( ) [ ] ( ).;75;-3-8;-7-:Ответ ∞∪∪](https://image.slidesharecdn.com/random-150128153034-conversion-gate02/85/slide-34-320.jpg)
![;0
3612
log 2
4
6 ≤
+−
−
xx
x
x
≠
≠−
>−
≤
−
−
;0
,16
,06
,0
6
log
2
6
х
х
х
х
х
х
;0
6
log
22
6 ≤
−
−
х
x
x
;0
6
log2
2
6 ≤
−
−
х
x
x
≠
≠
<
≤−
−
−−
;0
,5
,6
,0)1
6
)(16(
2
х
х
х
х
х
х
≠
≠
<
≤
−
−+
−
;0
,5
,6
,0)
6
6
)(5(
2
х
х
х
х
хх
х
[ ) ( ] ( ).6;52;0.3;0-:Ответ ∪∪x
+
x
2 5
5
-3
++
6
6
--
0](https://image.slidesharecdn.com/random-150128153034-conversion-gate02/85/slide-35-320.jpg)
![;0
3612
log 2
4
6 ≤
+−
−
xx
x
x
;0
6
log
22
6 ≤
−
−
х
x
x
≠
≠
<
≤+
−
−
−
−
;0
,5
,6
,0)1
6
)(1
6
)(5(
22
х
х
х
х
х
х
х
х
≠
≠
<
≤
−
−+−
;0
,5
,6
,0
)6(
)6)(5(
2
2
х
х
х
х
ххх
D<0, .062
хх >+−
Для тех, кто боится «модулей» -Для тех, кто боится «модулей» -
2 способ2 способ::
x
-
x
2 5
5
-3
++ --
0 6
6
≠
≠
<
≤
−
−+
−
+−
−
;0
,5
,6
,0)
6
6
)(
6
6
)(5(
22
х
х
х
х
хх
х
хх
х
[ ) ( ] ( ).6;52;0.3;0-:Ответ ∪∪](https://image.slidesharecdn.com/random-150128153034-conversion-gate02/85/slide-36-320.jpg)
