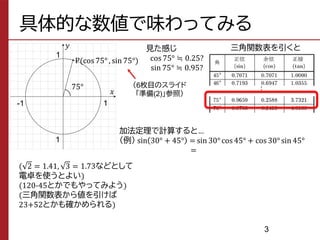
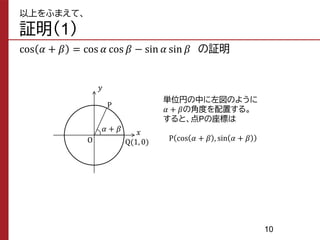
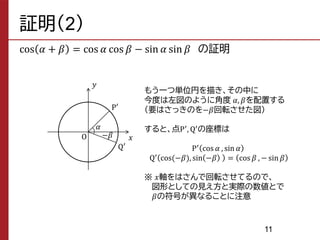
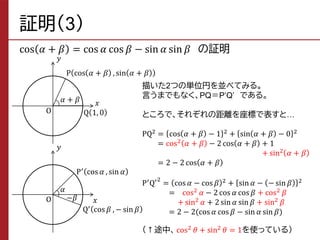
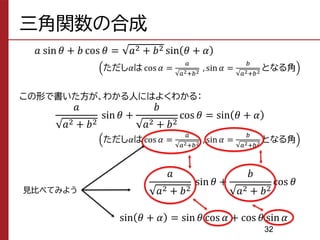
The document summarizes trigonometric addition formulas and related formulas. It provides proofs of the formulas using properties of coordinates on the unit circle. Specifically, it proves formulas for cosine, sine, and tangent of the sum or difference of two angles α and β using the x-y coordinates of points on two superimposed unit circles with angles of α, β, α+β, and -β.

1. 基礎数学 補足資料
三角関数の加法定理と関連公式
もう全部あいつ一人でいいんじゃないかな
作者： @masa_hiroo_kano （twitter ID）
1

2. 三角関数の加法定理
1. cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽
2. cos 𝛼 − 𝛽 = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽
3. sin 𝛼 + 𝛽 = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
4. sin 𝛼 − 𝛽 = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
5. tan 𝛼 + 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
6. tan 𝛼 − 𝛽 =
tan 𝛼−tan 𝛽
1+tan 𝛼 tan 𝛽
• その心
– 三角関数の値がわかってる角度があれば、その角度を
足したり引いたりで作れる別の角度の三角関数が求められる
– たとえば30°, 45°, 60°の三角関数の値は知ってるので、
それらを使えば15°, 75°, 105°などの三角関数の値が求められる

3. 具体的な数値で味わってみる
1
1
-1
1
・P(cos 75° , sin 75°)
75°
見た感じ
cos 75° ≒ 0.25?
sin 75° ≒ 0.95?
三角関数表を引くと
𝑦
𝑥
…
加法定理で計算すると…
（例） sin 30° + 45° = sin 30° cos 45° + cos 30° sin 45°
=
( 2 = 1.41, 3 = 1.73などとして
電卓を使うとよい)
(120-45とかでもやってみよう)
(三角関数表から値を引けば
23+52とかも確かめられる)
3
（6枚目のスライド
「準備(2)」参照）

4. 三角関数の加法定理
1. cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽
2. cos 𝛼 − 𝛽 = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽
3. sin 𝛼 + 𝛽 = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
4. sin 𝛼 − 𝛽 = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
5. tan 𝛼 + 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
6. tan 𝛼 − 𝛽 =
tan 𝛼−tan 𝛽
1+tan 𝛼 tan 𝛽
• ここから、これらを順に証明していきます
• 単に読んでもたぶんわかりません
• でも紙とペンで計算をなぞれば、不思議とわかります
– たぶん…
4

5. その前に…2
準備（1）三角関数の相互関係
5

6. 準備 (2) 三角関数と動径の端点の座標
• 単位円の動径OPが𝑥軸と𝜃の角をなすとき、
点Pの座標(𝑥, 𝑦)は
𝑥 = cos 𝜃
𝑦 = sin 𝜃 …と表せる
（単位円の中の直角三角形でsin 𝜃と cos 𝜃を考えれば明らか）
P(𝑥, 𝑦)
𝜃
O 𝑥
𝑦
1
𝜃
O
P
1
𝑥
𝑦
6

7. 準備 (3) cos −𝜃 とsin −𝜃
P(cos 𝜃 , sin 𝜃)
𝜃
O 𝑥
𝑦
1
−𝜃
P′(cos −𝜃 , sin −𝜃 )
= (cos 𝜃 , −sin 𝜃)
• 下図のように、動径OPについて𝑥軸対称な位置に
動径OP’をとり、その座標を三角関数で考えてみると…
角度は負の方向にできるので−𝜃
準備(2)に放り込んだだけ
点Pとの位置関係を考えると、−𝜃でなく
𝜃の角度で表すことができる
つまり
cos −𝜃 = cos 𝜃
sin −𝜃 = − sin 𝜃
7

8. 準備 (4) 90° − 𝜃 の三角関数
P(cos 𝜃 , sin 𝜃)
𝜃
O 𝑥
𝑦
O 𝑥
𝑦
𝜃
90° − 𝜃
H
H′
𝑥軸と𝜃の角度で交わる動径OP（上図）と、
𝑥軸と90° − 𝜃の角度で交わる動径OP’を
考えてみる（下図）。
見ての通り △OPH≡△OP’H’ なので、
PH = OPの𝑦座標 = P′H′ = (動径OP′の𝑥座標)
OH = OHの𝑥座標 = O H′ = (動径OP′の𝑦座標)
（↑上図の世界） ｜ （↑下図の世界）
P’(cos 90° − 𝜃 , sin 90° − 𝜃 )
= sin 𝜃 , cos 𝜃
したがって、
cos 90° − 𝜃 = sin 𝜃 (OP′の𝑥 = OPの𝑦)
sin 90° − 𝜃 = cos 𝜃 (OP′の𝑦 = OPの𝑥)
が成り立つ

9. 準備 (5) 座標平面上の2点間の距離
• 座標平面上の2点P 𝑥1, 𝑦1 , Q 𝑥2, 𝑦2 間の距離PQは、
PQ = 𝑥1 − 𝑥2
2 + 𝑦1 − 𝑦2
2
（または PQ2
= 𝑥1 − 𝑥2
2
+ 𝑦1 − 𝑦2
2
）と表せる
𝑥
𝑦
O
・P 𝑥1, 𝑦1
・Q 𝑥2, 𝑦2
𝑥2 − 𝑥1
𝑦1 − 𝑦2
ここに直角三角形があると思って
縦・横の長さを座標で表し、
三平方の定理で斜辺PQの長さを
求めればわかる
（QがPの右か左か、上か下かは、
2乗するので関係なくなる）
9

10. 以上をふまえて、
証明（1）
cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 の証明
単位円の中に左図のように
𝛼 + 𝛽の角度を配置する。
すると、点Pの座標は
P cos 𝛼 + 𝛽 , sin 𝛼 + 𝛽
O
𝑥
𝑦
𝛼 + 𝛽
P
Q(1, 0)
10

11. 証明（2）
cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 の証明
もう一つ単位円を描き、その中に
今度は左図のように角度 𝛼, 𝛽を配置する
（要はさっきのを−𝛽回転させた図）
すると、点P′, Q′の座標は
P′ cos 𝛼 , sin 𝛼
Q′ cos(−𝛽), sin −𝛽 = cos 𝛽 , − sin 𝛽
※ 𝑥軸をはさんで回転させてるので、
図形としての見え方と実際の数値とで
𝛽の符号が異なることに注意
O 𝑥
𝑦
𝛼
−𝛽
P′
Q′
11

12. 証明（3）
cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 の証明
O
𝑥
𝑦
𝛼 + 𝛽
P cos 𝛼 + 𝛽 , sin 𝛼 + 𝛽
Q 1, 0
O 𝑥
𝑦
𝛼
−𝛽
P′ cos 𝛼 , sin 𝛼
Q′ cos 𝛽 , − sin 𝛽
描いた2つの単位円を並べてみる。
言うまでもなく、PQ＝P’Q’ である。
ところで、それぞれの距離を座標で表すと…
PQ2 = cos 𝛼 + 𝛽 − 1 2 + sin 𝛼 + 𝛽 − 0 2
= cos2 𝛼 + 𝛽 − 2 cos 𝛼 + 𝛽 + 1
+ sin2 𝛼 + 𝛽
= 2 − 2 cos 𝛼 + 𝛽
P′Q′2
= cos 𝛼 − cos 𝛽 2 + sin 𝛼 − − sin 𝛽 2
= cos2 𝛼 − 2 cos 𝛼 cos 𝛽 + cos2 𝛽
+ sin2 𝛼 + 2 sin 𝛼 sin 𝛽 + sin2 𝛽
= 2 − 2(cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽)
（ ↑ 途中、 cos2 𝜃 + sin2 𝜃 = 1を使っている）

13. 証明（4）
O
𝑥
𝑦
𝛼 + 𝛽
P cos 𝛼 + 𝛽 , sin 𝛼 + 𝛽
Q 1, 0
O 𝑥
𝑦
𝛼
𝛽
P′ cos 𝛼 , sin 𝛼
Q′ cos 𝛽 , − sin 𝛽
cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 の証明
つまり、
PQ2 = 2 − 2 cos 𝛼 + 𝛽
P′Q′2
= 2 − 2(cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽)
そして PQ2 = P′Q′2
以上から、
cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽
が成り立つことがわかる
13

14. 加法定理の証明
1. cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽
2. cos 𝛼 − 𝛽 = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽
3. sin 𝛼 + 𝛽 = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
4. sin 𝛼 − 𝛽 = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
5. tan 𝛼 + 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
6. tan 𝛼 − 𝛽 =
tan 𝛼−tan 𝛽
1+tan 𝛼 tan 𝛽
• 1つめクリア。
• 後の5つは、準備しておいた公式を使って
芋づる式に導出できます
• これからそれを示します
14

15. 証明（5）
cos 𝛼 − 𝛽 = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽 の証明
• cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽 において、
𝛽を−𝛽に置き換えてやればよい。つまり…
cos 𝛼 − 𝛽 = cos 𝛼 + (−𝛽)
= cos 𝛼 cos(−𝛽) − sin 𝛼 sin(−𝛽)
= cos 𝛼 cos 𝛽 − sin 𝛼 × (− sin 𝛽)
= cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽
• 2つめクリア。
• 次は sin 𝛼 + 𝛽 = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽 を示す。
15

16. 証明 (6)
sin 𝛼 + 𝛽 = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽 の証明
• 準備(4)から、
sin 𝛼 + 𝛽 = cos 90° − 𝛼 + 𝛽 = cos 90° − 𝛼 − 𝛽
と変形できる。さらに、さっき証明した
cos 𝛼 − 𝛽 = cos 𝛼 cos𝛽 + sin𝛼 sin𝛽
を使うと…
sin 𝛼 + 𝛽 = cos 90° − 𝛼 − 𝛽
= cos 90° − 𝛼 cos 𝛽 + sin 90° − 𝛼 sin 𝛽
= sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
（↑赤字のところでまた準備(4)を利用している）
16

17. 証明（7）
sin 𝛼 − 𝛽 = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽 の証明
• cos 𝛼 − 𝛽 のときと同じやり口でいける。
sin 𝛼 − 𝛽 = sin 𝛼 + −𝛽
= sin 𝛼 cos −𝛽 + cos 𝛼 sin −𝛽
= sin 𝛼 cos 𝛽 + cos 𝛼 × − sin 𝛽
= sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
赤字部：準備（3）を利用
17

18. 加法定理の証明
1. cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽
2. cos 𝛼 − 𝛽 = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽
3. sin 𝛼 + 𝛽 = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
4. sin 𝛼 − 𝛽 = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
5. tan 𝛼 + 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
6. tan 𝛼 − 𝛽 =
tan 𝛼−tan 𝛽
1+tan 𝛼 tan 𝛽
• 4つめまでクリア。
• あと2つ、タンジェントは…？
18

19. その前に…
準備（1）三角関数の相互関係
これを使う
19

20. 証明（8）
tan 𝛼 + 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
の証明
tan 𝛼 + 𝛽 =
sin 𝛼+𝛽
cos(𝛼+𝛽)
=
sin 𝛼 cos 𝛽+cos 𝛼 sin 𝛽
cos 𝛼 cos 𝛽−sin 𝛼 sin 𝛽
=
sin 𝛼 cos 𝛽+cos 𝛼 sin 𝛽 ×
1
cos 𝛼 cos 𝛽
(cos 𝛼 cos 𝛽−sin 𝛼 sin 𝛽)×
1
cos 𝛼 cos 𝛽
=
sin 𝛼
cos 𝛼
×
cos 𝛽
cos 𝛽
+
cos 𝛼
cos 𝛼
×
sin 𝛽
cos 𝛽
1−
sin 𝛼
cos 𝛼
×
sin 𝛽
cos 𝛽
ｷﾞｮｴｰ...あっでもよく見たら
あ
← ！？！？！？
20

21. 証明（8）
tan 𝛼 + 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
の証明
tan 𝛼 + 𝛽 =
sin 𝛼+𝛽
cos(𝛼+𝛽)
=
sin 𝛼 cos 𝛽+cos 𝛼 sin 𝛽
cos 𝛼 cos 𝛽−sin 𝛼 sin 𝛽
=
sin 𝛼 cos 𝛽+cos 𝛼 sin 𝛽 ×
1
cos 𝛼 cos 𝛽
(cos 𝛼 cos 𝛽−sin 𝛼 sin 𝛽)×
1
cos 𝛼 cos 𝛽
=
sin 𝛼
cos 𝛼
×
cos 𝛽
cos 𝛽
+
cos 𝛼
cos 𝛼
×
sin 𝛽
cos 𝛽
1−
sin 𝛼
cos 𝛼
×
sin 𝛽
cos 𝛽
ｷﾞｮｴｰ...あっでもよく見たら
=
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
タンジェントを作るために掛けてやった
← ！？！？！？
21

22. 準備（6）tan −𝜃
合体
tan −𝜃 =
sin −𝜃
cos −𝜃
=
− sin 𝜃
cos 𝜃
= − tan 𝜃

23. 証明（9）
tan 𝛼 − 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
の証明
• 例のやり口
tan 𝛼 − 𝛽 = tan 𝛼 + −𝛽
=
tan 𝛼+tan −𝛽
1−tan 𝛼 tan −𝛽
=
tan 𝛼−tan 𝛽
1+tan 𝛼 tan 𝛽
23

24. 三角関数の加法定理
1. cos 𝛼 + 𝛽 = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽
2. cos 𝛼 − 𝛽 = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽
3. sin 𝛼 + 𝛽 = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
4. sin 𝛼 − 𝛽 = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
5. tan 𝛼 + 𝛽 =
tan 𝛼+tan 𝛽
1−tan 𝛼 tan 𝛽
6. tan 𝛼 − 𝛽 =
tan 𝛼−tan 𝛽
1+tan 𝛼 tan 𝛽
MISSION COMPLETE
24

25. 三角関数の公式を覚えるポイント
• 全部を丸暗記しては絶対いけません
– 多すぎるので、正しく思い出すことは不可能です
（私は絶対無理）
– 「準備」のやつらは単位円を描くだけでわかります
• sin, cos, tanの定義を理解できていればですが…
• どうしても覚えるなら加法定理だけにする
– 加法定理の計算ができれば他は芋づる式に導出可能
• 最悪 90° ± 𝜃 も 180° ± 𝜃 も加法定理で作れる
• −𝜃 の公式も 0° − 𝜃 と思えば加法定理で作れる
• 合成も積→和、和→積もけっきょく加法定理の変形
• 証明をなぞれば公式を使った計算の練習にもなるので、
最高の教材です。やってみましょう
25

26. やってみましょう
↑単位円や加法定理を使って導出してみよう 26

27. やってみましょう2
↑加法定理を使って導出してみよう 27

28. やってみましょう3
↑加法定理を使って導出してみよう 28

29. これはまあ、示しておきます
29

30. 三角関数の合成
𝑎 sin 𝜃 + 𝑏 cos 𝜃 = 𝑎2 + 𝑏2 sin 𝜃 + 𝛼
ただし𝛼は cos 𝛼 =
𝑎
𝑎2+𝑏2
, sin 𝛼 =
𝑏
𝑎2+𝑏2
となる角
この形で書いた方が、わかる人にはよくわかる：
𝑎
𝑎2 + 𝑏2
sin 𝜃 +
𝑏
𝑎2 + 𝑏2
cos 𝜃 = sin 𝜃 + 𝛼
ただし𝛼は cos 𝛼 =
𝑎
𝑎2+𝑏2
, sin 𝛼 =
𝑏
𝑎2+𝑏2
となる角
30

31. 三角関数の合成
𝑎 sin 𝜃 + 𝑏 cos 𝜃 = 𝑎2 + 𝑏2 sin 𝜃 + 𝛼
ただし𝛼は cos 𝛼 =
𝑎
𝑎2+𝑏2
, sin 𝛼 =
𝑏
𝑎2+𝑏2
となる角
この形で書いた方が、わかる人にはよくわかる：
𝑎
𝑎2 + 𝑏2
sin 𝜃 +
𝑏
𝑎2 + 𝑏2
cos 𝜃 = sin 𝜃 + 𝛼
ただし𝛼は cos 𝛼 =
𝑎
𝑎2+𝑏2
, sin 𝛼 =
𝑏
𝑎2+𝑏2
となる角
𝑎
𝑎2 + 𝑏2
sin 𝜃 +
𝑏
𝑎2 + 𝑏2
cos 𝜃
見比べてみよう
sin 𝜃 + 𝛼 = sin 𝜃 cos 𝛼 + cos 𝜃 sin 𝛼
31

32. 三角関数の合成
𝑎 sin 𝜃 + 𝑏 cos 𝜃 = 𝑎2 + 𝑏2 sin 𝜃 + 𝛼
ただし𝛼は cos 𝛼 =
𝑎
𝑎2+𝑏2
, sin 𝛼 =
𝑏
𝑎2+𝑏2
となる角
この形で書いた方が、わかる人にはよくわかる：
𝑎
𝑎2 + 𝑏2
sin 𝜃 +
𝑏
𝑎2 + 𝑏2
cos 𝜃 = sin 𝜃 + 𝛼
ただし𝛼は cos 𝛼 =
𝑎
𝑎2+𝑏2
, sin 𝛼 =
𝑏
𝑎2+𝑏2
となる角
𝑎
𝑎2 + 𝑏2
sin 𝜃 +
𝑏
𝑎2 + 𝑏2
cos 𝜃
見比べてみよう
sin 𝜃 + 𝛼 = sin 𝜃 cos 𝛼 + cos 𝜃 sin 𝛼
32

33. 合成の肝
• 三角関数の合成 𝑎 sin 𝜃 + 𝑏 cos 𝜃 = 𝑎2 + 𝑏2 sin 𝜃 + 𝛼
「適当な角𝛼を持ち出してきて加法定理を考えれば、
sin 𝜃とcos 𝜃が混じった式が sin(𝜃 + 𝛼) だけで表せる」
「角 𝛼 としては、cos 𝛼 =
𝑎
𝑎2+𝑏2
, sin 𝛼 =
𝑏
𝑎2+𝑏2
となるものを持ち出してくればよい」 ということ
• グラフで言えば、
「sin 𝜃とcos 𝜃を足した場合は変な形にはならず、
位相がずれた違う大きさのサイン波ができる｣ということ
𝛼
・P 𝑎, 𝑏
O 𝑥
𝑦
𝑎2 + 𝑏2
𝑎
𝑏
つまりこういう角 𝛼 →
33

34. 合成の例
• sin𝜃 + 3cos 𝜃 = 2 sin 𝜃 + 60°
• 3 sin𝜃 + cos 𝜃 = 2 sin 𝜃 + 30°
• sin𝜃 + cos 𝜃 = 2 sin 𝜃 + 45°
• sin𝜃 + 3cos 𝜃 = 2 sin 𝜃 + 60°
• sin𝜃 − cos 𝜃 = 2 sin 𝜃 − 45°
（右辺を加法定理で展開し、一致することを確かめてみよう）
（Excelや科学計算ソフトなどで両辺それぞれグラフを描いてみるのもよい）
34

35. (再)三角関数の公式を覚えるポイント
• 全部を丸暗記しては絶対いけません
– 多すぎるので、正しく思い出すことは不可能です
（私は絶対無理）
– 「準備」のやつらは単位円を描くだけでわかります
• sin, cos, tanの定義を理解できていればですが…
• どうしても覚えるなら加法定理だけにする
– 加法定理の計算ができれば他は芋づる式に導出可能
• 最悪 90° ± 𝜃 や 180° ± 𝜃 なども加法定理で作れる
• −𝜃 の公式も 0° − 𝜃 と思えば加法定理で作れる
• 合成も積→和、和→積もけっきょく加法定理の変形
• 証明をなぞれば公式を使った計算の練習にもなるので、
最高の教材です。やってみましょう
35