More Related Content
PDF
DataRobotを用いた要因分析 (Causal Analysis by DataRobot) PDF
数学カフェ 確率・統計・機械学習回 「速習 確率・統計」 PPTX
PDF
Optuna Dashboardの紹介と設計解説 - 2022/12/10 Optuna Meetup #2 PPTX
深層強化学習による自動運転車両の経路探索に関する研究 PDF
PPTX
PPTX
What's hot
PDF
PDF
最近強化学習の良記事がたくさん出てきたので勉強しながらまとめた PDF
PPTX
PDF
PDF
PDF
PDF
Surveyから始まる研究者への道 - Stand on the shoulders of giants - PDF
PDF
Pythonによる、デジタル通信のための ビタビ符号化・復号ライブラリの作成 PDF
PPTX
これからの Vision & Language ~ Acadexit した4つの理由 PDF
マイクロマウスのための MATLAB/Simulink 講座 第1回 - MATLAB入門 PDF
「あなたがいま読んでいるものは文字です」~画像情報学から見た文字研究のこれから PDF
PDF
SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法 PPTX
【DL輪読会】Is Conditional Generative Modeling All You Need For Decision-Making? PDF
【DL輪読会】Mastering Diverse Domains through World Models PDF
PDF
Viewers also liked
PDF
PDF
超小型クアッドロータ "Quadruptor" の製作とその制御 PDF
PDF
グローバル理工人材のための今日から使える検索テクニック ―もう日本語でググるのはやめよう PDF
PDF
PPTX
PPTX
さるでも分かりたい9dofで作るクォータニオン姿勢 PDF
PDF
PDF
PDF
北部九州における産学連携による小型電気飛行機の開発 PDF
PDF
楽しいクォータニオンの世界 田所 第二回Rogyゼミ PPTX
PPTX
PPTX
オープンソースによるドローン開発の概要( #ABC2015S ) PDF
ROS の活用による屋外の歩行者空間に適応した自律移動ロボットの開発 PPTX
PDF
論文紹介 Semi-supervised Learning with Deep Generative Models Similar to クモ型ロボットにおける逆運動学計算
PDF
PPTX
PDF
201110 01 Polytech Center 1 PDF
PDF
PDF
PDF
coma Study Room vol.2 Arduino Workshop PPTX
[DL輪読会]Learning agile and dynamic motor skills for legged robots PDF
PDF
PDF
PDF
RTミドルウェアによるロボットプログラミング技術 �1.コース概要 PDF
Variable Stiffness Mechanism(VSM):可変剛性機構に関する研究紹介 PDF
ODP
PDF
ロボットマニピュレーションの作業・動作計画 / rosjp_planning_for_robotic_manipulation_20240521 PPTX
[DL輪読会]Learning quadrupedal locomotion over challenging terrain クモ型ロボットにおける逆運動学計算
- 1.
- 2.
- 3.
- 5.
- 6.
どうせなら
モーション:自動生成
フレームレート :高
外界のフィードバック :モーション自動生成なので可
→楽しい!!✌(‘ω’✌ )三✌(‘ω’)✌三(✌‘ω’)✌
- 7.
でも制御用のプログラムも…
→楽しい!!✌( ◞‸◟✌)三✌(◞‸◟)✌三(✌◞‸◟)✌
ことになってしまう
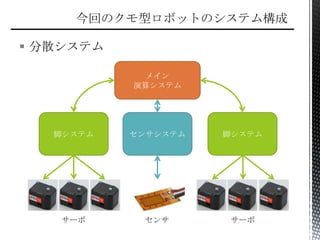
複雑なシステムを構築する際の考え方
分散システム (システムを並列化) (´・ω・`)(´・ω・`)
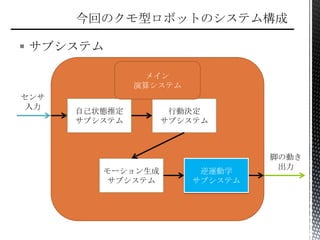
サブシステム (システムを入れ子状化)(´・(´・ω・`)・`)
双方を利用して,処理を分散・コンポーネント化
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.