1. パターン認識と機械学習
C.M.ビショップ
第1回 2013/05/08

2. 第1章 序論
• 以下のような手書き文字の認識を考える。
• 機械学習ではまず訓練集合(training set)と呼ばれる N 個の手書き文字の大きな
集合{x1, x2, x3, …, xN}を使ってモデルのパラメータを適応的に調節する。
• ただし、訓練集合の手書き文字は予め人間が手作業でラベル付けするなどして既知。
訓練集合 x
目標ベクトル t
0 3 4 5 6 7 ８ 91 2

3. • 機械学習のアルゴリズムによって判明するのは関数 y(x) であり、この関数の詳細は訓
練データに基づいて求まる。
• このプロセスを訓練(training)段階ないし学習(learning)段階という。
• モデルが学習された後はテスト集合(test set)と呼ばれる新たな数字データに対してカ
テゴリが判別される。
• 訓練で使ったのと異なるデータを分類する能力を汎化(generalization)という。
• 実際の手書き文字データはフォーマットがバラバラであることが多いため適度に前処理
(特徴抽出、属性抽出)し訓練集合としている。
訓練集合(既知)
{x1, x2, x3, …, xN}
目標ベクトル(既知)
{t1, t2, t3, …, tN}
関数(未知)
y(x)
テスト集合(既知)
{x’1, x’2, x’3, …, x’N}
カテゴリベクトル(未知)
{t’1, t’2, t’3, …, t’N}
関数(既知)
y(x’)
前処理前 前処理後

4. 教師あり学習(教師付き学習、supervised learning)
• 訓練データが入力ベクトルと目標ベクトルから構成される問題
– クラス分類(classification) : 各入力ベクトルを有限個の離散カテゴリに分類
– 回帰(regression) : 出力ベクトルが1つないしそれ以上の連続変数
教師なし学習(unsupervised learning)
• 訓練データが入力ベクトルのみで対応する目標値が存在しない問題
– クラスタリング(clustering) : 類似したグルーピングを発見する
– 密度推定(density estimation) : 入力空間におけるデータの分布を求める
強化学習(reinforcement learning)
• 所与の条件下で報酬最大化を達成する行動を発見する問題
• 探査と利用のトレードオフが存在
– 探査(exploration) : 新しい種類の行動がどれくらい有効であるか試す
– 利用(exploitation) : 高い報酬が得られることがわかっている行動をとる

5. 多項式曲線フィッティング
• N 個の観測値の組 x ≡ (x1, x2, x3, …, xN)T と t ≡ (t1, t2, t3, …, tN)T から関
係性を調べたい。(有限個のデータから汎化を行いたい。)
• 曲線フィッティングに基づいて考えるために次のような多項式を考える。
• M を多項式の次数と呼ぶ。
• y 自体は非線形関数であるが係数ベクトル w に関しては線形関数。
⇨ 未知のパラメータに関して線形である関数は線形モデル(linear model)と呼ばれる。
• 訓練データに多項式をフィットさせることで係数ベクトル w を求める。
• 単純な方法としてモデルの出力 y と観測値の出力 t の差を2乗したものを誤差と考え
これを最小にする w を求める。
• この時の誤差を二乗和誤差(sum-of-squares error)と呼び次のように書く。

6. • 二乗和誤差を最小にする係数ベクトル w* を得た。(モデルの推定)
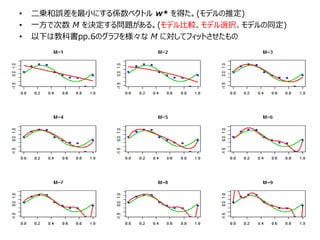
• 一方で次数 M を決定する問題がある。(モデル比較、モデル選択、モデルの同定)
• 以下は教科書pp.6のグラフを様々な M に対してフィットさせたもの

7. 参考 : 以下の多項式にフィットさせた時の係数行列

8. • M = 3, 4の時は真値(緑の線)に対してフィッティングが良いように見える。
• 一方で M = 9の時はデータの全点を通っており理論的に二乗和誤差は0である。
⇨ 発振したグラフであり真値に対する表現としては不適 (= 過学習(over-fitting) )
⇨ そもそも汎化とは新しい入力(テスト集合)に対しての分類能力だった。
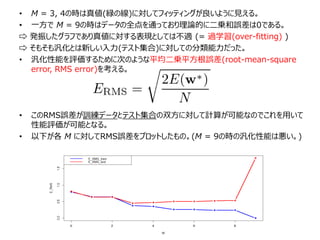
• 汎化性能を評価するために次のような平均二乗平方根誤差(root-mean-square
error, RMS error)を考える。
• このRMS誤差が訓練データとテスト集合の双方に対して計算が可能なのでこれを用いて
性能評価が可能となる。
• 以下が各 M に対してRMS誤差をプロットしたもの。(M = 9の時の汎化性能は悪い。)

9. • (3次多項式) ⊂ (9次多項式)なのに9次多項式のほうが汎化性能が悪いのはパラド
クスのように思える。
⇨ 9次多項式の係数は非常に大きな値をとっており無理やりデータにフィットさせている。
⇨ 過去のデータに対する過適合であり、説明力は上がるが予測力は下がっている。
• cf.オッカムの剃刀
• M が大きく自由度の高い多項式は目的値のランダムノイズに引きずられてしまうと思
えば良い。(意味不明)
過学習に対するアプローチ
1. データ数を増やす。
2. ベイズ的アプローチを用いる。
3. 正則化(regularization)を行う。
• 正則化とは過学習を制御するためのテクニックであり、二乗和誤差に係数爆発を考慮
した罰金項を加えた誤差関数を用いるものである。具体的には以下。
• このようなテクニックを縮小推定(shrinking)という。

10. 曲線フィッティング再訪
• 目標変数の値に関する不確実性は確率分布を用いて表現可能で所与の x に対する t は平
均が以下であるガウス分布に従うと考える。
• 具体的には以下
• 上記は密度表現だが分布で表現すれば以下のようになる。( t が従う確率変数を T とした。)
• 結局のところ通常のNCRM(古典的正規回帰モデル)と同じ表現になる。
• 誤差の分布を仮定したことにより最尤法によるパラメータ推定が可能になる。

11. • 尤度関数、対数尤度関数として次式を得る。
• MLEを求める際に考える は二乗和誤差を最小にする推定量を
求めることと等価である。
⇨ OLSEはMLEの特別な場合と等価だとわかる。
• 同様にガウス分布の精度パラメータ β を求めると以下のようになる。
• 正規分布の分散のMLEは標本分散だったのでその点でも整合的。

12. • MLEを得たので新たな x に対する予測分布として以下が導出できる。
• 簡単のため次のような事前分布を導入する。
• この表現を用いることで事後分布を事前分布と尤度の積で表現できる。
• これにより所与のデータから最も尤もらしい w を見つけることができる。
• すなわち、事後分布を最大化する w を決めることができる。
• これを最大事後確率推定(maximum posterior)ないしMAP推定と呼ぶ。
• 事後確率の最大値は下式の最小値として与えられ正則化された二乗和誤差の最小
化問題と等価である。

13. モデル選択
• 最尤アプローチは過学習の問題がある。よって訓練集合に対して良いパフォーマンスを
あげていても汎化性能が低い場合がある。
確認用集合(validation set)を用意
– 確認用集合で最も汎化性能の高いモデルを採択
– 確認用集合に対して過学習してしまう懸念があるためテスト集合を新たに用意する必要がある。
交差確認(cross-validation)
– データの (S - 1) / S を学習に使い全データで汎化性能を測る
– データが極小のときは S = N とし、この時LOO法と呼ぶ
– パラメータ数に対して指数関数的に訓練回数が増える
情報量基準
– 最尤推定バイアスを罰金項により修正する
– 赤池情報量基準(AIC)
– ベイズ情報量基準(BIC)
– これらはモデルパラメータの不確実性を考慮しておらず過度に単純なモデルが採用されやすい。
次元の呪い(curse of dimensionality)
– 高次元空間に伴う困難性のこと。
– 高次元空間は低次元空間の単なる拡張ではない。
– e.g. 1~3次元球の体積は中心の寄っているが高次元球ではそうならない。

14. 情報理論
• 情報とは「驚きの度合い」
⇨ 起きそうに無い事象の発生はそうでない事象の発生に比して多くの情報を持つ
⇨ 情報量を測る尺度は確率分布 p(x) に依存しているはず
• 情報量を表す関数 h(*) を発見したい。 ⇨ 情報量と確率の性質について考えてみる。
• 事象 x, y が独立ならば次の2式が成立するのが自然。
1. h(x, y) = h(x) + h(y)
2. p(x, y) = p(x) p(y)
• この関係を満たす関数として情報量は次のように表現できる。
• この関数を用いることにより情報量の平均を次のように期待値で表現可能。
• これをエントロピー(entropy)という。(多重度を用いた表現も可能)

15. • 最大エントロピーを持つ分布を持つ確率分布を考えたいが以下の定義では不十分
• 条件付き極値問題に帰着させるために確率を規格化する項を追加した以下を考える。
• この式は p(xi), p(xj)に関して偏微分すると要素が負になるので最大値が存在する。
• 最終的に次のような極値問題を解くことによって最大エントロピーを持つ分布を導く。
• 結果としてエントロピー最大となる分布は離散一様分布だとわかる。

16. • 離散エントロピーを連続変数に拡張することを考える。
• x を ⊿ 分割し p(x) が連続だと仮定することにより(積分の)平均値の定理から以下を
満足する xi が必ず存在する。
• xi の観測する確率は p(xi)⊿ となるので離散エントロピーは次のように計算できる。
• この式の第2項を無視し ⊿ → 0 の極限を取ると以下のように収束する。

17. • 複数の連続変数をまとめてベクトル表記をすれば微分エントロピーとして以下を定義で
きる。
• 離散の場合と同様にこのエントロピーを最大にする分布を特定したい。
• 最大値が定義されるために規格化制約と1,2次モーメントを制約として課す。
• 上記の極値問題を解くことで微分エントロピーが最大となる分布は正規分布だとわかる。

18. 相対エントロピー / Kullback-Leibler divergence
• 未知の分布 p(x) があり、これを近似的に q(x) でモデル化することを考える。
• 真の分布 p(x) の代わりに q(x) を使うと x の値を特定するのに必要な追加情報量
の平均は次のように書ける。