This document is written about "Data-Intensive Text Processing with MapReduce" Chapter 6.1. Chapter 6 describes how to design Expectation Maximization with MapReduce algorithm. Section 6.1 focus to Expectation Maximization algorithm itself, and so there are no description about MapReduce.

1. Data-Intensive Text Processing
with MapReduce
(Ch6 EM Algorithms for Text Processing, Part 1)
2010/10/17
shiumachi
http://d.hatena.ne.jp/shiumachi/
http://twitter.com/shiumachi
http://www.facebook.com/sho.shimauchi

2. Agenda
● 6章 テキスト処理のためのEMアルゴリズム
● イントロダクション
● 6.1 Expectation Maximization(期待値最大化)
– 6.1.1 最尤推定
– 6.1.2 潜在変数つきビー玉ゲーム
– 6.1.3 潜在変数つき最尤推定
– 6.1.4 Expectation Maximization
– 6.1.5 EMの例

3. Chapter 6
EM Algorithms for Text Processing
6章
テキスト処理のためのEMアルゴリズム

4. イントロダクション

5. テキスト処理の歴史
● 1980年代の終わりまではルールベース
● 分析や変換のルールをひたすら人力で書く形式
● ルールに当てはまればいいけど、推定が全くできな
い
● 1990年から現代まではデータドリブンが主流
● 訓練データを用いてパラメータ調整
– スパムフィルタとか
● やがて、アルゴリズム自体も訓練データで改善して
いくように→機械学習の世界へ

6. データドリブンの利点
● 気が利く
● 訓練データにより徐々にアルゴリズムを修正できる
ので、現実世界の複雑さに対応しやすい
● 安い
● 元のデータはこのシステムを作るために新しく生成
する必要がないことが多い
– テキスト処理用の訓練データだったら、本やwebに既に
大量に存在している
● ルールベースだと毎回書き直す必要がある

7. 統計モデル
● この章で扱うデータドリブンの手法は統計モデル
● 3つの課題がある
● モデル選択
– HMM(隠れマルコフモデル)
● パラメータ推定・学習
– 最尤推定とEMアルゴリズム
● デコーディング
● この章ではパラメータ推定がメインだが、デ
コーディングにも触れる

8. 記号の定義とか
X : 入力データセット(観測可能)
Y : 存在し得るアノテーションの集合
(アノテーションとはメタデータのようなもの)
x ∈ X, y ∈ Y
このとき与えられた x に対する y の確率を以下の
2通りで表記する
Pr(x, y) … ジョイントモデル
Pr(y | x) … コンディショナルモデル

9. デコーディングの手法
与えられた x に対してPrの最大値をとる y を出す
ジョイントモードで書くとこんな感じ
いずれにせよ片っ端から計算すれば算出可能

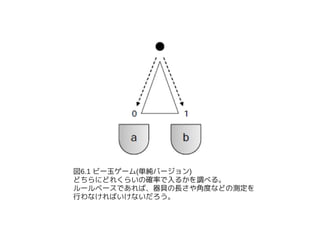
10. 機械学習の分類
● 教師あり学習
● “事前に与えられたデータをいわば「例題（＝先生から
の助言）」とみなして、それをガイドに学習（＝デー
タへの何らかのフィッティング）を行う” [5]
● 例) SVM, ナイーブベイズ
● 教師なし学習
● “出力すべきものがあらかじめ決まっていないという点
で教師あり学習とは大きく異なる。 データの背後に存
在する本質的な構造を抽出するために用いられる” [6]
● 例) クラスタリング, 自己組織化マップ

11. 教師あり学習
既に x と y の対応が分かっているデータセットを
訓練データとする
Z = < <x1, y1>, <x2,y2> ...>
ここで <xi, yi> ∈ X * Y
この対応づけはマニュアルで行わなければいけな
いため非常に大変

12. 教師なし学習
x さえ用意しておけばOK
Z = < x1, x2, x3 ...> ここで xi ∈ X
集合Yを定義して学習基準とモデル構造を作って
おけば、事前にラベリングしていなくても学習で
きる
教師なし学習アルゴリズムの一つ、EMアルゴリ
ズム と MapReduce の相性がいいため、この本
ではEMアルゴリズムを取り扱う

13. 6.1 Expectation Maximization

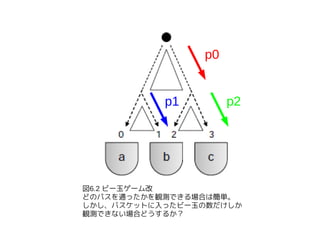
14. EMアルゴリズム
● "確率モデルのパラメータを最尤法に基づいて推定する手
法のひとつであり、 観測不可能な潜在変数に確率モデル
が依存する場合に用いられる" [7]
● Eステップ、Mステップの繰り返しで処理を行う
● Eステップ
● 与えられたパラメータを元に、尤度関数の期待値を算出
● Mステップ
● 期待値を最大化するパラメータを算出
● このセクションでは、このEMアルゴリズムについて解説
する(MapReduce一切なし)

15. 6.1.1 最尤推定

16. 最尤推定(MLE)
● 与えられたデータ x に対し一番尤もらしいパラ
メータ θ を推測する方法(式6.1)
● 例えばビー玉ゲーム(図6.1、次ページ)では、
ルールベースであれば物理モデルを作らなけれ
ばいけないが、MLEであればどちらのバスケッ
トに何回入ったかを観測するだけでいい

17. 図6.1 ビー玉ゲーム(単純バージョン)
どちらにどれくらいの確率で入るかを調べる。
ルールベースであれば、器具の長さや角度などの測定を
行わなければいけないだろう。

18. 確率を出してみる
10回試行し、a に2回、b に8回入ったとする。
a に入る確率を p とすると、
Pr を最大にするときの p を出すには微分すれば
いい

19. 確率を出してみる(続き)
対数をとって微分するとこうなる
これを解けば p = 0.2 とわかる。
さらに調べていけば、N回試行でaにN0回、bにN1回入ったときに
尤もらしい p は、p = N0 / (N0 + N1)
※ テキストの式は誤植

20. 6.1.2 潜在変数つきビー玉ゲーム

21. ビー玉ゲーム改
● バスケットを3つにし、段を1つ増やす
● 第1段で右に行く確率を p0, 第1段で左に行き、
第2段で右に行く確率を p1, 第1段・第2段とも
に右に行く確率を p2 とする(次ページ参照)
● 「どのパスを通ったか」が観測できる場合は
とっても簡単

22. p0
p1 p2
図6.2 ビー玉ゲーム改
どのパスを通ったかを観測できる場合は簡単。
しかし、バスケットに入ったビー玉の数だけしか
観測できない場合どうするか？

23. 6.1.3 潜在変数つき最尤推定

24. パスを観測できないとき
● 教師なし学習の出番
● 部分的な情報だけで Pr を推定する
● Ys を全ての潜在変数 y の合計として前述の式
を書き直す
● ここでの y は x と同様インプット側のパラメータ
であることに注意(最終的には求める値だが)

25. 最尤値を求める
ある観測値 x に対する Pr は、
全ての観測ベクトル x = <x1, x2 ...> に対する Pr は、
よって一番尤もらしいパラメータ θ は、

26. 6.1.4 Expectation Maximization

27. EMアルゴリズムの解説
● EMアルゴリズムは訓練データの周辺確率を増
加させていく一連のパラメータを求めるための
繰り返しアルゴリズム
● EMアルゴリズムは以下の式を保証する

28. Eステップ
現在のパラメータに基づき、それぞれの観測値 x に対する y の事
後確率を求める
このとき、x が集合 X に出てくる相対確率に基づき重み付けする
この事後確率を q(X = x, Y = y; θ(i)) とする

29. Mステップ
Eステップで求めた qの分布における結合分布の確率の対数を最大
化する θ(i+1) を求める
θ(i+1) による尤度は必ず θ(i) 以上になるということは証明されて
るらしい(テキストではそこまで説明していない)

30. 6.1.5 EMの例

31. ビー玉問題にEMを適用する
x ∈ {a,b,c}, y ∈ {0,1,2,3} として EM アルゴリズムを適用する
まず x の相対頻度は、
図6.2から、明らかに Pr(0|a)=1, Pr(3|c)=1 なので計算不要。
残りの y = {1,2} について計算すると、

32. Mステップで最大化
結局最適化すると、p は以下のようになる。
これは完全に観測できた場合と非常に似ている。

33. 参考文献

34. 1. Facebook has the world's largest Hadoop cluster!, Facebook has the world's largest
Hadoop cluster!, http://hadoopblog.blogspot.com/2010/05/facebook-has-worlds-largest-
hadoop.html
2. ユーティリティコンピューティング, wikipedia, http://ja.wikipedia.org/wiki/
%E3%83%A6%E3%83%BC%E3%83%86%E3%82%A3%E3%83%AA
%E3%83%86%E3%82%A3%E3%82%B3%E3%83%B3%E3%83%94%E3%83%A5%E3
%83%BC%E3%83%86%E3%82%A3%E3%83%B3%E3%82%B0
3.Hadoop 第1版, Tom White, オライリー・ジャパン, 2009
4.Simple-9について解説 – tsubosakaの日記,
http://d.hatena.ne.jp/tsubosaka/20090810/1249915586
5.”教師あり学習”, wikipedia, http://ja.wikipedia.org/wiki/%E6%95%99%E5%B8%AB
%E3%81%82%E3%82%8A%E5%AD%A6%E7%BF%92
6. “教師なし学習”, wikipedia, http://ja.wikipedia.org/wiki/%E6%95%99%E5%B8%AB
%E3%81%AA%E3%81%97%E5%AD%A6%E7%BF%92
7.”EMアルゴリズム”, wikipedia, http://ja.wikipedia.org/wiki/EM
%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0

35. Thank you !