Recommended
PDF
【メタサーベイ】Video Transformer
PPTX
[DL輪読会]Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets
PDF
自己教師学習(Self-Supervised Learning)
PPTX
[DL輪読会]“Spatial Attention Point Network for Deep-learning-based Robust Autono...
PPTX
PDF
PDF
PDF
【DL輪読会】Self-Supervised Learning from Images with a Joint-Embedding Predictive...
PDF
SSII2022 [TS1] Transformerの最前線〜 畳込みニューラルネットワークの先へ 〜
PDF
PPTX
PPTX
PDF
PDF
人間の視覚的注意を予測するモデル - 動的ベイジアンネットワークに基づく 最新のアプローチ -
PDF
PDF
最近のディープラーニングのトレンド紹介_20200925
PPTX
【DL輪読会】Towards Understanding Ensemble, Knowledge Distillation and Self-Distil...
PDF
[DL輪読会]Understanding Black-box Predictions via Influence Functions
PDF
PDF
【DL輪読会】NeRF in the Palm of Your Hand: Corrective Augmentation for Robotics vi...
PDF
PDF
[DL輪読会]NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
PDF
【DL輪読会】Perceiver io a general architecture for structured inputs & outputs
PPTX
【DL輪読会】Decoupling Human and Camera Motion from Videos in the Wild (CVPR2023)
PPTX
[DL輪読会]ドメイン転移と不変表現に関するサーベイ
PDF
PDF
トピックモデルの評価指標 Perplexity とは何なのか?
PPTX
【DL輪読会】The Forward-Forward Algorithm: Some Preliminary
ODP
PDF
隠れマルコフモデル - Speech and Language Processing : Appendix A : Hidden Markov Models
More Related Content
PDF
【メタサーベイ】Video Transformer
PPTX
[DL輪読会]Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets
PDF
自己教師学習(Self-Supervised Learning)
PPTX
[DL輪読会]“Spatial Attention Point Network for Deep-learning-based Robust Autono...
PPTX
PDF
PDF
PDF
【DL輪読会】Self-Supervised Learning from Images with a Joint-Embedding Predictive...
What's hot
PDF
SSII2022 [TS1] Transformerの最前線〜 畳込みニューラルネットワークの先へ 〜
PDF
PPTX
PPTX
PDF
PDF
人間の視覚的注意を予測するモデル - 動的ベイジアンネットワークに基づく 最新のアプローチ -
PDF
PDF
最近のディープラーニングのトレンド紹介_20200925
PPTX
【DL輪読会】Towards Understanding Ensemble, Knowledge Distillation and Self-Distil...
PDF
[DL輪読会]Understanding Black-box Predictions via Influence Functions
PDF
PDF
【DL輪読会】NeRF in the Palm of Your Hand: Corrective Augmentation for Robotics vi...
PDF
PDF
[DL輪読会]NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
PDF
【DL輪読会】Perceiver io a general architecture for structured inputs & outputs
PPTX
【DL輪読会】Decoupling Human and Camera Motion from Videos in the Wild (CVPR2023)
PPTX
[DL輪読会]ドメイン転移と不変表現に関するサーベイ
PDF
PDF
トピックモデルの評価指標 Perplexity とは何なのか?
PPTX
【DL輪読会】The Forward-Forward Algorithm: Some Preliminary
Similar to マルコフモデル,隠れマルコフモデルとコネクショニスト時系列分類法
ODP
PDF
隠れマルコフモデル - Speech and Language Processing : Appendix A : Hidden Markov Models
PDF
ODP
PDF
PDF
続・わかりやすいパターン認識 第7章「マルコフモデル」
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Casual learning machine learning with_excel_no4
PPTX
MASTERING ATARI WITH DISCRETE WORLD MODELS (DreamerV2)
PPTX
KDD2015読み会 Matrix Completion with Queries
PPTX
PPTX
マルコフモデル,隠れマルコフモデルとコネクショニスト時系列分類法 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. パラメータの最尤推定
x = x1x2...xt...xn
s = s1s2...st...sn
・・・得られた出目の系列
・・・得られた状態の系列
このような結果が得られる確率は
P(x, s) = P(s)P(x|s)
P(x|s) = P(x1x2...xn|s1s2...sn)
= P(x1|s1)P(x2|s2)...P(xn|sn)
b(st, xt) = P(xt|st)ここから、 を用いて
P(x|s) =
nY
t=1
b(st, xt)
と書ける。
n…観測回数
12. 13. パラメータの最尤推定
P(x, s) =
nY
t=1
a(st−1, st)b(st, xt)
微分しやすいように対数を取る
P(x, s) = log P(s1) +
n−1X
t=1
log a(st, st+1) +
nX
t=1
log b(st, xt)
下線部はそれぞれ ⇢i, aij, bjk のみを含む
なので、下線部それぞれについて独立にパラメータを最大化
すれば良い
14. (補足)最尤推定に必要な定理
n個の正の定数 がある.
ここで,n個の変数 x1, x2, ..., xn (0 < xi < 1)
が拘束条件
nX
i=1
xi = 1 を満たしている時
f(x1, x2, ..., xn) =
nX
i=1
wi log xi を最大にする xi は
xi =
wi
Pn
k=1 wk
(i = 1, 2..., n)
w1, w2, ..., wn
15. 16. (補足)最尤推定に必要な定理【証明】
両辺に を施すと
λxi = wi (i = 1, 2..., n)
nX
i=1
λ
nX
i=1
xi =
nX
i=1
wi
ここで、
nX
i=1
xi = 1 という拘束条件があったので
λ =
nX
i=1
wi
従って、λxi = wi (i = 1, 2..., n) より、求めるxiは
xi =
wi
λ
=
wi
Pn
k=1 wk
(i = 1, 2..., n)
となる。
(証明終)
17. パラメータの最尤推定
P(x, s) = log P(s1) +
n−1X
t=1
log a(st, st+1) +
nX
t=1
log b(st, xt)
La =
n−1X
t=1
log a(st, st+1)
=
cX
i=1
(
cX
j=1
mij log aij)
c …状態の数
mij …ωi,ωjと連続して
取り出した回数
パラメータ に関して最大化するには各i毎に
を最大化すれば良い
aij
cX
j=1
mij log aij
18. パラメータの最尤推定
cX
j=1
aij = 1 という拘束条件が成り立つ
cX
j=1
mij = ni なので
よって、先の定理を用いると
ˆaij =
mij
Pc
h=1 mih
また、
ˆaij =
mij
ni
と求められる(パラメータAの最尤推定値)
19. パラメータの最尤推定
P(x, s) = log P(s1) +
n−1X
t=1
log a(st, st+1) +
nX
t=1
log b(st, xt)
Lb =
cX
j=1
mX
k=1
njk log bjk
!
サイコロ を取り出した回数をwj nj とし
サイコロ を投げて出た目が であった回数を とするwj vk njk
m…出力記号の数
各j毎に
mX
k=1
njk log bjk を最大化すれば良い
20. パラメータの最尤推定
mX
k=1
bjk = 1 (j = 1, 2..., c)
mX
k=1
njk = nj
bに関しても以下の拘束条件が成り立っているので
先と同様の定理を用いることができる
ˆbjk =
njk
Pm
l=1 njl
=
njk
nj
より
(パラメータBの最尤推定値)
21. パラメータの最尤推定
P(x, s) = log P(s1) +
n−1X
t=1
log a(st, st+1) +
nX
t=1
log b(st, xt)
初期状態は既知であるものとしている
Lp = log P (s1 = !i)
s1=ωiだとしたとき
= log ⇢i
⇢
ˆ⇢i = 1
ˆ⇢j = 0 (j 6= i)
上式を最大にするパラメータρは
(パラメータρの最尤推定値)
22. 23. 24. 25. 26. 27. 28. 29. 前向きアルゴリズム
↵t(i) は再帰的な計算方法で求めることができる
↵t(j) = [
cX
i=1
↵t−1(i)aij]b(!j, xt)
(t = 2, 3..., n) (j = 1, 2..., c)
↵1(i) = p(x1, s1 = !i)
= ⇢ib(wi, x1)
各パラメータが既知なのでここは
計算できる
ただし
(i = 1, 2, ..., c)
このような計算方法は前向きアルゴリズムと呼ばれている
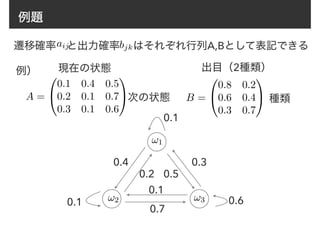
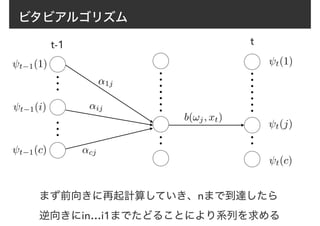
30. 31. 32. 33. 34. 35. 36. 37. ビタビアルゴリズム
ある時点tで状態ωjに到達し,かつxtが観測される確率を考え
その最大値をψt(j)で表す
t(j) = max
s1,...,st−1
P(x1...xt, s1...st−1, st = !j)
この式は再帰的な形で表せる
1(i) = ⇢ib(!i, x1)
(t = 2, 3, ..., n) (i, j = 1, 2, ..., c)
t(j) = max
i
[ t−1(i)aij]b(!j, xt)
38. 39. 40. ビタビアルゴリズム
1.初期化 1(i) = ⇢ib(wi, x1)
1(i) = 0 (i = 1, 2, ..., c)
2.再帰的計算
t(j) = max
i
{ t−1(i)aij}b(!j, xt)
t(j) = argmaxi{ t−1(i)aij}
3.終了 P(x, s⇤
) = max
i
{ n(i)}
(i = 1, 2, ..., c)
4.系列の復元(
it = t+1(it + 1)
s⇤
t = !it
(
in = argmaxi{ n(i)}
s⇤
t = !in
(t = n − 1, ..., 2, 1)
41. 42. バウム・ウェルチアルゴリズム
(1)初期化
パラメータaij, bjk, ⇢i に適当な初期値を与える
(2)再帰的計算
ˆaij =
Pn−1
t=1 at(i)aijb(!j, xt+1)βt+1(j)
Pn−1
t=1 ↵t(i)βt(i)
ˆbik =
Pn
t=1 δ(xt, vk)↵t(j)βt(j)
Pc
t=1 ↵t(j)βt(j)
ˆ⇢i =
↵1(i)β1(i)
Pc
j=1 ↵n(j)
δ(xt, vk) =
(
1(xt = vk)
0(otherwise)
これらの式から を求める。
α,β等は前向き・後向きアルゴリズムによって求める。
ˆaij,ˆbjk, ˆ⇢i
43. 44. 45. 46. コネクショニスト時系列分類法
真のラベル l = ‘cbab’
L = {a,b,c} ・・認識対象となるラベルの集合
L0
= {a, b, c, }・・Lに空白を表すラベルを追加した集合
真のラベルの冗長な系列は無数にある
例){c b aab} { c ba b} {cc b aaa bb}
冗長性のない系列lと冗長な系列πは多:1の以下の
写像によって結ばれる
l = ß(⇡) l = ß(c b aab) = ß( c ba b)
47. 48. 49. 50. 51. コネクショニスト時系列分類法
に関して再帰的に計算↵s,t
l’sが空白の場合,もしくはl’sが空白ではないが空白をまた
いで同じラベルの場合
1)
それ以外の場合2)
↵s,t = yt
l0
s
(↵s−1,t−1 + ↵s,t−1)
↵s,t = yt
l0
s
(↵s−2,t−1 + ↵s−1,t−1 + ↵s,t−1)
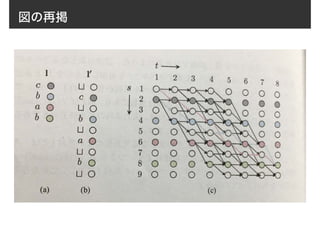
t=Tまで計算ができるとp(l|X)は
p(l|x) = ↵|l0|,T + ↵|l0|−1,T で計算できる(図参照)
52. 53. 54. 55. 56.



























![前向きアルゴリズム
↵t(i) は再帰的な計算方法で求めることができる
↵t(j) = [
cX
i=1
↵t−1(i)aij]b(!j, xt)
(t = 2, 3..., n) (j = 1, 2..., c)
↵1(i) = p(x1, s1 = !i)
= ⇢ib(wi, x1)
各パラメータが既知なのでここは
計算できる
ただし
(i = 1, 2, ..., c)
このような計算方法は前向きアルゴリズムと呼ばれている](https://image.slidesharecdn.com/random-170127062436/85/slide-29-320.jpg)
![前向きアルゴリズム
t-1 t
↵t−1(1)
↵t−1(i)
↵t−1(c)
↵1j
↵ij
↵cj
b(!j, xt)
↵t(1)
↵t(j)
↵t(c)
↵t(j) = [
cX
i=1
↵t−1(i)aij]b(!j, xt)](https://image.slidesharecdn.com/random-170127062436/85/slide-30-320.jpg)






![ビタビアルゴリズム
ある時点tで状態ωjに到達し,かつxtが観測される確率を考え
その最大値をψt(j)で表す
t(j) = max
s1,...,st−1
P(x1...xt, s1...st−1, st = !j)
この式は再帰的な形で表せる
1(i) = ⇢ib(!i, x1)
(t = 2, 3, ..., n) (i, j = 1, 2, ..., c)
t(j) = max
i
[ t−1(i)aij]b(!j, xt)](https://image.slidesharecdn.com/random-170127062436/85/slide-37-320.jpg)














![コネクショニスト時系列分類法の学習
∆E(w)
∆yt
k
= −
1
p(d|X)
∆p(d|X)
∆yt
k
ここで、αβを利用する
↵s,tβs,t =
X
⇡2ß−1(d)⇡t=d0
s
p(d|X)
α_stとβ_stの積は(s,t)を通る全パスにわたる同じ確率の総和
任意のtに対し,全てのs ∈[1,|d’|]にわたる和を取ると
p(d|X) =
|d0
|
X
s=1
↵s,tβs,t
d’はdの系列の間,最初,最後に空白
ラベルを入れたもの](https://image.slidesharecdn.com/random-170127062436/85/slide-54-320.jpg)

